The Role of Negative Selection in Protein Evolution Revealed through the Energetics of the Native State Ensemble

Abstract

Knowing the determinants of conformational specificity is essential for understanding protein structure, stability, and fold evolution. To address this issue, a novel statistical measure of energetic compatibility between sequence and structure was developed, using an experimentally validated model of the energetics of the native state ensemble. This approach successfully matched sequences from a diverse subset of the human proteome to their respective folds. Unexpectedly, significant energetic compatibility between ostensibly unrelated sequences and structures was also observed. Interrogation of these matches revealed a general framework for understanding the origins of conformational specificity within a proteome: specificity is a complex function of both the ability of a sequence to adopt folds other than the native, and ability of a fold to accommodate sequences other than the native. The regional variation in energetic compatibility indicates that the compatibility is dominated by incompatibility of sequence for alternative fold segments, suggesting that evolution of protein sequences has involved substantial negative selection, with certain segments serving as “gatekeepers” that presumably prevent alternative structures. Beyond these global trends, a size dependence exists in the degree to which the energetic compatibility is determined from negative selection, with smaller proteins displaying more negative selection. This partially explains how short sequences can adopt unique folds, despite the higher probability in shorter proteins for small numbers of mutations to increase compatibility with other folds. In providing evolutionary ground rules for the thermodynamic relationship between sequence and fold, this framework imparts valuable insight for rational design of unique folds or fold switches.

Introduction

Why does an amino acid sequence adopt one particular unique fold and not one of the few thousands of alternatives? How do new folds arise and change during evolution of the proteome? Insight into these essential biological questions will be obtained by understanding the determinants of conformational specificity, the well-known ability of structured proteins to retain a finite population of native fold even under destabilizing conditions. One particularly interesting aspect of this problem is revealed by the repeated observation of “chameleon sequences” [1–4], which can adopt different folds, and the emerging discovery of “metamorphic proteins” [5, 6], which change fold as part of their function. Such extremes of conformational specificity, which have already been shown to be amenable to protein engineering [7–11], may prove to be an evolutionarily important mechanism for both fold change [9, 12–15] and functional versatility (as a prominent sub-class of “moonlighting proteins” [16, 17]). However, current bioinformatics tools and molecular dynamics simulations, using sequence or structure information, fail to reliably identify chameleon or metamorphic proteins [8, 18–20]. Novel information, not entirely based on either sequence or structure alone, may facilitate development of a more effective compatibility measurement between sequence and structure.

Our approach to addressing the problem is rooted in the ensemble nature of proteins [21], leveraging the long-standing realization that fold stability and conformational specificity are both thermodynamic in origin, and partially separable [22, 23]. Proteins in solution sample myriad conformations according to a Boltzmann distribution. Even when a single folded conformation is dominant, alternative structures could be transiently populated, albeit at vanishingly small amounts. Indeed, if protein sequences do obey Boltzmann statistics, each sequence has some probability of adopting every fold. Thus, the question of conformational specificity may be more tractable if rephrased: what is the difference in stability between one sequence adopting each of two alternative folds? Answering this question requires knowledge of the energetics of the compatibility between amino acid sequence and protein structure.

In this work, conformational specificity [22] is addressed from such a thermodynamic standpoint by development of a statistical framework for measurement of the compatibility between sequence and structure. An ensemble-based description of protein thermodynamics [24] is applied to a diverse database of protein folds, for which the positional thermodynamic stability of every residue is estimated. Importantly, this computational stability has been experimentally demonstrated [21, 24–28] to largely capture the cooperativity imparted by both local and global interactions, and from both enthalpic and entropic contributions. Thus, every residue in a protein can be described, not by residue letter or structural type, but instead by a so-called “thermodynamic environment” [29, 30].

Using a previously validated threading algorithm [30, 31], the energetic compatibility of amino acid sequence fragments adopting varied thermodynamic environment contexts was exhaustively computed, exploring general principles for conformational specificity and the organization of protein fold space. The results indicate that there is substantial energetic compatibility between ostensibly unrelated proteins, composed of energetically compatible and incompatible contributions that are heterogeneously distributed throughout the sequence. We find that conformational specificity, operationally defined as the high energetic compatibility of one sequence with one fold, is a function of both sequence and fold, and that evolution of one fold from another may not be energetically improbable.

Furthermore, because energetic compatibility is correlated with the number of incompatible contributions, negative design appears to be important for conformational specificity, particularly for small, single domain proteins. This finding suggests that negative selection could be an evolutionary strategy to minimize the effects of metamorphic structure, as small proteins are expected to be more susceptible to fold-switching [11].

Materials and Methods

Ensemble-Based Thermodynamic Database of Diverse Human Proteins

This database has been described and used in previous analyses, of note is the presence of diverse secondary structural classes and fold types as curated by the SCOP database [32]. Briefly, 122 H. sapiens proteins of known structure (Table S1) were taken from the Protein Data Bank (PDB) [33] and native state Boltzmann-weighted thermodynamic ensembles were generated using the COREX/BEST algorithm [21, 34]. A summary of the computational procedure used to generate this database is given in Figure 4, below. When present in the PDB coordinates, selenomethionine residues were manually edited to methionine to permit execution of the algorithm. Parameters for the algorithm were: window size of 5 residues, minimum window size of 4 residues, simulated temperature of 25 °C, entropy weighting of 0.5, Monte Carlo sampling of at least 10,000 microstates per partition. Clustering of the COREX/BEST thermodynamic parameters ΔG, ΔH_ap, ΔH_pol, TΔS_conf to obtain eight thermodynamic environments was performed by partitioning-around-medoids, implemented in S-PLUS 6 (Insightful Corporation, Seattle, WA), as previously described [30, 31]. Thermodynamic parameters for the 17,801 residues in this database are given in Table S2. Log-odds scores (Figure 1), quantifying the observed to expected ratios of amino acids in thermodynamic environments, were computed from this database as previously described [29–31]. Secondary structure elements were assigned to each residue using STRIDE [35] and are listed in Table S2.

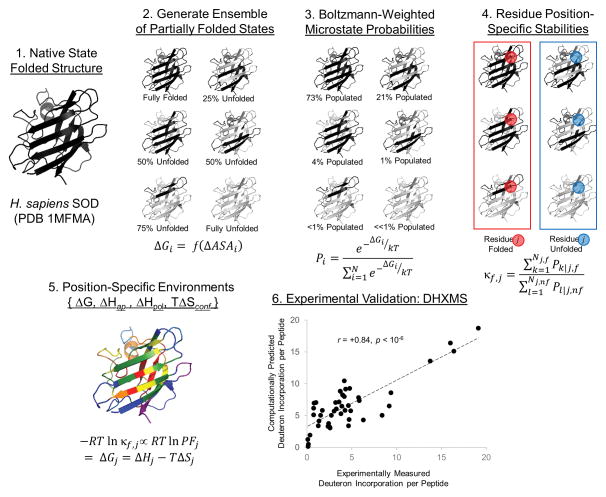
Figure 4. Conceptual basis for native state ensemble-based thermodynamic environments.

The human superoxide dismutase (SOD) protein (Step 1) is used as an example for the COREX/BEST algorithm, briefly explained in the main text. An experimentally validated positional thermodynamic stability ΔG_j measured at a residue position j in the protein (Steps 4 and 6), is obtained from the Boltzmann-weighted ensemble of partially folded microstates (Steps 2 and 3). Clustering of a large number of positional stabilities from diverse proteins, with respect to the relative contributions of enthalpy and entropy to those stabilities, results in eight colored “thermodynamic environments”. These colors correspond to the average Gibbs free energy of the position: purple/blue colors are less stable and orange/red colors are more stable (as displayed in Figure 5). Black regions of the molecular cartoon represent folded, native-like conformations in a greatly simplified COREX ensemble, and gray represents regions of unfolded conformations. Experimental data was obtained from Liu, et al. [28]. Abbreviations: ASA = solvent accessible surface area, ap = apolar surface area, pol = polar surface area, conf = conformational, PF = hydrogen exchange protection factor, DHXMS = deuterium – hydrogen exchange mass spectrometry. The thermodynamic environments for this protein are listed in Table S2.

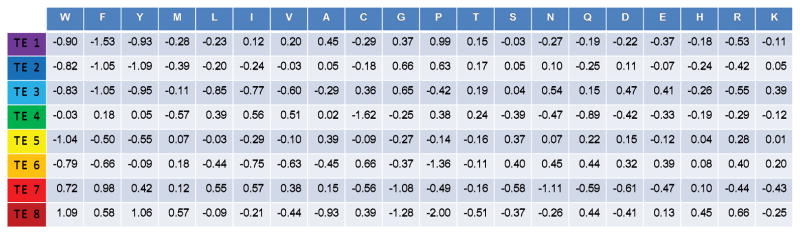
Figure 1. Log-odds compatibility scores relating amino acids to native state ensemble-based thermodynamic environments.

These scores were computed as previously described [29–31] using the amino acids and thermodynamic environments data given in Table S2. A positive value indicates that the amino acid is found more often than expected in a particular thermodynamic environment within globular proteins, while a negative value indicates occurrence less often than expected. Colors are identical to those used in Figures 4 and 5, i.e. violet, blue, green are lower predicted stability and yellow, orange red are higher stability.

Exhaustive Gapless Scoring Between Sequence and Thermodynamic Environments

All amino acid sequences in the database were quantitatively compared with all proteins’ thermodynamic environments. This was performed twice, first using complete sequence strings compared with complete environment strings, and second after dividing complete strings into overlapping 13 residue fragments starting at all possible registers. The second procedure was deliberately chosen for three reasons: to reveal regional contributions to energetic compatibility, to avoid possible length-dependent artifacts, and to keep the total amount of computations tractable. (Fragments of lengths 6 and 25 were also explored, with little qualitative change in results, data not shown.) Each comparison of sequence to environments used gapless scoring, popularly referred to as gapless “threading” [36] of an amino acid string against an environment string. A comparison was simply defined as a sum of the log-odds scores given by each residue/environment pair in Figure 1, using custom scripts written in Mathematica 9.0 (Wolfram Research, Champaign, IL). For example, the 13 residue amino acid sequence fragment starting at position 155 in the PDB coordinate file 1BYQ is NDDEQYAWESSAG. The threading score of this sequence fragment compared with the 13 residue thermodynamic environments fragment from the PDB file 1GP0 starting at position 1538, i.e. 5742211111248, is calculated as the sum of all 13 log-odds scores corresponding to each amino acid/environment pair, as listed in Figure 1. For this example, the sum would be 0.07 − 0.61 − 0.42 − 0.07 − 0.25 − 0.93 + 0.45 − 0.90 − 0.37 − 0.03 + 0.05 + 0.02 − 1.28 = −4.27. These computations were repeated until all sequence fragments were scored against all environments fragments. For comparisons of full-length proteins, the shorter protein was matched in all possible registers against the longer protein, such that the number of terms in the sum for each register was identical to the length of the shorter protein. Then, the maximum score over all registers was taken to be the single final score for that protein pair.

Parameterization of Probability Distributions: Significance of Energetic Compatibility

To assess the quality of these raw summed scores, a mathematical model was developed to estimate the expected chance occurrence of any particular raw score. Proteins of random composition and varying length were created by randomly choosing amino acids according to background frequencies in the Table S1 database (which were similar to background frequencies of amino acids seen in large sequence databases). These random sequences of amino acids were compared to identical length random sequences of similarly chosen thermodynamic environments and the total raw scores computed as described above. 120,000 such random proteins were scored at each chain length to obtain the reported histograms and curve fits (Fig. S1). Random protein creation, scoring, curve and distribution fitting were performed in Mathematica using custom scripts.

Empirical distributions of random gapless summed scores between amino acid sequences and thermodynamic environments were discovered to be statistically Gaussian for all lengths tested (Fig. S1). This result allowed the parameterization of a useful probability model for a gapless match of any length protein (Fig. S1b). In this model, as the length of a gapless match increased, it became progressively less likely to obtain a positive log-odds score (Fig. S1a); in other words, a randomly chosen sequence was expected to be energetically incompatible with a randomly chosen structure. In contrast, an extremely high positive score is uncommon in the model, and thus a significantly high score would be consistent with an empirical observation of “conformational specificity”: defined here as the extreme case where one amino acid sequence is energetically compatible with only one unique structure (Fig. S1a).

Computing Compatibility Index of Significant Matches and Principal Components Analysis

The 122 database proteins were exploded into 16,337 overlapping fragments of length 13 residues. Exhaustive all-vs-all comparisons of these 16,337 fragments resulted in greater than 266 million raw scores. Each raw score was then treated as a limit of integration in the length 13 Gaussian random score distribution, and the probability of obtaining a score of at most the observed raw score was computed using custom scripts. This list of p-values was filtered such that the best (most positive) and worst (most negative) of all comparisons, defined as those exhibiting p < 0.01 or p > 0.99, were retained. The resulting filtered comparisons were then mapped back on to the positions of amino acid sequence or thermodynamic environments in the full-length proteins from which they originally came. Counts at each position were tabulated to produce a density of significant best, or worst, comparisons with regard to either sequence or structure. Thus, this analysis resulted in a total of four new attributes measured at every position in every protein: most significant matches of amino acid sequence against all other thermodynamic environments, least significant matches of amino acid sequence against all other thermodynamic environments, most significant matches of thermodynamic environments against all other amino acid sequences, and least significant matches of thermodynamic environments against all other amino acid sequences. These four attributes were, respectively, named “positive compatibility index (PCI with respect to sequence)”, “negative compatibility index (NCI with respect to sequence)”, “positive compatibility index (PCI with respect to structure)”, and “negative compatibility index (NCI with respect to structure)” throughout the rest of this paper. To minimize possible end effects, the N-terminal 12 and C-terminal 13 values for each protein were ignored, resulting in a total of 14,751 residue positions, with four density counts at each position. These data were treated as a four-dimensional space and were subjected to standard eigenvalue decomposition [37] using an in-house C program (Figure 2). “Aggregate Negative Compatibility Indices” with respect to sequence or structure of an individual protein were defined as the integrated area along the entire protein of these respective densities (i.e. the area under the blue curves in Figs. 7a and 7b, respectively).

Figure 2. Principal components analysis of positive and negative energetic compatibilities demonstrates the dominance of incompatibility in a representative sample of globular proteins.

Values in the last four columns of Table S2 were subjected to standard eigenvalue decomposition. [37] The vast majority of the information content of the four-dimensional data can be described by the first two principal components, dominated by energetically incompatible sequence and structure indices, respectively, interpreted as effects of negative selection in the organization of protein fold space. Red circles indicate the indices contributing the most to the information content.

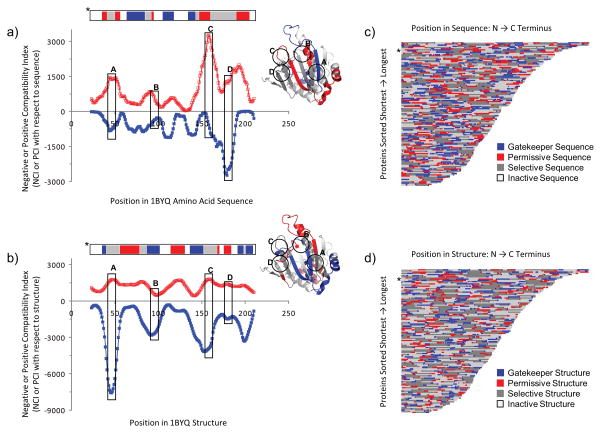
Figure 7. Energetic scoring varies with sequence and structure position, as energetically “compatible” and “incompatible” regions ubiquitous within the proteome.

The y-axes in panels a) and b) indicate the number of times any 13-residue fragment from any other protein was significantly compatible with the 1BYQ protein at the residue positions located on the x-axes. Panel a) displays compatible structure fragments with 1BYQ sequence, and panel b) displays compatible sequence fragments with 1BYQ structure. “Significantly” was defined as exhibiting an energetic compatibility of at least p < 0.01 (red open squares) or p > 0.99 (blue filled squares). For most proteins analyzed, the density of incompatible matches dominated the most compatible matches, suggesting the importance of energetic incompatibility in conformational specificity. Horizontal colored bar above the chart indicates regions of compatibility defined in the text and in Figure 3: “gatekeeper” (blue), “permissive” (red), “selective” (gray), and “inactive” (white); these regions are colored on the molecular cartoon. Labeled vertical boxes A – D denote regions of interest discussed in the text. Panels c) and d) summarize the energetic compatibilities of a representative subset of 122 human proteome amino acid sequences and structures, respectively. Colors are identical to those in panels a) and b) and the locations of the data for the protein displayed in panels a) and b) are indicated by asterisks in panels c) and d), respectively. Panels c) and d) indicate that, for both sequence and structure, total amounts of gatekeeper and permissive regions are less than amounts of inactive and selective regions. Within the sequence and structure of any particular protein, gatekeeper and permissive regions, thought to be important for conformational specificity, are located at different positions.

Provisional Classification of Energetic Compatibility: Susceptibility to Fold Switch

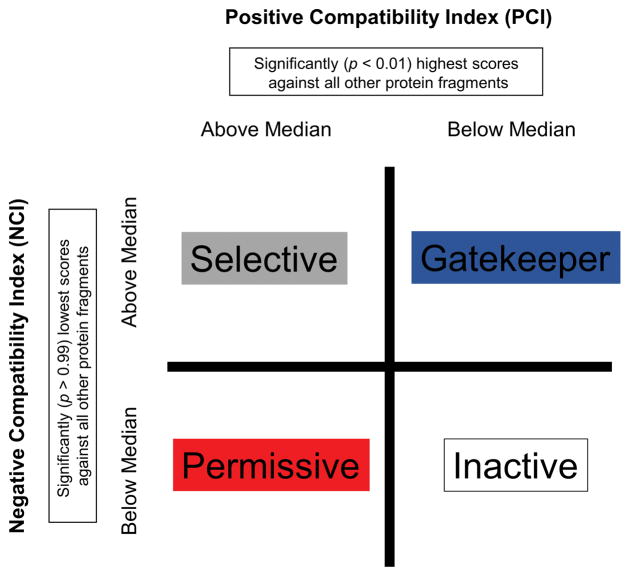
The median PCI and NCI within each protein was used to classify residue positions according to the following definitions. Figure 3 is a visual representation of this classification that may be referenced when the various categories are discussed later in the text. “Gatekeeper” positions exhibited an NCI greater than median and a PCI less than median; the term “Gatekeeper” was meant to capture the intuitive notion of a protein fragment being energetically unlikely to adopt any known conformation. “Permissive” positions exhibited an NCI less than median and a PCI greater than median; the term “Permissive” was meant to capture the intuitive notion of a protein fragment being energetically likely to adopt many conformations. “Selective” positions exhibited NCI and PCI both greater than median; the term “Selective” was meant to capture the intuitive notion of a protein fragment being energetically likely to adopt multiple conformations but simultaneously being unlikely to adopt others. In other words, “Selective” positions could indicate regions of a protein more susceptible to fold switching. “Inactive” positions exhibited NCI and PCI both less than median; the term “Inactive” was meant to capture the intuitive notion of no strong conformational preference. Since NCI and PCI were separate attributes of both sequence and structure, each residue position was assigned two classifications, one in terms of sequence and one in terms of structure. These classifications are listed in Table S2 for the proteins analyzed in this work.

Figure 3. Provisional classification scheme for energetic compatibility indices within proteins.

The scheme is a simple contingency table wherein categories are defined based on the median Positive Compatibility Index (PCI) and median Negative Compatibility Index (NCI) for an individual protein. Attributes for the category labels are described in Methods, and the colors correspond to those in Figure 6.

Results

Proteins Represented in Energetic Terms

Previous work has established that proteins can be represented in energetic rather than in structural terms [30]. The conceptual basis of this energetic representation is that the positional thermodynamic stability of a folded protein can be computationally estimated, by treating the protein as a Boltzmann-weighted ensemble of partially folded microstates [24]. This process, algorithmically named COREX/BEST [34], can be summarized as follows (Figure 4). The experimental coordinates (i.e. crystallographic or NMR structure) are the input for COREX/BEST (Fig. 4, Step 1). A large number, typically millions, of partially folded microstates involving all regions of the protein are generated based on the input (Fig. 4, Step 2); a key simplification here are the assumptions that any folded conformation is native-like and any unfolded conformation is expressed by average amounts of newly exposed polar and apolar surface area, relative to the PDB structure. [21, 24, 38] Each microstate is assigned a Gibbs free energy from a surface-area based function, and statistical weights and populations are calculated for every microstate in the ensemble (Fig. 4, Steps 2 & 3). For every residue position j in the protein, the entire ensemble is partitioned into sub-ensembles in which the position is either in a folded conformation or an unfolded conformation (Fig. 4, Step 4), thus defining a position-specific equilibrium constant, κ_f,j, between folded and unfolded. This equilibrium constant can be converted (Fig. 4, Step 5) to a position-specific stability, ΔG_j, which quantitatively matches experimental position-specific stabilities measured from hydrogen exchange (Fig. 4, Step 6). Statistical analysis of the COREX/BEST output from a large number of diverse proteins results in a meaningful simplification of all position-specific stabilities into a small number (i.e. eight [30]) of clusters that share similar average values of stability.

Using our structure-based model of the native state ensemble (i.e. COREX/BEST) [21], it has been shown that these eight different “thermodynamic environments” [29] exist within any protein [30]. Furthermore, the propensities of amino acids to appear in these environments could be used as the basis of a fold recognition algorithm, much in the same way that helical sequences can be predicted from known helix propensities. Figure 5 shows an example protein color-coded according to the ensemble-based thermodynamic description of proteins, which is represented as eight color-coded environments [30]. Each energetic environment has a characteristic average stability resulting from enthalpic and entropic contributions associated with the computed change in solvent accessible polar and apolar surface upon locally unfolding each segment (Fig. 5, bottom) [21]. Importantly, these environments report on the energetics observed at a particular position rather than the contribution of the individual amino acid occupying that position, thus revealing how homologous proteins with marginal sequence identity can nonetheless share common thermodynamic signatures, and thus identical folds [29, 39]. As demonstrated, this representation has recapitulated numerous experimental observations that ground-state structures of proteins have regions of relatively high and low thermodynamic stability, and that these regions are not always intuitive upon visual inspection of the structure [28, 40].

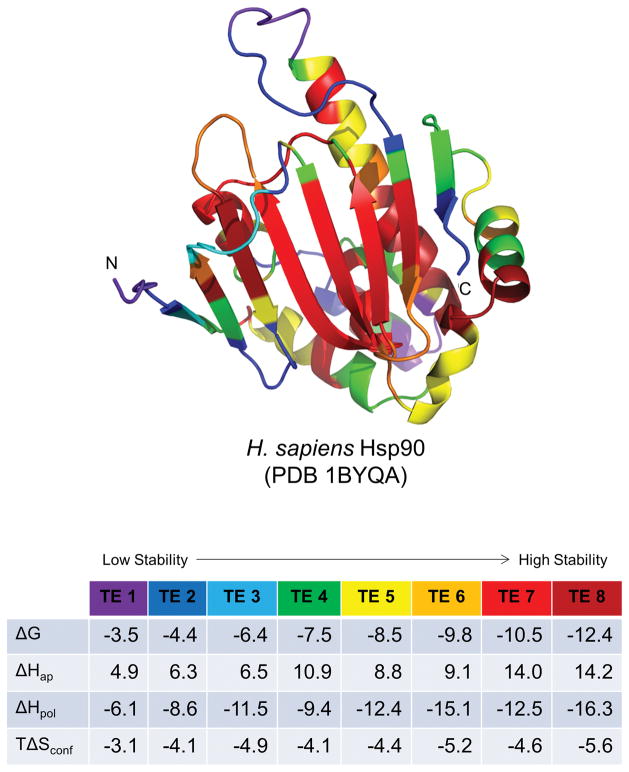
Figure 5. Representation of protein structure in terms of native state ensemble-based thermodynamic environments.

Example protein Hsp90 1BYQ from the thermodynamic environments database (top). Residue cartoon color coding corresponds to the average thermodynamic quantities in the environments table (bottom). Values in the table are in units of kcal/mol under simulated folding conditions: 25 °C, pH = 7.0. Rainbow coloring follows the order of average thermodynamic stability: purple, blue, green exhibit lowest stability (least negative ΔG), yellow, orange, red exhibit highest stability (most negative ΔG). The beta-strand core of this protein contains most (but not all) of the highest stability regions, while some (but not all) of the loops and turns are lower in stability.

As noted previously, several key features of this representation are exemplified in the Hsp90 protein (Fig. 5). First, the most stable regions are often in the core of the protein, which is true of this Hsp90. Second, elements of secondary structure, even those located in the core, are not uniformly stable: it is often observed that the middle residue positions of elements are more stable than the termini [41]. Third, although the most unstable regions are loops and turns, not all loops and turns are necessarily unstable, a counterintuitive result that has been borne out by experiment [42]. Although there are at least two low stability turns in this example (purple or blue), there is a prominent higher stability (orange) turn between strands 4 and 5 (upper left, Fig. 5), and the apparently coil-like linker (dark red) between strand 3 and helix 3 is among the highest stability regions of any protein in the database.

This energetic representation of proteins alone has formed the basis of an effective fold recognition algorithm, whereby sequences could be matched with their respective folds [29–31], even if the secondary structure information of the fold was not present in the training set [43]. This last result, that the energetic information of entirely alpha-helical proteins permitted recognition of entirely beta sheet proteins, compellingly established the universality of this energetic representation with regard to protein structure classification [44].

Quantifying Energetic Compatibility between Homologous and Non-Homologous Proteins

To test whether structured full-length proteins exhibit significant energetic compatibility with their respective sequences using the probability model described in Methods, we applied the model to the scores of all amino acid sequences in the database against all sets of thermodynamic environments (Fig. 6). Because the log-odds scores (Fig. 1) are dependent on both amino acid and thermodynamic environment, an all-vs.-all plot is necessarily separated into scoring of sequences against a structure (rows in Fig. 6), and structures against a sequence (columns in Fig. 6). Unlike scoring derived from symmetric amino acid substitution matrices, this analysis is not symmetric and thus may reveal differential scoring contributions from either a sequence or a structure perspective.

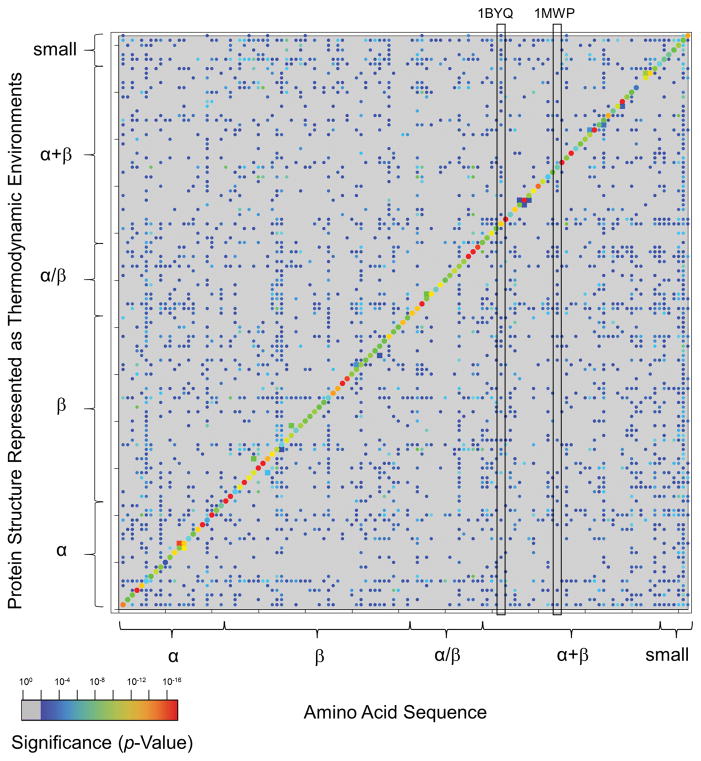
Figure 6. Parameterized random model recapitulates expected sequence-structure conformational specificity as statistically significant.

122 H. sapiens proteins are listed on each axis in the order given in Table S1. SCOP secondary structure classes [32] of each protein are indicated by braces. Dots represent significance levels of either sequence-environment or environment-sequence energetic compatibilities of full length proteins of p < 0.01. Rainbow coloring indicates the statistical significance of the energetic scores, with dark blue corresponding to p ~ 0.01 and red corresponding to p ~ 10⁻¹⁵. The most significant scores are located along the diagonal, corresponding to sequences that are conformationally specific for known structures. Homologous proteins, displayed as squares, also display significant sequence-environment scores. Gray areas, largely off-diagonal, indicate insignificant scores of p > 0.01. Unexpectedly, approximately one-half of the off-diagonal points are significant to at least p = 0.01. The column locations of two proteins discussed in the text, 1BYQ and 1MWP, are indicated by vertical boxes: the values within these column vectors are plotted as the x-axes in Figs. 8a and 8b.

There are several noteworthy observations in Fig 6. First, the diagonal of this plot, representing “self” matches of an amino acid sequence to its known correct fold, was clearly populated by substantial and significant scores, indicating that the algorithm works. These correct matches were highly specific: except for known homologous proteins (as classified in the SCOP database), no non-self match exhibited a p-value more significant than approximately 0.001. Although expected conformational specificities were thus recapitulated by the significant energetic compatibilities, no obvious relationship was observed that differentiated conformational specificity with respect to sequence or environments (the median correlation coefficients between rows and columns of Fig. 6 was r = + 0.5, data not shown). Also not observed was any general pattern between fold type (e.g. all-alpha or all-beta, Fig. 6 braces) and energetic compatibility. For example, the mixed alpha + beta proteins 1BYQ and 1MWP did not exhibit increased energetic compatibility to other mixed alpha + beta proteins (boxed vertical columns in Fig. 6).

Unexpectedly, however, there was a large amount of marginal, yet significant, energetic compatibility between otherwise unrelated proteins: more than half of the non-self matches were significant at the 0.01 < p < 0.001 level (blue dots in Fig. 6). To investigate the source of this unexpected observation, the energetic compatibility between regions of individual proteins and the rest of the sequence or fold space was quantified.

Negative Contributions Dominate Energetic Compatibility between Sequence and Structure

The most statistically significant best and worst matches of 13 residue fragments were mapped to their locations on the full-length protein, and the densities of the matches were tabulated, as described in Methods. These densities were recorded in two ways: 1) mapping structure fragments to the full-length sequence, and 2) mapping sequence fragments to full-length structure. Thus, the highs and lows of density approximated the average energetic compatibility of a protein’s sequence or structure with a representative sample of the entire sequence or structure space. Since these densities were composed of the most extreme energetically compatible and incompatible matches between arbitrary sequences and arbitrary structures of globular proteins, they are referred to as “positive” and “negative” compatibility indices, respectively. In short, the fragment matches revealed regions of full-length proteins likely (or unlikely) to exhibit non-self conformational specificity, due to energetic characteristics shared between other globular proteins.

One example of these compatibility indices is displayed from the perspective of sequence (i.e. how a sequence scored in other fold fragments - Fig. 7a) and from the perspective of structure (i.e., how other sequence fragments scored in its fold – Fig. 7b). The variability of indices within an individual protein suggests that energetic compatibility is not uniformly distributed. Also clear is that sequence and structural compatibility indices are asymmetric. In other words, at a given position within an individual protein, the amino acid sequence at that position could have a very different compatibility for other environments than does the environments at that position for other sequences. For example, in labeled regions A, B, and C (Fig. 7), the negative compatibility index between the 1BYQ structure and all other sequences was relatively high, while the negative compatibility index between the sequence at this position and all other structures was low. This means that while the structure at that position does not accommodate many sequences, the sequence that is there, is compatible with many folds. A third observation is that the magnitude of the negative compatibility index is, in general, much greater than the magnitude of the positive compatibility index. In other words, the blue curves in Fig. 7, and in most other proteins, are larger in magnitude than the red curves, consistent with the higher likelihood of obtaining negative random scores in the probability model. No obvious relations between fold type, secondary structure type, location of secondary structure, and the compatibility indices were seen.

It was hypothesized that these indices contained detailed information about energetic compatibility with multiple structures, and thus would provide insight into conformational specificity. To explore this hypothesis, eigenvalue decomposition (principal components analysis) was used to simplify these four-dimensional compatibility indices (Fig. 2). As expected, the first two principal components of the decomposition were dominated by the sequence and structure negative compatibility indices (red circles in Fig. 2), and constituted almost the entire information content (60% + 35% = 95%). Unexpectedly, the decomposition also revealed a secondary, but substantial, correlation in the patterns of positive and negative compatibility indices, as the coefficients of these quantities are of the same sign and order of magnitude (Fig. 2). Thus, the locations of the largest negative compatibility indices with respect to structure are also often the locations of the largest positive compatibility indices with respect to structure. Examples of this phenomenon can be seen in Fig. 7b, boxes A and B, where the peaks and valleys of both red and blue curves (positive and negative indices, respectively) roughly track each other. In summary, 95% of the information about positive and negative energetic compatibility could be retained by considering only the first two principal components, which are largely due to negative compatibility. Therefore, despite the necessity of a high positive score for one sequence to be conformationally specific for one structure, thermodynamically incompatible regions of sequence and structure largely organize the energetic compatibility, and thus possibly the conformational specificity, of this representative sample of protein fold space.

The trends in Figure 7 were used as the basis for provisionally classifying the susceptibility of a sequence to switch fold (Fig. 7a) or the ability of a fold to accommodate other sequences. (Fig. 7b). Four types of sequence segments were defined (Fig. 3); “permissive”, “selective”, “inactive”, and “gatekeeper” (Fig. 7 a&b – upper bar). Permissive sequence, which accounts for 15% of the total sequence space, is so named because it is highly compatible with other folds, but rarely is it highly incompatible with other folds. In other words, these sequence segments may contribute to stabilizing a fold, but do little to select against other folds. Selective sequences, which at 35% of sequence space, constitutes one of the highest fractions, are those that score very highly in, and are thus highly compatible with, many folds, but are also highly incompatible with other folds. These sequence segments contribute to stabilizing the native fold, but also significantly select against other folds. Inactive sequences are those that appear to not contribute significantly to determining any particular fold and do little to select against any fold. Finally, there are so-called “gatekeeper” sequences that are not compatible with most other folds, and indeed significantly select against many folds, these comprise approximately 15% of sequence space. A similar analysis was performed to categorize the compatibility of fold segments; fractions of gatekeeper and permissive structure were each found to be approximately 11% and fractions of inactive and selective structure were each found to be approximately 39%.

Importantly, all proteins in this representative subset of the human proteome contained variable sized segments of each type of sequence (Fig. 7c) and fold (Fig. 7d) revealing an overall architecture, which indicates that sequence and fold contributions to energetic compatibility are heterogeneously distributed throughout individual proteins. Indeed, the relatively large fractions of inactive sequence and fold segments suggests that the specific folds, which some sequence segments adopt, may be context dependent, lacking significant intrinsic propensity. Ideas such as context dependent sequence propensities have been discussed for the particular case of beta strands, [7] although for these proteins we find no significant correlation between beta sheet and inactive sequence (data not shown).

Protein Size Dependence of Negative Energetic Compatibility

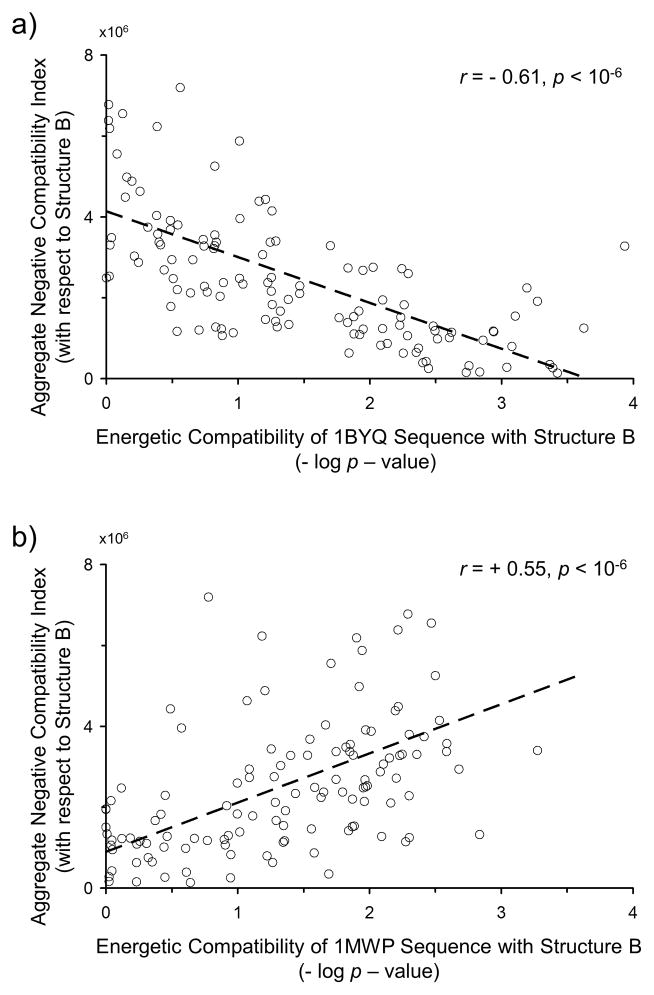
Although the magnitudes of negative (i.e. incompatible) and positive (i.e. compatible) scoring sequences were comparable, the amount of the incompatibilities was observed to be significantly higher than the amount of compatibilities. The dominance of energetic incompatibility is consistent with the idea of “negative selection” [23, 45–48], i.e. that through evolution most other competing folds become thermodynamically incompatible with a particular amino acid sequence. It was hypothesized that the total amount of negative energetic compatibility (i.e. the integrated area of the blue curves in Fig. 7) exhibited by a protein, from either sequence or structure, could be related to the widespread non-self energetic compatibility seen in Fig. 6. In other words, does the amount of negative selection scale with the overall ability of a sequence to adopt other folds? To address this question, the p-value of the optimal non-self scores in Fig. 6 were plotted against the aggregate energetic incompatibility of each protein (Fig. 8). Significant, though modest, correlations were indeed observed between aggregate negative compatibility and the energetic compatibility between sequence and structure, suggesting that negative selection exerts a significant influence on conformational specificity.

Figure 8. Aggregate negative energetic compatibility of a structure correlates with energetic compatibility of a sequence for that structure.

Two protein sequences, 1BYQ (Fig. 8a) and 1MWP (Fig. 8b), are compared with each of 122 structures, the latter represented as native state ensemble-based thermodynamic environments. The p-value of the optimal gapless match, computed by the random model described in Fig. S1, is displayed as a log value on the x-axis, negated so that increased energetic compatibility between sequence and structure is represented by a more positive value. The y-axis represents the aggregate negative compatibility of a second protein, examples of which are displayed by the blue curves in Fig. 7. For many proteins studied, modest but significant correlations are observed (Pearson correlation coefficient r shown [37]). Across the entire database of studied proteins, these correlations trend with length: length inversely varies with correlation coefficient: longer proteins such as 1BYQ exhibit negative correlations (Fig. 8a) while shorter proteins such as 1MWP exhibit positive correlations (Fig. 8b). This trend, displayed in Fig. 9, is interpreted as increased importance of negative selection in the conformational specificity of smaller, single-domain proteins.

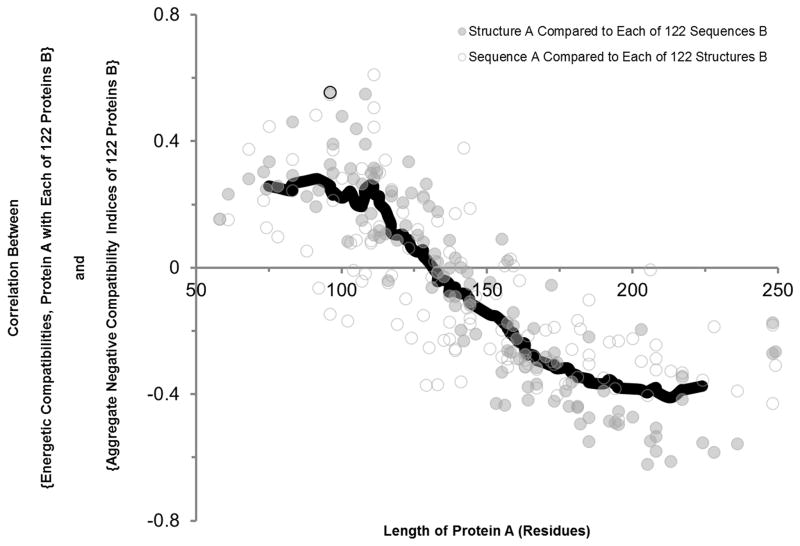
However, an unexpected pattern was observed in these correlations: the relationship between aggregate negative compatibility and energetic compatibility changed sign as a function of protein size (Fig. 9). Longer proteins, such as the 228-residue Hsp90 1BYQ, exhibited a negative correlation between negative compatibility and energetic compatibility (Fig. 8a), while shorter proteins, such as the 96-residue N-terminal domain of amyloid precursor protein 1MWP, exhibited a positive correlation (Fig. 8b). In other words, shorter proteins exhibited increased conformational specificity towards an alternative fold when that alternative fold exhibited increased energetic incompatibility with fragments from all other proteins. The positive correlation reached a maximum value at a protein size of approximately 100 residues (Fig. 9). The fact that the correlation changed sign indicates that both compatibility and incompatibility influence the specificity of proteins of all sizes, but that the relative contribution of incompatibility monotonically decreases with protein length. In other words, the requirement for negative selection appears to be released as sequence length increases.

Figure 9. Relationship between energetic compatibility and negative compatibility depends on protein size.

Small, single domain proteins exhibit a positive Pearson correlation [37] between negative energetic compatibility and energetic compatibility of sequence with structure. This relationship is interpreted as evidence of the effect of negative selection on conformational specificity. Examples of such correlations are shown in Fig. 8. Open circles indicate aggregate negative compatibility index with respect to structure (as displayed in Fig. 7b), and filled circles indicate aggregate negative compatibility index with respect to amino acid sequence (as displayed in Fig. 7a). The solid dark curve is to guide the eye, a window size 11 moving average over all the data. Energetic compatibilities are expressed as negative log p-value, as shown on the x-axes of Fig. 8. The correlation coefficients for proteins 1BYQ and 1MWP shown in Fig. 8 are labeled for reference.

Discussion

Energetic Incompatibility Influences Protein Conformational Specificity

Two significant insights emerge from these studies, accepting the hypothesis that energetic compatibility is a measure of the degree of conformational specificity. First, conformational specificity of a representative sample of the human proteome, and presumably the entire protein fold space, appears to be organized by energetic incompatibility. This key insight could not be obtained by inspection of the amino acid sequences or ground state structures. Second, protein conformational specificity is a complex function of both the sequence and the fold, with both positive and negative contributions. Just as not all sequence and structure segments contribute equally to protein stability, neither do they contribute equally to conformational specificity. Importantly, although a weak trend exists for more stable regions to exhibit higher negative compatibility index with respect to structure, there is imperfect correlation between stability and specificity; the most stable regions are not always the most specific nor are the least stable regions always the least specific. Thus, gatekeeper residues located in high-stability regions may be informative determinants of conformational specificity and potential targets for fold-switch engineering. Conversely, mutation or removal of permissive residues may permit increased specificity for a desired fold.

For all proteins, regardless of size, “designing-in” favorable interactions is important for adopting stable structure, a conclusion that can be drawn directly from the highly significant diagonal scores in Fig. 6. Indeed, structure-guided protein engineering has repeatedly employed this idea of “positive design” with much success [49–51]. However, the present analysis suggests that in natural proteins extremely unfavorable interactions in alternative folds (energetic incompatibility) dominate conformational specificity. Furthermore, the intriguing sign switch observed in Fig. 9 reveals that negative selection has an even more pronounced influence for proteins of small size.

Local Structure and Sequence Contributions to Negative Selection

The regions of highest NCI are enriched in proline (Pro) and glycine (Gly) residues (with respect to sequence, Fig. S2a) and are enriched in high-stability (with respect to structure, Fig. S2c). These enrichments suggest that the mechanisms for negative selection can be localized to individual positions of a protein’s structure and sequence: high stability environments, and the amino acids Gly and Pro. Examples include Box A of Fig. 7b, which is a high stability region of 1BYQ that exhibits high NCI with respect to structure, and Box D of Fig. 7a, a region enriched in Gly and Pro that exhibits high NCI with respect to sequence. Conformational restriction and freedom afforded by Pro and Gly side chains, respectively, are likely to be two physical mechanisms for mediating negative selection [52].

Localization of negative selection could guide protein engineering efforts to promote desired, or alternative, structure using targeted Pro or Gly substitutions [53] and core destabilization. The similarity in environmental propensities of negative compatibility and gatekeeper positions (Fig. S2c&d) suggests co-localization of gatekeeper positions, high structural stability, and negative selection. Bearing in mind that mutational effects of sequence and stability changes could be opposing (e.g. Fig. 1 indicates that a Pro substitution in a high stability region, intentioned to increase NCI with respect to sequence, is unfavorable and could be destabilizing with respect to structure), such changes might afford a crude tool to introduce or remove specificity. In any event, the analysis presented here provides the locations on each protein where such efforts should be targeted to increase chances for success.

Negative Selection Mediates Protein Domain Evolution

The average domain size of structured proteins is approximately 100 residues [54], and 90% of all known domains are less than 200 residues [55], spanning the size range of proteins sampled here. One implication for protein evolution is that single domain proteins, usually thought of as modular “building blocks” in the organization of larger proteins [56], might be particularly susceptible to sampling alternative structures. Fold-switching is expected to be more prevalent in smaller size proteins [11] and is expected to be less prevalent in larger size proteins [15]. These expectations are supported by strong positive correlations between experimental thermodynamic stability and size [38, 57], as well as from lattice models that exhibit a larger fraction of alternative minimum energy compact structures as the chain length decreases [58, 59]. Thus, increased negative design would be important for small proteins to preserve structure and function when faced with the constraints of small stability and large numbers of alternative folds.

Consistent with this conjecture is the SCOP classification of “small proteins”, whose membership consists of proteins that explicitly require disulfide bonds or metal ions for increased stability [32]. In this scenario, primordial small proteins would have had the tendency for metamorphic behavior, thus negative evolutionary selection would have been a necessary adaptation for dependable metabolic processes mediated by such molecules. Figure 9 suggests that as proteins increase in length they gradually lose the requirement for negative selection. Perhaps this implies the conformational space for a large protein is so vast that preservation of fold is energetically “easier”, as long as aggregation is avoided [60]. Alternatively, larger proteins, which are sometimes composed of several smaller domains, contain functionally important intra-domain interfaces that alter the energetic landscape relative to the individual domains. The role of negative design in larger multi-domain proteins remains to be investigated.

Protein Design Strategy Based on Negative Selection

Aside from effects of negative selection for small proteins, we believe that thermodynamic environments data (Fig. 5) could be practically used as a template for fold design. The log-odds scores (Fig. 1) may be used to generate reasonable amino acid choices for site directed mutagenesis and/or de novo design of full-length proteins. A possible advantage of using thermodynamic environments as a design template, as opposed to structural coordinates, is that environments avoid the difficulty of a “frozen approximation” of the backbone [51]. Instead, thermodynamic environments intrinsically incorporate a range of small conformational adjustments that are approximately isoenergetic within the average stability, enthalpy, and entropy of the environment. One possible design strategy, leveraging both the theory and techniques in this paper, would be to simultaneously maximize the positive score of sequence choices for a desired fold target using the log-odds scores while maximizing the negative score of the same sequence against a large library of alternative folds. This strategy could mimic the “energy gap” between desired and alternative structures that has been demonstrated to be useful in protein design [61]. Such a strategy would be computationally fast to implement using the thermodynamics environment data in Table S2. The pursuit of such avenues is currently under way [62].