Network synchronization in hippocampal neurons

Significance

We show that neurons from the hippocampus and cortex fire in an oscillatory manner, both individually and as a network. When disconnected, the majority of neurons are independent intrinsic oscillators, each with its own natural frequency. Synchronization of the neurons occurs when coupling is introduced. Weak coupling already leads to convergence of all of the oscillators to one common oscillation frequency. Strikingly, this common frequency is close to the mean distribution of their natural frequencies. Strengthening the coupling decreases the phase differences of the oscillators to practically zero, leading to synchronous periodic network bursts. Overall, we show that periodic network bursts originate in collective effects rather than in specialized pacemaking elements that control the rest of the network.

Abstract

Oscillatory activity is widespread in dynamic neuronal networks. The main paradigm for the origin of periodicity consists of specialized pacemaking elements that synchronize and drive the rest of the network; however, other models exist. Here, we studied the spontaneous emergence of synchronized periodic bursting in a network of cultured dissociated neurons from rat hippocampus and cortex. Surprisingly, about 60% of all active neurons were self-sustained oscillators when disconnected, each with its own natural frequency. The individual neuron’s tendency to oscillate and the corresponding oscillation frequency are controlled by its excitability. The single neuron intrinsic oscillations were blocked by riluzole, and are thus dependent on persistent sodium leak currents. Upon a gradual retrieval of connectivity, the synchrony evolves: Loose synchrony appears already at weak connectivity, with the oscillators converging to one common oscillation frequency, yet shifted in phase across the population. Further strengthening of the connectivity causes a reduction in the mean phase shifts until zero-lag is achieved, manifested by synchronous periodic network bursts. Interestingly, the frequency of network bursting matches the average of the intrinsic frequencies. Overall, the network behaves like other universal systems, where order emerges spontaneously by entrainment of independent rhythmic units. Although simplified with respect to circuitry in the brain, our results attribute a basic functional role for intrinsic single neuron excitability mechanisms in driving the network’s activity and dynamics, contributing to our understanding of developing neural circuits.

Periodicity emerges as a key physiological characteristic at all levels of neuronal activity, from the dynamics of neurons at subthreshold potentials (1, 2), through rhythmic neuronal ensembles within local networks, and all of the way up to global oscillations measured by electroencephalography (EEG) (3). The range of observed frequencies is surprisingly wide, from the millisecond range typical for interspike intervals all of the way to several seconds in the case of slow EEG. Over the years, accumulating evidence and theory have attributed different mechanisms for the origin of each measured periodic activity. Within local networks, the role of known collective mechanisms for periodicity, such as the balance between excitatory and inhibitory neurons and recurrent network architecture (4–6), is often contrasted with single neuron contributions, for example, the role of pacemaker neurons in oscillatory network dynamics (7). Although the physiological properties of single neurons are diverse and well documented (2, 8), their role in emergent network oscillations was predicted theoretically (9), but has not been observed experimentally. This contribution may involve a subtle interplay between intrinsic excitability and network connectivity (10, 11).

The connectivity and excitability together determine the behavior of the network. The connectivity can be decreased either at the receiving, postsynaptic neuron or at the sending, presynaptic neuron. The postsynaptic end is blocked by the use of appropriate synaptic blockers. The presynaptic end can be modified by decreasing [Ca²⁺]_o in the environment and effectively stopping synaptic vesicle release.

To understand excitability, one must take into account the origin of membrane potential fluctuations, which can drive a single neuron to fire action potentials (APs). Although APs of coupled neurons are usually triggered via an “integrate and fire” process, there is also evidence for synapse-independent intrinsic processes capable of driving APs (11). Both synaptic and intrinsic processes affect the excitability state of the cell, which, in turn, determines how close to threshold the cell hovers before firing.

The excitability can also be modulated by the balance between intracellular and extracellular ionic concentrations. Changes in the extracellular ionic environment can be globally controlled and take effect immediately without relying on adaptive mechanisms. The effect of changes in the ionic environment on intrinsic excitability can be striking (7, 12). The potassium concentration directly affects the resting membrane potential of the neuron, but other subtle effects can also arise from divalent ions that affect specific channel activity, and thus the internal excitability of the cell.

In particular, calcium plays an important role in controlling collective behavior by participating in synaptic transmission between neurons, regulating the release of neurotransmitter vesicles (13). Furthermore, calcium is important for determining the single cell excitability, for example, by regulating leak currents into the neuron via the NALCN (sodium leak channel) (14, 15).

In this study, we modified both excitability and connectivity by systematically varying the network environment, and we used multielectrode arrays (MEAs) to follow the spontaneous activity of up to 59 single neurons continuously and simultaneously in a dissociated culture. The large-scale network bursting that is characteristic of dissociated culture activity is easily monitored with single spike resolution in this system (16). The precise control of external conditions, along with a high temporal resolution and the relatively large number of recorded neurons in this system, makes it possible to search for the role of heterogeneous intrinsic properties of single neurons in the emergence of synchronized network bursts.

Results

The characteristic behavior of mature [14–17 d in vitro (DIV)] neuronal cultures in standard physiological medium (1–1.5 mM [Ca²⁺]_o, 1 mM [Mg²⁺]_o, and 4–5 mM [K⁺]_o) consisted of periodic bursting. As seen in Fig. 1 A and B, these periodic bursts were highly synchronized network bursts in which activity typically lasted up to several seconds. The activity was separated by windows of complete silence, which may vary in duration depending on the ionic composition of the medium.

Fig. 1.

Bursting network activity at 1 mM Ca²⁺ vs. independent, asynchronous intrinsic neuronal activity at 0 mM Ca²⁺. Typical raster plots (A) and integrated network firing rates (B, red) of MEA electrodes (n = 25) at 1 mM Ca²⁺ show periodic bursting behavior. (C and D) Same culture at 0 mM Ca²⁺ exhibits asynchronous firing with no bursts, whereas the single neurons maintain their firing rate (statistics in I). (E and F) Application of synaptic blocks at 1 mM Ca²⁺ abolishes practically all activity, whereas depolarization using 7 mM K⁺ instead of 4 mM K⁺ recuperates a considerable fraction of the activity, which is asynchronous and not bursting (statistics in I). (G and H) At 0 mM Ca²⁺, the same synaptic blockade has practically no effect on the firing pattern (statistics in K). Network firing rates reported in B, D, F, and H are the total number of spikes measured over all of the active electrodes in 20-ms bins. In contrast, the single neuron firing rate given in I and K is calculated by dividing the total number of spikes that a single neuron fired in a given experimental condition by the duration of the measurement, and then averaging over neurons. The burst rate reported in J is the number of network bursts detected (criteria in Materials and Methods and SI Materials and Methods, Analysis) divided by the duration. Membrane potentials (−70.5 mV and −64.5 mV) in F were obtained from the Goldman–Hodgkins–Katz equation for 4 mM K⁺ and 7 mM K⁺, respectively. (I) Summary of statistics for firing rates at different Ca²⁺ and K⁺ concentrations, with and without synaptic blockers (*P < 0.05; ***P < 0.001). (Inset) Number of active electrodes under the same conditions. (J) Synchronous network bursts appear at 1 mM Ca²⁺. At 0.5 mM Ca²⁺, some cultures already exhibited zero-lag synchronous bursting, but most did not, creating an intermediate state (***P < 0.001). (K) Comparison of average single neuron firing rate at 0 mM Ca²⁺ before and after application of synaptic blockers (normalized by the maximal single neuron firing rate in the culture). No significant change is apparent (t test: P = 0.197; NS, not significant).

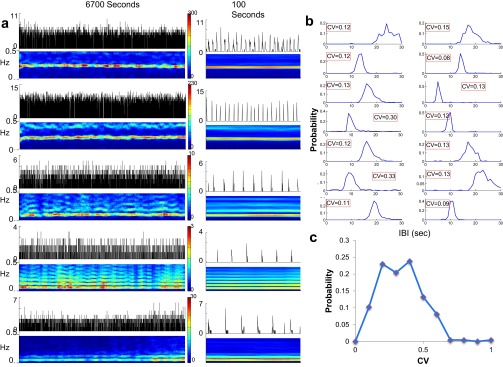
The stability of the periodic bursts was demonstrated by using the three different measurement techniques of MEAs, patch-clamp electrophysiology, and fluorescent imaging in parallel (data are shown in Figs. S1–S4). Fast Fourier analysis of the bursting behavior in the MEAs showed a stable bursting amplitude and frequency for as long as the measurement continued (over 2 h; Fig. S1). Analysis of the interburst intervals (IBIs), or quiet time between bursts, showed peaked distributions for all three measurement modalities in more than 20 cultures measured. The coefficient of variation (CV) of the IBI distribution was typically CV ∼ 0.4, which is indicative of well-defined oscillation frequencies (MEA, fluorescence, and patch-clamp measurements are shown in Figs. S2–S4, respectively). Each neuron fired, on average, 7.6 ± 1.0 (mean ± SEM) spikes per burst (n = 8 cultures, total number of electrodes = 259). The bursting network activity involved the participation of all of the recorded neurons, with a typical recruitment time (as defined in SI Materials and Methods, Analysis) of 30–40 ms.

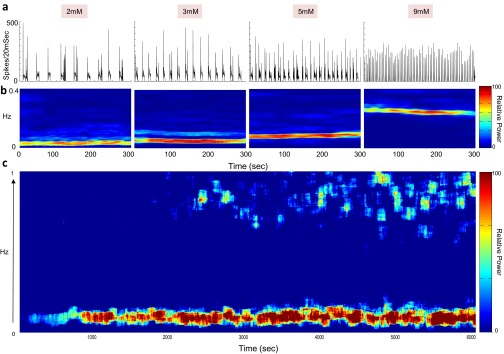
Fig. S1.

Stability of network bursts in 1 mM Ca²⁺ medium. (A) Network firing rate indicates the appearance of bursts, which increase in frequency as the potassium concentration in the medium is increased from 2 to 9 mM. The increased potassium concentration elevates the resting membrane potential, and is associated with an increase in neuronal excitability. (B) Shown are windows of 300 s. FFT spectrograms, calculated over consecutive overlapping windows of 1 min, depict the spectrum of the network activity in A as a function of time. (C) Example of long-term stability over 6,000 s under constant conditions of 5 mM potassium and 1 mM Ca²⁺.

Fig. S4.

IBI stability in 1 mM Ca²⁺ medium measured by whole-cell patch clamp. (A, Lower) Ten minutes of membrane potential activity recorded by patch clamp at room temperature. (A, Upper) Forty-second zoom-in view of the voltage trace. (B) IBIs were measured either as the interval between the end of one burst and the start of next burst (blue) or from start of one burst to the start of the following burst (red). (C) Spectral analysis of the fluorescent trace shown above in A.

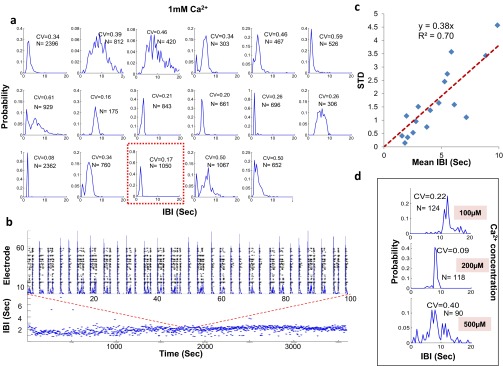
Fig. S2.

IBI stability in 1 mM Ca²⁺ medium. (A) IBI histograms of 17 cultures, each recorded by a MEA at 1 mM Ca²⁺. The red outlined panel represents an example of the experiment shown below. (B, Lower) One hour of the measured IBI plotted by time. (B, Upper) Zoom-in view showing the neuronal activity in the form of a raster plot (black) and total network firing rate (blue overlay) to demonstrate the appearance of bursts. (C) Summary of all experiments shown in A. The CV appears to be fixed at CV ∼ 0.4 and to be insensitive to the actual IBI. (D) IBI histograms at lower Ca²⁺ concentrations.

Fig. S3.

IBI stability in 1 mM Ca²⁺ medium measured by calcium imaging. (A) IBI histograms of three cultures, each recorded at 1 mM Ca²⁺ at room temperature. IBIs were measured either as the interval between the end of one burst and the start of next burst (blue) or from start of one burst to the start of the following burst (red). Representative calcium-imaging fluorescent activity (B) and its equivalent spectral analysis (C). arb. arbitrary.

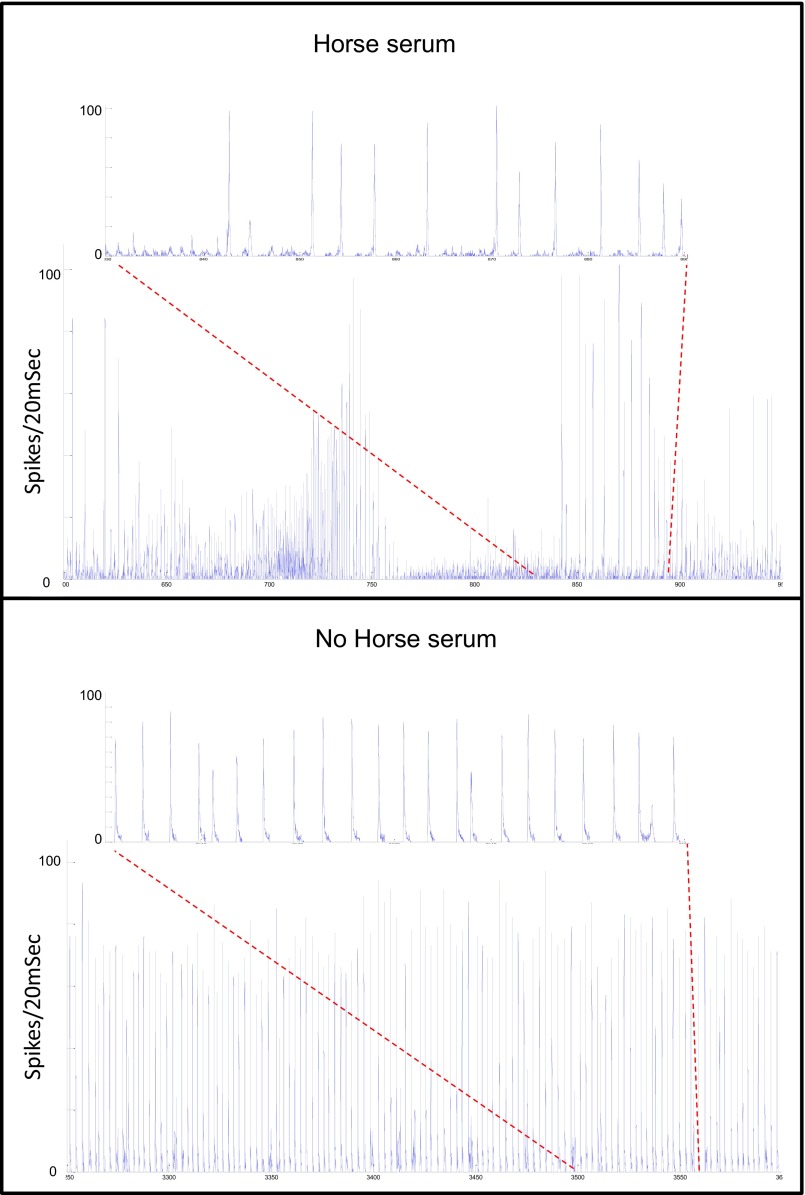
In contrast, we found that varying the medium to include undefined components by addition of horse serum immediately changes the culture’s behavior to a less stable, more complex repertoire of dynamics with no obvious periodicity (Fig. S5). Reverting back to medium with no horse serum results in immediate recovery to the stable oscillatory state. In both cases, the change is abrupt with little apparent adaptation.

Fig. S5.

Horse serum (HS) has a strong impact on network dynamics stability. Three hundred fifty seconds of ongoing network activity were recorded with (Upper) and without (Lower) the addition of 10% (vol/vol) HS, both under 1 mM extracellular concentration of Ca²⁺. All other medium components (i.e., ionic composition) were the same. Zoom-in view of 60 s is shown in each condition. Although network activity without HS (Lower) is stable and periodic, in the presence of HS (Upper), the network behavior becomes irregular with no obviously dominant dynamics. Focus on the individual bursts (zoom-in view) reveals condition-dependent differences in the emergent dynamics and in the overall shape and size of the bursts.

Upon removal of the extracellular calcium (0 mM [Ca²⁺]_o), we found that over 85% of the single neurons maintained their firing with only a small reduction in the mean firing rate (Fig. 1I). However, the drastic and immediate change was in the complete abolishment of collective behavior, as shown in Fig. 1 C, D, and J. The loss of connectivity within the population led to the disappearance of network bursts, whereas activity persisted in over 85% of the single neurons (Fig. 1 C and D). Controlling for the existence of residual calcium in the medium with the calcium chelator EGTA (1 mM) showed no change in the behavior (Fig. S6).

Fig. S6.

Control for 0 mM Ca²⁺. Addition of the Ca²⁺ chelator EGTA to the extracellular medium containing 1 mM Ca²⁺ is similar to changing the extracellular concentration of Ca²⁺ to 0 mM. (Left) EGTA eliminated the synchronization between the neurons with little change to the individual neuron’s mean firing rate. (Right) Likewise, the addition of EGTA to a calcium-free medium had no additional effect.

The calcium-free medium is known to affect the connectivity in the network by reducing presynaptic vesicle release (17, 18). For comparison, we also blocked the postsynaptic end by addition of saturating concentrations of the synaptic blockers 6-cyano-7-nitroquinoxaline-2,3-dione; 2-amino-5 phosphonovaleric acid; and bicuculline, completely abolishing synaptic transmission. Fig. 1 E–H shows its effect on both network bursting (at 1 mM [Ca²⁺]_o) and single neuron activity (at 0 mM [Ca²⁺]_o). In the calcium-free case, there was little to no effect of the additional blocking (Fig. 1 G and H), indicating that the activity recorded under calcium-free conditions was intrinsic and already independent of synaptic communication. Surprisingly, the synaptic blockers caused the cessation of all activity in the standard calcium-containing medium (Fig. 1I). Although this drastic disruption of activity by blockers has been reported previously, its origin was unknown. Fig. 1 E and F shows an intermediate effect of synaptic blockers under the condition of 1 mM [Ca²⁺]_o, where some single neuron activity persisted but the network bursts disappeared.

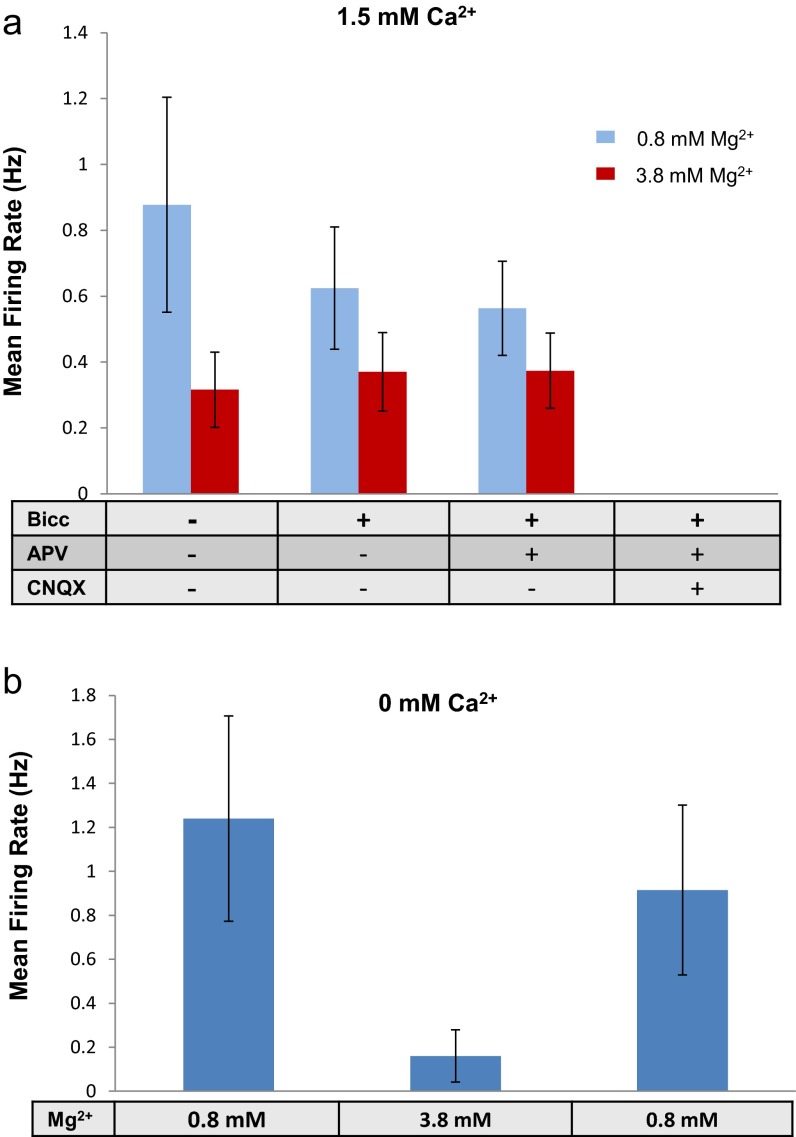
A fundamental question is therefore why single neuron activity persists when synaptic connectivity is disrupted by eliminating vesicle release, but ceases when it is disrupted by blocking receptors. The fact that the single neuron activity is reduced when the concentration of [Ca²⁺]_o is increased suggests the involvement of neuronal excitability in determining the intrinsic neuronal firing. Indeed, holding the [Ca²⁺]_o level at 1.5 mM while increasing the potassium level to 7 mM, equivalent to about 6 mV of depolarization of the membrane resting potential, led 40% of the active neurons to resume the intrinsic activity even with synaptic blockers, at a level of about one-third of the firing rate at 0 mM [Ca²⁺]_o (Fig. 1 E, F, and I). As expected, however, the synchronized network bursting activity did not recover. Decreasing the excitability by addition of 3 mM Mg²⁺ (19) had the opposite effect of reducing the intrinsic single neuron activity either with or without synaptic blockers, and for both 0 mM [Ca²⁺]_o and 1.5 mM [Ca²⁺]_o (Fig. S7).

Fig. S7.

Synapse-independent effect of elevated extracellular Mg²⁺ on single neuron firing rate. (A) Divalent ion magnesium (3 mM) was added to a medium containing the physiological magnesium concentration (0.8 mM) in the presence of 1.5 mM Ca²⁺. A high magnesium concentration considerably reduced the firing rate. Synaptic blockers were then added to control for a specific magnesium effect stemming from increased blockage of NMDA receptors. Indeed, addition of GABA and NMDA blockers in the presence of high magnesium had no further effect on the mean firing rate of single neurons. As shown in Fig. 1, complete synaptic blockage in the presence of 1.5 mM Ca²⁺ eliminated all activity. (B) Similar effect of magnesium was also found at a 0 mM extracellular concentration of Ca²⁺.

The Majority of Dissociated Neurons Are Self-Sustaining Oscillators.

Inspection of the intrinsic firing pattern of single neurons during the asynchronous activity at 0 mM [Ca²⁺]_o revealed that about two-thirds of the neurons were, in fact, oscillators (Fig. 2). Because about 85% of all of the active neurons continue to fire at 0 mM [Ca²⁺]_o, in total about 2/3 of 0.85, or ~60% of all active neurons are oscillators. The oscillating neurons fired a number of spikes once per cycle and were quiescent during the rest of the cycle. As seen in Fig. 2 A–C, both the fast Fourier transform (FFT) power spectrum and the autocorrelation function show a clear signature of the dominant frequency. The remaining 30–40% of the neurons did not show a clear periodic signature (Materials and Methods and SI Materials and Methods, Analysis).

Fig. 2.

Oscillatory firing of disconnected neurons in zero-calcium medium. (A) Example of firing rate traces for 12 of about 40 neurons from one culture. (Insets) Oscillations where the oscillation rate is high but the firing rate is low (typically one to three spikes per oscillation) are emphasized. (B and C) Power spectrum and autocorrelation of the traces shown in A capture the robust and stable oscillatory behavior of the single neurons. (D) Probability distribution function of the oscillation frequency for hippocampus under 5 mM [K⁺]_o (blue, n = 216 electrodes from eight cultures) and 7 mM [K⁺]_o (green, n = 59 electrodes from three cultures) and for cortical cells under 5 mM [K⁺]_o (red, n = 60 electrodes from four cultures). (Inset) Comparison of the average of the distribution for hippocampus vs. cortex (***P < 0.001). (E) Average oscillation frequency (Osc; blue) and firing rate (FR; red) of the single neurons increase significantly (ANOVA: P < 0.001; P < 0.0001, respectively) as a function of potassium concentration (shown are 1, 3, 5, and 7 mM [K⁺]_o with corresponding n = 58, n = 61, n = 62, and n = 59 electrodes from three cultures). The x axis is in units of the membrane rest potential. Note that firing rate units are scaled in hertz/10. (F) As in E for the average number of spikes per oscillation.

The distribution of oscillation frequencies for the different neurons within the same culture was rather broad, and could range from 0.05 to 0.8 Hz (Fig. 2D), with a few outliers (3 of 277) that oscillate at up to 1.5 Hz. These frequencies were stable for as long as we monitored them, and the distribution of IBIs had a CV of ∼0.3 (Fig. S8). Although most of the experiments were performed with hippocampal neurons, we verified that cortical cultures exhibit similar oscillatory behavior. The fraction of oscillatory neurons in cortical and hippocampal cultures was the same, but the frequencies were shifted to higher values in cortical neurons (Fig. 2D).

Fig. S8.

Stability of individual neuron oscillations in a calcium-free medium. (A) Five examples of oscillating neurons are shown, taken from the same culture. The long-term stability measured over about 110 min (Left) and a zoom-in view over 100 s (Right) are shown. The firing rate (black, spikes per 200 ms) of the individual neuron (Upper) with its corresponding FFT spectrogram (Lower), taken in overlapping windows of 60 s, are shown. (B) IBI histograms and CVs of 14 oscillating neurons. (C) Histogram of all individual oscillator CVs.

The effect of changes in excitability was assessed by steps of increased potassium concentration so as to control membrane potential. As shown in Fig. 2D, the distribution of frequencies at 7 mM [K⁺]_o was similar but slightly shifted to higher frequencies compared with 5 mM [K⁺]_o. A more detailed dependence is shown in Fig. 2 E and F, where the increase in average frequency is seen to be threefold over the range of 1–7 mM [K⁺]_o. The firing rate also increased proportionally (Fig. 2E), whereas the number of spikes per burst did not change significantly (Fig. 2F). Taken together, as excitability was increased by increased [K⁺]_o levels, the neurons decreased the time of quiescence between bursts with little change in the burst spike composition.

Synchrony Emerges as a Transition from Independently Oscillating Single Neurons into Coherent Network Bursts.

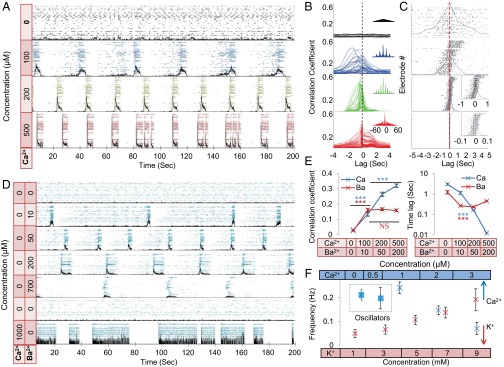
The coupling of intrinsic oscillators and the subsequent emergence of network dynamics are of conceptual interest and have been systematically treated theoretically (20, 21). Following the finding of intrinsic oscillators (Fig. 2), we further explored the issue of coupling. As the calcium concentration was gradually increased from 0 to 500 μM (Fig. 3A), thus enabling connectivity, a transition from an ensemble of individually firing oscillators to a coherent synchronized network of bursts was evident (the transition is displayed in Movies S1–S4). One hundred micromolar [Ca²⁺]_o was sufficient to coordinate the neuronal activity along a slow time scale measured in seconds. Although no network bursts emerged at this concentration, the neurons had already adjusted their activity to one common oscillation frequency, shifted in phase across the population. Phase-shift adjustment of the neuron oscillations to zero-lag gradually developed with increased [Ca²⁺]_o until the activity was fully synchronized at 500 μM.

Fig. 3.

Transition from independently oscillating single neurons into synchronized network bursts. (A) Raster of single neuron activity for 42 electrodes in a sample culture under 5 mM K⁺ and increasing [Ca²⁺]_o. Black traces are the sum over spikes in all of the electrodes per 20-ms bins, representing total network activity. (B) Sample of cross-correlation function for one electrode with all of the other electrodes in the culture shown in A, taken over 25 min. (Insets) Zoom-out view of each cross-correlation function, emphasizing the long-term coherence of the oscillations, and therefore the stability of the synchrony. (C) Lags at which the peak of the correlation functions (like the examples shown in B) were attained for all of the electrodes in A. The blue trace is the normalized histogram of the electrodes per lag in 200-ms bins. (Insets) Lags and histograms in 20-ms bins. Electrodes have been ordered along the y axis by the sum over the lags in the x axis (this order is different from the order in A), and the general monotonic tilt of the data shows that the order between electrode firing is maintained. (D) Raster of single neuron activity for 41 electrodes in a sample culture under an increasing concentration of barium. In the lowest two panels, the barium was washed away, and in the lowest panel, 1 mM [Ca²⁺]_o was added. Black traces are the sum over spikes in all of the electrodes per 20-ms bins, representing total network activity. (E) Average over all electrodes of the peak values of the cross-correlation coefficients (Left) and the corresponding lags themselves (Right), under increasing [Ca²⁺]_o (blue) and barium (red). This lag gives a characteristic of the synchrony (Materials and Methods and SI Materials and Methods, Analysis). P values were computed using single-factor ANOVA (***P < 0.001). Interactions were significant for all [Ca²⁺]_o values but only for 0 mM barium (post hoc analysis). (F) Change in frequency as a function of [Ca²⁺]_o (blue) and of [K⁺]_o (red). The lower two concentrations of [Ca²⁺]_o (dashed rectangle) have independently oscillating neurons, and the value given is the average over their frequencies; all other frequencies are for the synchronized network bursts. No difference (t test: P = 0.423) was found between the average oscillation frequency (at 0 mM) and the network burst frequency (at 1 mM). Both calcium and potassium effects on network burst frequency were significant (ANOVA: ***P < 0.001; NS, not significant).

The gradual synchronization was well captured by the cross-correlation among the activities of all individual neurons (Fig. 3C). Although the phases were widely distributed at 100 and 200 µM [Ca²⁺]_o, the neurons did maintain a fixed phase shift between each other, demonstrating a constant firing order within a global cycle. A reliable measure of network synchronization is the correlation time lag (Materials and Methods and SI Materials and Methods, Analysis), which is an indicator of the mean phase shifts between the different oscillators. As Fig. 3 C and D shows, there was a strong decrease in this measure, going from 1.5 s at 100 μM down to 0.015 s at 500 μM [Ca²⁺]_o, corresponding to a similar decrease in the mean phase shifts. Zero-lag occurred at 500 μM, as manifested by synchronized periodic network bursts. Note that the peak in Fig. 3B is shown for the correlation of a single electrode, typically the first to fire, with all of the rest of the electrodes.

Fig. 3 points to a two-stage synchronization process. The first stage is an adjustment to one frequency that occurs already at 100 μM. The second stage is full synchronization, with very small or zero time lag and fast recruitment times (SI Materials and Methods, Analysis), which arises at 500 μM. Interestingly, the mean single neuron oscillation frequency at 0 mM [Ca²⁺]_o and the mean network burst frequency at 1 mM [Ca²⁺]_o coincide, as shown in Fig. 3F (n = 6 cultures).

As mentioned above, there are two mechanisms of calcium-triggered neurotransmitter release at the presynaptic sites. Barium is known to facilitate only the slow-asynchronous release (13, 22). To investigate the relative involvement of the slow-asynchronous (scale of seconds) release, we introduced a gradual increase of [Ba²⁺]_o while keeping [Ca²⁺]_o at 0 mM (Fig. 3D).

Similar to calcium, adding barium gradually increased the tendency of the whole population to oscillate at one frequency. However, the added barium did not cause the zero-lag synchrony and network bursts that characterize the presence of calcium. Washing the Ba²⁺ retrieved the intrinsic single neuron behavior, whereas further addition of Ca²⁺ brought back the fast, synchronized network bursts, although they were longer than the standard.

Intrinsic Excitability Mechanism Is Mediated by a Sodium Leak Current I_NaP.

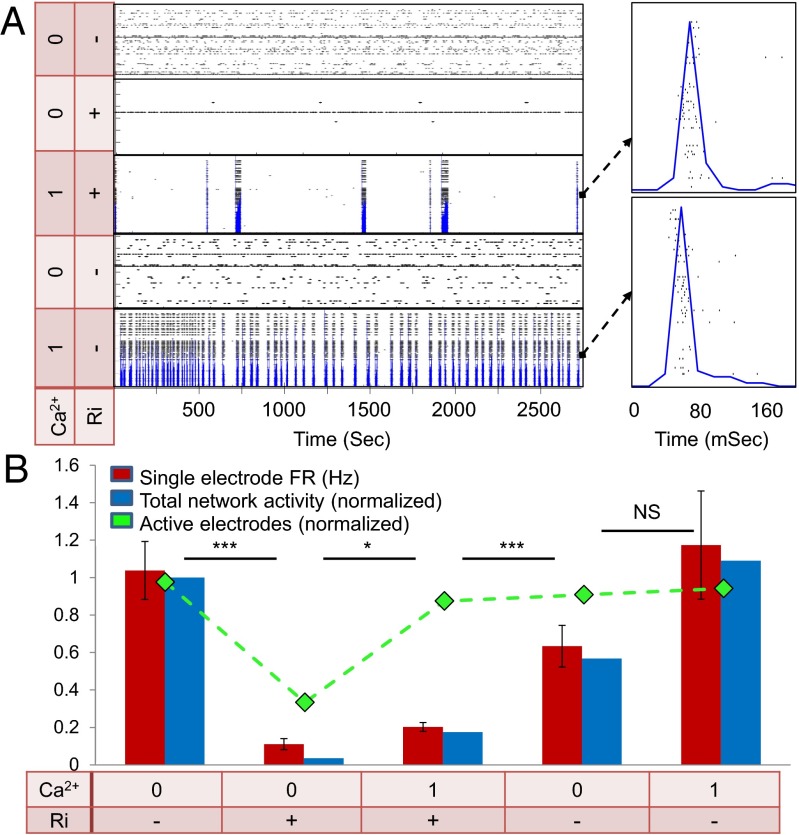
Intrinsic firing mechanisms of individual neurons have been suggested to rely on leak currents, which affect neuronal excitability and support oscillatory behavior (14, 23). This leak current often involves the persistent noninactivating sodium current I_NaP. The relevance of I_NaP can be tested by its antagonist riluzole (24, 25). As shown in Fig. 4A, the addition of 1 μM riluzole immediately and dramatically reduced all activity of the neurons. At 0 mM [Ca²⁺]_o and 1 μM riluzole, over 70% of the active neurons ceased their activity completely, whereas the mean firing rate decreased by about 90% in the remaining 30%.

Fig. 4.

Intrinsic excitability mechanism is mediated by a persistent sodium leak current. (A) Raster of single neuron activity for 30 electrodes in a sample culture under different conditions of calcium and riluzole. Blue traces are the sum over spikes in all of the electrodes per 20-ms bins, representing total network activity. The lowest two panels are after washing out of the riluzole. (Right) Blow-up view of a single network burst in the 1 mM [Ca²⁺]_o conditions, either with riluzole (Top) or after washing it out (Bottom). (B) Effect of riluzole on single electrode and network activity. As a baseline for comparison and normalization, 0 mM [Ca²⁺]_o and no riluzole (Ri) are used. Single electrode firing rates (red bars), relative number of active electrodes (green curve), and network activity (blue bars) are greatly reduced by riluzole application at 0 mM [Ca²⁺]_o (n = 57; t test: P < 0.0001). The network activity was calculated as the total number of recorded spikes divided by time (in seconds) and is presented as the change relative to the condition before riluzole. Adding 1 mM calcium results in only a small recovery in firing rates (t test: *P < 0.05; ***P < 0.001) and total activity, but the number of active electrodes is concurrently almost completely recovered in these conditions. The effect of riluzole is most pronounced in the total network activity (blue bars), which actually equals the value of the single electrode activity (red bars) multiplied by the value of the number of active electrodes (green curve).

Upon addition of 1 mM Ca²⁺, practically all of the neurons regained synchronous activity, but the burst rate remained extremely low (Fig. 4B), with quiescent periods on the order of minutes between bursts. Most suggestive is that the bursts that did occur with riluzole exhibited zero-lag synchrony, which is characteristics of regular connected networks at 1 mM [Ca²⁺]_o. Washout of the riluzole brought about almost full recovery of the intrinsic neuronal firing at 0 mM [Ca²⁺]_o and of the network activity at 1 mM [Ca²⁺]_o.

SI Materials and Methods

MEA.

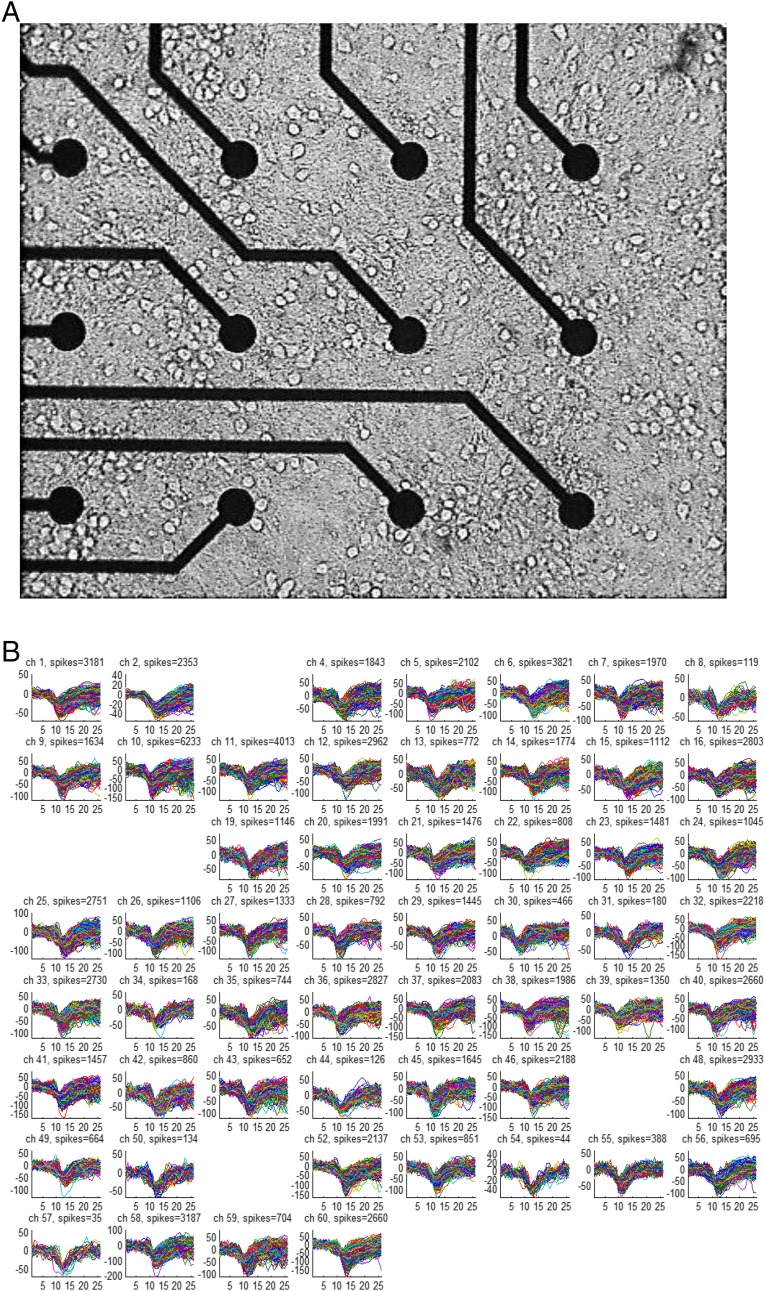
MEAs of 60 electrodes with a diameter of 30 μm and a spacing of 200 μM (MultiChannelSystems) were prepared by autoclaving and oxygen plasma discharge treatment (Fig. S9). The plasma cleaner (PDC-32G-2; Harrick Plasma) was first purged by oxygen flow with the MEAs inside for 20 min and then operated at the high-power setting for 3 min. Plasma cleaning was followed by overnight application at room temperature of poly-l-lysine (P4707; Sigma) diluted 1:5 in borate buffer. After three rinses with double-distilled water (DDW), the MEAs were left overnight in the incubator with plating medium [5% (vol/vol) FCS; Gibco] and 5% (vol/vol) heat-inactivated horse serum (HIHS; Gibco) in Earle’s MEM (Gibco) enriched with 0.6% glucose, 1% Glutamax (Invitrogen), 0.02 mg/mL gentamicin, and 0.1% B-27 supplement. After 4 DIV, 30% of the medium was replaced by final medium [10% (vol/vol) HIHS in Earle’s MEM enriched with 0.6% glucose, 1% Glutamax, and 0.02 mg/mL gentamicin]. At 8 DIV, the MEAs were transferred to the final medium, after which one-third of the medium was replenished at intervals of 3 d for 1 wk, followed by 2-d intervals after that time.

Fig. S9.

Multielectrode recording of hippocampal culture. (A) Microscope image of 12 of 60 electrodes in 14 DIV hippocampal culture. The spacing between electrodes is 200 μm, and each electrode is 30 μm in diameter. (B) Overlay of all spike waveforms detected during a measurement of 1,800 s in each of the 55 active electrodes in this MEA. All electrode amplifier channels (ch) were recorded simultaneously, and the ongoing spike detection was based on the signal-to-noise ratio measured at each of the electrodes separately. The sampling rate was 13 kHz, and the x axes are given in units of the sampling points, showing a total of 26 sampling points, equivalent to 1 ms before and 1 ms after spike detection. The y axes are given in microvolts.

Culture Preparation.

Rat hippocampal neurons from 19-d-old embryos were used. All procedures were approved by the Weizmann Institute’s Animal Care and Use Committee. Following the method of Segal and Manor (39), dissection was carried out in ice-cold L-15 medium enriched with glucose (0.6%) and gentamicin (0.02 mg/mL; Sigma–Aldrich). The hippocampus was dissociated first by enzymatic and then by mechanical trituration. As in previous work (29), neurons were seeded into 3 mm of medium at a typical initial density of 3,000–4,000 neurons per square millimeter, with survival rates that lead to a typical final density of 800 neurons per square millimeter (Fig. S9A). Measurements were almost always carried out on 14–17 DIVs (one measurement was on 19 DIV) in a chamber placed on a thermally regulated plate held at 38 °C by water flowing through it. Each culture was measured over one experiment that typically lasted 8–9 h.

Serum-Free Media.

We experimented with several different fluid media for the measurement, and found that media containing horse serum led to less regular activity than the serum-free media (Fig. S5). Horse serum (Biological Industries) is collected from a donor herd and tested for its ability to support the growth of Sp2/O-Ag14 (murine myeloma) cells in control medium containing the test lot of serum. Horse serum (different from what is used to develop vaccines) is often used as a component in the growth medium of neuronal cultures. In particular, previous reports on bursting network activity of neural cultures have used it at times in maintaining their cultures even while measuring the activity, particularly over long periods. The ingredients of the horse serum are variable, because it is obtained from an animal, and are not regulated. We use HIHS in which proteins are deactivated by the heat treatment. We present the data with horse serum as an “uncontrolled” environment, where the ionic concentrations and other factors are not well known. This behavior is in stark contrast to the “controlled” medium that we use, in which all of the components are well known and the concentrations of all of the different ions are precisely determined. We have seen that adding the antibiotic gentamicin to the measurement medium affects the stability, so one interesting possibility is that traces of antibiotics that may be present in the horse serum affect the activity.

We therefore conducted the measurements in a controlled medium: DDW containing 5.3 mM potassium, 144 mM sodium, 155 mM chloride, 0.81 mM magnesium, 39 mM glucose, 16 mM sucrose, 10 mM Hepes, and 10 mM Glutamax, but with no serum. Potassium and calcium concentrations were varied according to the experimental protocol described in the main text. Neuronal activity usually equilibrated within several minutes of the transfer to calcium-free medium, which was the first condition that experiments began with as a standard. The calcium-free condition also usually served as a final control at the end of each experimental run, ensuring that the culture had not deteriorated significantly during the experiment. Changes in membrane potential due to ionic content were calculated using the Goldman–Hodgkin–Katz equation with our ionic concentrations (www.physiologyweb.com/calculators/ghk_equation_calculator.html).

Electrophysiology.

The electrical signals were amplified 1,200-fold and then low-pass-filtered with a 3-kHz cutoff (MEA1060 amplifier; MultiChannelSystems) and sampled at 13 kHz, using a general-purpose data acquisition board (PCI-6071E; National Instruments). Data were acquired and processed using MATLAB (The MathWorks). The condition for spike detection was that the absolute value of the sampled signal exceeds an amplitude threshold for duration of at least 0.2 ms. The threshold was set at the higher of either 15 μV or sixfold the rms of the signal. Only one dominant form of spike was taken per electrode, eliminating the need for spike sorting and ensuring a clear signature for every electrode. The resulting spike waveforms are shown in Fig. S9B, and we verified by spike sorting that in a large portion of the electrodes, typically 90%, the spike shapes were consistent with a single source. The remaining 10% did not give a clear separation into two spikes but could not be assigned unambiguously to one cluster. We can safely conclude that there is only one neuron measured for each of the electrodes we measured, which is confirmed by the fact that no electrode gave consequent spikes that were separated by less than 2 ms and, rarely, less than 5 ms apart. We thus equate an electrode with a single neuron, and use the terms “neuron” and “electrode” interchangeably.

Patch Clamp.

Hippocampal cultures at 14 DIV were transferred to a recording chamber placed on the stage of an inverted Olympus IX70 microscope and washed with a serum-free controlled medium. Neurons were recorded with patch pipettes containing 136 mM K-gluconate, 19 mM KCl, 5 mM NaCl, 10 mM Hepes, 0.1 mM EGTA, 0.3 mM Na-GTP, 1 mM Mg-ATP, and 5 mM phosphocreatine (pH 7.2) with a resistance in the range of 5–8 MΩ. Signals were amplified with a MultiClamp 700B instrument and recorded with a pClamp10 (Axon Instruments). Data were analyzed offline using MATLAB.

Calcium Imaging at 1 mM Ca²⁺.

Neuronal cultures (SI Materials and Methods, Culture Preparation), grown on 13-mm glass coverslips, were preincubated for 1 h in serum-free media containing 1 mM Ca²⁺ and Fluo-4 calcium indicator (Molecular Probes) and placed in a chamber with fresh serum-free media. The chamber was mounted on a Zeiss inverted microscope with a 10× objective. Imaging was obtained using a CCD camera (SensiCam) with a 20-Hz sampling rate and at room temperature. Data were analyzed using MATLAB.

Analysis.

The neuronal firing rate is given by the number of spikes or APs measured in a given electrode per bin of 20 ms. The mean firing rate was calculated for each electrode as the total number of spikes measured in a corresponding time interval divided by the time interval (in seconds). Electrodes were deemed active and retained for further analysis if the mean firing rate during the measurement was above 0.01 Hz.

Oscillations were identified from the FFT of the firing rate, which was calculated by dividing the total interval into segments of 60 s and then averaging over the interval. A neuron was classified as an oscillator if the largest peak in the FFT was 2 SDs larger than the background of the FFT and its full width at two-thirds maximum was 0.15 Hz or less. Fig. S8A shows the stability of five representative oscillators, recorded simultaneously over time periods of 6,700 s (Left) or 100 s (Right) and plotted along with their spectrograms. Fig. S8B shows the distribution function of the IBIs for 14 representative neurons, whereas Fig. S8C shows the distribution function of the CVs of the IBIs obtained for 235 neurons. The average CV was 0.28.

Summing over all APs in all of the electrodes in bins of 20 ms gives the network activity as a function of time. A network burst is defined to have occurred if 1 s of complete quiescence in all active electrodes was followed by over 60% electrodes that fired within one 20-ms bin. A burst continues until the occurrence of another second of complete silence in the network (Fig. 1 A and B). The abrupt onset characterizing these global bursts is a well-documented feature of strongly connected neuronal networks (29–31). The burst rate (different from the firing rate) was calculated as the total number of detected network bursts divided by the corresponding time interval (in seconds). The frequency of the network bursts was calculated by the peak in the FFT of the network activity, similar to the single neuron oscillation criterion.

IBIs were measured from the end of one burst until the beginning of the next one. For the fluorescence and patch-clamp data, the end of the burst was harder to evaluate; thus, we also present for comparison the interval between the first spike of one burst and the first spike of the next burst, which are easy to identify. These intervals differ because the length of the burst may vary, as indeed happens at the higher calcium values (1 and 1.5 mM calcium). Significantly, we found that the CV of both distributions was small, indicative of a well-defined period.

Synchrony was examined by looking at the cross-correlation of all of the electrodes with each other, measured for segments of 60 s, which are then averaged over the duration of the experimental condition. The time lag at which this averaged cross-correlation peaks for each pair of electrodes was extracted. When single neurons share a common oscillation frequency, this time lag reflects the mean phase shift between the pair of oscillators. As the synchronization increases, the neuronal spikes bunch into smaller and smaller time intervals and the peaks in the correlation converge to a correspondingly shorter interval around zero-lag. This convergence is shown in Fig. 3C. The average over the absolute value of these time lags represents this bunching of the neurons and serves as a quantitative measure of network synchrony. The absolute value needs to be taken, because in Fig. 3C, both values for the cross-correlation of two electrodes are given, where one value is the negative of the other. In principle, synchrony can be quantified by this time lag, and one may think of synchrony as the inverse of the time lag in appropriately normalized units, although we do not use this definition in the current work.

Upon increase of the connectivity, correlation emerges in the network and the lags decrease from values on the order of seconds to tens of milliseconds. For the fast-rising bursts, which are characteristic of a strongly connected network (above 1 mM [Ca²⁺]_o), the averaged time lag drops to less than 20 ms (Fig. 3C, Bottom). We define this condition as equivalent to zero-lag synchrony.

A tricky point is that if the network is not bursting, as is the case for 0 mM Ca (Fig. 3C, Top), then a spurious peak can appear simply because the single neuron frequencies are widely distributed and neurons with short periods will have cross-correlations with peaks closer to zero-lag. However, this peak will be very shallow and very broad, on the order of the inverse of the mean frequency. To demonstrate that the phase shift between the neurons is fixed, and thus the order of firing of the neurons within the burst is fixed, the electrodes have been ordered in Fig. 3C according to the mean lag with all of the other electrodes.

Recruitment time is related to synchrony, and was defined by the time that passed from the firing of the first spike in the burst until 80% of the neurons that participated in the burst had fired their first spike.

Pharmacology.

Synaptic blockers were applied by bath application to block AMPA, NMDA, and GABA receptors, using their respective antagonists: 6-cyano-7-nitroquinoxaline-2,3-dione (10–20 μM), of 2-amino-5 phosphonovaleric acid (50 μM), and bicuculline (40 μM). The calcium chelator EGTA was used at 3 mM in two experiments under the zero calcium condition as a control verifying that no additional effects appeared. Barium was added in the form of BaCl₂ at concentrations varying from 2 μM to 3 mM. Riluzole (R116-25MG; Sigma) was administered at 0.3–10 μM to block the persistent sodium current I_NaP.

Discussion

We have shown that under sufficient excitability conditions, about 60% of dissociated, disconnected hippocampal or cortical neurons will oscillate. This intrinsic excitability is supported by the sodium leak current I_NaP, and is strongly affected by calcium levels. Upon a gradual increase in connectivity, the entrainment of these intrinsic oscillations through decreasing phase shifts was found to underlie the emergence of synchronized and periodic network bursts. Our use of synaptic blockers elucidated the involvement of neurotransmission in coupling the individual neurons, but coupling mechanisms such as gap junctions (26, 27) and glial cells should also be considered (SI Discussion).

The importance of elevated calcium concentrations is twofold, enabling network connectivity by increasing the synaptic release while concurrently reducing the single neuron excitability. The effect of excitability is dominant in allowing the intrinsic oscillations and in determining their frequency. A minimal excitability is also required for the activation of the sodium leak current I_NaP. The increase in excitability obtained by depolarizing the resting membrane potential via the potassium concentration leads to an increase in the single neuron oscillation frequencies. Addition of magnesium, a divalent ion-like calcium, decreased the excitability without affecting the connectivity.

The effect of calcium on excitability also explains why disconnecting the network via synaptic blockers at elevated calcium levels stops practically all activity. Our picture of the bursting network activity at elevated calcium is based on the idea that without blockers, a background of spontaneous synaptic activity exists and makes the neurons slightly more excitable. We have shown previously that under these conditions of strong connectivity, firing of a small fraction of the neurons, presumably those neurons that are more sensitive to inputs and lead the activity, suffices to ignite the rest of the network (28–30). An additional effect of increased network synchronization with elevated [Ca²⁺]_o was recently reported in cortical slices (31), but through differential sensitivity of excitatory and inhibitory synapses to calcium.

The contribution of calcium in enabling connectivity and the build-up of synchronization is also dual, this time because of the two main mechanisms for vesicle release. The interplay between calcium-dependent fast-synchronous and slow-asynchronous neurotransmitter release is central to understanding the dynamics in this system. The slow-release mechanism is sufficient to adjust the frequencies of the individual oscillators into a unified oscillation frequency, but not to synchronize the oscillators, which requires the addition of fast release. This effect is also seen in conditions of no calcium but with barium, which enables only the slow release. Zero-lag synchronization occurs at elevated calcium concentrations, presumably when the fast-release mechanism is activated as well, making the coupling stronger. This interplay is explained by different sensitivities of the two mechanisms to intracellular calcium concentrations (32).

Within theoretical models for self-entrainment of independent oscillators (20, 21, 33, 34), the coupling strength determines the synchronization process. In our system, the connectivity, or coupling, is controlled by the calcium concentration. The original model by Kuramoto (20) makes a clear prediction that the network will oscillate at a fixed frequency that equals the average of the frequencies of the single oscillators. For more complex pulse-coupled models, the network burst frequency may be a complex function of the coupling strength (20, 34–36). Our measurements indicate that at least at one point (5 mM [K⁺]_o and 1 mM [Ca²⁺]_o), there is a correspondence between the burst frequency and the average of single neuron frequencies, much like the model prediction of Kuramoto (20). However, from Fig. 3, it can be seen that increasing the coupling strength also decreases the burst frequency, which is different from the simple scenario of Kuramoto (20). Interestingly, Hansel et al. (35) showed that the frequency tends to a steady value as the coupling increases to unity. This result may indicate that at 1 mM [Ca²⁺]_o, the system has reached a strong coupling limit.

Another deviation of our data from the predictions of theoretical models can be seen in the comparison between the stability of the single neuron oscillations and those oscillations of the network bursts. Theoretically, the coupling of the oscillators should lead to an improvement of the precision of the oscillators (37). However, we have seen clearly that the single neuron oscillations are, in fact, 30% more precise than the network bursts, as measured by the IBI distribution functions and their CV.

The deviations may be because these models often make assumptions that are not borne out experimentally, for example, that the coupling is uniform, that there is no inhibition, and that the distribution function of the frequencies is symmetrical around the mean. The coupling in our system is more complex because it is composed of two components, the slow-vesicle release and the fast-vesicle release. Furthermore, we have shown that neuronal excitability is important in determining the frequency of oscillations and the extent of network activation, a factor usually ignored in models of synchronizing oscillators. For example, the excitability must cross a threshold to enable the oscillatory behavior. Another difference from the models is that a small subpopulation of active neurons suffices to ignite the rest of the network (29).

An interesting point is that in our experimental setup, both single neuron and network oscillation frequencies are robust and stable for hours. However, in a medium with horse serum, a totally different behavior emerges (Fig. S5). The same network architecture can thus switch between different modes of dynamics by only changing the fluid environment, with no need for an associated change in the hardwiring of synaptic connectivity.

In summary, cultured neurons comprise a network of coupled intrinsic oscillators that may be described by theoretical models for self-emergent synchronization. In this scenario, the slow, calcium-dependent, asynchronous release is a weak coupling that suffices to entrain the frequencies of the oscillators, whereas the fast, calcium-dependent, synchronous release is required to attain zero-lag synchrony. Once coupling is established in the network, the oscillators converge onto one frequency, which is close to the mean distribution of their natural frequencies. Thus, the intrinsic oscillations characteristic of the majority of neurons, and the resultant network periodicity in the shape of rhythmic bursts, may play an important role in defining the dynamical states in many neuronal processes (38).

SI Discussion

A possible alternative mechanism for creating synchronous neuronal oscillation is electrical coupling (EC) by gap junctions (GJs). This coupling has been suggested as a synchronizing mechanism in emergent high-frequency (200 Hz) oscillations (27), although the action of the specific GJ blocker used there is controversial (28). We observed in our cross-correlation results at 0 mM Ca²⁺ that all pairs of neurons were uncorrelated; thus, if independent and separate synchronizing networks of neighbors are acting, then they must be very small and localized around each electrode. Given the scarcity of GJs in cultures, the EC scenario for synchronization thus seems highly improbable. Another possible scenario is a linkage of glial cells to the neurons that creates a separate frequency at each neuron, but we have found no evidence either for or against such a mechanism.

Materials and Methods

Rat hippocampal neurons from 19-d-old embryos were used (39). All procedures were approved by the Weizmann Institute’s Animal Care and Use Committee. Measurements were typically carried out on 14–17 DIV (one measurement was on 19 DIV) in a chamber placed on a plate that was temperature-controlled by circulation of water at 38 °C. MEAs of 60 electrodes of with a diameter of 30 μm and a spacing of 200 μM (MultiChannelSystems) were used for recording (Fig. S9). The electrical signals were amplified 1,200-fold and sampled at 13 kHz, using a general purpose digital-to-analog converter. Data were acquired and processed using MATLAB (The MathWorks). Electrodes were deemed active and retained for further analysis if the mean firing rate during the measurement was above 0.01 Hz. Both single neuron oscillations and periodic network bursts were identified by the FFT. Synchrony was defined by the cross-correlation of all of the electrodes with each other. The time lag at which the averaged cross-correlation has a peak was extracted for each pair of electrodes. The average over these time lags serves as a quantitative measure of network synchrony. Zero-lag (maximal) synchrony was defined to occur if this average time lag drops to less than 20 ms (Fig. 3C, Bottom). Recruitment time was defined as the duration between the first spike in the burst and when 80% of the participating neurons fired their first spike. To demonstrate that the phase shift between the neurons is fixed, and thus the order of firing of the neurons within the burst is fixed, the electrodes have been ordered in Fig. 3C according to the mean lag with all of the other electrodes. Barium was added in the form of BaCl₂ at concentrations varying from 2 μM to 3 mM. Riluzole (R116-25MG; Sigma) was administered at 0.3–10 μM to block the persistent sodium current I_NaP. Details are provided in SI Materials and Methods.