Dynamic Coupling and Allosteric Networks in the α Subunit of Heterotrimeric G Proteins

Abstract

G protein α subunits cycle between active and inactive conformations to regulate a multitude of intracellular signaling cascades. Important structural transitions occurring during this cycle have been characterized from extensive crystallographic studies. However, the link between observed conformations and the allosteric regulation of binding events at distal sites critical for signaling through G proteins remain unclear. Here we describe molecular dynamics simulations, bioinformatics analysis, and experimental mutagenesis that identifies residues involved in mediating the allosteric coupling of receptor, nucleotide, and helical domain interfaces of Gα_i. Most notably, we predict and characterize novel allosteric decoupling mutants, which display enhanced helical domain opening, increased rates of nucleotide exchange, and constitutive activity in the absence of receptor activation. Collectively, our results provide a framework for explaining how binding events and mutations can alter internal dynamic couplings critical for G protein function.

Introduction

Heterotrimeric G proteins are key mediators of intracellular signaling pathways that control diverse cellular processes ranging from movement and division to differentiation and neuronal activity (1). G proteins consist of three subunits: Gα, Gβ, and Gγ. Bound with GDP, Gα forms an inactive complex with its Gβγ subunit partners. Interaction with activated receptor (GPCR)³ promotes the exchange of GDP for GTP on Gα and its separation from Gβγ. Both isolated Gα and Gβγ can then bind and activate or inhibit downstream effectors. GTP hydrolysis deactivates Gα, which subsequently reassociates with Gβγ completing the cycle. This cycle is further regulated by two classes of additional proteins called regulators of G protein signaling. These function as either GTPase-activating proteins (which promote GTP hydrolysis) or GDP dissociation inhibitors (GDIs, which hinder exchange of GDP for GTP) (2). Important conformational transitions occurring at each stage of this regulated cycle have been characterized from extensive crystallographic studies. These include GDP, GTP analogue, Gβγ, GTPase-activating protein, GDI and most recently GPCR bound complex structures of Gα. However, the link between the observed conformations and the atomic level mechanisms involved in coupling receptor association, G protein activation, and effector interaction remain unclear.

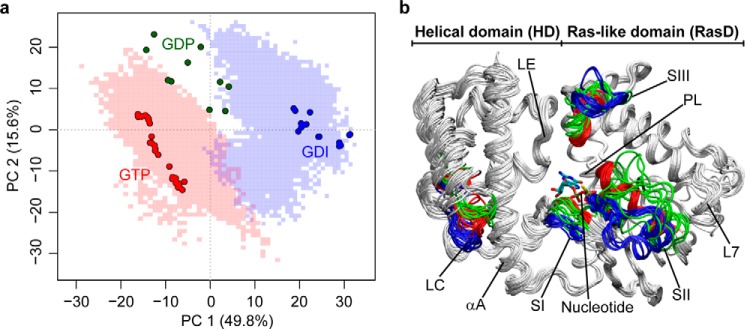
All Gα proteins consist of a catalytic GTP binding Ras-like domain (termed RasD) and a heterotrimeric G protein specific helical domain (HD). Recent principal component analysis (PCA) of 53 available Gα crystallographic structures identified three major conformationally distinct groups (Fig. 1 and Ref. 3). These groups correspond to structures with bound GTP analogues, GDP, and GDI (red, green, and blue points in Fig. 1a, respectively). The major variation in the accumulated structures is the concerted displacements of three nucleotide-binding site loops termed the switch regions (SI, SII, and SIII), as well as a relatively small scale (<10°) rotation of the constituent HD and RasD regions. A much larger (127°) clam-shell like displacement of the HD with respect to RasD was reported recently in the crystallographic structure of Gαs (the α subunit of the stimulatory G protein for adenylyl cyclase) in complex with Gβγ and the β2 adrenergic receptor (4). This conformational change, which effectively exposes the otherwise buried nucleotide binding site, has been linked to GPCR-mediated nucleotide exchange (4). Evidence for domain opening has also been obtained from recent electron microscopy (5), double electron-electron resonance analysis (6), hydrogen-deuterium exchange mass spectrometry (7), biochemical analysis (8), and molecular dynamics (MD) simulations (3, 9, 10). In addition, the structure of Rasmussen and co-workers (7) together with mass spectrometry results also confirm that both N-terminal β1 strand and C-terminal α5 helix are major interaction sites for receptors. This supports the previously suggested role of these regions in coupling receptor binding and nucleotide dissociation activities (11–17). Despite these advances, critical questions remain unanswered: How do the distinct conformations evident in the accumulated structures interconvert? And critically, how do distal functional sites responsible for GPCR, nucleotide, and partner protein binding allosterically coordinate their activities? Addressing these questions requires information on protein dynamics, which is not directly available from the accumulated static experimental structures.

FIGURE 1.

Principal component analysis of crystallographic Gα structures reveals three major conformations. a, projection of 53 available Protein Data Bank crystal structures of Gα (represented by round points; see also supplemental Table S1) onto the first two principal components (PC) that together account for 65.4% of the total structural variance. Three conformational clusters correspond to GTP-bound (red), GDP-bound (green), and GDI-bound (blue) structures. Projection of conformations sampled from MD simulations under GTP- and GDI-bound conditions are also shown as transparent red- and blue-shaded areas, respectively. b, superimposition of structures with high variance regions (SI, SII, SIII, and LC) colored by conformational cluster.

In this study, we aimed to dissect detailed mechanisms of allostery in Gα by employing a combined computational and experimental approach. This entailed long time MD simulations, ensemble-based correlation network analysis of dynamic couplings related to allostery, and experimental mutagenesis and functional assays. This approach identified fluctuations and dynamic residue couplings in functional regions that distinguished GTP, GDP, and GDI states. Network analysis revealed a consistent bilobal dynamic partitioning of the RasD region. Partitioning of residues into these correlated segments was similar in different states but displayed distinct nucleotide dependent coupling strengths between segments. The active GTP state was shown to have the strongest overall couplings, exhibiting “dynamical tightening” with respect to GDP and GDI states. Furthermore, network path analysis delineated the detailed mechanism of dynamic coupling and revealed residues predicted to be involved in mediating the distal (>30 Å) allosteric coupling of receptor, nucleotide, and HD interfaces. Results from mutational simulations further supported the functional relevance of the identified allosteric paths with selected path mutations displaying a dynamic decoupling of distal sites along with an enhanced rate of spontaneous RasD-HD domain opening. Experimental mutagenesis of a number of these sites together with in vitro cAMP and [³⁵S]GTPγS assays indicated that the signaling properties of Gα_i can indeed be modulated by these single point mutations that act allosterically. In particular, the novel L32A mutation (numbering based on the α subunit of bovine transducin) was predicted to enhance domain opening and was found to increase nucleotide exchange rates, increase G protein activation, and decouple G protein from receptor activation leading to constitutive activity.

Experimental Procedures

All structure and trajectory analysis was performed with Bio3D version 2.0 (18, 19). Molecular graphics were generated with VMD version 1.9 (20).

Crystallographic Structures Preparation

Atomic coordinates for all crystallographic structures of the G_i protein family were obtained from the RCSB Protein Data Bank (21) via sequence search utilities in the Bio3D package. Structures with unresolved residues in the switch regions were excluded from analysis leading to a data set containing 53 structural species (see supplemental Table S1 for full listing). Prior to assessing the variability of the structures, iterated rounds of structural superposition were performed to identify the most structurally invariant region. During this procedure, residues with the largest positional differences (measured as the volume of an ellipsoid determined from the Cartesian coordinates of the Cα atoms) were removed, before each round of superposition, until only invariant core residues remained (22). The identified “core” structure was used as the reference frame for the superposition of crystal structures and subsequent MD trajectories prior to further analysis.

Principal Component Analysis

PCA was performed for the 53 crystallographic structures of Gα to characterize interconformer relationship. The application of PCA to both distributions of experimental structures and MD trajectories, along with its ability to provide considerable insight into the nature of conformational differences in a range of protein families has been previously discussed (23–26). Briefly, PCA is based on the diagonalization of the variance-covariance matrix, Σ, with elements Σ_ij calculated from the Cartesian coordinates of Cα atoms, r, after the superposition of all structures under analysis,

where i and j enumerate all 3N Cartesian coordinates. The eigenvectors, or principal components, of Σ form a linear basis set matching the distribution of structures. The variance of the distribution along each principal component is given by the corresponding eigenvalue. Projection of the distribution onto the subspace defined by principal components with the largest eigenvalues provides a low dimensional representation of structures facilitating analysis of interconformer relationships (Fig. 1a).

Molecular Dynamics Simulations

MD simulations were performed with AMBER12 (27) and corresponding force field ff99SB (28). Additional parameters for guanine nucleotides were taken from Meagher et al. (29). The Mg²⁺·GDP-bound transducin crystal structure (Protein Data Bank code 1TAG) was employed as the starting model for GDP-bound simulations. The Mg²⁺·GTPγS structure (Protein Data Bank code 1TND) was used as the starting model for GTP-bound simulations. The sulfur atom (S1γ) in the GTPγS was replaced with the corresponding oxygen (O1γ) of GTP. In addition, GDP-bound Gα_i/GoLoco motif complex structure (Protein Data Bank code 1KJY) was employed as the starting model for GDI-bound simulations. These structures were identified as cluster representatives from PCA. In all systems, Arg and Lys were protonated, whereas Asp and Glu were deprotonated. The protonation states for His residues were determined based on an inspection of the residues local environment and their pK_a values as calculated by PROPKA (30). Simulation structures were solvated in a truncated cubic box of pre-equilibrated TIP3P water molecules, which extended 12 Å in each dimension from the surface of the solute. Sodium counter ions (Na⁺) were added to neutralize the systems. Additional ions were not added to mimic physiological ionic strength. This may have the effect of accentuating electrostatic interactions. Energy minimization was performed in four stages, with each stage employing 500 steps of steepest decent followed by 1500 steps of conjugate gradient. First, minimization for solvent only was performed with fixed positions of protein and ligand atoms. Second, side chain and ligand were relaxed with backbone still fixed. Third, all protein and ligand atoms were relaxed with fixed solvent. Fourth, all atoms were free to move without any restraint. Following minimization, 10 ps of MD simulation was performed to heat the system from 0 to 300 K under constant volume periodic boundary conditions. A further 1 ns of equilibration simulation was performed at constant temperature (T = 300 K) and constant pressure (p = 1 bar). Subsequent 80-ns production phase MD was then performed under the same conditions as equilibration. For both energy minimization and MD simulations, the particle mesh Ewald summation method was adopted to treat long range electrostatic interactions. In addition, an 8 Å cutoff was used to truncate the short range nonbonded van der Waals' interactions. Additional operational parameters for MD included a 2-fs time step, removal of the center of mass motion every 1000 steps and update of the nonbonded neighbor list every 25 steps. All hydrogen atoms were constrained using the SHAKE algorithm.

Correlation Network Construction

Network analysis of correlated motions was employed to identify protein segments with coupled dynamics. A weighted network graph was constructed where each node represents an individual residue and the weight of the connection between nodes, i and j, represents their respective cross-correlation value, c_ij (31). This well established cross-correlation approach is based on linear atomic displacements during the course of simulations. Our evaluation of more recently developed nonlinear mutual information of dihedral angle changes (32, 33) indicated that prohibitively longer simulation and analysis time were likely required for the generation of robust networks (data not shown). We used a network construction method similar to that introduced by Luthey-Schulten and co-workers (34). However, instead of employing a [4.5 Å] contact map of non-neighboring residues to define network edges (that are then weighted by a single correlation matrix), our network edges were constructed based on the minimum Cα-Cα cross-correlation value between all residues across five replicate simulations. Specifically, cross-correlations were calculated for each trajectory after mass-weighted superposition. Network edges were added for (i) residue pairs with |c_ij| ≥ 0.6 in all simulations and (ii) residues satisfying |c_ij| ≥ 0.6 in at least one simulation and with a Cα-Cα distance d_ij ≤ 10 Å for at least 75% of total simulation frames. Edge weights were calculated as −log(|<c_ij>|), where <·> denotes the average across simulations. Networks constructed with a c_ij cutoff between 0.5 and 0.7 yielded equivalent networks with similar community structure (data not shown). This procedure was found to reduce potentially false positive couplings that exist when using only a single trajectory, as well as minimize the arbitrary exclusion of consistent strong couplings that are just beyond a given distance cutoff.

Network Community and Centrality Analysis

For each correlation network, hierarchical clustering was performed to generate aggregate nodal clusters, or communities, that are highly intraconnected but loosely interconnected, using a betweenness clustering algorithm similar to that introduced by Girvan and Newman (35). However, instead of using the partition with the maximum modularity score, as is common with unweighted networks, we took the partition closest to the maximal modularity value that resulted in the smallest number of overall communities (i.e. the earliest high scoring partition). This avoided the common situation where many small communities with equally high scoring modularity values were generated. Using this approach networks under different states showed a largely consistent community partition, with differences localized to the nucleotide binding P-loop (PL), SI, SII, and α1 regions that were observed to repartition between major communities in the different states (data not shown). Consensus communities that abstracted these regions to new separate communities to facilitate further comparisons were derived from partitioning these regions at the boundaries of their known conserved sequence motifs. Intercommunity correlations were then calculated as the sum of the mean correlation values across simulation replicates associated with all the intercommunity edges. A standard t test was also performed to measure the significance of the mean difference between intercommunity correlations of distinct states.

Node centralities that assess the density of connections per node were calculated as follows,

where x_i is the centrality of node i, A_ij is the ijth entry of the adjusted adjacent matrix A, λ is a constant to be determined, and G indicates all nodes. A_ij is not 0 if node i and j are linked, and it is equal to e^−w_ij, where w_ij is the edge weight. Solving Equation 2 for every i (i ∈ G) is equivalent to finding the eigenvalues and eigenvectors of matrix A. Node centralities can then be obtained from the eigenvector with the largest eigenvalue, after scaling all entries with the largest entry set to be 1.

Network Path Analysis

Given a pair of nodes treated as “source” and “sink,” respectively, optimal (shortest) and suboptimal (close to but longer than optimal) connecting network paths were identified using the algorithm in Ref. 36. Five hundred paths were collected for each source/sink pair in each network. Comparative path length distributions indicating the strength of correlated motions under distinct conditions were then calculated. In addition, normalized node degeneracy, i.e. the fraction of the number of paths going through each node, was calculated. Residues with high node degeneracy (≥0.1 or 50 paths) in any network were specified as “on-path” residues and were subjected to further analysis including, for select cases, mutagenesis simulations and experimental characterization.

Molecular Cloning

cDNA for human adenosine A₁ receptor (A₁R) and Gα_i2 isoform 1 were acquired from DNASU Plasmid Repository and Open Biosystems, respectively. N-terminal Flag-tagged Gα_i2 or A₁R-Gα_i2 fusions and N-terminal mCerulean-tagged Gα_i2 were cloned into pBiex1 and pCDNA5/FRT plasmids, respectively. A₁R and Gα_i2 were fused together using the previously described SPASM technique (37). Briefly, A₁R-Gα_i2 fusions were cloned from N to C terminus as follows: A₁R, mCitrine, ER/K linker, mCerulean, and Gα_i2. Repeating (Gly-Ser-Gly)₄ sequences were inserted in between domains to ensure rotational freedom. Gα_i2 and Gα_t (Bos taurus) residues were aligned to identify the conserved Leu³², Phe¹⁹⁵, and Asp³³³ residues in Gα_i2. L36A, F200L, or D338A mutations in Gα_i2 were induced via PCR using oligonucleotide-directed mutagenesis (QuikChange site-directed mutagenesis kit; Stratagene). All constructs were confirmed via sequencing.

Mammalian Cell Culture

HEK293T-Flp-in (Invitrogen) cells were cultured in DMEM supplemented with 10% FBS (v/v), 4.5 g/liter d-glucose, 1% GlutaMAX, 20 mm HEPES, pH 7.5, at 37 °C in a humidified atmosphere at 5% CO₂. The cells were plated at ∼30% confluence into 6-well tissue cultured treated dishes. 16–20 h later, the cells were transfected with indicated construct using XtremeGene HP DNA transfection reagent. Where indicated, 24 h post-transfection, cells were incubated with 100 ng/ml pertussis toxin (PTX) for 20–24 h. Experiments were conducted when fusions or mCerulean-Gα_i2 constructs expressed predominately at the plasma membrane with minimal internal localization as evaluated at 20× and 40× magnification on a Nikon tissue culture microscope with fluorescence detection. Experiments were performed at equivalent fusion expression at a cell density of 2 × 10⁶ cells/ml. Fusion expression was quantified by measuring mCitrine and mCerulean fluorescence by exciting cells at 490 and 430 nm, respectively. Excitation and emission bandpass were correspondingly set to 8 and 4 nm. For mCerulean tagged Gα_i2 experiments, the cells were harvested at similar wild type and mutant Gα_i2 expression levels. It should be noted that wild type, F195L, and D333A expressed twice as much as L32A mutant as indicated by mCerulean fluorescence counts. Fusion integrity was evaluated by measuring mCitrine to mCerulean emission ratio. This ratio was held between 1.7 and 2.1 because mCitrine is twice as bright as mCerulean. All fluorescence measurements were conducted using FlouroMax-4 fluorometer (Horiba Scientific) in an optical glass cuvette.

Quantification of cAMP Levels

Protocol was conducted as previously described using the cAMP Glo luminescence based assay (Promega) (38). Briefly, 28–30 h post-transfection, the cells were spun down (300 g, 3 min), resuspended at 1 × 10⁶ cells/ml in PBS solution supplemented with 0.02% glucose and 800 μm ascorbic acid and aliquoted into 96-well round bottom opaque microplates. The cells were treated with 0.25 mm 3-isobutyl-1-methylxanthine, 1 μm forskolin, or 10 μm forskolin in the presence or absence of A₁R agonist (12.5 nm N⁶-cyclopentyladenosine) for 5 min at 37 °C. After incubation with indicated compounds, the cells were lysed, and protocol was followed according to the manufacturer's recommendations. Luminescence was recorded using a microplate luminometer (SpectraMax M5; Molecular Devices). cAMP levels (relative luminescence units) were calculated by subtracting the untransfected untreated background from the indicated conditions. Each experiment had four repeats per condition and was repeated at least three times (n > 12).

Insect Cell Culture and Protein Purification

Sf9 cells were cultured and maintained in suspension with shaking at 28 °C in Sf900-II medium (Life Technologies) containing 1% Antibiotic-Antimycotic (Life Technologies). Constructs were transiently transfected into Sf9 cells using Escort IV transfection reagent (Sigma-Aldrich) in antibiotic-free medium. The cells were lysed 3 days post-transfection in HEPES lysis buffer (20 mm HEPES, pH 7.5, 0.5% Igepal, 4 mm MgCl₂, 200 mm NaCl, 7% sucrose, 5 mm DTT, 50 μg/ml PMSF, 5 μg/ml aprotinin, 5 μg/ml leupeptin). Lysates were clarified by ultracentrifugation (175,000 × g, 4 °C, 45 min) and bound to anti-FLAG M2 affinity resin (Sigma-Aldrich). Resin was washed with HEPES wash buffer (20 mm HEPES, pH 7.5, 150 mm KCl, 5 mm MgCl₂, 5 mm DTT, 50 μg/ml PMSF, 5 μg/ml aprotinin, 5 μg/ml leupeptin) and eluted using FLAG peptide (Sigma-Aldrich). Protein concentration and integrity were assessed by SDS-PAGE and Coomassie staining in comparison to BSA standards.

Nucleotide Exchange and [³⁵S]GTPγS Incorporation

Binding of [³⁵S]GTPγS to purified Gα_i protein was based on the method outlined in Ref. 39. Briefly, the assay mixture contained 0.5 μg of purified Gα_i protein in TED buffer (20 mm Tris-HCl, pH 7.4, 1 mm DTT, 1 mm EDTA, 0.1 mm MgCl₂) with 2 μm GTPγS and 0.1 nm [³⁵S]GTPγS, unless otherwise stated, in a total volume of 200 μl. Experiments were performed at room temperature (25 °C), unless stated otherwise, and 50-μl samples were withdrawn and diluted 1:4 in ice-cold TED buffer to stop the reaction at various time points. Aliquots were vacuum-filtered through GF/C filters, and the amount of bound radioactivity was quantified by scintillation counting. Data were analyzed using GraphPad Prism as one-phase association curves.

Results

GTP-, GDP-, and GDI-bound States Display Distinct Flexibilities and Dynamic Couplings in Known Functional Regions

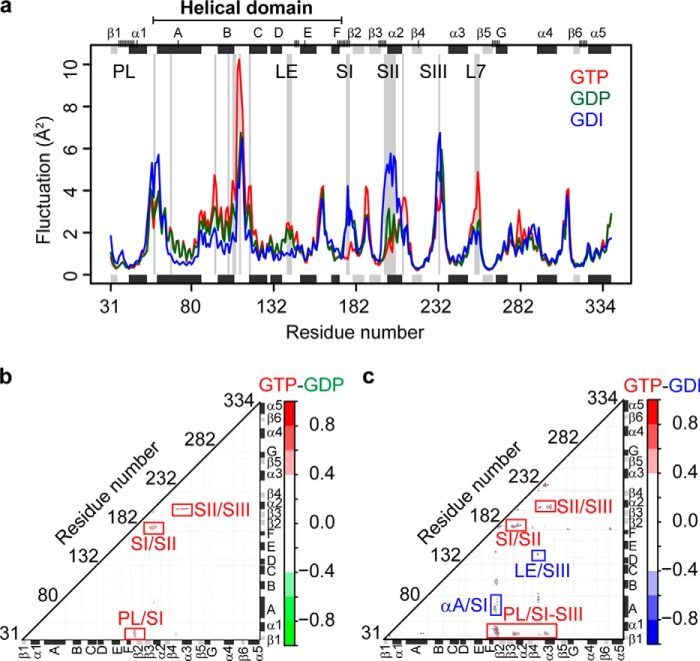
Five 80-ns MD simulations for each state (GTP, GDP, and GDI totaling 1.2 μs; see “Experimental Procedures”) revealed residue fluctuations that clearly distinguished states (Fig. 2a). Specifically, the SI, SII, and SIII regions were found to be more flexible in GDP and GDI states than in the GTP state. Conversely, a more flexible L7 region (the loop between α3 and β5) was apparent for the GTP state only. The possible role of L7 in receptor binding has been suggested by both crystallographic studies (4) and mutagenesis experiments (40). Furthermore, fluctuation analysis revealed a more rigid HD region in the GDI state, with fluctuations at multiple sites predicted to be smaller in the GDI state than those in either GTP or GDP state.

FIGURE 2.

State-specific residue fluctuations and dynamic couplings in Gα from molecular dynamic simulations. a, ensemble averaged fluctuation analysis reveals structural regions with significantly distinct flexibilities in GTP (red), GDP (green), and GDI (blue) states. Sites with a p value < 0.05 are highlighted with a light gray background on the main plot. Short vertical tick lines on the top axis indicate the location of nucleotide binding site residues. Marginal black and gray rectangles indicate the location of major α helix and β strand secondary structure elements. b and c, state-specific residue couplings. Difference correlation values between GTP and GDP (b) and between GTP and GDI (c) states are shown. Major regions displaying distinct couplings are indicated with red (GTP) and blue (GDI) labels. Note that no major GDP specific couplings were evident from comparison with GTP (b) or GDI (data not shown) states.

MD derived residue-residue couplings also clearly distinguished GTP, GDP, and GDI states (Fig. 2, b and c). This analysis revealed that the GTP state had significantly stronger couplings in the PL and switch regions, whereas the GDI state had uniquely strong couplings around the region between RasD (SIII) and HD (the loop between αD and αE, or LE) and the region between αA and SI (Fig. 2, b and c). It is important to note that results from a simple difference contact map analysis of trajectories did not reveal the full extent of the dynamic coupling difference reported here (data not shown). This highlights the importance of employing dynamic coupling analysis to provide additional context for the interpretation of both global and local structural dynamic changes of potential functional relevance. In the next section, we further dissect these apparent dynamic couplings with network analysis to obtain insight into potential mechanisms of long range dynamic coupling in Gα of relevance to allostery.

Correlation Network Analysis Further Characterizes State-specific Dynamic Couplings and Reveals the Intrinsic Dynamical Modularity of Gα

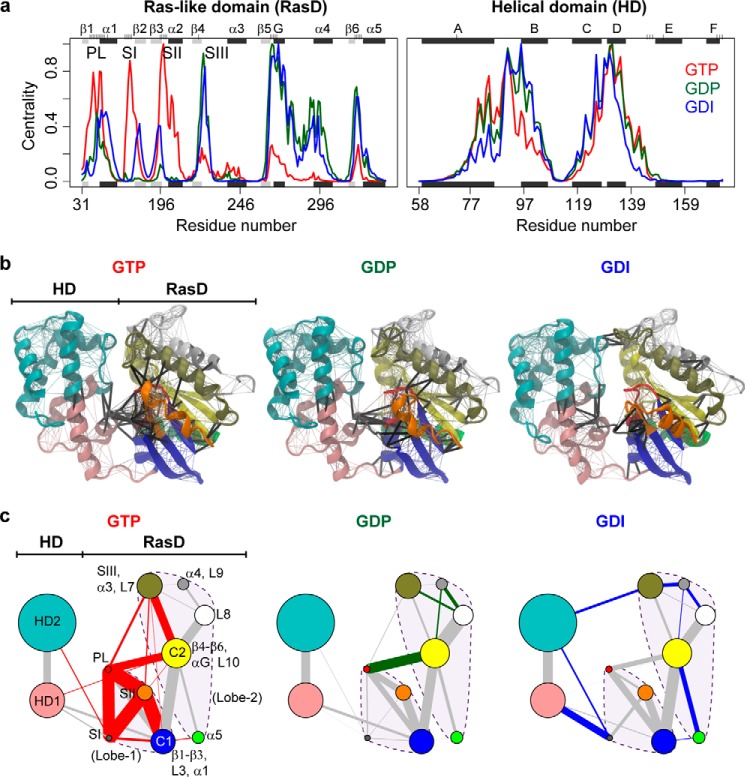
For each state, a weighted correlation network graph was constructed from the MD simulation results. Each node of the graph represented an individual residue, and the weight of the connection between nodes was proportional to their respective correlation value calculated from multiple replicate MD simulations. To reduce noise, i.e. “false positive” couplings that may exist only in a single trajectory, we inspected the robustness of each coupling over multiple simulation trajectories and constructed an ensemble-averaged network with each edge representing only significant residue-residue correlations present in the entire simulation set for a given state (see “Experimental Procedures”). Eight highly connected network regions are evident in Fig. 3a. This analysis assesses the density of connections per node (i.e. node centrality) and highlights six regions in RasD and two regions in HD with a comparatively high level of coupling. Within RasD, these six regions can be equally partitioned into two major groups with the boundary located near L5 (the loop between α2 and β4). These correspond to the two major lobes reported first for Ras itself using structural and evolutionary sequence analysis (24). Lobe 1, which includes all switch regions and the N-terminal half of the β-sheet, is highly conserved across distinct Ras isoforms, whereas lobe 2, which includes α3-α5 and the C-terminal half of the β-sheet, contains significant amino acid variations. Intriguingly, dynamic coupling analysis here identified the same two lobes in Gα, which also exhibit distinct nucleotide-dependent dynamics. In the GTP state, lobe 1 displays stronger coupling than lobe 2. Major regions of high density network connections (i.e. high centrality values) are located at the PL, SI, and SII. In contrast, in the GDP and GDI states, coupling in lobe 2 is stronger, and high density connections occur at SIII, αG, and L10 (the loop between β6 and α5). This further supports the functional relevance of the conserved bilobal substructure and reveals how nucleotide modulates the transition between active and inactive states by altering the dynamic coupling within and between these conserved structural lobes. In contrast, regions in the HD with high density connections do not show significant differences between states, indicating that changes in dynamic coupling upon nucleotide cycling are largely limited to the RasD region.

FIGURE 3.

Correlation network analysis reveals state-specific differences in residue couplings. a, node centrality values that assess the density of connections per node for RasD and HD regions in GTP (red), GDP (green), and GDI (blue) states. b, molecular structure mapping of consensus network communities (colored regions) and residue couplings (lines). Intercommunity couplings are indicated with thick black lines. c, community networks depicted with colored circles (as in b) whose relative radius indicates the number of residues in a particular community. The widths of linking lines are determined by their relative intercommunity coupling strength. Red-, green-, and blue-colored linking lines indicate enhanced GTP, GDP, or GDI couplings that are significantly stronger (p value <0.005) in one state than another. All other lines are colored gray.

Correlation network analysis further dissects residue couplings and reveals residue communities having the potential to facilitate long range allosteric signal propagation. Clustering was performed to define local communities of correlated residues that represent highly intraconnected but loosely interconnected substructures (see “Experimental Procedures” and Fig. 3, b and c). Consistent with centrality analysis, the RasD region can be clearly partitioned into two major lobes (Fig. 3c, dashed lines). Lobe 1 includes the large β1–β3, L3, and α1 community (blue in Fig. 3, b and c and labeled “C1”) plus the PL, SI and SII elements. Lobe 2 includes the large β4-β6, αG, and L10 community (yellow in Fig. 3, b and c, labeled C2) plus four smaller communities corresponding to individual helices and their associated loops distributed on both sides of the β-sheet. The HD N-terminal αA, αE, and αF were grouped into one community with the C-terminal αA, αB, αC, and αD forming a second HD community. The overall community structure reflects the intrinsic dynamic couplings within Gα and provides a level of abstraction at which significant commonalities and differences in potential allosteric coupling can be further understood.

Analysis of intercommunity coupling strengths reveals state-specific allosteric coupling paths and an overall dynamical tightening in the GTP state. In particular, lobe 1 couplings including PL/SI, PL/SII, SI/SII, and SII/C1 are significantly enhanced in the active GTP state and weakened or absent in the inactive GDP and GDI states (Fig. 3c, red edges). Interlobe couplings to SIII (α3) and C2 are also significantly enhanced in the GTP state. In contrast intralobe 2 couplings, including SIII/L8, α4/L8, and α4/C2 are stronger in the GDP state than those in the GTP and GDI states (Fig. 3c, green edges). Also noteworthy are the significantly stronger HD to RasD couplings evident for the GDI state (Fig. 3c, blue edges). These state-specific dynamical coupling differences are robust to variations of network model parameters and have potential implications for the nucleotide-dependent modulation of long range signal propagation. However, detailed dissection of these potential pathways and the residues involved can be better addressed with the more fine-grained path analysis approach described below together with targeted mutagenesis studies aimed at assessing their functional significance.

Network Path Analysis Reveals Distinct Features of GTP-, GDP-, and GDI-modulated Couplings of Distal Functional Sites

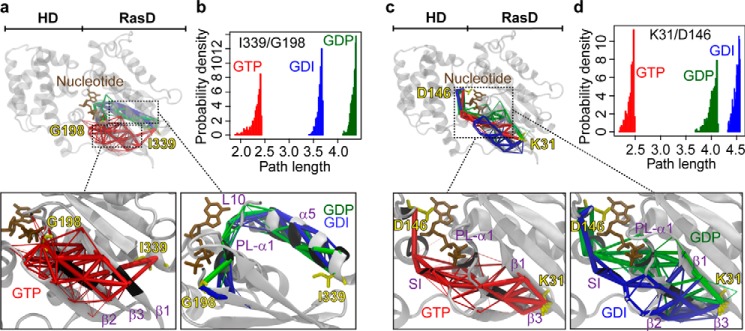
Given a pair of residues, termed source and sink, 500 suboptimal connecting coupling paths through each network were calculated. Path lengths were computed as a summation over the weights of traversed edges. Shorter paths represent stronger dynamic coupling. Source and sink pairs were chosen that represent receptor binding site to nucleotide γ-phosphate (γ-Pi) binding site (Ile³³⁹/Gly¹⁹⁸) and receptor binding site to the RasD-HD interface (Lys³¹/Asp¹⁴⁶ and Ile³³⁹/Lys²⁶⁶; Fig. 4 and supplemental Table S2). Note that both RasD-HD interface residues, Asp¹⁴⁶ and Lys²⁶⁶, were chosen based on the experimental observation that significantly enhanced mobility around LE and αG occurred after Gα activation (7). The first pair of residues is located at the C terminus of α5 and the γ-P_i coordinating SII region, respectively. For the GTP state, calculated paths predominantly traversed the lobe 1 β-strands (β1, β2, and β3), whereas in the GDP and GDI states the dominant paths involved α5, α1, and L10 from lobe 2 (Fig. 4a). Examining the distributions of path lengths indicated that the GTP state had much shorter overall paths (Fig. 4b). This is indicative of the apparent dynamical tightening of the lobe 1 region in the active state evident from network community analysis (Fig. 3, b and c). Paths from receptor coordinating β1 (Lys³¹) to the RasD-HD interface (Asp¹⁴⁶) displayed differing favored routes in distinct states. In the GTP network, paths mainly traversed β1, β3, SI, and PL, whereas in the GDI network, the traversed regions extended to β2 but excluded PL (Fig. 4c). In the GDP network, the traversing region was mainly β1, β3, PL, and α1 (Fig. 4c). Moreover, the path length distributions show that the GTP state had much shorter paths than either GDP or GDI state, again demonstrating the dynamical tightening of the active state (Fig. 4d). Path analysis from receptor coordinating α5 (Ile³³⁹) to RasD-HD interface (Lys²⁶⁶) revealed a common major route through α5-L10-αG (supplemental Table S2) and similar path length distributions across GTP, GDP, and GDI states (data not shown). This indicates that the β1-HD pathway is more dynamic during G protein cycling and potentially more sensitive to external modulations such as small molecule binding and point mutations.

FIGURE 4.

State-specific coupling from receptor to nucleotide and helical domain interfaces. a, suboptimal paths linking α5 and SII for GTP (red), GDP (green), and GDI (blue) states. Line thickness scales with relative path length within a state with the shortest path rendered as the thickest line. Source and sink residues Ile³³⁹ and Gly¹⁹⁸ are labeled and rendered in stick representation. The bottom panels magnify path regions and have residues with high (>0.5) node degeneracy (proportion of paths traversing a given node) colored on the protein cartoon. b, probability density distribution of path lengths between α5 (Ile³³⁹) and SII (Gly¹⁹⁸). c and d, suboptimal paths between β1 and the RasD-HD interface (with source/sink pair Lys³¹/Asp¹⁴⁶) and corresponding probability density distribution of path lengths. See also supplemental Table S2 for details of path analysis from receptor coordinating α5 to the RasD-HD interface (with source/sink pair Ile³³⁹/Lys²⁶⁶).

Normalized network node degeneracy, which characterizes the percentage of total paths that traverse a given node, revealed that many high degeneracy residues are also highly conserved in sequence (supplemental Table S2). Furthermore, previous in vitro mutagenesis of predicted on-path residues (occurring on >10% of total paths) indicates that many are functionally relevant. In particular, point mutations of residues from SI (Arg¹⁷⁴ and Thr¹⁷⁷), β3 (Phe¹⁹²), L10 (Cys³²¹), and α5 (Asn³²⁷, Val³²⁸, Phe³³⁰, Val³³¹, Phe³³², Asp³³⁷, Ile³³⁸, and Ile³³⁹) have shown significantly altered basal and receptor-catalyzed nucleotide exchange rates (13, 17, 41, 42). All of these residues are characterized as playing a prominent role in coupling paths linking receptor-binding and domain-binding interfaces (i.e. high node degeneracy values; supplemental Table S2). Below we explore further how perturbations, introduced via point mutations, can potentially affect these apparent coupling networks.

On Path Mutations Promote Domain Opening and Disrupt Long range Couplings Linked to Receptor-catalyzed Nucleotide Exchange

Five replicate 80-ns GTP-bound MD simulations and subsequent network analysis were performed on each of five mutant variants: L32A, F195L, F332A, D333A and I339A. These positions were highlighted by path analysis as contributing to the coupling of receptor, nucleotide and HD binding interfaces. The highly conserved α5 residue Ile³³⁹ and β1 residue Leu³² were identified as key mediators of GTP specific couplings between α5 and the β-sheet (Fig. 4a and supplemental Table S2). The β3 residue Phe¹⁹⁵ was predicted to participate in the coupling paths between β1 and the RasD-HD interface (supplemental Table S2). We note that a leucine substitution at an equivalent position in Gα_i2 has been reported to be associated with ventricular tachycardia (43). The conserved residue Phe³³² in α5 was identified to participate in the paths between α5 and RasD-HD interface (supplemental Table S2), and substitution of an equivalent position in Gα11 has been reported to be associated with hypocalcemia (44). The importance of Phe³³² on nucleotide exchange has also been demonstrated in both in vitro experiments and computational energetic analysis (13, 17, 45, 46). The α5 residue Asp³³³ is solvent-exposed and not directly involved in contact with other structural elements outside of α5 but is predicted here to be a prominent on-path site (supplemental Table S2).

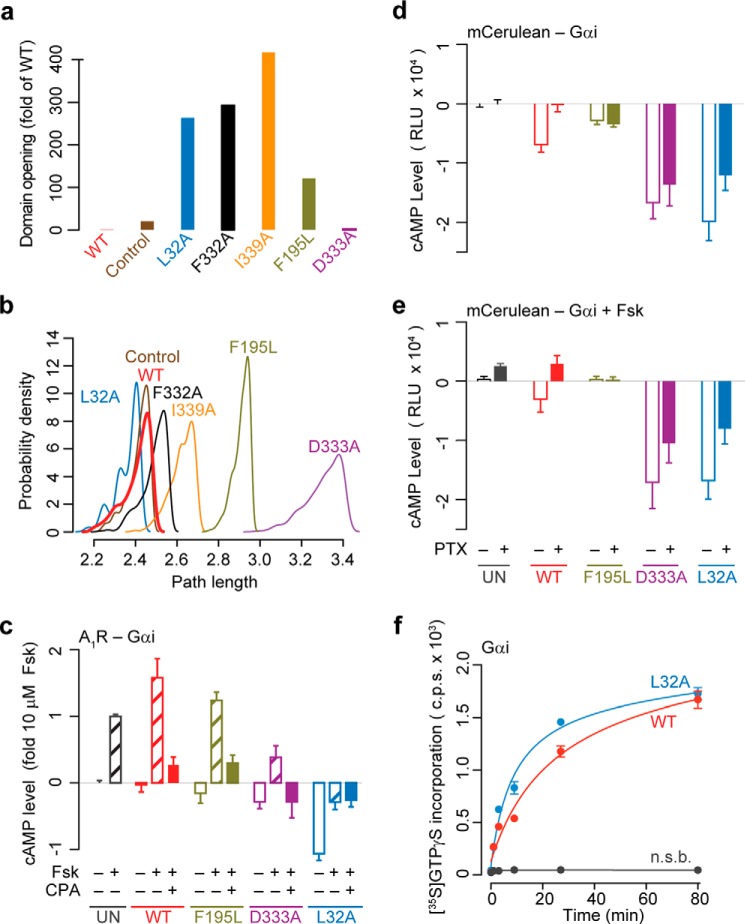
Our MD simulations of L32A, F332A, and I339A showed a substantial effect on the rate of RasD-HD domain opening. Specifically, these mutants displayed a 200-fold more populated open conformation than wild type during equivalent simulations (Fig. 5a). These mutants also displayed Cα-based root mean square deviation from the initial structure of up to 5–6 Å, because of this relative domain opening. Interestingly, the D333A mutant simulations under the same conditions displayed a similar level of domain opening to that of wild type, whereas F195L showed a more moderate level of enhanced domain opening (Fig. 5a). Network path analysis indicated that the mutants with the most perturbed coupling paths (D333A and F195L) displayed the least domain opening events. Conversely, mutants with relatively unperturbed coupling paths (L32A, F332A, and I339A) displayed enhanced opening. This suggests that mutations mimicking the effect of receptor binding may utilize wild type-like coupling paths for eliciting their allosteric effect on domain opening. Detailed inspection further revealed that only D333A and F195L mutations displaced on-path residues, most notably the SI region, leading to elongated path lengths. Collectively, these results indicate that both path analysis and subsequent mutant simulations are required for prediction of the structural dynamic effects of mutation. Our predictions parallel previous in vitro experimental measurements of enhanced spontaneous nucleotide exchange rates for mutations equivalent to F332A and I339A (13, 17). The current results indicate that enhanced domain opening can lead to enhanced nucleotide exchange. However, currently very little is known experimentally about the potential allosteric role or effect of mutations at sites Leu³² and Asp³³³.

FIGURE 5.

Computational and experimental mutagenesis of on path residues. a, fraction of domain opening events observed relative to WT simulations for L32A, F195L, F332A, D333A, and I339A. The same WT simulation protocols and network analysis methods were implemented for all mutant simulations. Domain opening was detected whenever the minimum Cα-Cα distance between LE (on the HD side) and SIII (on RasD) exceeded 10 Å in the cumulative 5 × 80-ns simulations. Control refers to a set of five separately performed WT simulations. Note that all simulations were structurally stable as indicated by standard geometric analysis (data not shown). b, probability density distribution of path lengths from receptor coordinating β1 (Lys³¹) to RasD-HD interface (Asp¹⁴⁶) in WT and mutants. c, cAMP levels for the WT and mutant A₁R-Gα_i fusions for indicated conditions in live HEK293 cells (Untransfected (UN), 10 μm Fsk, and 12.5 nm N⁶-cyclopentyladenosine (CPA, A₁R agonist)). d and e, cAMP levels for HEK293 cells expressing WT or mutant mCerulean labeled Gα_i, treated without (d) or with (e) forskolin (10 μm Fsk) in the presence or absence of PTX. PTX treatment inhibits WT but not D333A and L32A activity, indicating that the latter display receptor-independent constitutive activity. f, representative time course of [³⁵S]GTPγS binding to purified WT and L32A mutant Gα_i. n.s.b., nonspecific binding.

Gα_i Signaling Properties Are Modulated by the Predicted Single Point Mutations That Act Allosterically

To examine the effect of our potential receptor-decoupling Gα_i mutants, we experimentally assayed cAMP levels in HEK293 cells using the recently described SPASM GPCRs construct (see “Experimental Procedures” and Ref. 37). Briefly, adenosine type 1 receptor (A₁R) was fused to the N terminus of wild type or mutant Gα_i using the SPASM module. At equivalent expression levels, measurements were performed in the presence and absence of the adenylyl cyclase activator, forskolin (Fsk), and adenosine receptor agonist, N⁶-cyclopentyladenosine in live cells (Fig. 5c). As expected, Fsk addition increased cAMP levels compared with basal for all systems. However, the relative magnitude of this increase differs between mutants and wild type (Fig. 5c, dashed bars), as does the relative reduction of Fsk-stimulated cAMP levels upon agonist addition (Fig. 5c, dashed versus filled bars). Treatment with Fsk alone resulted in a 1.6, 1.2, 0.4, and −0.3-fold increase in cAMP levels for wild type, F195L, D333A, and L32A mutants, respectively, compared with untransfected cells (Fig. 5c, dashed bars). The reduced basal cAMP levels for D333A and L32A compared with untransfected and wild type indicate an enhanced level of G_i activity for these mutants even in the absence of receptor stimulation (agonist free conditions; Fig. 5c, open bars). Furthermore, for L32A agonist addition had little effect on Fsk-stimulated cAMP levels indicating that this mutant, and to a lesser extent D333A, are constitutively active and do not require agonist stimulated receptor to exert their effect on adenylyl cyclase. The constitutive activities of L32A and D333A were also supported by independent PTX experiments. PTX inhibits GPCR-mediated activation of G_i (47). The cAMP levels for D333A and L32A mutants were much lower than that for wild type even after PTX inhibition (Fig. 5, d and e). We note that D333A displays more moderate activity than L32A in the absence of receptor agonist (Fig. 5c). This is consistent with its predicted reduced domain opening activity relative to L32A (Fig. 5a). However, it is important to note that our accessible simulation time (5 × 80 ns) likely provides only a partial characterization of these rare events for such mutants. In such cases, enhanced sampling methods, such as accelerated MD, may provide additional insight as we have previously demonstrated (3).

Binding of the nonhydrolyzable GTP analogue [³⁵S]GTPγS (48) to Gα_i was used to compare nucleotide binding to L32A and WT. Steady state levels of [³⁵S]GTPγS binding were the same in both L32A and WT, but the rate of association at 25 °C was faster in the L32A (t_½ = 12.9 ± 2.6 min) than the WT (t_½ = 19.1 ± 2.5 min; p = 0.04, paired t test) (Fig. 5f). In an additional experiment at 37 °C using 0.4 nm [³⁵S]GTPγS, rates of association were faster, but a similar difference was seen between L32A (t_½ = 1.8 min) and WT (t_½ = 5.3 min). These results are consistent with both cAMP assays (Fig. 5c) and MD simulations (Fig. 5a) and reveal the faster GTP binding kinetics of L32A.

Discussion

Our extensive MD simulations predicted nucleotide-dependent modes of motion and internal dynamic coupling of functional regions including SI, SII, SIII, PL, and HD. Correlation network analysis characterized the conserved bilobal dynamic substructure of RasD reminiscent of that observed in Ras itself. Nucleotide turnover led to a modulation of the coupling between these substructures with an overall dynamical tightening in the GTP state and enhanced HD-RasD couplings in the GDI state. Network path analysis and subsequent mutant simulations highlighted residues of potential importance for the coordination of receptor and nucleotide-binding site to the RasD-HD interface. In particular, the on-path mutation D333A displayed disrupted dynamic coupling between distal functional sites, whereas L32A, F332A, and I339A led to an enhanced helical domain opening. Experimental characterization of D333A and L32A revealed constitutive activity in the absence of receptor supporting the functional relevance of these allosteric mutations. Mutations of the additionally highlighted Phe³³² and Ile³³⁹ have been shown previously to result in enhanced spontaneous rates of nucleotide exchange (13, 17).

Recent alanine scanning mutagenesis and thermostability assays by Sun et al. (46) identified clusters of hydrophobic residues that confer differential stability to GDP-, GTPγS-, and rhodopsin-bound Gα_i1. In particular, residues in α5 (most notably Phe³³⁶, which is equivalent to our Phe³³²), α1 (including Ile⁴⁹, Gln⁵², and Met⁵³), and β1 (Leu³⁸ equivalent to Leu³⁴, which is a neighboring residue to our Leu³²) were found to confer greater thermal stability to GDP- and GTPγS-bound states. Importantly, F336A was revealed to be the only substitution that resulted in both loss of stability and altered nucleotide binding kinetics. Using independent biophysical modeling, we report here that this substitution results in increased domain opening rates. This provides a clear structural dynamic perspective consistent with the previous finding that this mutation increases the rate of nucleotide release (17). In a similar manner, we report that the novel L32A mutation results in enhanced helical domain opening, increased nucleotide binding rates, and constitutive activity in the absence of receptor.

Using differential contact analysis of Gα crystal structure subsets, Flock et al. (49) recently suggested that structural contacts between α1 and α5 act as a “hub” for Gα allosteric activation. In this model, activation is mediated by the breaking of contacts between α5 and α1, leading to an increased flexibility of α1 that promotes GDP release. The allosteric importance of α5 was also highlighted in recent long time scale MD simulations by Dror et al. (10). These simulations suggested that α5 displacement upon receptor binding results in an increased flexibility of the β6-α5 loop. This loop, located at the N terminus of α5, coordinates the guanosine moiety of a bound nucleotide. Interestingly, Flock et al. state that residues contacting the guanosine moiety, including the β6-α5 “are not extensively reorganized during Gα activation.” In both the Flock et al. and Dror et al. models, α5 acts as the primary initial conduit of information transfer between the receptor and nucleotide binding sites. The models differ in that Dror et al. propose that flexibility differences of the β6-α5 loop complete the connection to the guanosine moiety, whereas Flock et al. propose that increased α1 dynamics is the primary determinant of allosteric coupling. Our path analysis results support the importance of α5 in general and the β6-α5 loop in particular (Dror et al. model). However, we provide new evidence for a dominant alternate allosteric coupling route through β1 that directly links from receptor to the phosphate coordinating P-loop. Both the C-terminal of α5 and the N-terminal β1 are known GPCR binding interfaces. The increased dynamics of both regions upon receptor binding were also evident in earlier hydrogen/deuterium exchange data (7). Moreover, our analysis of the structural dynamic effects of mutations in these regions reveals the novel role of β1 together with β2, β3, P-loop, and SI in the regulation of domain opening that is critical for nucleotide exchange.

More frequent RasD-HD domain separation has previously been suggested to underlie the self-activation of the G protein GPA1 from Arabidopsis thaliana (9). GPA1 is permanently activated, has enhanced nucleotide exchange rates, and displays enhanced domain opening in simulations relative to Gα_i. Intriguingly, investigations of chimeric proteins established that the HD αA helix of GPA1 is almost entirely responsible for this enhanced activation. We note that the αA helix spans the two major HD communities (Fig. 3, b and c) and that perturbations to αA have the potential to effect dynamic couplings in the entire HD region. Collectively, our mutational analysis and the GPA1 chimeric analysis indicate that sites distant from regions involved in binding to receptors, effectors, and nucleotides can perturb the structural dynamics and function of G proteins.

Our results indicate that network analysis of dynamic couplings from multiple replicate MD simulations is a promising method to delineate features of protein allostery. Similar network approaches have been successfully applied to a number of important biological systems (3, 34, 50–54). The major improvement in our current implementation versus our previous work (3, 52, 53) and that of others is the use of many multiple replicate trajectories instead of results from single simulations. This reduces statistical errors in the calculated cross-correlation matrix and resulting correlation network and importantly allows for a more robust statistical assessment of within state and between state dynamic coupling differences. It is important to note that this widely applicable approach provides structural and dynamic insights that are not immediately available from accumulated crystal structures or individual pairs of trajectories. Furthermore, combining this approach with targeted computational and experimental mutagenesis lays the foundation for dissecting the dynamic consequences of disease-associated mutations and the potential generality of allosteric coupling mechanisms in related GTPase and ATPase systems.

Author Contributions

B. J. G., X.-Q. Y., S. S., and J. R. T. designed the study. X.-Q. Y. and B. J. G. performed and analyzed the MD simulations. R. M. and N. W. G. performed and analyzed the experiment. X.-Q. Y., B. J. G., and L. S. developed methods for the computational modeling and analysis. All authors reviewed the results and wrote the manuscript.