Corepressive interaction and clustering of degrade-and-fire oscillators

Abstract

Strongly nonlinear degrade-and-fire (DF) oscillations may emerge in genetic circuits having a delayed negative feedback loop as their core element. Here we study the synchronization of DF oscillators coupled through a common repressor field. For weak coupling, initially distinct oscillators remain desynchronized. For stronger coupling, oscillators can be forced to wait in the repressed state until the global repressor field is sufficiently degraded, and then they fire simultaneously forming a synchronized cluster. Our analytical theory provides necessary and sufficient conditions for clustering and specifies the maximum number of clusters that can be formed in the asymptotic regime. We find that in the thermodynamic limit a phase transition occurs at a certain coupling strength from the weakly clustered regime with only microscopic clusters to a strongly clustered regime where at least one giant cluster has to be present.

I. INTRODUCTION

Many gene regulatory networks contain negative feedback loops as their core elements [1]. The negative feedback provides robustness and noise resistance to signaling pathways [2]. They also lie at the center of many natural rhythmic circuits (such as circadian clocks [3]) and synthetic gene oscillators [4–6]. In our recent work [7] the delayed negative feedback was identified as the mechanism of oscillations in the synthetic two-gene oscillator [5]. It is well known that delayed autorepression can lead to oscillatory gene expression even with only a single regulatory element [8–12]. Typically the period of delay-induced oscillations is comparable with the delay time, and thus this mechanism seemingly could not explain rather slow oscillations observed in gene circuits. However, it turns out that in a strongly nonlinear regime, the period of oscillations is determined by the rate of enzymatic degradation of the repressor protein and therefore can be arbitrarily longer than the transcriptional and translational delay. The essential mechanism of oscillations in this circuit is based on the alternation of two regimes: slow degradation of repressor protein, and the fast production of the repressor (firing) that occurs only when the repressor is degraded below a certain critical concentration; hence we termed these sawtooth-like oscillations “degrade-and-fire” (DF) in analogy with integrate-and-fire oscillations in neuronal circuits. Bacterial cells containing the DF circuit demonstrated robust oscillations, but due to cell-to-cell variability and stochastic effects, in the absence of cell-cell communication the bacterial colony quickly becomes desynchronized. In our subsequent work [13] we succeeded in synchronizing gene oscillators across the bacterial colony; however, the synchronized regime was achieved with a different circuit design that incorporated a quorum-sensing machinery producing small-molecule Acyl-Homoserine Lactone (AHL), which served as signaling element necessary for cell-cell synchronization.

In this paper we study synchronization of DF oscillators through a purely co-repressive interaction. To enable analytical calculations, we replace the original nonlinear delay-differential model of the DF oscillator [7] by a discontinuous piecewise linear model that assumes that the concentration x degrades from the maximum value (which can be scaled to 1) linearly with unit rate, ẋ= −1 (mimicking enzymatic decay with high enzyme affinity), until it reaches the (small) threshold value η > 0, after which repressor concentration x is immediately reset to 1 (“fire”), and the process repeats. It is easy to see that the protein concentration oscillates with period 1 − η. This model closely resembles the classical “integrate-and-fire” (IF) neuron model, which has been extensively studied in the literature [14–17]. We introduce global co-repressive coupling of DF oscillators by assuming that each DF oscillator increases the repressor field of all other oscillators in proportion to its own repressor field. Equivalently, it can be interpreted as if all DF oscillators contribute their respective repressor concentrations to a global “repressor field,” that in turn is added to the repressor field of individual oscillators and therefore delays their firing. This mechanism is qualitatively similar to the inhibitory coupling of IF neurons that has been studied by Ernst et al. [17]. However, the important difference is that the oscillators are coupled all the time, and not just during the firing events, and as we see below, the dynamics of co-repressive synchronization of DF oscillators is fundamentally different from those of inhibitory coupled IF neurons. In particular, a critical value of coupling strength exists at which a phase transition from the no-clustering regime to the strong clustering regime occurs.

Consider a population of N DF oscillators coupled through a common repressor field. We postulate that the dynamics of the concentration of repressor protein x_i is given by the following rules:

1. If positive, x_i degrades linearly with rate 1, i.e., ẋ_i=−1, or remains constant if it has reached 0,

2. When the locally averaged concentration χ_i(t) = (1−ε)x_i(t) + εX(t) [where $X(t)=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i(t)}$and 0 ≤ ε ≤ 1 is the coupling strength parameter] reaches threshold η, the ith oscillator fires, and its concentration is reset to 1, i.e., x_i(t+) = 1.

With these simple evolution rules, one can readily see that all oscillators must fire indefinitely (i.e., there cannot be “oscillator death” regime for any of the oscillators). Indeed, starting from an arbitrary configuration ${\{x_i\}}_{i=1}^N$ for which all χ_i > η, all concentrations decay toward 0 with time (those that have reached x_i = 0, remain at zero) and so do all χ_i. Thus the oscillator with the lowest x_i (possibly more than one if several oscillators have identical concentrations x_i) eventually fires when the corresponding χ_i reaches η. After that, the oscillator j with new lowest x_j has to fire when its χ_j reaches η, and so on. It is also clear that if any two oscillators in a population are in sync at certain time t_*, i.e., x_i = x_j, they will remain in sync for all t > t_*. What is not obvious, however, is under which conditions oscillators that are initially out of sync will synchronize in the course of the dynamics, and what the properties of the resulting clusters are. To answer these questions, we begin with the simple case of two oscillators.

II. INTERACTION OF TWO DF OSCILLATORS

In this case oscillator i (i = 1,2) fires when χ_i (1−ε/2)x_i+εx_3−i/2=η. Without loss of generality, we can assume that initially one oscillator has just fired [i.e., (x₁, x₂) = (x, 1) with η < x ≤ 1] and denote t_f (x) > 0 the firing time associated with this configuration. The dynamics can be described through the return map R between ordered concentration pairs just after firings, (x,1) ↦ R(x,1) := (1 − t_f (x),1).

The two-dimensional dynamics of two DF oscillators is contained in a parameter-dependent subset of the unit square [0,1]² (Fig. 1). For ε = 0, firing occurs when either of the individual concentrations x_i = χ_i touches the threshold η. A simple computation shows that R²(x,1) = (x,1) for all x; i.e., we have a continuum of periodic orbits equivalent to the rigid rotation on a two-dimensional torus [Fig. 1(a)].

FIG. 1.

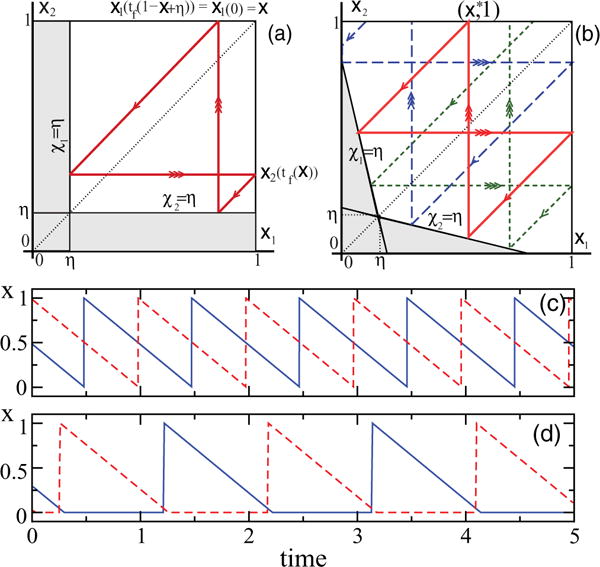
(Color online) (a, b) Typical phase trajectories of two coupled DF oscillators (solid red line indicates periodic orbits and dashed blue and green lines two transients). Simple arrows indicate motions between firings when both concentrations decay with rate 1. Triple arrows denote firings when the trajectory jumps from critical line χ_i = η to x_i = 1. (a) ɛ = 0, every trajectory is periodic. (b) ɛ > 0, for every initial condition except x₁ = x₂ the system asymptotically converges to a unique periodic trajectory passing through (x^*,1), where x^* = 1 − 2(1 − η)/(4 – ɛ) (thick red line). (c, d) time series of two coupled DF oscillators for η = 0.01 and different values of ɛ: (c) ɛ = 0.01; (d) ɛ = 0.5.

For ε > 0, the dynamics changes drastically, as expected. Instead of a continuum of neutral periodic orbits, a single stable periodic orbit emerges that attracts all trajectories, except for the unstable periodic orbit lying on the diagonal x₁= x₂ [Fig. 1(b)]. These are direct consequences of Lemmas 2 and 3 below. Furthermore, it can be shown that a unique and globally stable periodic orbit exists in arbitrary systems of two coupled DF oscillators with any monotonous degradation of both concentrations. Note that this result implies a somewhat unexpected corollary that two initially distinct oscillators never synchronize and always remain distinct. As seen from Fig. 1(c) and 1(d), the two oscillators in the asymptotic regime are always in antiphase, and, for large ε, one oscillator remains repressed (x_i = 0) almost the entire time when the other repressor is present (more precisely, it fires when the other concentration reaches the small value 2η/ε) and vice versa.

III. MANY COUPLED DF OSCILLATORS

Now we turn to the analysis of the clustering dynamics of a population of N co-repressively coupled DF oscillators. Before we proceed with analytical results, we illustrate the typical behavior of the system numerically. Figure 2 shows the time series of 50 oscillators with initially distinct values of x for η = 0.01 and different values of the coupling parameter ε. For small ε = 0.01 [Fig. 2(a)], all oscillators fire before they ever reach zero, and so they remain distinct (no clustering). For larger ε = 0.03 [Fig. 2(b)] some oscillators reach zero, and some of them (not all) synchronize, and thus asymptotically, only eight clusters remain. Note that this number is not universal, as it depends on specific initial conditions. For ε = 0.05 [Fig. 2(c)], only two clusters remain. Their “weights,” however, are not equal, in this example one cluster contains 24 oscillators, and another 26 oscillators. Again, this weight distribution is nonuniversal. And for very large ε = 0.5 [Fig. 2(d)] oscillators produce the repressor protein in almost exact antiphase, one repressor is present, and the other one is absent.

FIG. 2.

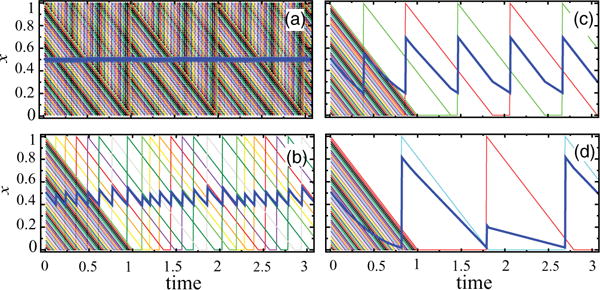
(Color online) Typical time series of 50 coupled DF oscillators and of their mean value X(t) (thick/blue line) for η = 0.01 and different values of ɛ: (a) 0.01; (b) 0.03; (c) 0.05; (d) 0.5.

By grouping oscillators with identical value of x_i into one cluster, the population dynamics can be described via ${\{(n_k,x_k)\}}_{k=1}^K$ where n_k ∈ {1,…,N} denotes the size of the cluster k and x_k the corresponding repressor concentration (K ⩾ N is the total number of clusters). In this viewpoint the cluster size distribution {n_k} obviously remains unaffected in time unless two clusters k and k′ fire together.

As before, we consider the map between consecutive firings. Any ordering in {(n_k,x_k)} is irrelevant because of the permutation symmetry in this system. However, it is more convenient to deal with ordered values of x_k. Thus we assume that 0 < x₁ < x₂ <⋯< x_K−1 < x_K=1. Given {n_k}, this defines the state configuration set where the firing map $R\equiv R_{\{n_k\}}$ is effectively defined, viz., ${\mathcal{T}}_{\{n_k\}}=\{(x_1,\dots ,x_K):0<x_1<\cdots <x_K=1\text{ and }(1-\epsilon )x_1+\frac{\epsilon }{N}{\displaystyle {\sum }_{k=1}^K{n}_k{x}_k>\eta }\}$. In order to maintain the ordering of protein concentrations in time, we must include cyclic permutations of indices in the firing map dynamics. Similar considerations have been used in the analysis of the population dynamics analysis in [15]. The absence of clustering requires that, when starting in ${\mathcal{T}}_{\{n_k\}}$, the after-firing configuration has to lie in ${\mathcal{T}}_{\{n_k+1\}}$ (where all indices are understood mod K), and this should hold for each k = 1,…,K_per where K_per is the minimal size distribution period. This property globally holds in state configuration sets provided that the coupling strength is small enough.

Lemma 1

$R_{\{n_k\}}{\mathcal{T}}_{\{n_k\}}\subset {\mathcal{T}}_{\{n_k+1\}}$ for all k = 1,…,K_per iff

$${\epsilon }_{\eta }\le \underset{k=1,\dots ,K_{\mathrm{per}}}{min}\frac{N}{N-n_k-n_{k+1}}\text{where }{\epsilon }_{\eta }:=\epsilon /\eta .$$ (1)

In particular, for ε_η < N/(N − 2), which is the minimal right-hand side in (1) over all cluster distributions {n_k}, no clustering can ever occur, independently of the initial configuration. Notice that N/(N − 2) > 1 and → 1 as N → ∞. Lemma 1 is rigorously proven in Appendix A.

The nonclustering condition (1) can be intuitively understood as follows. The only way two clusters can merge is when one cluster reaches zero (collapses) and remains at zero at least until the following cluster also reaches zero. It is easy to see that in the worst case scenario two clusters 1 and 2 should be very close to zero when the other K − 2 clusters are very close to 1. In the limit x_1,2 → 0,x₃,…,x_K →1, after x₁ has collapsed, the value of x₂ is equal to [N − ε_η(N − n₁ − n₂)]/(Nε_η) when χ₁ reaches η, and in order to avoid merging of n₁ and n₂, this value has to be positive. Of course, the same condition has to be satisfied for all consecutive pairs n_k,n_k+1, hence the minimum in inequality (1).

Independently of (1), we may ask about the fate of the trajectories for which no clustering occurs. Since the sequence of merging events is always finite, this actually would determine every possible asymptotic regime. In absence of clustering, the firing map in ${\mathcal{T}}_{\{n_k\}}$ becomes $R_{\{n_k\}}^{\ast }(x_1,\dots ,x_K):=(x_2-t_f,\dots ,x_K-t_f,1)$, where t_f still denotes the firing time. [This map is actually K − 1-dimensional because ${(R_{\{n_k\}}^{\ast }x)}_K=x_K=1$.] Since the image $R_{\{n_k\}}^{\ast }x$ belongs to ${\mathcal{T}}_{\{n_{k+1}\}}$, one needs to iterate further until the point returns back to ${\mathcal{T}}_{\{n_k\}}$; hence the dynamics to study is the return map $R_{\{n_{k+K_{\text{per}}-1}\}}^{\ast }\circ \cdots \circ R_{\{n_{k+1}\}}^{\ast }\circ R_{\{n_k\}}^{\ast }$. It can be shown (see Appendix B) that this map is always a pure contraction.

Lemma 2

For every ${\{n_k\}}_{k=1}^K$and 0 < ε ≤ 1, there is a norm in ${{ℝ}^K}^{-1}$for which $R_{\{{n_k}_{+K\text{per}-1}\}}^{\ast }\circ \cdots \circ R_{\{n_{k+1}\}}^{\ast }\circ R_{\{n_k\}}^{\ast }$ is a global contraction.

It follows that, in absence of clustering, every trajectory initially in ${\mathcal{T}}_{\{n_k\}}$ must approach a unique periodic orbit (whose single element in ${\mathcal{T}}_{\{n_k\}}$ is the fixed point of the return map). More generally, every trajectory in a population of N oscillators must converge to the periodic orbit associated with some {n_k}. Hence, the asymptotic cluster size distributions and periodic orbits are in one-to-one correspondence. Accordingly, to get asymptotically attainable cluster distributions, it suffices to compute the existence domains of the corresponding periodic orbits. These domains are given by the following statement.

Lemma 3

The periodic orbit in ${\mathcal{T}}_{\{n_k\}}$ exists iff

$${\epsilon }_{\eta }<\zeta (\{n_k\}):=\frac{2N^2}{N^2-{\displaystyle {\sum }_k{n}_k^2}}\frac{1}{1-{min}_k\frac{n_k}{N-n_{k+1}}}.$$ (2)

This claim is proved in Appendix C where we also give the explicit expressions for the periodic orbit. Note that when n_K = N − n₁ (i.e., K = 2), we have ζ({n_k})=+∞, which means that every two-cluster periodic orbit exists for any ε. In particular, for n₁=n₂=1 this observation implies the result for two coupled oscillators presented above.

For K > 2, the critical value ζ({n_k}) is minimal for the (equi-)distribution where all n_k = 1 (in this case K=N), and the corresponding minimum is ζ_c = 2N/(N−2). So all possible periodic orbits exist for ε_η up to ζ_c. For larger ε_η, some periodic orbits disappear, certainly the one associated with equidistribution, and the number of clusters K must eventually be less than N.

A closer look at the formula (2) reveals that when {n_k} is only composed of microscopic clusters, i.e., when ${\displaystyle {\sum }_k{n}_k^2}=O(N)$, the corresponding critical value ζ({n_k}) approaches 2 in the thermodynamic limit N → ∞. Therefore, such distributions do not perdure asymptotically beyond ε_η ≃ 2 when N is large, and at least some of the clusters size n_k reach O(N) in the course of time. Moreover, distributions that contain macroscopic cluster(s) (i.e., n_k ≃ ρ_kN with ρ_k > 0 for some k) all have critical value ζ({n_k}) larger than 2 in the thermodynamic limit. Thus, there is a sharp transition in the system at a certain ε_c = ζ_c (which is close to 2η for large N), from a dynamical regime in which all kinds of cluster size distributions may exist asymptotically, to a regime where every asymptotic distribution contains at least one giant O(N) cluster.

IV. MAXIMAL NUMBER OF CLUSTERS

The transition at ε_η = ζ_c can be quantitatively described by estimating the number of asymptotic clusters as a function of ε_η. Since the precise number actually depends on the initial condition and can be as little as 2, the appropriate quantity to compute is the maximal possible number K_max. It can be proven (see Appendix D) that for any given K ⩾ 3 and N ⩾ K (and N ≠ 6 if K = 3), the critical value $\zeta ({\left\{n_k\right\}}_{k=1}^K)$ in (2) reaches its maximum for the distribution consisting of K − 1 unitary clusters of weight n_k = 1 and one big cluster n_K = N − K + 1. In this case, we have

$$\zeta (\{n_k\})={\zeta }_{max}(K)=\frac{2N^2(N-1)}{(K-1)(2N-K)(N-2)},$$

and therefore all distributions with K clusters exist for 0 ≤ ε_η < ζ_max. This immediately yields the maximum number of clusters at a given N and ε_η:

$$\begin{array}{l}{K}_{max}({\epsilon }_{\eta })=N\text{if}{\epsilon }_{\eta }<{\zeta }_c\\ =N-\lfloor \frac{1}{2}+\sqrt{\frac{1}{4}+N(N-1)(1-\frac{{\zeta }_c}{{\epsilon }_{\eta }})}\rfloor \\ \text{if }{\zeta }_c\le {\epsilon }_{\eta }<{\zeta }_{max}(3)\\ =2\text{if }{\epsilon }_{\eta }⩾{\zeta }_{max}(3).\end{array}$$ (3)

This result indicates that a kind of second order phase transition takes place at ε_η = ζ_c with K_max that behaves like $N(1-\sqrt{1-{\zeta }_c/{\epsilon }_{\eta }})$ slightly above the threshold. Formula (3) implies that for each 1 ≤ K≤ K_max(ε_η), there exists a nonempty set of initial conditions that produces a stable periodic trajectory with K clusters. However, the “typical” number of clusters emerging from an arbitrary set of initial conditions can be much less than this upper bound. We performed numerical simulations of the full model with initial conditions randomly selected from the [0,1]^N hypercube. Figure 3 shows that the typical number of clusters for a given ε can be well approximated by the number K_e corresponding to the uniformly distributed initial condition x_i=i/N. However, the number of asymptotic clusters depends strongly on the width of the distribution of initial states. We performed simulations for initial conditions x_i equidistributed between 1 − δ and 1 and found that the number of asymptotic clusters strongly increases as the width of the initial distribution δ gets smaller and approaches the values close to the upper bound K_max [Fig. 3(a), inset].

FIG. 3.

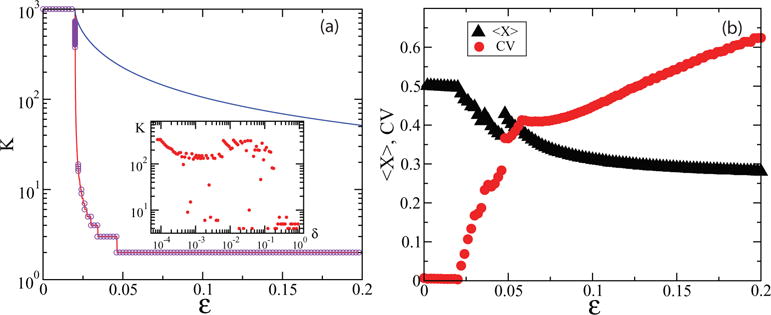
(Color online) (a) Number of clusters in the asymptotic regime for 1000 coupled oscillators with η = 0.01 and 1000 different random initial conditions for each ɛ. The solid blue line indicates the upper bound (3), and the solid red line shows the number of clusters K_e(ɛ) for the uniform initial distribution. Inset: The number of clusters as a function of the initial distribution width δ for ɛ = 0.03; (b) time-averaged mean field 〈X〉 and the coefficient of variation CV as a function of ɛ for δ = 0.01 and firing noise η = 0.05 for 10 000 oscillators and 500 periods.

We addressed the robustness of the clustering transition against noise. DF oscillators are most sensitive to noise during the firing, so we modeled this by resetting x_i to a random number uniformly distributed in [1 − η, 1 + η] (η characterizes the noise strength). In this case, the clusters are not “exact,” since after firing identical x_i become different; however, for small noise groups of oscillators remain closely correlated. We can characterize the degree of correlation by the coefficient of variation of the mean field X(t), CV = [〈X²〉 − 〈X〉²]^1/2/〈X〉. CV is small in the nonclustered regime but increases rapidly as soon as the clustering occurs [Fig. 3(b)].

V. CONCLUDING REMARKS

We presented an analytically solvable model of co-repressively coupled degrade-and-fire oscillators in a strongly nonlinear regime. At a certain coupling strength this model exhibits a phase transition from a regime when any cluster distributions including the nonclustered state can be attained to the regime of strong clustering characterized by the appearance of at least one giant O(N) cluster. This phenomenology is reminiscent of the synchronization in the Kuramoto model of globally coupled oscillators [18] or populations of integrate-and-fire neurons [14–17]; however, the details of the transition are different. In particular, in the Kuramoto and IF models with identical oscillators synchronization occurs for any positive coupling strength, while in the array of co-repressively coupled DF oscillators the nonclustered regime is stable for sufficiently small coupling strength.

Our model neglected the variability in parameters of individual oscillators. It also ignores the spatial localization of coupling or the time delays in exchange of the repressor concentrations among the oscillators. It is well known that these effects may play significant role in the synchronization phenomena [17,19,20]. We plan to address these effects in our future work. The experimental realization of coupled gene oscillators [13] incorporated a different (co-excitatory) mechanism of coupling through a quorum-sensing mechanism. However, we believe that co-repressive coupling may also be realized experimentally, if, for example, oscillators produce an enzyme that degrades a freely diffusing inducer or the quorum sensing molecule activates a repressor protein. Our results demonstrate that a strong clustering can be expected in this case, and large out-of-phase synchronized clusters are likely to emerge.

APPENDIX A: PROOF OF LEMMA 1

Recall that $R_{\left\{n_k\right\}}$ denotes the mapping in the ordered configuration set ${\mathcal{T}}_{\left\{n_k\right\}}$ that defines the new (ordered) configuration after firing. Recall also that ε_η := ε/η.

We first prove that (1) is a sufficient condition. Assume that initially ${\left\{x_k\right\}}_{k=1}^K\in {\mathcal{T}}_{\left\{n_k\right\}}$. Prior to firing, we have ${\chi }_1(t)=(1-\epsilon )x_1+\frac{\epsilon }{N}{\displaystyle {\sum }_{k=1}^K{n}_k{x}_k-t}$. Accordingly, the quantity χ₁ reaches η at time t_f defined by

$$t_f:={\chi }_1(0)-\eta =x_1+\frac{\epsilon }{N}{\displaystyle \sum _{k=2}^K{n}_k(x_k-x_1)-\eta .}$$

The quantity t_f is the actual firing time provided that x₁(t_f) ⩾ 0, viz., t_f ≤ x₁. The latter is equivalent to

$${\epsilon }_{\eta }{\displaystyle \sum _{k=2}^K{n}_k(x_k-x_1)\le N.}$$ (A1)

Using that 0 ≤ x_k − x₁ ≤ 1 for state configurations in ${\mathcal{T}}_{\left\{n_k\right\}}$, a sufficient condition for this inequality is ${\epsilon }_{\eta }\le \frac{N}{N-n_1}$. Applying cyclic permutations, we conclude that, for every configuration in any of the ${\mathcal{T}}_{\left\{n_{k+\mathit{\ell }}\right\}}$, the lowest cluster of oscillators fires before (or exactly when) it reaches 0 if

$${\epsilon }_{\eta }\le \underset{i=1,\dots ,K}{min}\frac{N}{N-n_i}.$$ (A2)

When this condition is violated, cluster configurations with all coordinates x_k, k⩾2, sufficiently close to 1 and x₁ sufficiently close to 0 satisfy the inequality ${\chi }_1(x_1)=\frac{\epsilon }{N}{\displaystyle {\sum }_{k=2}^K{n}_k(x_k-x_1)⩾\eta }.$ Accordingly, the concentration x₁ reaches 0 before χ₁ reaches η, and, to prevent clustering, we have to make sure that χ₂(t_f) > η i.e., t_f < x₂ if t_f still denotes the time when x₁ fires. For t⩾x₁, we have ${\chi }_1(t)=\frac{\epsilon }{N}{\displaystyle {\sum }_{k=2}^K{n}_k(x_k-t)}$. The condition χ₁(t_f) = η defines the time firing as follows $t_f=\frac{1}{N-n_1}({\displaystyle {\sum }_{k=2}^K{n}_k{x}_k-N{\eta }_{\epsilon }})$, where η_ɛ=η/ɛ. Now, the inequality t_f < x₂ turns out to be equivalent to

$${\displaystyle \sum _{k=3}^K{n}_k{x}_k-N{\eta }_{\epsilon }<(N-n_1-n_2)x_2,}$$ (A3)

which is certainly satisfied when ${\displaystyle {\sum }_{k=3}^K{n}_k{x}_k-N{\eta }_{\epsilon }}\le 0$. Solving this inequality for all permutations {n_k+l} gives the desired condition (1) on the coupling parameter.

We now show that $R_{\left\{n_k\right\}}$ maps ${\mathcal{T}}_{\left\{n_k\right\}}$ into ${\mathcal{T}}_{\left\{n_{k+1}\right\}}$ when (1) holds. This consists in checking three conditions:

1. First, we have x₂ − t_f > 0 either because x₁ − t_f ⩾0 and x₂ > x₁ or simply because of (A3) when (A2) fails.

2. Then, the strict ordering x₂ < ⋯ < x_K−1<1 implies a similar ordering for the coordinates of R_{nk}x where x = (x₁,…,x).

3. Finally, we have

   $$\begin{array}{l}(1-\epsilon ){\left(R_{\left\{n_k\right\}}x\right)}_1+\frac{\epsilon }{N}{\displaystyle \sum _{k=1}^K{n}_{k+1}{\left(R_{\left\{n_k\right\}}x\right)}_k}\\ =(1-\epsilon )(x_2-t_f)+\frac{\epsilon }{N}\left({\displaystyle \sum _{k=1}^{K-1}{n}_{k+1}(x_{k+1}-t_f)+n_1}\right)\\ =(1-\epsilon )(x_2-t_f)+\frac{\epsilon }{N}\left[{\displaystyle \sum _{k=2}^K{n}_k(x_k-t_f)+n_1}\right]\\ >(1-\epsilon )(x_1-t_f)+\frac{\epsilon }{N}{\displaystyle \sum _{k=1}^K{n}_k(x_k-t_f)=\eta },\end{array}$$ (A4)

   where we used x₂ > x₁ and 1 ⩾ x₁ – t_f to obtain the inequality. Thus the last inequality in the definition of ${\mathcal{T}}_{\left\{n_{k+1}\right\}}$ is satisfied for $R_{\left\{n_k\right\}}^{\ast }$, and the proof is complete.

Finally, that (1) is a necessary condition is easy to check. Indeed, when ${\epsilon }_{\eta }>\frac{N}{N-n_1-n_2}$, initial conditions in ${\mathcal{T}}_{\left\{n_k\right\}}$ with x₁ and x₂ sufficiently close to 0 and the other x_i close enough to 1 simultaneously violate (A1) and (A3). Accordingly, the clusters n₁ and n₂ fire simultaneously, and a K′-cluster distribution results with K′≤ K−1. In particular, the image $R_{\left\{n_k\right\}}x$ cannot belong to ${\mathcal{T}}_{\left\{n_{k+1}\right\}}$. The proof is complete.

APPENDIX B: PROOF OF LEMMA 2

Recall that $R_{\left\{n_k\right\}}^{\ast }(x_1,\dots ,x_K):=(x_2-t_f,\dots ,x_K-t_f,1)$ denotes the firing map acting in ${\mathcal{T}}_{\left\{n_k\right\}}$ in the absence of clustering. The proof of Lemma 2 essentially consists in showing that, due to the dissipative nature of the coupling, all eigenvalues of the linear parts of each map $R_{\left\{n_k\right\}}^{\ast }$ lie inside the unit circle.

We first prove contraction for the individual map $R_{\left\{n_k\right\}}^{\ast }$. Its form depends upon whether the initial condition x = (x₁,…,x_K) satisfies (A1) or not.

Stability in the domain where x satisfies (A1)

When only considering the first K − 1 coordinates, we obtain

$${\left(R_{\left\{n_k\right\}}^{\ast }x\right)}_k=x_{k+1}-t_f=\eta +x_{k+1}-x_1-\frac{\epsilon }{N}{\displaystyle \sum _{\mathit{\ell }=2}^K{\alpha }_{\mathit{\ell }}(x_{\mathit{\ell }}=x_1)}$$

for all k = 1,…,K − 1. Applying the change of variable x ↦ y defined by

$$\begin{array}{l}{y}_k=\{\begin{array}{lll}{x}_k-x_{k+1}\hfill & \text{if}\hfill & k=1,\dots ,K-2\hfill \\ x_{K-1}\hfill & \text{if}\hfill & k=K-1\hfill \end{array}\iff \\ x_k={\displaystyle \sum _{\mathit{\ell }=k}^{K-1}{y}_{\mathit{\ell }},}k=1,\dots ,K-1\end{array}$$

the linear part of the previous expression becomes $y\mapsto L_{\left\{n_k\right\}}y$ where

$${(L_{\left\{n_k\right\}}y)}_k=\{\begin{array}{lll}{y}_{k+1}\hfill & \text{if}\hfill & k=1,\dots ,K-2\hfill \\ -{\displaystyle {\sum }_{\mathit{\ell }=1}^{K-1}{y}_{\mathit{\ell }}\left(1-\frac{\epsilon }{N}{\displaystyle {\sum }_{j=\mathit{\ell }+1}^K{n}_j}\right)}\hfill & \text{if}\hfill & k=K-1.\hfill \end{array}$$

(We used ${\displaystyle {\sum }_{j=2}^{K-2}{n}_j}{\displaystyle {\sum }_{\mathit{\ell }=1}^{j-1}{y}_{\mathit{\ell }}}={\displaystyle {\sum }_{\mathit{\ell }=1}^{k-2}{y}_{\mathit{\ell }}}{\displaystyle {\sum }_{j=\mathit{\ell }+1}^{k-1}{n}_j}$.) The corresponding (K − 1) × (K −1) matrix $L_{\left\{n_k\right\}}$is a companion matrix whose characteristic polynomial $P_{\left\{n_k\right\}}$immediately follows by reading the bottom line, namely,

$$P_{\left\{n_k\right\}}(\mathrm{\lambda })={\displaystyle \sum _{\mathit{\ell }=0}^{K-1}{\mathrm{\lambda }}^{\mathit{\ell }}\left(1-\frac{\epsilon }{N}{\displaystyle \sum _{j=\mathit{\ell }+2}^K{n}_j}\right)}.$$

The polynomial coefficients $1-\frac{\epsilon }{N}{\displaystyle {\sum }_{j=\mathit{\ell }+2}^N{n}_j}$ are positive and decaying (as l decreases) when 0 < ɛ ≤ 1. By a classical result in numerical analysis (see, e.g., Ref. [21], p. 116), this property implies that $P_{\left\{n_k\right\}}$ is Schur stable, viz., all its roots lie inside the unit disk.

Stability in the domain where x does not satisfy (A1)

In this case, the map reads

$$(R_{\left\{n_k\right\}}^{\ast }x)k=x_{k+1}-\frac{N}{N-n_1}\left({\displaystyle \sum _{\mathit{\ell }=2}^K{n}_{\mathit{\ell }}{x}_{\mathit{\ell }}-{\eta }_{\epsilon }}\right)$$

for all k = 1,…,K − 1. After applying the same change of variable as before the corresponding linear part becomes

$$\left(L_{\left\{n_k\right\}}^{\prime }y\right)k=\{\begin{array}{lll}{y}_{k+1}\hfill & \text{if}\hfill & k=1,\dots ,K-2\hfill \\ -\frac{1}{N-n_1}{\displaystyle {\sum }_{\mathit{\ell }=2}^{K-1}{y}_{\mathit{\ell }}{\displaystyle {\sum }_{j=2}^{\mathit{\ell }}{n}_j}}\hfill & \text{if}\hfill & k=K-1,\hfill \end{array}$$

now based on ${\displaystyle {\sum }_{j=2}^{K-1}{n}_j{\displaystyle {\sum }_{\mathit{\ell }=j}^{K-1}{y}_{\mathit{\ell }}}}={\displaystyle {\sum }_{\mathit{\ell }=2}^{K-1}{y}_{\mathit{\ell }}{\displaystyle {\sum }_{j=2}^{\mathit{\ell }}{n}_j}}$. The associated characteristic polynomial in this case reads

$$P_{\left\{n_k\right\}}^{\prime }(\mathrm{\lambda })=\frac{1}{N-n_1}{\displaystyle \sum _{\mathit{\ell }=1}^{K-1}{\mathrm{\lambda }}^{\mathit{\ell }}{\displaystyle \sum _{j=2}^{\mathit{\ell }+1}{n}_j}.}$$

As before, the polynomial ${\mathrm{\lambda }}^{-1}{P}_{\left\{n_k\right\}}^{\prime }(\mathrm{\lambda })$ has positive and decaying coefficients; hence all roots of $P_{\left\{nk\right\}}^{\prime }(\mathrm{\lambda })$ lie inside the unit disk.

Proof that the return map is a contraction

Given that both spectral radii $r(L_{\left\{n_k\right\}})$ and $r(L_{\left\{n_k\right\}}^{\prime })$ are less than 1, the end of the proof is quite standard. Take any norm |·| in ℝ^K−1. We have $r(L_{\left\{n_k\right\}})=\underset{t\to \infty }{\text{lim}}|L_{\left\{n_k\right\}}^t{|}^{1/t}$ (see, e.g., Ref. [22]). Take δ > 0 sufficiently small so that $r(L_{\left\{n_k\right\}})+\delta <1$ and let t_δ enough be large so that

$${\left|L^t\right|}^{\frac{1}{t}}\le r\left(L_{\left\{n_k\right\}}\right)+\delta ,\forall t⩾t_{\delta }.$$

Consider the analogous ${t^{\prime }}_{\delta }$ for the operator $L_{\{nk\}}^{\prime }$ and take $s_{\delta }=max\{t_{\eta },{t^{\prime }}_{\eta }\}$ [this requires electing δ so that both inequalities $r(L_{\{n_k\}})+\delta <1$ and $r(L_{\{nk\}}^{\prime })+\delta <1$ simultaneously hold]. By choosing $\Vert x\Vert :=|x^{s_{\delta }}{|}^{1/s_{\delta }}$ in ℝ^K−1, we conclude that the linear parts of $R_{\{n_k\}}^{\ast }$ have norm ‖·‖ less than 1, viz., $R_{\{n_k\}}^{\ast }$ is a global contraction.

Finally, the return map $R_{\left\{n_{k+K_{\text{per}}-1}\right\}}^{\ast }\circ \cdots \circ R_{\left\{n_{k+1}\right\}}^{\ast }\circ R_{\left\{n_k\right\}}^{\ast }$ will be contracting for the norm ‖x^s‖^1/s where s is any integer larger than each s_δ of the $R\left\{n_{k+\mathit{\ell }}\right\}$ and δ is such that all these maps are contracting. The proof is complete.

APPENDIX C: PROOF OF LEMMA 3

Lemma 3 is a consequence of existence conditions for the periodic orbit associated with each cluster size distribution {n_k}. This analysis of these conditions directly follows from the explicit computation of periodic orbits coordinates.

Without loss of generality, we study the solution in ${\mathcal{T}}_{\left\{n_k\right\}}$ of the equation

$$R_{\left\{n_{k+K-1}\right\}}^{\ast }\circ \cdots \circ R_{\left\{n_{k+1}\right\}}^{\ast }\circ R_{\left\{n_k\right\}}^{\ast }(x)=x$$ (C1)

for any K-cluster configuration ${\left\{n_k\right\}}_{k=1}^K$. For the sake of notation, we use the symbol R^ℓ instead of $R_{\left\{n_{k+\mathit{\ell }-1}\right\}}^{\ast }\circ \cdots \circ R_{\left\{n_{k+1}\right\}}^{\ast }\circ R_{\left\{n_k\right\}}^{\ast }$ and R⁰ = Id.

Periodic orbits have a property that remarkably simplifies their analysis; namely, all coordinates fire from the same value. In particular, this implies that they either all fire before reaching 0 or all reach 0 before firing. To see this, recall that t_f(x) denotes the firing time for x. The firing map definition obviously implies (R^Kx)_K = 1, but also (R^Kx)_K−1 = 1 − t_f(R^K−1x) since (R^K−1x)_K−1 = 1 and t_f (R^K−1x) is the firing time of the configuration R^K−1x. By repeating the argument for the other coordinates (R^Kx)_k, we easily obtain the following expression:

$${(R^{K}x)}_k=1-{\displaystyle \sum _{\mathit{\ell }=k}^{K-1}{t}_f(R^{\mathit{\ell }}x)},k=1,\dots ,K.$$ (C2)

Together with the periodicity assumption R^Kx=x and the firing map definition, this expression implies

$$\begin{array}{l}{(Rx)}_1-t_f(Rx)={(R^{K}x)}_2-t_f(Rx)-t_f(x)\hfill \\ ={(R^{K}x)}_1-t_f(x)=x_1-t_f(Rx)\hfill \end{array}$$

By induction, we conclude that successive firing levels (R^ℓx)₁ − t_f(R^ℓx) do not depend on l = 0,…,K−1, and the announced alternative follows. To proceed, we consider both cases separately.

Case 1: All coordinates fire before reaching 0

In this case, we assume that t_f(R^ℓx) ≤ (R^ℓx)₁ for all l = 0,…,K−1, and we accordingly solve the equation (C1), i.e., R^K(x) = x.

Using the notation τ_k = x_k+1 − x_k, it is convenient to rewrite the periodic orbit coordinates as follows:

$$x_k=1-{\displaystyle \sum _{\mathit{\ell }=k}^{K-1}{\tau }_{\mathit{\ell }},}k=1,\dots ,K,$$

which in particular yields x_K=1. In addition, periodicity conditions (C1) and (C2) imply

$$t_f(R^{k}x)={\tau }_k,k=1,\dots ,K-1.$$ (C3)

To proceed, we use the assumption $t_f(x)\le x_1$ to rewrite $t_f(x)=x_1+\frac{\epsilon }{N}{\displaystyle {\sum }_{\mathit{\ell }=2}^K{n}_{\mathit{\ell }}(x_{\mathit{\ell }}-x_1)-\eta }$ as follow:

$$t_f(x)=1-{\displaystyle \sum _{\mathit{\ell }=1}^{K-1}{\tau }_{\mathit{\ell }}-{\mathrm{\Delta }}_0},$$

where

$$\begin{array}{l}{\mathrm{\Delta }}_k=\eta -\frac{\epsilon }{N}{\displaystyle \sum _{\mathit{\ell }=2}^K{n}_{\mathit{\ell }+k}({(R^{k}x)}_{\mathit{\ell }}-{(R^{k}x)}_1}),\\ k=0,\dots ,K-1\end{array}$$

Accordingly, the definition of the firing map implies ${(Rx)}_k=x_{k+1}-t_f(x)={\displaystyle {\sum }_{\mathit{\ell }=1}^k{\tau }_k}+{\mathrm{\Delta }}_0$ for all k = 1,…,K and then $t_f(Rx)={(Rx)}_1+\frac{\epsilon }{N}{\displaystyle {\sum }_{\mathit{\ell }=2}^K{n}_{\mathit{\ell }+1}({(Rx)}_{\mathit{\ell }}-{(Rx)}_1)}-\eta ={\tau }_1+{\mathrm{\Delta }}_0-{\mathrm{\Delta }}_1$ since we are assuming t_f(Rx) ≤ (Rx)₁ Repeating this argument inductively, we obtain

$${(R^{\mathit{\ell }}x)}_k={\displaystyle \sum _{j=\mathit{\ell }}^{k+\mathit{\ell }-1}{\tau }_j+{\mathrm{\Delta }}_{\mathit{\ell }-1}},k=1,\dots ,K-\mathit{\ell }$$ (C4)

and

$$t_f(R^{\mathit{\ell }}x)={\tau }_{\mathit{\ell }}+{\mathrm{\Delta }}_{\mathit{\ell }-1}-{\mathrm{\Delta }}_{\mathit{\ell }},\mathit{\ell }=1,\dots ,K-1.$$ (C5)

From equation (C3), it results that ${\mathrm{\Delta }}_{\mathit{\ell }-1}={\mathrm{\Delta }}_{\mathit{\ell }}$ for all l = 1,…, K−1, Which is equivalent to

$$\begin{array}{l}{\displaystyle \sum _{j=2}^K{n}_{j+\mathit{\ell }-1}[{(R^{\mathit{\ell }-1}x)}_j-{(R^{\mathit{\ell }-1}x)}_1]}\\ ={\displaystyle \sum _{j=2}^K{n}_{j+\mathit{\ell }}[{(R^{\mathit{\ell }}x)}_j-{(R^{\mathit{\ell }}x)}_1]}.\end{array}$$

Using again the firing map definition we have

$${(R^{\mathit{\ell }}x)}_k=\{\begin{array}{lll}{(R^{\mathit{\ell }-1}x)}_{k+1}-t_f(R^{\mathit{\ell }-1}x)\hfill & \text{if}\hfill & 1\le k<k\hfill \\ 1\hfill & \text{if}\hfill & k=K,\hfill \end{array}$$

and, together with the relation ${\displaystyle {\sum }_{j=1}^K{n}_{j+\mathit{\ell }-1}=N}$, the previous relation thus simplifies to

$$N[{(R^{\mathit{\ell }}x)}_2-{(R^{\mathit{\ell }}x)}_1]=n_{\mathit{\ell }+1}[1-{(R^{\mathit{\ell }}x)}_1+t_f(R^{\mathit{\ell }}x)],$$

for ℓ = 0,…,K−2. For ℓ = 1,…,K−2 we can use relations (C4) and (C5) to get (R^ℓx)₂−(R^ℓx)₁ = τ_ℓ+1 and (R^ℓx)₁= τ_ℓ+Δ_ℓ−1. Accordingly, the previous relation results in

$${\tau }_{\mathit{\ell }}=\frac{n_{\mathit{\ell }}}{N}(1-{\mathrm{\Delta }}_{\mathit{\ell }}),\mathit{\ell }=2,\dots ,K-1.$$

For ℓ = 0, using the expressions of x₁ and t_f(x) the previous equality becomes

$${\tau }_1=\frac{n_1}{N}(1-{\mathrm{\Delta }}_0).$$

Since all Δ_ℓ = Δ the are equal, we finally get the condensed expression ${\tau }_{\mathit{\ell }}=\frac{n_{\mathit{\ell }}}{N}(1-\mathrm{\Delta })$ for all 1 ,…, K−1.

In order to compute Δ we introduce the latter into the definition of Δ₀ via the coordinates x_k. This gives a first-order equation for Δ, whose solution is

$$\mathrm{\Delta }=\frac{\eta -\epsilon {\sum }_K}{1-\epsilon {\sum }_K},$$

where ${\sum }_K=\frac{1}{N^2}{\displaystyle {\sum }_{k=2}^K{n}_k}{\displaystyle {\sum }_{\mathit{\ell }=1}^{k-1}{n}_{\mathit{\ell }}}$. Direct combinatorics implies

$$N^2={\displaystyle \sum _{k=1}^K{n}_k}{\displaystyle \sum _{\mathit{\ell }=1}^K{n}_{\mathit{\ell }}}=2N^2{\sum }_K+{\displaystyle \sum _{k=1}^K{n}_k^2},$$

showing that ${\sum }_K=\frac{N^2-{\sum }_k{n}_k^2}{2N^2}$. Notice that Δ is well defined when ɛ < 1 since Σ_K < 1. Moreover, we have Δ < 1 when η < 1. From the expression of Δ, we immediately get ${\tau }_k=\frac{n_k(1-\eta )}{N(1-\epsilon {\sum }_K)}.$

To conclude the analysis in the present case, it remains to check the conditions on parameters, for which we have

$$t_f(x)\le x_1\text{and}{R}^{\mathit{\ell }}x\in {\mathcal{T}}_{\left\{n_{k+\mathit{\ell }}\right\}},\mathit{\ell }=0,\dots ,K-1.$$

Using (C4) and (C5), the first inequality amounts to Δ > 0, viz., ${\epsilon }_{\eta }\le \frac{1}{{\sum }_K}$. As for the second conditions, the only nontrivial restriction is (R^ℓx)₁ > 0 for all = 0,…,K−1, since the other ones are automatically satisfied from the definition of R and the nonclustering assumption. Again, (C4) and (C5) show that ${(R^{\mathit{\ell }}x)}_1={\tau }_{\mathit{\ell }}+\mathrm{\Delta }>0$ for all l = 1,…,K−1. For ℓ = 0, we have ${\displaystyle {\sum }_{k=1}^{K-1}{\tau }_k}=(1-\frac{n_k}{N})(1-\mathrm{\Delta })<1$, i.e., x₁ > 0. Summarizing, the periodic orbit passing ${\mathcal{T}}_{\left\{n_k\right\}}$ exists with all coordinates firing before they reach 0 iff

$${\epsilon }_{\eta }\le \frac{1}{{\sum }_K}=\frac{2N^2}{N^2-{\displaystyle {\sum }_k{n}_k^2}}.$$

Case 2: All coordinates reach 0 before firing

This case can only occur when ${\epsilon }_{\eta }>\frac{1}{{\sum }_K}$. We claim that the solution reads

$$x_k=\frac{1}{N}\left[{\displaystyle \sum _{\mathit{\ell }=0}^{k-1}{n}_{\mathit{\ell }}}-\left(1-\frac{{\eta }_{\epsilon }}{{\sum }_K}\right){\displaystyle \sum _{\mathit{\ell }=k+1}^K{n}_{\mathit{\ell }}}\right]$$ (C6)

for all k = 1,…,K − 1 and obviously x_K = 1. To check this assertion, according to (C2), it suffices to verify that

$$t_f(R^{\mathit{\ell }}x)=\frac{1}{N}\left[n_{\mathit{\ell }}+\left(1-\frac{{\eta }_{\epsilon }}{{\sum }_K}\right)n_{\mathit{\ell }+1}\right],\mathit{\ell }=1,\dots ,K-1.$$

We shall indeed show by induction that this relation holds for all k = 0,…,K − 1. Since we now assume that t_f (x) > x₁ we have $t_f(x)=\frac{1}{N-n_1}\left({\displaystyle {\sum }_{k=2}^K{n}_k{x}_k-N{\eta }_{\epsilon }}\right)$. Using (C6) and the definition of Σ_K we obtain

$$\begin{array}{l}N\left({\displaystyle \sum _{k=2}^K{n}_k{x}_k-N{\eta }_{\epsilon }}\right)\\ ={\displaystyle \sum _{k=2}^K{n}_k}{\displaystyle \sum _{\mathit{\ell }=0}^{k-1}{n}_{\mathit{\ell }}}-{\displaystyle \sum _{k=2}^K{n}_k}{\displaystyle \sum _{\mathit{\ell }=k+1}^K{n}_{\mathit{\ell }}}+(\frac{{\displaystyle {\sum }_{k=2}^K{n}_k}{\displaystyle {\sum }_{\mathit{\ell }=k+1}^K{n}_{\mathit{\ell }}}}{{\sum }_K}-N^2){\eta }_{\epsilon }\\ ={\displaystyle \sum _{k=2}^K{n}_k}{\displaystyle \sum _{\mathit{\ell }=0}^{k-1}{n}_{\mathit{\ell }}}-{\displaystyle \sum _{k=3}^K{n}_k}{\displaystyle \sum _{\mathit{\ell }=2}^{k-1}{n}_{\mathit{\ell }}}+\left(\frac{{\displaystyle {\sum }_{k=3}^K{n}_k}{\displaystyle {\sum }_{\mathit{\ell }=2}^{k-1}{n}_{\mathit{\ell }}}-{\displaystyle {\sum }_{k=2}^K{n}_k}{\displaystyle {\sum }_{\mathit{\ell }=1}^{k-1}{n}_{\mathit{\ell }}}}{{\sum }_K}\right){\eta }_{\epsilon }\\ =(N-n_1)(n_0+n_1-\frac{n_1}{{\sum }_K}\eta \epsilon ),\end{array}$$

which gives the desired result for k = 0. The other cases proceed similarly by induction.

The existence conditions now become

$$x_1<t_f(x),t_f(R^{\mathit{\ell }}x)\le {(R^{\mathit{\ell }}x)}_2$$

and

$$R^{\mathit{\ell }}x\in {\mathcal{T}}_{\left\{n_{k+\mathit{\ell }}\right\}},\mathit{\ell }=0,\dots ,K-1.$$

The inequalities x_k < x_k+1 for all k = 1,…, K − 1 are equivalent to the following ones:

$${\eta }_{\epsilon }<\left(1+\frac{n_k}{n_{k+1}}\right){\sum }_K,k=1,\dots ,K-1,$$

which certainly hold when ${\epsilon }_{\eta }>{\sum }_K^{-1}$. Moreover, x₁ > 0 is equivalent to ${\eta }_{\epsilon }>\left(1-\frac{n_k}{N-n_1}\right){\sum }_K$, and naturally, we obtain x₁ < t_f(x) iff η_ɛ < Σ_K.

For ℓ > 0, the only nontrivial constraint in $R^{\mathit{\ell }}x\in {\mathcal{T}}_{\left\{n_{k+\mathit{\ell }}\right\}}$ is (R^ℓx)₁ > 0, i.e., (R^ℓ−1x)₂ > t^f(R^ℓ−1x), since all other constraints follow from the definition of the firing map and the nonclustering assumption. Therefore, all that remains to be checked is t^f(R^ℓx) ≤ (R^ℓx)₂ for all ℓ = 0,…, K − 1.

By induction we get ${(R^{\mathit{\ell }}x)}_2-t_f(R^{\mathit{\ell }}x)=x_{\mathit{\ell }+2}-{\displaystyle {\sum }_{j=0}^{\mathit{\ell }}{t}_f}(R^{j}x)$. Using the explicit expression above, we obtain

$${(R^{\mathit{\ell }}x)}_2-t_f(R^{\mathit{\ell }}x)=-(N-n_{\mathit{\ell }+2}-n_{\mathit{\ell }+1})+\frac{{\eta }_{\epsilon }}{{\sum }_K}(N-n_{\mathit{\ell }+2}),$$

for all ℓ = 0,…, K − 1. Altogether, we conclude that the existence condition in the case when all coordinates reach 0 before firing reduces to

$$\begin{array}{c}\frac{1}{{\sum }_K}<{\epsilon }_{\eta }<\underset{k=1,\dots ,K}{min}\frac{1}{{\sum }_K}\frac{N-n_k}{N-n_k-n_{k+1}}\\ =\frac{2N^2}{N^2-{\sum }_k{n}_k^2}\frac{1}{1-{min}_k\frac{n_k}{N-n_{k+1}}}.\end{array}$$

APPENDIX D: MAXIMIZING CONFIGURATIONS

Lemma 4

Given K ⩾ 3 and N ⩾ K (and N ≠ 6 if K = 3), the K-cluster configuration that maximizes the critical value ζ({n_k}) is the one defined by

$$n_k=\{\begin{array}{lll}1\hfill & \text{if}\hfill & k=1,\dots ,K-1\hfill \\ N-K+1\hfill & \text{if}\hfill & k=K.\hfill \end{array}$$ (D1)

This result is not as obvious as it may first appear. Indeed, collapsing extensive clusters together and splitting off unitary clusters in a way to keep the total number K constant increases the left term in the expression of ζ({n_k}) [see (2)] but simultaneously decreases the right term; so the overall shift of the critical value needs to be carefully evaluated. In addition, Lemma 4 does not hold in the case K = 3 and N = 6 since one can check that ζ({1, 1, 4}) < ζ({2,2,2}).

Proof

To show that the configuration (D1) minimizes the denominator in ζ ({n_k}), we can assume without loss of generality that {n_k} is a permutation of the configuration ${\left\{q_k\right\}}_{k=1}^K$ where 1 ≤ q_k ≤ q_k+1 and ${\displaystyle {\sum }_{k=1}^K{q}_k}=N$. Let ℓ ≤ K − 1 be the largest index for which q_k = 1. We separate the cases $\mathit{\ell }⩾\lfloor \frac{K}{2}\rfloor +1$ and $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$.

If $\mathit{\ell }⩾\lfloor \frac{K}{2}\rfloor +1$, then we have ℓ > K − ℓ; i.e., the configuration {q_k} has more clusters with a single unit than it has clusters with more than one unit. Thus every permutation {n_k} must have two consecutive clusters with a single unit. In this case, the quantity

$$S=\underset{k=1,\dots ,K}{min}\frac{n_k}{N-n_{k+1}}=\frac{1}{N-1}$$

reaches its global maximum. Moreover, adding units to the largest cluster q_K by taking off units from smaller clusters q_k has the effect to increase the quantity ${\displaystyle {\sum }_k{q}_k^2}$. Thus the configuration (D1) minimizes the denominator in ζ ({n_k}) over all permutations of increasing configurations {q_k} with $\mathit{\ell }⩾\lfloor \frac{K}{2}\rfloor +1$. The corresponding minimum is

$$Q=(K-1)(2N-K)\frac{N-2}{N-1}.$$

To deal with the case $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$, we begin by showing that for every K-cluster configuration we have $1-S⩾\frac{K-2}{K-1}$. Consider the following alternative. Either all $n_k\le \lceil \frac{N}{K}\rceil$ or there is a pair (n_k,n_k+1) for which $max\{n_k,n_{k+1}\}>\lceil \frac{N}{K}\rceil$. In the second case, by contradiction there must be another pair (n_k′,n_k′+1) where $min\{n_{k^{\prime }},n_{k^{\prime }+1}\}<\lceil \frac{N}{K}\rceil$ (otherwise we would have Σ_k n_k > N which is impossible) implying that

$$S\le \frac{\lceil \frac{N}{K}\rceil -1}{N-\lceil \frac{N}{K}\rceil }\le \frac{1}{K-1}.$$

In the first case, if $\lceil \frac{N}{K}\rceil =\frac{N}{K}$, then we have

$$S\le \frac{\frac{N}{K}}{N-\frac{N}{K}}=\frac{1}{K-1}.$$

Otherwise there must be k such that $n_k\le \lceil \frac{N}{K}\rceil -1$ (otherwise we would again have Σ_k n_k > N) and then again

$$S\le \frac{\lceil \frac{N}{K}\rceil -1}{N-\lceil \frac{N}{K}\rceil }\le \frac{1}{K-1}.$$

Thus in all cases, we have $S\le \frac{1}{K-1}$, which implies the desired inequality.

Still for $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$, the configuration that maximizes the sum ${\displaystyle {\sum }_k{q}_k^2}$ is

$$q_k=\{\begin{array}{lll}1\hfill & \text{if}\hfill & k=1,\dots ,\mathit{\ell }\hfill \\ 2\hfill & \text{if}\hfill & k=\mathit{\ell }+1,\dots ,K-1\hfill \\ N-2(K-1)+\mathit{\ell }\hfill & \text{if}\hfill & k=K.\hfill \end{array}$$

[Notice that the assumption that ${\left\{q_k\right\}}_{k=1}^K$ has exactly ℓ sites for which q_k = 1 implies that N − 2(K − 1) + ℓ ⩾ 2.] Altogether we conclude that when $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$, the denominator of ζ ({n_k}) is certainly not smaller than

$$\begin{array}{l}{Q}_{\mathit{\ell }}=\{[2(K-1)-\mathit{\ell }][2N-2(K-1)+\mathit{\ell }]\\ -4(K-1)+3\mathit{\ell }\}\frac{K-2}{K-1},\mathit{\ell }=0,\dots ,\lfloor \frac{K}{2}\rfloor .\end{array}$$

Now, the quantity Q_ℓ − (K − 1)(2N − K) increases with N provided that $[2(K-1)-\mathit{\ell }]\frac{K-2}{K-1}⩾K-1$. This inequality holds for every $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$ when K ⩾ 5. Moreover, the quantity $\left(K-1\right)\frac{2N-K}{N-1}$ also increases with N for K ⩾ 2. Thus the quantity Q_ℓ − Q increases with N, and to ascertain that Q is a global minimum, it suffices to check that each Q_ℓ − Q is non-negative for N = 2K − ℓ. This amounts to verify that the following inequalities hold:

$$\begin{array}{l}2K\left(K-1\right)\left[2\left(2K-1\right)-3\frac{{\left(K-1\right)}^2}{K-2}\right]\\ \begin{array}{cc}⩾\mathit{\ell }\left[c\left(K\right)+b\left(K\right)\mathit{\ell }+{\mathit{\ell }}^2\right],& \mathit{\ell }=0,\dots ,\lfloor \frac{K}{2}\rfloor \end{array},\end{array}$$

where

$$c\left(K\right)=12K^2-14K+3-\frac{{\left(K-1\right)}^2}{K-2}\left(7K-4\right)$$

and

$$b\left(K\right)=2\left[\frac{{\left(K-1\right)}^2}{K-2}-3K+2\right].$$

The right-hand side in the inequality above is a third-order polynomial in ℓ that is decreasing between 0 and $\lfloor \frac{K}{2}\rfloor$ when K ⩾ 5. Moreover, it is easy to check that

$$2\left(2K-1\right)-3\frac{{\left(K-1\right)}^2}{K-2}⩾0$$

for every K ⩾ 4; i.e., we indeed have Q_ℓ ⩾ Q for every $\mathit{\ell }\le \lfloor \frac{K}{2}\rfloor$ when K ⩾ 5.

For the cases K = 4 and K = 3, the proof needs to be improved because the quantity $Q_{\lfloor \frac{K}{2}\rfloor }-Q$ actually decreases with N when this integer is large. We begin with assuming K = 4 and check separately cases j = 0, 1, and 2.

For K = 4 and j = 0, the inequality 2(K − 2)⩾K − 1 shows that Q₀ − Q increases with N. Moreover, we have just checked in the general case that Q₀ ⩾ Q for all N ⩾ 2K when K = 4; thus Q is also a global minimum in this case.

For K = 4 and j = 1, since $\left[2\left(K-1\right)-1\right]\frac{K-2}{K-1}⩾K-1$, we still have Q₁ − Q increases with N. By numerically computing the values Q₁ and Q for N = 7 = 2K − 1, we conclude that Q remains a global minimum in this case.

For K = 4 and j = 2, we claim that given an increasing configuration (1, 1,q,N − q − 2) with $2\le q\le \lfloor \frac{N}{2}\rfloor -1$, the minimum S is maximal for the permutation (1, N − q − 2,1,q). Indeed, up to a cyclic permutation, there are three distinct permutations, and (1, N − q − 2, 1, q) is the only one that has nonconsecutive “1.” For (1, N − q − 2, 1, q), we have $S=\frac{1}{N-q}$ due to the assumptions on q, and the corresponding denominator of ζ({n_k}) reads

$$2[N\left(q+2\right)-q^2-2q-3]\frac{N-q-1}{N-q}.$$

This quantity is convex for q between 2 and $\lfloor \frac{N}{2}\rfloor -1$ (as a product of two positive functions, one increasing with decreasing derivative and the other one decreasing with decreasing derivative). Thus we only have to check that the values for q = 2 and $q=\lfloor \frac{N}{2}\rfloor -1$ are not smaller than the value for q = 1. Direct calculations reveal that the former quantity eventually grows with N faster than the latter when N is large enough. A numerical check shows that these values for q = 2 and $q=\lfloor \frac{N}{2}\rfloor -1$ are not smaller than the value for q = 1 provided that N ⩾ 6 (which is the minimal N for j = 2), and so the proof is complete for K = 4.

For K = 3, there are two types of configurations to consider, namely, the ordered ones (q₁,q₂,q₃) and those of the form (q₁,q₃,q₂). For (q₁, q₂, q₃), due to the assumption q_i ≤ q_i+1, the minimum S is given by $S=\frac{q_1}{N-q_2}$. For (q₁,q₃,q₂), depending on the sign of $q_2^2-q_1{q}_3$, the minimum S is either $\frac{q_2}{N-q_1}$ or $\frac{q_1}{N-q_3}$. Since both these quantities are never smaller than $\frac{q_1}{N-q_2}$, the nonordered configuration always minimizes the denominator of ζ({n_k}).

Using that $S\le \frac{q+p}{N-q}$ for the configuration (q, N − 2q − p, q + p) (where $0\le p\le \lfloor \frac{N-3q}{2}\rfloor$ and $1\le q\le \lfloor \frac{N}{3}\rfloor$), we get that the denominator of the critical value is at least

$$[2N\left(2q+p\right)-{\left(2q+p\right)}^2-{\left(q+p\right)}^2-q^2]\frac{N-2q-p}{N-q}.$$ (D2)

Using similar arguments as above, one concludes that this quantity is convex for p between 0 and $\lfloor \frac{N-3q}{2}\rfloor$. Therefore, it reaches its minimum at the boundaries of this interval.

For p = 0, the quantity (D2) becomes

$$2q\left(2N-3q\right)\frac{N-2q}{N-q},$$

which is again convex with q between 1 and $\lfloor \frac{N}{3}\rfloor$. Moreover, the value for $q=\lfloor \frac{N}{3}\rfloor$ grows faster with N than the value for q = 1 does. A numerical investigation reveals that the former is not smaller than the former provided that N ⩾ 7, i.e., ζ(1, N − 2, 1) ≤ ζ(q, N − 2q, q) for all $q\le \lfloor \frac{N}{3}\rfloor$ when N ⩾ 7.

For $p=\lfloor \frac{N-3q}{2}\rfloor$, (D2) becomes

$$\left(2N\lfloor \frac{N+q}{2}\rfloor -{\lfloor \frac{N+q}{2}\rfloor }^2-{\lfloor \frac{N-q}{2}\rfloor }^2-q^2\right)\frac{\lceil \frac{N-q}{2}\rceil }{N-q}.$$

Using once again the convexity argument, we obtain that this quantity reaches its minimum for either q = 1 or $q=\lfloor \frac{N}{3}\rfloor$. In the first case we want to check the inequality

$$\begin{array}{l}(2N\lfloor \frac{N+1}{2}\rfloor -{\lfloor \frac{N+1}{2}\rfloor }^2-{\lfloor \frac{N-1}{2}\rfloor }^2-1)\frac{\lceil \frac{N-1}{2}\rceil }{N-1}\\ ⩾2(2N-3)\frac{N-2}{N-1}.\end{array}$$

Again, as N increases, the l.h.s grows faster than the right-hand side, and numerics show that the inequality holds for all N ⩾ 10. For $q=\lfloor \frac{N}{3}\rfloor$, one can prove that the corresponding inequality holds for all N ⩾ 7. Therefore, we have shown that (1, 1, N − 2) maximizes ζ(n₁, n₂, N − n₁ − n₂) provided that N ⩾ 10. For N between 4 and 9, we have listed all three-cluster configurations and checked that the property remains valid, except for N = 6, as stated above.