Accurate Information Transmission Through Dynamic Biochemical Signaling Networks

Abstract

Stochasticity inherent to biochemical reactions (intrinsic noise) and variability in cellular states (extrinsic noise) degrade information transmitted through signaling networks. We analyze the ability of temporal signal modulation, that is dynamics, to reduce noise-induced information loss. In the extracellular signal-regulated kinase (ERK), calcium (Ca²⁺), and nuclear factor kappa-B (NFκB) pathways, response dynamics resulted in significantly greater information transmission capacities compared to non-dynamic responses. Theoretical analysis demonstrated that signaling dynamics has a key role in overcoming extrinsic noise. Experimental measurements of information transmission in the ERK network under varying signal-to-noise confirmed our predictions and showed that signaling dynamics mitigate, and can potentially eliminate, extrinsic noise induced information loss. By curbing the information-degrading effects of cell-to-cell variability, dynamic responses substantially increase the accuracy of biochemical signaling networks.

The role of biological signaling networks is to reliably transmit specific information about the extracellular environment to downstream effectors, allowing the cell to adjust its physiological state to changing conditions. The stochasticity of molecular interactions that underlies various forms of “noise” in biological systems can interfere with signal transduction and degrade the transmitted information. How signaling networks perform their core functions in the presence of noise is a fundamental question. Information-theoretic approaches allow estimating the maximal possible information transmission capacity of noisy biochemical networks (1–11). Previous applications of such methods to the analysis of signaling networks suggested that due to noise, cells lose most of the information about the concentration of ligands (12–14). Thus far, the information-theoretic analyses of signaling networks have been based on scalar measurements performed at a single time point. However, the information on activating ligands is often encoded using a dynamic signal represented by a multivariate vector that contains a single cell’s response at multiple time points (15–18).

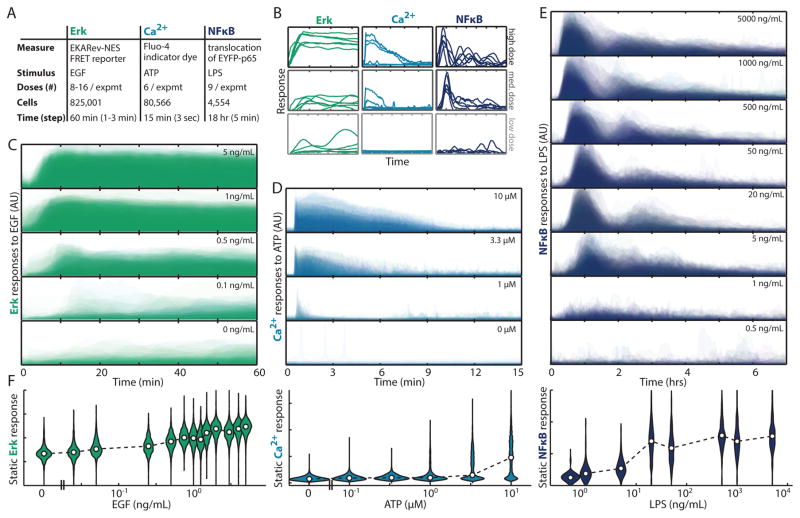
To test the hypothesis that dynamic responses contain more information than static responses, we performed single live-cell measurements of three key signaling pathways (Fig. 1): ERK, Ca²⁺, and NFκB (19). Fully automated computational image analysis (19) allowed us to measure the response of 910,121 individual live cells (Fig. S1–6, Tables S1–3). The large sample size was instrumental for analyzing high-dimensional multivariate responses. In all three pathways there was substantial variability within the dynamic (Fig. 1CDE) and non-dynamic (Fig. 1F) single cell responses across multiple concentrations of activating ligands.

Figure 1. Single cell measurement of the dynamic response of ERK, Ca²⁺ and NFκB.

A. Overview of single cell data analyzed in this work. B. Examples of single cell response dynamic trajectories. CDE. Temporal histograms of several representative dosages for ERK (C) Ca²⁺ (D) and NFκB (E). Color intensity reflects the probability density of a cellular response magnitude at each time point. Y-axis in BCDE is the same for each pathway and is of Arbitrary Units representing the FRET/CFP ratio reported by the EKARev ERK biosensor (C), intensity of Ca²⁺ indicator dye Fluo-4 (D), and ratio of nuclear to cytoplasmic localization of an EYFP-p65 reporter (E). F. Violin plot of the maximally separable static response in the three signaling pathways. Shape width shows response distribution (areas are equal), and point is the median response in each condition.

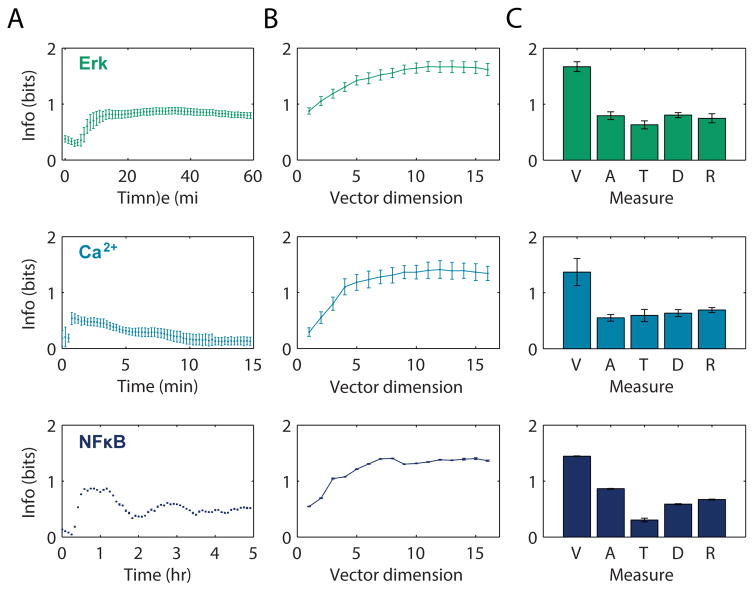
To analyze the implications of noise on information loss we used an information-theoretic approach to calculate the information transmission capacity of a dynamic signaling network. The information transmission capacity [also referred to as channel capacity (20)] is measured as the maximal possible mutual information between the measured response and the activating ligand concentration. To calculate the mutual information between a dynamic response (a vector) and the ligand concentration (a scalar), we expanded on a previously described algorithm (14). The algorithm uses continuous multi-dimensional response data and a k-nearest-neighbor approach to estimate the conditional probability density for each cell’s response (19). We thus estimated the information transmission capacity of the dynamic response and of several types of static responses. For all single time point static scalar responses we found transmission capacity (<1 bit) (12, 13) (Fig. 2A). However, across all three signaling pathways, the dynamic response had significantly higher information transmission capacity than several scalar responses previously described (21, 22) (Fig. 2BC, Student’s t-test p-value <0.05 for all comparisons, Fig. S16, Table S6). These estimates should be considered as lower bounds because they do not exclude variability resulting from experimental imperfections.

Figure 2. Information transmission capacity of static and dynamic ERK, Ca²⁺ and NFκB responses.

A. Information transmission capacity calculated from static scalar response distribution based on single time point measurements. B. Information transmission capacity calculated from multivariate dynamic responses as a function of the dimension of the multivariate vector. The multivariate vector was subsampled using a uniform grid centered on the middle time point (Fig. S20) C. Comparison of the multivariate vector (V) measurement to the following scalar responses: maximum response amplitude (A), maximum response time (T), maximal rate of response (D), ratio of maximum response amplitude to initial response amplitude (R). Error-bars are s.e.m from 6 biological replicates for ERK, 4 for Ca²⁺, and s.d. from 5 jackknife iterations for NFκB (Table S1–3). The multivariate vector information transfer was significantly greater than all scalar measures (p-values <0.05, Student’s t-test, Table S6).

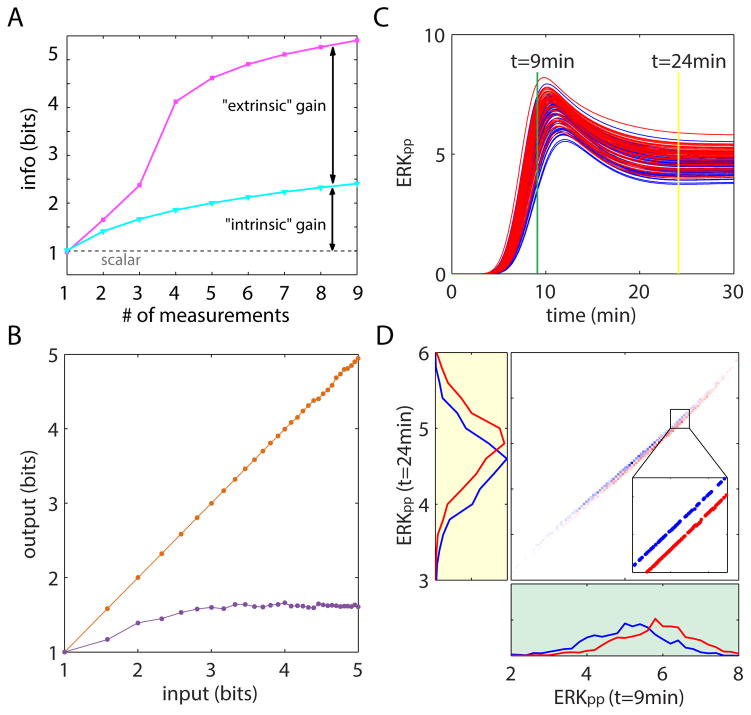
To elucidate the origins of the enhanced information transmission capacity of dynamic signaling responses we developed a mathematical theory using information-theoretic formalism (19). The theory explicitly accounts for the information-degrading effects of intrinsic and extrinsic noise sources in the context of multivariate responses. Intrinsic noise adds to uncertainty in all dimensions (i.e. time points) independently from one another. In contrast, the extrinsic variability in cellular states produces fluctuations that are constrained by the signaling network that generates the dynamics. Therefore, the fluctuating components generated by extrinsic noise at different time points are deterministically dependent on one another. As a result, intrinsic and extrinsic noise sources have different effects on the information transmission capacity of multivariate responses. In the case of purely intrinsic noise, additional measurements increase the information logarithmically due to simple ensemble averaging (12). In the case of purely extrinsic noise, sufficient number of dynamical measurements can provide complete information about the a priori uncertain internal state of the cell and therefore lead to a substantial gain in the information about the activating ligand (Fig 3A).

Figure 3. Theoretical decomposition of information loss caused by intrinsic and extrinsic noise.

A. graphical representation of the analytical expression for the gain in mutual information from overcoming intrinsic (cyan) and extrinsic (magenta) noise sources obtained from random linear gaussian inputs and outputs with three parameters (19). B. information transmission capacity of dynamic (orange) and static (maximal response, purple) responses calculated using simulated trajectories from the computational model of ERK (22) with only the extrinsic noise contributing to cell response variability. C. Example of ERK trajectory variability for two different inputs levels (red and blue). Variability was generated using a uniform distribution of a single parameter, MEK values that was varied by +/- 20%. D. Two dimensional histogram (center) and marginal distributions (left and bottom) for the two input levels (shown in red and blue) at two time points (T=9 & 24min) from the trajectories in C. Because only a single parameter was varried, the responses vary on a one-dimensional curve. As a result, although the univariate marginal distributions show substantial response overlap, the two dimensional distribution shows completely seperated response levels (inset).

To test our analytical prediction that the multivariate dynamic response can completely eliminate the information loss that results from introduction of extrinsic noise (19) we used computer simulations of ERK responses based on a published kinetic model (19, 23) (Fig. S14). We generated sets of simulated ERK activity trajectories in response to an increasing number of ligand concentrations. We varied model values for ERK and Mitogen-activated protein kinase kinase (MEK) according to a uniform distribution (+/−20% mean value) to mimic extrinsic noise and measured the information transmission capacity. Our analysis supported the analytical prediction and showed that while the univariate response, based on maximal ERK dynamics, had limited information transmission capacity, the dynamic multivariate response can transmit complete information about ligand concentration (Fig. 3B). An intuitive demonstration for the limitation of univariate response and the ability of multivariate response to overcome extrinsic noise is shown in Fig. 3C and D. Superficially, the trajectories of two populations of simulated responses of ERK activity to two input concentrations of Epidermal growth factor (EGF) appear overlapping (Fig. 3C), but in fact, they are completely separable when considering joint distributions (24). Plotting the distribution of ERK activity at t=9 and t=24 minutes on a two-dimensional plane (Fig. 3D) shows that the responses to a single varied parameter input lies on a one-dimensional curve within a two-dimensional space. The two one-dimensional manifolds for different inputs are completely separated from each other (inset), but overlap considerably in any one-dimensional projection. This simple example demonstrates how the extrinsic variability of a single parameter can in principle be completely eliminated using measurements from only two time points.

The accuracy of a response can be characterized by its signal-to-noise ratio (SNR). The mutual information and the system’s SNR are related, however this relationship is strongly affected by the noise properties (intrinsic vs. extrinsic) and the type of the response. Our analytical theory predicts different relationship between mutual information and SNR for three different types of responses: (i) scalar responses that do not distinguish between intrinsic and extrinsic noise, (ii) multivariate responses without any dynamic component (redundant measurements) that can only reduce intrinsic noise, and (iii) dynamic responses that combine the benefits of redundant measurements with efficient mitigation of extrinsic variability. We varied the SNR in the ERK network by partial inhibition of the ERK kinase MEK with six different dosages of the inhibitor U0126. At each MEK inhibition level we measured ERK response to eight EGF levels. A total of 48 conditions were measured in four biological replicates (Fig. S24). At each MEK inhibitor level we calculated the mutual information and the SNR from single cell responses (19). In total, Fig. 4 contains 535,107 cell responses (Table S4,5). As expected, for a scalar response, the formula relating the mutual information and the overall SNR is in very good agreement with our experimental measurements. The theoretical prediction of mutual information for the redundant measurement case requires knowledge of intrinsic to extrinsic noise ratio (IER). IER was estimated in two ways by: (i) quantifying the fluctuations in the later (quasi-stationary) portion of the response time series of our ERK data (Fig. S22C) (ii) using data for repeated measurements of single cell responses (25) (Fig S22). The predicted mutual information based on redundant responses required IER values that are 2–4 orders of magnitude higher than experimentally estimated IER (19)(Fig S17). In contrast, the measured mutual information values were in good agreement with the theoretical prediction for a dynamic response based on a computational ERK model (19)(Fig. S19). Overall this analysis demonstrates that the substantial information gain from multivariate measurements is indeed the direct result of the dynamic nature of ERK response.

Figure 4. Measured information gain is a result of ERK dynamics ability to mitigate extrinsic noise.

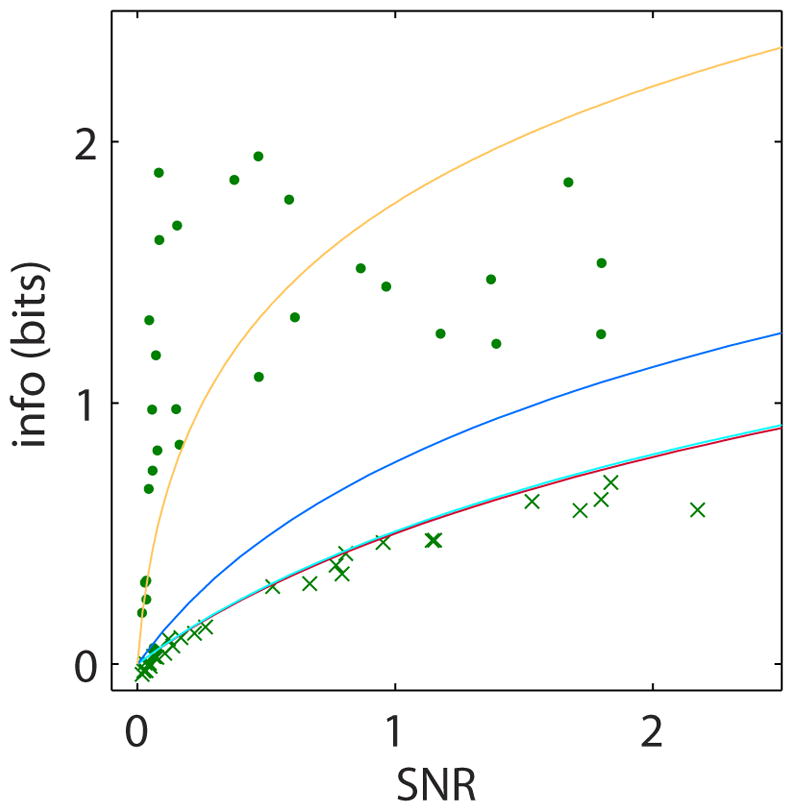
Experimental measurement of the mutual information between ERK response and EGF measured as a function of the response signal-to-noise (SNR). Each marker represents calculations of SNR and mutual information from the dynamic (dot) and maximal scalar (cross) responses of cells from an 8-well dose-response experiment. Shown data are calculated based on 535,107 single cell responses from 29 experiments with six doses of MEK inhibitor U0126 (Table S4–5). Lines represent theoretical predictions of the mutual information as a function of SNR for three types of responses: static scalar (red line), redundant measurements where the multivariate response has no dynamics (dark and light blue lines) calculated based on two independent estimates of IER (19)(Fig S22), and dynamic response (orange) that can mitigate both intrinsic and extrinsic noise (Fig S19).

The robustness of biological systems is epitomized by their ability to function in the presence of large variability in cellular states (26, 27). Signaling dynamics allow biochemical networks to mitigate variability in the cellular state and thereby maximize the information transmission capacity of signaling networks. Although the theory and observations presented here focus on the information transmission capacity of the dynamics of a single signaling molecule, the extension of our analysis to the case of multiple signaling molecules responding to one ligand is straightforward. Not all of the information contained in the dynamical responses may actually be used by cells. Yet, because reliable information transmission is a fundamental function of cellular signaling networks, it is plausible that evolutionary pressures shaped the cellular machinery to maximize the reliable decoding of multivariate dynamic signals.