A hybrid method for protein–protein interface prediction

Abstract

The growing structural coverage of proteomes is making structural comparison a powerful tool for function annotation. Such template‐based approaches are based on the observation that structural similarity is often sufficient to infer similar function. However, it seems clear that, in addition to structural similarity, the specific characteristics of a given protein should also be taken into account in predicting function. Here we describe PredUs 2.0, a method to predict regions on a protein surface likely to bind other proteins, that is, interfacial residues. PredUs 2.0 is based on the PredUs method that is entirely template‐based and uses known binding sites in structurally similar proteins to predict interfacial residues. PredUs 2.0 uses a Bayesian approach to combine the template‐based scoring of PredUs with a score that reflects the propensities of individual amino acids to be in interfaces. PredUs 2.0 includes a novel protein size dependent metric to determine the number of residues that should be reported as interfacial. PredUs 2.0 significantly outperforms PredUs as well as other published interface prediction methods.

Introduction

Knowledge of a protein's interaction partners is important for elucidating a protein's function and for a detailed characterization of protein networks. High‐throughput experimental techniques are beginning to identify interacting partners on a genome‐wide scale,1 but the physical basis of these interactions is generally unknown. The location on a protein surface where it is likely to bind to its partners (its interfacial residues) is important in determining the mechanism by which a protein carries out its function as well as for understanding the effects of mutations and for designing experiments to perturb targeted biological networks. The prediction of interfacial residues is therefore an important goal which, among other applications, can be used in elucidating an organism's complete interactome computationally.2, 3

A variety of approaches have been developed to predict interfacial residues. These have typically relied on the observation that proteins often interact with their partners at locations in the primary sequence with characteristic sequence motifs4, 5, 6 or evolutionarily conserved sequence patterns.7, 8, 9 The growing availability of protein structures through crystallography and computational modeling has enabled other approaches that typically depend on the fact that protein surface patches involved in protein‐protein interactions (PPIs) tend to have certain characteristics that distinguish them from the rest of the surface.10 These characteristics typically include physico‐chemical and geometric properties, evolutionary conservation and the tendency of different types of amino acids to be involved in protein‐protein interfaces.11, 12, 13, 14, 15 When a binding partner is known, other structure‐based approaches, are based on docking procedures which rely on shape complementarity and use broad conformational sampling combined with physical–chemical force fields to identify favorable interaction sites on a protein surface.16, 17 Such methods are difficult to apply to a large number of proteins because of their computational complexity.

Template‐based approaches use comparison of protein structures to make functional inferences. They have proven to be a powerful technique for function prediction in general18 and interfacial residue prediction in particular19, 20 and can be applied on a genome‐wide scale. Their success is based on the fact that expanded structural coverage of genomes has resulted in a situation where, given a query protein of unknown function, it is highly likely that there is a structurally similar protein in databases that binds to other proteins in similar way. Such functional similarities are not necessarily evident from sequence similarity, and their identification requires the exploitation of both remote sequence20 and structural relationships.21

The information used in prediction methods based on surface patch features or templates is largely orthogonal, so combining them should result in improved performance. Here we describe PredUs 2.0, a protein–protein interface prediction method that uses a template‐based score implemented in our program PredUs19 and a novel patch‐based score. Combined with a dynamic approach to estimating the size of an interface for individual query proteins, the method is shown to be quite effective in predicting interfacial residues and outperforms both the original PredUs and other widely used interface prediction methods.

Results

To predict an interface, we calculate two scores for each residue r _i on a query protein surface. The first is calculated using PredUs which has been described previously.19, 21 Briefly, for a residue at a given position on the surface, the PredUs score reflects the frequency with which residues at geometrically equivalent positions in structurally similar proteins are involved in a protein–protein interaction. The second score (patch) reflects the properties of r _i and its local environment, which include the propensities of individual residue types to be involved in a PPI [see Fig. 1(A)], and the relative accessible surface areas (RASA) of residue r _i and residues in a surface patch surrounding r _i. The propensities are calculated from a dataset of 2766 non‐redundant complexes in the PDB (see Methods). A likelihood ratio (LR) is calculated for each score using a Bayesian approach and a final LR reflecting the likelihood that r _i is interfacial is calculated with a naïve Bayesian network as LR_interface = LR_PredUs × LR_patch.

Figure 1.

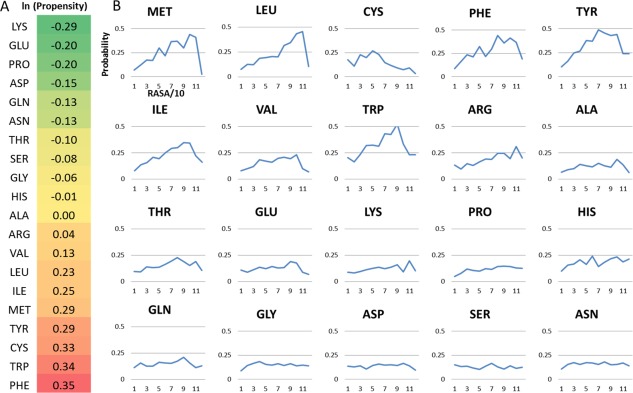
Propensities and surface area‐dependent probabilities for amino acids to be interfacial. (A) Interface propensities for the 20 amino acids (see Materials and Methods). Positive numbers indicate that residues of that type are enriched in interfaces and negative numbers indicate that they are reduced. (B) Probabilities (y axis) for residues to be interfacial conditioned on the level of accessible surface area. Each number on the x axis represents a bin of relative accessible surface area (0–10%, 10–20%, etc.).

The propensity for residues of a given type to be interfacial and accessible surface area have been used as components of patch‐based interface prediction methods reported previously.10, 11 Figure 1(B) reports probabilities for a residue type to be interfacial conditioned on its accessible surface area. As shown in the figure, large relative accessible surface area is a significant factor in determining whether hydrophobic/aromatic amino acids are interfacial, but has no effect for the polar amino acids. Hence, to take this into account when calculating our patch score, we weight the amino acid propensities by the associated conditional probability for that amino acid. How the weighted propensities are combined into a single patch score, construction of the patch and calculation of the propensities and ASA dependent probabilities are described in detail in Materials and Methods.

Figure 2 contains precision‐recall (PR) curves showing the performance of the combined score applied to a set of proteins (denoted DB34) taken from Docking Benchmark 3.022 and 4.023 (see Materials and Methods). As shown in the figure, PredUs 2.0 (solid black line) outperforms the previous version of PredUs (solid orange line). To decide which residues to report as interfacial in a given application, it is necessary to develop an algorithm which provides such a list. Most interface prediction methods derive this list from predicted residues with a score higher than some cutoff value, or use the top scoring n residues where n is some preset value. In addition, a number of other methods require that interfacial residues be in a contiguous surface patch and report only top scoring residues in the largest such patch. The original PredUs19 does not require that residues be in a patch but simply reports all residues with a score, calculated by a support vector machine (SVM), above a cutoff (0.0). PredUs 2.0 does not directly identify contiguous patches but the LR of a particular residue is dependent on properties of neighboring residues as defined by its patch score (see Methods).

Figure 2.

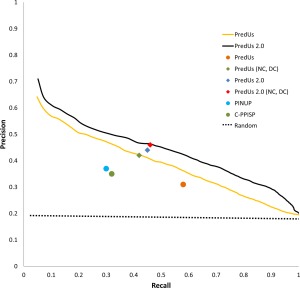
Prediction performance. Solid lines show the precision calculated as a function of recall which was varied at 1% increments, and averaged over all query proteins in our benchmark. Single points show precision/recall using different approaches to deciding which residues to include in a predicted interface for the methods shown in the legend. For PredUs and PredUs 2.0 this is described in the text. Predicted interfaces for PINUP and cons‐PPISP are obtained using the default parameters for those methods.

The use of a fixed cutoff can adversely affect precision and recall achieved for a given query protein. This can be understood by assuming a perfect predictor, for which the true interfacial residues are always top ranked. If a cutoff on the score is used, recall suffers if it is too strict (some true interfacial residues do not meet the cutoff) and precision suffers if it is too liberal (non‐interfacial residues are incorrectly predicted). Using a fixed number of residues to include in the prediction, a similar reduction in performance occurs if this number is smaller (recall suffers) or larger (precision suffers) than the true interface size. These issues cause the average performance achieved in practice to fall below the performance represented by the PR curve. This is illustrated in Figure 2 which shows the performance of PredUs using the fixed cutoff for its SVM score (orange circle) and PredUs 2.0 taking the top 27 residues ranked by LR_interface (blue diamond, 27 was the average number of true interface residues in our benchmark).

Hence, for a perfect predictor, optimal performance can be achieved by taking the top n residues ranked by the score as the predicted interface, and allowing n to vary to reflect the true interface size for a specific query protein. Even for an imperfect predictor, it is reasonable to take the true interface size into account in this way, assuming it can be expected that true interfacial residues are highly ranked. Although the true interface size is not known of course, it has been shown24 that it can be approximated by a power law function of the number of surface residues of a protein. We therefore implemented a dynamic cutoff (DC) where we choose the number, n, of residues to include in a predicted interface for each query protein using the function

$$n=6.1N^{0.3}$$

where N is the total number of surface residues for that protein (see Supporting Information Fig. S1 for how this function was derived).

As shown in Figure 2 this brings the average precision/recall for both PredUs (green diamond) and PredUs 2.0 (red diamond) to their optimal values represented by the precision/recall curve. In fact, this performance essentially equivalent to what can be achieved using a cutoff based on “native contacts” (NC, Fig. 2), that is, assuming the actual number of residues in an interface is known for each query protein.

Finally, we note that the method has potential applications in the identification of “crystal contacts,” that is, interfaces formed in a crystal structure that do not occur in a biological context. Given that we use properties of real interfaces to make predictions and the general accuracy of our method, we expect that residues in crystal contacts will be less likely to be predicted as interfacial by PredUs 2.0. To examine this, we used the program Pymol25 to reconstruct the the unit cell for the complexes in our benchmark and calculated the percentage of residues predicted to be interfacial in interfaces that are formed only upon unit cell reconstruction. On average, 16% of residues in these interfaces are predicted to be interfacial, compared to 47% of residues in the true interfaces defined in the benchmark. Hence, the percentage of predicted residues in an observed interface in a crystal structure should provide a simple indication of whether it is likely to be biologically relevant and provides a complementary approach to crystal contact prediction methods based, for example, on identification of interfaces with poor affinity26 or the consistent presence of an interface under different crystalllization conditions.27

Discussion

As we have previously shown,21 the overall shape of a protein is a strong determinant of where on a protein surface other proteins are likely to bind. That is, two proteins with sets of secondary structure elements with similar relative orientations and positions are likely to bind partners at structurally equivalent locations. This allows prediction of interfaces from structurally similar templates, but an obvious drawback of this approach is that not all structural fragments with a particular arrangement of secondary structure elements will bind other proteins. We have addressed this problem here by combining a template‐based score with a score that accounts for the propensities of individual residues to be in an interface. Bayesians statistics provides a convenient means of integrating the contributions of different sources of evidence and indeed Bayesian methods have found increasing application in structural biology. We also trained a linear regression model to combine a patch‐based score and a template‐based score for interface prediction with four‐fold cross validation. The performance with a linear regression model is similar to that with Bayesian methods.

A novel feature of our scoring scheme for interfacial residues is the method used to weight residue propensities by probabilities to be interfacial conditioned on accessible surface area. In particular, the high propensity, hydrophobic/aromatic amino acids are no more likely to be in interfaces than low propensity amino acids when they have low accessible surface area. However, high accessible surface area has a strong effect. Taking tryptophan as an example [Fig. 1(B)], it is no more likely than random to be interfacial when it is on the surface with low accessible surface area, but interfacial half of the time when it is highly exposed.

Other structural features incorporated into the final PredUs2.0 score include the local environment of a given residue reflected in the patch‐based score and the size of the query protein which is used to determine the dynamic cutoff on the number of residues to include in a predicted interface. A concern with predicting an interface by taking the top n residues is that they may be distributed over the surface without forming contiguous patches. The identification of the true binding site would be problematic in such a situation, despite the levels of precision/recall we report.

We therefore identified contiguous patches formed by predicted interfacial residues (a residue was included in a patch if any atom in that residue was within 6.5 Å of another residue in the patch) and found that only a single patch was formed for half of the query proteins. As shown in Table 1 the performance for the set of proteins with a single predicted patch is actually better than the performance averaged over all query proteins, hence predictions for proteins that have only a single patch reliably indicate the binding site. However, Table 1 also shows that the prediction performance decreases for those proteins where multiple patches are predicted, likely because these patches may indicate additional interaction sites that are not defined in our benchmark data set as discussed in previous studies.13, 28, 29

Table 1.

Relationship Between Prediction Performance and the Number of Contiguous Patches of Predicted Interfacial Residues

		Average precision	Average recall
DB34	All query proteins	0.46	0.46
	Query proteins with one patch	0.56	0.55
	Query proteins with multiple patches	0.36	0.37
HET‐TRI	All query proteins separate interfaces	0.31	0.25
	All query proteins combined interfaces	0.57	0.24
	All query proteins combined interfaces with 25% increase in dynamic cutoff	0.55	0.38

To test for this possibility, we collected 25 proteins (non‐redundant at a sequence identity cutoff of 40%) not in DB34 that are involved in heterotrimeric interactions at non‐overlapping interfaces (denoted the HET‐TRI set and listed in Supporting Information Table SI). For this set, only 20% of the predictions formed single patches and, consistent with multiple known interaction sites, there was a higher proportion of multiple patch predictions (see Supporting Information Figure S2 which compares the distribution of the number of contiguous patches for the DB34 and HET‐TRI proteins).

Table 1 shows that prediction performance depends on how the separate interfaces are treated. When each interface in the heterotrimer is considered as a separate target (i.e., falsely classifying the second interface as non‐interfacial) prediction precision was similar to multiple patch predictions in the DB34 (0.31 vs. 0.36). However, when the union of both interfaces is classified as a true positive, the average precision is comparable to the single patch predictions in DB34 (0.57 vs. 0.56), suggesting that PredUs2.0 is correctly predicting the second interface in HET‐TRI as well as the first. Although the average recall does not improve when considering both interfaces together, this is because our dynamic cutoff assumes a single interface and, thus, PredUs2.0 under‐predicts when there is more than one. When the number of interfacial residues included in the prediction is arbitrarily increased 25% beyond the dynamic cutoff for all proteins in the HET‐TRI dataset, recall increases from 0.24 to 0.38 with precision decreasing moderately from 0.57 to 0.55. These results suggest that future algorithmic developments will enable the prediction of multiple binding sites on protein surfaces.

The combined use of the set structural features incorporated into PredUs 2.0 more completely reflects the properties of real interfaces. The final score addresses problems with a purely template‐based approach, and results in a method that, as shown in Figure 2, outperforms PredUs as well as other top performing programs11, 24 as determined by recent surveys of interface prediction techniques.30, 31 PredUs2.0 should therefore represent the current state‐of‐the‐art in interfacial residue prediction.

Materials and Methods

Datasets

The 302 protein structures contained in DB34 are taken from the Docking Benchmark 3.0 and 4.022, 23 and listed in Supporting Information Table SII. They form 52 enzyme–inhibitor complexes and 99 “other” categories of protein‐protein complexes. Twenty‐five antibody–antigen complexes in Docking Benchmark 3.0 and 4.0 were excluded from this work. Our benchmark is non‐redundant at the SCOP32 family level except for 10 proteins that are in complexes with different partners. We treat these as separate targets since, although the interfaces with their partners overlap, they are not identical. Two copies of each protein are available, one in the context of its interacting partner (bound form) and one in its isolated state (unbound form). Only the unbound form was used as a query protein.

A residue in a benchmark protein was considered to be interfacial if any atom of that residue was within 6 Å of any atom from its interacting partner in the complex.

PredUs interface score

The PredUs program was run locally but identical software is available from the PredUs web server.19

Interface propensity

We calculated the propensity for each residue type r to be in an interface using a set of 2,766 heterodimeric complexes (listed in Supporting Information Table SIII). This set represents all heterodimers (excluding proteins in our benchmarks) in the PDB as of April 2015 which satisfied the following criteria: non‐redundant at the 40% sequence identity level, interface size ≥1500Å2 and no disulfide bonds in the interface. Propensity measures the enrichment of accessible surface area (ASA) from residues of type r in protein–protein interfaces compared to the protein surface in general and is calculated as follows:

$$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}\left(\mathrm{r}\right)=\left(\frac{\frac{{\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{r}}^{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}{{\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{a}\mathrm{l}\mathrm{l}}^{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}}{\frac{{\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{r}}^{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}{{\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{a}\mathrm{l}\mathrm{l}}^{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}}\right)$$

Here ${\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{r}}^{\mathrm{X}}$is the sum of the relative accessible surface areas of all residues of type r that have characteristic X (on the interface or on the surface) in all proteins from the benchmark, and ${\mathrm{R}\mathrm{A}\mathrm{S}\mathrm{A}}_{\mathrm{a}\mathrm{l}\mathrm{l}}^{\mathrm{X}}$ is the sum of relative ASAs of residues of all types with characteristic X. Relative ASA for a given residue is defined as the solvent exposed area of that residue in the context of the protein structure, normalized by the area of that residue in the context of an extended ALA‐r‐ALA tripeptide.33, 34 An amino acid was considered to be at protein surface if its RASA ≥ 5%. Areas were calculated with a probe size of 1.4 Å using the surfv program.35

Although propensity to be in an interface should implicitly reflect the general properties of residue types that make them more or less likely to be involved in PPIs, whether a specific residue in a given query protein is involved in an interaction will also depend on its structural context. To take this into account, we weighted the propensity for specific residues based on that residue's RASA. To do this, we defined 10 general levels of RASA (RASA < 10%, 10% < RASA < 20%, etc.) and calculated $P_{\mathrm{r}}\left(\mathrm{I}|\text{RASA}\right)$, i.e., the probability that a residue of type r is involved in an interface, given that it has a certain level of RASA. For a specific residue r _i of type r in a query protein the weighted propensity (WP) for that residue is then

$$\text{WP}\left(r_{\mathrm{i}}\right)=\text{propensity}\left(r\right)\times P_{\mathrm{r}}\left(\mathrm{I}|\text{RASA}\right)$$

Conditional probabilities were calculated from directly from our benchmark.

Definition and Scoring of Surface Patches

To take into account the local environment of each amino acid in predicting its interfacial likelihood, we implemented the algorithm described in Ref. 10 to define patches on a protein surface. For each surface residue r _i, another residue r _j is considered to be in the patch if its Cα atom is within 10 Å of the Cα of r _i, and if the angle between the solvent vectors of r _i and r _j are <120°. The solvent vector points from the Cα atom of r _i to the center of mass of the Cα atoms of the 10 residues nearest to r _i. As discussed in Ref. 10, the solvent vector comparison is designed to avoid including residues from the opposing face of a protein surface, which may lead to discontinuous patches.

Each surface residue of a query protein is thus associated with a surface patch, Patch(r _i)={x ₁, x ₂,…,x _n}, containing residues x ₁‐x _n. Two scores were calculated for each patch: (a) the average of the weighted propensities of residues calculated as

$$〈\text{WP}(\text{Patch}\left(r_{\mathrm{i}}\right))〉=\text{Average}\left(\text{WP}\left(x_1\right),\mathrm{...},\text{WP}\left(x_{\mathrm{n}}\right)\right)$$

(b) the joint probability for residues in the patch to be in a protein‐protein interface given their levels of RASA calculated as:

$$\prod \text{Patch}\left(r_{\mathrm{i}}\right)={\displaystyle \sum _{j=1}^n\log \left(p_{{\mathrm{x}}_{\mathrm{j}}}\left(I|\text{RASA}\right)\right)}$$

The Pearson's correlation coefficient between $〈\text{WP}(\text{Patch}\left(r_{\mathrm{i}}\right)〉$ and $\prod \text{Patch}\left(r_{\mathrm{i}}\right)$ was found to be 0.21 so they are providing orthogonal information. A single patch‐based score, patch, was calculated using a voting method. Voting methods which combine multiple classifiers have demonstrated superior performances compared to individual classifier.36 In our voting approach, if a residue r_i appears as a member in n of the top 15 patches ranked by $〈\text{WP}(\text{Patch}\left(r_{\mathrm{i}}\right)〉$ and in m out of the top 15 patches ranked by $\prod \text{Patch}\left(r_{\mathrm{i}}\right)$, its patch score would be (n+m). The number 15 was chosen by examining the performance using values from 5 to 22.

Bayesian network

The Pearson's correlation coefficient between the PredUs score and the patch‐based score was 0.38 so they are also providing orthogonal information. We used a naïve Bayes approach to combine them, dividing the scores into uniform bins and calculating an LR for each bin. We arbitrarily chose 10 as the total number of bins for each of the PredUs and patch scores. We further required that the LRs increase monotonically from bin to bin as the score increased. This was mostly satisfied for the PredUs score but the behavior of the LR was erratic for the patch score. Testing different values for the total number of bins for the patch score showed that 14 bins produced largely monotonic increases in LR. The bin ranges and LRs are provided in Supporting Information Table SIV. LRs for each bin are calculated as the percentage of interfacial residues with a score in a given bin divided by the percentage of non‐interfacial residues with a score in that bin and were obtained from our benchmark using 10‐fold cross validation. The product of the PredUs LR and patch LR becomes the PredUs 2.0 score for each residue.

Performance evaluation

Precision was calculated as TP/(TP+FP) and recall was calculated as TP/(TP+FN) where TP means “true positive,” FP means “false positive,” and FN means “false negative.”

Supporting information

Supporting Information Tables.