Receptor-ligand H-bond pairings have evolved to promote high-affinity binding by reducing competitive interference with water.
Keywords: Hydrogen bonds, Drug design, Computational chemistry, Biological activity, Enzyme catalysis, Hydrogen bond pairing, Hydrogen bonding capability, Binding affinity, Clostridium difficile toxin
Abstract
Hydrogen (H)-bonds potentiate diverse cellular functions by facilitating molecular interactions. The mechanism and the extent to which H-bonds regulate molecular interactions are a largely unresolved problem in biology because the H-bonding process continuously competes with bulk water. This interference may significantly alter our understanding of molecular function, for example, in the elucidation of the origin of enzymatic catalytic power. We advance this concept by showing that H-bonds regulate molecular interactions via a hitherto unappreciated donor-acceptor pairing mechanism that minimizes competition with water. On the basis of theoretical and experimental correlations between H-bond pairings and their effects on ligand binding affinity, we demonstrate that H-bonds enhance receptor-ligand interactions when both the donor and acceptor have either significantly stronger or significantly weaker H-bonding capabilities than the hydrogen and oxygen atoms in water. By contrast, mixed strong-weak H-bond pairings decrease ligand binding affinity due to interference with bulk water, offering mechanistic insight into why indiscriminate strengthening of receptor-ligand H-bonds correlates poorly with experimental binding affinity. Further support for the H-bond pairing principle is provided by the discovery and optimization of lead compounds targeting dietary melamine and Clostridium difficile toxins, which are not realized by traditional drug design methods. Synergistic H-bond pairings have therefore evolved in the natural design of high-affinity binding and provide a new conceptual framework to evaluate the H-bonding process in biological systems. Our findings may also guide wider applications of competing H-bond pairings in lead compound design and in determining the origin of enzymatic catalytic power.
INTRODUCTION
Hydrogen (H)-bonds are ubiquitous in nature and play an important role in protein folding (1), protein-ligand interactions (2), and catalysis (3, 4). Despite extensive investigations, there remain many challenges that prevent us from completely understanding how H-bonds modulate molecular function. In biological systems, an H-bond competing process is always present with water. Because bulk water interferes with reversible biological processes and enthalpy-entropy compensation occurs during H-bond formation, the mechanisms and the extent to which H-bonds contribute to molecular function are not well understood. In particular, whether H-bonds regulate receptor-ligand binding remains a long-standing problem with poorly defined mechanisms (5–9).
H-bonds are generally considered to be facilitators of protein-ligand binding (2, 10). However, introducing H-bond donors or acceptors to establish stronger protein-ligand interactions often results in the absence of net gain in binding affinity (5, 11). Rather than targeting protein-ligand interactions per se, H-bonds are also reported to promote ligand binding affinity by displacing protein-bound water molecules into the bulk solvent (12–15). Contrasting H-bonding mechanisms are also evident in enzyme catalysis where the effects of H-bonds on the free energy barrier reduction of enzymatic reaction are identical to their role in protein-ligand binding. Whether electrostatic (H-bond) interactions represent the major origin of enzymatic catalytic power is still under debate (16–18). We recently reported that accurate quantification of the free energy contribution of H-bonds to both enzymatic reactions and the corresponding reference reactions in aqueous solution is vital for exploring the origin of enzymatic catalytic power (19). A deeper understanding of the effects of water H-bond interactions on biological processes is therefore needed to advance our appreciation of how such systems are regulated and to facilitate lead compound design without compromising ADMET (absorption, distribution, metabolism, excretion, and toxicity) properties or escalating drug development costs (20).
To better delineate how water regulates H-bonding between a receptor and its ligand, we used water/hexadecane partition coefficients to determine whether the H-bonding capability of receptor-ligand atoms is stronger or weaker than that of hydrogen or oxygen atoms in water. Here, we provide theoretical and experimental demonstration in which synergistic receptor-ligand H-bond pairings potentiate high-affinity binding by effectively eliminating competitive interference with water.
RESULTS
To better define the nature of H-bonds in biological systems, two key aspects need to be considered. First, the protein-ligand H-bonding process will invariably compete with bulk water. This process is represented in Eq. 1, which shows a reversible competing H-bonding process between a ligand H-bond acceptor (L; note that L stands for a ligand atom, not the whole ligand) and a protein receptor H-bond donor (PH), where the square bracket indicates that the water molecule’s orientation and position is constrained by the protein
| (1) |
| (2) |
| (3) |
The free energy change (ΔG) of this process is usually considered as the Gibbs free energy change from PH…[OH2] to PH…OH2 (Eq. 2). The difference between Eqs. 1 and 2 describes an H-bond competing process associated with small molecules in aqueous solution (Eq. 3). Because this relationship is poorly understood and often ignored, a common misperception—that is, generating stronger protein-ligand H-bonds leads to a net gain in binding affinity—exists. The ΔG in Eq. 2 is not dependent on the strength of protein-ligand interactions, whereas the ΔG in Eq. 3 is associated with protein-ligand H-bonds. Thus, the ΔG in Eq. 3 provides useful quantitative information in deciphering how protein-ligand H-bonds may modulate ligand binding affinity. To address the first issue of competing H-bonds in bulk water, we propose a new H-bond pairing principle to evaluate the ΔG in Eq. 3, and we demonstrate that the nature of these H-bonds depends on the pairing of the donors and acceptors (see the next section).
Second, H-bonding in biological systems is highly complicated. Some key determinants, such as solvent entropy changes during the H-bonding process, are difficult to measure accurately using either experimental or theoretical methods. This limitation is a significant reason why the contribution of H-bonds to biological function remains poorly defined. Furthermore, the net free energy contribution of an H-bonding process represents the sum of several parts, with individual values being much larger than the net contribution in some cases. Even if each component can be measured with small relative error, the net contribution cannot be obtained with accuracy. To address this second issue, we developed a novel parameter derived from experimental partition coefficients to calculate the contribution of specific H-bonds to ligand binding affinity. Because this parameter includes the factors that influence the free energy contribution of H-bonds, notably electrostatic interactions, desolvation, entropy change of solvent, and van der Waals interactions, this makes the calculation simple and accurate because summarizing the individual parts that are hard to quantify accurately is not necessary. By applying both the H-bond pairing principle and the novel parameter, we examined the mechanism and the extent to which protein-ligand H-bonds modulate ligand binding affinity.
The H-bond pairing principle
The H-bond competing process can be defined by the following general equation, where two acceptors (A1 and A2) and donors (D1 and D2) form mixed pairings
| (4) |
When A2 and H-D2 have stronger H-bonding capabilities than A1 and H-D1, respectively, Eq. 4 favors (both in enthalpy and in free energy) the pairing A2…H-D2 (Fig. 1A and fig. S1). We estimated the H-bonding capability of an atom using the free energy required to transfer the atom from water to hexadecane. We then used a modification of the method of Kenny et al. (21) to evaluate the H-bonding capability of the respective atoms in the protein-ligand complex by calculating the difference (ΔlogP16) between water/hexadecane partition coefficients (logP16) and logP16 of saturated hydrocarbon molecules with the same molecular surface area (Table 1 and fig. S2). It is known that ΔlogP between hexadecane (or alkane)/water and 1-octanol/water provides a measure of the H-bond potential of a molecule (22–24), and the calculated standard errors for the H-bonding capabilities listed in Table 1 appear acceptable. The H-bonding capabilities of some atoms are highly accurate [low root mean square error (RMSE) values] because values can be obtained directly from one-step calculation (Eq. 2) and the RMSE value for the basic equation (Eq. 1) is lower. For atoms where the experimental hexadecane/water partition coefficients for their relevant compounds are lacking, RMSE values increase (>1) because the calculation steps increase. Systematic measurement of experimental hexadecane/water partition coefficients for the compounds containing the atom type and/or the relevant compounds will improve future calculations of H-bonding capability.
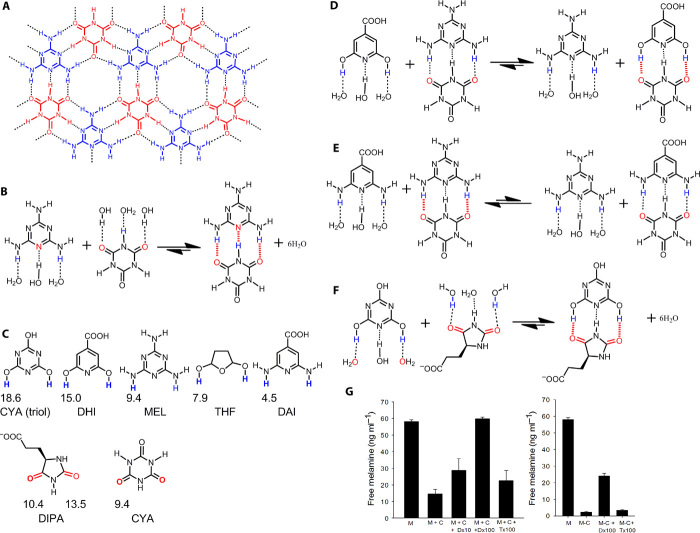
Fig. 1. The s-s/w-w H-bond pairing principle and the effect of protein-ligand H-bonds on protein-ligand binding.
(A) General schematic of the principle. Red and blue circles indicate H-bond acceptors and donors, respectively, with the symbol representing the relative H-bonding capability. (B) Competing H-bonds of two ligand atoms (LA and LB) to a protein atom P: this illustrates the effect of the H-bonding capability on the ligand binding affinity. (C) Relationship between the ΔG° of process (B) and HB − HA; HA and HB are the H-bonding capability of LA and LB, respectively. The slopes of the lines are directly proportional to HW – HP (the difference in H-bonding capability between water and the protein atom). (D) Relationship between ΔGHB for protein-ligand H-bonds and the H-bonding capability of ligand atom (HL). ΔGs-s° is the contribution of s-s pairing H-bonds shown in Fig. 3B to the ligand binding affinity; ΔGw-s° is associated to the polar-apolar interaction (w-s pairing H-bonds) shown in Fig. 3B. The yellow region represents H-bonds that have little effect on binding affinity.
Table 1. H-bonding capabilities (in kilojoules per mole) of defined atoms (red) in basic functional groups calculated from water/hexadecane partition coefficients (fig. S2): R, R1, and R2 represent alkyl groups.
The H-bonding capability for oxygen atoms is the value of a lone pair (±SDs).
| H-bond acceptors | H-bond donors | ||
| Atom | H-bonding capability | Atom | H-bonding capability |
| H2O | 7.02 (±0.11) | H2O | 7.02 (±0.11) |
| Apolar atom | 0 | Apolar atom | 0 |
| Alcohol | Alcohol | 6.6 (±0.21) | |
| RCH2OH | 8.7 (±0.42) | RCH2OH | |
| RR1CHOH | 9.5 (±0.58) | RR1CHOH | 6.3 (±0.20) |
| SerCH2OH | 8.1 (±0.42) | CF3CH2OH | 10.2 (±0.45) |
| Ether | Amide | ||
| THF: (CH2)4O | 8.2 (±0.22) | RCH2C(=O)NHR1 | 7.6 (±0.65) |
| RCH2OCH2R | 7.2 (±0.35) | C6H5C(=O)NHR1 | 7.2 (±0.86) |
| Aldehyde | Phenol | ||
| RCH2CHO | 8.9 (±0.45) | 4-R-C6H4OH | 10.8 (±0.74) |
| 4-RC6H4CHO | 7.6 (±0.26) | 4-NO2-C6H4OH | 16.9 (±0.75) |
| Ketone | Aniline | ||
| 4-RC6H4COMe | 10.4 (±0.27) | C6H5NH2 | 2.7 (±0.51) |
| RCH2COCH2R | 9.8 (±0.55) | 4-NO2-C6H4NH2 | 6.1 (±0.78) |
| Ester (O.2) | Amino | ||
| 4R-C6H4C(=O)OCH3 | 8.4 (±0.26) | RCH2NH2 | 1.3 (±0.34) |
| RCH2C(=O)OCH2R | 9.6 (±0.47) | (RCH2)2NH | 1.5 (±0.61) |
| Amide | Acid | ||
| RCH2C(=O)NH2 | 14.5 (±0.62) | RCH2COOH | 11.2 (±0.86) |
| RCH2C(=O)NHCH3 | 14.9 (±0.64) | C6H5COOH | 11.5 (±1.03) |
| RCH2C(=O)N(CH3)2 | 15.9 (±0.22) | Cl3CCOOH | 20.4 (±0.77) |
| C6H5C(=O)NH2 | 12.0 (±0.88) | 3NO2-C6H4COOH | 13.2 (±1.06) |
| Amino | Others | ||
| RCH2NH2 | 19.7 (±0.58) | CHCl3 | 3.6 (±0.42) |
| (RCH2)2NH | 22.9 (±0.42) | CHBr3 | 2.7 (±0.31) |
| (RCH2)3N | 22.8 (±0.31) | RCH2NO2 | 0.85 (±0.16) |
| Nitrile | RCH2CN | 0.6 (±0.14) | |
| RCH2CN | 18.1 (±0.36) | ||
| C6H5CN | 15.4 (±0.43) | ||
| Pyridine | |||
| C5H5N | 18.2 (±0.62) | ||
| 4-CN-C4H4N | 12.3 (±0.64) | ||
| Others | |||
| C6H5O*H | 6.4 (±0.51) | ||
| Furan: C4H4O* | 2.9 (±0.65) | ||
| RC6H5 (pi electron) | 1.6 (±0.18) | ||
*Because the two lone pairs of electrons are not identical, H-bonding capability is the value of the oxygen atom.
Experimental support for the strong-strong or weak-weak (s-s/w-w) H-bond pairing principle is provided by the observation that the H-bond competing process between two halide ions and two hydrogen halides in a gaseous system (Eq. 5) favors the s-s/w-w pairing in enthalpy
| (5) |
The enthalpy change (ΔH) in Eq. 5, calculated from the experimental data for the H-bond energies, is −19.9 kcal/mol (Table 2) (25), indicating that the equation favors s-s/w-w H-bond pairing in enthalpy because HCl is a stronger H-bond donor than HF and F− is a stronger H-bond acceptor than Cl−. This phenomenon is universal because all H-bond competing processes listed in Table 2 favor s-s/w-w pairing in enthalpy. Although entropy-enthalpy compensation exists, the favorable enthalpic contributions of H-bond competing processes are only partially canceled by unfavorable entropic contribution (TΔS) (fig. S1). Thus, H-bond competing processes favor s-s/w-w pairing in free energy.
Table 2. Enthalpy changes for the H-bond competing processes (A + B ↔ C + D) of strong ionic H-bonds (ΔH, in kilocalories per mole).
On the basis of the H-bond energies given (25), we list H-bond competing processes, the energy of each H-bond, and the enthalpy change (ΔH) of each process. The strongest H-bond of each process is D, which is on the right side of the process. Because all processes have negative ΔH values, we conclude that the reversible H-bond competing process favors the s-s/w-w H-bond pairing in enthalpy. A, B, C, and D denote the hydrogen bonds of the H-bond competing processes. EA, EB, EC, and ED denote the hydrogen bond energy of A, B, C, and D in kilocalories per mole.
| A | B | C | D | EA | EB | EC | ED | ΔH | |
| 1 | Cl…H-Cl | F…H-F | Cl…H-F | F…H-Cl | 23.1 | 38.6 | 21.8 | 59.8 | −19.9 |
| 2 | Cl…H-Br | F…H-F | Cl…H-F | F…H-Br | 29.0 | 38.6 | 21.8 | 65.0 | −19.2 |
| 3 | Cl…H-I | F…H-F | Cl…H-F | F…H-I | 32.0 | 38.6 | 21.8 | 72.0 | −23.2 |
| 4 | Cl…H-CN | F…H-F | Cl…H-F | F…H-CN | 21.0 | 38.6 | 21.8 | 39.5 | −1.7 |
| 5 | Br…H-Cl | F…H-F | Br…H-F | F…H-Cl | 19.0 | 38.6 | 17.0 | 59.8 | −19.2 |
| 6 | Br…H-Br | F…H-F | Br…H-F | F…H-Br | 20.0 | 38.6 | 17.0 | 65.0 | −23.4 |
| 7 | Br…H-CN | F…H-F | Br…H-F | F…H-CN | 16.0 | 38.6 | 17.0 | 39.5 | −1.9 |
| 8 | I…H-Cl | F…H-F | I…H-F | F…H-Cl | 13.0 | 38.6 | 15.0 | 59.8 | −23.2 |
| 9 | CN…H-Cl | F…H-F | CN…H-F | F…H-Cl | 37.0 | 38.6 | 21.1 | 59.8 | −5.3 |
| 10 | F…H-F | CN…H-Br | CN…H-F | F…H-Br | 38.6 | 42.0 | 21.1 | 65.0 | −5.5 |
| 11 | CN…H-CN | F…H-F | CN…H-F | F…H-CN | 20.0 | 38.6 | 21.1 | 39.5 | −2.0 |
| 12 | Cl…H-I | F…H-Cl | Cl…H-Cl | F…H-I | 32.0 | 59.8 | 23.1 | 72.0 | −3.3 |
| 13 | Cl…H-Cl | F…H-CN | Cl…H-CN | F…H-Cl | 23.1 | 39.5 | 21.0 | 59.8 | −18.2 |
| 14 | Br…H-Br | F…H-Cl | Br…H-Cl | F…H-Br | 20.0 | 59.8 | 19.0 | 65.0 | −4.2 |
| 15 | Br…H-Cl | F…H-CN | Br…H-CN | F…H-Cl | 19.0 | 39.5 | 16.0 | 59.8 | −17.3 |
| 16 | CN…H-Cl | F…H-CN | CN…H-CN | F…H-Cl | 37.0 | 39.5 | 20.0 | 59.8 | −3.3 |
| 17 | Cl…H-I | F…H-Br | Cl…H-Br | F…H-I | 32.0 | 65.0 | 29.0 | 72.0 | −4.0 |
| 18 | Cl…H-Br | F…H-CN | Cl…H-CN | F…H-Br | 29.0 | 39.5 | 21.0 | 65.0 | −17.5 |
| 19 | Br…H-Br | F…H-CN | Br…H-CN | F…H-Br | 20.0 | 39.5 | 16.0 | 65.0 | −21.5 |
| 20 | F…H-CN | CN…H-Br | CN…H-CN | F…H-Br | 39.5 | 42.0 | 20.0 | 65.0 | −3.5 |
| 21 | Cl…H-I | F…H-CN | Cl…H-CN | F…H-I | 32.0 | 39.5 | 21.0 | 72.0 | −21.5 |
| 22 | Br…H-Br | Cl…H-F | Br…H-F | Cl…H-Br | 20.0 | 21.8 | 17.0 | 29.0 | −4.2 |
| 23 | I…H-Cl | Cl…H-F | I…H-F | Cl…H-Cl | 13.0 | 21.8 | 15.0 | 23.1 | −3.3 |
| 24 | CN…H-F | Cl…H-Cl | Cl…H-F | CN…H-Cl | 21.1 | 23.1 | 21.8 | 37.0 | −14.6 |
| 25 | CN…H-F | Cl…H-Br | Cl…H-F | CN…H-Br | 21.1 | 29 | 21.8 | 42.0 | −13.7 |
| 26 | Br…H-Br | Cl…H-Cl | Br…H-Cl | Cl…H-Br | 20.0 | 23.1 | 19.0 | 29.0 | −4.9 |
| 27 | CN…H-CN | Cl…H-Cl | Cl…H-CN | CN…H-Cl | 20.0 | 23.1 | 21.0 | 37.0 | −14.9 |
| 28 | Br…H-Br | Cl…H-CN | Br…H-CN | Cl…H-Br | 20.0 | 21.0 | 16.0 | 29.0 | −4.0 |
| 29 | CN…H-CN | Cl…H-Br | Cl…H-CN | CN…H-Br | 20.0 | 29.0 | 21.0 | 42.0 | −14.0 |
| 30 | I…H-Cl | Br…H-F | I…H-F | Br…H-Cl | 13.0 | 17.0 | 15.0 | 19.0 | −4.0 |
| 31 | Br…H-Cl | CN…H-F | Br…H-F | CN…H-Cl | 19.0 | 21.1 | 17.0 | 37.0 | −13.9 |
| 32 | Br…H-Br | CN…H-F | Br…H-F | CN…H-Br | 20.0 | 21.1 | 17.0 | 42.0 | −17.9 |
| 33 | Br…H-Br | CN…H-Cl | Br…H-Cl | CN…H-Br | 20.0 | 37.0 | 19.0 | 42.0 | −4.0 |
| 34 | Br…H-Cl | CN…H-CN | Br…H-CN | CN…H-Cl | 19.0 | 20.0 | 16.0 | 37.0 | −14.0 |
| 35 | CN…H-CN | Br…H-Br | Br…H-CN | CN…H-Br | 20.0 | 20.0 | 16.0 | 42.0 | −18.0 |
| 36 | I…H-Cl | CN…H-F | I…H-F | CN…H-Cl | 13.0 | 21.1 | 15.0 | 37.0 | −17.9 |
The H-bond pairing principle applied to protein-ligand interactions
The ΔG for the reversible competing protein-ligand H-bonding process shown in Eq. 1 has two components: (i) the ΔG associated with the release of a well-ordered water molecule into the bulk solvent (Eq. 2), which does not depend on protein-ligand interactions, and (ii) the ΔG associated with protein-ligand H-bonds (Eq. 3). The ΔG in Eq. 3 cannot be obtained from experimental data. However, because the H-bond competing process between the same H-bonding protein atom and different ligand atoms (Fig. 1B) obeys the H-bond pairing principle, ΔG can be calculated by comparing the experimental binding affinities of the two ligands. The ΔG for the H-bond competing process of two ligand atoms with the same protein atom(s) (Fig. 1B) can be expressed as shown in Eq. 6 (for theoretical proof and validation, see text S2)
| (6) |
where k is a constant and is equal to 1/HWH; HPH, HWH, HA, and HB are the H-bonding capabilities of the protein atom(s), the H-bond donor or H-bond donor of water, and the atoms of ligands A and B, respectively. The effect of H-bond geometry on ΔG is factored into the H-bonding capability of the protein atom(s) (see text S3 for details). The relationship between the ΔG for the H-bond competing process of two ligands is shown in Fig. 1B, and the difference between the H-bonding capabilities of the two ligand atoms (HB − HA) is shown in Fig. 1C.
Equation 6 is a mathematical expression of the H-bond pairing principle. Because this derivation is complex, some approximations are used to develop the models. For example, to derive Eq. 6, we assume that single H-bonds of similar distance make up the pairings. However, the calculated ΔG for the H-bond pairing process—in which two H-bonding acceptors compete and bind to the same nonpolar site on a protein receptor—is the same as the ΔG obtained from the experimental water/hexadecane partition coefficients for any H-bond pairings (Fig. 2). These experimental findings validate the model as fitting beyond its approximations (see Fig. 2 and text S2). We further validate Eq. 6 by showing that strong H-bonds in different pairing models have opposing effects on experimental binding free energy. A notable example is provided in Fig. 3, which shows that strong s-s pairing H-bonds between 2 and its protein receptor enhance binding affinity, whereas the strong-weak (s-w) pairing between 4 and its protein receptor is not as favorable as the w-w pairing provided in the form of a polar-apolar interaction. Moreover, the reported binding affinities of two structurally similar scytalone dehydratase inhibitors 1 and 2 (Fig. 3A) (26) indicate that substitution of an apolar H atom (H-bonding capability, 0) for a cyano group (H-bonding capability, 16.0) enhances receptor antagonism by ~30,000-fold (fig. S3). The binding free energy difference (ΔΔG) between 1 and 2 mainly results from (i) H-bond interactions with Tyr30 and Tyr50 (ΔGHB) and (ii) the relative flexibility of the OH groups in Tyr30 and Tyr50 (ΔGflex) because the OH groups interacting with 2 are less flexible. The first term, ΔGHB, is the ΔG of the H-bond competing process as shown in Fig. 3B, which is −33.2 ± 3.2 kJ/mol because the HPH, HA, and HB of the process are 21.6 ± 1.5, 0, and 16.0 ± 0.5, respectively. The free energy required for fixing two rotatable bonds (ΔGflex) is ~7.4 ± 1.8 kJ/mol because the predicted free energy cost for rotor restrictions is close to 3.7 ± 0.9 kJ/mol per rotor (27, 28). Thus, the calculated ΔΔG is −25.8 ± 3.7 kJ/mol, which is in close agreement to the experimental ΔΔG (−25.6 kJ/mol at 298 K). On this basis, we conclude that the s-s pairing H-bonds between the cyano group of 2 and the receptor tyrosine hydroxyls can markedly increase the binding affinity. Further evidence that shows that the H-bond interactions between the inhibitor 2 CN group and the receptor tyrosine hydroxyls are strong and favorable to binding affinity is based on their geometry and large effects on binding affinity (fig. S4).
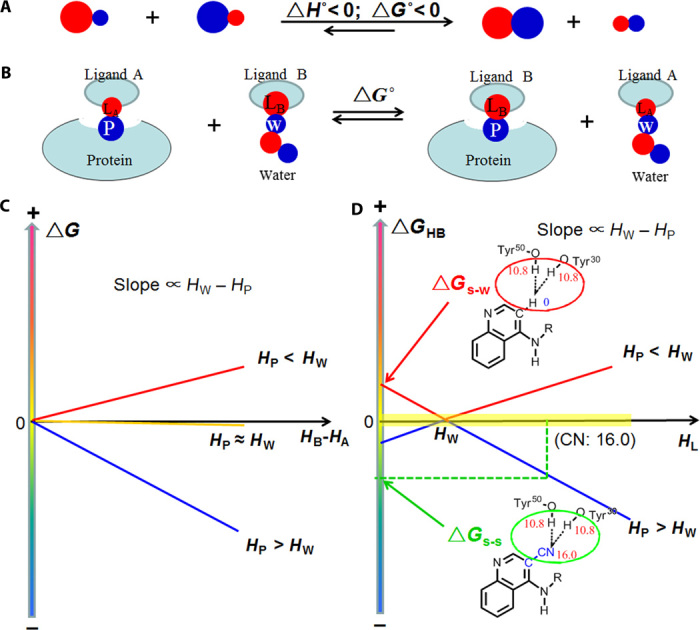
Fig. 2. Validation of Eq. 6 based on the definition of H-bonding capability.
(A) A competing H-bond pairing process shows the binding of two H-bonding acceptors A and B bound to the same nonpolar site of a protein receptor. (B and C). Because the nonpolar environment is similar to hexadecane, process (A) can be represented as two subprocesses (B and C), which are relevant to the definition of H-bonding capability. The free energy change of process (A) is HB − HA (H-bonding capability) and is derived from experimental water/hexadecane partition coefficients. Because the H-bonding capability of nonpolar atoms is zero, the calculated free energy change based on Eq. 6 is similar to the experimental data, irrespective of the nature of HB and HA. Further validation is provided in text S2.
Fig. 3. Validation of Eq. 6 with reported experimental data.
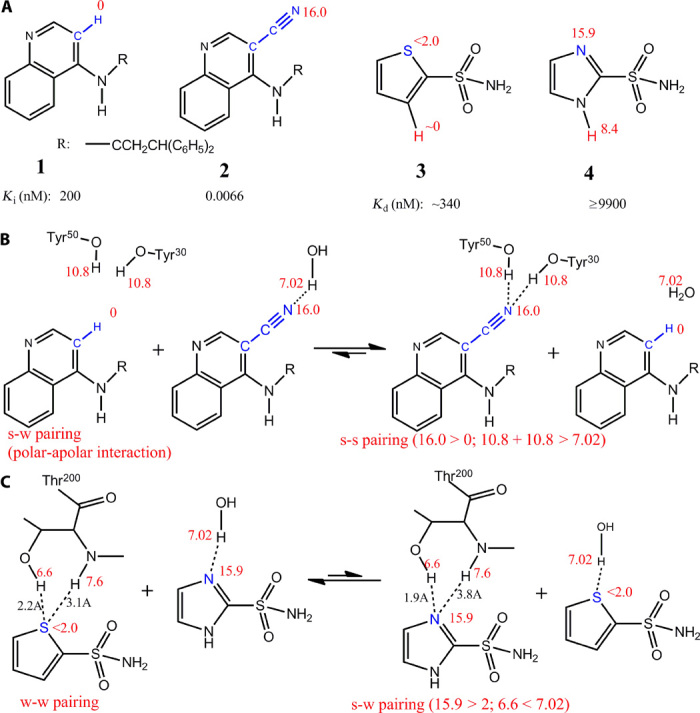
(A) Structures of the inhibitors used in this figure. Inhibitors 1 and 2 are scytalone dehydratase inhibitors. Inhibitors 3 and 4 are carbonic anhydrase inhibitors. (B) The competing H-bond pairing process between inhibitors 1 and 2 is used to calculate whether s-s H-bond pairings enhance ligand binding affinity. (C) The competing H-bond pairing process between inhibitors 3 and 4 demonstrates that the strong H-bond between 4 and Thr200 (s-w pairing) is less favorable to binding affinity than the weak interaction between 3 and Thr200 (w-w pairing).
By contrast, the reported binding affinities of two heterocyclic aromatic sulfonamide inhibitors of carbonic anhydrase (3 and 4; Fig. 3, A and C, and fig. S5) indicate that the strong H-bond between 4 and Thr200 is not as favorable as the weak (polar-apolar) interaction between 3 and Thr200. The binding affinity of 4 is ~30-fold lower than 3. Two factors contribute to the difference in binding affinity: (i) differential H-bond interactions with Thr200 (ΔGHB), which is equal to the ΔG for the H-bond pairing shown in Fig. 3C, and (ii) the free energy difference in transferring the hydrogen atoms from water to protein (ΔGsol; colored red on the aromatic rings of 3 and 4 in Fig. 3A). Because protein has a higher dielectric constant than hexadecane, ΔGsol is less than the free energy difference in transferring the hydrogen atoms from water to hexadecane (which is 8.4 kJ/mol based on the H-bonding capabilities of the hydrogen atoms). Thus, transferring the hydrogen atom of 4 reduces the activity <30-fold (=108.4/5.71) compared with the hydrogen atom of 3. Because the difference in activity between 4 and 3 is ~30-fold, the strong H-bond between 4 and Thr200 (s-w pairing) is not as favorable as the weak H-bond between 3 and Thr200 (w-w pairing).
Free energy contribution of a protein ligand H-bond to ligand binding affinity
Concordance between experimental and calculated results is supportive of Eq. 6, and from this, the free energy contribution of a protein ligand H-bond (ΔG in Eq. 3) can be calculated from Eq. 7
| (7) |
where k is a constant and HW, HL, and HP are the H-bonding capabilities of the H-bond donor/acceptor of water, ligand atom, and protein atom, respectively. The relationship between ΔGHB and HL, HP (Fig. 1D) offers insight into how specific protein-ligand H-bonds contribute to binding affinity in the following ways:
(i) H-bonds with s-s pairings increase ligand binding affinity. An example is provided by the strong binding affinity of the scytalone dehydratase inhibitor 2 (Fig. 3A) (26). The s-s H-bond pairings between the cyano group (HL = 16.0 > HW) and two strong donors from Tyr30 and Tyr50 (HL = 21.6 > HW) increase the binding affinity by ~300-fold (fig. S3). Another noteworthy analogy exists in nature, where the high-affinity binding of biotin to streptavidin (Ka = 2.5 × 1013 M−1) (29) represents a prototypic example of how s-s H-bond pairings facilitate exceptionally strong interactions for a molecule with such few heavy atoms (Fig. 4). All H-bond–forming atoms from the ureido ring of biotin form s-s receptor-ligand H-bond pairings. The H-bonds for the ureido oxygen contribute significantly to the binding affinity because of the extreme H-bonding capabilities of both donors and acceptors. For the H-bond acceptor, the ureido oxygen has two lone pairs of electrons with an H-bonding capability of 14.3 per lone pair. For the H-bond donors, the sum of the H-bond capability of the three H atoms in Asn23, Ser27, and Tyr43 is 25.0, much stronger than the sum of the H-bonding capability of two water H-bond donors (14.04). Critical importance of this s-s H-bond pairing in reducing competitive interference with water is demonstrated by the biotin analog 2-iminobiotin, where binding affinity to streptavidin is reduced by more than 3 million–fold (Fig. 4) (30). Although there is some unfavorable positive-positive repulsion between 2-iminobiotin and the side chains of streptavidin, these interactions are minor because these side chains are rotatable (Fig. 4). Thus, the s-s H-bond pairings of the ureido oxygen atom are important for the high affinity of biotin to streptavidin.
Fig. 4. Streptavidin-biotin as a prototypical example of the contribution of s-s/w-w H-bond pairings to high binding affinity.
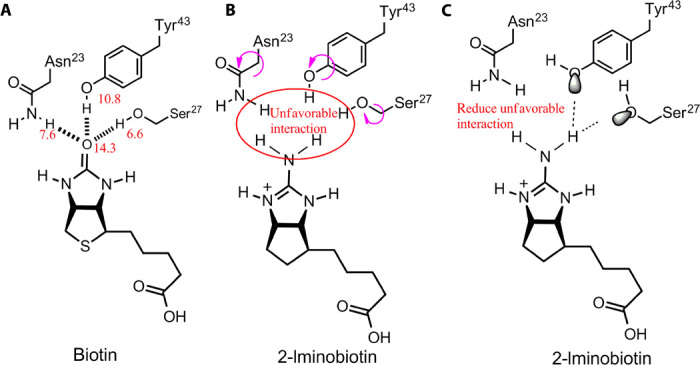
(A) H-bond interactions between the ureido oxygen atom from biotin and streptavidin. The H-bonds contribute significantly to binding affinity because of the extreme H-bonding capabilities for both H-bond donors and H-bond acceptors. (B) Structure and interactions of the biotin analog 2-iminobiotin, which is highly similar in structure to biotin, yet its binding affinity to streptavidin is >3 million–fold lower (30). (C) The unfavorable positive-positive interactions between the imino group and H-bond donors in (B) are minimal because the side chains are rotatable.
(ii) Ligand binding affinity is relatively unaffected by the strength of H-bonds when the H-bonding capability of the ligand or protein atom is close to that of water (ΔGHB ≈ 0; Fig. 1D). The binding of the heterocyclic aromatic sulfonamide inhibitors (5, 6, and 7 in Fig. 5) to carbonic anhydrase (31) represents an example where significant modification of H-bond strength fails to improve the binding affinity. The ligand acceptors form H-bonds with OH and NH of Thr200, but the latter H-bond is weak because of large donor-acceptor distances. Because the H-bonding capability of the protein is close to that of water, ligands 5, 6, and 7 have similar binding affinities, although the H-bond acceptors have markedly different H-bonding capabilities.
Fig. 5. Ligand binding affinity is relatively unaffected when the H-bonding capability is close to water.
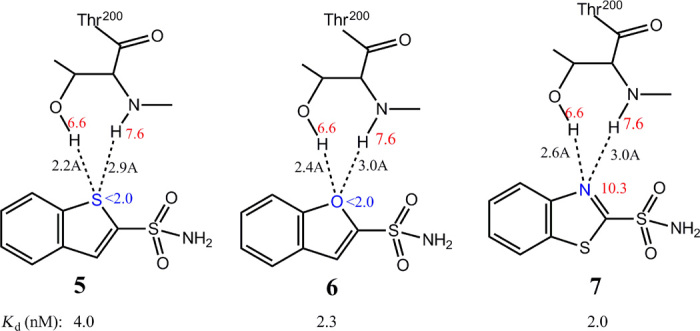
Interactions between the H-bond acceptors of three heterocyclic aromatic sulfonamide inhibitors (5, 6, and 7) with large differences in H-bonding capabilities and the H-bond donors from the receptor Thr200. Because the H-bonding capability of the receptor Thr200 protein is close to that of water, the ligand binding affinity is relatively unaffected by the varying strengths of the H-bonds that are formed. A similar inhibitor, 1H-benzimidazole-2-sulfonamide, is excluded from our comparison because its extra polar hydrogen atom affects binding affinity.
(iii) s-w H-bond pairings are less favorable than w-w pairings, although they might be stronger. A typical example in Fig. 3C indicates that the nature of the H-bond pairing is more important than H-bond strength. This phenomenon is further illustrated by the favorable interactions between aromatic rings and polarized CH groups (32, 33). Aromatic rings are weak H-bond acceptors (32, 34), whereas CH groups are weak H-bond donors (34, 35). The favorable hydrophobic interaction with a weak H-bond (w-w pairing) explains the inhibitory action of antagonists on factor Xa activity (Fig. 6) (36). The compound with a quaternary ammonium cation [–N(Me)3+] (8) is ~1100-fold more active than the ammonium ion (–NH3+) compound (9), indicating that hydrophobic pairings with weak (w-w) H-bonds are more favorable than the s-w interactions. Although the –NH3+ of 9 may not interact with the aromatic rings, logic analysis indicates that –NH3+-π interactions are less favorable than –N(Me)3+-π interactions (fig. S6). Also, van der Waals interactions are insufficient to explain the large potency differences. Thus, mixed s-w H-bond pairings can decrease protein-ligand binding affinity even when H-bonds are strong, offering new mechanistic insight into why some strong H-bonds do not enhance ligand binding affinity; generalizations that H-bonds contribute minimally to binding affinity may therefore be inaccurate. Notably, s-w H-bond pairings with a ligand atom can significantly reduce its binding affinity as is demonstrated by the relatively weak binding affinity of the scytalone dehydratase inhibitor 1 (Fig. 3A) (26), with its apolar hydrogen atom (HL = 0 < HW) interacting with two strong H-bond donors from Tyr30 and Tyr50 (HP = 21.6 > HW). The s-w pairing interaction decreases binding affinity by ~90-fold (fig. S3).
Fig. 6. Favorable π–quaternary ammonium cation interactions with w-w H-bond pairings.
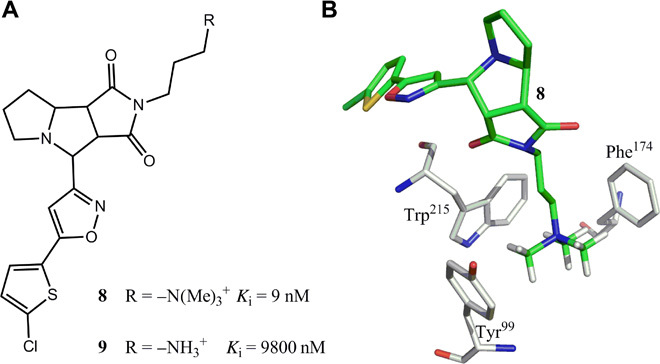
(A and B) Structures of two factor Xa antagonists 8 and 9. Antagonist 8 is ~1100-fold more active than 9 because of the w-w pairing interactions between the hydrophobic aromatic rings of factor Xa and polarized CH groups [–N(Me)3+] shown in (B) (Protein Data Bank: 2JKH).
Application of the H-bond pairing principle to drug design
Our findings demonstrate that protein-ligand binding affinity is dependent on H-bond pairing effects on ΔG (Fig. 1D), and altering one ligand atom/group may significantly modulate the binding affinity (Figs. 3 to 6). On this basis, precision-based drug design can be modeled on the H-bond pairing principle. The simplest approach is to optimize ligands on the basis of available crystal structures of the protein-ligand complexes. By analyzing H-bond pairings between each receptor-ligand interaction, ligand atoms requiring modification can be identified (and the manner in which the modification should be effected) to achieve maximum ligand binding affinity.
As an experimental example, we applied the H-bond pairing principle in the lead discovery for pathogenic molecular self-assembly involving s-s H-bond pairings that contribute to renal toxicity in humans. In principle, toxicity caused by the formation of insoluble kidney stones, when dietary melamine forms a complex with cyanuric acid (Fig. 7, A and B, and fig. S7) (37), can be reduced by increasing the solubility of the melamine–cyanuric acid complex using water-soluble molecules that form stronger s-s H-bond pairings with melamine or cyanuric acid. By screening the ZINC database (38) for compounds that are structurally similar to cyanuric acid or melamine, but have stronger H-bonding capability and contain an ionic group for better solubility, we identified two compounds—DHI and DIPA (Fig. 7C)—that specifically target the s-s H-bonds in the insoluble melamine–cyanuric acid complex, releasing free melamine into solution (Fig. 7, D and F, and fig. S7). This approach is not limited to biological systems because certain compounds containing both strong H-bond donors and acceptors can form strong intermolecular s-s pairing H-bonds that prevent them from solubilizing in water and apolar solvents. Thus, the H-bond pairing principle may also be applied to identify solvents that form favorable s-s H-bond pairings with candidate insoluble compounds, making them more soluble.
Fig. 7. Pathogenic s-s H-bond pairings in melamine toxicity.
(A) Structural analysis of melamine (MEL, blue)–cyanuric acid (CYA, red) interactions demonstrates an extensive H-bonding network (dashed lines) that promotes the formation of toxic insoluble crystals. (B and C) The MEL and CYA complex forms s-s H-bond pairings (fig. S7), with H-bonding capabilities of MEL and CYA and of inhibitors 2,6-dihydroxyisonicotinic acid (DHI), 3-(2,5-dioxo-4-imidazolidinyl)propanoic acid (DIPA), and tetrahydrofurandiol (THF) shown in (C). (D and E) Although DHI (D) and 2,6-diaminoisonicotinic acid (DAI) (E) are structurally similar, the hydrogen atoms of DHI have a much stronger H-bonding capability (C). (G) (left) We used this calculation of H-bonding capability to demonstrate that DHI preferentially forms a complex with CYA when compared with DAI or MEL (F). Statistically significant inhibition of MEL-CYA complex formation was also demonstrated with DIPA, which forms s-s H-bond pairings with the triol tautomer of CYA. The triol tautomer predominates in solution because of its aromatic character. DIPA also dissolved MEL-CYA crystal in solution (whereas THF did not) (G; right), illustrating how the s-s/w-w H-bond pairing principle may be applied to lead optimization in diseases caused by low solubility (error bars show SEM; P < 0.05 was considered significant using t test or Mann-Whitney U test for ranks).
The H-bond pairing principle can also be applied to targets where traditional drug design methods are difficult to implement. One approach is to evaluate the H-bonding capability of the receptor atoms based on the effect of H-bonding capability on free energy contribution; ligands can then be modified based on the H-bond pairing principle (Fig. 8A). We adopted this approach in the redesign of the Clostridium difficile toxin inhibitor inositol hexakisphosphate (InsP6). C. difficile is the most prevalent cause of nosocomial infectious diarrhea and life-threatening colitis worldwide, and has rapidly become a significant unmet medical problem in hospitals, long-term care facilities, and the community (39). Patients typically develop C. difficile infection after the use of broad-spectrum antibiotics, immunosuppressive agents, or chemotherapy, which disrupt the normal gut microbiota. C. difficile clinical isolates produce two pathogenic enterotoxins, TcdA and TcdB, which are allosterically regulated by InsP6 (40, 41). We and others have demonstrated that InsP6 is a natural allosteric inhibitor of these toxins in vitro, by inducing autocatalytic self-cleavage (42). However, InsP6 shows suboptimal efficacy when orally administered in vivo (42). Traditional methods cannot be used to optimize InsP6, because the binding site contains a disproportionally high ratio of charged versus hydrophobic residues (Fig. 8A) and the positively charged residues already have strong interactions with the negatively charged phosphate groups of InsP6 (42).
Fig. 8. Lead optimization of the C. difficile toxin inhibitor InsP6 using the s-s/w-w H-bond pairing principle.
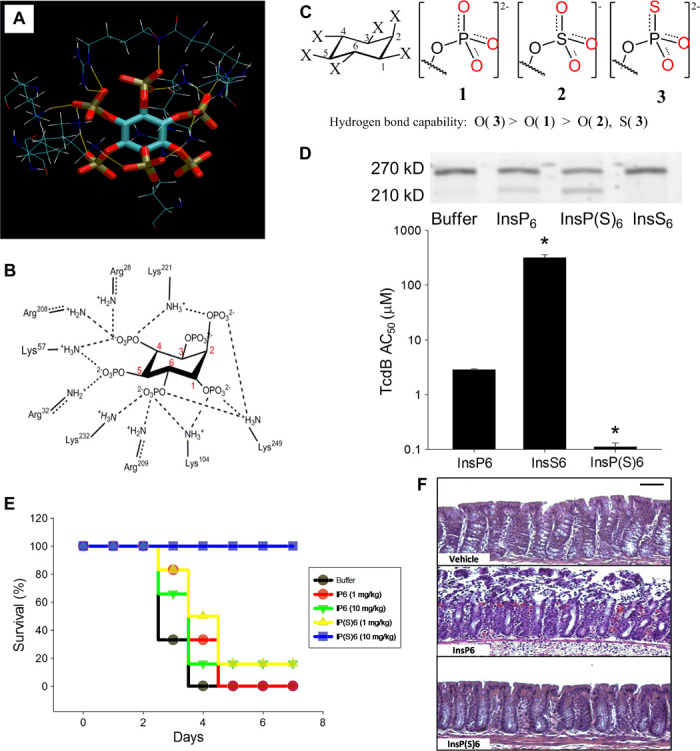
(A and B) H-bond interactions between InsP6 and allosteric binding site residues on TcdB based on the crystal structure 3PA8. (C) Structures of InsP6, its derivative InsP(S)6, and the structural analog InsS6 and the relative H-bonding capability of the oxygen atoms. (D) (Top) TcdB autocleavage induced by 100 nM InsP6, InsP(S)6, or InsS6 shows intact unprocessed (270 kD) and processed toxin cleavage products (205 kD). Processed toxin is inactive as the virulent glucosyltransferase domain fails to enter the target cell. (Bottom) InsP6 binding affinity for TcdB as measured by its self-cleavage activity in vitro (half-maximum activation constant, AC50, in micromole per liter). Increasing the H-bonding capability of the oxygen atoms in InsP(S)6 enhances the AC50 by 26-fold, whereas decreasing the H-bonding capability in InsS6 leads to a 110-fold reduction of AC50 (*P < 0.05 compared with InsP6). (E) Kaplan-Meier survival plots of C57BL/6 mice inoculated intragastrically with 103 C. difficile VPI 10463 spores and with InsP6 or InsP(S)6 (1 or 10 mg kg−1 day−1; n = 5 per group; survival at day 4; P < 0.05, analysis of variance on ranks). (F) Histopathology showing that oral InsP(S)6 is protective for colonic mucosa when administered at 10 mg.kg−1 day−1 (scale bar, 50 μm).
We decreased the H-bonding capability of the oxygen atom by converting the phosphate groups into sulfate groups (–O-SO3−); this led to a decrease (by two orders of magnitude) in the antitoxin activity (Fig. 8, C and D), indicating that the phosphate groups may interact with donors that have a higher H-bonding capability than the water hydrogen. Chemical conversion of the phosphate groups of InsP6 into −O-P(S)O22− significantly improved (26-fold increase) the toxin inhibitory activity (Fig. 8, C and D). This compound also demonstrated good efficacy in a clinically relevant infectious disease model of C. difficile infection, which could not be achieved with native InsP6 (Fig. 8, E and F). Thus, the InsP6 toxin neutralizing activity was successfully optimized by increasing the H-bonding capability of its phosphate groups.
Application of the H-bond pairing principle to enzymatic reactions
There is much interest in the role of electrostatic (H-bond) interactions on enzyme reactions. Because the contribution of H-bonds to the reduction of free energy barriers in enzyme reactions equates to that of substrate-enzyme binding in transition state (fig. S8), we applied the H-bond pairing principle to explore the role of H-bonds in the origin of enzymatic catalytic power. Well-oriented electrostatic (H-bond) interactions in the oxyanion hole of ketosteroid isomerase are reported to provide a major source of catalytic power (16). This view is based on models where H-bonding in the reference reaction in aqueous solution is assumed not to contribute to free energy barrier reduction. The well-oriented H-bonds in the oxyanion hole of ketosteroid isomerase (Fig. 9A) can reduce the free energy barrier to ~7.3 kcal/mol as compared to the reaction without H-bond interactions (Fig. 9B) (16). Thus, the free energy change for the competing H-bond pairing process (Fig. 9C) is the difference between the reactions in Fig. 9 (A and B) (7.3 kcal/mol). The free energy change for a similar competing H-bond pairing process (Fig. 9D), where all H-bonds are not restricted, is <−6.13 kcal/mol because the free energy required to fix two strong H-bonds is less than that required to fix two HOH…OH2 H-bonds in bulk water [~1.17 kcal/mol at room temperature (19)]. Calculations based on Eq. 6 indicate that the corresponding H-bonds in aqueous solution contribute >3.91 kcal/mol to the reduction of free energy barrier for the reference reaction (Fig. 9E), which is close to the data estimated from the experimental free energy barriers of ketosteroid isomerase mutants (19). Our findings indicate that electrostatic interactions in ketosteroid isomerase appear to contribute far less to the origin of catalytic power than has been previously reported, although the precise role for H-bond pairing in this enzymatic process needs to be verified through future experimentation.
Fig. 9. Estimating the contribution of H-bond interactions to the free energy barrier reduction for the isomerization of 5-androstene-3,17-dione (5-AND) in aqueous solution.
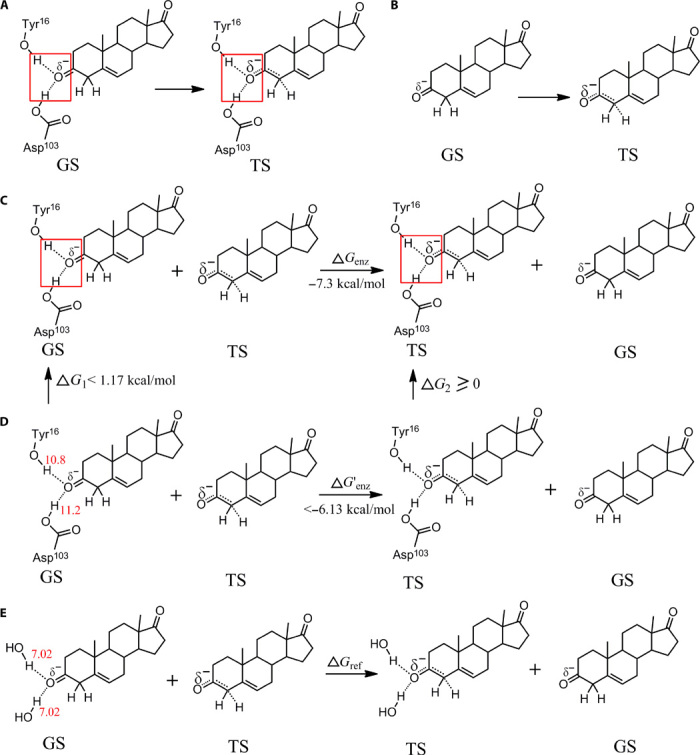
(A) H-bond interactions in the oxyanion hole of the ketosteroid isomerase for the ground state (GS) and transition state (TS). The H-bonds in red boxes are well oriented. (B) GS and TS without H-bond interactions. (C) Difference between (A) and (B), which is a competing H-bond pairing process. (D) H-bond pairing process in which the H-bond interactions are similar to (C) but are not restricted and can adopt a broad distribution of conformations as is seen in solution. (E) Competing H-bond pairing process for estimating the free energy barrier reduction contributed by the H-bond interactions of the reference reaction. We assume that the H-bonding capabilities for the atoms in the ketosteroid isomerase are close to those in solution. On the basis of Eq. 6, we get ΔG′enz = k × (0 − Henz)(HO_TS − HO_GS) and ΔG′ref = k × (0 − HW)(HO_TS − HO_GS). G′ref = ΔG′enz × (0 − HW)/(0 − Henz) < −6.13 × 14.04/22.0 = −3.91 (kcal/mol). Thus, the free energy barrier reduction for the isomerization of 5-AND in aqueous solution is larger than 3.91 kcal/mol.
DISCUSSION
Increasing hydrophobic interactions is a major consideration for lead optimization, as this often requires enhancing ligand molecular weight, rotatable bonds, and lipophilicity, all affecting the ADMET properties of ligands. Designing ligands with high binding affinity and satisfactory ADMET properties is therefore a major and often cost-prohibiting challenge (20). Here, we address these issues by establishing an s-s/w-w H-bond pairing principle to reveal a previously unappreciated mechanism by which H-bonds modulate receptor-ligand binding affinity. On the basis of theoretical calculation and reported experimental binding affinities, we demonstrate that receptor-ligand H-bonds contribute significantly to binding affinity by establishing synergistic s-s or w-w pairings in H-bonding capability. We also demonstrate that mixed s-w H-bond pairings can decrease protein-ligand binding affinity, even when H-bonds are significantly stronger than water, offering new mechanistic insight into why some strong H-bonds do not enhance ligand binding affinity. Generalizations that H-bonds confer minimal contribution to binding affinity may therefore be inaccurate because we show that an s-s pairing H-bond can increase the ligand binding affinity by a few hundredfold or more. On the basis of this premise, H-bonds can be made more favorable by increasing the H-bonding capability of the ligand atom without increasing the lipophilicity of ligands. Because enthalpy gains of s-s or w-w paired protein-ligand H-bonds are only partially canceled out by entropy, such H-bonds always remain favorable in terms of free energy. Thus, the H-bond pairing principle may be effective in designing ligands with high binding affinity and satisfactory ADMET properties, ultimately reducing drug design costs.
Our approach can also be applied to the precision design of ligands with high selectivity. With crystal structures of target proteins available, it is feasible to design ligands with high predictable binding affinity to specific target protein receptors because variations in a single H-bond can significantly alter the binding interactions. The H-bond pairing principle is also applicable to hydrophobic interactions, which can be considered as w-w H-bond pairings between atoms with an H-bonding capability approaching zero. We demonstrate feasibility by designing drug candidates showing in vitro efficacy against pathogenic dietary melamine. This type of an approach may find other important applications in pathogenic self-assembly, including inhibition of amyloid protein aggregation (43) and prevention of l-cystine stones (44).
The H-bonding capability parameter presented in this study is obtained from experimental partition coefficients. It has significant thermodynamic and interaction information encoded within it and represents the foundation for the accuracy of Eq. 6. The thermodynamic and interaction information includes the factors that potentially contribute to ligand binding affinity, including electrostatic interactions, desolvation, entropy (entropy related to rotatable bond is not included), and van der Waals interactions. Thus, the combination of the H-bond pairing principle and H-bonding capability makes the estimation of free energy contribution of H-bonds simpler and more accurate when compared with traditional approaches. This approach can similarly be applied to determine the origin of the catalytic power of an enzyme reaction. We demonstrate the use of this novel approach to estimate the contribution of H-bond interactions to the free energy barrier reduction of the reference reaction in aqueous solution, which is usually not experimentally accessible. Our approach also has application to certain compounds containing both strong H-bond donors and acceptors that form strong intermolecular s-s pairing H-bonds and, as such, are insoluble in water and apolar solvents. The H-bond pairing principle can potentially identify solvents that form more favorable s-s H-bond pairings with candidate insoluble compounds, making them more soluble.
Although almost all protein-ligand interactions include H-bond interactions, our studies are restricted to experimental examples where suitable reference compounds are available to accurately calculate the free energy contributed by specific H-bonds. The diverse examples and theoretical proof presented indicate the accuracy and the wide applications of the principle. Because of H-bonding cooperativity, the H-bonding capability of an atom within a protein may be slightly different from the H-bonding capability calculated based on the methods of this manuscript. For more accurate future interpretation of protein-ligand interactions, the effects of H-bonding cooperativity on H-bonding capability will also need to be investigated. Even if precise H-bonding capabilities cannot be obtained, Eq. 6 (or Eq. 7) may still be used in a qualitative capacity for drug design. The lead optimization of the C. difficile toxin inhibitor provides an example where Eq. 6 was successfully applied in a qualitative manner. Qualitative application of Eq. 6 is especially instructive when the information for protein-ligand interactions is unknown or the accurate H-bonding capability of the interacting atoms (for example, the ionic groups) is not available.
In conclusion, as water plays a crucial role in all known biological systems, synergistic s-s and w-w H-bond pairings have evolved to promote high-affinity receptor-ligand interactions by reducing competitive interference for H-bonds with water. This fundamentally new principle is potentially important for precision-based drug design because numerous studies have demonstrated that lead compounds cannot be optimized by indiscriminately increasing the strength of protein-ligand H-bonds. We expect these findings to be useful in any field relevant to H-bond pairing, including enzyme catalysis and drug solubility.
MATERIALS AND METHODS
Materials were obtained from Sigma-Aldrich Chemical Company or Invitrogen unless otherwise stated.
Methods for calculating H-bonding capability
Three-dimensional structures of small organic molecules used for calculating H-bonding capabilities were created using the SYBYL molecular modeling package (Tripos Inc.) and minimized with a Tripos force field. Molecular surface-accessible surface areas (SASAs) were calculated from atomic coordinates, and the radii of solvent were set to 1.4 Å. Data for Phxd (hexadecane/water partition coefficient) and Poct (1-octanol/water partition coefficient) were obtained from earlier experimental reports (23, 24). Experimental Phxd values for some compounds were also calculated from alkane/water partition coefficients. All partition coefficient data were converted to standard free energy by multiplying 2.303 by RT (R = 0.008314 kJ mol−1 K−1 and T = 298 K). The basic method to calculate H-bond capability is illustrated in fig. S2. The basis for this method is the strong correlation of free energy for phase transferring (Galk) with SASA for saturated hydrocarbons and the flexibility of the molecules (Flex), evaluated from the rotatable bonds
| (M1) |
A similar conclusion was also obtained from the method of Kenny et al. (21). The H-bond capability for a molecule (EM) was calculated directly as illustrated in fig. S2, and the calculation can be expressed as in Eq. M2
| (M2) |
Molecules that have intramolecular H-bond interactions were not used for the initial calculations. Thus, the H-bond capability of a molecule is the sum of the H-bond capabilities of all H-bond–forming atoms in the molecule
| (M3) |
where Ei is the H-bonding capability of atom i.
Electronic effects on H-bonding capability
A major modification of this method over that of Kenny et al. is that it considers the relationship between the H-bonding capability of an atom and the electronic effects of its connections, which include resonance and inductive effects. For example, the H-bonding capabilities of the oxygen and hydrogen atoms of the substituted phenol structure shown below are affected by the resonance and inductive effects of the substituent X.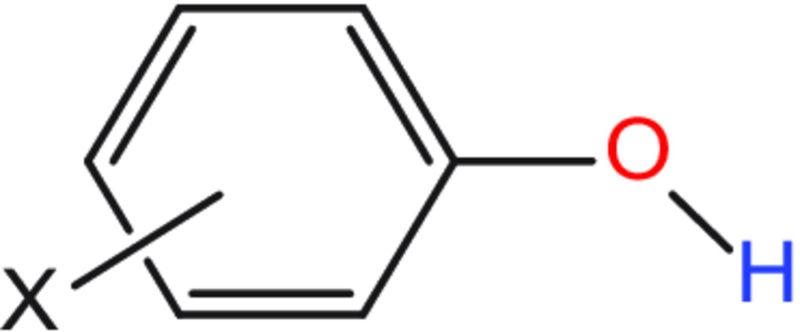
Because Hammett substituent constants (σ) (45) can be used as descriptors of resonance and inductive effects, they were used to build models. The following model was used to calculate the H-bonding capability (E) of an atom
| (M4) |
where E0 is H-bonding capability of the atom not affected by other atoms, ρ is a constant for certain atom types, and σ is the Hammett substituent constant of X.
Methods for calculating the H-bonding capability of atoms
The methods are classified into three types:
(i) The H-bonding capability of an atom (Ei) was calculated directly from the H-bonding capability of its molecule (EM) when the molecule contains only one H-bond–forming atom (such as ketone) or the H-bond capabilities of all H-bond–forming atoms are the same (for example, the six sp2 carbons in benzene are the same).
(ii) The H-bonding capability of an atom was calculated by subtracting the H-bonding capability of other H-bond–forming atoms in the molecule from the sum H-bonding capability of its molecule.
| (M5) |
(iii) The H-bonding capability of some atoms cannot be calculated from Phxd because more than one atom’s H-bonding capabilities in the molecule are unknown. Take substituted phenol as an example. Only the H-bonding capability of the OH group (EH) can be calculated from the hexadecane/water partition coefficient, whereas the H-bonding capability of O (EO) and H (EH) atoms cannot be calculated. In this case, 1-octanol/water partition coefficients (Poct) were used to cancel out one of the two unknown items. The energies for transferring the OH group of the substituted phenol from water to 1-octanol () were calculated using the same method as for calculating EOH
| (M6) |
where and are the energies for transferring oxygen and hydrogen atoms in the substituted phenol from water to 1-octanol.
Data analysis of H-bond acceptors indicated that there are strong correlations between E and Eoct, especially when the atom type and the steric environment are the same. Thus, , and fO was assumed to be the same for all substituted phenol and was set to 0.7092, which was estimated from compounds like ketones and alcohols.
Similarly, . Thus
| (M7) |
Also
| (M8) |
Dividing Eq. M7 by fO, and then abstracting the result from Eq. M8, we get
| (M9) |
Thus, the unknown item for oxygen was canceled and the H-bond capability for the H atom of phenol () and the constant k was obtained by building QSAR (quantitative structure-activity relationship) models based on a series of data for the substituted H. At this point, the parameters for the oxygen atom can be calculated. Standard errors for calculated H-bonding capabilities are shown in Table 1.
Synthesis of inositol hexakisphosphorothioate, InsP(S)6
Thin-layer chromatography was performed on 0.25-mm precoated glass plates (Merck silica gel 60F254) and detection was carried out using ceric ammonium molybdate. Chromatography was performed on an Isco Combiflash Companion using prepacked silica columns (Silicycle). All reagents were purchased from Sigma-Aldrich or Acros and used without further purification. 1H (400 MHz) and 31P (162 MHz) nuclear magnetic resonance (NMR) spectra were recorded at 25°C on a Varian INOVA instrument. Chemical shifts are given in parts per million. Mass spectra were measured at the University of Utah Medicinal Chemistry Department using electrospray ionization (ESI) or matrix-assisted laser desorption/ionization (MALDI).
1: Dibenzyl N,N-diisopropylphosphoramidite (450 μl, 1.37 mmol) was added to a suspension of myo-inositol (30 mg, 0.17 mmol) and 1H-tetrazole (140 mg, 2.0 mmol) in dry CH3CN (6 ml) and DMF (N,N′-dimethylformamide; 5 ml) under Ar. After stirring at room temperature for 24 hours, sulfur (135 mg, 4.2 mmol) was added followed by a mixture of carbon disulfide (120 μl, 2.0 mmol) and pyridine (120 μl, 1.2 mmol). The reaction was stirred overnight and then diluted with ethyl acetate (50 ml). The mixture was washed with saturated NaHCO3 (10 ml), dried (MgSO4), and evaporated under reduced pressure. The product was purified by chromatography (5 to 20% ethyl acetate in hexanes, 12 g silica). RF = 0.26 (4:1 hexanes/ethyl acetate). Yield: 142 mg (40%). 1H NMR (CDCl3): 6.92 to 7.23 (m, 60H), 5.16 to 5.52 (m, 5H), 4.86 to 5.10 (m, 25H). 31P NMR (CDCl3): 70.34, 69.90, 69.86, 69.11 (1:2:1:2). MALDI-MS: 1859.4 (M + Na)+.
InsP(S)6: Anhydrous ammonia (10 ml) was condensed into a flask that was cooled in a dry ice/isopropanol bath. Sodium (50 mg) was added and stirred until it completely dissolved, yielding a blue solution. A solution of 1 (37 mg, 0.20 mmol) in dry dioxane (2 ml) was added dropwise. The reaction was stirred for 15 min in the cooling bath and then quenched with ethanol (1 ml). The reaction was gradually allowed to warm to room temperature, and the residual solvents were evaporated under reduced pressure. The residue was dissolved in deionized H2O (50 ml), filtered through a syringe filter (0.45 μm), and applied to a column of DEAE cellulose (20 × 55 mm). The column was eluted with a linear gradient of 0 to 2 M triethylammonium bicarbonate buffer (pH 8). The desired fractions eluting at ~1.2 M were pooled and lyophilized. The product was resuspended in deionized water and converted to sodium salt by treatment with Dowex 50X8-100 (Na+) resin followed by lyophilization. Yield: 13.7 mg (69%). 1H NMR (D2O): 5.08 (d, J = 11.6 Hz, 1H), 4.71 (m, 2H), 4.50 (m, 1H), 4.35 (t, J = 11.6 Hz, 2H). 31P NMR (D2O): 53.89, 53.03, 52.8, 51.16 (1:2:2:1). ESI-MS 754.8 (M-H)−.
Melamine–cyanuric acid complex inhibition studies
Cyanuric acid, melamine, melamine–cyanuric acid crystal compound, DHI, DAI, DIPA, and THF were purchased from Sigma-Aldrich and Thermo Fisher Scientific. Cyanuric acid and melamine were separately solubilized in water at 10 mM by shaking at 60 rpm at room temperature for 4 hours with three 10-min incubations at 70°C. DHI, DAI, DIPA, and THF were solubilized in water at 250 mM. Inhibition of cyanuric acid–melamine complex formation was investigated by measuring free melamine in solution using the Melamine H.S. Plate Kit (Beacon Analytical Systems Inc.) briefly as follows: Up to 100-fold excess (25 mM) DHI, DAI, DIPA, or THF was incubated in phosphate-buffered saline (PBS) for 30 min, with shaking (30 rpm) at room temperature with 250 μM melamine in 1.5-ml Eppendorf LoBind tubes. After which, 250 μM cyanuric acid was added and incubated for 1 hour. Tubes were centrifuged at 22,000g for 5 min. The concentration of free melamine in the supernatant was measured using the Plate Kit. Release of free melamine from the cyanuric acid–melamine crystal was measured after sonicating 10 mM melamine–cyanuric acid complex in 1 ml of PBS for 10 s, followed by 1:40 dilution with PBS, DIPA, or THF (25 mM each) for 90 min, after which free melamine was measured. Assays were repeated three times in triplicate.
In vitro toxin cleavage assays
Autocleavage of 1 μg of TcdA and TcdB holotoxins was performed in 25 μl of 20 mM tris-HCl and 150 mM NaCl (pH 7.4 or pH 8.0) with and without InsP6, InsP(S)6, or InsS6 for 2 hours at 37°C as previously described (42). Cleavage reactions were stopped with SDS–polyacrylamide gel electrophoresis loading buffer and boiled at 96°C for 5 min. Samples were then run under reducing conditions on 4 to 20% gradient gels, and cleavage products were stained with GelcodeBlue (Pierce) for 1 hour and cleared in water overnight. AC50 concentrations were calculated by measuring the relative absorbance of cleavage fragments relative to intact toxin using a LiCor Odyssey infrared scanner (λ = 680 nm). Cleavage was plotted against ligand concentration using four-parameter logistic curve fitting on SigmaPlot12.0 software.
Infectious murine C. difficile infection model
A conventional mouse model of antibiotic-induced C. difficile infection, that resembles the spectrum of disease that is manifest in humans, was used as previously described (42). Disease severity varies from fulminant, with typical histopathologic features of C. difficile infection, to minimal diarrhea, depending on challenge dose. Twelve-week-old C57BL/6 mice were pretreated for 3 days with a mixture of antibiotics shown to disrupt the intestinal microflora. After 2 days, mice were injected with clindamycin and then challenged intragastrically with 103 C. difficile VPI 10463 spores the following day. Therapeutic efficacy of InsP6 and InsP(S)6 was tested by oral gavage of 1 or 10 mg kg−1 day−1 in 0.2 ml of PBS. All procedures were performed with Institutional Animal Care and Use Committee approval and in accordance with National Institutes of Health guidelines for use of live animals.
Supplementary Material
Funding
This work was supported by grants RO1AI100914, DK096323, P30DK56338, UL1TR0000711, and KL2TR000072 from the National Institute of Allergy and Infectious Diseases, National Institute of Diabetes and Digestive and Kidney Diseases, and National Center for Advancing Translational Sciences and the National Science Foundation of China (21473041 and 21303024). Author contributions: D.C. designed the study, wrote the manuscript, established the proof, and calculated the H-bonding capabilities; N.O. performed structural modeling of H-bonds; P.U. performed in vitro melamine and toxin studies; C.F. synthesized the InsP(S)6 analog; S.M.D. performed animal infectious disease studies; and T.S. designed the study and wrote the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/3/e1501240/DC1
Text S1. Theoretical proof of the H-bond pairing principle.
Text S2. Relationship between the free energy change for a reversible protein-ligand H-bond competing process and the H-bonding capability of the H-bond–forming atoms.
Text S3. The H-bonding capability of the protein atoms with which a ligand atom interacts and the effect of H-bond geometry on the H-bond interaction.
Fig. S1. Schematic illustration of the free energy change for the H-bond competing process.
Fig. S2. Calculation of H-bonding capability based on water/hexadecane partition coefficients.
Fig. S3. Contributions of the H-bonds between CN and the Tyr-OH from scytalone dehydratase to protein-ligand interactions.
Fig. S4. Proof for the strong H-bond interactions between the CN group of inhibitor 2 and tyrosine hydroxyls from scytalone dehydratase.
Fig. S5. Binding affinities of 1H-imidazole-2-sulfonamide and thiophene-2-sulfonamide.
Fig. S6. Quaternary ammonium cation [–N(Me)3+]-π interactions are more favorable than ammonium ion (–NH3+)-π interactions.
Fig. S7. A pathogenic role for the s-s/w-w H-bonding principle in melanin toxicity.
Fig. S8. The thermodynamic cycle that demonstrates the contribution of H-bonds to enzymatic catalytic power equates to their contribution to protein-ligand binding.
REFERENCES AND NOTES
- 1.Gao J., Bosco D. A., Powers E. T., Kelly J. W., Localized thermodynamic coupling between hydrogen bonding and microenvironment polarity substantially stabilizes proteins. Nat. Struct. Mol. Biol. 16, 684–690 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Salentin S., Haupt V. J., Daminelli S., Schroeder M., Polypharmacology rescored: Protein–ligand interaction profiles for remote binding site similarity assessment. Prog. Biophys. Mol. Biol. 116, 174–186 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Natarajan A., Schwans J. P., Herschlag D., Using unnatural amino acids to probe the energetics of oxyanion hole hydrogen bonds in the ketosteroid isomerase active site. J. Am. Chem. Soc. 136, 7643–7654 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taylor M. S., Jacobsen E. N., Asymmetric catalysis by chiral hydrogen-bond donors. Angew. Chem. Int. Ed. Engl. 45, 1520–1543 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Chodera J. D., Mobley D. L., Entropy-enthalpy compensation: Role and ramifications in biomolecular ligand recognition and design. Annu. Rev. Biophys. 42, 121–142 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Olsson T. S. G., Ladbury J. E., Pitt W. R., Williams M. A., Extent of enthalpy–entropy compensation in protein–ligand interactions. Protein Sci. 20, 1607–1618 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leigh D. A., Summing up ligand binding interactions. Chem. Biol. 10, 1143–1144 (2003). [DOI] [PubMed] [Google Scholar]
- 8.Li Y., Han L., Liu Z., Wang R., Comparative assessment of scoring functions on an updated benchmark: II. Evaluation methods and general results. J. Chem. Inf. Model. 54, 1717–1736 (2014). [DOI] [PubMed] [Google Scholar]
- 9.Wang R., Lai L., Wang S., Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput. Aided Mol. Des. 16, 11–26 (2002). [DOI] [PubMed] [Google Scholar]
- 10.Sawada T., Fedorov D. G., Kitaura K., Role of the key mutation in the selective binding of avian and human influenza hemagglutinin to sialosides revealed by quantum-mechanical calculations. J. Am. Chem. Soc. 132, 16862–16872 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Lafont V., Armstrong A. A., Ohtaka H., Kiso Y., Amzel L. M., Freire E., Compensating enthalpic and entropic changes hinder binding affinity optimization. Chem. Biol. Drug Des. 69, 413–422 (2007). [DOI] [PubMed] [Google Scholar]
- 12.Ross G. A., Morris G. M., Biggin P. C., Rapid and accurate prediction and scoring of water molecules in protein binding sites. PLOS One 7, e32036 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sarkar A., Kellogg G. E., Hydrophobicity-shake flasks, protein folding and drug discovery. Curr. Top. Med. Chem. 10, 67–83 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abel R., Young T., Farid R., Berne B. J., Friesner R. A., Role of the active-site solvent in the thermodynamics of factor Xa ligand binding. J. Am. Chem. Soc. 130, 2817–2831 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Barillari C., Taylor J., Viner R., Essex J. W., Classification of water molecules in protein binding sites. J. Am. Chem. Soc. 129, 2577–2587 (2007). [DOI] [PubMed] [Google Scholar]
- 16.Fried S. D., Bagchi S., Boxer S. G., Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 346, 1510–1514 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kamerlin S. C. L., Sharma P. K., Chu Z. T., Warshel A., Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proc. Natl. Acad. Sci. U.S.A. 107, 4075–4080 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ruben E. A., Schwans J. P., Sonnett M., Natarajan A., Gonzalez A., Tsai Y., Herschlag D., Ground state destabilization from a positioned general base in the ketosteroid isomerase active site. Biochemistry 52, 1074–1081 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen D., Savidge T., Comment on “Extreme electric fields power catalysis in the active site of ketosteroid isomerase”. Science 349, 936 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mullard A., New drugs cost US$2.6 billion to develop. Nat. Rev. Drug Discov. 13, 877 (2014). [Google Scholar]
- 21.Kenny P. W., Montanari C. A., Prokopczyk I. M., ClogPalk: A method for predicting alkane/water partition coefficient. J. Comput. Aided Mol. Des. 27, 389–402 (2013). [DOI] [PubMed] [Google Scholar]
- 22.El Tayar N., Tsai R.-S., Testa B., Carrupt P.-A., Leo A., Partitioning of solutes in different solvent systems: The contribution of hydrogen-bonding capacity and polarity. J. Pharm. Sci. 80, 590–598 (1991). [DOI] [PubMed] [Google Scholar]
- 23.Abraham M. H., Chadha H. S., Whiting G. S., Mitchell R. C., Hydrogen bonding. 32. An analysis of water-octanol and water-alkane partitioning and the Δlog P parameter of seiler. J. Pharm. Sci. 83, 1085–1100 (1994). [DOI] [PubMed] [Google Scholar]
- 24.Toulmin A., Wood J. M., Kenny P. W., Toward prediction of alkane/water partition coefficients. J. Med. Chem. 51, 3720–3730 (2008). [DOI] [PubMed] [Google Scholar]
- 25.Larson J. W., McMahon T. B., Gas-phase bihalide and pseudobihalide ions. An ion cyclotron resonance determination of hydrogen bond energies in XHY- species(X, Y = F, Cl, Br, CN). Inorg. Chem. 23, 2029–2033 (1984). [Google Scholar]
- 26.Chen J. M., Xu S. L., Wawrzak Z., Basarab G. S., Jordan D. B., Structure-based design of potent inhibitors of scytalone dehydratase: Displacement of a water molecule from the active site. Biochemistry 37, 17735–17744 (1998). [DOI] [PubMed] [Google Scholar]
- 27.Gerhard U., Searle M. S., Williams D. H., The free energy change of restricting a bond rotation in the binding of peptide analogues to vancomycin group antibiotics. Bioorg. Med. Chem. Lett. 3, 803–808 (1993). [Google Scholar]
- 28.Pluth M. D., Bergman R. G., Raymond K. N., Acceleration of amide bond rotation by encapsulation in the hydrophobic interior of a water-soluble supramolecular assembly. J. Org. Chem. 73, 7132–7136 (2008). [DOI] [PubMed] [Google Scholar]
- 29.Green N. M., Avidin and streptavidin. Methods Enzymol. 184, 51–67 (1990). [DOI] [PubMed] [Google Scholar]
- 30.Reznik G. O., Vajda S., Sano T., Cantor C. R., A streptavidin mutant with altered ligand-binding specificity. Proc. Natl. Acad. Sci. U.S.A. 95, 13525–13530 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Snyder P. W., Mecinović J., Moustakas D. T., Thomas S. W. III, Harder M., Mack E. T., Lockett M. R., Héroux A., Sherman W., Whitesides G. M., Mechanism of the hydrophobic effect in the biomolecular recognition of arylsulfonamides by carbonic anhydrase. Proc. Natl. Acad. Sci. U.S.A. 108, 17889–17894 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Steiner T., Koellner G., Hydrogen bonds with π-acceptors in proteins: Frequencies and role in stabilizing local 3D structures. J. Mol. Biol. 305, 535–557 (2001). [DOI] [PubMed] [Google Scholar]
- 33.Imai Y. N., Inoue Y., Yamamoto Y., Propensities of polar and aromatic amino acids in noncanonical interactions: Nonbonded contacts analysis of protein–ligand complexes in crystal structures. J. Med. Chem. 50, 1189–1196 (2007). [DOI] [PubMed] [Google Scholar]
- 34.Bissantz C., Kuhn B., Stahl M., A medicinal chemist’s guide to molecular interactions. J. Med. Chem. 53, 5061–5084 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pierce A. C., Sandretto K. L., Bemis G. W., Kinase inhibitors and the case for CH…O hydrogen bonds in protein–ligand binding. Proteins 49, 567–576 (2002). [DOI] [PubMed] [Google Scholar]
- 36.Salonen L. M., Bucher C., Banner D. W., Haap W., Mary J.-L., Benz J., Kuster O., Seiler P., Schweizer W. B., Diederich F., Cation–π interactions at the active site of factor Xa: Dramatic enhancement upon stepwise N-alkylation of ammonium ions. Angew. Chem. Int. Ed. Engl. 48, 811–814 (2009). [DOI] [PubMed] [Google Scholar]
- 37.Perdigão L. M. A., Champness N. R., Beton P. H., Surface self-assembly of the cyanuric acid–melamine hydrogen bonded network. Chem. Commun. 538–540 (2006). [DOI] [PubMed] [Google Scholar]
- 38.Irwin J. J., Shoichet B. K., ZINC—A free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 45, 177–182 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kelly C. P., LaMont J. T., Clostridium difficile—More difficult than ever. N. Engl. J. Med. 359, 1932–1940 (2008). [DOI] [PubMed] [Google Scholar]
- 40.Pruitt R. N., Chagot B., Cover M., Chazin W. J., Spiller B., Lacy D. B., Structure-function analysis of inositol hexakisphosphate-induced autoprocessing in Clostridium difficile toxin A. J. Biol. Chem. 284, 21934–21940 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Reineke J., Tenzer S., Rupnik M., Koschinski A., Hasselmayer O., Schrattenholz A., Schild H., von Eichel-Streiber C., Autocatalytic cleavage of Clostridium difficile toxin B. Nature 446, 415–419 (2007). [DOI] [PubMed] [Google Scholar]
- 42.Savidge T. C., Urvil P., Oezguen N., Ali K., Choudhury A., Acharya V., Pinchuk I., Torres A. G., English R. D., Wiktorowicz J. E., Loeffelholz M., Kumar R., Shi L., Nie W., Braun W., Herman B., Hausladen A., Feng H., Stamler J. S., Pothoulakis C., Host S-nitrosylation inhibits clostridial small molecule–activated glucosylating toxins. Nat. Med. 17, 1136–1141 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cheng P.-N., Liu C., Zhao M., Eisenberg D., Nowick J. S., Amyloid β-sheet mimics that antagonize protein aggregation and reduce amyloid toxicity. Nat. Chem. 4, 927–933 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rimer J. D., An Z., Zhu Z., Lee M. H., Goldfarb D. S., Wesson J. A., Ward M. D., Crystal growth inhibitors for the prevention of L-cystine kidney stones through molecular design. Science 330, 337–341 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hansch C., Leo A., Taft R. W., A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 91, 165–195 (1991). [Google Scholar]
- 46.Kitchen D. B., Decornez H., Furr J. R., Bajorath J., Docking and scoring in virtual screening for drug discovery: Methods and applications. Nat. Rev. Drug Discov. 3, 935–949 (2004). [DOI] [PubMed] [Google Scholar]
- 47.Cornell W. D., Cieplak P., Bayly C. I., Gould I. R., Merz K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., Kollman P. A., A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117, 5179–5197 (1995). [Google Scholar]
- 48.de Azevedo W. F. Jr, Dias R., Computational methods for calculation of ligand-binding affinity. Curr. Drug Targets 9, 1031–1039 (2008). [DOI] [PubMed] [Google Scholar]
- 49.Le Questel J.-Y., Berthelot M., Laurence C., Hydrogen-bond acceptor properties of nitriles: A combined crystallographic and ab initio theoretical investigation. J. Phys. Org. Chem. 13, 347–358 (2000). [Google Scholar]
- 50.Zheng X., Zhao A., Xie G., Chi Y., Zhao L., Li H., Wang C., Bao Y., Jia W., Luther M., Su M., Nicholson J. K., Jia W., Melamine-induced renal toxicity is mediated by the gut microbiota. Sci. Transl. Med. 5, 172ra22 (2013). [DOI] [PubMed] [Google Scholar]
- 51.Meylan M. W., Howard P. H., Estimating log P with atom/fragments and water solubility with log P. Perspect. Drug Discov. 19, 67–84 (2000). [Google Scholar]
- 52.Miao H., Fan S., Wu Y.-N., Zhang L., Zhou P.-P., Chen H.-J., Zhao Y.-F., Simultaneous determination of melamine, ammelide, ammeline, and cyanuric acid in milk and milk products by gas chromatography-tandem mass spectrometry. Biomed. Environ. Sci. 22, 87–94 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/3/e1501240/DC1
Text S1. Theoretical proof of the H-bond pairing principle.
Text S2. Relationship between the free energy change for a reversible protein-ligand H-bond competing process and the H-bonding capability of the H-bond–forming atoms.
Text S3. The H-bonding capability of the protein atoms with which a ligand atom interacts and the effect of H-bond geometry on the H-bond interaction.
Fig. S1. Schematic illustration of the free energy change for the H-bond competing process.
Fig. S2. Calculation of H-bonding capability based on water/hexadecane partition coefficients.
Fig. S3. Contributions of the H-bonds between CN and the Tyr-OH from scytalone dehydratase to protein-ligand interactions.
Fig. S4. Proof for the strong H-bond interactions between the CN group of inhibitor 2 and tyrosine hydroxyls from scytalone dehydratase.
Fig. S5. Binding affinities of 1H-imidazole-2-sulfonamide and thiophene-2-sulfonamide.
Fig. S6. Quaternary ammonium cation [–N(Me)3+]-π interactions are more favorable than ammonium ion (–NH3+)-π interactions.
Fig. S7. A pathogenic role for the s-s/w-w H-bonding principle in melanin toxicity.
Fig. S8. The thermodynamic cycle that demonstrates the contribution of H-bonds to enzymatic catalytic power equates to their contribution to protein-ligand binding.