Status competition, inequality, and fertility: implications for the demographic transition

Abstract

The role that social status plays in small-scale societies suggests that status may be important for understanding the evolution of human fertility decisions, and for understanding how such decisions play out in modern contexts. This paper explores whether modelling competition for status—in the sense of relative rank within a society—can help shed light on fertility decline and the demographic transition. We develop a model of how levels of inequality and status competition affect optimal investment by parents in the embodied capital (health, strength, and skills) and social status of offspring, focusing on feedbacks between individual decisions and socio-ecological conditions. We find that conditions similar to those in demographic transition societies yield increased investment in both embodied capital and social status, generating substantial decreases in fertility, particularly under conditions of high inequality and intense status competition. We suggest that a complete explanation for both fertility variation in small-scale societies and modern fertility decline will take into account the effects of status competition and inequality.

1. Introduction

Recent research on human fertility and the demographic transition suggests that fertility decisions are affected by differences in mortality risk, access to resources, pay-offs to investment in future economic productivity, and access to information and technology [1–3]. There is also evidence suggesting that status competition may play a key role in fertility outcomes, above and beyond these other factors. This paper explores why and how social status (and its corollary inequality) may play this role in human reproduction.

In this paper, we define social status as a person's ordinal position or rank in a locally relevant social community. Defined this way, status can include elements of both dominance (size, strength, and coercive ability) and prestige (respect and reputation). In contrast, we define wealth as ownership of or access to material resources. Wealth can be produced directly through embodied capital (health, status, and skills [4]) but can also be affected by social position (status). While we acknowledge that wealth (resources) and status (social position) are often correlated, we believe there is theoretical clarity to be gained by explicitly modelling how the dynamics of status competition are likely to affect fertility, rather than treating wealth and status as interchangeable. The nature of status as a ‘positional good’—the value of which depends fundamentally on how much is possessed by other members of the community [5]—has important implications for the dynamics of fertility decision-making.

In the first part of the paper, we offer two motivating propositions that underlie the hypothesis that status competition affects reproductive decisions and has played a role in modern fertility decline. The first proposition is that in existing small-scale societies, status affects many aspects of social life including reproductive outcomes. This suggests that concerns for status are likely to be ancient and may have played a role in the evolution of fertility decision-making processes. The second proposition is that under certain ecological circumstances—particularly the presence of heritable wealth and modern markets—investment in status trades off with the number of children parents are able to support, providing a motivation for decreased fertility. We argue that economic and risk-based models are necessary yet insufficient to explain modern levels of fertility decline and suggest that failure to consider status competition is a key reason why.

In the second part of the paper, we present a theoretical model of status competition and parental investment. A numerical form of the model is analysed, and a set of predictions are derived regarding how investments in social status and fertility are altered under different ecological conditions. We specifically focus on the effects of the intensity of status competition and the level of social inequality. The paper concludes with a discussion of the results of our model and their implications for understanding patterns of fertility variation and fertility decline.

(a). Proposition 1: despite their egalitarian nature, status affects both well-being and fitness in small-scale societies

A review of the published data suggests that status hierarchies may be present in all or at least most human societies [6,7]. In fact, many researchers argue that status seeking is a basic human motivation [8,9]. Most human societies have multiple dimensions of status. Among hunter-gatherers and forager-horticulturalists, strength, hunting skill, persuasive ability, and healing ability are important inputs to status; livestock and lineage membership are important among pastoralists; inherited caste or class are important among agriculturalists; while education and profession are important in market economies (e.g. [10]).

Hierarchical systems of ranking are not exclusive to humans. Most anthropoid primates, and more generally mammals that live in multi-male multi-female groups, have within-sex dominance hierarchies [11–13] that affect reproductive outcomes. High-ranking males often out-reproduce lower-ranking males as a result of greater success in mating [14,15], resulting in higher lifetime reproductive success. High-ranking females often have higher reproductive success than lower-ranking females as they may have better access to resources, longer reproductive careers, shorter interbirth intervals, and higher rates of infant survival [15–17]. In some cases, the reproduction of lower-ranking females (or the survival of their offspring) is suppressed through aggression and other forms of social stressors [18].

Human status rankings, however, may be much less overt than dominance hierarchies among other primates, especially among ‘egalitarian’ foragers. Such foragers rarely have formalized status hierarchies among adult men [19], and women tend to enjoy relatively high levels of autonomy [20]. Many foragers share food widely within groups, and the high returns to risk reduction (i.e. consumption smoothing) through food sharing may mitigate against overt competition [21]. Many foraging societies have been noted for their egalitarian ethos, insistence on the autonomy of individuals, strong norms of sharing, and reciprocity and disapproval of aggrandizers [6,22]. Some researchers have suggested that among egalitarian foragers, dominance hierarchies may have been replaced by prestige hierarchies based on reputation, with an emphasis on gaining high-quality social partners for production and reproduction [6–8,23].

Detailed research on the social, productive, and reproductive lives of relatively egalitarian foragers and forager-horticulturalists suggests several important pay-offs to status (reviewed in [7]), most of which have potential reproductive consequences. The most important are access to more or better mates or marriage partners [24–27], access to more productive and reliable sharing partners [23], more help when sick or injured [28–30], and an improved ability to form coalitions, especially among men [27]. Status in more egalitarian groups appears to be achieved primarily on the basis of an individual's activities during their lifetime, and the ability of parents to influence the status of their children is limited compared with other types of societies [31,32].

Yet there is reason to believe that some hunting and gathering societies during the ‘age of foraging’ (i.e. before plant and animal domestication became widespread) may have been more complex than the extant foraging groups who have been studied in recent decades (e.g. [33,34]). This complexity may take the form of hierarchies within settled groups, or occasionally involve broader institutions across groups. Complex foragers, for example, existed for centuries on the Northwest Coast of North America before and after the European expansion. The most complex of these groups were characterized by sedentary villages, hereditary chiefs, heritable rights to foraging areas (i.e. salmon runs, fish weirs), isogamous marriages between men and women of elite rank, elaborate norms of competitive feasting, and enslavement of war captives [34,35]. While few such cultures survived to the ethnographic present, some authors have argued that complex foraging societies may also have existed in early Holocene Australia [36] and Upper Palaeolithic Europe [37].

Aspects of social complexity related to status can also be found in otherwise egalitarian foragers. Aboriginal Australian groups had status-related institutions such as inherited land tenure, trade in prestige goods and initiation-based social groups extending across bands and linguistic communities (e.g. [38–40]). Age-graded men's societies constrained access to ritual information and determined marriage decisions, allowing men with high ritual status to achieve higher levels of polygyny than in other foraging groups. In the Kalahari, Wiessner [24] has described social institutions among Ju/’hoansi foragers including a system of land rights inherited through mothers and fathers and a system of prestige-good exchange (xaro) that was important in individual prestige, forged social networks between families in different bands, and facilitated alliances and arranged marriages. In the distant past the Ju/’hoansi may have had territory-based exogamous name groups, though knowledge of how they operated is lost [24]. It is unclear whether and to what degree such social institutions existed in other world regions before they were disrupted by conquest, colonialism and assimilation, though emerging archaeological data should provide better answers.

The ability of parents to influence their children's status is likely to be much greater in complex foraging, pastoralist, and agricultural societies with heritable wealth and heritable statuses [31,41–43]. Among settled horticulturalist and forager-horticulturalist groups, explicit forms of status competition are often present, for example, yam festivals in Pohnpei [44], the moka among ‘big man’ societies in Papua New Guinea [45], and the Kula ring in the Trobriand Islands [46]. These examples are likely to reflect dynamics of ecological and social circumscription, economic defensibility, and resource accumulation common to territorial, herding, and insular communities [41,47,48]. On the basis of the—still limited—cross-cultural evidence, we suggest that a concern about status may be a universal feature of the social organization of human groups, including foragers, and thus a relevant aspect of the environment in which human fertility behaviour evolved.

(b). Proposition 2: under ecological conditions of heritable wealth and modern markets, investment in social status trades off with fertility

In pre-demographic transition societies, positive relationships between status (as measured by wealth, income, occupation, or social class) and fertility have been found, with some research suggesting that these relationships are stronger for males than females (e.g. [49–51]). This relationship appears to change during the demographic transition, with greater reductions in fertility found among people with higher socio-economic status [52,53]. Most studies of modern populations have shown negative or null relationships between status and fertility [50,54,55], though longitudinal studies generally find positive effects of wealth on fertility [56], suggesting that such relationships need to be carefully measured. A positive association between status and fertility appears more likely to hold true for males, at least when status is measured by income [50,57]. Yet socio-economic status is multifaceted, and some research suggests that income and education may have opposite effects, with income being more likely to increase fertility, and education being more likely to decrease it [50,51,57].

Mace [58] and Luttbeg et al. [59] have argued that even in pre-transition societies most humans are not maximizing the number of surviving offspring but instead optimizing the number of offspring versus the wealth provided to offspring. Yet much of the data on which this argument is based come from pastoralist societies with appreciable amounts of heritable wealth in animals, and consequently higher levels of inequality than are common in small-scale foraging and horticultural societies, leaving open the question of how broadly such evidence applies [60–63]. Moreover, Lawson & Borgerhoff Mulder [64], question the logic of Mace and Luttbeg et al., arguing instead that the solution to sibling competition over wealth inheritance often consists of high fertility and biased investment rather than fertility limitation.

While we know that status affects fertility in many small-scale societies (see [7, table 9.1] for a summary), current empirical studies do not tell us if status trades off with fertility in societies without significant forms of heritable wealth or social complexity. One possibility is that status has always traded off with fertility, just as investment in child nutrition trades off with fertility, but the extent of the trade-off is limited by food sharing, alloparental care, high exogenous mortality risks, and limited returns to investment per child. Another possibility is that status does not trade off with fertility in small-scale social contexts because status is primarily achieved through personal behaviour. From this perspective, while parents can directly invest in a child's nutritional status and skillset, they may only have indirect, partial, and somewhat unpredictable effects on a child's adult status. In post-transition societies, in contrast, high levels of parental investment are often needed to make children socially competitive. In such environments, the quantity–quality trade-off between offspring becomes a dominant reproductive dynamic (e.g. [55]), alongside a related trade-off between investment in parents' own status (especially through education and status-related consumption) and investment in offspring (e.g. [65]).

In sum, while we do not know whether fertility and status trade off in small-scale societies, we know that under certain ecological circumstances—particularly where heritable material wealth and/or intensive investment in embodied capital in education are important inputs to status—investment in status does indeed trade off with the number of children parents are able or willing to support. While this insight is related to the quantity–quality trade-off models of fertility of Kaplan [4] and Becker & Lewis [66], the distinction here is that investment in status may only trade off with offspring number in particular kinds of environments.

(c). Hypothesis: investment in economic productivity and mortality risk are insufficient to explain the full extent of fertility decline, because status competition plays an important role in determining fertility in modern contexts

A close reading of recent empirical results on the causes of fertility decline suggests that while economic measures and mortality risk are highly important in predicting the demographic transition, they are insufficient to fully explain observed levels of fertility decline (e.g. [3,67,68]). Not only is it often true that statistical models that incorporate aspects of multiple types of causation perform best in explaining actual fertility decisions (e.g. [3,68–70]), but important predictors are often consistent with multiple types of interpretation (e.g. [3,71]). Specifically, many of the most important predictors of fertility in the literature—women's education, the family's occupation, wealth, and income—are important not just as measures of resource access or mortality risk, but also as direct and indirect indicators of social status. This means that while parents may invest in their own or their children's education to increase access to resources, they are simultaneously securing social rank and favourable positions in social networks, local communities, and society as a whole. Even if reproductive fitness were replaced by a utility function¹ in which the wealth of descendants was what parents attempted to maximize, the empirical estimates of the effect of offspring number on offspring adult wealth are not large enough to explain the two-child family (see, for example, estimates in [54,72]).

Several lines of evidence suggest a potentially important role for status concerns in fertility behaviours and a trade-off between investment in status and fertility in demographic transition contexts. The economics literature suggests that the consumption levels of parents and children may trade off with child quantity (e.g. [66]). Investment in ‘child quality’ in more unequal societies often involves signalling with status-related goods, services, or experiences. Instead of just providing access to better food, skills, or resources, investments such as gold-jewellery dowries or an Ivy League education may also serve as signals of status [73,74]. These types of investment may in part drive the steeper quantity–quality trade-offs observed in developed [75] and some developing [63] countries.

These data suggest that status considerations are likely to be important in determining fertility decisions, particularly in contexts where: (a) investment in status trades off with fertility, as observed in societies where heritable wealth or education are key; and (b) there are high levels of status competition, resulting from high levels of social inequality or other factors. We hypothesize that ecological circumstances in which both (a) and (b) hold are likely to result in higher investment per child—and concomitantly lower fertility—compared with circumstances where status does not trade off with fertility and/or status competition is less intense.

(d). Towards an evolutionary theory of fertility that incorporates status

On the basis of the above discussion, we present a simple model of optimal parental investment and fertility that attempts to address (a) how the inclusion of status in the fitness function affects predicted fertility, and (b) how predicted fertility changes as the scope for status competition increases. In this optimality model, parents attempt to maximize fitness, which depends on both the quantity and quality of offspring. The model treats investments in offspring that directly increase survival and economic productivity (independent of status), and investments in offspring status as separate decision variables. It explores the dynamics of reproduction and parental investment over multiple generations under different socio-ecological conditions. While, for simplicity, the model focuses on investment in offspring status, similar results are expected to hold for investments in parental status, as long as status investments affect parental fitness and trade off against fertility. The model is first presented in a more general form. We then introduce specific functional forms for a numerical simulation, and then analyse how optimal investments and fertility respond to variation in key ecological parameters.

2. Model

The model represents an individual's attempt to optimize investments in offspring and the number of offspring in order to maximize fitness. For simplicity, reproduction occurs asexually with semelparity and non-overlapping generations. The number of offspring is treated as a continuous variable (i.e. it can take non-integer values²), and investments are assumed to be identical across offspring.

A parent's investments are envisioned as a bundle or portfolio of goods that are provided to support the development and success of each offspring—for example, food, childcare, education, social connections, money, livestock, land, etc. Each good in the bundle may enhance offspring success in an ‘absolute’ sense (i.e. its value is independent of how much others possess), and/or in a ‘relative’ or positional sense (i.e. its value is dependent on how much others possess [5]). Basic foods, for example, are likely to contribute to one's survival and productivity primarily in an absolute way, with very little dependence on the consumption levels of other individuals in the population. Conspicuous luxury goods with little practical utility, on the other hand—e.g. designer clothing or meticulous landscaping—probably contribute to success almost entirely through their effect on one's social status or standing relative to others. Many other goods—such as a college education, automobiles, or the quality of one's residential neighbourhood—are likely to contribute to offspring success in both absolute and relative ways.

We conceive that the goods packaged in a given bundle together give rise to an aggregate stock of capital a, which affects offspring survival and productivity in an absolute/non-positional/rank-independent way. Each bundle also gives rise to an aggregate stock of social capital , which affects offspring success in a relative/positional/rank-dependent way. In terms of the examples above, basic food would increase a alone; designer clothing would increase ; while a prestigious education would increase both a and . For analytical clarity, we rephrase the problem of choosing which goods to include in the investment bundle, and in what quantities, in terms of the problem of choosing a and .

The ‘fitness value’ of a single offspring, V, is assumed to increase with both a and . We expect that the effects of these two stocks are complementary and multiplicative. We thus specify that V is proportional to the product of two functions, A(a) and :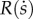

2.1

The function A(a) represents the effect of a, while 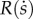represents the effect of . The survival-and-productivity stock a is directly optimized by the parent. The social capital stock is itself defined as the product of two terms 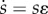. s is a decision variable directly optimized by the parent, while ɛ is an exogenous and stochastic ‘shock’ variable (revealed by nature after the parent decides s), which is used to model inequality in the distribution of social capital, described in greater detail below.

The parent's fertility, or number of offspring, is represented by f. The total fitness of the parent W is the product of the fitness value of a single offspring V multiplied by fertility f:

2.2

A budget constraint requires that the total capital given to all offspring f(a + s) does not exceed (and in practice equals) the parent's budget Y:

2.3

We assume that the parent's budget Y is proportional to the fitness value established by the parent's parent in the previous generation (V_p) multiplied by an exogenous constant g representing the (presumably positive) effects of growth and maturation on the value of the investment. Thus:

2.4

The numerical simulation uses specific functional forms to model the relationship between socio-ecological variation and realized fertility outcomes. A(a) and 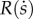are both represented by logistic functions, which are S-shaped and monotonically increasing in the capital stocks. The function A(a) representing the effect of the survival-and-productivity stock a is given by:

2.5

The exogenous ecological parameter 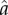in this function sets the inflection point for the S-shaped curve (i.e. the value of a that yields A = 0.5), while α determines the steepness of the curve around the inflection point. A higher value of 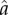implies that a higher level of a is necessary to hit the ‘knee of the curve’ (for example, more years of training are required to achieve competency in some productive task).

The function 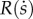representing the effect of the social capital stock is given by:

2.6

The pay-off to social capital is mediated entirely through the effect of on relative rank. One's rank r—ranging from 0 (lowest) to 1 (highest)—is equal to the quantile of her/his social capital within the full distribution of in the local population (the vector 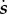). The parameter 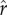sets the inflection point for the S-shaped curve (i.e. the value of r that yields R = 0.5). This parameter can be interpreted as the ‘intensity of status competition’, which is related to the exclusivity of the benefits of social capital. For low values of 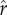, a greater fraction of the population can be expected to have R values close to 1; for high values, only an elite minority benefits. The parameter ρ determines the slope of the S-shaped curve around the inflection point (i.e. the point in the function where the positive slope stops increasing and begins decreasing). This parameter can be interpreted as the ‘decisiveness' of rank in determining R: low values of ρ reflect benefits that increase gradually with rank, while high values result in a decisive cut-off between those who benefit and those who do not.

The final essential ecological parameter in this system is the degree of inequality in social capital , represented as CV(ɛ). This inequality is conceived as an exogenous random ‘shock’ to the parent's chosen value of s that occurs over the course of development (similar in conception to the shocks in the model of Borgerhoff Mulder et al. [41]). The net effect of these shocks on social capital may be either negative (losses) or positive (windfalls), depending on stochastic events in individual lives. More unequally distributed shocks reflect greater inequality in social capital resulting from ecological conditions and social processes that are not explicitly modelled (e.g. storage, economic defensibility, differential accumulation of wealth, etc.). In the simulation, this shock is realized as a value ɛ drawn from a gamma distribution with mean 1 and an exogenous shape parameter determining the degree of inequality around 1.³ Each value of s chosen by parents is multiplied by ɛ to yield the post-shock value 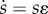. Inequality in shocks is reported in terms of their coefficient of variation, CV(ɛ).

In the simulation, each run consists of multiple generations that reproduce, invest in their offspring, and die. In each generation, each parent optimizes a and s (and thus f) in order to maximize expected fitness (equation (2.2)) given current ecological parameters and the distribution of observed in their own generation. The values of V_p defining the endowments (budgets) of the subsequent generation (equation (2.4)) are determined by sampling with replacement from the V values that result from the choices of the parental generation with probability proportional to the realized fitness of each parent (W).

For the runs reported in figures 1–3, three key ecological parameters are held constant within a run, but vary across runs: the inflection point for the returns to rank (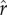), the slope of the returns to rank (ρ), and inequality in the inputs to rank (CV(ɛ)). For simplicity of presentation, the parameters defining the returns to non-rank parental investment ( 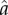and α) are held constant across runs (but see figure 4). We track parental investment and fertility as the dynamics of best-response play out over approximately 50 generations in each run. Further model details are described in electronic supplementary material, §1.

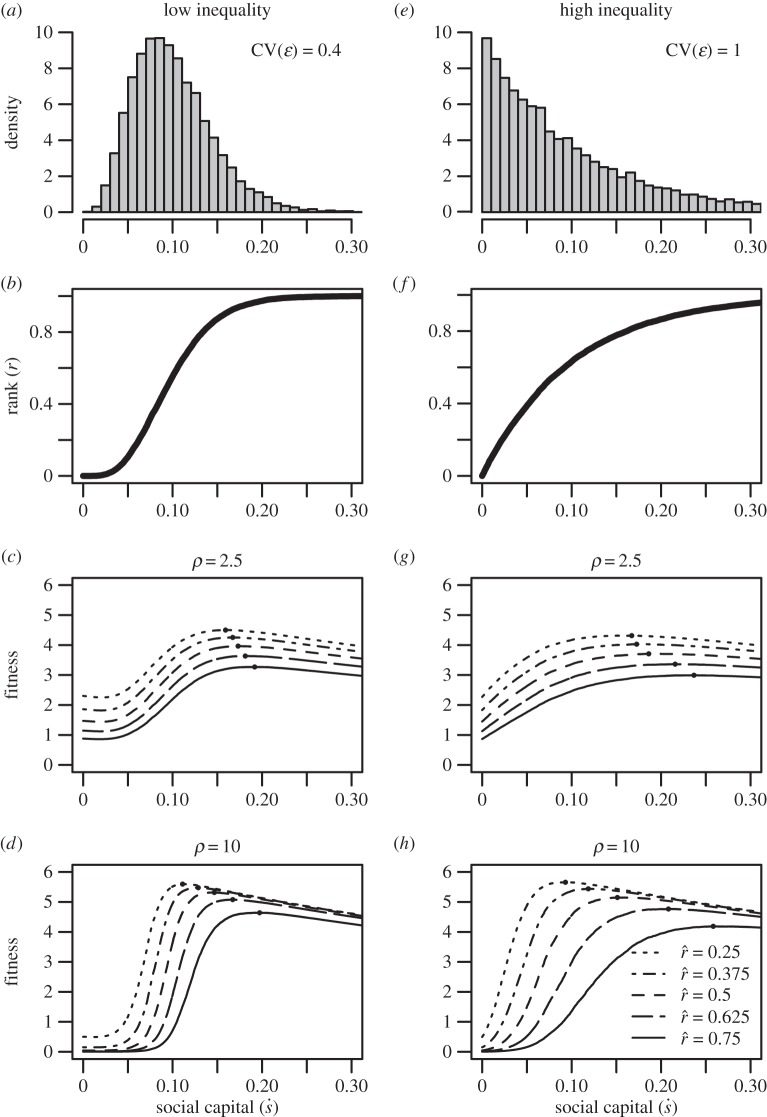
Figure 1.

An illustration of the effect of ecological parameters on the core mechanics of the model. The left-hand column represents conditions of lower inequality in the inputs to social rank (the distribution in panel (a)), while the right-hand column represents conditions of higher inequality (the distribution in panel (e)). Panels (b,f) indicate the rank achieved for a given level of investment in social capital. Panels (c,d,g,h) plot parental fitness as a function of investment in social capital given different values for the inflection point (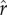, varying across the solid and dashed lines) and slope (ρ, varying across panels) of the effect-of-social-capital function. Solid black points indicate the optimal (fitness-maximizing) levels of investment in social capital.

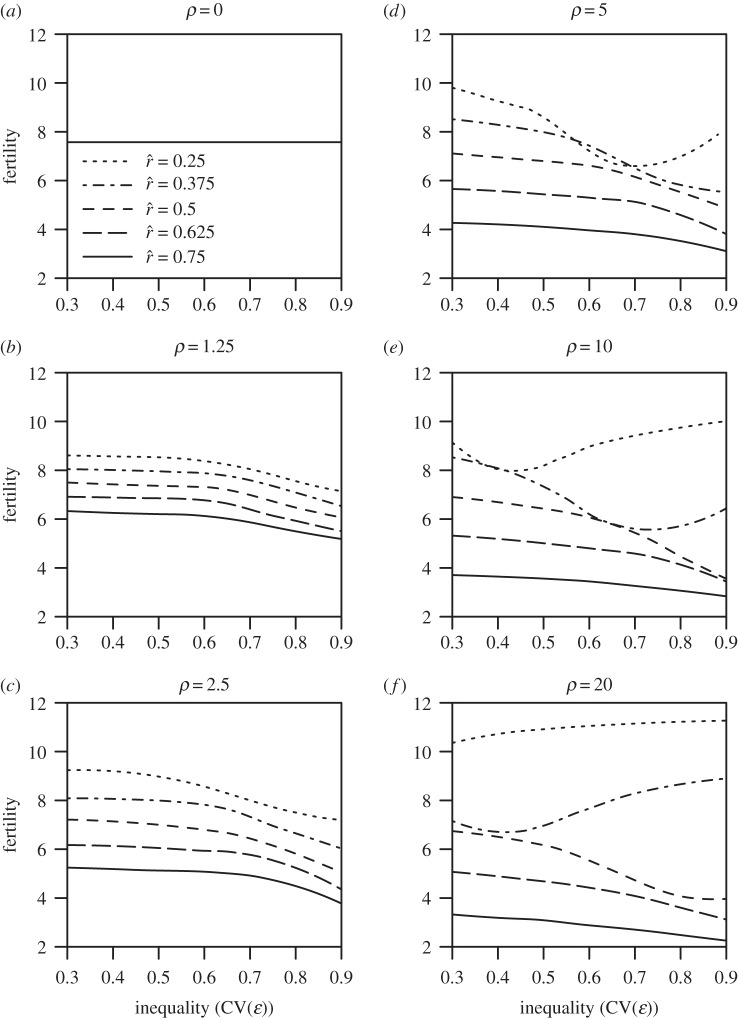
Figure 2.

(a–f) Mean fertility as a function of inequality in the inputs to status (CV(ɛ), varying across the horizontal axis) and the inflection point (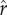, varying across the dashed and solid lines) and slope (ρ, varying across panels) of the effect-of-social-capital function.

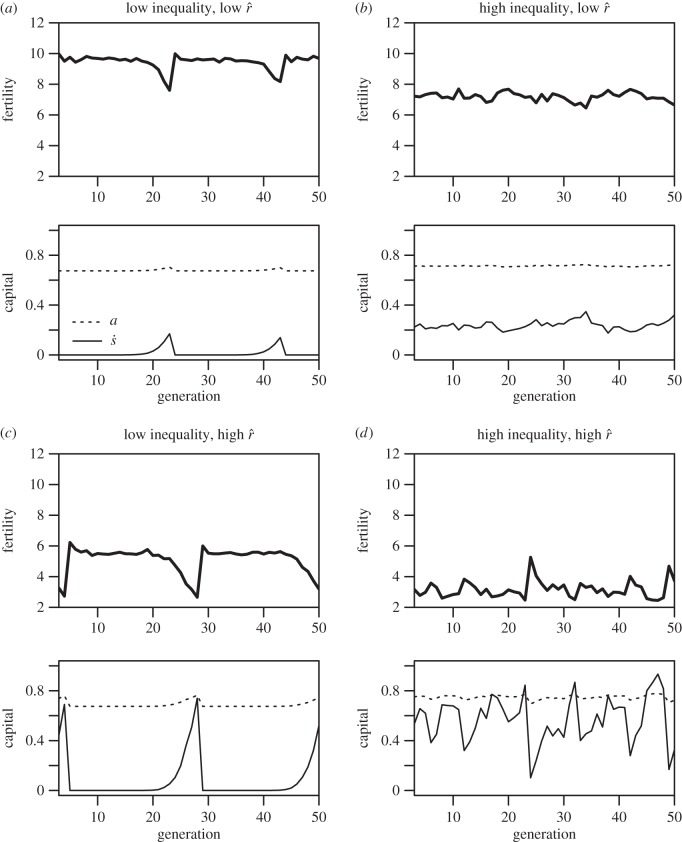
Figure 3.

(a–d) Dynamics of fertility and investment in offspring quality through time in four different ecologies. The thick solid line plots mean fertility, the dotted line plots mean investment in survival-and-productivity capital (a), while the thin solid line plots mean investment in social capital (). The left-hand column represents lower inequality in the inputs to status (CV(ɛ) = 0.4), whereas the right-hand column represents higher inequality (CV(ɛ) = 1). The top row represents a lower intensity of status competition (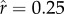), whereas the bottom row represents a higher intensity (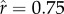). ρ is held constant at 2.5 across ecologies.

Figure 4.

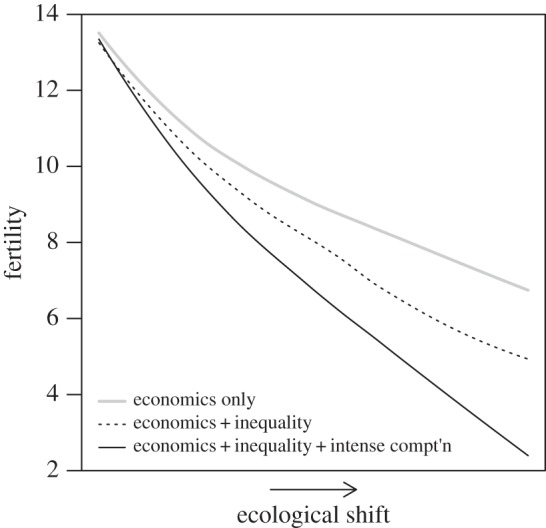
The predicted effect of increasing status competition on fertility with a shift from pre- to post-demographic transition ecological conditions. We hypothesize that fertility falls across the demographic transition not only due to an increase in the gains to direct investment in productivity, but also due to an increase in investment in status competition. The grey curve shows the effect of increasing gains to direct investment in productivity alone. The dashed black curve shows the additional effect of increasing inequality in the inputs to status, while the solid black curve shows the additional effects of increasing both inequality and the intensity of status competition. (The gains to direct productivity investment are assumed to increase for all three curves. For simplicity, other factors that we recognize as important, such as reduced infant mortality rates, are not explicitly modelled. See the electronic supplementary material for a description of the model parameters used to generate this plot.)

3. Model results

Figure 1 shows the returns to social capital for ecologies with two different levels of inequality: the left-hand column represents a case of lower inequality, while the right-hand column represents a case of greater inequality. Figure 1a depicts a distribution of social capital with relatively low inequality, with a coefficient of variation equal to 0.4 (and a gini coefficient of 0.25, similar to measures of wealth/social capital in relatively egalitarian small-scale societies; Borgerhoff Mulder et al. [41]). The relationship between social capital and relative rank for this distribution is plotted in figure 1b: more social capital results in a higher social rank, equal to one's percentile of social capital in the population. Figure 1c shows the fitness achieved at each possible value of social capital, with black points marking optimal (fitness-maximizing) levels of social capital, depending on the intensity of status competition (). The different solid, dashed, and dotted curves plot parental fitness for different values of from 0.25 to 0.75. All else equal, as the intensity of status competition increases, the optimal level of social capital increases. The differences between figures 1c and d illustrate the effect of increasing the slope parameter ρ, which affects the steepness of the curve around the inflection point. Figure 1c plots the curves given a relatively shallow slope parameter (ρ = 2.5), while figure 1d plots curves with a steeper slope parameter (ρ = 10). As ρ increases, the effect of increasing the intensity of status competition on optimal investment tends to be greater.

Figure 1e depicts a more unequal distribution of social capital, with a coefficient of variation equal to 1 (and a gini coefficient of 0.5, similar to measures of wealth/social capital in more unequal human societies; Borgerhoff Mulder et al. [41]). The relationship between social capital and relative rank for this distribution is plotted in figure 1f. Comparing figure 1f with the more equal case in figure 1b, one can see that the amount of social capital necessary to achieve a high rank is greater when the distribution of social capital is more unequal. Figure 1g shows fitness as a function of social capital for the more unequal case. Again, optimal investment in social capital increases with higher intensity of competition 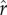. Comparing figure 1g with figure 1c, optimal social capital investment tends to be greater in the more unequal case for any given value of 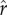. Figure 1h again shows that the effects of increasing intensity of competition 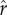on the optimum tend to be greater for higher values of the slope parameter ρ.

Figure 2 reports the effect of increasing inequality (varying across the horizontal axis) on mean optimal fertility when the dynamics of investment, growth, and re-investment play out across multiple generations. As in figure 1, the different solid, dashed, and dotted curves represent different values of the intensity of competition 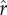. The different panels from figure 2a to figure 2f illustrate the results for different values of the slope parameter ρ from 0 to 20. The model yields the following three principal results:

• (1) When there are no returns to social capital or social capital does not trade off with fertility—i.e. ρ = 0, as plotted in figure 2a—optimal fertility is unaffected by inequality.

• (2) When there are gains to social capital that trade off with fertility (i.e. ρ > 0), optimal fertility decreases with greater inequality in social capital under most conditions. This result is reflected in the downward slope of optimal fertility as a function of inequality for most parameter values represented in figure 2b–f. The exception to the rule of a negative inequality–fertility relationship occurs where there is a strict cut-off in the returns to rank (i.e. very high ρ), yet the majority of the population falls above the cut-off (low 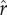), as observed in the non-monotonic or increasing relationship between inequality and optimal fertility shown by the dotted curves in figure 2d–f. Interestingly, very extreme levels of inequality (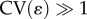) can also sometimes lead to the collapse of investment in status, with parents opting for minimal social capital investment rather than paying the heavy costs of ascending from one rank to the next.

• (3) Optimal fertility declines consistently with a higher intensity of status competition (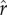). This result is apparent by comparing the solid, dashed, and dotted curves representing different values of 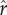within each panel of figure 2.

For non-zero values of the slope parameter ρ, increasing ρ tends to inflate the effect of changes in 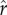on fertility outcomes, and may thus either increase or decrease realized fertility as illustrated across figure 2b through figure 2f. (For reference, electronic supplementary material, figure S1, plots the corresponding levels of mean optimal social capital investment from the same simulations as in figure 2.)

The dynamics of the simulated system as they vary with ecology are illustrated in figure 3. Because the returns to status vary depending on the distribution of social capital (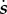) in the population, optimal social capital investment changes dynamically through time. Figure 3a shows that where there are some returns to social capital (i.e. ρ > 0) but low inequality and low intensity of competition (low 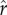), the maximal extent of status competition is quite limited. As inequality increases (as in figure 3b) or the intensity of competition increases (as in figure 3c), the scope for status competition increases, with attendant drops in fertility. Figure 3d illustrates a case with both high inequality and high intensity of competition, which manifests the highest levels of social capital investment and lowest fertility. The system tends to exhibit either regular cycles of escalating status competition then collapse, as in figure 3a and c, or stochastic fluctuations around a mean (particularly for higher levels of inequality) as in figure 3b and d. The complementarity between returns to social capital and non-rank-based capital—i.e. that the value of non-rank-based capital is greater when one invests more in social capital, and vice versa—is evident in the subtle but consistent positive correlation between optimal social capital investment () and non-rank-based capital (a) across time in each panel.

4. Discussion

We hypothesized that a concern for social status is an important element in explaining human fertility variation and recent fertility decline. This follows from the proposals that (1) status is important for fitness across most, perhaps all, human societies, and (2) status trades off with fertility, particularly under conditions of heritable wealth and modern markets. We developed a simple model for the relationship between the intensity of status competition and realized fertility. The model predicts that when investment in status is important for fitness and trades off with fertility, fertility tends to decrease with either greater inequality in the inputs to status, or greater intensity of status competition. An increase in the intensity of status competition amidst high levels of social inequality may thus be important for explaining the observed extent of modern fertility decline.

Status competition alone is not sufficient to fully explain modern fertility decline. Status aside, expectations for juvenile and adult survival and returns to embodied capital (i.e. investment in direct economic productivity including the economic returns to education) have increased across the demographic transition [4,65]. Instead, our findings suggest that the demographic transition occurred in response to a set of correlated shifts in ecological conditions, including decreased mortality and increased gains to investment in economic productivity, coupled with increasing scope for costly status competition. Our intuition regarding the role of increasing status competition is illustrated in figure 4. The solid grey line in the figure shows that fertility falls with an increase in direct economic returns (the parameter 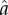in the model) alone. The rate and extent of decline becomes more severe when the economic changes are accompanied by increasing social inequality (CV(ɛ)) and/or intensity of status competition (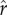), as represented by the dashed and solid black lines. The complementarity between direct economic benefits and the benefits of status posited by the model implies that investments in these two domains reinforce each other, interacting to deepen declines in fertility.

(a). Comparison with previous models, limitations and extensions

The current model builds on important previous evolutionary models positing links between fertility and wealth and/or status with implications for the demographic transition. Rogers [77,78] and Harpending & Rogers [79] modelled the trade-off between the number of offspring and the wealth that they inherit, finding that where offspring are in danger of falling short of a minimal threshold of wealth necessary for reproduction, limiting fertility to maintain high socio-economic status could be beneficial for long-term reproductive success. Boone & Kessler [80] suggested that low fertility strategies that are more likely to survive periodic population crashes (e.g. due to differential access to resources) could sometimes outcompete higher fertility strategies. Yet Low et al. [68] show that the conditions under which late breeding, low fertility lineages are predicted to be successful are difficult to create, while Rogers [78] was unable to replicate all the results of Rogers [77] under more realistic conditions. In a model with several similarities to the current model (e.g. the form of the budget constraint and sigmoidal returns to investment), Hill & Reeve [81] derived an evolutionary stable strategy for a balance between fertility and resource production, and intuitively show that optimal fertility decreases with higher marginal gains from investment in resource production.

The current theory has a number of features that set it apart from these models: its ecological analysis explicitly evaluates the effects of social inequality (in terms of the variance in inputs to and intensity of status competition). It also explicitly models the (often cyclical) dynamics of status competition, rather than a static equilibrium, and represents both non-status- and status-based investment in the same model. In a different strain, Rayo & Robson ([82]; building on Robson [83]) have recently modelled the evolution of preferences for investments in offspring quality that depend on the investment levels of other members of the population; their results suggest that imitation of others' fertility behaviour can evolve when there is uncertainty surrounding the pay-offs to investment, potentially resulting in suboptimally low fertility under modern conditions. In our model, a concern for others' investment in offspring quality is driven by direct cost-benefit calculus given perfect information, rather than by imperfect information.

The present modelling framework can be elaborated in a number of directions. This model does not explicitly address the effects of differentiation into subpopulations (e.g. social stratification into classes or castes) that might limit social mobility in ways that affect model results. The finding that the returns to status competition collapse under extreme levels of inequality due to the high costs of social climbing, for instance, may be relevant for poorer segments of societies who have little hope of upward mobility. The model does not incorporate differences in the returns to investment for parents depending on their inherited endowments, which has proved important for the outcome of past demographic transition models [4]. While the current model represents inequality in the inputs to social status, it does not address the role of inequality in non-rank investment (a). Introducing inequality in a would certainly induce greater variance in fertility. However, given that the benefits of a are explicitly non-relative (i.e. absolute), the same social dynamics of escalation observed here for investment in relative social capital would not occur for a since agents would not benefit from attempting to outdo their competitors.

The model can also be modified to address the different roles of investment in one's own status (affecting principally the initiation of reproduction) versus the status of one's children (affecting the rate and cessation of reproduction). Extending the model from its relatively abstract current form to represent more concrete ecological and behavioural variables (e.g. absolute versus relative returns to education, competition for social partners and their effects on fitness) will prove particularly productive for linking the model's theoretical intuitions with empirical reality.

(b). Empirical connections

Empirical work is required to test both the assumptions and the predictions of the model. Most importantly, cross-cultural and cross-temporal comparisons are necessary to quantify relationships between ecological parameters, key behavioural variables, and demographic outcomes. Is there evidence that status trades off with fertility in small-scale societies, or is this effect limited to societies relying on material wealth and/or modern labour markets? Where there is an effect, what is its shape and magnitude? All else equal—i.e. controlling for direct economic returns, mortality risks, and other factors—are the predicted relationships between inequality, status investment, and fertility borne out across populations? If so, how much of the observed variation in fertility is attributable to variation in inequality and status competition? Do these relationships depend in important ways on other aspects of ecology (e.g. subsistence regime, importance of material wealth)? Does status competition in real-world systems exhibit the kind of cyclical dynamics exhibited by the model, as illustrated in figure 3? If so, on what time scales do they occur, and to what extent is variation across time and space a result of endogenous dynamics versus variation in socio-ecological parameters? We hope that the current formalization will stimulate the empirical work necessary to evaluate whether status competition plays the role hypothesized here.

Additionally, while we have framed the model in terms of capital stocks whose effects are purely rank-independent or purely rank-dependent, these stocks in fact arise from bundles or portfolios of goods with a mix of rank-independent and rank-dependent effects. An important empirical goal is thus to quantify the direct and indirect effects of different goods on health, economic productivity, and social status, and the relationship between these intermediate factors and outcomes of survival and reproduction. These data would allow the development of more precise models with greater relevance to particular times and places.

Empirical work focusing on the relationships between social inequality and fertility is still nascent. Our findings are consistent with the work of Kremer & Chen [84], who found that the fertility differential between the more educated (who have lower fertility) and less educated (who have higher fertility) is greater in countries with higher levels of inequality. Our findings are not prima facie consistent with Colleran et al. [85], who found that fertility is higher in more unequal communities in rural Poland. This inequality, however, arises in part due to variation in subsistence strategies (farmers and non-farmers), so might be better represented in our model by people experiencing different ecological circumstances rather than the kind of inequality that motivates greater effort toward social climbing.

There are other points of evidence that apparently run counter to our model results. Why do societies relying on intensive agriculture with high levels of inequality [43] appear to maintain relatively high fertility? If our model is correct, these results may be explained by counter-balancing effects of other correlated changes, such as increased mortality risk and (especially) increased productivity of children in agricultural economies (e.g. [3,86–88]). Agricultural societies that face land limitation also frequently decrease fertility and/or adopt strategies to limit the number of legitimate heirs in order to increase investment in particular children through primogeniture, ultimogeniture, or single-sex inheritance (e.g. [35,89,90]). These societies are also likely to have high levels of inequality (e.g. [10,35,89]). On the other hand, the nascent demographic transitions experienced by the elites of ancient Rome and China (e.g. [1]) may be due, in part, to the intensity of status competition in these empires. Yet why is fertility not higher in socialist or communist countries with redistributive policies that limit social inequality? Again, the explanation may lie in other correlated changes, including lower availability of resources or anti-natal policies. Alternatively, when social policies limit economic inequality, parents may increase investment in other forms of social capital. Moreover, some countries engage in many modern market economic practices despite an official ‘communist’ identity (e.g. modern China).

In our model, inequality and status competition drive fitness-maximizing actors to decrease fertility. Yet because the ecological circumstances have changed so rapidly beyond the range of conditions typical of the remote or even the recent past, there is a great potential for mismatch and suboptimal outcomes in modern fertility behaviour. The low levels of fertility found in post-demographic transition societies appear to be maladaptive, occurring as they do alongside radical increases in material wealth, nutrition, and modern healthcare, which should allow parents to raise larger families [91]. While increasing investment in individual children could be adaptive if it puts them at a long-term advantage in survival and/or reproduction [58,78,80,81,92], empirical tests of increasing scope and sophistication have found that short-term reproductive success is consistently correlated with longer-term reproductive success after two to four generations [72,93–95]. Such studies also find that while low fertility decreases reproductive success, it substantially increases the socio-economic success of descendants (e.g. [72,94]), suggesting that fertility is being traded off for socio-economic standing. We see that our model provides a baseline for examining the relationship between status and fitness in an optimization context, from which future models can approach questions of mismatch and deviations from fitness maximization.

In our model, actors are able to adjust their strategies to ecological changes without the type of lag we might expect when evolved psychological machinery faces new environmental conditions. Yet we know that mismatch may arise as individuals attempt to apply ‘rules-of-thumb’ appropriate for the past, or experiment with new rules that may or may not yield success under changed circumstances [4,91]. The potential for mismatch may be particularly great in the domain of status competition, given the diversity and novelty of the means by which people can compete for social standing in modern contexts, and the opacity of information (such as the distribution of different forms of social capital) relevant for ascertaining the ‘true’ optimum. It is also possible that mechanisms of cultural transmission are operating to drive fertility decline under novel conditions (e.g. [96]) in ways that do not track optimality, making it tricky to disentangle mismatch from cultural forces. Future models should incorporate the possibility of informational constraints and adaptive lag in individuals' reactions to new environments. Research focusing on the proximate cognitive mechanisms involved in fertility regulation can also help us understand the potential for, and direction of, mismatches under novel conditions. It would be particularly useful to know what ‘reference populations' are relevant for fertility decision-making [97] and how different levels of inequality are perceived, mentally represented, and translated into different behavioural outcomes.

5. Conclusion

The important role that social status plays in small-scale societies suggests that status may be important for understanding the evolution of human fertility decisions, and how such decisions play out in the modern world. Much fertility research has treated status as synonymous with wealth, without addressing relative social position. This paper has attempted to tackle this problem by asking whether modelling competition for status—in the sense of relative rank within a society—can give greater traction for understanding fertility decline and fertility decisions more generally. We find that ecological conditions similar to those in demographic transition societies yield increased investment in both embodied capital and social status, generating substantial decreases in fertility, particularly under conditions of high inequality and intense status competition. We suggest that a complete explanation for both fertility variation in small-scale societies and modern fertility decline will take into account the effects of status competition and inequality. Future research can test the specific predictions of this model and the assumptions that underlie it.

Authors' contributions

M.K.S. conceived of the study, drafted the manuscript, and revised the manuscript. P.H. conceived of the study, constructed and analysed the model, drafted the manuscript, and revised the manuscript. H.K. conceived of the study and revised the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

The National Evolutionary Synthesis Center (NESCent) and the School for Advanced Research (SAR) funded the working groups that inspired this paper.