Step-Growth Polymerization of Inorganic Nanoparticles

Abstract

Self-organization of nanoparticles is an efficient strategy for producing nanostructures with complex, hierarchical architectures. The past decade has witnessed great progress in nanoparticle self-assembly, yet the quantitative prediction of the architecture of nanoparticle ensembles and of the kinetics of their formation remains a challenge. We report on the marked similarity between the self-assembly of metal nanoparticles and reaction-controlled step-growth polymerization. The nanoparticles act as multifunctional monomer units, which form reversible, noncovalent bonds at specific bond angles and organize themselves into a colloidal polymer. We show that the kinetics and statistics of step-growth polymerization enable a quantitative prediction of the architecture of linear, branched, and cyclic self-assembled nanostructures; their aggregation numbers and size distribution; and the formation of structural isomers.

The focus of nanoscience is gradually shifting from the synthesis of individual nanoparticles (NPs) to the organization of larger nanostructures. Ensembles of NPs show optical, electronic, and magnetic properties that are determined by collective interactions of individual NPs (1). To fully understand and exploit these cooperative properties, it is important to achieve control of the structural characteristics of NP ensembles. Self-assembly has emerged as a promising, cost-efficient methodology for generating different types of nanostructures (2–10). In particular, one-dimensional (1D) NP arrays have potential applications in optoelectronics (11–15) and sensing (16, 17). Currently, the lack of models describing the kinetics and statistics of the self-assembly of 1D arrays does not allow the quantitative prediction of their structural features (for instance, the length of NP chains; the degree of branching; or the coexistence of rings, linear chains, and branched structures). Phase diagrams provide useful information on the equilibrium architectures of the linear NP assemblies (18); however, they do not currently describe their detailed structural characteristics and do not characterize the kinetics of NP organization.

Recently, several research groups reported on the assembly of colloidal particles in 1D polymerlike structures. Binding of particles into chains was achieved by chemical cross-linking or physical attraction of ligands (4, 10, 19, 20), external field-induced attraction between colloids (9, 21), and oriented attachment and fusion of nanocrystals (22, 23). No quantitative approach has been successfully applied to the prediction of chain topology and the kinetics of chain growth. For example, in contrast to step-growth polymerization, the rate of growth of nanowires by oriented attachment of NPs could not be characterized by a characteristic rate constant (22), whereas in chemically mediated assembly, the description of the kinetics of polymerization was complicated by the ligand-exchange step (4).

We report an approach to the quantitative prediction of the structural characteristics of linear, branched, and cyclic ensembles of NPs, as well as their structural isomers. We hypothesized that NPs act as multifunctional monomer units that, in a process analogous to step-growth polymerization, organize themselves into macromolecule-like assemblies. Polymerization occurred because of the formation of reversible (controlled by solvent quality), noncovalent bonds at specific bond angles, and it yielded a colloidal polymer. The growth of NP chains was described by the kinetics and statistics of step-growth polymerization (24–26), which, for a particular time, allowed the prediction of the aggregation number and the size distribution of NP ensembles, similar to the degree of polymerization and polydispersity index (PDI) of polymers, respectively.

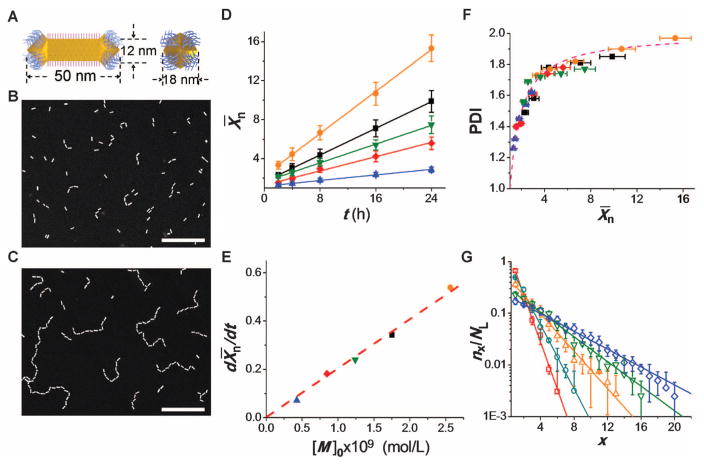
Figure 1A shows the architecture of the individual asymmetric NP. A gold nanorod (NR) was coated with a bilayer of cetyl trimethyl ammonium bromide (CTAB) along its sides, and the two arrowhead edges were coated with thiol-terminated polystyrene (PS) molecules (10, 27). Arrowhead gold NRs with a mean length and width of 50 and 12 nm, respectively, were prepared by seed-mediated synthesis of cylindrical NRs (28), followed by the synthesis of two arrowhead ends, each with four {111} facets (figs. S1 and S2) (29). Preferential binding of CTAB to the {100} facets of the longitudinal side of the NRs left the {111} facets of the arrowheads deprived of CTAB and allowed for the attachment of thiol-terminated PS molecules to the facets of the arrowheads (10). After ligand exchange, the NRs were dispersed in dimethyl formamide, a good solvent for both CTAB and PS.

Fig. 1.

Growth of colloidal polymer chains. (A) Schematics of the side view of the long face (left) and the edge (right) of the NR carrying CTAB on the long side and thiol-terminated PS molecules on the ends. (B and C) Dark-field TEM images of the NR chains after 2 (B) and 24 (C) hours assembly. [M]₀ = 0.84 × 10⁻⁹ (mol/L). Scale bar, 100 nm (both panels). (D to F) Polymerization of NRs at [M]₀ of 0.42 × 10⁻⁹ (solid blue triangles), 0.84 × 10⁻⁹ (solid red diamonds), 1.24 × 10⁻⁹ (solid green inverted triangles), 1.76 × 10⁻⁹ (solid black squares), and 2.56 × 10⁻⁹ (solid orange circles) (mol/L). (D)Variation in the number average degree of polymerization, X̄_n, with time t. h, hours. (E) Dependence of chain growth rate on [M]₀. (F) Variation in the PDI of the chains with X̄_n. The dashed line shows the relation PDI = (2 – 1/X̄_n). For each data point in (D) and (F), the total number of NRs used in the analysis was 5000. (G) The experimental (symbols) and theoretically predicted (lines) fractions of linear x-mer chains, plotted as a function of their degree of polymerization, x, for the time of 2 (open red squares), 4 (open teal circles), 8 (open orange triangles), 16 (open green inverted triangles), and 24 (open blue diamonds) hours. [M]₀ = 0.84 × 10⁻⁹ (mol/L). Error bars indicate SD.

The self-assembly of the NRs was mediated by reducing the solubility of the PS tethers after adding 15 weight percent of water to the solution of NRs in dimethyl formamide (10). To minimize the surface energy of the system in a poor solvent, the hydrophobic PS molecules formed a physical bond between the arrowheads of the neighboring NRs, thereby organizing them into chains (Fig. 1, B and C). The use of PS with an intermediate molecular weight of 12,000 g/mol ensured that the polymer-coated facets of the arrowheads acted as distinct functional groups. In the chains, the length of the bond—defined as the average distance between the facets of the arrowheads of adjacent NRs—was 7.5 ± 0.5 nm. The self-assembly of the NRs was monitored by ultraviolet (UV)–visible spectroscopy (fig. S3) and by the analysis of transmission electron microscopy (TEM) and scanning electron microscopy images of the NR chains on various substrates.

With increasing time t, the number of NRs in the chains gradually increased (Fig. 1, B and C) (30). Inspection of the TEM images of the chains revealed that most of the NRs reacted as bifunctional monomers and formed one bond per arrowhead: After 24 hours, even at the highest initial NR concentration, the fraction of arrowheads forming two bonds per arrowhead was only 1.4% versus 91% of monoreacted arrowheads (~7.6% of arrowheads did not react). A reduced reactivity of the three remaining facets of the arrowheads after the formation of the first bond was presumably caused by steric hindrance.

We used an analogy to polymer molecules to characterize the evolution of the NR chains by the change in their number-average degree of polymerization (X̄_n), weight-average degree of polymerization (X̄_w), and PDI as in (25)

$${\overline{X}}_{\mathrm{n}}=\frac{\sum n_{x}x}{\sum n_x}{\overline{X}}_{\mathrm{w}}=\frac{\sum n_x{x}^2}{\sum n_{x}x}\text{PDI}=\frac{\overline{X_{\mathrm{w}}}}{{\overline{X}}_{\mathrm{n}}}$$ (1)

where x is the number of NRs in the chain and n_x is the number of chains containing x NRs. The individual NRs were included in the calculations, and the increasing values of X̄_n or X̄_w reflected conversion of the polymerization reaction.

We initially focused on the linear chains. The initial concentration of active functional groups of the NRs was found as [M]₀ ≈ 2[C_NR]₀, where [C_NR]₀ is the initial mole concentration of the NRs. The value of [C_NR]₀ was determined by measuring the intensity of extinction of the NRs at the wavelength corresponding to their longitudinal plasmon-band maximum (table S1) (31). In the concentration range of 0.42 × 10⁻⁹ ≤ [M]₀ ≤ 2.56 × 10⁻⁹ mol/liter, the value of X̄_n increased linearly with time (Fig. 1D). The relation X̄_n ~ t was characteristic of reaction-controlled step-growth polymerization, in which the reactivity of functional groups of the monomers is independent of the chain length [the Flory’s assumption (24)].

The assembly of the chains occurred at a low rate: At [M]₀ = 2.56 × 10⁻⁹ mol/L, the increase of X̄_n by one unit took 6.7 × 10³ s (Fig. 1D). The long time of bond formation was caused by the small reactive volume of the arrowheads, the excluded volume repulsion between CTAB-coated sides of the NRs, and the requirement for a particular NR orientation to bond the facets of the arrowhead (32).

In the range of initial concentrations of functional groups studied, the variation in the average-number degree of polymerization X̄_n = 2 [M]₀kt + 1, where k is the rate constant (Fig. 1D), was characteristic of the kinetics of externally catalyzed polymerization of bifunctional monomers with identical functional end groups (24). The rate of chain growth, dX̄_n/dt, was linearly proportional to the initial concentration of functional groups (Fig. 1E), which yielded a rate constant for the self-assembly process of k = 2.9 × 10⁴ M⁻¹s⁻¹. For all values of [M]₀, the PDI of the growing chains changed asPDI = 2 − 1/X̄_n, approaching the value of two for the nearly complete reaction (Fig. 1F), also characteristic of step-growth polymerization.

For different self-assembly times, we determined the distribution of degrees of polymerization of the chains (equivalent to the distribution of chain lengths). Figure 1G shows the variation in the fraction of x-mers among linear chains (n_x/N_L), where n_x is the number of chains with degree of polymerization x, and N_L is the total number of linear chains in the system at time t. The value of n_x/N_L for linear step-growth polymerization was theoretically determined as in (33)

$$n_x/N_{\mathrm{L}}=(1-p)p^{x-1}$$ (2)

where p is the fraction of arrowheads of the NR forming a single bond. (We note that p is the extent of polymerization reaction, equal to the probability of an arrowhead of a NR to form a single bond with another NR at time t.) The value of p as a function of time was determined by analyzing TEM images. A good agreement between the experimental and theoretical values of n_x/N_L (Fig. 1G) implied that the statistics of step-growth polymerization predicted the distribution of chain lengths at different reaction times.

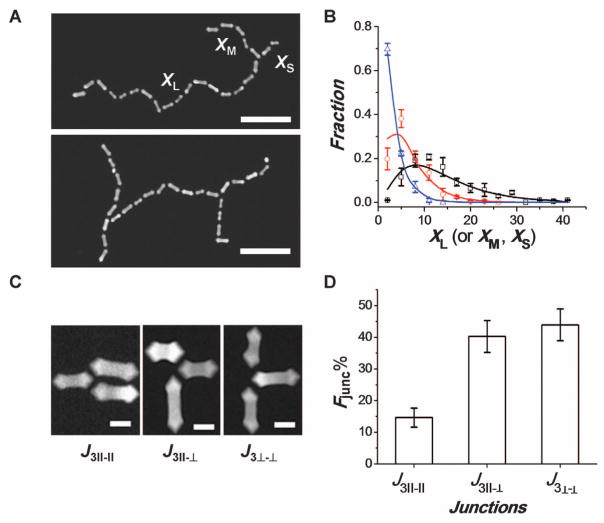
The self-assembly of the NRs generated several types of structural isomers. First, in chains with a low degree of polymerization (x ≤ 4) most of the NRs were aligned with their long axes either parallel or perpendicular to each other (that is, with a bond angle θ = 90° or 180°, respectively) (Fig. 2, A and B). The distribution of bond angles resulted in two energy minima and the formation of structures resembling trans-gauche isomers. With increasing x, the fraction of bond angles of θ = 90° diminished because of the stronger stretching of the longer chains on the surface, caused by the surface tension–driven flow. Second, due to the existence of facets on the arrowheads, the preceding and subsequent NRs attached to the two opposite arrowheads of a particular NR were in a cis- or a trans-position with respect to each other (Fig. 2C). Cis- and trans-isomers randomly alternated along the chain, and for x ≤ 20, the relative ratio (R_cis/trans) of cis-to-trans isomers was close to a unit (Fig. 2D). Third, we also observed a small (below 0.5%) number of cyclic polymers forming triangles, squares, pentagons, or hexagons (Fig. 2E). With an increasing degree of polymerization of the chains, the fraction of cycles reduced (Fig. 2F). A low fraction of cycles stemmed from the low probability of the assembly of all the NRs in the cycle at specific bond angles. For example, the probability of the formation of the tetramer cycle was estimated as $P_{\text{c-tetra}}={P_{90}}^3\times P_f^2$, where P₉₀ is the average probability of attaching an ith and the (i – 1)th NRs at a bond angle θ = 90°, and P_f is the average probability of linking an ith NR to a particular facet of the arrowhead of the (i – 1)th NR, so that the ith NR was located in the plane determined by the (i – 1)th and (i – 2)th NRs. The value of P₉₀ = 0.26 was found by integrating the area below the angle distribution curve for tetramer chains at 75° ≤ θ ≤ 105° (Fig. 2B), and the value of P_f = 1/4 was used for four equally reactive facets on each arrowhead of the NR for i > 2. The value of P_c-tetra was estimated to be 1.2 × 10⁻³, in agreement with the experimentally determined fraction of tetramer rings of 1.4 × 10⁻³ among chains with x = 4.

Fig. 2.

Structural isomerism of the self-assembled polymer chains. (A) TEM images of the NRs linked at a bond angle of θ = 90° (left) and θ = 180° (right). (B) Variation in the distribution of bond angles for dimers (black), tetramers (red), and octamers (blue). (C) TEM images of the chains with cis-isomers (left) and trans-isomers (right). (D) Variation in the ratio of the number of trans-to-cis isomers (R_trans/cis), plotted as a function of the number of NRs in the chain. (E) TEM images of cyclic molecules assembled at [M]₀ = 0.84 × 10⁻⁹ (mol/L) and t = 6 hours. (F) Variation in the fraction of cyclic isomers (F_c), as in (E), plotted for chains with different degrees of polymerization. Scale bars in (A), (C), and (E), 50 nm. Error bars indicate SD.

The value of the bond angle of 90° led to reduced strain in small cycles, in comparison with carbon-based polymers. In addition, mismatch of the bond angles with respect to the optimal angles between the arrowhead facets could result in a larger surface energy of PS molecules in a poor solvent. Linkage of the NRs with PS molecules exposed to the solvent allowed for the adjustment of the bond angles between the facets to minimize the energy of the system.

We analyzed the structure of branched NR chains formed at t = 24 hours and [M]₀ = 2.56 × 10⁻⁹ mol/L. Approximately 30% of the chains formed three-arm stars [~5% of the chains had two branches, similar to H-polymers (33)] (Fig. 3A). For star chains, the PDI of 1.25 ± 0.14 was lower than the PDI of the linear chains with an identical degree of polymerization, and it was close to the expected value of 1.33 (33). To characterize the architecture of star assemblies, we denoted the degrees of polymerization of the long, medium, and short arms of the chains as X_L, X_M, and X_S, respectively (Fig. 3A, top). The number average degrees of polymerization of the arms were 16, 8, and 3, in very good agreement with the theoretical predictions of 17, 8, and 4, respectively, as determined in (33)

Fig. 3.

Structure of branched NR chains. (A) TEM images of three-arm star polymer (top) and H-shaped polymer (bottom). The corresponding degrees of polymerization of the long, medium, and short arms of the star polymers are denoted as X_L, X_M, and X_S, respectively. Scale bars, 200 nm. (B) Experimentally determined fractions of long (black squares), medium (red circles), and short (blue triangles) arms of star polymers, plotted as a function of the corresponding degrees of polymerization. Solid lines show the corresponding theoretically estimated fractions of the long (Eq. 4), medium, and short arms (eqs. S7 and S9). (C) TEM images of the junctions at branching points in NR chains. The subscripts in the notations define the number of NRs in the junction and the orientation of NRs with respect to each other. Scale bars, 20 nm. (D) Distribution of the fractions of junctions with different orientations of NRs for t = 24 hours and [M]₀ = 2.56 × 10⁻⁹ mol/L. Error bars indicate SD.

$${\overline{X}}_{\mathrm{L}}=\frac{1+2p+3p^2+3p^3+2p^4}{(1-p^2)(1+p+p^2)}$$ (3)

where p = 0.9 (for X̄_M and X̄_S, see eqs. S8 and S10). In addition, we characterized the distribution of arm lengths by determining the fraction of each arm as a function of its degree of polymerization (Fig. 3B). The fractions of the long, medium, and short arms (P_L, P_M, and P_S, respectively) were theoretically predicted using the statistics of polymerization of branched polymers (Eq. 4 and eqs. S7 and S9, respectively). For example, the fraction of the long arm with degree of polymerization X_L was determined as in (33)

$$P_{\mathrm{L}}(X_{\mathrm{L}})=\frac{p^{X_{\mathrm{L}}}{\displaystyle \sum _{X_{\mathrm{M}}=1}^{X_{\mathrm{L}}}}{p}^{X_{\mathrm{M}}}{\displaystyle \sum _{X_{\mathrm{S}}=1}^{X_{\mathrm{M}}}}{p}^{X_{\mathrm{S}}}}{{\displaystyle \sum _{X_{\mathrm{L}}=1}^{\infty }}{p}^{X_{\mathrm{L}}}{\displaystyle \sum _{X_{\mathrm{M}}=1}^{X_{\mathrm{L}}}}{p}^{X_{\mathrm{M}}}{\displaystyle \sum _{X_{\mathrm{S}}=1}^{X_{\mathrm{M}}}}{p}^{X_{\mathrm{S}}}=(1-p^3)(p^{X_{\mathrm{L}}-1}-p^{2X_{\mathrm{L}}-1}-p^{2X_{\mathrm{L}}}+p^{3X_{\mathrm{L}}})}$$ (4)

The experimental and theoretical distributions of the arm length in star molecules were in good agreement (Fig. 3B).

In the branching points, we observed three types of mutual orientation of the NRs (Fig. 3C). We labeled the junctions as J_3||-||, J_3⊥-⊥, and J_3||-⊥ where the number 3 in the subscripts denotes the number of NRs in the junction, and the symbols ||-||, ⊥-⊥, and ||-⊥ reflect two parallel, two perpendicular, and one parallel/one perpendicular NR alignments, respectively. The histogram of the fractions of each type of junction in the chains showed a lower fraction of J_3||-|| junctions in comparison with J_3⊥-⊥ and J_3||-⊥ junctions (Fig. 3D), due to the steric constraints in attaching the second NR in the parallel orientation to the reacted arrowhead.

The polymerization model was applicable to the self-assembly of arrowhead and cylindrical gold NRs (28), with a length in the range from 30 to 50 nm, which were end-tethered with PS molecules with a molecular weight ranging from 5000 to 20000 g/mol. We anticipate that the approach can be applied to the organization of other types of NPs, as long as their self-assembly follows a reaction-limited process.

This work bridges the gap between polymerization reactions taking place at a molecular level and NP self-assembly occurring at the length scale two orders of magnitude larger. It shows that the theory of step-growth polymerization is valid for the assembly of NPs linked by physical bonds. The polymerization approach enables pre-programming the dimensions of 1D nanostructures by assembling NP chains with a predetermined length. It can facilitate the design of new, complex nanostructures by mimicking a large library of polymers produced by step-growth polymerization, e.g., hyperbranched (dendritic) polymers, polymer networks, and copolymerization of different NPs (e.g., metal and semiconductor NPs) with a high degree of control over the structure of alternating, block and graft-copolymers. Owing to the progress in NP synthesis, the self-assembly of NPs with asymmetric functional groups can be explored and modeled using the theory developed for polymerization of more complex monomers. On the other hand, the capability to visualize the polymerization process by imaging emerging nanostructures provides the unique ability to test theoretical models developed for step-growth polymerization.