Network-Based Analysis of eQTL Data to Prioritize Driver Mutations

Abstract

In clonal systems, interpreting driver genes in terms of molecular networks helps understanding how these drivers elicit an adaptive phenotype. Obtaining such a network-based understanding depends on the correct identification of driver genes. In clonal systems, independent evolved lines can acquire a similar adaptive phenotype by affecting the same molecular pathways, a phenomenon referred to as parallelism at the molecular pathway level. This implies that successful driver identification depends on interpreting mutated genes in terms of molecular networks. Driver identification and obtaining a network-based understanding of the adaptive phenotype are thus confounded problems that ideally should be solved simultaneously. In this study, a network-based eQTL method is presented that solves both the driver identification and the network-based interpretation problem. As input the method uses coupled genotype-expression phenotype data (eQTL data) of independently evolved lines with similar adaptive phenotypes and an organism-specific genome-wide interaction network. The search for mutational consistency at pathway level is defined as a subnetwork inference problem, which consists of inferring a subnetwork from the genome-wide interaction network that best connects the genes containing mutations to differentially expressed genes. Based on their connectivity with the differentially expressed genes, mutated genes are prioritized as driver genes. Based on semisynthetic data and two publicly available data sets, we illustrate the potential of the network-based eQTL method to prioritize driver genes and to gain insights in the molecular mechanisms underlying an adaptive phenotype. The method is available at http://bioinformatics.intec.ugent.be/phenetic_eqtl/index.html

Introduction

Because of their short generation times, large population sizes and quasi clonal behavior, experimental evolution of microorganisms offers great potential for trait selection and testing evolutionary theory (Dettman et al. 2012; Kawecki et al. 2012). Evolution experiments start from a single clone propagated for many generations under a predefined conditional set up defined as the selection regime. As the organisms propagate they gradually accumulate genetic variation (single nucleotide polymorphism (SNP’s), INDELs, etc.). Some of this variation will cause a clonal fitness increase and a concomitant selective sweep, which ultimately increases population fitness. The acquired genetic variation can be identified in the evolved lines of the population through sequencing. Genes containing mutations that are fixed in the population, that reach a high frequency in the population, or of which the origin coincides with an increase in fitness (Herron and Doebeli 2013; Kvitek and Sherlock 2013; Hong and Gresham 2014) are pinpointed as likely drivers, where a driver in this context is defined as any gene carrying adaptive mutations, that in isolation or in combination with other drivers can elict a fitness increase and concomittant clonal expansion.

In most evolution studies, however, a mechanistic understanding of how the selected driver mutations elicit the adaptive phenotype is still lacking. Such a mechanistic interpretation depends on correctly identifying and interpreting driver genes in terms of the genome-wide interaction network of the organism of interest to find the molecular pathways that drive the observed adaptive phenotype. The identification of the driver genes is in itself nontrivial because during a selection sweep, passenger mutations, that is mutations that do not contribute to the phenotype, are likely to hitchhike to fixation along with driver mutations (Barrick and Lenski 2013). Furthermore, because under strong selection pressures hypermutators frequently arise (Foster 2007; Wielgoss et al. 2013), the ratio of driver genes to passenger genes can become low, further complicating the identification of driver genes.

To identify driver genes, one can exploit parallelism of mutations at the gene/nucleotide level. Genes observed to be recurrently mutated in independently evolved lines with a similar phenotype are more likely to be drivers (Tenaillon et al. 2012; Hong and Gresham 2014). However, independently evolved lines can also acquire similar adaptive phenotypes by mutations in different genes that affect the same molecular pathways (Tenaillon et al. 2012; Kvitek and Sherlock 2013; Hong and Gresham 2014), rather than by sharing exactly the same mutations or mutated genes. Identifying driver genes underlying an observed phenotype thus requires identifying mutational parallelism between independently evolved lines at the molecular pathway level (Lin et al. 2007; Wood et al. 2007; Ding et al. 2014; Lang and Desai 2014). In other words, driver gene identification and acquiring a network-based understanding of the adaptive phenotype are confounded problems that have to be solved simultaneously.

In this study, we illustrate how a network-based method in combination with coupled genotype-expression phenotype data (eQTL data) of parallel evolved lines can aid in simultaneously prioritizing driver genes and providing a network-based interpretation of the molecular mechanisms underlying the evolved adaptive traits. To this purpose, the network-based eQTL method uses an organism-specific genome-wide interaction network, compiled from publicly available interactomics data (Cloots and Marchal 2011; Sánchez-Rodríguez et al. 2013) to drive the search for mutational consistency at the pathway level.

By generating a semisynthetic experimental evolution benchmark, the ability of the method to prioritize driver genes is demonstrated. To illustrate the performance of both driver gene prioritization and network-based interpretation of the data in a real setting, the method is applied to eQTL data obtained from two previously described evolution experiments in Escherichia coli. The first data set aims at identifying the adaptive pathways that gave rise to improved Amikacin resistance in four independently evolved lines (Suzuki et al. 2014). The second data set focuses on unveiling the molecular interactions between two distinct ecotypes that evolved from a common ancestor in the long-term evolution experiment of Lenski et al. (1991) (Plucain et al. 2014). For both data sets, the method prioritizes driver genes that contribute to the adaptive phenotypes and unveils their molecular modes of action.

Materials and Methods

Network-Based eQTL Method

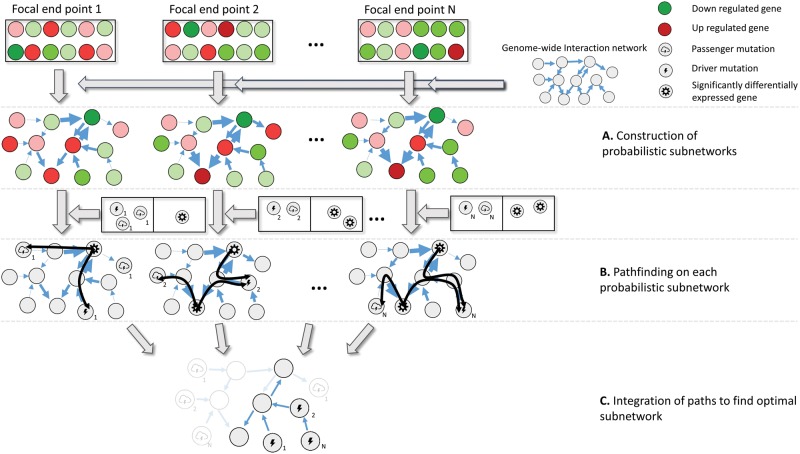
The eQTL analysis method is based on the probabilistic logical querying language ProbLog (De Raedt et al. 2007). To simultaneously prioritize driver genes and unveil adaptive molecular pathways, elicited by these driver mutations, the driver gene identification problem is reformulated as a decision theoretic subnetwork inference problem (Van den Broeck et al. 2010) over multiple probabilistic networks $Q_i$, derived from the genome-wide interaction network $G$. The method consists of three steps (fig. 1).

Fig. 1.—

Overview of the network-based eQTL method. The input of the method consists of, respectively, coupled genotype and expression phenotype data for a set of evolved lines with the same phenotype and a genome-wide interaction network. Red and green indicate, respectively, over- and underexpression with respect to a reference. Genes that are considered to be significantly differentially expressed according to a test statistic are indicated by a specific symbol as displayed on the figure legend. Mutated driver and passenger genes are indicated with two different symbols as displayed on the legend. The numbering of each mutated gene indicates the evolved line in which this mutated gene occurred. (A) Construction of the end point specific probabilistic subnetworks: for each evolved line the genome-wide interaction network is converted into a probabilistic subnetwork by assigning to each edge in the genome-wide interaction network a weight that is interpreted as the probability that the edge has an influence on the assessed phenotype. These weights depend on the level of differential expression of the terminal node of the edge. Genes that are more differentially expressed (darker red/green) will give rise to higher weights on the edges (indicated by the width of the edge). (B) Pathfinding in each of the probabilistic subnetworks. The mutated and significantly differentially expressed genes occurring in each of the evolved lines are mapped to the corresponding end point specific probabilistic subnetworks. For each significantly differentially expressed gene, all possible paths from this gene to all mutated genes in the same end point are searched for (paths are shown as black curves). (C) Optimal subnetwork selection. Optimization is performed by integrating the paths found in all end point specific probabilistic networks according to a predefined cost function that positively scores the addition of paths connecting pairs of mutated genes-differentially expressed genes observed in any of the end points, but that penalizes the addition of edges. As a result, paths that are strongly connected to the expression phenotype and that overlap with each other are selected as the optimal subnetwork.

Construction of Probabilistic Networks

For each of the parallel evolved lines $i$ of an evolution experiment, the genome-wide directed interaction network $G$ is converted into a probabilistic network $Q_i$ by assigning to each edge a weight that reflects the probability the edge is playing a role under the assessed condition, given the differential expression data as depicted in figure 1A. To this end, per node the probability is calculated that an expression value at least as extreme as the one associated with that node would be observed by chance, given the null hypothesis that the expression value of the gene which corresponds to the node is not significantly differentially expressed, is true. Calculation is performed using a two-tailed P-test assuming that the log₂ fold changes follow a normal distribution $N\left(\mu ,\sigma \right)$ (Pawitan et al. 2005; Feng et al. 2012). By standardizing, this distribution to $N(0,1$) this probability can be calculated for any differential expression value $D_{gene}$ using Formula 1 in which $Z_{gene}$ corresponds to the standard score associated with $D_{gene}$.

$$P_{gene}=\{\begin{array}{c}P\left(X>Z_{gene}\right)+P\left(X<-Z_{gene}\right)if{Z}_{gene}>0\\ P\left(X<Z_{gene}\right)+P\left(X>-Z_{gene}\right)if{Z}_{gene}<0\end{array}GivenN(0,1)$$ (Formula 1)

As in the network-based eQTL method the edges, not the nodes, are weighted, the value $P_{gene}$ is propagated to the edges that terminate in it. A high value for the probability that a specific edge is involved in a specific experimental condition is assigned to edges that terminate in highly differentially expressed genes. Therefore, 1 − $P_{endgene}$ will be assigned to all edges. Using the cumulative normal distribution of $N\left(\mu ,\sigma \right)$ which is written as $\Phi \left(\mu ,\sigma \right)$, this can be simplified as shown in Formula 2.

$$P_{edge}=(|0.5-{\Phi }_{\left(\mu ,\sigma \right)}(D_{endgene})|)\text{*}2$$ (Formula 2)

Where $D_{endgene}$ is the differential expression data of the end gene of the interaction. If no differential expression data is available for $D_{endgene}$, $P_{edge}$ is set to 0.5.

Pathfinding in Probabilistic Networks

Each probabilistic network $Q_i$ allows for determining the probability of connectedness between a gene $C_{i,j}$, from a set of genes $C_i$, and a gene set $A_i$, defined as $P\text{(}path\left(C_{i,j},A_i\right)\text{|}{Q}_i)$. This probability of connectedness expresses how likely it is that there exists a path that connects the gene $C_{i,j}$ to any gene in the gene set $A_i$, in the probabilistic network $Q_i$. A path between two nodes is a sequence of consecutive edges from the genome-wide interaction network that connects these two nodes and for which all edges are directed in the same direction. The probability of such a path is simply the product of the probabilities of the edges it contains. In the proposed eQTL setting, each gene $C_{i,j}$ is defined as significantly differentially expressed in evolved line $i$ and gene set $A_i$ is the set of mutated genes obtained from evolved line $i$. A path connects a significantly differentially expressed gene to genes mutated in the same evolved line. The rationale behind this is that the significantly differentially expressed genes are effects of mutations and thus connect to the “causal” mutations through the probabilistic network. The probability of connectedness $P\text{(}path\left(C_{i,j},A_i\right)\text{|}{Q}_i)$ represents the probability with which the differential expression of $C_{i,j}$ can be induced by the set of mutations, given the probabilistic interaction network $Q_i$ and quantifies which mutations are most likely to cause the differential expression of $C_{i,j}$.

Inference of the Optimal Subnetwork by Combining the Data from All Evolved Lines

Identifying driver mutations from a set of independent end points with the same phenotype corresponds to inferring a single subnetwork $K_{optimal}$ over all independent end points that best connects the significantly differentially expressed genes $C_{i,j}$ and the set of mutations $A_i$ for all end points together as depicted in figure 1C. A subnetwork $K$ of a network $G$ is defined as a subset of the edges in $G$ together with the nodes occurring in the selected edges. Note that a subnetwork in this context can thus consist of any number of disconnected parts of the original network $G$.

For each subnetwork, $K$ from $G$ the probability of connectedness changes to $P\text{(}path\left(C_{i,j},A_i\right)\text{|}{Q}_i,K)$ as paths that are valid in $Q_i$ are not necessarily valid in a subnetwork $K$. Therefore, the probability of connectedness changes to $P\text{(}path\left(C_{i,j},A_i\right)\text{|}{Q}_i,K)$ when working with subnetworks $K$, denoting that the edges along the path have to be present in both $Q_i$ and $K.$ Each subnetwork $K$ should be scored based on the sum of probabilities that there exists a path between each significantly differentially expressed gene $C_{i,j}$ in $C_i$ and the list of mutated genes $A_i$, for each independently evolved line $i$, out of a total of $n$ independently evolved lines as described in Formula 3. Between different end points, it is expected that the same adaptive pathways are triggered (parallel evolution). Also, within every end point separately, multiple paths are expected to be found in regions with many significantly differentially expressed genes that are likely to be important for the phenotype. Therefore, paths between driver genes selected from different end points and their respective sets of differentially expressed genes should overlap in the optimal subnetwork. By restricting the size of the network through a cost based on the number of edges$|K|$ in the subnetwork, the method will preferentially select these overlapping paths. This edge cost can be modulated using the cost factor $x_e$. $K_{optimal}$ is defined as the subnetwork that has the maximum possible value of the score function $S(K)$ (Formula 3).

$$S\left(K\right)={\displaystyle \sum }_i^n({\displaystyle \sum }_j^l(P(path(C_{i,j},A_i)|Q_i,K)))-\left|K\right|*x_e$$ (Formula 3)

Computing the probability that there exists a path between two nodes in a probabilistic network is known as the two-terminal reliability problem, which is nondeterministic polynomial time hard (NP-hard). This explains why there is no known efficient exact inference algorithm and why we employ an approximation algorithm to compute $P(path(C_{i,j},A_i)|Q_i)$. This probability is approximated by using only the N most likely paths of maximal length $l$ between the differentially expressed gene $C_{i,j}$ and any mutated gene of $A_i$ (De Raedt et al. 2007; De Maeyer et al. 2013). The resulting paths (for all $C_i$) are then represented as a Boolean formula (as in probabilistic logic programming languages [De Raedt et al. 2007]): each path corresponds to a conjunction of the edges that are present in the path, and a set of such paths corresponds to the disjunction of the conjunctions corresponding to these paths. This formula is then compiled into an equivalent deterministic decomposable negation normal form (d-DNNF) using knowledge compilation techniques (Darwiche and Marquis 2002). The advantage of the d-DNNF is that it contains the same information as the original set of paths and that it can efficiently be evaluated in polynomial time for each subnetwork $K$ (Darwiche and Marquis 2001). Selecting such a subnetwork $K$ corresponds to setting all edges not in $K$ to false when evaluating the d-DNNFs. The optimal subnetwork $K_{optimal}$ is determined by sampling different subnetworks $K$ from $G$ by performing a random-restart hill climbing optimization as outlined in Van den Broeck et al. (2010). Note that, as $K_{optimal}$ is a subset of $G$, it is possible that $K_{optimal}$ is not necessarily connected.

Driver Gene Prioritization

Because subnetworks obtained using a higher edge are more enriched in driver genes than subnetworks obtained using a low edge cost (higher positive predictive value [PPV], more stringent conditions) and subnetworks detected at high edge costs are in general contained within the ones retrieved at lower edge costs, mutated genes are prioritized based on the highest edge cost for which they are still selected (i.e. ranks of mutated genes are based on the most stringent condition under which they are still selected). The reason for this is that mutated genes that are detected at the highest edge cost (most stringent parameter) represent the most pronounced signals in the data. Mutated genes that represent weaker signals (mutations that explain less of the expression data) are only retrieved at less stringent edge parameter costs. To this end, for each data set multiple optimal subnetworks are inferred using a gradually decreasing edge cost, that is a parameter sweep over the edge cost. Mutated genes that are retrieved using a high edge cost are strongly connected to the expression phenotype and thus receive the lowest (best) rank. Note that this prioritization strategy can result in assigning identical ranks to different mutated genes. These prioritized mutated genes, together with the inferred subnetworks are visualized by depicting the union of all edges and nodes present in the different inferred subnetworks.

Parameter Settings

To infer subnetworks, the maximum length of a path is set to four edges based on both biological (Gitter et al. 2011; Navlakha et al. 2012) and computational considerations. To approximate the probability of connectedness $P\text{(}path\left(C_{i,j},A_i\right)\text{|}{Q}_i,K)$_, the 20-best paths were used that connect each differentially expressed gene $C_{i,j}$ to the set of mutated genes $A_i$. The edge cost parameter determines the size of the inferred subnetwork and forces the selection of overlapping paths. The behavior of the edge cost is characterized on a semisynthetic data set as indicated in the Result section. As described in the Driver Gene Prioritization paragraph, a parameter sweep of the edge cost was performed to prioritize the mutated genes.

As lower edge costs do not affect ranks of genes prioritized at higher edge costs, the choice of the lower bound on the edge cost does not interfere with the results of the highest ranked genes. For convenience and visualization purposes, we choose a cut off on the sweep at a cost that corresponds to finding a network of no more than 120 nodes. Conversely, when setting the conditions too stringent that is very high edge cost, subnetworks can no longer be inferred. Therefore, as smallest edge cost we chose the most stringent value at which a subnetwork could be inferred. This resulted in a parameter sweep of the edge cost from 1.75 to 0.25 for the Amikacin (AMK) resistance data set and from 0.975 to 0.025 for the coexistence ecotypes data set. The edge cost sweep was performed with a step size of 0.025. Note that the upper limit of the edge cost in the sweep corresponds to the value for which no subnetwork was inferred anymore.

Data Sets

Semisynthetic Benchmarking Set

The semisynthetic benchmark data set was based on data published by Stincone et al. (2011) (has been deposited at Gene Expression Omnibus under the accession GSE13361) assessing for 27 E. coli K-12 MG1655 single gene knockout strains involved in acid resistance, the expression profiles relative to a wild-type E. coli K-12 MG1655. Levels of differential expression of single gene knockout strains (27 strains) with respect to the reference were obtained from COLOMBOS (Engelen et al. 2011). As no repeats were available for the different experiments, and thus no relevant P values were available, significantly differentially expressed genes were determined as genes having a log₂ fold expression change larger than 2. For each KO strain, the knocked out gene was considered a “known” driver gene and the measured levels of differential expression as the corresponding expression phenotype. Five of those strains, namely phoH, cadB, ycaD, spy, yjbJ, and grxA, were discarded for benchmarking, because these genes only have incoming interactions in the genome-wide interaction network or, in the case of yjbJ, are not present in the interaction network. In addition, the experiment corresponding to the hns KO strain was removed as the COLOMBOS database did not contain the appropriate data. For each of the remaining 20 strains, the presence of passenger genes was mimicked by randomly selecting a nucleotide position in the reference genome and mapping this position to a gene. Passenger mutations had to obey following conditions: 1) randomly selected genes did not belong to the set of driver genes and 2) they were connected in the genome-wide interaction network with outgoing interactions. The number of passenger mutations assigned to each data set was selected from a binomial distribution with n, the total number of selected mutations, being equal to 9 and P, the chance of adding a passenger mutation, being equal to 0.5. On average, this mimics an addition of five passenger mutations with a standard deviation of 1.5 for each of the 20 strains in each data set. This way the total number of mutated genes in the semisynthetic data set is of the same order of magnitude as the number of passenger mutations per driver mutation observed in real data sets (Tenaillon et al. 2012; Herron and Doebeli 2013; Suzuki et al. 2014).

AMK Resistance Data Set

The genomic data for the four Amikacin resistant strains was obtained from Suzuki et al. (2014). Raw sequencing has been deposited at the DNA Data Bank of Japan sequence read archive under the accession PRJDB2980. Only the Illumina reads were used. The data of the four Amikacin resistant lines was mapped to the ancestral E. coli K-12 MDS42 strain using Bowtie2 (Langmead and Salzberg 2012). SNPs and small INDELs were called using freebayes (Garrison and Marth 2012) while large INDELs were called using Pindel (Ye et al\\. 2009). This resulted in a total of 59 mutations throughout the four strains. These mutations were mapped to genes as follows: mutations within the coding region of a gene were mapped to the encoded gene, mutations in intergenic regions were mapped to the closest gene if there was a gene within 250 bp of the intergenic region. This resulted in 51 mutated genes. Of these 51 mutated genes, 41 could be mapped to the E. coli K-12 MDS42 reference genome.

Normalized expression data for each of the four Amikacin resistant strains and the ancestral line has been deposited at GEO under the accession GSE59408. Differentially expressed genes were defined as genes having an absolute log₂ fold expression change value higher than 2. This cut off value was selected as no repeated measurements were available and thus no P values could be calculated. Differential expression values were obtained between the Amikacin resistant strains and an ancestral line.

Coexisting Ecotypes Data Set

Genomic data was obtained from Plucain et al. (2014). Mutations present in both clones of the same ecotype, but not in clones of the other ecotype, were selected as candidate driver mutations that could explain the origin of speciation into the observed coexisting ecotypes. It was hereby assumed that potential driver mutations are likely to be ecotype-specific, as mutations common to all clones most likely originated before divergence of the ecotypes. This resulted in the selection of 87 candidate driver mutations, which could be mapped to 86 potential driver genes. The mapping of mutations to genes was taken from Plucain et al. (2014). Of those 86 genes, 62 genes could be mapped to the E. coli B REL606 genome-wide interaction network, which were used as input.

As expression phenotype, we used the degree to which gene expression differed between, respectively, the L and S ecotype as determined by microarray experiments performed by Le Gac et al. (2012) (has been deposited at GEO under the accession GSE30639). Microarrays of 6 biological replicates of the L ecotype, 6 biological replicates of the S ecotype, and 5 biological replicates of the ancestor were available. Using PCA analysis one microarray of the S ecotype and one microarray of the ancestor were found to be outliers and were discarded from subsequent analyses (supplementary fig. 1, Supplementary Material online). The LIMMA package (Smyth 2004) was used to identify the degree of differential expression between the ecotypes. As for this data set repeated measurements for the expression data were available, significantly differentially expressed genes are defined as genes having a P value of maximum 0.05 and an absolute value of log₂ fold change of minimal 0.75. The cut off on the log₂ fold change was taken lower than in the other data sets as here we impose an additional cut off on the P value.

Genome-Wide Interaction Networks

In this article, a genome-wide interaction network refers to a comprehensive representation of current interactomics knowledge on the organism of interest. Networks are represented as graphs $G(N,E)$ in which nodes $N$ correspond to genetic entities (genes, proteins, or sRNAs) and edges $E$ to the interactions between these entities. Every edge is assigned an edge type, indicating the molecular layer to which the interaction represented by the edge belongs (e.g. protein–DNA, protein–protein, metabolic, or signaling interactions). Depending on its type and provided the proper information is available, an edge will be added as a single-directed interaction (e.g. protein–DNA interactions, sRNA–DNA, kinase-target, etc.) or two-directed interactions (protein–protein interactions, undirected metabolic interactions, etc.).

An overview of the genome-wide interaction networks used in this study for the three different E. coli strains: E. coli K-12 MDS42, E. coli B REL606, and E. coli K-12 MG1655 is given in table 1. To compile these networks metabolic interactions and (de)phosphorylation interactions were derived from KEGG (Kanehisa et al. 2014) version 72.1, protein–DNA, sigma interactions, and sRNA–DNA interactions from RegulonDB version 8.6 (Salgado et al. 2013) and high-confidence physical protein–protein interactions from String (Jensen et al. 2009) version 10. Interactions involving RpoD, the primary sigma factor, were removed from these interaction networks as RpoD regulates over one-half of the genes in the interaction network.

Table 1.

Selected mutated genes prioritized as driver genes

AMK Resistance				Coexisting Ecotypes
Gene name	Rank	Line	Type	Gene name	Rank	Line	Type
CyoB	1	2,4	frameshift	gntR	1	S	missense
CpxA	2	1,3	missense, in-frame del	arcA	1	S	missense
NuoG	3	2	nonsense	evgA	1	S	missense
rseA	3	4	nonsense	dnaK	2	S	intergenic
nuoN	3	4	In-frame del	acs	3	S	intergenic
nuoC	4	4	missense	flgG	4	S	synonymous
fusA	5	1,2,3,4	missense	fbaB	5	L	missense
phoQ	6	1	missense	cpsG	5	L	Large del
arcB	7	3	Frameshift del	fruK	6	S	missense
gapA	8	2	missense	rpiR	7	L	intergenic
ClsA	9	1	missense	glk	7	S	intergenic
rho	10	1	missense

Results

Method Overview

A network-based eQTL method was devised to simultaneously prioritize driver genes and unveil molecular pathways involved in the adaptive phenotype. As input, the method requires a genome-wide interaction network of the organism of interest and coupled genotype-expression phenotype (eQTL) data for a set of independently evolved lines (strains/populations) with similar phenotypes (fig. 1). The expression phenotype is defined as the level of differential expression of every gene between an evolved line and a reference.

To prioritize driver genes, all genes from the end points carrying allelic variants (hereafter referred to as mutated genes) will be assessed for their ability to explain the adaptive expression phenotype. Hereto the method infers from the genome-wide interaction network the subnetwork that best connects the mutated genes in each of the evolved lines to the set of significantly differentially expressed genes in the corresponding evolved lines, assuming that 1) the expression phenotype is at least partially a consequence of the driver mutations and 2) the adaptive molecular pathways, but not necessarily the driver genes, are to some extent similar, resulting in parallelism at the molecular pathway level.

An overview of the proposed network-based eQTL method is given in figure 1. The method consists of three steps (see Materials and Methods). In a first step (fig. 1A), the genome-wide interaction network is for each evolved line separately converted into a condition-specific probabilistic network using the expression data of the corresponding evolved line. These condition-specific probabilistic networks are subsequently, in a second step (fig. 1B), used to find all paths between mutated and significantly differentially expressed genes for each evolved line separately. A path is here defined as a sequence of consecutive edges in the genome-wide interaction network. These paths represent possible molecular mechanisms by which mutations could induce the observed pattern of differential expression. In the third step, (fig. 1C) all these paths are analyzed together to find the optimal subnetwork, which aims at selecting the subnetwork of the genome-wide interaction network that captures the molecular mechanisms that drive the adaptive phenotype common to all evolved lines. The optimization enforces the selected subnetwork to have two properties. First, it selects the subnetwork that contains the most likely paths that explain the connection between the mutated and differential expressed genes. Second, it enforces the network to contain parallel molecular pathways between the different evolved lines. The optimal subnetwork thus contains the molecular mechanisms likely to drive adaptation. Possible driver mutations which occur in the optimal subnetwork are prioritized based on the strength of their connectivity with downstream effects and their involvement in parallel molecular pathways (see Materials and Methods).

Performance of Network-Based eQTL Method on a Semisynthetic Data Set

To assess the performance of prioritizing causal mutations by the network-based eQTL method, a semisynthetic benchmark data set was constructed based on a previously published knockout expression profiling experiment (Stincone et al. 2011). This study assesses differential expression profiles between 20 knockout strains with altered fitness in acidic conditions and the wild-type E. coli K12 strain. To mimic the eQTL set up, each of the knocked out genes was considered a “driver gene” and the presence of passenger genes was simulated by adding a number of randomly selected genes to each knockout data set (see Materials and Methods). Differential expression profiles between each knockout strain and the wild type were derived from the original publication data (see Materials and Methods). The performance of the network-based eQTL method was measured in terms of correctly distinguishing driver from passenger genes.

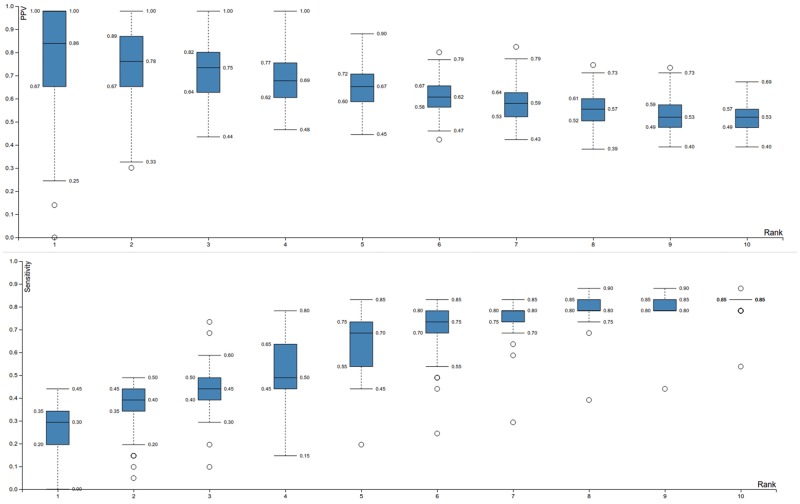
The main parameter of the method is the edge cost, that is the cost for selecting an edge in the inferred subnetwork (see Materials and Methods). As a lower amount of mutated genes will be selected using a higher edge cost, mutated genes can be prioritized by the maximum edge cost for which they are selected. This allows assigning a rank for every selected mutated gene based on the maximum edge cost. This prioritization is motivated by the fact that mutations which are selected at high edge costs need to be better connected to the expression and/or have a higher degree of parallelism with other mutations than mutations which are selected at lower edge costs. This reasoning was tested by analyzing the semisynthetic data set for a wide range of edge costs (see Materials and Methods for specific parameter settings). As can be seen in figure 2, the PPV is high for low ranks and decreases for higher ranks, meaning mutated genes having low ranks are likely to be driver genes. Furthermore, the sensitivity clearly increases with increasing rank, leading to a trade-off between selecting few passenger mutations and selecting many driver mutations. Even for high ranks, results are still better than a random selection of genes as this would correspond to a PPV of 0.2 (on average for every driver gene, four passenger genes were added).

Fig. 2.—

Performance assessment of the network-based eQTL method on the semisynthetic data set. Data of all selected mutated genes at specific ranks are presented as Tukey boxplots. Note that multiple mutated genes can have identical ranks as ranks are assigned based on the maximal edge cost for which a mutation is present within the subnetwork and thus multiple mutated genes can have identical maximal edge costs for which they are present within the subnetwork. The upper plot shows the PPV, (fraction of the selected mutations which are true positives, i.e. driver mutations) in terms of the ranks of the selected mutations. It can be seen that low ranks have higher PPV values. Note that at rank 1, the variance is high. This is because inferred subnetworks for rank 1 are small, and therefore more prone to random effects. That is the selection of one additional false positive in a particular random set largely affects the PPV. Solutions are clearly less variable from rank 2 onwards. The lower plot shows the sensitivity (fraction of all possible true positives selected) in terms of the ranks of the selected mutations. Sensitivity increases with rank, implying a trade-off between PPV and sensitivity.

Unveiling the Molecular Mechanisms Underlying Amikacin Resistance

We applied the eQTL analysis on the eQTL data set from the study of Suzuki et al. (2014). In this study, four independent E. coli MDS 42 lines were grown in the presence of the aminoglycoside antibiotic until all four strains attained increased Amikacin resistance compared with the parental strains.

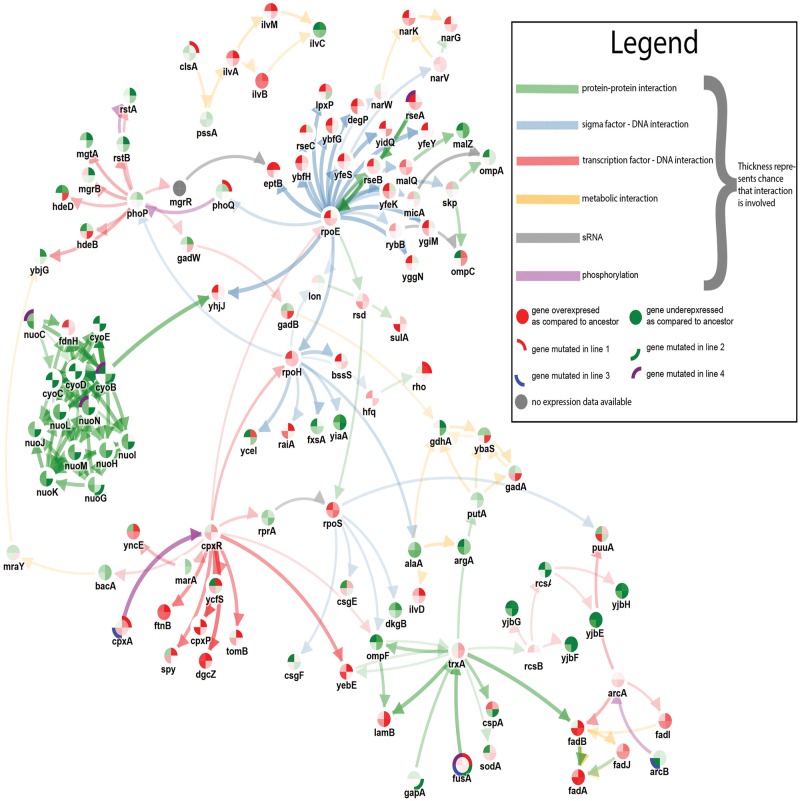
The network-based eQTL method was applied using the genome-wide interaction network of E. coli MDS 42 and the data of the four parallel evolved strains (see Materials and Methods). Out of 41 mutated genes, we prioritized 12 as potential drivers based on their association with the expression data (table 2). The inferred adaptive pathways containing those prioritized genes are visualized in figure 3.

Table 2.

Data sets used to compile the Escherichia coli genome-wide interaction networks

Interaction Type	E. coli K12 MG1655	E. coli B REL606	E. coli K12 MDS42a
Protein–protein	2,737 (Jensen et al. 2009)	2,721 (Jensen et al. 2009)	2,534 (Jensen et al. 2009)
Protein–DNA	4,492 (Salgado et al. 2013)	3,415 (Salgado et al. 2013)	3,890 (Salgado et al. 2013)
Sigma	727 (Salgado et al. 2013)	1,225 (Salgado et al. 2013)	592 (Salgado et al. 2013)
Metabolic	2,798 (Kanehisa et al. 2014)	5,136 (Kanehisa et al. 2014)	2,462 (Kanehisa et al. 2014)
Phosphorylation and dephosphorylation	44 (Kanehisa et al. 2014)	38 (Kanehisa et al. 2014)	40 (Kanehisa et al. 2014)
Srna	213 (Salgado et al. 2013)	2 (Salgado et al. 2013)	171 (Salgado et al. 2013)
Size (edges)	11,011	12,537	9,689
Size (nodes)	2,732	2,650	2,418

^aThe E. coli K12 MDS42 network was derived from the E. coli K12 MG1655 network by deleting all edges connecting genes that do not exist in E. coli K12 MDS42.

Fig. 3.—

Visualization of subnetworks inferred from the Amikacin resistance data set based on data from 100 randomizations. The visualization was created by merging separate inferred subnetworks resulting from a parameter sweep of the edge cost from 0.25 to 1.75. The width of the edge displays the stringency at with the edge was selected (the wider the edge the more stringent the condition. More Stringent conditions correspond to higher edge costs). Node borders are subdivided into four parts to visualize in which line a mutation occurred (evolved lines compared with ancestral line). The inner color of the nodes is also subdivided into four parts where each part represents the degree of differential expression in the corresponding line. The colors of the edges represent the edge types.

One very plausible driver mutation is fusA, encoding the elongation factor G which is consistently carrying a missense mutation in all four strains (mutational consistency at gene level). Mutations in the fusA ortholog have previously been found to confer aminoglycoside resistance in Staphylococcus aureus (Norstrom et al. 2007).

Prioritized genes that are also plausible candidate drivers are those that are consistently mutated at pathway level. Examples of those are the highly prioritized genes cyoB, nuoG, nuoN, and nuoC, affected in lines 2 and/or 4 by nonsense or frameshift mutations. These genes are members of the electron transport chain which are known to downregulate the protein complexes to which they belong (NADH dehydrogenase or terminal oxidase, see supplementary fig. 2, Supplementary Material online) implying an involvement of the electron transport chain in the adaptive phenotype. cpxA is another likely driver as it shows mutational consistency at gene level in two lines (lines 1 and 3). cpxA is a sensor kinase that is known to regulate the cpx response in conjunction with the transcription factor cpxR. The mutations in cpxA seem to result in lines 1 and 3 in an activation of the cpx response with the targets of cpxR being overexpressed compared with the ancestral strain. This increased cpx response has previously been found to have an effect on the electron transfer chain (Raivio et al. 2013).

These results are consistent with what is described in the original article of Suzuki et al. (2014) and are in line with the knowledge that Amikacin uptake is dependent on proton-motive force (Allison et al. 2011). Our results confirm these previous findings although the different lines seem to be triggered through two different molecular systems either by directly affecting the electron transfer chain or through mutations in cpxA.

In addition to genes associated with the proton-motive force, the method prioritizes additional genes, such as rseA explain a large part of the expression phenotype and therefore receive a high rank. However, as a mutation in the antisigma factor which inhibits rpoE leads to large effects on the expression phenotype and other independently evolved lines do not show effects in molecular pathways associated with rseA or rpoE, we would need more data to completely rule out the rseA mutation in line 4 being a false positive.

Unveiling the Molecular Mechanisms of Coexisting Ecotypes in Glucose-Limited Minimal Medium

A second test case consisted of transcriptomics data and genomics data, described, respectively, by Plucain et al. (2014) and Le Gac et al. (2012). These data sets provide the molecular characterization at generation 6,500 of Ara-2, one of the 12 populations that were evolved in the E. coli long-term evolution experiment in glucose minimal medium (Lenski et al. 1991; Barrick et al. 2009). By this time, the ancestral line had diverged into two distinct, stable ecotypes (Le Gac et al. 2012). Associated studies by Rozen et al. (Rozen and Lenski 2000; Rozen et al. 2005, 2009) showed that the L ecotype grows faster on glucose, but secretes byproducts that S can exploit, implying a cross-feeding mechanism between the L and S ecotypes that can explain their stable coexistence.

Plucain et al. (2014) experimentally identified a minimal set of mutations. Two S-specific mutations in, respectively, arcA and gntR and one in spoT, shared by both the L and S strains that when reintroduced together in the ancestral strain were sufficient to mimic the evolved S ecotype in invading and stably coexisting with the L ecotype. However, the fitness level of this reconstructed S ecotype was lower than the fitness level of the evolved S ecotype (Plucain et al. 2014), suggesting that additional mutations play a role in establishing the phenotype of the evolved S ecotype. Both the L and S ecotypes are hypermutators and have accumulated a large number of mutations. Such setting complicates the identification of the correct driver genes.

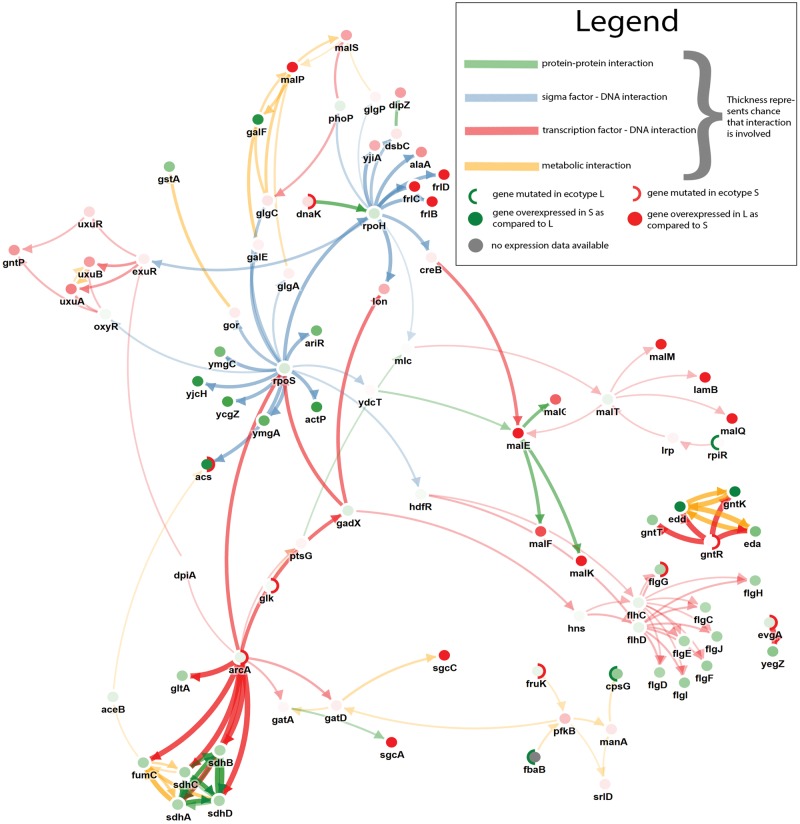
By applying the network-based eQTL method on this coupled genomics-transcriptomics (eQTL) data (Le Gac et al. 2012; Plucain et al. 2014) (see Materials and Methods), we tested to what extent we could successfully prioritize the known important driver genes in a data-driven way and could identify missing drivers explaining the adaptive phenotype. The network-based eQTL method resulted in prioritizing 11 mutated genes out of 62 identified mutated genes (table 2, fig. 4).

Fig. 4.—

Visualization of subnetworks inferred from the coexisting ecotypes data set. The visualization was created by merging separately inferred subnetworks resulting from a parameter sweep of the edge cost from 0.025 to 0.975. The width of the edges represents the maximal 30 mutation cost for which these edges were selected. The width of the edge displays the stringency at with the edge was selected (the wider the edge the more stringent the condition. More Stringent conditions correspond to higher edge costs). Node borders are subdivided into two parts to visualize in which strain a mutation occurred. The inner color of the nodes represents the degree of differential expression (L ecotype compared with S ecotype). The colors of the edges represent the edge types.

Given the available data, we could only focus on identifying drivers that originated after the divergence between both ecotypes. Using this input data, we were able to successfully prioritize the driver genes originally identified by Plucain et al. (2014), which are arcA and gntR, but not spoT as this mutation was present before the divergence of the two ecotypes. The selected subnetwork (fig. 4) shows that, consistent with the prioritized mutations in arcA and gntR, the TCA cycle and the Entner–Doudoroff pathway are upregulated in S as compared with L (supplementary figs. 3 and 4, Supplementary Material online). Figure 4 shows how the S-specific mutation in gntR is responsible for the observed upregulation of the Entner–Doudoroff pathway (gntT, gntK, edd, eda). As gntT is a gluconate transmembrane transporter protein, the inferred subnetwork provides an explanation of one of the previously described mechanisms of the cross-feeding phenotype (Rozen et al. 2005) in which the gluconate released by the L ecotype is metabolized by the S ecotype. The S-specific mutation in the arcA gene relates to the S-specific upregulation of the TCA cycle (gltA, fumC, sdhC, sdhD, sdhA, sdhB). arcA was previously found to be repetitively mutated in strains of fast switching phenotypes (Luli and Strohl 1990), meaning that the S ecotype could have a fast switching phenotype. Besides the already previously prioritized adaptive alleles, the method could prioritize several additional mutated genes.

acs carrying an S-specific mutation in a cis binding site element known to promote acs expression (Beatty et al. 2003) was prioritized. Consistently, the network shows how acs is highly upregulated in the S-strain as compared with the L strain. acs is an extracellular acetate scavenger involved in the conversion of acetate to acetyl coenzyme which implies that, in addition to gluconate, acetate might also be (partly) responsible for the cross-feeding phenotype between L and S. Acetate consumption has previously been linked to the origin of cross-feeding phenotypes in experimental evolution (Barrick and Lenski 2013; Herron and Doebeli 2013).

Interestingly, an intergenic mutation associated to dnaK in the S ecotype appears highly prioritized (table 2). Overexpression of the gene dnaK, a heat shock chaperone, has previously been found to mitigate the effect of deleterious mutations in hypermutators (Maisnier-Patin et al. 2005). Although in our network, this mutation does not lead to significantly higher expression levels of dnaK, the mutation could indirectly interfere with for example the stability of the mRNA and as such affect protein expression (Burgess 2011), hereby protecting both hypermutator strains.

For the S ecotype, the molecular mechanism involved in triggering the coexistence phenotype are clear, the mechanism of the L ecotype in the coexistence phenotype is, given the available data, less obvious. However, the uxuA and uxuB genes are more pronouncedly expressed in the L strain than in the S strain. Both genes are involved in catalyzing the reaction of D-fructuronate to 2-dehydro-3-deoxy-D-gluconate, which could play an important role in gluconate cross feeding.

Discussion

Here, we present a network-based eQTL method that exploits parallelism between independently evolved lines to search for mutational consistency at the molecular pathway level. Because the method searches for parallel molecular pathways between the different evolved lines, these identified driver mutations are likely to be adaptive. In the context of this article, this adaptive effect is different from directly affecting fitness as some of the adaptive mutations will elicit their effect on the phenotype only in the presence of additional adaptive mutations (epistasis).

Key to the method is the use of the interaction network to guide the search. The method belongs to the class of subnetwork selection methods that have been used to interpret differential expression data on networks (Ma et al. 2011; Alexeyenko et al. 2012; Glaab et al. 2012), for gene prioritization (Verbeke et al. 2013; Hu et al. 2014) or for linking KO genes or genes from a genetic screen to an expression phenotype (Ourfali et al. 2007; Lan et al. 2011), but that have not yet been used to solve the combined problem of searching for molecular pathway consistency in independently evolved clones and driver gene identification.

Several recent studies in cancer have shown how searching for mutational consistency at pathway level between independently evolved samples can aid in prioritizing drivers. These methods use genomic information as input and identify driver genes as genes carrying somatic mutations that are frequently mutated in different tumor samples and/or that are in each other’s neighborhood in a human genome-wide interaction network (Vandin et al. 2011; Babaei et al. 2013; Hofree et al. 2013; Verbeke et al. 2015) and/or that display patterns of mutual exclusivity over different tumor samples (Vandin et al. 2012; Leiserson et al. 2013). All of the aforementioned techniques rely mainly on genomic information and are applicable only when large numbers of independent samples are available (in a cancer setting often at least 1,000 tumor samples are available (Cancer Genome Atlas Research et al. 2013). This in contrast to evolution experiments in microorganisms which contain too few independently evolved samples (clones) to directly apply the aforementioned data-driven methods that mainly rely on genotype data.

Therefore, we combine molecular profiling data (expression data) with genomic data to increase the signal of mutational consistency at the molecular pathway level. This compensates partly for the number of evolved samples usually available in studies on microbial clonal systems. Because of the eQTL setting drivers that affect expression are more likely to be identified. Based on the few eQTL studies that have been performed it appears that at least in microbes adaptive mutations often result in a sometimes marginal but significant expression response compared with their (immediate) ancestor (Carroll and Marx 2013; Rodriguez-Verdugo et al. 2015).

Furthermore, in contrast to the statistical and diffusion-based methods used in cancer research, we have developed a method that can more explicitly exploit prior information to drive the search for drivers. To that end, our method relies on a probabilistic subnetwork selection technique that in a first pathfinding step uses an explicit path definition to find paths in a weighted (by expression data), probabilistic subnetwork. This allows integrating prior and/or condition-specific data on the biological process of interest to steer the search toward specific parts of the genome-wide interaction network by exploiting the directionality of the network to define biologically relevant paths and by assigning prior weights to the edges of the network that are likely to be active under the assessed conditions.

The optimization function actively searches for overlap in the selected subnetworks allowing to detect mutational consistency at molecular pathway level, despite even a low number of independently evolved lines. The required overlap between paths can be tuned using the edge cost parameter. Driver mutations exhibit a high degree of mutational consistency at the molecular pathway level. Therefore, using a high edge cost, which forces the selection of subnetworks with a large overlap between paths over the different evolved lines, leads to fewer false positives amongst the identified driver mutations. On the semisynthetic data set, it was illustrated how a sweep on the edge cost parameter can be used to successfully prioritize the most likely candidate drivers.

Using two biological data sets, the potential of applying the method on eQTL data for studying the molecular mechanisms underlying adaptive traits was illustrated. From a large number of potential mutations, the method was able to select previously identified driver mutations. In addition to this, potential driver mutations could be identified and verified with literature. The potential of the method to distinguish passengers from driver mutations was also shown on mutator phenotypes, where a large amount of passenger mutations are present but where the method was able to rank the previously identified driver genes as highly likely to be driver genes.

It is important to note that even if few mutations are available, it is often not clear which of those are the drivers (as is illustrated in the case of the Amikacin resistance) and which are potentiating mutations. Microbial systems are not guaranteed to display mutational consistency at gene level, solely relying on mutational consistency of the same mutation in independent lines to identify drivers might fail. Because of this, the experimental identification of drivers is tedious as it requires reintroducing all possible individual driver mutations and, in case of complex phenotypes, their possible combinations in the ancestral strain (Barrick and Lenski 2013). As illustrated with the biological test cases, the combination of an eQTL setting with the dedicated network-based approach allows to drastically reduce the list of possible driver genes.

Using a dedicated network-based analysis to an eQTL data sets is key to better understanding basic concepts of microbial evolution. Experimental evolution has become an important experiment in wet-lab practice to study interesting phenotypes, for example the role of epistasis (Chou et al. 2011; Khan et al. 2011; Kvitek and Sherlock 2011; Woods et al. 2011) or to understand the degree to which parallelism occurs (Khan et al. 2011; Tenaillon et al. 2012; Herron and Doebeli 2013; Kvitek and Sherlock 2013). Interpreting identified drivers in terms of the molecular interaction network can potentially contribute to a better understanding of why epistasis or parallelism occurs beyond the level of mutational consistency. An illustration of such parallelism was shown in the analysis of the Amikacin data set, where based on only four independently evolved lines, the network method was able to identify two different mechanisms by which strains alter their proton-motive force to lower Amikacin uptake. Each of these mechanisms was identified by exploiting parallelism at molecular pathway level. Interestingly both mechanisms, one involving direct mutations in the electron transport chain and one involving mutations in cpxA, appeared mutually exclusive that is strains had either mutations in their electron transfer chain or in cpxA but never simultaneously in both. This shows that the network-based eQTL method is not only able to successfully exploit parallelism but also allows identifying convergent ways of evolution that lead to the same adaptive phenotype.

In this study, we presented a network-based analysis method that exploits public interactomics knowledge to analyze eQTL data sets. The results of this method provide a simultaneous prioritization of driver mutations and an understanding of the adaptive phenotype at the molecular pathway level. This method exploits the potential of coupled genotype-expression data sets to study experimental evolution and bacterial trait selection in bacteria.

Supplementary Material

Supplementary figs. S1–S4 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).