Abstract
Background
In influenza epidemiology, analysis of paired sera collected from people before and after influenza seasons has been used for decades to study the cumulative incidence of influenza virus infections in populations. However, interpretation becomes challenging when sera are collected after the start or before the end of an epidemic, and do not neatly bracket the epidemic.
Methods
Serum samples were collected longitudinally in a community-based study. Most participants provided their first serum after the start of circulation of influenza A(H1N1)pdm09 virus in 2009. We developed a Bayesian hierarchical model to correct for non-bracketing sera and estimate the cumulative incidence of infection from the serological data and surveillance data in Hong Kong.
Results
We analysed 4843 sera from 2097 unvaccinated participants in the study, collected from April 2009 through December 2010. After accounting for non-bracketing, we estimated that the cumulative incidence of H1N1pdm09 virus infection was 45.1% (95% credible interval, CI: 40.2%, 49.2%), 16.5% (95% CI: 13.0%, 19.7%) and 11.3% (95% CI: 5.9%, 17.5%) for children 0–18y, adults 19–50y and older adults >50y respectively. Including all available data substantially increased precision compared to a simpler analysis based only on sera collected at 6-month intervals in a subset of participants.
Conclusions
We developed a framework for the analysis of antibody titers that accounted for the timing of sera collection with respect to influenza activity and permitted robust estimation of the cumulative incidence of infection during an epidemic.
INTRODUCTION
Serological data are commonly used to identify past exposures to antigens either through natural infection or vaccination. In influenza epidemiology, serologic studies have been used for decades to study the cumulative incidence of influenza virus infections in persons of different ages [1–3]. There are two basic types of serologic study. In a serial cross-sectional study, sera are collected before and after an influenza epidemic, and infection risks are estimated by comparing the proportions of participants with antibody titers greater than a certain threshold [4–6]. In some situations when pre-epidemic seroprevalence is very low, a cross-sectional study with only post-epidemic specimens can be used to estimate cumulative incidence [7]. The second type corresponds to longitudinal studies in which sera are collected from the same persons before and after an epidemic, and the cumulative incidence of infection is estimated by the proportion of persons with 4-fold or greater rises in antibody titers in paired specimens [3,8]. Smaller rises are traditionally ignored because of the potential for assay variability and measurement error [9–11]. However, one recent study suggested that the exclusion of 2-fold rises might lead to under-ascertainment of some infections particularly for seasonal influenza [9].
Interpretation of serologic data may be challenging. For example, in certain serologic studies sera are collected after the start or before the end of an epidemic. This can be called “non-bracketing” and contrasts with the ideal scenario that consists of collection of paired sera that neatly bracket the epidemic period. This can happen either because of unpredictability in influenza seasonality for example in tropical and subtropical regions, or for an unpredictable influenza pandemic [7,12–19]. For example, in some locations, the first wave of H1N1pdm09 occurred quite soon after the new virus was identified, and most serologic studies therefore failed to collect baseline sera before the start of the first wave [19]. In some studies multiple sera are collected at various times before, during and after epidemics, with consecutive pairs of sera providing information on incidence of infection during the corresponding periods, but it can be challenging to integrate all of this information into estimates of cumulative incidence across the entire epidemic. In general, failing to account for the timing of sera collection relative to influenza activity may lead to underestimation of the cumulative incidence of influenza virus infections. Furthermore, if there is a long delay between the end of an epidemic and the collection of post-epidemic sera, waning in antibody that occurs in the months to years after infection might lead to under-ascertainment of some infections.
The objective of our study was to develop a unifying framework to address the issue of timing of sera collection, and particularly non-bracketing in sera, with a view to estimate more accurately the cumulative incidence of influenza virus infections. We also aim to characterize the distribution of boosting of antibody titers after infection and that of waning of antibody titers without infection. We used these methods to estimate the cumulative incidence of infection with pandemic A(H1N1) influenza virus in 2009 (H1N1pdm09) in different age groups in Hong Kong.
METHODS
Study participants
We used data on longitudinal serum samples collected in two community-based trials of the direct and indirect benefits of influenza vaccination [20,21]. In 2008–09 we enrolled 119 households and randomly allocated one child 6–15 years of age in each household to receive either a single dose of TIV or saline placebo. Serum specimens were collected from each household member three times: at enrolment to the study in November-December 2008, in April 2009, and in August-October 2009 [20].
In a larger trial in 2009–10 we enrolled 796 households, including 83 of the 119 households from the previous study, and randomly allocated one child 6–17 years of age per household to receive either a single dose of TIV or saline placebo. Serum specimens were collected from every household member at enrolment to the study in August 2009 through February 2010, and at the end of the study in August-December 2010, and a third sample was collected from all persons in a random sample of 25% of households plus in all 83 households that continued from the prior study in April 2010 [21]. For those 83 households, the specimens collected at the end of the 2008–09 study were used as the baseline specimens for 2009–10. In both studies, children who received TIV or placebo also provided one additional serum specimen one month after vaccination. Therefore in total we collected up to 7 sequential serum specimens from participants over a 2-year period covered by the two trials, while the majority of participants in the large 2009–10 study provided 2 serum specimens.
Ethics
Written consent was obtained for participants ≥18 years of age. Proxy written consent from parents or legal guardians was obtained for participants who were ≤17 years of age, with additional written assent from those aged 8 to 17 years. The study protocol was approved by the Institutional Review Board of Hong Kong University.
Surveillance data
Influenza activity in the general community is monitored through a sentinel surveillance network in outpatient clinics, which report the proportion of patients with influenza-like illness defined as a fever >37.8°C plus a cough or sore throat. The public health laboratory also collects data on the weekly proportion of specimens from sentinel outpatient clinics and local hospitals that tested positive for influenza virus. We used a proxy measure of the weekly incidence rate of influenza virus infections in the community, derived as the weekly proportion of outpatients with influenza-like illness multiplied by the weekly proportion of laboratory specimens testing positive for H1N1pdm09 virus [22–25]. We previously reported that this particular proxy provided a good indication of incidence of H1N1pdm09 virus infection in the community based on hospital admissions [26].
Laboratory methods
All serum samples were stored in a refrigerated container immediately at 2–8ºC immediately after collection and delivered to the Department of Microbiology, HKU before the end of the day. Serum samples were extracted and stored at −70°C within 24 hours of receipt at the laboratory. Serum specimens were tested against the H1N1pdm09 virus A/California/7/2009 in parallel by hemagglutination inhibition (HAI) assays in serial doubling dilutions from an initial dilution of 1:10 using standard methods as previously described [21,27].
Statistical methods
While in theory there could be as many as 7 serum samples for some participants, in practice there was no pandemic influenza activity when pre-vaccination and post-vaccination sera were collected in the 2008/09 study, hence we used the sera collected in April 2009 as the baseline titers for every individual. Post-vaccination sera were ignored in the analysis since they were only available for a subset of children in the 2009/10 study. We therefore included data from 4 rounds of sera collection spaced at intervals of approximately 6 months. All participants who had at least one antibody titer measurement during the study period were included in the study.
Participants who reported vaccination or who were randomly assigned to receive vaccination as part of our study were excluded from analyses, because vaccination reduced risk of infection and also because interpretation of serology in vaccinated persons can be challenging [28]. Infection was defined by having 4-fold rise or greater in consecutive pairs of sera. We built a 3-level hierarchical model to estimate the cumulative risk of infection across an epidemic accounting for non-bracketing. The first level of the model described the distribution of the pre-epidemic antibody titer levels among participants (Supplementary section 1.1). The second level of the model described the risk of infection during the epidemic, by assuming that the weekly hazard of infection was proportional to an influenza proxy, constructed by the method mentioned in the surveillance data subsection above [26]. Hence, the hazard of infection at time t is
where a is the age group of the participant, ψc,a is the scaling factor for the influenza risk of infection for the age group a and Pt is the influenza activity proxy at time t based on local surveillance data. Hence, the probability of infection in time period (tj−1, tj is (Supplementary section 1.2). The third level of the model described the pattern of boosting of antibody titers for infected participants and the pattern of waning of antibody titers for uninfected participants. We used multinomial distributions to model the boosting distribution after infection and waning without infection. Since we defined infection by using 4-fold rise in pair sera, boosting distributions were estimated conditioning on participants with at least 4-fold rise after infection and we assumed there was no waning in the paired sera that have greater than or equal to 4-fold rise (Supplementary section 1.3). Those patterns were observed between rounds of sera collection at intervals of approximately 6 months. We assumed that antibody titers were boosted exactly at 14 days after infection and there was no change from 0 to 14 days, and that it was not possible for an individual to be infected more than once during a single epidemic. For those participants with missing pre-epidemic antibody titer measurements, we imputed the pre-epidemic antibody titer based on the estimated individual posterior distribution of the antibody titer levels combining the information from the estimated cumulative incidence of infection before the individual’s serum collection and estimated pre-pandemic antibody titer distribution from other individuals with data available.
In our study, we collected sera once per year (in rounds 2 and 4) for two thirds of participants and inferences from these paired sera may not be directly comparable with the paired sera that were collected on two occasions (in rounds 2, 3 and 4) each year for the other participants. To account for this potential impact on estimation of cumulative incidence, we assumed that there was a missing mid-year serum sample (assumed to be collected at the time when the round 3 sera were collected for other participants) for those participants that provided once-annual sera and estimated it within the inferential framework by combining the information on the individual’s antibody titer on round 2 and 4, the estimated boosting and waning distribution from the study participants and the estimated cumulative incidence of infection in the corresponding periods.
During the first wave of pandemic influenza H1N1 in 2009, the sentinel surveillance system was affected by the establishment of special Designated Flu Clinics (not part of the sentinel network), before and during the peak in the first wave, which provided subsidized consultation and medication for patients [13]. Additionally, there were changes in health-care seeking behaviors during that period because of the increased media and government attention on influenza [29]. To account for these changes, we assumed that the scaling factor relating the influenza proxy to incidence rates changed after a fixed date that we denoted the change point. To evaluate uncertainty in the change point, we evaluated models with different change points and selected the change point that minimized the differences between the expected and observed number of infections in each age group.
A Bayesian Markov Chain Monte Carlo algorithm [30] was constructed to impute antibody titer levels when they were missing. Censoring of the antibody boosting or waning (eg: drop from 1:40 to <1:10) was accounted for. Simulation studies demonstrated that this algorithm could give unbiased parameter estimates (Appendix). The adequacy of model fit was assessed by comparing the observed and expected distributions of number of 4-fold rise in consecutive sera collected between rounds in different age groups. A sensitivity analysis of the delay from infection to boosting in antibody titer was conducted (eAppendix). Statistical analyses were conducted using R version 3.1.1 (R Foundation for Statistical Computing, Vienna, Austria) and MATLAB 7.8.0 (MathWorks Inc, Natick, MA). Additional technical details of the methods are provided in the eAppendix.
RESULTS
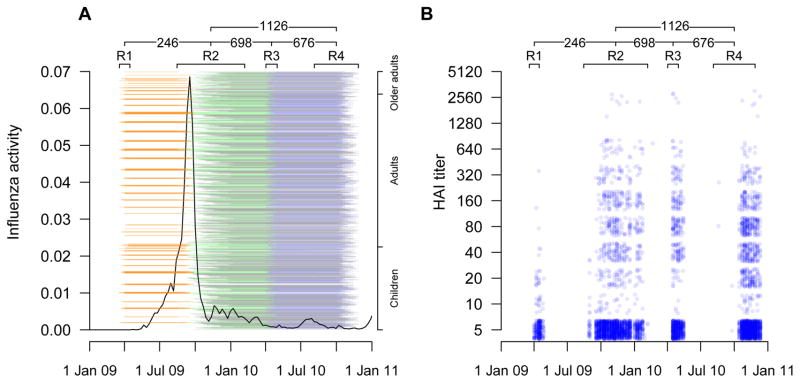
A total of 3160 participants participated in the studies in 2008–09 or 2009–10 including 301 who participated in both. After excluding participants who received influenza vaccination either as part of the trials (n=530) or privately (n=217), and 316 participants who did not provide any sera, 2097 participants remained for analysis of antibody titers. There were 4 rounds of serum collection in our study (Figure 1), and the characteristics of participants who provided a serum sample in each round were similar (Table 1). The time of collection of sera in our study and distribution of antibody titers in different rounds are shown in Figure 1. While in total we collected 4843 sera from 2097 unvaccinated participants in the study, a relatively smaller number of samples were collected in rounds 1 and 3, and only 2396 sera could be used if restricting analysis to participants with consecutive sera in rounds 1+2, rounds 2+3, and rounds 3+4.
Figure 1.
Panel A: Timeline of the study and local influenza virus activity for H1N1pdm09 epidemic. Black lines represent the local influenza activity. Orange, green, blue and black lines represent the pairs of sera draw from round 1+2 (246 pairs), round 2+3 (698 pairs), round 3+4 (676 pairs) and round 2+4 (1126 pairs), respectively. Collection dates are adjusted for the 2-week delay from infection to rise in antibody titer. Participants were ordered vertically by age. Panel B: Antibody titer measurements over calendar time. A value of 5 corresponds to a titer measured at <10.
Table 1.
Characteristics of participants in community-based serologic study
| Characteristic | Round 1 | Round 2 | Round 3 | Round 4 |
|---|---|---|---|---|
| Date range of sera collection | April 2 to April 29, 2009 | August 29, 2009 to February 20, 2010 | April 16 to May 15, 2010 | August 19 to December 11, 2010 |
| Median sample collection date | April 15, 2009 | November 17, 2009 | April 30, 2010 | November 12, 2010 |
| No. of participants | 259 | 2057 | 703 | 1824 |
| Age | ||||
| ≤18 years | 77 (29.7%) | 660 (32.1%) | 214 (30.4%) | 596 (32.7%) |
| 19–50 years | 159 (61.4%) | 1217 (59.2%) | 438 (62.3%) | 1076 (59%) |
| >50 years | 23 (8.9%) | 180 (8.8%) | 51 (7.3%) | 152 (8.3%) |
| Sex | ||||
| Male | 117 (45.2%) | 933 (45.4%) | 315 (44.8%) | 819 (44.9%) |
| Serum available in other rounds | ||||
| Round 1 | 246 (12%) | 172 (24.5%) | 173 (9.5%) | |
| Round 2 | 246 (95%) | 698 (99.3%) | 1798 (98.6%) | |
| Round 3 | 172 (66.4%) | 698 (33.9%) | 676 (37.1%) | |
| Round 4 | 173 (66.8%) | 1798 (87.4%) | 676 (96.2%) | |
The proportions of persons with 4-fold rises in paired titers for different age groups are shown in Table S1. However, the interpretation of these proportions is complicated because of the non-bracketing shown in Figure 1. We used the statistical methods described above to address this issue. The model with a change point on November 21, 2009 gave the best fit to the data (Figure S1). This change point was consistent with findings of a previous study [13]. Hence we used this model as our baseline scenario.
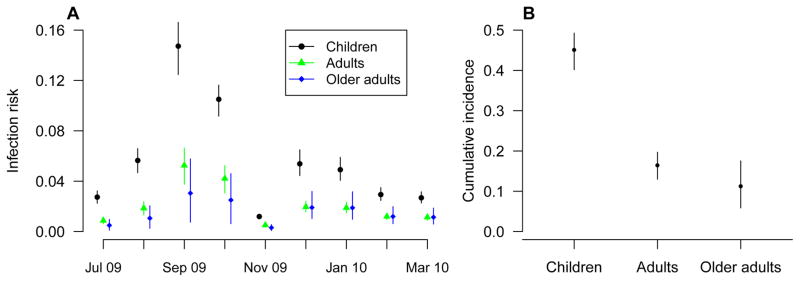
Estimates of the cumulative risk of infection for different age groups during the H1N1pdm09 epidemic are shown in Figure 2. Based on our model, we estimated that the cumulative risks of H1N1pdm09 infection from 5 July 2009 to 16 January 2010 were: 45.1% (95% CI: 40.2%, 49.2%), 16.5% (95% CI: 13.0%, 19.7%) and 11.3% (95% CI: 5.9%, 17.5%) for children, adults and older adults respectively. Estimates from sensitivity analyses assuming that the delays from infection to boosting were 10 days or 21 days were similar (Table S2).
Figure 2.
Panel A: Estimated monthly risk of infection during the H1N1pdm09 epidemic. Circles, triangles and diamonds represent the point estimates of the infection risks of H1N1pdm09 each month and the vertical lines represent the corresponding 95% credible intervals. Panel B: Estimated cumulative risk of infection over the entire epidemic of H1N1pdm09 for different age groups with 95% credible intervals.
We evaluated how accounting for the timing of sera collection relative to influenza activity could affect estimates in more naive analyses. Without the methodology described above we would need to make arbitrary choices about the data to retain in analyses, for example restricting analysis to participants with consecutive sera in rounds 1+2, rounds 2+3, and rounds 3+4 (Figure 1), and summing the cumulative incidence in each of the three corresponding periods (Table S1). This would lead to estimates of 51.3% (95% CI: 34.0%, 73.0%), 21.1% (95% CI: 13.3%, 32.0%) and 13.9% (95% CI: 3.8%, 65.6%) for children, adults and older adults respectively. The corresponding estimates based on our statistical model that included all data, and accounted for the timing of sera collection relative to influenza activity, were 58.2% (CI: 53.1%, 62.5%), 22.2% (CI: 18.6%, 25.6%) and 17.1% (CI: 10.5%, 24.4%). Using all available data and accounting for the timing of sera collection therefore gave more precise estimates of incidence, which could shorten the length of confidence intervals by 4.1-fold, 2.7-fold and 4.5-fold for children, adults and older adults respectively.
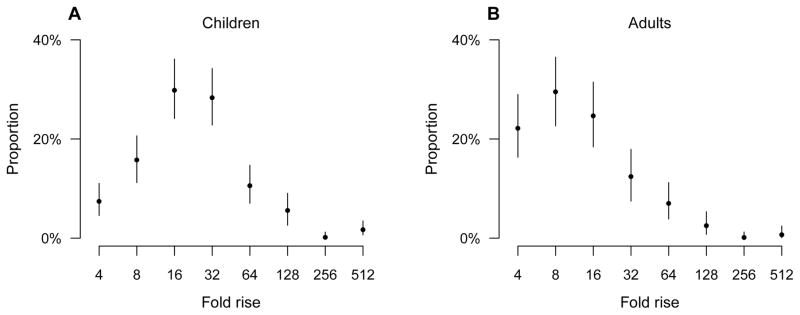
In our main analysis, the estimated distributions of pre-epidemic antibody titers indicated that more than 80% of children and adults had titers below 1:10 (Table S3). We found that the geometric mean boosting in antibody titers after infection was significantly higher for children (22.0-fold; 95% CI: 19.6 to 24.8-fold) than for adults (12.6-fold; 95% CI: 11.0 to 14.6-fold) (Figure 3). We also estimated the distribution of antibody titer waning after accounting for censoring. The estimated probabilities of having 2-fold rise, no change in titer, or a drop in titer of various magnitudes in paired sera were shown in Table S4. The average waning rate of antibody titers across a period of six months was significantly faster for adults (3.5-fold drop over 6 months; 95% CI: 3.0 to 4.2-fold drop) than for children (1.7-fold drop over 6 months; 95% CI: 1.6 to 1.9-fold drop).
Figure 3.
Estimated antibody titer boosting distribution for children and adults infected with H1N1pdm09 virus. Panel A: boosting distribution for children infected with H1N1pdm09 virus. Panel B: boosting distribution for adults infected with H1N1pdm09 virus.
We then examined the advantage of collecting additional sera halfway through a year from 1/3 of participants (i.e round 3), in the context of waning in antibody titers after infection. Using only the paired sera in rounds 1+2 and then in rounds 2+4, the estimates of the cumulative incidence of infection were 44.4% (95% CI: 31.4%, 60.1%), 12.5% (95% CI: 7.4%, 19.9%) and 6.1% (95% CI: 2.3%, 28.2%) for children, adults and older adults respectively, which underestimated the cumulative incidence of infection by 23.7%, 43.6% and 64.3% relatively when compared with estimates obtained from the model that included the mid-year sera in round 3.
DISCUSSION
In this study, we proposed a method to account for the timing of sera collection relative to influenza activity, by combining the information from surveillance data, distribution of pre-epidemic antibody, patterns of antibody boosting after infection, and waning. We applied the method to estimate the cumulative incidence of H1N1pdm09 virus infection across the entire first epidemic wave in Hong Kong which spanned from April 2009 through to November 2010. While our estimate for the cumulative incidence of H1N1pdm09 virus infection in children was similar to that in other studies, the estimate for adults and elderly were higher than in other studies [7,16,18]. One potential explanation for this observation is that our data were from a vaccine trial that involved families of school-age children, and therefore excluded adults that did not live with children and might therefore generally be at lower risk of infection [31]. However, we would expect that our method could provide more accurate estimates if the participants were a more generalizable sample, while the data from the present study might allow population-based estimates under a series of assumptions and estimates of transmission dynamics within households of different types.
We described a typical problem in serologic studies namely collection of sera that do not neatly bracket an epidemic (Figure 1). While we collected pairs of sera across 6-month intervals from a smaller number of participants that permitted reasonable estimates of cumulative incidence summing across each period, the methodology developed here enabled us to include a much larger number of sera collected once per year that did not bracket the epidemic (Figure 1). Inclusion of all available data improved precision in estimates. In addition, using only data from the participants that provided sera once per year led to underestimation of cumulative incidence because of waning in titers over time. This implies that in sero-epidemiological studies, the cumulative incidence of infection may be underestimated if sera are collected once per year, in particular for adults, unless waning is addressed in the analysis. Collection of mid-year sera from a subset of participants provided the required information on waning for our analysis.
We estimated the distribution of boosting in antibody titers after infection (defined as having at least 4-fold rise in paired sera) and found the average boosting after infection for children was higher than for adults, conditional on having at least a 4-fold rise in titer. The pattern shown in Figure 3 suggests that infection might lead to less than 4-fold rises in titers in some adults, and consequently that the cumulative incidence of infection for adults might have been underestimated, compared with children [9].
Waning of antibody titers after infection or vaccination is a well-known problem [32–35], which may lead to under-ascertainment of infections if post-epidemic sera are not collected soon after the end of the epidemic [12–15]. We estimated that waning of antibody titers was considerable over six-month time periods, which was consistent with other studies [32–34]. The distribution of waning of antibody titers was faster in adults than in children. We found that children had both higher boosting of antibody after infection and slower waning, suggesting that most children infected in the first wave of H1N1 pandemic were still immune in the second wave of H1N1 pandemic, and may partly explain the observed shift in age distribution of infected people (from children to adults) in the second wave of H1N1 pandemic in Hong Kong [25]. Waning in antibody titers over a calendar year may also partly explain the generally lower boosting distributions inferred in an earlier study [9].
Our model accounted for missing data on antibody titers which allowed us to fully use the information from all participants, even those for whom pre-epidemic antibody titers were missing, although such data were required on a subset of participants. While our study showed that the non-bracketing problem would seriously influence the estimation of cumulative incidence of infection and should be avoided in future serology studies, we demonstrated an approach addressing this problem when unavoidable.
In our model, we used a proxy measure of influenza activity in the community (Figure 1) based on surveillance data, and the reliability of estimates from our model are dependent to some extent on the accuracy of this proxy in reflecting the risk of influenza virus infection in study participants. Moreover, the proxy used here was not age-specific, and it is possible that patterns in the risks of influenza vary for different age groups for example because of faster depletion of susceptibles in school-age children. However, we did have age-specific data on incidence in 2009 and found that patterns in the incidence rates of H1N1pdm09 were similar for different age groups [26].
Our study had a number of limitations. First, infections were defined by a 4-fold rise or greater in paired titers, which may not have ideal sensitivity and specificity to identify influenza virus infections owing to cross-reactive antibody associated with other infection or unreported vaccination. Moreover, to ensure identifiability of the model, we assumed that there would be no waning in the paired sera that have greater than or equal to 4-fold rise, which may lead to underestimation of the boosting distribution. The boosting distributions were estimated conditioning on participants with at least 4-fold rise after infection which may overestimate the boosting distribution if some infected persons did not have a 4-fold or greater rise in antibody titer after infection, as we believe may have occurred for adults (Figure 3).. Second, measurement error in titers may be important [9] and its impact on estimation of cumulative incidence remains unclear. Third, because serum samples were collected at different times for different participants, 23% of the consecutive intervals in sera collection (i.e. R1–R2,R2–R3 and R3–R4) were longer or shorter than 6 months by at least 1 month and this may have affected the estimation of waning and imputation of missing antibody titers. Finally, our study was household-based and hence the estimation of cumulative incidence of infection could be improved by taking transmission dynamics in households into account, so that more accurate estimates of cumulative incidence of infection for population could be provided.
In conclusion, we found that failing to account for the timing of sera collection could inhibit accurate and precise estimation of cumulative incidence of infection. We presented a methodological framework to address this issue and permit more accurate estimates of the cumulative incidence of infection during an epidemic.
Supplementary Material
Acknowledgments
SOURCES OF FINANCIAL SUPPORT
This project was supported by the National Institute of Allergy and Infectious Diseases under contract no. HHSN266200700005C; ADB No. N01-AI-70005 (NIAID Centers for Excellence in Influenza Research and Surveillance), a commissioned grant from the Health and Medical Research Fund from the Government of the Hong Kong Special Administrative Region (grant no. HK-10-04-02), the Harvard Center for Communicable Disease Dynamics from the National Institute of General Medical Sciences (grant no. U54 GM088558), and the Area of Excellence Scheme of the University Grants Committee of Hong Kong (grant no. AoE/M-12/06). TKT was supported by a Research Scholarship from L’Oreal Hong Kong. SC thanks the National Institute of General Medical Sciences MIDAS initiative (grant 1U01GM110721-01) and the Laboratory of Excellence Integrative Biology of Emerging Infectious Diseases for research funding.
The authors thank Chan Kit Man, Calvin Cheng, Lai-Ming Ho, Ho Yuk Ling, Nicole Huang, Lam Yiu Pong, Tom Lui, Tong Hok Leung, Edward Ma, Loretta Mak, Sophia Ng, Hau Chi So, Winnie Wai, Jessica Wong, Kevin Yau, and Jenny Yuen for research support.
Footnotes
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript
POTENTIAL CONFLICTS OF INTEREST
DKMI has received research funding from Hoffmann-La Roche Inc. JSMP receives research funding from Crucell NV and serves as an ad hoc consultant for GlaxoSmithKline and Sanofi. BJC has received research funding from MedImmune Inc. and Sanofi Pasteur, and consults for Crucell NV. GML has consulted for Janssen Pharmaceuticals, and received speakers’ fees from HSBC and CLSA. The authors report no other potential conflicts of interest.
References
- 1.Monto AS. Studies of the community and family: acute respiratory illness and infection. Epidemiol Rev. 1994;16:351–373. doi: 10.1093/oxfordjournals.epirev.a036158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fox JP, Cooney MK, Hall CE, Foy HM. Influenzavirus infections in Seattle families, 1975–1979. II. Pattern of infection in invaded households and relation of age and prior antibody to occurrence of infection and related illness. Am J Epidemiol. 1982;116:228–242. doi: 10.1093/oxfordjournals.aje.a113408. [DOI] [PubMed] [Google Scholar]
- 3.Monto AS, Kioumehr F. The Tecumseh Study of Respiratory Illness. IX. Occurence of influenza in the community, 1966–1971. Am J Epidemiol. 1975;102:553–563. doi: 10.1093/oxfordjournals.aje.a112193. [DOI] [PubMed] [Google Scholar]
- 4.Wu JT, Leung K, Perera RA, Chu DK, Lee CK, et al. Inferring influenza infection attack rate from seroprevalence data. PLoS Pathog. 2014;10:e1004054. doi: 10.1371/journal.ppat.1004054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kelly H, Peck HA, Laurie KL, Wu P, Nishiura H, et al. The age-specific cumulative incidence of infection with pandemic influenza H1N1 2009 was similar in various countries prior to vaccination. PLoS One. 2011;6:e21828. doi: 10.1371/journal.pone.0021828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Widelock D, Schaeffer M, Millian ST. Surveillance of Infectious Disease by Serologic Methods. I. Asian Influenza, 1957–1964. Am J Public Health Nations Health. 1965;55:578–586. doi: 10.2105/ajph.55.4.578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu JT, Ma ES, Lee CK, Chu DK, Ho PL, et al. The infection attack rate and severity of 2009 pandemic H1N1 influenza in Hong Kong. Clin Infect Dis. 2010;51:1184–1191. doi: 10.1086/656740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee VJ, Chen MI, Yap J, Ong J, Lim WY, et al. Comparability of different methods for estimating influenza infection rates over a single epidemic wave. Am J Epidemiol. 2011;174:468–478. doi: 10.1093/aje/kwr113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cauchemez S, Horby P, Fox A, Mai le Q, Thanh le T, et al. Influenza infection rates, measurement errors and the interpretation of paired serology. PLoS Pathog. 2012;8:e1003061. doi: 10.1371/journal.ppat.1003061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Katz JM, Hancock K, Xu X. Serologic assays for influenza surveillance, diagnosis and vaccine evaluation. Expert Rev Anti Infect Ther. 2011;9:669–683. doi: 10.1586/eri.11.51. [DOI] [PubMed] [Google Scholar]
- 11.Wood JM, Gaines-Das RE, Taylor J, Chakraverty P. Comparison of influenza serological techniques by international collaborative study. Vaccine. 1994;12:167–174. doi: 10.1016/0264-410x(94)90056-6. [DOI] [PubMed] [Google Scholar]
- 12.Chen MI, Cook AR, Lim WY, Lin R, Cui L, et al. Factors influencing infection by pandemic influenza A(H1N1)pdm09 over three epidemic waves in Singapore. Influenza Other Respir Viruses. 2013;7:1380–1389. doi: 10.1111/irv.12129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cowling BJ, Perera RA, Fang VJ, Chan KH, Wai W, et al. Incidence of influenza virus infections in children in Hong Kong in a 3-year randomized placebo-controlled vaccine study, 2009–2012. Clin Infect Dis. 2014;59:517–524. doi: 10.1093/cid/ciu356. [DOI] [PubMed] [Google Scholar]
- 14.Horby P, Mai le Q, Fox A, Thai PQ, Thi Thu Yen N, et al. The epidemiology of interpandemic and pandemic influenza in Vietnam, 2007–2010: the Ha Nam household cohort study I. Am J Epidemiol. 2012;175:1062–1074. doi: 10.1093/aje/kws121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cauchemez S, Ferguson NM, Fox A, Mai le Q, Thanh le T, et al. Determinants of influenza transmission in South East Asia: insights from a household cohort study in Vietnam. PLoS Pathog. 2014;10:e1004310. doi: 10.1371/journal.ppat.1004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wu JT, Ho A, Ma ES, Lee CK, Chu DK, et al. Estimating infection attack rates and severity in real time during an influenza pandemic: analysis of serial cross-sectional serologic surveillance data. PLoS Med. 2011;8:e1001103. doi: 10.1371/journal.pmed.1001103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Klick B, Nishiura H, Ng S, Fang VJ, Leung GM, et al. Transmissibility of seasonal and pandemic influenza in a cohort of households in Hong Kong in 2009. Epidemiology. 2011;22:793–796. doi: 10.1097/EDE.0b013e3182302e8e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Riley S, Kwok KO, Wu KM, Ning DY, Cowling BJ, et al. Epidemiological characteristics of 2009 (H1N1) pandemic influenza based on paired sera from a longitudinal community cohort study. PLoS Med. 2011;8:e1000442. doi: 10.1371/journal.pmed.1000442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Van Kerkhove MD, Hirve S, Koukounari A, Mounts AW group HNpsw. Estimating age-specific cumulative incidence for the 2009 influenza pandemic: a meta-analysis of A(H1N1)pdm09 serological studies from 19 countries. Influenza Other Respir Viruses. 2013;7:872–886. doi: 10.1111/irv.12074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cowling BJ, Ng S, Ma ES, Cheng CK, Wai W, et al. Protective efficacy of seasonal influenza vaccination against seasonal and pandemic influenza virus infection during 2009 in Hong Kong. Clin Infect Dis. 2010;51:1370–1379. doi: 10.1086/657311. [DOI] [PubMed] [Google Scholar]
- 21.Cowling BJ, Ng S, Ma ES, Fang VJ, So HC, et al. Protective efficacy against pandemic influenza of seasonal influenza vaccination in children in Hong Kong: a randomized controlled trial. Clin Infect Dis. 2012;55:695–702. doi: 10.1093/cid/cis518. [DOI] [PubMed] [Google Scholar]
- 22.Wu P, Cowling BJ, Wu JT, Lau EH, Ip DK, et al. The epidemiological and public health research response to 2009 pandemic influenza A(H1N1): experiences from Hong Kong. Influenza Other Respir Viruses. 2013;7:367–382. doi: 10.1111/j.1750-2659.2012.00420.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu P, Goldstein E, Ho LM, Yang L, Nishiura H, et al. Excess mortality associated with influenza A and B virus in Hong Kong, 1998–2009. J Infect Dis. 2012;206:1862–1871. doi: 10.1093/infdis/jis628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wu P, Goldstein E, Ho L-M, Wu JT, Tsang T, et al. Excess mortality impact of two epidemics of pandemic influenza A(H1N1pdm09) virus in Hong Kong. Influenza and Other Respiratory Viruses. 2013 doi: 10.1111/irv.12196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wu P, Goldstein E, Ho LM, Wu JT, Tsang T, et al. Excess mortality impact of two epidemics of pandemic influenza A(H1N1pdm09) virus in Hong Kong. Influenza Other Respir Viruses. 2014;8:1–7. doi: 10.1111/irv.12196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wong JY, Wu P, Nishiura H, Goldstein E, Lau EH, et al. Infection fatality risk of the pandemic A(H1N1)2009 virus in Hong Kong. Am J Epidemiol. 2013;177:834–840. doi: 10.1093/aje/kws314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cowling BJ, Chan KH, Fang VJ, Lau LL, So HC, et al. Comparative epidemiology of pandemic and seasonal influenza A in households. N Engl J Med. 2010;362:2175–2184. doi: 10.1056/NEJMoa0911530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Petrie JG, Ohmit SE, Johnson E, Cross RT, Monto AS. Efficacy studies of influenza vaccines: effect of end points used and characteristics of vaccine failures. J Infect Dis. 2011;203:1309–1315. doi: 10.1093/infdis/jir015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Marmara V, Cook A, Kleczkowski A. Estimation of force of infection based on different epidemiological proxies: 2009/2010 Influenza epidemic in Malta. Epidemics. 2014;9C:52–61. doi: 10.1016/j.epidem.2014.09.010. [DOI] [PubMed] [Google Scholar]
- 30.Gilks WR, Richardson S, Spiegelhalter D. Markov Chain Monte Carlo in Practice. London: Chapman & Hall; 1996. [Google Scholar]
- 31.Cauchemez S, Carrat F, Viboud C, Valleron AJ, Boelle PY. A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data. Stat Med. 2004;23:3469–3487. doi: 10.1002/sim.1912. [DOI] [PubMed] [Google Scholar]
- 32.Hsu JP, Zhao X, Chen MI, Cook AR, Lee V, et al. Rate of decline of antibody titers to pandemic influenza A (H1N1-2009) by hemagglutination inhibition and virus microneutralization assays in a cohort of seroconverting adults in Singapore. BMC Infect Dis. 2014;14:414. doi: 10.1186/1471-2334-14-414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chan KH, To KK, Hung IF, Zhang AJ, Chan JF, et al. Differences in antibody responses of individuals with natural infection and those vaccinated against pandemic H1N1 2009 influenza. Clin Vaccine Immunol. 2011;18:867–873. doi: 10.1128/CVI.00555-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang M, Yuan J, Li T, Liu Y, Wu J, et al. Antibody dynamics of 2009 influenza A (H1N1) virus in infected patients and vaccinated people in China. PLoS One. 2011;6:e16809. doi: 10.1371/journal.pone.0016809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ng S, Fang VJ, Ip DK, Chan KH, Leung GM, et al. Estimation of the association between antibody titers and protection against confirmed influenza virus infection in children. J Infect Dis. 2013;208:1320–1324. doi: 10.1093/infdis/jit372. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.