Identification of Differentially Expressed Genes in RNA-seq Data of Arabidopsis thaliana: A Compound Distribution Approach

Abstract

Gene expression is the process by which information from a gene is used in the synthesis of a functional gene product, which may be proteins. A gene is declared differentially expressed if an observed difference or change in read counts or expression levels between two experimental conditions is statistically significant. To identify differentially expressed genes between two conditions, it is important to find statistical distributional property of the data to approximate the nature of differential genes. In the present study, the focus is mainly to investigate the differential gene expression analysis for sequence data based on compound distribution model. This approach was applied in RNA-seq count data of Arabidopsis thaliana and it has been found that compound Poisson distribution is more appropriate to capture the variability as compared with Poisson distribution. Thus, fitting of appropriate distribution to gene expression data provides statistically sound cutoff values for identifying differentially expressed genes.

1. Introduction

In biological system, for better understanding of complex conditions, there is a need for advancements in identifying genes related to that trait. This can be achieved by enhancing our knowledge about gene expression through statistical models so as to perform statistical analysis of gene expression profiles. To measure gene expression (or transcript abundance), the sequencing reads obtained are aligned to a known reference genome sequence and the proportion of reads matching a given transcript is used as quantification of its expression level followed by statistical testing of difference in quantification values between samples (Bloom et al., 2009; Costa et al., 2010; Oshlack et al., 2010).

RNA-seq is rapidly emerging as the method of choice for comprehensive transcript abundance estimation (Li and Xie, 2013). TopHat and Cufflinks (Trapnell et al., 2012) are free, open-source software tools for gene discovery and comprehensive expression analysis of high-throughput mRNA sequencing (RNA-seq) data. Later on, Cuffdiff 2 (Trapnell et al., 2013) was developed, which is an algorithm that estimates expression at transcript-level resolution and controls for variability evident across replicate libraries.

A gene is declared differentially expressed if a difference or change observed in read counts or expression levels/index between two experimental conditions is statistically significant. Transcription is the expression analysis of population of genes or analysis of differences in expression of gene populations under different environments, conditions, treatments, and stages. Several statistical methods are there for gene expression analysis. Statistical distributions are used to approximate the pattern of differential gene expression. Such genes are selected based on a combination of expression change threshold and score cutoff, which are usually generated by statistical modeling.

The Poisson distribution and the negative binomial distribution are the most commonly used models. The main advantage associated with Poisson distribution is its simplicity, and it has only one parameter, but it has a constraint that variance of the model is equal to the mean. Several researchers have tested for differential expression using Poisson distributions (Marioni et al., 2008; Bullard et al., 2010; Wang et al., 2010). The Poisson assumption, however, does not account for biological variability in the data (Robinson and Smyth, 2007; Nagalakshmi et al., 2008). Biological replicates are more variable than technical replicates (McIntyre et al., 2011). Ignoring this issue on datasets with biological replicates will result in false-positive rates because of underestimation of sampling error (Anders and Huber, 2010). The negative binomial distribution has two parameters, encoding the mean and the dispersion, which allows modeling of more general mean–variance relationships. The negative binomial distribution, which requires an additional dispersion parameter to be estimated, is often used to deal with the biological variability in the data. Variations of negative-binomial-based differential expression analysis of count data have been proposed (Robinson and Smyth, 2007; Anders and Huber, 2010; Hardcastle and Kelly, 2010) along with models that extend the Poisson model by including overdispersion (Srivastava and Chen, 2010).

Several R packages are available for expression analysis, like DEGseq (Wang et al., 2010). The Bioconductor software package edgeR (Anders and Huber, 2010; Robinson et al., 2010) has been developed to examine replicated gene count data using an overdispersed Poisson model. The statistical tests based on negative binomial distributions (DESeq, edgeR, and baySeq) had notably good control of false-positive errors with comparable specificity and sensitivity resulted from the tests (Rapaport et al., 2013). Soneson and Delorenzi (2013) conducted an extensive comparison of 11 methods for differential expression analysis of RNA-seq data. All methods are freely available within the R framework and take as input a matrix of counts.

Different distributions have been fitted to the data as a whole and inferences drawn from it. These distributions do not handle different experimental sources of variation and the variability of the data is not properly addressed. Analysis of differences in expression of gene populations under different conditions, treatments, and developmental stages is required. Further, within a whole data set there are different subsets that possess different properties that can be modeled separately. The interest is to know whether there is statistically significant evidence that any of the genes under study exhibit a difference in expression across the groups/conditions/subpopulations.

The concept of compound distribution has been used here for identification of differentially expressed genes. Compound distributions represent a useful way of describing heterogeneity in the distribution of a variable. In the present study, the focus is mainly to investigate the differential gene expression analysis for sequence count data based on compound distribution model as this model is able to capture extra variation. Compound mixture of Poisson–gamma distribution is used. The joint likelihood density function is obtained and the parameters of the model are estimated.

2. Materials and Methods

It is very important to find statistical distribution to approximate the nature of differential gene expression data. It is found from the literature that, for differential expression analysis of count data, Poisson distribution is most commonly used.

A discrete random variable X (number of reads per gene) is said to have a Poisson distribution with parameter λ > 0 if it assumes only nonnegative values, and the probability mass function of X is given by

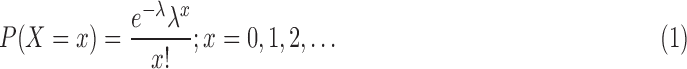Here, mean = variance = λ. The Poisson distribution has the advantage of simplicity and has only one parameter, λ. Poisson distribution occurs when there are events that do not occur as outcomes of a definite number of trials of an experiment but that occur at random points of time and space wherein the interest lies only in the number of occurrences of the event, not in its nonoccurrences. However, it constrains the variance of the modeled variable to be equal to the mean. It has been noted that the assumptions of Poisson distribution are too restrictive: it predicts smaller variations that are observed in data. Therefore, the resulting statistical test does not control type 1 error (the probability of false discoveries). Overdispersion problem was solved in count data by using negative binomial distribution.

A random variable X is said to follow a negative binomial distribution with parameters r and p if its probability mass function is given by

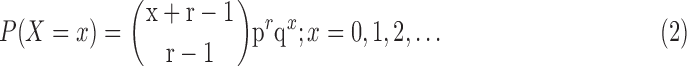The negative binomial distribution has two parameters, the mean and the dispersion, and hence allows modeling of more general mean–variance relationships. But the number of replicates in the data set of interest is normally too small to estimate both the parameters mean and variance reliably for each gene. For RNA-seq, it has been suggested that the Poisson distribution is well suited for analysis of technical replicates, whereas the higher variability between biological replicates necessitates a distribution incorporating overdispersion, such as the negative binomial.

The theory of compound mixture distribution model has been attempted here to know whether there is statistically significant evidence that any of the genes under study exhibit a difference in expression across the groups/conditions/subpopulations.

2.1. Compound distribution

Consider a random variable X following a Poisson distribution with parameter λ as given in Eq. (1), where the Poisson parameter λ is itself a random variable, distributed according to a gamma distribution with parameters α and β; that is,

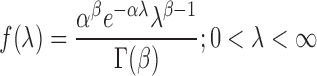The compound Poisson follows negative binomial distribution with parameters 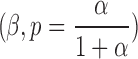with the following probability function:

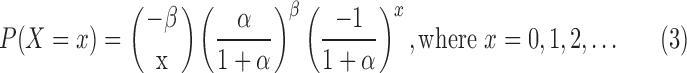The mean of this compound Poisson distribution is 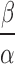and variance is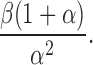

The negative binomial distribution is thus here a mixture of a family of Poisson distributions with gamma mixing weights. Thus, the negative binomial distribution is known as a Poisson–gamma mixture. In case of a single biological sample (RNA extract), aliquots are taken to make technical replicates. These technical replicates will be distributed as Poisson. In case of multiple biological samples, multiple technical replicates out of each biological replicate will have multiple Poisson distributions for each biological replicate. The multiple Poisson distributions for each biological replicate can be described by a gamma distribution.

Negative binomial as compound Poisson is more capable of capturing the variability as compared with Poisson distribution and hence identified more differentially expressed genes in case of RNA-seq data.

2.2. RNA-seq data

RNA-seq data of Arabidopsis thaliana have been considered for this investigation. The small size, simplicity, convenience and abundance, susceptibility to T-DNA insertions, short generation time, large number of progeny per plant, and small genome of A. thaliana make it attractive for molecular genetic analysis. The details of the RNA-seq data in terms of number of read counts of A. thaliana are given below:

Source: GEO. Accession No. GSE 25818 (Cumbie et al., 2011). Conditions: two—hrcC mutant of Pseudomonas syringae, pv. tomato DC3000 (PtoDC3000), and mock inoculated with 10 mM MgCl₂ 7 hpi. Number of genes: 22,626. Replicates: Three.

The steps followed for analyzing differential gene expression are as follows:

• 1. The expression data under the two conditions (hrcC and mock) for different genes are arranged.

• 2. The difference in read counts is taken over two conditions and is plotted.

• 3. The positive values are up-regulated gene expression values and the negative values are down-regulated gene expression values.

• 4. The compound Poisson distribution is fitted to both these values separately, and accordingly the parameters of the distribution are estimated.

• 5. The goodness-of-fit of the model is tested and the fitted distribution is compared with the single-component Poisson distribution using likelihood ratio test.

3. Results

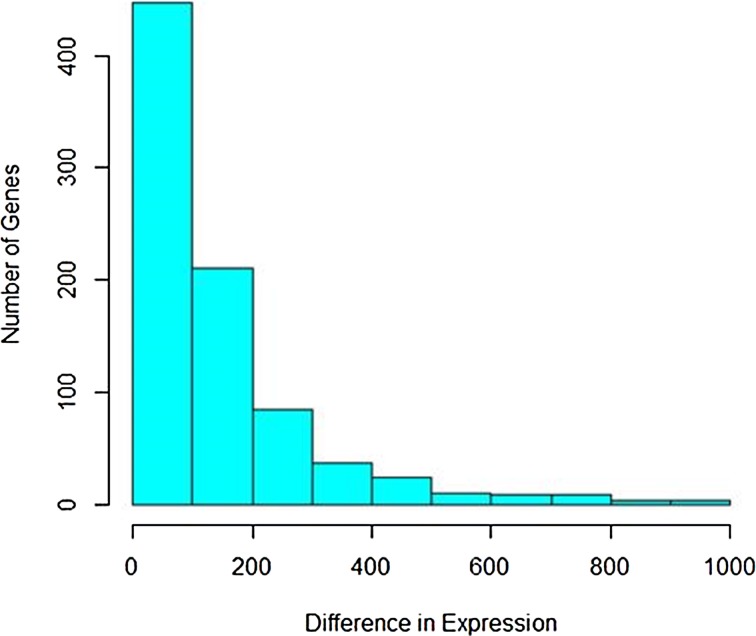
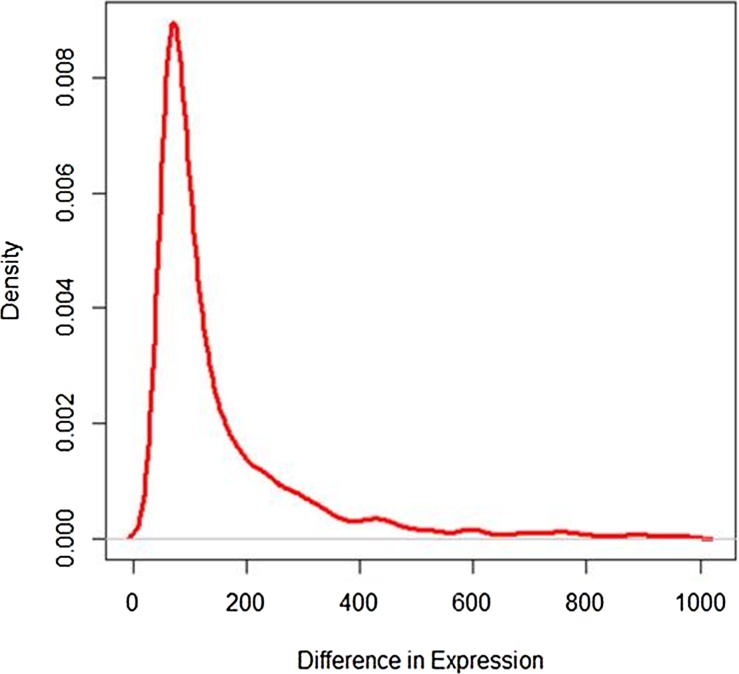
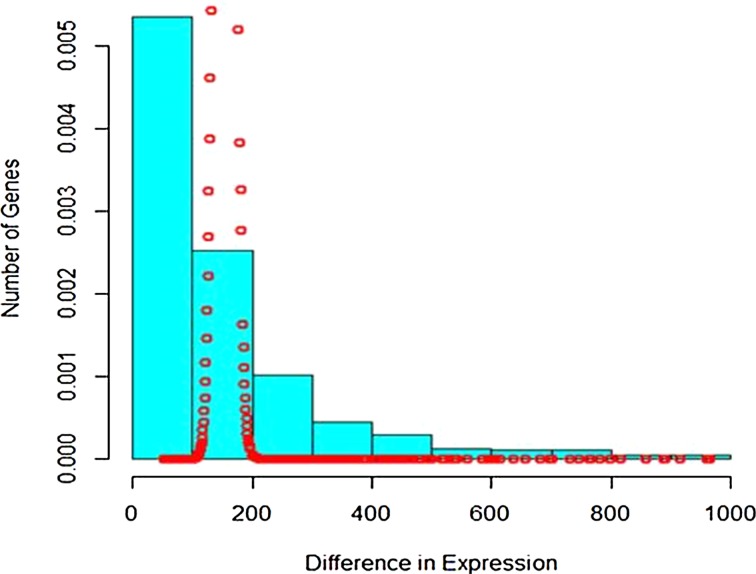
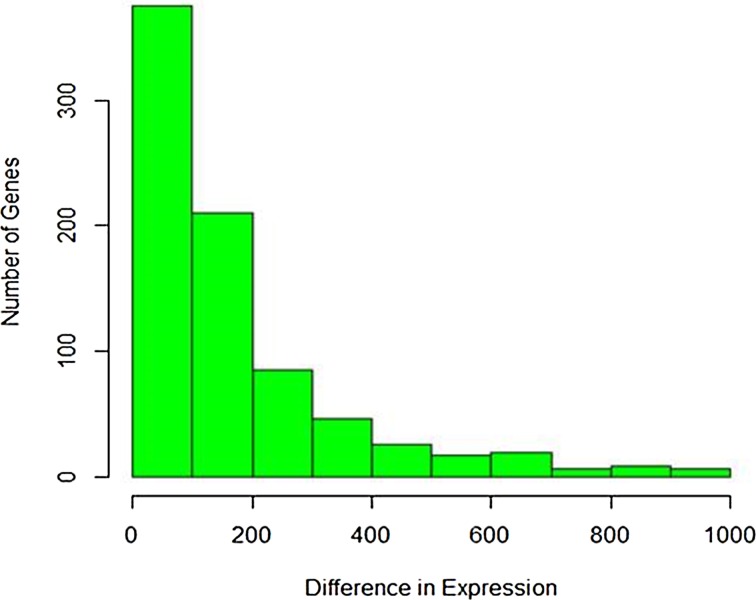
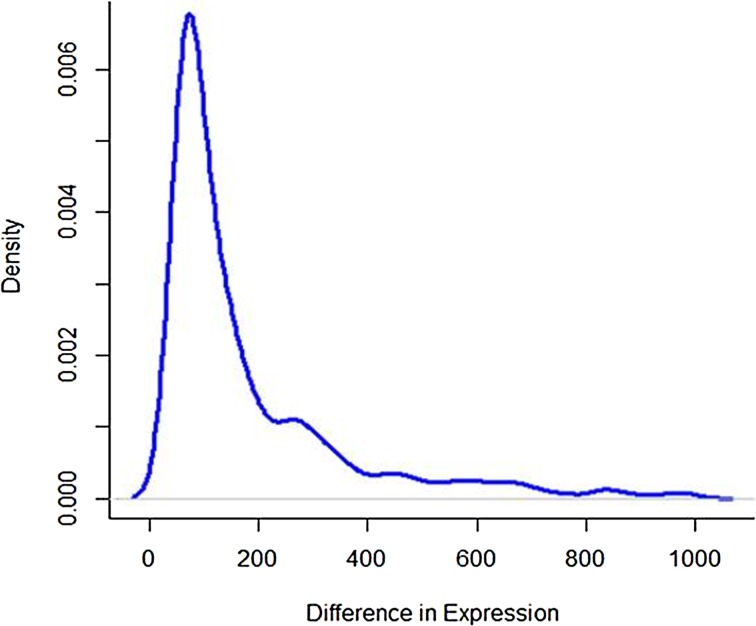
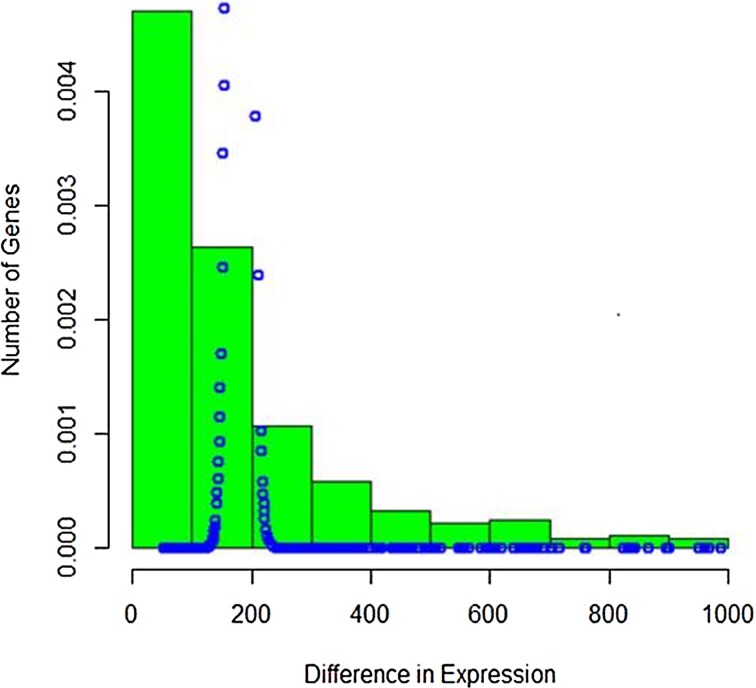
The difference in read counts of A. thaliana is taken over two conditions (hrcC and mock) and is plotted. The changes in one direction in up-regulated gene expression can be clearly seen from the graphs in Figures 1 and 2. Poisson distribution was fitted to the data and the fitted plot is shown in Figure 3.

FIG. 1.

Histogram of up-regulated gene expression.

FIG. 2.

Plot of up-regulated gene expression.

FIG. 3.

Poisson fitting to up-regulated gene expression.

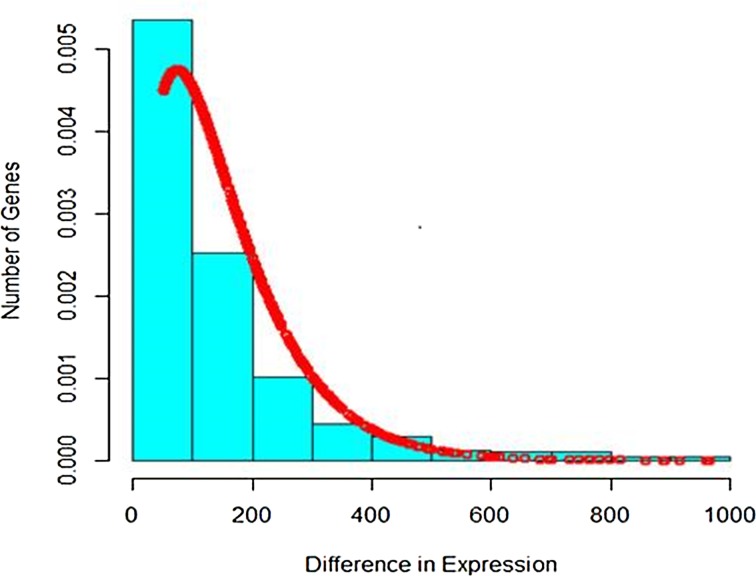
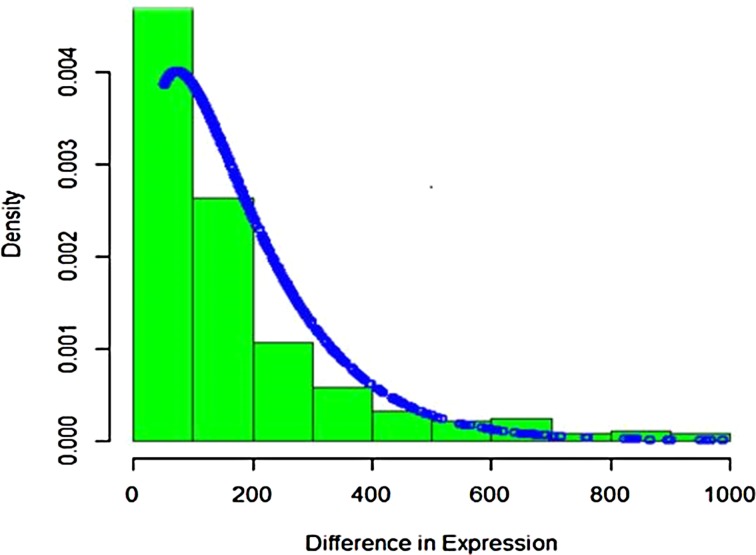
It is seen that Poisson distribution is not able to capture the entire variability. Therefore, the mixture of Poisson distribution with gamma mixing weights (Poisson–gamma mixture) that results in negative binomial distribution was fitted to the up-regulated gene expression RNA-seq data. The fitted plot is shown in Figure 4. It is seen that it covers more variability and takes care of overdispersion.

FIG. 4.

Compound Poisson fitting to up-regulated gene expression.

Similarly for the down-regulated gene expression values, changes in one direction are clearly seen (Figs. 5 and 6). Poisson distribution was fitted to the down-regulated gene expression data and the fitted plot is shown in Figure 7.

FIG. 5.

Histogram of down-regulated gene expression.

FIG. 6.

Plot of down-regulated gene expression.

FIG. 7.

Poisson fitting to down-regulated gene expression.

It can be seen that Poisson distribution is not a good fit of the data, and hence the mixture of Poisson distribution with gamma mixing weights (Poisson–gamma mixture) was fitted to the down-regulated gene expression RNA-seq data. The fitted plot is shown in Figure 8. It is seen that it covers more variability and takes care of overdispersion.

FIG. 8.

Negative binomial fitting to down-regulated gene expression.

The parameter estimates of the Poisson and the compound Poisson were obtained as given in Table 1. Further, the likelihood ratio test was performed and the LRT was computed, which follows a chi-square with 1 degree of freedom. It is found that the null model of Poisson distribution is rejected in favor of the alternative model of compound Poisson distribution.

Table 1.

Parameter Estimates

		Compound Poisson
Gene expression	Poisson λ	β	α	Likelihood Ratio Test (LRT)
Up-regulated	25.24	0.40	0.0158	1,312,396
Down-regulated	34.19	0.36	0.0105	1,608,147

The total number of genes identified as differentially expressed is shown in Table 2 based on the probability value p < 0.01 under the Poisson and compound Poisson distributions.

Table 2.

Number of Genes Identified

	No. of genes (p < 0.01)
Gene expression	Poisson	Compound Poisson
No. of up-regulated genes identified from a total of 10,483	9649	2081
No. of down-regulated genes identified from a total of 11,607	10,357	1954

4. Discussion

Here we have predicted differentially expressed genes by using the compound distribution approach, which is a way of mixing the distributions by assuming the parameter of the distribution to be random variable following certain distribution. It has been found that in case of RNA-seq data, compound Poisson distribution, which is a mixture of Poisson and gamma distribution, is more appropriate to capture the variability as compared with Poisson distribution and could identify the differentially expressed genes more accurately. Separate fitting was done for up-regulated and down-regulated genes.

In case of up-regulated genes, out of 10,483 genes, 9649 genes were identified as differentially expressed based on the probability value cutoff with respect to Poisson distribution and 2081 were identified with compound Poisson distribution. Out of a total of 11,607 down-regulated genes, 10,357 were identified as differentially expressed by fitting Poisson distribution, whereas only 1954 were identified with compound Poisson distribution. It is seen that Poisson distribution is able to identify a large number of genes even for very small differences in read counts, which is not realistic. Table 3 lists few selected genes along with the read count values under two conditions (mock and hrcC). All the genes are differentially expressed using Poisson distribution irrespective of large or small differences. Gene numbers AT5G67640, AT1G01355, and AT5G67550 with a small difference of 2, 1, and 1, respectively, are identified as differentially expressed, whereas using compound Poisson these are not differentially expressed as p > 0.01. Hence, it can be seen that compound Poisson distribution, which is a mixture of Poisson and gamma, is able to identify the differentially expressed genes more accurately.

Table 3.

Gene Identification

Gene ID	Mock	hrcC	Difference	Poisson (Prob.)	Compound Poisson (Prob.)
AT5G67640	13	15	2	3.49E-09	0.051383
AT1G14670	145	205	60	1.75E-09	0.002830
AT5G66070	48	110	62	2.94E-10	0.002690
AT1G01355	0	1	1	2.76E-10	0.074767
AT5G67550	1	2	1	2.76E-10	0.074767
AT1G14320	240	303	63	1.18E-10	0.002623
AT4G12500	176	3686	3510	0	0
AT4G22470	2487	12,804	10,317	0	0
AT1G76930	6836	35,418	28,582	0	0

Thus, fitting of appropriate distribution to gene expression data provides statistically sound cutoff values for identifying differentially expressed genes.

5. R Code

For fitting the compound Poisson distribution to the data of RNA-seq, R codes have been written, which are given in the Supplementary File (Supplementary Material is available online at www.liebertonline.com/cmb). The code also calculates the likelihood value for testing these models.

Author Disclosure Statement

No competing financial interests exist.