Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Apr 12;6:24088. doi: 10.1038/srep24088

Directed dynamical influence is more detectable with noise

Jun-Jie Jiang 1,2, Zi-Gang Huang 1,2, Liang Huang 2, Huan Liu 3, Ying-Cheng Lai 1,4,a
PMCID: PMC4828632  PMID: 27066763

Abstract

Successful identification of directed dynamical influence in complex systems is relevant to significant problems of current interest. Traditional methods based on Granger causality and transfer entropy have issues such as difficulty with nonlinearity and large data requirement. Recently a framework based on nonlinear dynamical analysis was proposed to overcome these difficulties. We find, surprisingly, that noise can counterintuitively enhance the detectability of directed dynamical influence. In fact, intentionally injecting a proper amount of asymmetric noise into the available time series has the unexpected benefit of dramatically increasing confidence in ascertaining the directed dynamical influence in the underlying system. This result is established based on both real data and model time series from nonlinear ecosystems. We develop a physical understanding of the beneficial role of noise in enhancing detection of directed dynamical influence.

Two types of behaviors can show similar trends and may thus be highly correlated, but they may not have anything to do with each other. Three hundred years ago already, Bishop Berkeley famously declared that “correlation does not imply causation”1, but there is still tendency to confuse correlation with causation in modern scientific research. A widely known example2 occurred in epidemiological studies where it was found that women undergoing hormone replacement therapy (HRT) had a lower-than-average probability of incurring coronary heart disease (CHD), leading to the proposal that HRT can be effective at suppressing CHD. More carefully designed control experiments showed, however, that women who took HRT were more likely to belong to higher social-economic groups with healthier diet and regular physical exercise. In fact, the use of HRT and reduction in CHD can both be attributed to the common cause of social-economic origin, but they have no causal relation with respect to each other. To be able to correctly and accurately detect directed dynamical influence is generally of fundamental importance to many branches of science and engineering3,4 ranging from neuroscience5,6,7 and climatology8,9 to economics10,11,12.

In real world situations a precise mathematical model of the underlying system is often unavailable, thus one must rely on measured time series, data, or other types of information to uncover the directed dynamical influence in the system. Such influences generally are quite subtle - noise in the time series or uncertainties in the available information constitute a serious obstacle to successful unraveling of the influence. Conventional wisdom would stipulate that noise should be removed from data as much as possible. In this paper, however, we report a surprising phenomenon: in a recently developed, nonlinear dynamics based framework13, noise can counterintuitively enhance the detectability of directed dynamical influence. In fact, intentionally injecting a suitable amount of measurement noise into the time series can optimize a quantitative measure (to be described below) characterizing the detectability, which we establish using physical reasoning based on analyzing the interplay between nonlinearity and stochasticity, as well as examples from real data and model systems. Our results suggest that, in situations where ambiguity arises in the detection of directed dynamical influence injecting a certain level of noise into the time series may provide an effective resolution, leading to more reliable detection. We note that this phenomenon is distinct from stochastic resonance14,15, as noise in our case can be either additive or dynamical. In fact, the beneficial role of noise uncovered here is characteristically different because it emerges from a human designed framework/scheme to detect directed dynamical influence, one of the most subtle and elusive properties of dynamical systems.

Traditionally, causation detection is done using methods based on either the Granger causality test16 or transfer entropy17. The Granger test is a linear method operated on the hypothesis that the underlying system can be described as a multivariate stochastic process. Thus, in principle, the method is ineffective for nonlinear systems, in spite of efforts to extend the methodology to strongly coupled systems18,19,20. In the traditional Granger framework, measurement noise is generally detrimental in the sense that, as its amplitude is increased the value of the detected causal influence measure decreases monotonically, leading to spurious detection outcomes21. The transfer entropy framework is applicable17 to both linear and nonlinear systems, but often the required data amount is prohibitively large. In the special case of Gaussian dynamical variables, the two methods, one of the autoregressive nature (Granger test) and another based on information theoretic concepts (transfer entropy), are in fact equivalent to each other22. Quite recently, an alternative information theoretic measure, the causation entropy, was proposed23,24,25. In our study, we exploit the recent framework of convergent cross mapping (CCM)13 based on delay-coordinate embedding, the paradigm of nonlinear time series analysis26,27,28,29. The CCM method can deal with both linear and nonlinear systems with small data sets, and it has been applied to data from different contexts, such as EEG data30, FMRI31, fishery data32, economic data33, and cerebral auto-regulation data34. Here, we consider bivariate nonlinear time series from both experimental and model studies of a classic predator-prey system13,35, and investigate systematically the effects of intentionally injecting noise on detection of directed dynamical influence.

Results

Evidence of beneficial role of noise in detecting directed dynamical influence from an experimental data set

We consider a classic experimental prey-predator system with sustained oscillations in prey and predators, the system of Paramecium aurelia and Didinium nasutum13,36,37,38. In ref. 13, it was shown that there exists a stronger top-down control from Didinium x to Paramecium y, so x and y are the driving (predator) and driven (prey) variables, respectively, which naturally defines a directed dynamical influence. To demonstrate the beneficial role of noise in directed dynamical influence detection, we inject independent noise into the original x and y data (see Supplementary Note 1 for a description of the data set):

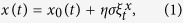graphic file with name srep24088-m1.jpg
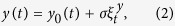graphic file with name srep24088-m2.jpg

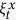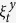where x0(t) and y0(t) are the original time series normalized to unit mean and variance, Inline graphic and Inline graphic are white noise of zero mean and unit variance, σ is the noise amplitude, and η is a control parameter characterizing the ratio of asymmetry of the noise perturbation to the original predator and prey variables. The quality of CCM index detection can be measured13 by the quantity R (see Methods), where a larger positive value of R indicates a stronger directed dynamical influence from x to y. For the experimental system studied here, for σ = 0 the value of R is about 0.035.

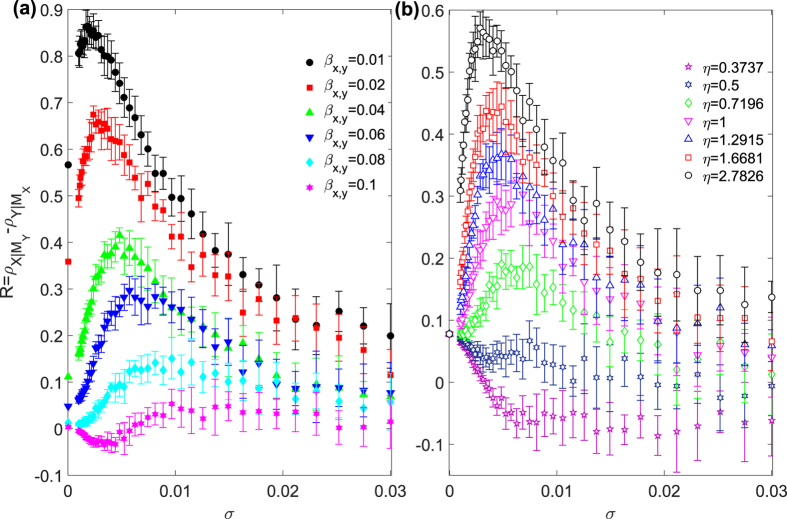
Figure 1 shows R versus the noise amplitude σ from the CCM method. We observe the phenomenon that R can be maximized for some optimal value of the noise amplitude when there is an asymmetry in the injected noise to the predator and prey data. As the noise amplitude σ is increased, R increases and reaches maximum. Strikingly, the maximally achievable value of R can be as large as 0.08 - more than 100% improvement as compared with the case of zero noise. This indicates that, when a proper amount of asymmetric noise is injected into the data set, our ability to detect directed dynamical influence can be enhanced significantly. We note that, there exists a critical value of the asymmetry ratio ηc that for η > ηc, the enhancement phenomenon occurs and the R − σ curve exhibits a characteristic non-monotonic behavior. However, for η < ηc, the non-monotonic behavior is lost, and no improvement in the detectability can be achieved (for too large noise amplitude σ, incorrect detection occurs). This provides a practically useful criterion to apply asymmetric noise: only when comparatively larger noise is injected into the driving variable (i.e., x for this experimental prey-predator system) will the R − σ curve be non-monotonic, as exemplified in Fig. 1. For a system of unknown relationship of directed dynamical influence, a non-monotonic behavior of R is indication that the correct the relationship has been detected. In addition, as shown in Fig. 1, small values of the asymmetry ratio and relatively large noise amplitude can lead to incorrect assessment of the directed dynamical influence13.

Figure 1. Effect of noise on detecting directed dynamical influence from an experimental data set.

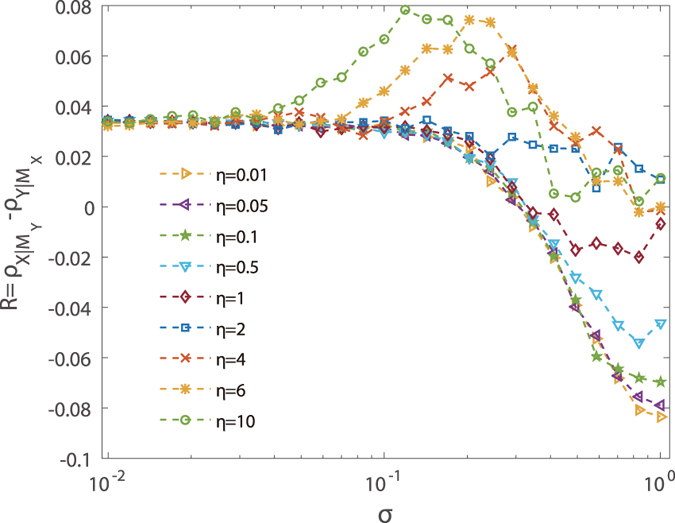
Figure 1

Open in a new tab

For the predator-prey system of paramecium and Didinium, quantity R characterizing the detectability versus the noise amplitude σ. The time series contains L = 61 records, into which noise is intentionally injected. The results are averaged over 1000 realizations of noise. The dimension of the reconstructed phase space is Ex = Ey = 3.

Beneficial role of noise in detecting directed dynamical influence from model data set

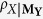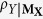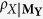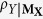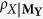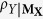In general, noise can cause two relevant quantities, Inline graphic and Inline graphic, to decay, where Inline graphic is the CCM measure from X to Y, with larger value indicating a higher casual effect of the variable x to the variable y, and Inline graphic has a similar meaning. 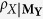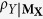(The detailed definitions of Inline graphic and Inline graphic are given in Methods.) The key point is that, due to the directed dynamical influence, the decay rates are different, so the difference R between Inline graphic and Inline graphic can be maximized for proper amount of noise, leading to enhancement of detectability. To develop a physical understanding of the counterintuitive phenomenon in a concrete setting and also to be able to compare results directly with those from real data in Fig. 1, we consider a two-dimensional ecosystem model13:

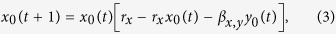graphic file with name srep24088-m13.jpg
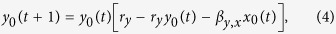graphic file with name srep24088-m14.jpg

where rx, ry ∈ [0, 4] are parameters of the intrinsic population dynamics, βx,y ∈ [0, 0.1] and βy,x ∈ [0, 0.1] are the coupling parameters from y0 to x0 and vice versa, respectively. The degree of directed dynamical interaction between the two variables can be adjusted by changing the relative values of the coupling parameters. As in our analysis of the experimental data, we inject measurement noise into the original time series x0 and y0 to obtain the corresponding new time series x and y. The dimensions of the reconstructed phase space for x and y are Ex = Ey = 2, and the length of the time series is L = 1001. We choose βx,y < βy,x so that the x-dynamics has a stronger influence on the y-dynamics than that in the opposite direction, indicating a larger directed dynamical influence from x to y. Indeed, we obtain from numerics that the value of R is positive and increases with the difference (βy,x − βx,y). Figure 2(a) shows R versus the noise amplitude σ for an increasing set of βx,y values (from 0.01 to 0.1) but for fixed βy,x = 0.1. We see that R can be maximized by noise (for σ ≈ 0.005), similar to the behavior observed from the experimental data set (Fig. 1). We also validate that, when coupling between the two dynamical variables is symmetric, i.e., for βx,y = βy,x = 0.1, the value of R tends to fluctuate about zero as σ is increased, as it should be. 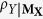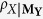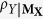Both the non-monotonic behavior of R and the overall increase in the value of R with η can be attributed to the more rapid decay of the correlation coefficient Inline graphic associated with larger η (see Supplementary Note 2 for additional examples and Figs S1 and S2 in Supplementary Information for the detailed behaviors of the correlation coefficients Inline graphic and Inline graphic). Figure 2(b) compares the results from different values of noise asymmetry ratio η for fixed dynamical coupling (βx,y = 0.05 and βy,x = 0.1). We see that, as η is increased, the overall curve of R versus σ is elevated, and the position of the peak moves toward the region of smaller σ values.

Figure 2. Enhancement of detectability of directed dynamical influence from model.

Figure 2

Open in a new tab

Measure of detectability R versus noise amplitude σ for a model ecosystem: (a) for different values of βx,y but fixed βy,x = 0.1 and η = 1, (b) for different values of the asymmetry parameter η but for fixed βx,y = 0.05 and βy,x = 0.1. The value of R for each parameter setting is averaged over 10 dynamical realizations and 10 different noise arrangements for each dynamical realization. Other parameters are rx = 3.8 and ry = 3.5.

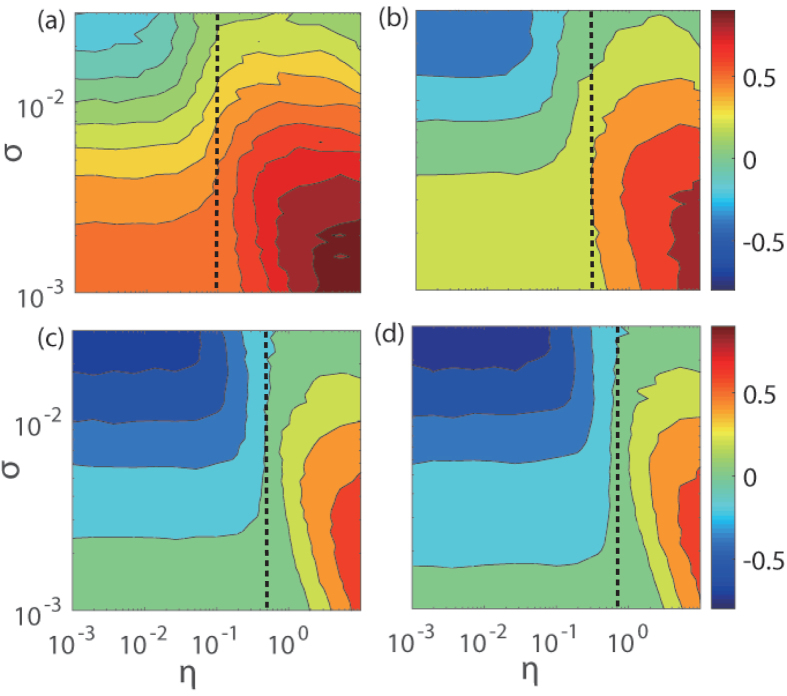
To obtain a comprehensive understanding of the role of noise in detecting the directed dynamical influence, we calculate R for the whole parameter plane (η,σ) characterizing the properties of measurement noise for βy,x > βx,y, as shown in Fig. 3. We see that the noise enhancement effect takes place in the region of η > ηc (for η < ηc, R decreases monotonically with the noise amplitude). In each panel, the value of ηc is indicated by a dashed line. We also note that, in the upper-left region of the parameter plane (i.e., small η and large σ), the values of R are negative, indicating incorrect identification of directed dynamical influence. This can be explained from the dynamical structures in the reconstructed phase space. In particular, for the case of extremely small values of η, noise in x makes the value of Dx = ησ too small to induce a significant decay of 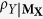Inline graphic with σ. However, 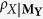Inline graphic decays to a smaller value (e.g., for η = 0.3727 in Fig. 2), leading to negative values of R. For the case where bidirectional causation is more homogeneous, i.e., βy,x and βx,y have approximately the same values, as shown in Fig. 3(a–d), the region of incorrect CCM index detection is enlarged. All these indicate that the applicability of the CCM method depends on how noise is introduced into the measured time series. When this is done properly, detectability of directed dynamical influence can be greatly enhanced.

Figure 3. Measure of detectability R in the parameter plane of noise.

Figure 3

Open in a new tab

The parameters characterizing the properties of measurement noise are σ and η. The model system has fixed βy,x = 0.1 and different values of βx,y: (a) 0.01, (b) 0.02, (c) 0.05, and (d) 0.07. Other parameters are rx = 3.8, ry = 3.5 and L = 1001. The values of the threshold ηc = βx,y/βy,x above which noise enhancement of CCM index measure occurs are marked by the dashed lines.

Physical theory

An effective approach to gaining a physical understanding of the role of noise in promoting directed dynamical influence detection is through examination of the relative effects of coupling and noise on “disturbing” the phase space structure. In general, the dynamics of the system is determined by the structure of the attractor manifold. In the model system, there is an influence of y0 on x0 through the coupling term −βx,y x0(t)y0(t). In this sense, we say that y0 has an effect on the ordered structure of the manifold MX, where MX is the shadow manifold constructed from the time series x0 with embedding dimension Ex and time-delay τ. Similarly, MY is the shadow manifold obtained from the time series y0 with the same parameter (see a detailed explanation in Methods). For a given value of x0(t), the points (x0(t), x0(t + 1)) in MX spread in a region with its upper and lower bounds determined by the possible minimum and maximum values of y0, respectively. The effect of y0 on MX can be characterized by the width in the reconstructed phase space:

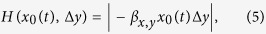graphic file with name srep24088-m20.jpg

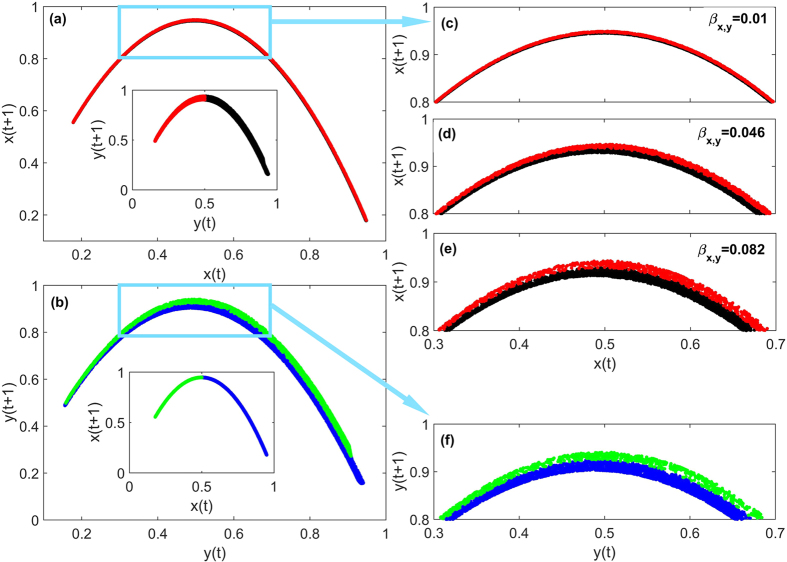
where Δy = max(y0) − min(y0). More specifically, the detailed behavior of y0 contributes to the formation of the structure of MX. For example, a continuously distributed y0 (e.g., for ry = 3.8) leads to a continuous strip of MX, as shown in Fig. 4, but two separated clusters of y0 (e.g., for ry = 3.5) produces a pair of long parallel strips in MX (see Fig. S3 in Supplementary Information).

Figure 4. Effect of noise on reconstructed phase space of dynamical variables.

Figure 4

Open in a new tab

Attractor manifolds MX (a,c–e) and MY (b,f) for σ = 0 and βy,x = 0.1. The insets in (a,b) show the manifold counterparts, respectively, with the color scheme indicated. For example, in (a), the dots (x(t), x(t + 1)) in MX is colored according to the corresponding point y(t) in MY, where points with y(t) ≥ 0.5 are in black and those with y(t) < 0.5 in red. The values of βx,y are 0.01 (a,c), 0.046 (d), and 0.082 (e), respectively. Panels (c,f) are magnifications of the squared frames in (a,b), respectively. Other parameters are rx = ry = 3.8.

To better understand the mutual influence between MX and MY, we color the dots in one state space according to their corresponding positions in the counterpart state space. Take the case shown in Fig. 4(a) as an example. We select a boundary in the middle of the manifold MY [e.g., y(t) = 0.5, as shown in the inset of panel (a)] and color the dots on the left-hand and right-hand sides in red and black, respectively, where each dot in MY corresponds to one point (y(t), y(t + 1)) for certain value of t. We set the same color to the dot (x(t), x(t + 1)) in the manifold MX. This color scheme presents us with a clear picture of the structural relationship between the manifolds MX and MY. For example, for the two clusters in MY (denoted by the value 0.5), the corresponding structure in MX consists of two stretched, thin strips that are close to each other. The dynamics on the two thin strips in MX are sensitive to noise, since a small perturbation can move a dot from one strip to another, visually leading to a mixing of dots of different colors. As we estimate 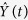Inline graphic according to the dots in MX through the neighbors of X(t), noise of amplitude about the thickness of the strips will result in a decrease in the prediction accuracy. The thickness of the strip in MX depends on the dynamical coupling from y. For the extreme case of βx,y = 0, i.e., y is decoupled from x, the thickness of the strip in MX becomes zero. As βx,y is increased, the strip in MX becomes thicker, as shown in Fig. 4(c–e).

The features of y0 thus determine how the structure of the manifold MX is modified through the coupling parameter βx,y. A relatively small value of βx,y indicates a weaker influence from y0 to x0, which results in a narrower strip in MX, and some larger value of βx,y will enlarge the width H(x0, Δy) of MX, as shown in Fig. 4(c–e). To illustrate the influence of y0 on x0, we mark the points in MY with y0(t) < 0.5 and y0(t) ≥ 0.5 with red and black colors, respectively. The corresponding points in MX at the same instants are marked by the same color. We see that the points in MX corresponding to different values of y0(t) tend to spread farther away from each other, and MX exhibits separated long pairing strips. Analogously, the effect of x0 on y0 is embedded in the structure of MY of size determined by

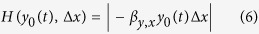graphic file with name srep24088-m22.jpg

and Δx = max(x0) − min(x0). The widths of MX and MY, as determined by the coupling between the two variables, play a crucial role in system’s response to noise associated with the detection of directed dynamical influence.

The phenomenon of noise enhanced detection of directed dynamical influence can be intuitively understood in terms of noise-induced diffusion. In particular, in the reconstructed phase space, noise can be viewed as inducing random diffusion of points on the attractor manifolds, which alters the originally ordered phase space structures that are result of the mutual dynamical interactions. On the manifold MX, what is relevant is the expected diffusion radius 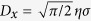Inline graphic of point X(t), with respect to the width H(x(t),Δy) of the manifold due to the influence from y0. In predicting Y(t) according to its weighted average 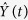Inline graphic, the E + 1 nearest neighbors of X(t), denoted as X(ti) in MX, are taken into account. However, diffusion can introduce “wrong” neighboring points from the region within the average distance Dx. When these points are mapped to MY, they correspond to the points Y(ti) with horizontal ordinate y(t) deviating by the amount

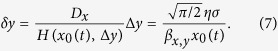graphic file with name srep24088-m25.jpg

The points in MY with the horizontal ordinates y(t) ± δy are actually used to estimate 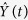Inline graphic (see Fig. S3 in Supplementary Information for a specific example). Here, δy is a measure of how errors in x(t) (due to noise) propagate to the corresponding errors in y(t). The accuracy of the estimation Y(t) decreases with δy. For the normalized time series (i.e., 〈x0〉 = 1), the average deviation is given by

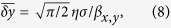graphic file with name srep24088-m27.jpg

where a smaller effective noise amplitude ησ on x0 or a larger coupling parameter βx,y from y0 to x0 will yield a smaller value of 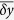Inline graphic, leading to more accurate estimation 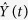Inline graphic. The quantity 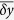Inline graphic thus characterizes the competition between the effects on y0 from x0 (denominator) and that from noise (numerator). A similar picture arises when estimating 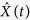Inline graphic based on MY, where the width of the manifold MY is H(y0(t), Δx), the expected vertical diffusion radius is 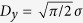Inline graphic, and the corresponding points X(ti) for the weighted average have the deviation

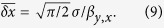graphic file with name srep24088-m33.jpg

We thus see that, interaction from the coupled variable contributes to forming a wider well-organized manifold of the focal variable, while noise tends to destroy the order of the structure. The competition between nonlinear interaction and noise in detecting directed dynamical influence is general and independent of the system and measurement details.

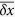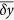Consider the setting where the variable x is the cause to y, as for βy,x > βx,y in the model system. The distinct responses of x and y to noise can lead to enhancement of R. Our analysis suggests Inline graphic and Inline graphic as the indicators of the competition between coupling and noise. The ratio

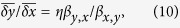graphic file with name srep24088-m36.jpg

quantifies the relative decay rate of 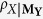Inline graphic with respect to 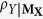Inline graphic as the noise amplitude σ is increased. A faster decay of 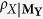Inline graphic to zero with σ, which in CCM prediction is associated with 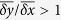Inline graphic, leads to the non-monotonic behavior in R versus σ. Furthermore, the condition 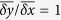Inline graphic defines the threshold ratio ηc (or critical value) for the emergence of the non-monotonic behavior (Fig. 3). For a real system with the directed dynamical relationship unknown a priori, the ratio βx,y/βy,x can be estimated by injecting asymmetric noise into the time series and calculating the threshold ηc. As shown in Fig. 1, the experimental system has the threshold ηc around 1.5. We also find that, for systems under dynamical noise, detection of directed dynamical influence can still be enhanced, as described in Supplementary Note 3 and shown in Fig. S4.

Discussions

We have uncovered a practically implementable mechanism to significantly enhance detection of directed dynamical influence in nonlinear dynamical systems: injecting asymmetric noise into the time series of the dynamical variables of interest. The general idea is that, since directed dynamical influence reflects the differential interaction of the dynamical variables on each other, noise can lead to an asymmetric degradation of the interactions. Because of the nonlinear dynamical underpinning of the CCM algorithm, its performance can in fact be enhanced and optimized by noise, which is the main result of our work. In particular, the CCM method relies on the asymmetry in the directed dynamical influence measures between the two dynamical variables in the two opposite directions. When noise of non-identical amplitude is added to the two variables, the asymmetry in the directed dynamical influence measures can be amplified, leading to better performance in the detection. For example, let x and y be the two dynamical variables, and assume that the directed dynamical influence from x to y is stronger than that for the opposite direction: βy,x > βx,y. As the noise amplitude is increased to a level corresponding to the weaker directed dynamical influence from y to x as characterized by βx,y but not yet up to that from x to y (characterized by βy,x), the ability to predict y from x will be dramatically reduced but that in the opposite direction will be affected less. As a result, the difference (βy,x − βx,y) will be enhanced. In other words, the beneficial role of noise can be attributed to the fact that weaker dynamical influence is destroyed earlier than the stronger one as the noise amplitude is increased. However, if the noise amplitude reaches the level of the stronger directed dynamical influence from x to y, the algorithm will not be able to detect any such influence. As a result, a non-monotonic relation between the detectability of directed dynamical influence and noise amplitude arises, in contrast to the monotonic decreasing behavior associated with the original Granger method.

It should be noted that, while a larger value of the metric R suggests a larger degree of asymmetry between the directed dynamical influence of dynamical variables in the two opposite directions, the task of enhancing the value of R should not be confused with that of detecting causality in the first place. Often, for any pair of variables in a nonlinear dynamical system, there is typically directed dynamical influence in both directions. That is, the question of whether there is causality has a trivial answer. The nontrivial and challenging task is to assess which direction possesses a stronger directed dynamical influence. Our main finding is that an appropriate amount of asymmetric noise can facilitate the assessment.

Intuitively, the phenomenon of noise enhanced detection of directed dynamical influence can be understood by resorting to the picture of noise induced diffusion in the phase space. The explanation is heuristic, calling for a quantitative or even rigorous analysis, which remains to be an outstanding issue at the present. Practically, the phenomenon noise can be induced extremely readily utilizing time series only, and we expect it to be appealing to ascertaining directed dynamical influence in experiments or data analysis of complex dynamical systems.

We remark that, while the intuitive argument that noise disrupts the structure of the noise-free manifold of the dynamical system is reasonable, it may not be generally true that the magnitude of the error can be preserved as measured by the directed dynamical influence metric R. For the systems studied in this paper, the coupling functions between the dynamical variables are assumed to be linear, i.e., the effect of one variable on the other is linear. This, however, may not be true generally. In particular, if the response of one variable to the other is nonlinear, small errors could be amplified and large errors could be reduced, and the nonlinear amplification/reduction effect can be state-dependent. In realistic systems there is no guarantee that the response of one variable to another is even a continuous function. For such cases, the effect of noise on detecting directed dynamical influences would depend on the system details. For complex dynamical systems with nonlinear or discontinuous coupling functions, whether a general relation exists between a measure of directed dynamical influence and the noise strength is an open question deserving further investigation.

Methods

CCM method

The nonlinear-dynamics based method was proposed recently13 to detect and quantify directed dynamical influence between a pair of dynamical variables through the corresponding time series. The starting point is to reconstruct a phase space, for each variable, based on the delay-coordinate embedding method26. Specifically, for time series x(t), the reconstructed vector is X(t) = [x(t), x(t − τ), …, x(t − (Ex − 1)τ)], where τ is the delay time and Ex is the embedding dimension. For variable y, a similar vector can be constructed in the Ey dimensional space. Let MX and MY denote the attractor manifold in the Ex- and Ey-dimensional space, respectively. If x and y are dynamically coupled, there is a mapping relation between MX and MY. The CCM method measures how well the local neighborhoods in MX correspond to those in MY. In particular, the cross-mapping estimate of a given Y(t), denoted as 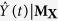Inline graphic, is based on a simplex projection39,40 that is essentially a nearest-neighbor algorithm involving E + 1 nearest neighbors of X(t) in MX. (Note that E + 1 is the minimum number of points required for a bounding simplex in the E-dimensional space.) The time indices of the E + 1 nearest neighbors are denoted as t1, t2, …, tE+1 in the order of distances to X(t) from the nearest to the farthest, i.e., point X(t1) is the nearest-neighboring point of X(t) in MX. These time indices are used to identify the points (putative neighborhoods) in MY, namely, to find the points at the corresponding instants: Y(t1), Y(t2), …, and Y(tE+1), which are used to estimate 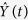Inline graphic through the weighted average

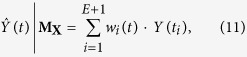graphic file with name srep24088-m44.jpg

where

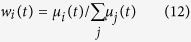graphic file with name srep24088-m45.jpg

is the weight of the vector Y(ti),

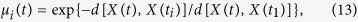graphic file with name srep24088-m46.jpg

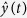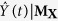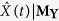and d[X(t), X(ti)] is the Euclidean distance between the two vector points X(t) and X(ti) in MX. An estimated time series Inline graphic can then be obtained from Inline graphic. Likewise, the cross mapping from Y to X can be defined analogously so that the time series of x(t) can be predicted from the cross-mapping estimate Inline graphic.

The correlation coefficient between the original time series y(t) and the predicted time series 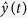Inline graphic from MX, denoted as 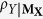Inline graphic, is a measure of CCM directed dynamical influence from y to x. Larger value of 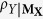Inline graphic implies that y is a stronger cause of x, while 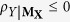Inline graphic indicates that y has no influence on x. The relative strength of directed dynamical influence can be defined as 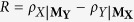Inline graphic, which is a quantitative measure of the casual relationship between x and y. A positive value of R indicates that x is the CCM cause of y. The measure R is used in Fig. 1 to quantify the degree of noise enhancement of CCM index detection.

Time delay and embedding dimension

The CCM method for detecting directed dynamical influence is derived from the standard delay-coordinate embedding method26 in nonlinear time series analysis. For properly chosen time delay41 (denoted as τ) and embedding dimension (denoted as E), the phase space of the underlying dynamical system can be faithfully reconstructed from time series. There are various methods for choosing the parameters42 τ and E, such as those based on the mutual information43, the correlation integral and dimension44,45,46,47,48,49, false nearest neighbors (FNN)50, and nonlinear prediction criteria51,52,53.

In the text, the time delay and embedding dimension for the experimental predator-prey data are chosen to be τ = 1 and Ex = Ey = 3, respectively. For the model systems with measurement noise and dynamical noise, we choose Ex = Ey = 2 and τ = 1. A comprehensive treatment of the effect of noise on phase space reconstruction can be found in ref. 53.

Additional Information

How to cite this article: Jiang, J.-J. et al. Directed dynamical influence is more detectable with noise. Sci. Rep. 6, 24088; doi: 10.1038/srep24088 (2016).

Supplementary Material

Supplementary Information
srep24088-s1.pdf (451.5KB, pdf)

Acknowledgments

This work was supported by ARO under Grant No. W911NF-14-1-0504 . Z.G.H. was supported by NSF of China under Grant No. 11275003. J.J. was partially supported by Lanzhou University.

Footnotes

Author Contributions Y.C.L. conceived the research. J.J. and Z.G.H. performed the analysis. L.H. and H.L. participated in discussions. Y.C.L. and Z.G.H. wrote the manuscript.

References

  1. Berkeley G. A Treatist Concerning the Principles of Human Knowledge (Lippincott’s Press, Philadelphia, USA, 1874). [Google Scholar]
  2. Lawlor D. A., Davey S. G. & Ebrahim S. Commentary: the hormone replacement-coronary heart disease conundruml is this the death of observational epidemiology? Int. J. Epidemiol. 33, 464–467 (2004). [DOI] [PubMed] [Google Scholar]
  3. Pearl J. Causality: Models, Reasoning, and Inference (Cambridge University Press, Cambridge, UK, 2000). [Google Scholar]
  4. Beebee H., Hitchcock C. & Menzies P. The Oxford Handbook of Causation (Oxford University Press, Oxford, UK, 2009). [Google Scholar]
  5. Chávez M., Martinerie J. & Le Van Quyen M. Statistical assessment of nonlinear causality: application to epileptic eeg signals. J. Neurosci. Meth. 124, 113–128 (2003). [DOI] [PubMed] [Google Scholar]
  6. Pereda E., Quiroga R. Q. & Bhattacharya J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 77, 1–37 (2005). [DOI] [PubMed] [Google Scholar]
  7. Chen Y., Bressler S. L. & Ding M. Frequency decomposition of conditional granger causality and application to multivariate neural field potential data. J. Neurosci. Meth. 150, 228–237 (2006). [DOI] [PubMed] [Google Scholar]
  8. Triacca U. Is granger causality analysis appropriate to investigate the relationship between atmospheric concentration of carbon dioxide and global surface air temperature? Theor. Appl. Climatol. 81, 133–135 (2005). [Google Scholar]
  9. Stern D. I. & Kaufmann R. K. Anthropogenic and natural causes of climate change. Climatic. Change. 122, 257–269 (2014). [Google Scholar]
  10. Rodrguez G. & Rowe N. Why us money does not cause us output, but does cause hong kong output. J. Int. Money. Financ. 26, 1174–1186 (2007). [Google Scholar]
  11. Stern D. I. & Enflo K. Causality between energy and output in the long-run. Energ. Econ. 39, 135–146 (2013). [Google Scholar]
  12. Ma Y. & Kanas A. Testing for nonlinear granger causality from fundamentals to exchange rates in the erm. J. Int. Finance Markets Insti. Money 10, 69–82 (2000). [Google Scholar]
  13. Sugihara G. et al. Detecting causality in complex ecosystems. Science 338, 496–500 (2012). [DOI] [PubMed] [Google Scholar]
  14. Benzi R., Sutera A. & Vulpiani A. The mechanism of stochastic resonance. J. Phys. A-Math. Gen. 14, L453–L457 (1981). [Google Scholar]
  15. Gammaitoni L., Hänggi P., Jung P. & Marchesoni F. Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998). [Google Scholar]
  16. Granger C. W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438 (1969). [Google Scholar]
  17. Schreiber T. Measuring information transfer. Phys. Rev. lett. 85, 461–464 (2000). [DOI] [PubMed] [Google Scholar]
  18. Chen Y., Rangarajan G., Feng J. & Ding M. Analyzing multiple nonlinear time series with extended granger causality. Phys. Lett. A 324, 26–35 (2004). [Google Scholar]
  19. Ancona N., Marinazzo D. & Stramaglia S. Radial basis function approach to nonlinear granger causality of time series. Phys. Rev. E 70, 056221 (2004). [DOI] [PubMed] [Google Scholar]
  20. Marinazzo D., Pellicoro M. & Stramaglia S. Kernel method for nonlinear granger causality. Phys. Rev. Lett. 100, 144103 (2008). [DOI] [PubMed] [Google Scholar]
  21. Nalatore H., Sasikumar N. & Rangarajan G. Effect of measurement noise on granger causality. Phys. Rev. E 90, 062127 (2014). [DOI] [PubMed] [Google Scholar]
  22. Barnett L., Barrett A. B. & Seth A. K. Granger causality and transfer entropy are equivalent for gaussian variables. Phys. Rev. lett. 103, 238701 (2009). [DOI] [PubMed] [Google Scholar]
  23. Sun J., Cafaro C. & Bollt E. M. Identifying coupling structure in complex systems through the optimal causation entropy principle. Entropy 16, 3416–3433 (2014). [Google Scholar]
  24. Cafaro C., Lord W. M., Sun J. & Bollt E. M. Causation entropy from symbolic representations of dynamical systems. Chaos 25, 043106 (2015). [DOI] [PubMed] [Google Scholar]
  25. Sun J., Taylor D. & Bollt E. M. Causal network inference by optimal causation entropy. SIAM J. Dyn. Syst. 14, 73–106 (2015). [Google Scholar]
  26. Takens F. Detecting strange attractors in fluid turbulence. Lecture Notes in Mathematics Vol. 898 (eds. Rand D. & Young L. S.) 366–381 (Springer-Verlag, 1981). [Google Scholar]
  27. Sauer T., Yorke J. A. & Casdagli M. Embedology. J. Stat. Phys. 65, 579–616 (1991). [Google Scholar]
  28. Kantz H. & Schreiber T. Nonlinear Time Series Analysis (Cambridge University Press, Cambridge, UK, 1997). [Google Scholar]
  29. Deyle E. R. & Sugihara G. Generalized theorems for nonlinear state space reconstruction. PLoS One 6, e18295 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. McBride J. C. Dynamic Complexity and Causality Analysis of Scalp EEG for Detection of Cognitive Deficits. Ph.D. thesis, University of Tennessee, Knoxville (2014).
  31. Wismüller A., Wang X.-X., DSouza A. M. & Nagarajan N. B. A framework for exploring non-linear functional connectivity and causality in the human brain: mutual connectivity analysis (mca) of resting-state functional mri with convergent cross-mapping and non-metric xlustering. arXiv:1407.3809 (2014).
  32. Harford W. et al. Can climate explain temporal trends in king mackerel (scomberomorus cavalla) catch-per-unit-effort and landings? Tech. Rep., SEDAR, SEDAR38-AW-04. SEDAR, North Charleston, SC (2014).
  33. Huffaker R. & Fearne A. Empirically testing for dynamic causality between promotions and sales beer promotions and sales in england. Proc. Food. Syst, Dyn 270–274 (2014). [Google Scholar]
  34. Heskamp L., Meel-van den Abeelen A. S., Lagro J. & Claassen J. A. Convergent cross mapping: a promising technique for cerebral autoregulation estimation. IJCNMH 1 (Suppl. 1), S20 (2014). [Google Scholar]
  35. Jost C. & Ellner S. P. Testing for predator dependence in predator-prey dynamics: a non-parametric approach. Proc. Biol. Sci 267, 1611–1620 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Luckinbill L. S. Coexistence in laboratory populations of paramecium aurelia and its predator didinium nasutum. Ecology 54, 1320–1327 (1973). [Google Scholar]
  37. Veilleux B. G. The analysis of a predatory interaction between Didinium and Paramecium. Master’s thesis, University of Alberta, Edmonton (1976).
  38. Gause G. F. The Struggle for Existence (Courier Dover Publications, 2003). [Google Scholar]
  39. Sugihara G. & May R. M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344, 734–741 (1990). [DOI] [PubMed] [Google Scholar]
  40. Sugihara G. Nonlinear forecasting for the classification of natural time series. Philos. T. Roy. Soc. A. 348, 477–495 (1994). [Google Scholar]
  41. Lai Y.-C., Lerner D. & Hayden R. An upper bound for the proper delay time in chaotic time series analysis. Phys. Lett. A 218, 30–34 (1996). [Google Scholar]
  42. Lai Y.-C. & Ye N. Recent developments in chaotic time series analysis. Int. J. Bif. Chaos 13, 1383–1422 (2003). [Google Scholar]
  43. Fraser A. M. & Swinney H. L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33, 1134–1140 (1986). [DOI] [PubMed] [Google Scholar]
  44. Grassberger P. & Procaccia I. Characterization of strange attractors. Phys. Rev. Lett. 50, 346–348 (1983). [Google Scholar]
  45. Albano A.-M., Mees A., De Guzman G. & Rapp P. Data requirements for reliable estimation of correlation dimensions. In Chaos in Biological Systems, 207–220 (Springer, 1987). [Google Scholar]
  46. Theiler J. Spurious dimension from correlation algorithms applied to limited time series data. Phys. Rev. A 34, 2427–2432 (1986). [DOI] [PubMed] [Google Scholar]
  47. Ding M., Grebogi C., Ott E., Sauer T. D. & Yorke J. A. Plateau onset for correlation dimension: when does it occur? Phys. Rev. Lett. 70, 3872–3875 (1993). [DOI] [PubMed] [Google Scholar]
  48. Osorio I., Harrison M. A., Lai Y.-C. & Frei M. Observations on the application of correlation dimension and correlation integral to prediction of seizures. J. Clin. Neurophysio. 18, 269–274 (2001). [DOI] [PubMed] [Google Scholar]
  49. Harrison M. A. F., Osorio I., Frei M. G., Asuri S. & Lai Y.-C. Correlation dimension and integral do not predict epileptic seizures. Chaos 15, 033106 (2005). [DOI] [PubMed] [Google Scholar]
  50. Kennel M. B., Brown R. & Abarbanel H. D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411 (1992). [DOI] [PubMed] [Google Scholar]
  51. Farmer J. D. & Sidorowich J. J. Predicting chaotic time series. Phys. Rev. Lett. 59, 845–848 (1987). [DOI] [PubMed] [Google Scholar]
  52. Casdagli M. Nonlinear prediction of chaotic time series. Physica D 35, 335–356 (1989). [Google Scholar]
  53. Casdagli M., Eubank S., Farmer J. D. & Gibson J. State space reconstruction in the presence of noise. Physica D 51, 52–98 (1991). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep24088-s1.pdf (451.5KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES