Crystallization, structural diversity and anisotropy effects in 2D arrays of icosahedral viruses

Abstract

We investigate two-dimensional (2D) assembly of the icosahedral turnip yellow mosaic virus (TYMV) under cationic lipid monolayers at the aqueous solution–vapor interface. The 2D crystallization of TYMV has been achieved by enhancing electrostatically induced interfacial adsorption, an approach recently demonstrated for another virus. In situ X-ray scattering reveals two close-packed 2D crystalline phases of TYMV that are distinct from the previously reported hexagonal and centered square ( $\sqrt{2}\times \sqrt{2}$) arrays of TYMV. One of the newly observed phases arises from either a dimeric double-square (2 × 1) or tetrameric square (2 × 2) unit cell. The other is a rhombic crystal with a lattice angle of 80°. The two observed crystal phases are substantially less dense (by over10%) than a 2D lattice of TYMV could be according to its known size and shape, indicating that local anisotropic interparticle interactions play a key role in stabilizing these crystals. TYMV’s anisotropy attributes and numerical analysis of 2D arrays of virus-shaped particles are used to derive a model for the rhombic crystal in which the particle orientation is consistent with the electrostatic lipid–TYMV attraction and the interparticle contacts exhibit steric complementarity. The interplay between particle anisotropy and packing is contrasted between the rhombic crystal model and the square ( $\sqrt{2}\times \sqrt{2}$) crystal. This study highlights how the high symmetry and subtle asphericity of icosahedral particles enrich the variety and complexity of ordered 2D structures that can be generated through self-assembly.

Introduction

A key challenge in the assembly of nanoparticles (NPs) is to understand and exploit the effects of anisotropy.¹ The need for progress has become increasingly urgent due to the advances in synthesizing a variety of NPs with well-defined nonspherical shapes.^2–4 Related recent efforts include intensive, largely computational, investigations into the packing of regular polyhedra^5–7 and patchy particles.^8–10 As emphasized recently,¹ an anisotropic NP usually possesses more than one type of anisotropy attributes, including their symmetry, shape, and chemical patchiness. An improved understanding of how a set of anisotropy attributes combine to dictate the interparticle interactions is essential for controlling the assembly of anisotropic NPs.¹ Thus far, experimental progress in addressing these issues has been limited mostly to cases involving highly nonspherical NPs or strong specific interactions.^11–15

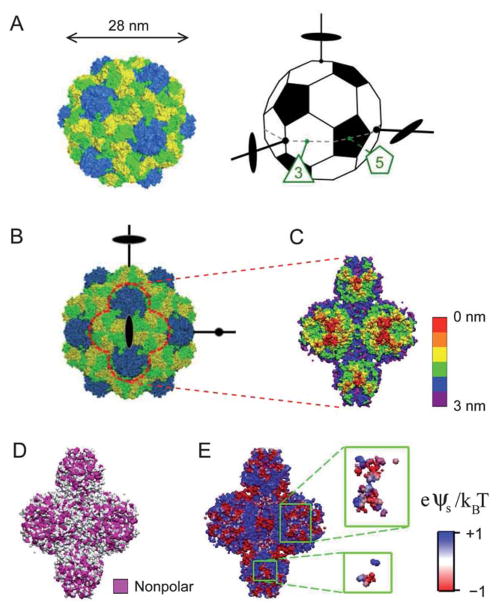
The present study aims to explore anisotropy effects and potential structural diversity in the assemblies of highly symmetric NPs. We studied the 2D assembly of turnip yellow mosaic virus (TYMV), a 28 nm icosahedral virus, formed under a cationic lipid monolayer at the aqueous solution–vapor interface (Fig. 1A and 2A). TYMV was chosen as a model NP since its topographical and chemical heterogeneities can be deduced from its known atomic coordinates.^16–18 For example, hexagonal and pentagonal knobs are known to protrude along TYMV’s 3-and 5-fold axes (Fig. 1A–C), respectively, and the knob surface displays distinct heterogeneous distributions of nonpolar residues (Fig. 1D) and electrostatic potential (Fig. 1E). The use of such structurally well-defined particles is essential to unraveling the interplay between the particle’s various anisotropy attributes and their effects on interparticle interactions and self-assembly. The lipid-coated aqueous interface provides a means to impose a specific particle orientation. This simplifying 2D geometry is used to help dissect the role of anisotropy in aqueous-media assembly,¹⁹ which involves various types of similarly weak interactions.²⁰

Fig. 1.

(A) The capsid of TYMV (left) consists of 180 copies of a protein subunit, with 60 subunits forming 12 pentamers (blue) and 120 subunits forming 20 hexamers (yellow and green). The truncated icosahedron (right) illustrates the virus orientation. A set of 3 orthogonal 2-fold axes, an equatorial 3-fold axis, and an equatorial 5-fold axis are indicated. (B) Projection of TYMV along a 2-fold axis. (C)–(E) The 2-fold axis views of TYMV’s exterior surface, corresponding to 2 hexagonal and 2 pentagonal knobs: (C) depth profile, (D) nonpolar residue distribution, and (E) electrostatic surface potential.¹⁸ Insets in (E) represent frontmost surfaces with depth ≤0.5 nm.

Fig. 2.

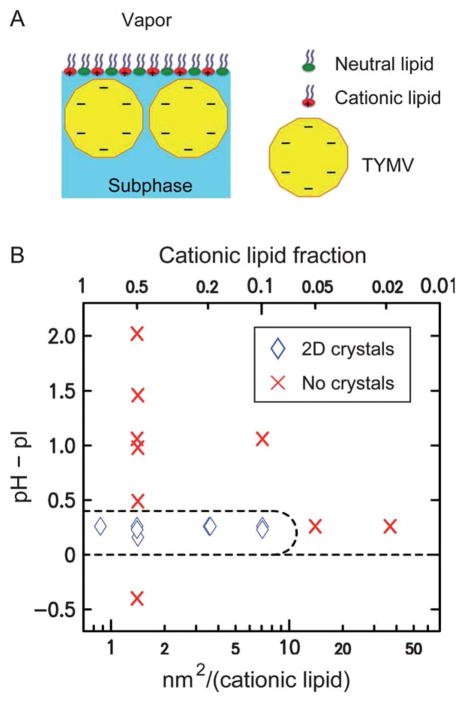
(A) A schematic illustrating the assembly of TYMV at the lipid-terminated solution–vapor interface (not drawn to scale). (B) Observed 2D assembly behavior of TYMV as a function of the solution pH relative to pI = 3.6 (see ESI, Fig. S1^†) and the area per cationic lipid (bottom abscissa) or the cationic lipid fraction (top). The points at which GISAXS measurements were carried out are indicated by diamonds and crosses, where diamonds represent the observation of GISAXS peaks for the 2D crystals of TYMV.

Although icosahedral viruses have been used in previous studies of interfacial self-assembly, most of the reported 2D-ordered assemblies consist of hexagonal arrays.^21–24 Exceptions include TYMV and cowpea mosaic virus (CPMV), for which true 2D crystals with well-defined virus orientation were observed.^19,25–28 In particular, electron microscopy (EM) studies^25–27 revealed 2D square crystals of TYMV that reflected the orthogonality of icosahedral 2-fold axes^29–31 (Fig. 1A and B). This unique crystallization behavior is interesting in light of the recent finding¹⁵ that the alignment of neighboring particles along common symmetry axes promotes long-range order. However, those previous EM studies of TYMV addressed neither the mechanism of 2D assembly nor the nature of prevalent anisotropic interactions.

The purpose of this paper is threefold. First, we show that the 2D crystallization of TYMV can be induced by enhancing the electrostatics-driven adsorption of the virus onto an oppositely charged lipid monolayer. Our results support the effectiveness of this crystallization strategy, which we recently demonstrated for CPMV.²⁸ Second, we demonstrate structural diversity in 2D assemblies of icosahedral particles. We present X-ray evidence for two previously unobserved 2D crystal phases of TYMV, which double the number of distinct ordered 2D packing motifs of TYMV to four. Third, we illustrate how the icosahedral particle’s high symmetry and subtle asphericity can help enrich 2D self-assembly behavior. We propose a packing model for the newly found rhombic crystal that is consistent with the known anisotropy attributes of TYMV, and contrast this model from the packing in the EM-derived square crystal.

Methods

The 2D crystallization was induced as follows (see Experimental for details). The aqueous solution (10 mM citric acid) was set to pH ~ 3.8 (Debye length = 3 nm), slightly above the isoelectric point pI = 3.6 of TYMV (see ESI, Fig. S1^†), so that the net particle charge was negative yet small to limit the interparticle electrostatic repulsion. A lipid monolayer was formed from a binary mixture of cationic and neutral lipids at a fixed lipid density of 0.7 nm² per lipid (surface pressure 10–13 mN m⁻¹), such that the interface charge density was controlled by the lipid composition. As shown previously for CPMV²⁸ and below for TYMV, the combination of weakly charged viruses and a highly charged lipid interface induced 2D crystallization by promoting dense lateral packing. The assembled structure was characterized by in situ grazing-incidence small-angle X-ray scattering (GISAXS) and X-ray reflectivity (XR).^28,32 The nature of the observed 2D crystals was examined further with the aid of numerical analysis of 2D packing based on model TYMV-shaped particles.

Results

X-ray scattering

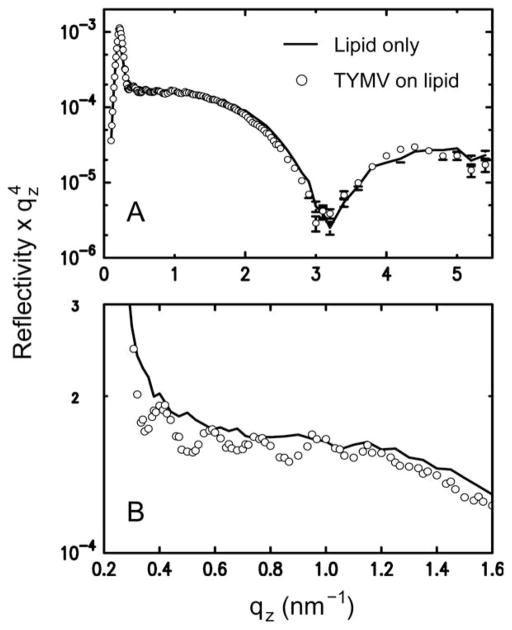
Fig. 2B summarizes the 2D assembly behavior of TYMV, derived from GISAXS measurements on stable structures. The 2D crystallization of TYMV is observed above a threshold cationic lipid fraction and only in a pH range just above the virus’ pI. As evident in Fig. 3 (and ESI, Fig. S2^†), the presence of 2D crystals gives rise to a series of sharp GISAXS peaks along q_xy, the surface-parallel component of the X-ray wavevector transfer. The broad intensity modulations of these peaks along q_z, the surface-normal component, arise from the form factor of TYMV, as in the case of CPMV.²⁸ Fig. 4 compares measured XR data from the lipid-coated interface without TYMV (solid lines) and with TYMV (circles). The latter data, obtained from the interface with TYMV crystals, exhibits intensity modulations at a period of Δq_z ≈ 0.2 nm⁻¹. The film thickness, 2π/Δq_z ≈ 30 nm, is therefore comparable to the TYMV diameter. These observations confirm the monolayer nature of the lipid-supported TYMV crystals. TYMV’s assembly behavior (Fig. 2B) and X-ray features noted above agree qualitatively with those for CPMV.²⁸

Fig. 3.

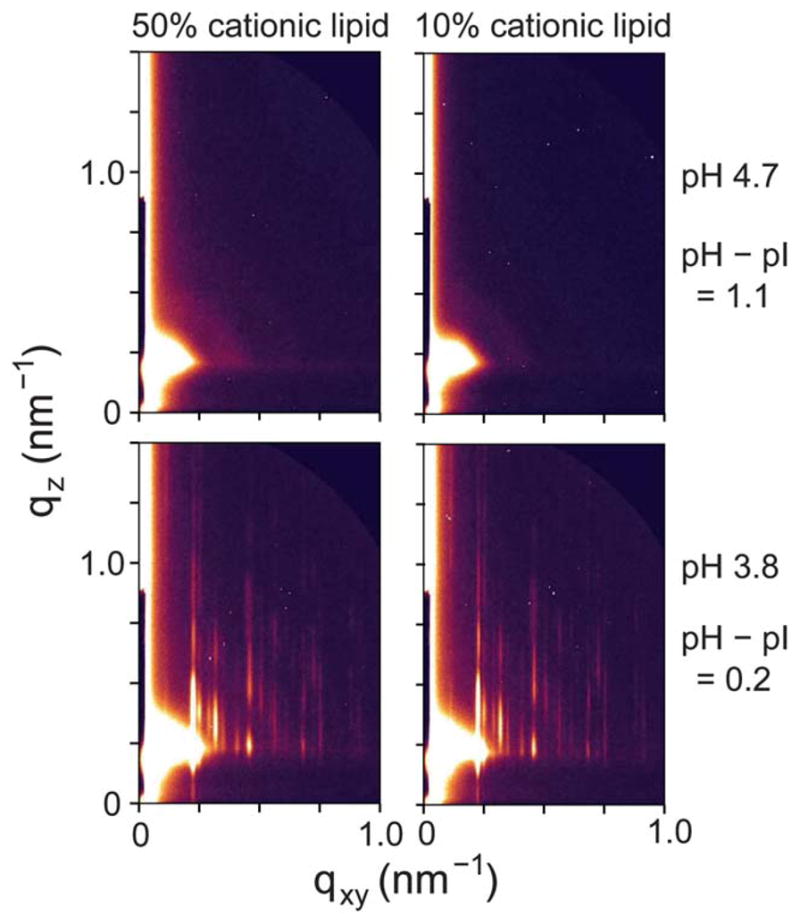
High-resolution GISAXS patterns measured at different values of the cationic lipid fraction and the solution pH (0.015 mg ml⁻¹ TYMV).

Fig. 4.

(A) Measured XR data from a lipid monolayer (10% cationic lipid) at the surface of a pH 3.9 solution (pH – pI = 0.3) without TYMV (line) and with TYMV (circles; 0.015 mg ml⁻¹), taken under the condition where 2D crystals were observed. (B) The same data sets over a smaller q_z range. In the presence of TYMV, the XR curve displays modulations at low q_z with a period of Δq_z ~ 0.2 nm⁻¹.

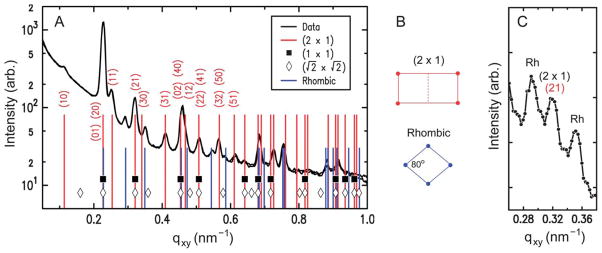
The lattice dimensions of the 2D crystals can be deduced from the GISAXS peak positions. Fig. 5A plots the q_xy-dependent profile of the GISAXS intensities. As indicated by the two sets of vertical lines, all of the observed peaks can be accounted for by coexistence of two 2D crystalline phases. The major component is consistent with a double-square (2 × 1) rectangular lattice with unit cell parameters a₁/2 = a₂ = 27.7 nm and γ = 90°. This phase, denoted hereafter as “rectangular,” exhibits intense peaks at the simple-square (1 × 1) positions, but it also displays clear (11), (31), and (51) peaks, which would be forbidden for the (1 × 1) and ( $\sqrt{2}\times \sqrt{2}$) lattices (filled squares and open diamonds in Fig. 5A). The near absence of the (10) and (30) peaks further implies that this rectangular phase is close-packed, consisting of 2 particles per (2 × 1) unit cell. The second component is a close-packed rhombic crystal with lattice parameters $a_1^{\prime }=a_2^{\prime }=28.0\text{nm}$ and γ′ = 80°. The rhombic crystal, with an area of S_Rh = 772 nm² per particle, is only slightly less dense (by 0.7%) than the rectangular crystal (S_rec = 767 nm² per particle). The q_xy widths of the observed peaks are resolution-limited, with the full-width-at-half-maximum of Δq_xy ~ 0.01 nm⁻¹ for the high-resolution GISAXS measurements (Fig. 5A). Thus, for each crystal phase, typical domain sizes are larger than the minimum coherence length³³ of 0.9 × 2π/Δq_xy ~ 600 nm, i.e., greater than ~20 times the virus diameter. These two crystal structures are distinct from the previously reported 2D assemblies of TYMV, i.e., hexagonal arrays^22,23,27 and the EM-based square crystal,^25–27 whose ( $\sqrt{2}\times \sqrt{2}$) unit cell contains 2 particles (Fig. 6B). They are also inconsistent with the lattice planes within the known 3D crystals of TYMV.^16,34,35

Fig. 5.

(A) Measured GISAXS intensity vs. q_xy (integrated over 0.2 ≤ q_z ≤ 0.6 nm⁻¹), obtained from 2D crystals of TYMV (pH 3.8, pH – pI = 0.2, cationic lipid fraction = 0.1, 0.015 mg ml⁻¹ TYMV). The tall vertical lines with indices represent the double-square (2 × 1) lattice (a₁/2 = a₂ = 27.7 nm, γ = 90°). The short vertical lines represent the rhombic lattice ( $a_1^{\prime }=a_2^{\prime }=28.0\text{nm}$, γ′ = 80°). The symbols indicate the positions that would be expected for simple square lattices with a = a₂ (filled squares) and $a=\sqrt{2}{a}_2$ (diamonds). (B) Unit cells for the (2 × 1) rectangular and rhombic lattices. (C) Measured GISAXS intensity vs. q_xy, obtained at a 3 times higher TYMV concentration (pH 3.8, pH – pI = 0.2, cationic lipid fraction = 0.5, 0.045 mg ml⁻¹ TYMV). The central peak is the (21) peak from the (2 × 1) rectangular lattice, and the adjacent “Rh” peaks are from the rhombic lattice.

Fig. 6.

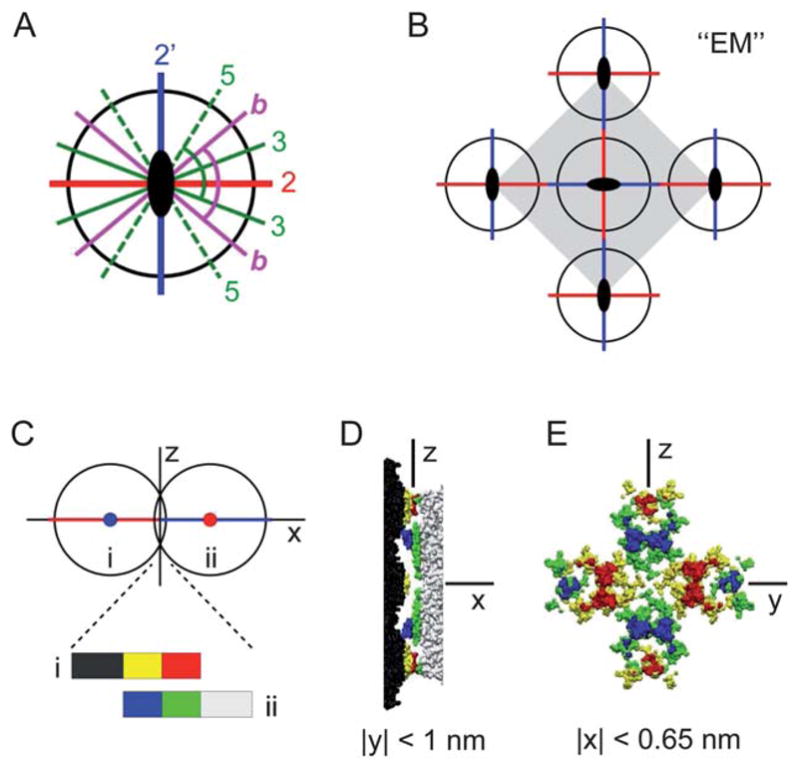
(A) The icosahedral symmetry axes in the equatorial plane normal to a 2-fold axis (out of page): two distinct 2-fold axes (“2” and “2′”), 3-fold axes (“3”), 5-fold axes (“5”), and the bisectors (“b”) between the adjacent 3- and 5-fold axes. The two indicated angles are both equal to 79.2° from symmetry. (B) The unit cell structure for the previously observed centered square crystal (“EM”).^25–27 (C)–(E) TYMV particles at the 2–2′ contact. (C) A side-view schematic defining the coordinate axes. (D) Side view and (E) contact-plane view of the two particles in the contact region, based on an interparticle spacing of 27.7 nm and the known TYMV structure.¹⁸

Coexistence of the two crystal forms has been verified by changes in the relative intensities of the corresponding GISAXS peaks. At a low TYMV concentration (0.015 mg ml⁻¹) and within the crystallization regime (Fig. 2B), the rectangular crystal is the predominant phase (Fig. 5A). However, the use of a higher TYMV concentration (0.045 mg ml⁻¹) is found to increase the relative peak intensities for the rhombic crystal (Fig. 5C). From the relative intensities of the (21) peak and the adjacent peak on each side, we estimate that the contribution of the rhombic phase to the crystalline area is ~25% or less at the TYMV concentration of 0.015 mg ml⁻¹ while it becomes comparable to the rectangular contribution at 0.045 mg ml⁻¹. Since fast adsorption tends to impede 2D ordering,^28,36 the rhombic crystal may be a metastable phase.

Although the atomic coordinates of TYMV are mostly known, direct GISAXS determination of the particle arrangements in the 2D crystals is hindered by limited q-range of the data, insensitivity of the TYMV form factor to particle asphericity at q < 0.7 nm⁻¹, and uncertainties in the form factor due to insufficient knowledge of the internal RNA and co-ion distributions. Nevertheless, qualitative GISAXS features provide insights to the peculiarity of the rectangular crystal. Let us assume that one of the basis particles resides at a corner of the (2 × 1) unit cell (as in Fig. 5B), representing half of the (1 × 1) lattice. Then, unlike in the EM-based square crystal, the second basis particle must deviate from the remaining (1 × 1) lattice points because of the clear (11) and (31) peaks (Fig. 5A). The second particle must also avoid the center of the (2 × 1) cell since the (21) and (32)/(50) peaks are present. Finally, the observed peaks can also be consistent with a square-symmetric (2 × 2) unit cell with a 4-particle basis, a possibility that cannot be ruled out at present. Detailed structural understanding of the rectangular phase requires further investigation.

Analysis of 2D arrays of model virus-shaped particles

To gain additional insight into the nature of the newly observed 2D crystals of TYMV, we numerically investigated the crystalline 2D packing of non-spherical particles that closely resembled TYMV in shape. According to the known atomic coordinates¹⁸ (also see ESI, Fig. S3D^†), the TYMV particle has the largest diameter of 32 nm along the 5-fold axis and the smallest diameter of 26 nm for the innermost exterior surfaces of the virus between knobs. Thus, the observed lattice constants a ≈ 28 nm for the 2D crystals indicate that the particles must come in close contact and the shape of the particle must play an important role in forming the observed 2D crystals. Therefore, in the following analysis, we take a simple approach in which we neglect the chemical and electrostatic heterogeneities of the TYMV surface and consider a series of ordered 2D arrays that are consistent with the particle size and shape. Details of the particle modeling and the simulations are provided in ESI.^† Here we briefly summarize the key results of these investigations.

The model particle (ESI, Fig. S3^†) consisted of one central spherical core combined with 12 and 20 spherical components to represent the pentagonal and hexagonal knobs, respectively, where the components were centered on the relevant icosahedral 5- and 3-fold axes. The core radius, the two component radii, and the two component-center distances were optimized to approximate the exterior surface of TYMV, which was derived from the known atomic coordinates. This model particle was then used to construct ordered 2D lattices with a fixed particle orientation relative to the lattice normal. For simplicity, we only considered the cases in which one of the following axes of the particles was aligned with the z-axis: 2-fold, 3-fold, 5-fold, or bisector axis, where the bisector was defined between adjacent 3- and 5-fold axes (Fig. 6A). These possibilities for the “vertical” particle orientation are physically reasonable since the tips of TYMV’s knobs tend to be anionic (Fig. 1E) and are therefore most likely to be attracted to the cationic lipid surface. Specifically, the 3- or 5-fold axis would be aligned with the z-axis for a single knob contact with the planar lipid monolayer, while the 2-fold or bisector axis would point along the z-axis for a 4-knob or 2-knob contact with the monolayer, respectively.

Two numerical approaches were used to generate ordered 2D lattices of the above model particle. For the first approach (ESI, Sec. IIID^†), a hard-core repulsion potential was used, and the densest 2D packing configurations were extracted numerically as a function of a₁, one of the two lattice constants, for a 1-particle unit cell; the other lattice constant a₂, the lattice angle γ, and the azimuthal particle orientation ϕ were varied to maximize the density. This approach is equivalent to the hypothetical case in which the 2D crystallization were driven solely by the lipid–TYMV attraction. The analysis shows that all the densest packing configurations thus generated display essentially hexagonal packing, with the corresponding area of S_min = 680 to 728 nm² per particle depending on the particle’s vertical orientation (ESI, Table I^†). In particular, the highest-density configuration (S_min = 680 nm² per particle) is obtained for the particle with its 3-fold axis aligned along the z-axis. These results indicate that the two newly observed 2D crystals (S ~ 770 nm² per particle) are substantially less dense than a crystalline 2D lattice of TYMV could be, based on its size and shape. This in turn suggests that the presence of local inter-particle interactions is essential to stabilizing the observed 2D crystals.

For the second approach (ESI, Sec. IIIE and F^†), a Morse potential, consisting of both a soft-core repulsion and a short-range attraction, was used for the core–core, core–knob, and knob–knob interactions. We emphasize that the Morse potential was used not to represent the actual interparticle interactions but to generate a series of ordered 2D lattices that are consistent with the shape and size of the TYMV particle. This potential was “homogeneous” in that it depended only on the distances between the exterior surfaces of the two interacting particles. As such, its anisotropic nature was solely due to the particle shape. The numerical minimization based on this potential generated global and local minimum-energy configurations for both 1- and 2-particle unit cells. Qualitatively, these configurations correspond to those that maximize the number of interparticle contacts. We find that none of the generated minimum-energy configurations are consistent with the observed rectangular crystal (ESI, Table III^†). On the other hand, the configuration that is most consistent with the observed rhombic crystal has an 1-particle unit cell with a₁ = a₂ = 28.0 nm, γ = 78.0°, and S = 765 nm² per particle (ESI, Table II^†). This configuration is obtained for the vertical orientation of the particle’s 3-fold axis (Fig. 7A) and displays an in-plane particle orientation in which one of the three equatorial 2-fold axes points toward the next-nearest-neighbor particles. These key features are captured in the packing model for the rhombic crystal shown in Fig. 7B. In the following section, we discuss the physical plausibility of this model.

Fig. 7.

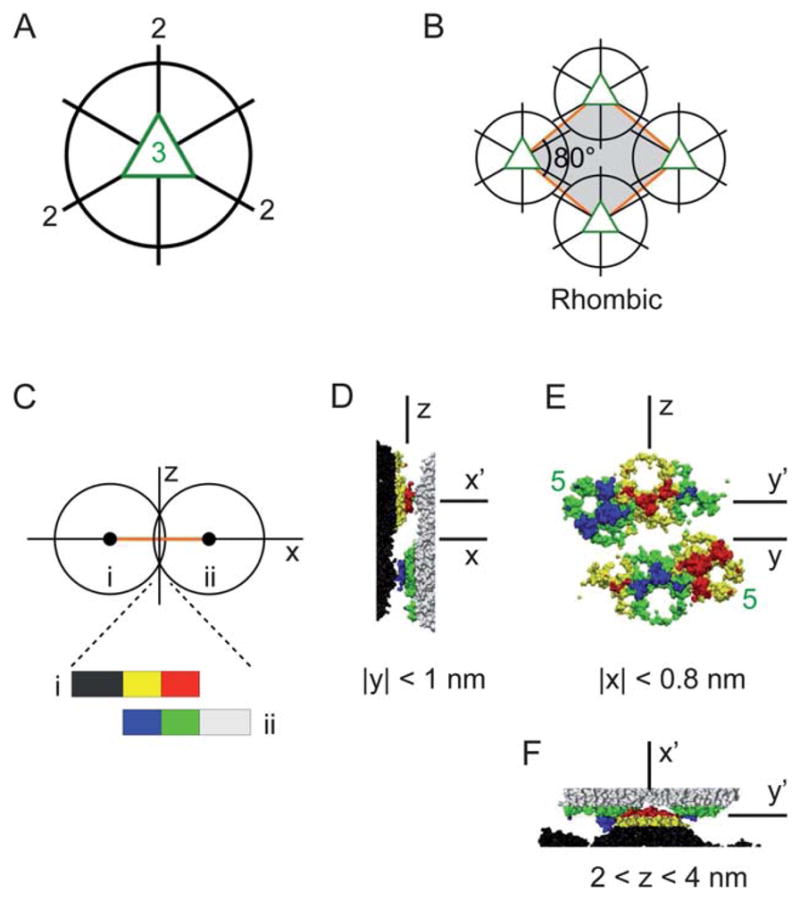
(A) Three icosahedral 2-fold axes lie in the equatorial plane normal to a 3-fold axis (out of page). (B) The unit cell structure of the proposed packing model for the rhombic crystal. (C)–(F) TYMV particles at the nearest-neighbor contact in the rhombic model. (C) A side-view schematic defining the coordinate axes. (D) Side view, (E) contact-plane view, and (F) top view of the two particles in the contact region, based on an interparticle spacing of 28.0 nm and the known TYMV structure.¹⁸ In (E), the pentagonal knobs are marked (“5”), and the hexagonal knobs are unmarked.

Discussion

General discussion

One of our objectives was to test the general applicability of the utilized 2D crystallization approach, which is based on promoting the electrostatically driven adsorption by means of weak particle charge and high interfacial charge density. We have previously applied this method to induce the 2D crystallization of CPMV.²⁸ The present results on TYMV support the method’s effectiveness as a general approach to 2D crystallization of charged nanoparticles.

Nevertheless, there is an important difference between the results of these two studies. In the case of CPMV, the same crystallization approach also yielded coexistence between two close-packed motifs.²⁸ One of them was a hexagonal lattice, which does not reflect particle anisotropy; the other was a centered rectangular lattice that resembled the densest lattice plane in the 3D crystals of CPMV, i.e., the (110) plane of the body-centered cubic lattice. By contrast, the two non-hexagonal 2D crystal phases discovered here for TYMV—the rectangular and rhombic crystals—are unique in that they both depend on the particle anisotropy and lack equivalent lattice planes in the known 3D crystals.^16,34,35 This suggests that the 2D confinement plays a vital role in inducing these phases.

Significantly, the two 2D crystal phases observed in the present study are distinct also from the previously reported hexagonal^22,23,27 and centered square^25–27 lattices of TYMV. The existence of these multiple 2D phases for TYMV illustrates that a rich variety of ordered packing motifs may be possible for icosahedral particles, even as a single-component system in 2D. This clearly follows from the icosahedral particle’s unique combination of high symmetry and subtle asphericity. However, the extent of structural diversity that such particles can exhibit has not attracted much attention.

A key result of the present study is that despite being close packed, the two newly observed 2D crystal phases are still substantially less dense than the densest possible lattice allowed by the size and shape of TYMV. The observed crystal densities (S_obs ~ 770 nm² per particle) are lower by 13% than the maximum possible density (S_min = 680 nm² per particle) obtained numerically for 2D lattices of model TYMV-shaped particles. This implies that the electrostatic lipid–virus attraction, which facilitates close packing by promoting interfacial adsorption, is nevertheless insufficient to direct the crystallization process. That is, the formation of the observed 2D crystals requires the presence of local anisotropic interparticle interactions.

The role of anisotropy in crystal formation can be scrutinized for the rhombic crystal, for which we have derived a model for the 2D packing arrangement (Fig. 7B). We note that this model is based on the numerical analysis in which the model particle captures only the shape of TYMV and the homogeneous (Morse) potential used to generate 2D lattices neglects TYMV’s chemical and electrostatic heterogeneities. Despite this simplification, the analysis provides a way to explore possible contact-optimizing configurations that are consistent with the particle shape and to identify those that may correspond to the experimentally observed crystals. Indeed, the proposed rhombic model is based on the configuration among the many generated that best satisfies the geometrical packing constraints imposed by the GISAXS-derived rhombic unit cell. Together with the known anisotropy attributes of TYMV, this model allows us to consider the possible role of anisotropy in stabilizing the rhombic crystal, as discussed further below.

Detailed understanding of the rectangular crystal is outside the scope of this work. Nevertheless, it is worth noting that none of the energy-minimum configurations generated in the numerical analysis is consistent with the GISAXS-derived rectangular unit cell. One possible reason for this is that the features neglected in the analysis, such as the chemical and electrostatic heterogeneities of TYMV or its fine structural details, play a prominent role in stabilizing the rectangular crystal. Another possibility, also not considered in the analysis, is that the crystal consists of a square (2 × 2) unit cell with a 4-particle basis, as noted earlier. One or both of these factors may need to be incorporated in the analysis to unravel the packing arrangement for this crystal.

Anisotropy effects in 2D crystals

We now turn to the discussion of the rhombic crystal model (Fig. 7B). A defining feature of this model is the alignment of the virus’ 2-fold axis along the minor diagonal of the rhombic unit cell. That is, the model preserves one of the particle’s 2-fold axes as a crystallographic 2-fold axis (in 3D space). This feature is consistent with what is expected of symmetry elements in molecular crystals, as follows. First, the rhombic lattice, with two unit cell vectors of equal length, implies the presence of a symmetry element along at least one of the two rhomb diagonals. For a virus crystal, this element can only be either a 2-fold or 2-fold screw axis since the virus is chiral and hence its crystal cannot exhibit a mirror or glide plane. Second, the vast knowledge of existing crystal structures has been used to establish certain general rules of crystal packing,^37,38 including frequently observed relationships between molecular and crystallographic symmetry elements. One such rule is that molecules possessing multiple 2-fold axes tend to preserve at least one of them within the crystal structure, as confirmed in more than 80% of the cases.³⁹ The proposed rhombic structure conforms with these expectations.

Another main feature of the rhombic model is the vertical, normal-to-lattice orientation of the particle’s 3-fold axis. To assess the physical plausibility of this orientation, it is useful to note that the protein shell or “capsid” of TYMV consists of 180 protein subunits with an identical amino-acid sequence, with 60 subunits forming 12 pentamers for the pentagonal knobs and 120 subunits contributing to 20 hexamers for the hexagonal knobs (Fig. 1A).^18,40 Thus, the part of the protein subunit that gives rise to the anionic knob tips (Fig. 1E), i.e., the region most likely to be attracted to the cationic lipid monolayer, should be identical whether it contributes to a hexagonal or pentagonal knob. This implies that the strength of the electrostatic interactions at the lipid–virus contact should scale roughly with the number of lipid-contacting subunits per particle. This number would be equal to: six subunits for the single hexagonal-knob contact along the 3-fold axis; about six in total for the 4-knob contact along the 2-fold axis (Fig. 1E inset); five for the single pentagonal-knob contact along the 5-fold axis; and about four in total for the 2-knob contact along the bisector axis. Therefore, among the four orientations considered, the vertical alignment of either the particle’s 3-fold or 2-fold axis should be favored by the electrostatic lipid–virus interactions. Our model is consistent with this expectation.

The particle shape also plays an important role in the interparticle packing in the rhombic model. This can be seen from the observation that the nearest-neighbor (NN) pair of particles present complementary shapes toward each other. Evidence for steric complementarity is provided in Fig. 7C–F, showing the topography of the two contacting particles in the rhombic model as derived from the atomic coordinates of TYMV.¹⁸ It can be seen that at each NN contact, one particle presents a set of three neighboring knobs toward the other particle. One of the three knobs is pentagonal, the other two are hexagonal, and all three extend beyond the mid-plane between the two particles. Close inspection shows that one of the hexagonal knobs from one particle docks between the apposing particle’s two knobs, one pentagonal and the other hexagonal. Each NN contact consists of two sets of such docking arrangements with opposite polarities.

To gain insight into the possible origin of this docking behavior, we consider the exterior surface heterogeneities of the TYMV particle. Fig. 1E shows that the knobs’ sloping sides tend to be cationic, while the “valley” region between a pair of adjacent knobs, corresponding to the innermost exterior surface of TYMV, tends to be anionic. For the rhombic model, this implies poor electrostatic complementarity at the interparticle contacts, since the docking puts the anionic knob tips from one particle near the anionic valleys on the other particle (Fig. 7D and E) and also brings the cationic knob sides from the two particles in close proximity (Fig. 7E and F). Thus, qualitatively, we expect the electrostatic contribution to the interparticle interaction potential to be repulsive at the NN contact. On the other hand, Fig. 1D shows that moderate concentrations of nonpolar residues reside on the knobs’ sloping sides, especially toward the top rims where the NN particles come in close contact (Fig. 7E and F). On the basis of these observations, we speculate that the interparticle contacts in the rhombic crystal originate primarily from local hydrophobic interactions. In the present experiment, the presence of short-range hydrophobic interactions^41,42 is qualitatively plausible since the 2D crystals were formed under close-packing conditions (pH ≈ pI) where the net particle charge is close to neutrality and the cationic and anionic contributions to TYMV’s surface charge were close to being balanced.

It is worth noting another model for the rhombic crystal that is guided by the particle symmetry rather than by the 2D packing constraints. In this alternative model, TYMV’s 2-fold axis is aligned normal to the lattice plane, leading to the electrostatically plausible 4-knob contact with the lipid surface (Fig. 1E). As shown schematically in Fig. 6A, the vertical alignment of an icosahedral 2-fold axis brings into the equatorial plane a pair of orthogonal and orientationally distinct 2-fold axes, labeled “2” and “2′,” and two each of the 3- and 5-fold axes, labeled “3” and “5,” respectively. Note that the symmetry-imposed angle of 79.2° between the indicated 3- and 5-fold axis in Fig. 6A agrees with the observed lattice angle of γ′ = 80° for the rhombic crystal. This raises the possibility that the two NN directions of the rhombic lattice are defined either asymmetrically by TYMV’s in-plane 3- and 5-fold axes or symmetrically by the equatorial bisectors (“b” in Fig. 6A). These possibilities appear appealing since the in-plane interparticle attraction could be understood to arise from local hydrophobic interactions between the equatorial knob tips (Fig. 1D). However, according to the atomic coordinates of TYMV,¹⁸ the corresponding NN distance upon interparticle contact would be about 30 nm for the 3–3 and b–b “bond” and about 32 nm for the 5–5 bond. These estimated distances are substantially greater than the observed distance of a′ = 28.0 nm and hence physically unattainable unless the particles could be deformed significantly at the knob tips. For this reason, the above symmetry-based model has been ruled out.

Finally, it is instructive to contrast the anisotropy effects in the rhombic model (Fig. 7B) with those in the EM-derived centered square crystal (Fig. 6). Although the formation mechanism of the EM square crystal remains uncertain,^25–27 it clearly results in the normal-to-lattice alignment of TYMV’s 2-fold axis and in-plane NN contacts along the equatorial 2-fold axes (Fig. 6B). Thus, the vertical particle orientation in the EM crystal differs from that in the rhombic model (3-fold axis along z). However, the two structures are similar in that the NN contacts exhibit substantial steric complementarity, which occurs at the 2–2′ bond for the ( $\sqrt{2}\times \sqrt{2}$) crystal. As evidence, Fig. 6C–E shows topography of the two particles at the 2–2′ contact, derived from the atomic coordinates of TYMV¹⁸ assuming a center-to-center spacing of 28 nm. Note that small portions of each particle’s 2 hexagonal and 2 pentagonal knobs penetrate beyond the 2–2′ bond’s mid-plane. The side and contact-plane views of these penetrating regions (Fig. 6D and E) demonstrate that the two particles present complementary shapes at the 2–2′ contact. Comparison with ψ_s in Fig. 1E further shows that the hexagonal knob’s anionic tip docks against the apposing pentagonal knob’s cationic side slope, with each 2–2′ bond forming 4 such docking pairs. These observations suggest that the 2–2′ bond may be partly stabilized by the local electrostatic complementarity. Moreover, the steric complementarity should also facilitate hydrophobic interactions by virtue of enhanced effective contact area. The presence of nonpolar residues on the sides of pentagonal knobs (Fig. 1D) suggests that their hydrophobic interactions with the apposing hexagonal tips may reinforce the 2–2′ bond. Thus, as far as the local NN interactions are concerned, the primary qualitative difference between the EM square crystal and the rhombic model appears to be in the sign of the electrostatic contribution.

Experimental

The wild-type turnip yellow mosaic virus (TYMV) was generated as previously reported.⁴⁰ The neutral lipid 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and the cationic lipid 1,2-dimyristoyl-3-trimethylammonium-propane (DMTAP) were purchased from Avanti Polar Lipids, Inc. All other chemicals were purchased from Sigma-Aldrich. Aqueous solutions were prepared using ultrapure water (Millipore; 18 MΩ cm).

All the experiments were performed at room temperature (23 to 25 °C), using the previously described sample cells and preparation procedures.^28,32 The Teflon cell or “trough” held 9–10 ml of aqueous subphase, had a surface area of 2540 mm², and was equipped with an injection port for injecting a virus solution into the subphase without disturbing the lipid-coated surface. Mechanical vibration of the liquid surface was reduced by immersing a Piranha-etched glass spacer (2″ × 1″ × 0.25″) such that the liquid was less than 0.5 mm thick over the X-ray illuminated region. The cell was enclosed in a sealed aluminium box filled with humidified helium to reduce background scattering and X-ray-induced oxidation.

The subphase contained 10 mM citric acid and its pH was adjusted with NaOH. An appropriate volume of a chloroform solution that contained the two lipids at known concentrations was spread at the interface to form a monolayer at a fixed molecular area of 0.7 nm² per lipid. Within 20 minutes the surface pressure stabilized in the range of 10–13 mN m⁻¹, consistent with the fluid-phase monolayer of double-tail lipids.⁴³ After the monolayer equilibrated, a concentrated solution of TYMV (1–2 mg ml⁻¹) was injected into the subphase through the injection port to initiate the 2D assembly. The final nominal concentration of dispersed TYMV was 0.015 mg ml⁻¹ for most of the samples, including those used to determine the phase behavior in Fig. 2. A higher TYMV concentration (0.045 mg ml⁻¹) was used for a few samples. Monitoring by GISAXS measurements (see below) indicated that the 2D crystallization was completed within ~24 h of injection, after which no change was observed in the GISAXS patterns. For one crystalline sample (pH 3.9, 20% DMTAP), the stability of the GISAXS pattern was ascertained up to 120 h. All the X-ray data presented herein are based on stable films.

The set-ups and data collection procedures for the X-ray measurements were similar to those described previously.^28,32 The interfacial assembly behavior of TYMV, summarized in Fig. 2, was determined by GISAXS and X-ray specular reflectivity measurements at Beamline X22B of the National Synchrotron Light Source (NSLS), using the Harvard-BNL liquid surface spectrometer operated at the X-ray wavelength of λ = 1.517 Å. The low-resolution GISAXS measurements at X22B utilized an area detector (Princeton Instruments) located 1 m from the sample center. The high-resolution GISAXS data, shown in Fig. 3 and 5A, were collected at NSLS Beamline X9 (λ = 0.918 Å). A microfocusing mirror was used to set the incident angle α close to the critical angle α_c = 0.091° for the water–vapor interface. The resulting incident angle spread was α = 0.07 ± 0.04°, the beam size was 0.3 mm (H) × 0.03 mm (V) at the sample, and the area detector (MarCCD 165) was located 5.1 m from the sample center. Additional GISAXS measurements at a high TYMV concentration (Fig. 5C) were carried out at Beamline 9ID-C of the Advanced Photon Source, using the liquid-surface spectrometer operated at λ = 1.550 Å and a Pilatus 100k detector (Dectris) located 0.7 m from the sample center.

Conclusions

The 2D assembly of TYMV on cationic lipid monolayers was studied by in situ X-ray scattering measurements at the aqueous solution–vapor interface. The results support the general applicability of the utilized 2D crystallization approach, which combines weak particle charge and high interfacial charge density to enhance the electrostatically induced adsorption.

This study has revealed two 2D crystal phases of TYMV that are distinct from the previously observed hexagonal and square arrays of TYMV.^{22,23,25–27} The structural diversity in the arrays of icosahedral particles, even as single-component 2D systems, suggests potential versatility of highly symmetric nanoparticles as building blocks for nanostructures. However, the coexistence behavior observed here for TYMV and previously for CPMV²⁸ highlights the need for exquisite manipulations of anisotropic interparticle interactions to control the nanostructures of highly symmetric particles. Icosahedral viruses are well suited to addressing this challenge since their exterior surface can be modified in a well targeted, site-specific manner by genetic or chemical methods.^44,45

For the newly observed rhombic crystal, a packing model has been derived with the aid of numerical analysis. Contrast between the rhombic model and the previously observed square crystal highlights how distinct combinations of TYMV’s multiple anisotropy attributes can generate different 2D packing structures. Each of these structures exhibits steric complementarity at the interparticle contact that suggests the presence of local hydrophobic interactions. However, the two crystals appear to differ in the electrostatic complementarity of the nearest-neighbor contact, which is good for the square crystal and poor for the rhombic model. While the critical role of these interactions in protein associations is well established,⁴⁶ our results illustrate their role in dictating the order that emerges in many-body assemblies.¹⁹ Resolving the structure of the newly found rectangular crystal remains a future challenge.