High Throughput Protein Nanocrystal Fractionation in a Microfluidic Sorter

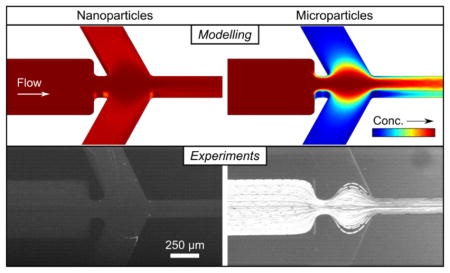
Abstract

Protein crystallography is transitioning into a new generation with the introduction of the X-ray free electron laser, which can be used to solve the structures of complex proteins via serial femtosecond crystallography. Sample characteristics play a critical role in successful implementation of this new technology, whereby a small, narrow protein crystal size distribution is desired to provide high quality diffraction data. To provide such a sample, we developed a microfluidic device that facilitates dielectrophoretic sorting of heterogeneous particle mixtures into various size fractions. The first generation device demonstrated great potential and success toward this endeavor; thus, in this work, we present a comprehensive optimization study to improve throughput and control over sorting outcomes. First, device geometry was designed considering a variety of criteria, and applied potentials were modeled to determine the scheme achieving the largest sorting efficiency for isolating nanoparticles from microparticles. Further, to investigate sorting efficiency within the nanoparticle regime, critical geometrical dimensions and input parameters were optimized to achieve high sorting efficiencies. Experiments revealed fractionation of nanobeads from microbeads in the optimized device with high sorting efficiencies, and protein crystals were sorted into submicrometer size fractions as desired for future serial femtosecond crystallography experiments.

Graphical Abstract

X-ray crystallography is the primary method of choice for protein structure determination and has been used for decades to solve more than 85,000 structures. While this method is powerful, there are biologically important classes of proteins that have eluded the traditional X-ray community, namely, difficult-to-crystallize membrane proteins and protein–protein complexes.^1–3 Out of the tens of thousands of protein structures deposited in the Protein Data Bank, less than 500 unique membrane protein structures have been solved to date,² largely due to the high degree of long-range disorder in their crystals often referred to as “mosaicity”.⁴ Furthermore, growing large, well-ordered single crystals of membrane proteins and large complexes for standard crystallography can take months or even decades. The recent advent of the X-ray free electron laser (XFEL) has allowed crystallographers to begin to uncover the structures of these complex proteins through serial femtosecond crystallography (SFX) experiments where smaller crystals can be utilized.^5,6 Submicrometer sized crystals also provide an added benefit since they contain only a few hundred or thousand unit cells, thus featuring minimal long-range disorder yielding better quality diffraction data for improved structure determination. Crystallization methods have been established to grow showers of small crystals, but these crystallization products are generally heterogeneous in size which can complicate SFX data analysis due to the necessary merging of tens of thousands of diffraction patterns from crystals of different sizes and orientations into a final product, the electron density map.^7,8

A further experimental challenge in SFX data collection is the small dynamic range of the X-ray detector, which is damaged by pixel overheating from strongly diffracting crystals larger than a few micrometers, requiring the XFEL beam to be heavily attenuated to protect the detector at the expense of data quality. Thus, having a less dispersed, submicrometer-sized crystal sample for SFX could reduce the number of diffraction patterns needed (thus reducing precious sample consumption and time at the XFEL), improve data quality (with an XFEL beam at full intensity), and simplify the process of data merging and indexing with more similar diffraction patterns.⁴

An effective way to obtain defined size homogeneity is to fractionate a bulk crystallization product to isolate smaller crystals for SFX. Ideally, such experiments should be automated, continuous, and not alter the sample. Traditionally, fractionation has been accomplished using common methods such as capillary electrophoresis,^9–11 chromatography,^12–14 and field flow fractionation (FFF);^15–18 however, several disadvantages arise such as stringent sample volume requirements or the sample needing specific inherent or additive chemical properties for the separation mechanism to work. With the rise of microfluidic technologies¹⁹ over the past decade, many traditional methodologies have been transferred to “labs-on-a-chip”^20–22 where in some cases greater experimental control and diversity can be accomplished. Due to the inherently small scale of such technologies, separation science has greatly benefitted, namely, in relation to biological applications. Examples of microfluidic separations have included proteins and DNA,^20,23 cells,^24–26 and magnetically functionalized particles,^27,28 and more recently, the use of dielectrophoresis (DEP) has been applied to separation-based particle manipulation. ^29,30 The latter has sparked great interest due to its applicability to a very broad spectrum of sample types in their native state without labels, specifically making it attractive for biological separations.

One requirement to invoke DEP is an inhomogeneous electric field under which gradients establish (∇E) that are directly proportional to the DEP force (F_DEP ∝ ∇E²). Such fields can be created by patterning electrodes within microchannels; however, fabricating electrodes this way can become arduous for more complex channel designs, and sample damage can result due to electrode fouling. Insulator-based DEP (iDEP) was introduced as an alternative in which creative microchannel designs are patterned in substrate materials (such as elastomers), deviating electric field lines to form DEP-inducing inhomogeneities.^31–35 This method follows all the aforementioned rules about maintaining sample integrity, while microfluidics provides a continuous and automated platform.

We previously developed a microfluidic method to sort nanoparticles from microparticles using iDEP with the goal of isolating protein nanocrystals for SFX.³⁶ The first generation device reported is presented in Figure 1a. As shown, this device contained a single inlet channel connected to a series of five outlet channels via a ∇E²-forming constricted channel region where negative iDEP (repulsion from high ∇E²) is induced. Briefly, the sorting mechanism is based on the correlation between F_DEP and particle size, whereby large particles repel from high ∇E² within the constriction and focus centrally in the device while small particles less influenced by DEP deflect away. The overall device length is ~5 mm, with a maximum reservoir diameter of 2 mm (dotted). Consequently, the possible throughput of this device is limited to a few μL/h with a reservoir capacity of 5–10 μL. For SFX, a minimum sample volume of ~300 μL is necessary; therefore, to prepare one sorted sample of adequate volume, at least 1 week was required. This is unfeasible, as such samples ideally should be prepared quickly for experimental progression and to ensure sample integrity.

Figure 1.

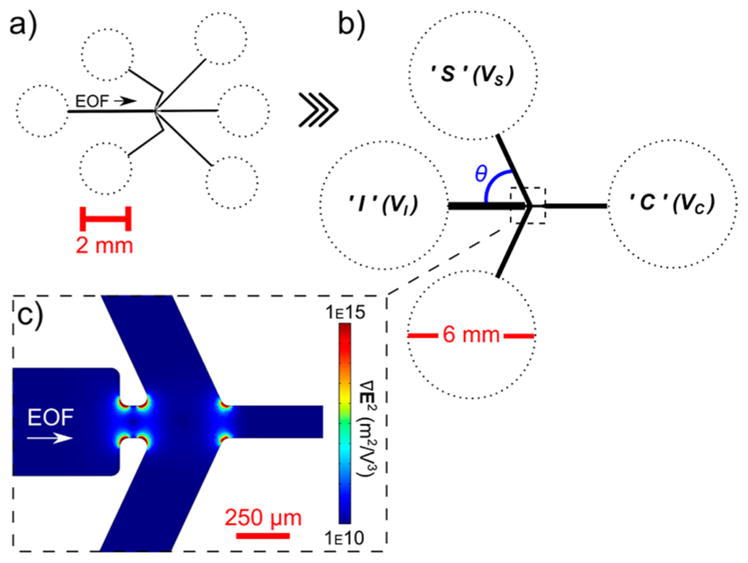
(a) Device schematic of the first generation microsorter with 2 mm reservoirs (dotted). The arrow indicates the fluid flow direction caused by EOF. (b) Schematic of the final device design for the second generation microsorter with 6 mm reservoirs (dotted). The location of the deflection angle (θ) is indicated in blue. (c) Zoom-in of the constriction region from (b) showing the computed ∇E² in the device exemplarily. A 4 order of magnitude increase in the maximum ∇E² occurs along the constricted channel walls compared to the pictured inlet region.

Here, we describe the development of a second generation microfluidic sorter based on the same sorting mechanism to achieve this goal in a more feasible timespan. The development process consisted of a numerical model to optimize a new design meeting various experimental requirements (discussed later). During this process, we determined several physical relationships between different controllable parameters allowing us to predict sorting outcomes from input variables. The theoretical study is based on nano- and microbeads with known migration properties since our previous study revealed that these parameters are suitable to predict photosystem I (PSI) nanocrystal sorting. After optimization with numerical modeling, fractionating two differently sized nanobeads from microbeads in the optimized device is demonstrated with high sorting efficiencies in addition to effectual sorting of submicrometer PSI protein crystal fractions allowing for their isolation from a bulk crystal suspension.

NUMERICAL MODELING

The theoretical study presented in this paper consisted of numerical modeling performed with the finite element analysis software COMSOL Multiphysics 4.4. Theoretical parameters were chosen to reflect experimental subjects (well understood polystyrene beads which show similar sorting behavior to PSI crystals³⁶). Two-dimensional device geometries were created with polylines and 40° fillets using AutoCAD software (Autodesk, USA) in the .dxf format. A detailed description of the various COMSOL modules used in the model is as follows.

Definitions and Geometry

Using the COMSOL Model Wizard, a blank 3D axisymmetric model was setup. The 2D AutoCAD-generated geometry was imported into COMSOL as a .dxf file with length unit μm. A work plane was created and the plane geometry was set as the imported file. The work plane was homogeneously extruded 100 μm in the z direction to form a three-dimensional structure. Settings were left as default unless otherwise specified, and parameters were set as global definitions.

Using the Materials Browser, liquid water was selected and applied to the entire geometry using room temperature values for viscosity and permittivity. Temperature (T) was set as 298 K, and electroosmotic flow (EOF) mobility (μ_EOF) equated 1.5 × 10⁸ m²/V·s.³⁷ Diffusion coefficients (D) were calculated for each particle diameter (d) using the Stokes–Einstein equation:

$$D=\frac{k_{\mathrm{B}}T}{3\pi \eta d}$$ (1)

where k_B is the Boltzmann constant and η is viscosity (8.9 × 10⁻⁴ Pa·s for water at 298 K). The DEP mobility (μ_DEP) was calculated for a spherical particle at each diameter as follows:³⁶

$${\mu }_{\text{DEP}}=\frac{d^2{f}_{\text{CM}}{\epsilon }_{\mathrm{m}}}{12\eta }$$ (2)

where ε_m is the medium permittivity (7.1 × 10⁻¹⁰ s⁴·A²/m³·kg for water). The Clausius-Mossotti factor ( f _CM) was assumed to be −0.5 (DC conditions and negligible particle conductivity with respect to medium conductivity).^36,38 Values of D and μ_DEP for each particle size examined can be found in Table 1.

Table 1.

Calculated Diffusion Coefficients and DEP Mobilities for All Particle Sizes Studied

d (nm)	D (m2/s)	μDEP (m4/V2·s)
100	4.90 × 10−12	−3.32 × 10−22
250	1.96 × 10−12	−2.08 × 10−21
500	9.81 × 10−13	−8.31 × 10−21
750	6.54 × 10−13	−1.87 × 10−20
1000	4.90 × 10−13	−3.32 × 10−20
2500	1.96 × 10−13	−2.08 × 10−19

Electric Currents (Electric Field Generation)

This module was used to generate the electric field within the device in accordance with Laplace’s equation. A current conservation equation is established here, whereby the current flux (J_Q) is defined as follows: J_Q ~ σ_mE, where σ_m is the medium conductivity. For physical channel boundary conditions, the channel walls were set to an insulating condition (J_Q = 0) and potentials were independently applied to the inlet (“I”), side outlet (“S”), and center outlet (“C”) channel extents.

Transport of Diluted Species

To model the particle transport through the microfluidic device, convection and diffusion mechanisms were applied to a single species in the transport of diluted species module:

$$\mathbf{J}=-D\nabla c+\mathbf{u}c$$ (3)

where J is the total flux, c is concentration, and u is the convective velocity field. u along the x axis (and similarly the y axis) was equated to

$$\mathbf{u}=\left[\frac{\mathrm{d}}{\mathrm{d}x}({E_x}^2+{E_y}^2)\times {\mu }_{\text{DEP}}\right]+{\mathbf{u}}_{\text{EOF}}$$ (4)

where E is the electric field along the corresponding axis and u_EOF is bulk velocity due to electroosmosis. Properties of the microfluidic device boundaries were also established, whereby a “no flux” (J = 0) boundary condition was setup along the channel walls. A relative particle concentration of 1 was set at the inlet (“I”) channel entrance. The end position of each outlet channel was set to an outflow condition (–D∇c = 0). Combining these particle and channel conditions, eq 3 was solved at steady state to obtain concentration distributions in the sorting device.

Creeping Flow (Bulk Fluid Transport)

To establish medium fluid transport, creeping flow was applied within the channels using incompressible flow neglecting inertial terms. At all channel ends, an open boundary condition was set. Bulk fluid properties were setup as previously described in the Definitions and Geometry section and set to remain constant. The in-channel velocity field was established according to the Navier Stoke’s equations obeying a no-flow condition at the channel walls. For an EOF-driven velocity (u_EOF) profile, this simplifies to the Helmholtz-Smoluchowski relationship (u_EOF = μ_EOFE), where the previously stated EOF mobility and solved electric field were applied.

Mesh, Study, and Results

The virtual mesh was built using the default setting for “physics controlled” using a “normal” element size. A study was setup as stationary to solve for all defined physics. The solver was set to a relative tolerance of 0.001 using the “MUMPS” solver type with default parameters. Surface plots were generated for species concentration distribution, fluid velocity, electric field, and ∇E². For the figures, surface plots were exported using the snapshot export function to 300 dpi resolution using a defined locked camera view for all models.

Data Analysis

To calculate sorting efficiency, concentration values were taken from the ends of each side channel outlet. A cutline was drawn spanning the entire channel end domain and >100 values were recorded along this line and averaged to determine the final side channel concentration. Both side channel means were then averaged to produce a final concentration value. To produce the ∇E² vs position plot, an interval-defined cutline was drawn as shown in Figure 3 and 30 values at the same x-axis locations for both constriction geometries were polled and exported. All final plots shown in the figures were created using Origin Pro software (OriginLab, USA).

Figure 3.

Experimental results of polystyrene bead sorting. (a) Fluorescence microscopy image overlay (100 frames) of 500 nm and 2.5 μm bead sorting showing the microbeads (thick lines) focusing into “C” while the nanobeads (thin lines) deflect into “S” at the model-optimized potential scheme (V_I = +200 V, V_S = −155 V, V_C = −750 V). (b) Fluorescence microscopy image overlay (100 frames) of 2.5 μm beads focusing into “C” while (c) shows 200 nm beads deflecting into “S” under lower applied potentials (V_I = +200 V, V_S = −155 V, V_C = −250 V). (d) Calculated Σ for both sorting events indicating high levels of sorting (>90%) in both cases.

EXPERIMENTAL METHODS

Device Fabrication

The microfluidic devices employed were fabricated with poly(dimethylsiloxane) (PDMS) using standard photolithography and soft lithography techniques.³⁶ Briefly, a silicon master wafer was patterned using SU-8 photoresist from a photomask containing the microchannel designs. Uncured PDMS/cross-linker was poured on the wafer and baked at 80 °C for 4 h to polymerize. The resulting PDMS slab was then irreversibly sealed to a glass slide using oxygen plasma treatment to create a closed channel system. Six mm diameter reservoirs were punched into channel ends to provide platinum electrodes access to the solutions in the channels. A high voltage source (HVS448, Labsmith, USA) controlled by Sequence software (Labsmith, USA) was connected to the electrodes to supply potentials to each reservoir, and a negative pressure pump (MFCS-EZ, Fluigent, France) was used to maintain even solution levels between the outlets and inlet reservoirs to reduce hydrodynamic pressure differences. 60 μL of each sample analyte suspension was added to the inlet reservoir prior to each experiment.

Sample Preparation and Data Analysis

Fluorescent polystyrene beads (Spherotech, USA) were suspended in 1 mM Pluronic F108 in water to reduce aggregation and adsorption to channel walls. The 200 nm (λ Ex: 470 nm; λ Em: 480 nm) and 500 nm (λ Ex: 590 nm; λ Em: 620 nm) beads were diluted 1:1000, and the 2.5 μm beads (λ Ex: 620 nm; λ Em: 650 nm) were diluted 1:500. PSI crystals were prepared as described previously.³⁹ Imaging was performed using a fluorescence microscope (IX71, Olympus, USA) with excitation, emission, and dichroic filters (Semrock, USA) suitable for each fluorophore incorporated in the beads and PSI crystal autofluorescence. For the 200 nm/2.5 μm bead sorting experiments, an optical beamsplitter (Optosplit, Cairn Research, UK) was used due to their widely different fluorescence characteristics allowing simultaneous imaging on spatially distinct regions of a sensitive camera. A CCD camera (iXon, Andor, UK) captured frames using Micro-Manager software (ver. 1.4, UCSF, USA) which were analyzed using ImageJ software (ver. 1.49, NIH, USA).

To determine sorting efficiency in the bead experiments, concentrations were quantified by particle counting of the microbeads and measuring average fluorescence intensities of the nanobeads spanning the visible “S” channel area since they are below the optical resolution limit of the microscope. PSI crystal size characterization was performed using dynamic light scattering (SpectroSize 302, Molecular Dimensions, UK) of an extracted “S” outlet reservoir solution by taking 10 measurements lasting 20 s each.

RESULTS AND DISCUSSION

Second Generation Device Design Process

The process to determine a device design for this second iteration of the microfluidic sorter (Figure 1b) entailed several criteria: (1) increase throughput, (2) increase channel and reservoir volume capacities, (3) reduce experimental complexity, and (4) minimize overall device size. To increase volume throughput, the original device was upscaled 5-fold in channel width and 10-fold in channel height. In early development of the first sorter, we envisioned collecting more than two fractions in different sets of outlet channels (hence having five); however, it was deemed unnecessary as we learned the device could be tuned to one desired size fraction and more of that single fraction could be attained by eliminating a third fraction. Furthermore, controlling the applied potentials in four reservoirs versus six reduces experimental complexity and equipment needs. As such, the number of outlet channels was reduced from five to three (two sides and one center), and the width of each of the side channels (where the desired fraction is usually collected) is double that of the center outlet channel to increase recovery. Lastly, to reduce the needed applied potentials, we shortened the channel lengths to the minimum length that would allow for a 6 mm reservoir (dotted) with a >100 μL solution capacity, a >25× increase over the first version. Figure 1b summarizes the geometry based on these improvements.

Upscaling included the constriction region which was boosted from 30 to 150 μm (Figure 1c). The increase in device dimensions allows for sorting larger volumes of sample in shorter time frames, yet since the ratio between the inlet channel and constriction widths was maintained, similar iDEP sorting properties were expected. Figure 1c shows the computed ∇E² within the constriction region, where high values (up to 10¹⁶) are found at the entrance and exit corners of the constriction (model details can be found in the Numerical Modeling section, and the applied potentials are discussed later). In that area, ∇E² increases up to 4 orders of magnitude from the inlet region shown, leading to iDEP comparable to but slightly higher in generated forces than the first generation design for similar particle sizes.

As shown in Figure 1b,c, the angle of the side channel with respect to the inlet channel (θ) was chosen to be 65°. Since two of the outlet channels were removed, we investigated which θ values between 65° and 135° could accommodate large reservoirs and provided the best sorting results (see the next section for optimized sorting input parameters). We selected particles with diameters of 500 nm and 2.5 μm, as these represent sizes relevant to our application of protein crystal fractionation to isolate nanoparticles/crystals from microparticles/crystals. We employed DEP parameters for polystyrene particles exhibiting negative DEP and scaled the DEP mobility with the size of the particles, as previously shown to provide a suitable model for crystal sorting in similar size ranges and with similar DEP characteristics.³⁶ From the calculated concentration distributions, sorting efficiencies were developed to gauge an effective sorting event. We defined the sorting efficiency (Σ) as follows:

$$\mathrm{\sum }=\left[1-\left(\frac{{\mathrm{C}}_{\mathrm{S},\text{large}}}{{\mathrm{C}}_{\mathrm{S},\text{small}}}\right)\right]\times 100$$ (5)

where C_S is the normalized side channel (“S”) concentration. A sorting condition is defined when the normalized concentration of the smaller particle (C_S,small) is greater than that of the larger particle (C_S,large). Instances where C_S,small < C_S,large were not considered. In all cases, the center outlet (“C”) channel normalized concentration was 1. Further details on how concentration values were sampled can be found in the Numerical Modeling section.

To find a suitable baseline potential scheme, two criteria were employed: (1) a target sorting efficiency of ≥90%, as this is generally considered acceptable in separation applications, ^40–43 namely, crystal sorting for SFX, and (2) a flow rate 2 orders of magnitude larger than the first generation device (≥75 μL/h) to reduce sorting time to hours. To accurately calculate the flow rate within the device, 3D modeling was performed (details in the Numerical Modeling section). A baseline inlet (V_I) and center outlet (V_C) voltage were established (V_I = +200 V, V_C = −750 V) to achieve flow rates ≥ 75 μL/h and side outlet voltage (V_S) was varied to achieve a maximum Σ for each given θ, as shown in Table 2.

Table 2.

Various Geometry Angles Tested and Their Corresponding Side Voltages Needed To Achieve the Maximum Sorting Efficiencies Listed

θ (°)	VS (V)	Σ (%)
65	−155	91.6
90	−160	90.2
115	−170	82.7
135	−190	72.9

At the voltage schemes selected, the flow rate did not vary considerably. Two significant trends were observed: as θ increased, V_S increased by as much as 35 V and Σ decreased by 20%. For larger θ, increasing V_S to boost E was necessary to achieve a nonzero Σ because the corner sharpness between the constriction and side channel decreased, reducing the values of ∇E² found in that region. However, in these types of microfluidic devices applied to biological systems, the lowest possible electric field is desired to avoid sample damage. Consequently, the minimal possible θ of 65° to fit large reservoirs was selected as the optimal configuration for low electric fields and high sorting efficiencies. All further studies presented in this Article are based on this geometry.

Sorting Voltage Threshold Study

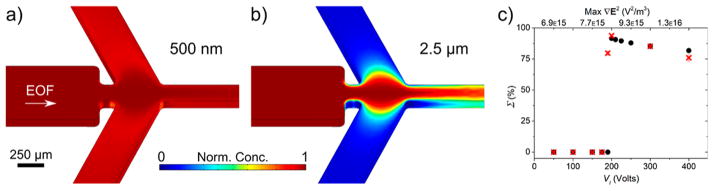
Next, we investigated optimized sorting schemes dependent on applied potentials, both with our numerical model and experimentally with polystyrene beads. Representatively, calculated concentration profiles for sorting 500 nm particles from 2.5 μm particles (V_I = +200 V, V_S = −155 V, V_C = −750 V) are shown in Figure 2a,b, respectively (profiles for θ = 90°, 115°, and 135° are provided in Supporting Information Figure S-1). Figure 2a shows 500 nm particles deflecting into the side channels with a C_S,small > 0.9, and Figure 2b shows 2.5 μm particles mainly focusing into the center of the device with a C_S,large < 0.1, leading to a Σ of 91.6%. During optimization of this potential scheme, we noticed a voltage threshold that occurred at the transition between DEP sorting and complete focusing due to “I”/”C” channel dominance by EOF. To investigate this effect further, we modeled varying V_I between +50 and +400 V (V_C = −155 V and V_S = −750 V) to examine how voltage and maximum ∇E² influence Σ, as represented by black circles in Figure 2c.

Figure 2.

(a) Concentration profile of 500 nm particles deflecting at the baseline voltage scheme (V_I = +200 V, V_S = −155 V, V_C = −750 V). (b) Concentration profile of 2.5 μm particles focusing at the same potentials. Color bar indicates normalized concentration values. (c) Threshold plot comparing variations in V_I to sorting efficiency (V_S = −155 V, V_C = −750 V). From the model (black circles), a maximum efficiency is apparent at +200 V. A similar threshold was also observed experimentally (red symbols).

A sharp transition is apparent (within ~5 V) after which bulk flow induced through EOF dominates the system when V_I < +200 V. This is supported experimentally (red symbols in Figure 2c) in which a similar behavior was observed when V_I ~ +190 V for sorting a mixture of 500 nm and 2.5 μm beads by varying V_I within a similar range. We attribute this to the fact that the inlet potential is effectively “pushing” the bulk fluid toward the outlets without discriminating between the sides or center. EOF into the side channels is dependent on the potential drop established between potential acting in the intersection and V_I and V_S. When V_I is too low, this potential drop is too small to support EOF into the side channels; thus, particles of all sizes are mainly transported into the center channel. Conversely, when V_I becomes too large (beyond the transition), more particles than necessary are pushed into the side outlet by EOF, thus decreasing Σ in a linear fashion. As expected, increasing V_I increases the maximum realized ∇E² which one might expect would improve the DEP sorting effect monotonically; however, we show here that other significant physics such as geometric distribution of the electric field and EOF also play a role in governing Σ and are equally important to explain the sharp transition in sorting efficiency.

To further confirm whether high sorting efficiencies are apparent at the optimal potential scheme established from the model (V_I = +200 V, V_S = −155 V, V_C = −750 V), two polystyrene bead pairs were tested experimentally. Figure 3a shows a fluorescence microscopy image overlay (100 frames) of the constriction region to enhance the particle trajectories during a sorting event for 500 nm and 2.5 μm bead sorting. The microparticles represented by the thicker lines focus into “C” (along the dotted yellow arrow) while nanoparticles (thin lines) deflect into “S” (along the dashed blue arrows), as expected, leading to a high Σ of 93.8 ± 0.4%. For further comparison, a second particle size pair was tested in the device using a slightly smaller nanoparticle (200 nm) and the same microparticle (2.5 μm). It was observed in this case that the potential scheme needed to drive sorting was lower than before (V_I = +200 V, V_S = −155 V, V_C = −250 V), likely due to the greater difference in particle size requiring lower ∇E² values for sorting. Figure 3b,c shows fluorescence microscopy image overlays (100 frames) of the 2.5 μm particles focusing and 200 nm particles (bulk fluorescence) deflecting, respectively, which were recorded simultaneously. Image frames were split using an optical beamsplitter due to differing fluorescence properties of the beads. A similarly high Σ of 94.8 ± 0.8% was calculated for this particle pair, which is shown in Figure 3d alongside Σ for the 500 nm/2.5 μm sorting event. Videos showcasing both sorting experiments can be found in the Supporting Information.

To study our application of interest whether protein crystals could be sorted using this optimized device, we applied a PSI crystal sample with a heterogeneous size distribution of ~200 nm to ~20 μm, as characterized by dynamic light scattering (DLS) in Figure 4a. Figure 4b shows a fluorescence microscopy snapshot of the sorting event (V_I = +50 V, V_S = −150 V, V_C = −100 V) illustrating large crystals centrally focusing in the device while smaller crystals deflect (bulk fluorescence indicates small nanocrystals and a few large nanocrystals and small microcrystals can be resolved). Interestingly, lower overall potentials were required for sorting, likely due to an electrophoretic component from the charged protein. Because of the more continuous size distribution, a similar quantitative analysis, as in the bead case, cannot be applied. Therefore, we again employed DLS to measure the size distribution of the deflected “S” fraction after recovery of the reservoir volume. Figure 4c shows a DLS signal heat map of this fraction indicating a submicrometer size distribution is attained as desired, with a major contribution lying between ~400 and ~800 nm. Some microcrystals are also detected, which is expected as the sorting efficiency is expected to be around 90% as previously observed in the bead experiments. As these sorted crystals were extracted for DLS measurement, they can also be directly loaded into a sample injector⁴ and delivered to the XFEL beam for SFX experimentation.

Figure 4.

PSI crystal sorting in the optimized design (V_I: +50 V, V_S: −150 V, V_C: −100 V). (a) DLS signal heat map illustrating the broad size distribution (~200 nm to ~20 μm) of a bulk PSI crystal suspension. (b) Fluorescence microscopy image of PSI crystals being sorted in the device where large crystals are focusing and small crystals deflect into “S”. (c) DLS signal heat map of the “S” fraction showing a submicrometer size distribution is isolated from the bulk.

Effect of Constriction Width

A main requirement of iDEP is the appearance of high ∇E² regions, which in our device is accomplished by converging the electric field from the inlet into a constriction region. The ratio between these widths was 3.3:1 in the first generation device and was maintained during upscaling. Because the device volume expanded, the applied potentials also increased accordingly to maintain similar ∇E² generation and thus DEP sorting effects. In the previous micro/nanosorting example, this increase was reasonable for biological applications. However, for smaller samples with smaller DEP mobilities (i.e., within the nanoregime) where ∇E² needs to be much higher for a DEP effect to be realized, alternatives to increasing voltage need to be considered.

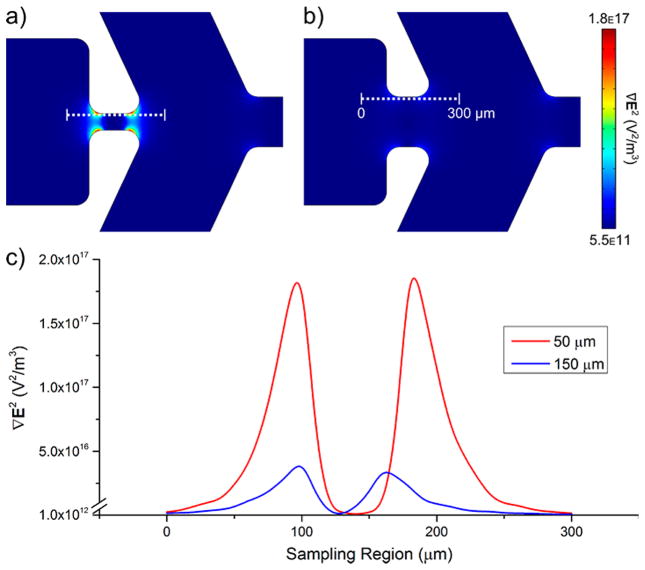
One way to do this is to increase the width ratio between inlet and constriction. Figure 5a,b illustrates one example where we reduced the constriction width by a factor of 3 from 150 to 50 μm (10:1 inlet width/constriction width) and modeled ∇E² in that area using the optimized sorting potentials discussed in the previous section. A cutline was drawn spanning 300 μm along the constriction wall, with corresponding ∇E² values given in Figure 5c. A significant difference arises between the two constriction types with a nearly 1 order of magnitude increase in ∇E² for the 50 μm constriction versus the 150 μm constriction, leading to a 6.5-fold increase in magnitude between the pictured inlet and constriction in Figure 5a. Additionally, the region of higher ∇E² values broadens (peak area increases) and a greater displacement between the two peak maxima occurs (60 to 80 μm) because the corner connecting the right constriction edge and side outlet shifts inward, leading to a slight lengthening of the constriction channel. Combined, these effects increase F_DEP to improve sorting.

Figure 5.

Comparison of two constriction widths. (a,b) Models of ∇E² for the 50 and 150 μm constriction designs, respectively. (c) Plot of ∇E² sampled from the dotted lines in (a) and (b) showing a significant difference in maximum values nearing 1 order of magnitude.

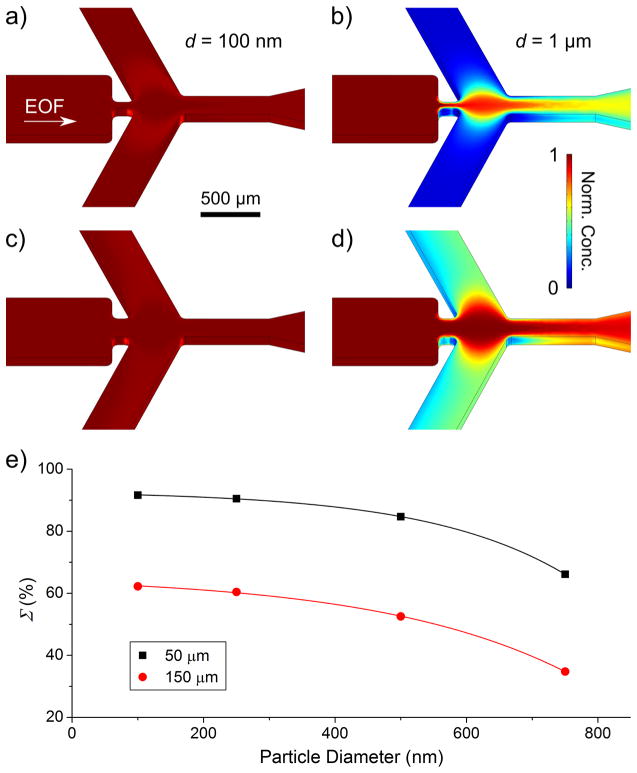
To examine the improvement in sorting, we tested whether 1 μm particles could be sorted from 100 nm particles with the 50 μm wide constriction. A potential scheme was developed to achieve a Σ of 92% (V_I = +600 V; V_S = −585 V; V_C = −2250 V) and resulting concentration profiles are shown in Figure 6a,b for 100 nm and 1 μm particles, respectively. It should be noted that, while potentials still had to be increased to achieve this level of sorting, the electric field remains nondestructive in magnitude for proteins.⁴⁴ Furthermore, this voltage increase was still 2.5 times less than that required to achieve a Σ > 90% for sorting 100 nm from 1 μm particles using the larger 150 μm constriction device. At the potential scheme yielding a Σ > 90% with the 50 μm constriction, the 150 μm constriction (Figure 6c,d) showed significant deflection of 1 μm particles and Σ declined to 62%. For both constrictions, we also examined sorting four intermediate particles sizes with respect to the 1 μm particles to study resolution (concentration profiles for 250, 500, and 750 nm are shown in Supporting Information Figure S-2). Figure 4e presents the calculated Σ for each particle sorting pair using the same potential scheme. As indicated, an acceptable Σ > 90% is obtained for 100 and 250 nm particles; however, it declines to 85% and 66% for 500 and 750 nm particles, respectively, indicating smaller differences in DEP mobility would need to be addressed with other geometries. Σ of these intermediate particle sizes was also calculated for the 150 μm constriction whereby no particles had an acceptable value as expected (maximum was 62% for 100 nm particles down to 35% for 750 nm particles). In both cases, the relationship between Σ and particle size could be fit exponentially (R² = 0.99), indicating that the degree of sorting between two particle sizes can be predicted for a given voltage scheme and device geometry. Note that the Supporting Information (Figure S-3) further discusses trends between V_I and V_S for both micro/nanosorting and nanosorting, which can also be studied with this model.

Figure 6.

Comparison of the nanoparticle sorting ability for both constriction widths. Concentration profiles showing (a) 100 nm particles deflecting and (b) 1 μm particles focusing in the 50 μm constriction under the same applied potentials (V_I = +600 V; V_S = −585 V; V_C = −2250 V). Under the same scheme, (c) and (d) show concentration profiles of each particle size in the 150 μm constriction. Through this wider constriction, the 1 μm particles exhibit a greater deflected concentration. (e) Shows the sorting efficiencies of various particles sizes with respect to the 1 μm particles. In the 50 μm constriction, 100 and 250 nm particles give acceptable sorting efficiencies (Σ > 90%), whereas in the 150 μm constriction, no particles sizes are sorted efficiently (Σ < 90%).

CONCLUSION

We have presented a detailed optimization strategy and procedure to develop a high throughput microfluidic sorter based on iDEP. Initially, several aspects of the second generation geometric design were finalized including channel width and length, angles between channels, and reservoir size. Physical limitations (i.e., reservoir crowding) were first considered, then a calculated sorting efficiency was used to optimize specific geometric parameters by testing the sorting mechanism at a baseline potential scheme. Voltage thresholds to give the best sorting result were presented, whereby the importance of voltage tuning was demonstrated to achieve the highest efficiency. The optimized design exhibited high theoretical and experimental sorting efficiencies of 91.6% and 93.8%, respectively, to sort 500 nm particles from 2.5 μm particles at the discovered optimal potential scheme. The possibility to sort smaller particles (100 nm from 1 μm) was also discussed, which can be accomplished with changes in geometry (constriction width) and further tuning of applied potentials. Lastly, it was shown that the optimized sorter can also be applied for isolating submicrometer fractions of PSI crystals, allowing us to provide an ideal sample for efficient and high quality SFX experimentation, noting that sample injection for SFX at XFELs is constantly improving toward accommodating sample volumes that the high throughput sorter is capable of processing in an hour. Furthermore, using the described methodology, we envision size fractionation of other impactful samples such as natural or artificial DNA or carbon nanotubes, which could also be investigated by similar theoretical and experimental processes covered in this study.