Quantity Versus Quality: A Survey Experiment to Improve the Network Scale-up Method

Abstract

The network scale-up method is a promising technique that uses sampled social network data to estimate the sizes of epidemiologically important hidden populations, such as sex workers and people who inject illicit drugs. Although previous scale-up research has focused exclusively on networks of acquaintances, we show that the type of personal network about which survey respondents are asked to report is a potentially crucial parameter that researchers are free to vary. This generalization leads to a method that is more flexible and potentially more accurate. In 2011, we conducted a large, nationally representative survey experiment in Rwanda that randomized respondents to report about one of 2 different personal networks. Our results showed that asking respondents for less information can, somewhat surprisingly, produce more accurate size estimates. We also estimated the sizes of 4 key populations at risk for human immunodeficiency virus infection in Rwanda. Our estimates were higher than earlier estimates from Rwanda but lower than international benchmarks. Finally, in this article we develop a new sensitivity analysis framework and use it to assess the possible biases in our estimates. Our design can be customized and extended for other settings, enabling researchers to continue to improve the network scale-up method.

Many important problems in science and policy require estimates of the sizes of hidden populations. For example, in order to respond to the human immunodeficiency virus (HIV)/acquired immunodeficiency syndrome (AIDS) epidemic, scientists and policy-makers need information about the sizes of key populations at risk for the disease: men who have sex with men, female sex workers, male clients of female sex workers, and people who inject illicit drugs (1). These size estimates are critical to designing HIV services, evaluating the outcomes of HIV-related interventions, and predicting the future course of the HIV/AIDS epidemic (1–3).

Unfortunately, traditional survey techniques are not well-suited to making accurate size estimates for hidden populations (2, 4). One promising alternative is the network scale-up method, which is based on the idea that ordinary people have embedded within their personal networks information that can be used to estimate the sizes of hidden populations, if that information can be properly collected, aggregated, and adjusted (4–6). The network scale-up method has many advantages over other population size estimation procedures, as has been described in detail elsewhere (4, 7): It can easily be standardized across times and locations; it can be used to concurrently produce estimates for several different hidden populations; it can be partially self-validating because it can easily be applied to populations of known size; it can produce estimates at the national, regional, or city level; it does not require respondents to report that they themselves are members of a stigmatized group; and it can be easily added to existing survey instruments. Because of its appeal, the network scale-up method has been used in studies around the world, and its use is accelerating (see Table 1 of the article by Feehan and Salganik (8)).

The current study makes 3 main contributions. First, we show that the type of network about which respondents are asked to report is a potentially crucial parameter that researchers are free to vary. Previous scale-up studies have asked respondents to report about their network of acquaintances, but there is no reason to think that this particular network will produce optimal or even near-optimal estimates. In order to explore this important issue, in 2011 we conducted a large, nationally representative survey experiment in Rwanda (3). By 1) randomizing respondents to report about one of 2 different types of personal networks and 2) estimating quantities whose true size was known, we were able to show that, somewhat surprisingly, asking respondents for less information can produce more accurate size estimates. The methodology we developed means that our study design can be replicated, customized, and extended in other settings, enabling cumulative improvement of the scale-up method over time.

Second, we use the results of our survey to produce substantively important hidden population size estimates for 4 key populations at increased risk of HIV infection in Rwanda: female sex workers, male clients of female sex workers, men who have sex with men, and people who inject illicit drugs. Sub-Saharan Africa is central to global efforts to combat HIV/AIDS, and Rwanda is an important example of the challenge that many countries in the region face: In 2010, the national prevalence of HIV infection among Rwandan adults was estimated to be 3%, yet little was known about the sizes of key populations at increased risk for HIV (9). Our study demonstrates that use of the scale-up method is feasible in Rwanda and is likely to be feasible in developing countries all over the world.

Third, we build on recent statistical research to introduce a new framework for sensitivity analysis that enables researchers to calculate estimates under different assumptions about potential biases. This framework for sensitivity analysis has been derived from first principles, meaning that it accounts for all of the sources of bias that have been previously discussed (but not resolved) in the scale-up literature; our framework also identifies new potential sources of bias not previously considered. This sensitivity framework can be used in future scale-up studies, regardless of whether they have an embedded experiment. We illustrate the framework by applying it to our estimates of the sizes of 4 key populations at increased risk of HIV infection in Rwanda.

METHODS

The network scale-up method

As Bernard et al. (4) have described elsewhere, network scale-up estimates come from survey data collected from a representative sample of the general population. Respondents are asked about their social connections with people in several hidden populations (e.g., “How many female sex workers do you know?”) and their connections with people in groups of known size (e.g., “How many teachers do you know?”). The responses are combined to produce estimates of the sizes of hidden populations using the basic scale-up estimator (5):

$${\hat{N}}_H=N\frac{{\sum }_i{\displaystyle \frac{y_{i,H}}{{\pi }_i}}}{{\sum }_i{\displaystyle \frac{{\hat{d}}_{i,U}}{{\pi }_i}}},$$ (1)

where ${\hat{N}}_H$ is the estimated size of a hidden population, N is the size of the total population, π_i is the probability of inclusion for the ith survey respondent, y_i,H is the number of members of the hidden population respondent i reports being connected with, and ${\hat{d}}_{i,U}$ is the estimated size of the personal network of respondent i (4, 8, 10). The personal network size estimates ${\hat{d}}_{i,U}$ come from the known population estimator, which is based on the number of connections respondents report having with the groups of known size:

$${\hat{d}}_{i,U}=\frac{{\sum }_j{\displaystyle \frac{y_{i,j}}{{\pi }_i}}}{{\sum }_j{N}_j}\times N,$$ (2)

where y_i,j is the number of people respondent i reports knowing in population j and N_j is the total size of known population j (5). The estimators in equations 1 and 2 will be consistent and unbiased under conditions described elsewhere (8). Intuitively, the basic scale-up estimator (equation 1) is like a sample proportion, but rather than being taken over all respondents, it is taken over all the members of respondents’ personal networks.

Definition of a social tie

In order to use the scale-up method in practice, researchers need to define what it means to be socially connected to another person. These connections are called ties in the social networks literature (11), and they can also be referred to as edges or links.

Almost all previous scale-up surveys have followed the definition of a social tie used in the original scale-up study (12): Two people are considered connected if they both know each other by sight and by name and have been in contact during the past 2 years (see Table 1). However, there is no particular reason to believe that this widely used definition leads to the best possible estimates. In fact, consideration of all possible definitions of a social tie along a continuum from very weak to very strong (13) highlights the fact that choosing a specific tie definition probably induces a trade-off between the quality and quantity of information collected from each respondent.

Table 1.

Definitions of Social Ties Used in a Survey Experiment, Rwanda, 2011

Acquaintance Definition (n = 2,236)	Meal Definition (n = 2,433)
1. People of all ages who live in Rwanda	1. People of all ages who live in Rwanda
2. People the respondent knows, by sight and by name, and who also know the respondent by sight and name	2. People the respondent knows, by sight and by name, and who also know the respondent by sight and name
3. People the respondent has had some contact with—either in person, over the phone, or on the computer in the previous 12 months	3. People the respondent has shared a meal or drink with in the past 12 months, including family members, friends, coworkers, or neighbors, as well as meals or drinks taken at any location, such as at home, at work, or in a restaurant

In order to understand this trade-off more carefully, it is useful to embed it within the total survey error framework. As with other survey-based methods, error in scale-up estimates can be decomposed into 2 broad categories: sampling error and nonsampling error (14). Sampling error arises from the fact that researchers interview only a sample of people rather than an entire population, and nonsampling error arises from all other sources of error, such as incompleteness in the sampling frame, mistakes in data processing, and inaccuracies in responses (see Groves and Lyberg (14) for a more detailed review). Previous network research leads us to predict that both sampling error and nonsampling error will depend on which definition of a social tie researchers choose for their survey. One set of findings suggests that nonsampling error will vary by tie strength, because people have more accurate information about their strong ties than their weak ties (15–19). A second set of findings suggests that sampling error will vary by tie strength, because people have more weak ties than strong ties (20, 21). Therefore, unless these two forces completely balance, total survey error will be a function of tie strength (see Figure 1 for a possible example).

Figure 1.

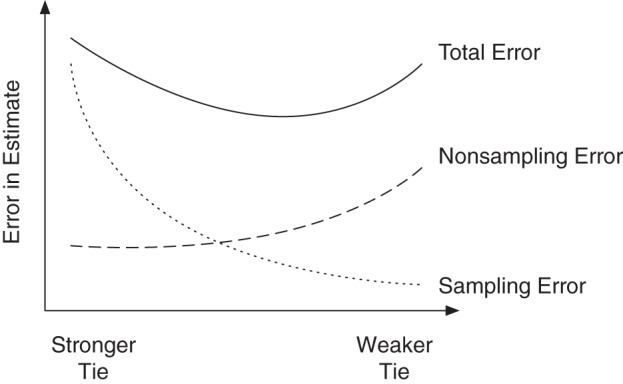
Possible relationship between the strength of social ties and total survey error. Previous social network research suggests that nonsampling error and sampling error will both likely be functions of tie strength. Therefore, we expect that total error will also be a function of tie strength. The curves in this figure illustrate one possible relationship between tie strength and total survey error.

The possible relationship between tie strength and total error means that by exploring other definitions of social ties, researchers can potentially obtain more accurate estimates at no additional cost. We assessed this possibility empirically by conducting a survey experiment to compare the accuracy of estimates made using 2 different tie definitions.

Survey experiment for evaluating tie definitions

In our survey experiment (3), each household was randomly assigned to one of 2 experimental arms. The questionnaires used in both arms were identical except for the definition of a social tie (Table 1). The first arm's tie definition, which we called the acquaintance definition, was modeled after the one used in all previous scale-up studies (4). The second arm's tie definition, which we called the meal definition, had never been used before. We designed the meal definition, in consultation with Rwandan researchers and policy-makers, so that 1) it would represent a stronger tie than the acquaintance definition and 2) it would be nested within the acquaintance definition, meaning that anyone who was connected to a respondent under the meal definition was also, by definition, connected to the respondent under the acquaintance definition (but not vice versa). We predicted that using the meal definition, we would learn about fewer people in each interview but the information we received would produce better size estimates.

Internal consistency checks for evaluating tie definitions

The information collected about ties to groups of known size (Table 2) makes it possible to check the accuracy of the scale-up estimates for these groups of known size (10), a practice known in the scale-up literature as internal consistency checks (4, 10). In order to do this, for each group of known size we 1) pretend its size is not known; 2) use the remainder of the groups of known size to estimate the respondents’ personal network sizes (equation 2); and 3) apply the scale-up method to estimate the size of the held-out group (equation 1). These internal consistency checks provide a natural method for deciding which of the tie definitions leads to more accurate estimates, at least for the groups of known size.

Table 2.

Groups of Known Size Used in Estimating Survey Respondents' Network Sizes, Rwanda, 2011

Group Name	Group Size (No. of Persons)	Source
Priests	1,004	Catholic Church
Nurses or physicians	7,807	Ministry of Health
Twahirwa	10,420	ID databasea
Mukandekezi	10,520	ID database
Nyiraneza	21,705	ID database
Male community health workers	22,000	Ministry of Health
Ndayambaje	22,724	ID database
Murekatete	30,531	ID database
Nsengimana	32,528	ID database
Mukandayisenga	35,055	ID database
Widowers	36,147	RDHS (2005, 2007, 2010)
Ndagijimana	37,375	ID database
Bizimana	38,497	ID database
Nyirahabimana	42,727	ID database
Teachers	47,745	Ministry of Education
Nsabimana	48,560	ID database
Divorced men	50,698	RDHS (2005, 2007, 2010)
Mukamana	51,449	ID database
Incarcerated people	68,000	ICRC 2010 report
Women who smoked	119,438	RDHS (2005)
Muslims	195,449	RDHS (2005, 2007, 2010)
Women who gave birth in last 12 months	256,164	RDHS (2010)

Abbreviations: ICRC, International Committee of the Red Cross; ID, identity; RDHS, Rwanda Demographic and Health Survey.

^a The ID database denotes groups of names from the Rwandan national identity card database.

Linear blending for size estimates

Our survey produced 2 estimates for the size of each key population, 1 from each tie definition. However, policy-makers typically require a single consensus estimate. Therefore, in Web Appendix 1 (available at http://aje.oxfordjournals.org/), we formally derive a linear blending technique to combine the results from both arms into a single consensus estimate, much like a meta-analysis (22). We consider all possible combinations of the estimates with the form

$$\hat{N}=w{\hat{N}}_{\mathrm{meal}}+(1-w){\hat{N}}_{\mathrm{acquaintance}}.$$ (3)

Web Appendix 1 proves that, under the assumption that the estimators from each experimental arm are unbiased and uncorrelated, the optimal linear blending weight is

$$w=\frac{{\sigma }_{\mathrm{acq}}^2}{{\sigma }_{\mathrm{acq}}^2+{\sigma }_{\mathrm{meal}}^2},$$ (4)

where ${\sigma }_{\mathrm{acq}}^2$ is the sampling variance for the acquaintance definition estimate and ${\sigma }_{\mathrm{meal}}^2$ is the sampling variance for the meal definition estimate. In narrative terms, equation 4 says that the larger the variance of the acquaintance definition's estimate relative to the variance of the meal definition's estimate, the more weight the meal definition estimate gets in the blended estimate. In practice, we use equation 4 by plugging in sample-based estimates of ${\sigma }_{\mathrm{acq}}^2$ and ${\sigma }_{\mathrm{meal}}^2.$

Framework for sensitivity analysis

There is a large body of literature describing many potential sources of bias in the basic scale-up estimator (4, 8, 23–29). Therefore, following a long tradition in epidemiology (30–32), we develop a framework for sensitivity analysis below. Our framework allows other researchers to calculate estimates under different assumptions about possible biases.

Using results developed by Feehan and Salganik (8), we consider the multiplicative bias of the basic scale-up estimator:

$$N_H=\alpha {\hat{N}}_H,$$ (5)

where α is an overall adjustment factor that captures all biases in the basic scale-up estimator. Web Appendix 2 shows that α can be written as the product of 4 quantities:

$$\alpha =\left(\frac{{\eta }_F}{{\tau }_F}\right)\left(\frac{1}{{\varphi }_F{\delta }_F}\right).$$ (6)

Each of the 4 adjustment factors is defined precisely in Web Appendix 2 and could potentially be estimated empirically. Together, the 4 adjustment factors account for the nonsampling errors discussed in the scale-up literature. In previous studies, investigators who have reported estimates from the basic scale-up estimators have implicitly assumed that the product of these 4 quantities is 1.

The 4 terms in equation 6 can be divided into 2 groups: reporting terms (η_F and τ_F), which summarize the accuracy of respondents' reports, and structural terms (δ_F and φ_F), which summarize the differences between the hidden population, the survey respondents, and the entire population. The precision, η_F, quantifies respondents' tendency to give false-positive reports (e.g., if respondents report that some members of their personal network are sex workers when they are not). On the other hand, the true positive rate, τ_F, quantifies respondents' tendency to give true-positive reports (e.g., if respondents are connected to sex workers and able to report this correctly). In general, we would expect the true positive rate to be less than 1, because members of hidden populations might attempt to keep this information secret from other people. The degree ratio, δ_F, quantifies whether members of hidden populations tend to have smaller personal networks than the survey respondents (e.g., if the average sex worker has fewer connections to adults than the average adult). Finally, the frame ratio, φ_F, quantifies whether survey respondents (e.g., adults) tend to have larger personal networks than the entire population (e.g., adults and children).

In addition to assessing the sensitivity of our estimates, our sensitivity framework (equation 6) enables our estimates to be improved over time as more is learned. If additional studies are conducted to estimate any of the quantities in equation 6 (η_F, φ_F, δ_F, and τ_F) (7, 8, 33), then, using the information given in Web Tables 1 and 2 and the procedure shown in Web Appendix 2, these new estimates can be combined with the results from our study to produce improved estimates of the sizes of hidden populations that are less dependent on assumptions about unobserved quantities.

Data collection and processing

To conduct our survey experiment, we collected original data using the same survey infrastructure as the 2010 Rwanda Demographic and Health Survey (3). The Demographic and Health Surveys Program, funded by the US Agency for International Development, is one of the largest and most widely used sources of reliable information about international health. Since 1984, the Demographic and Health Surveys Program has conducted over 260 surveys in more than 85 developing countries, and it has well-established protocols for developing questionnaires, training interviewers, supervising interviews, and processing data and for overall supervision of household-based surveys (34, 35). By using the infrastructure of the Demographic and Health Surveys Program, we ensured that our research design can be used in face-to-face surveys in developing countries around the world.

Our sample was drawn from the preparatory frame constructed for the 2012 Rwanda Census, which contained a complete list of 14,837 villages, which are the smallest administrative units in the country. We used a stratified, 2-stage cluster design with these villages as the primary sampling units.

We conducted interviews with 4,669 respondents from 2,125 households in 130 villages (household response rate: 99%; individual response rate: 97%) (3). All household members aged 15 years or more were interviewed in each selected household. Eight survey teams—each consisting of 1 supervisor, 2 male interviewers, and 2 female interviewers—conducted these interviews between June and August of 2011. Upon arriving in each sampled village, the survey team first updated the list of households. A number was assigned to each household in the updated listing, and the supervisor used a randomly pregenerated table to select households and assign them to tie definitions. Balance checks suggested that our randomization procedure was implemented according to the study design (Web Appendix 3, Web Table 3, and Web Figure 1). All interviews were conducted face-to-face in Kinyarwanda (the official language of Rwanda) in the respondent's home. All responses were recorded on paper forms, and data were entered twice using CSPro software (US Census Bureau, Washington, DC). Table 2 shows the definitions and data sources of the 22 known populations that we used to estimate the sizes of respondents' personal networks (equation 2). Full details on the sampling plan and the survey instrument have been provided elsewhere (3).

The survey protocol, including questionnaires and other instruments, was reviewed and approved by the Rwanda National Ethics Committee (Kigali, Rwanda), the Rwanda National Institute of Statistics (Kigali, Rwanda), and the institutional review boards of ICF International (Fairfax, Virginia), Princeton University (Princeton, New Jersey), the International Center for Research on Women (Washington, DC), and the US Centers for Disease Control and Prevention (Atlanta, Georgia). All participants were informed about their free choice to participate and their right to withdraw at any time during the study. Interviewers secured written consent from all respondents before the interview.

When analyzing our data, consistent with common scale-up practice, we truncated extreme outliers by top-coding all responses about connections with groups of known or unknown size at 30 (29), which affected 0.2% of responses. We used the rescaled bootstrap technique of Rao and Wu (36) to produce estimates of sampling uncertainty that accounted for the complex sample design (8) (see Web Appendix 4 and Web Figure 2). Unless otherwise noted, all estimates were produced using weights to account for the complex sample design. All of our calculations were done in R (R Foundation for Statistical Computing, Vienna, Austria) (37), using the following packages: networkreporting (38), plyr (39), ggplot2 (40), stringr (41), stargazer (42), RItools (43), and car (44). Our data set and a copy of the survey instrument are freely available for download (3), and code with which to replicate our analyses is available online (https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/CCC6HF).

RESULTS

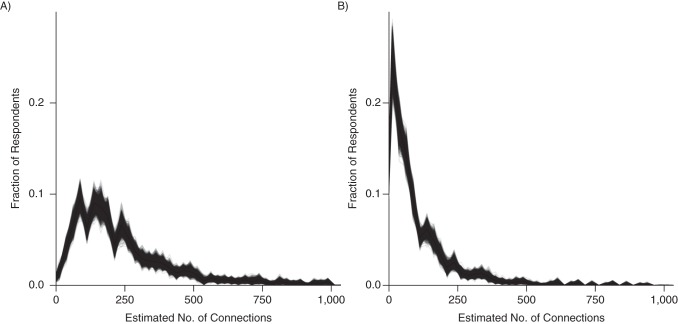
For each of the 22 groups of known size, respondents to the meal definition reported fewer average connections, indicating that our survey experiment manipulated responses (Web Figure 1). Using these reports to estimate the average size of respondents' personal networks (equation 2) showed that the meal definition elicited information about 60% fewer people than the acquaintance definition: The estimated mean network size for the meal definition was 108 persons (95% confidence interval: 99, 118), while for the acquaintance definition it was 251 persons (95% confidence interval: 237, 267) (Figure 2).

Figure 2.

Estimated distribution of network sizes by definition of a social tie, Rwanda, 2011. A) Network sizes produced from the acquaintance tie definition; B) network sizes produced from the meal tie definition. Results from each bootstrap resample are plotted with partial transparency, meaning that we were more confident about the distributions in regions that are more solidly colored. The histogram bin width was 25. The estimated mean network size for the acquaintance tie definition was 251 (95% confidence interval: 237, 267), while for the meal tie definition it was 108 (95% confidence interval: 99, 118).

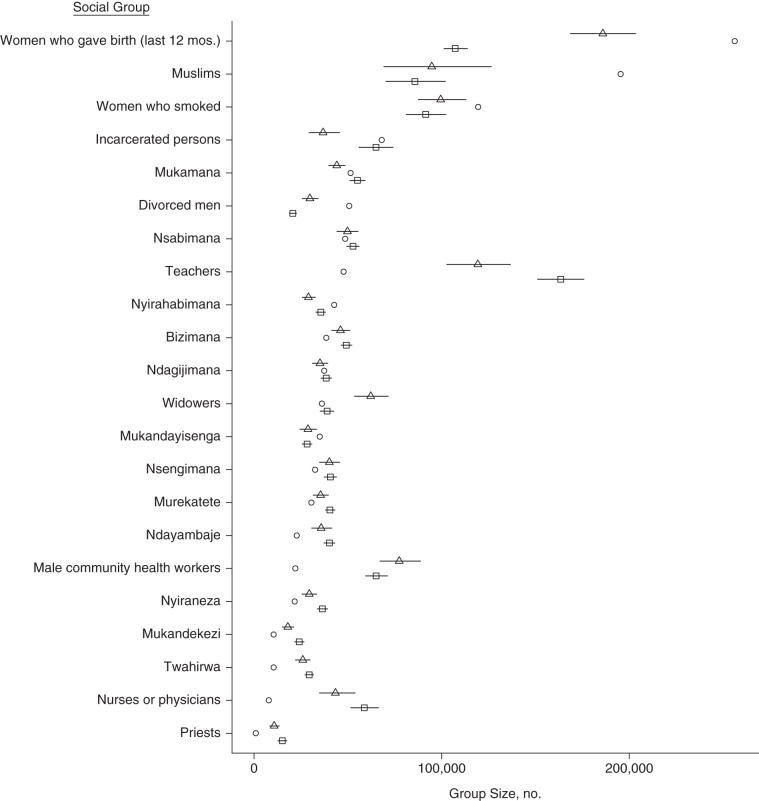
Internal consistency checks

The internal consistency checks, which compared the performance of both tie definitions in estimating the sizes of known populations, showed that in most cases, the estimates were close to the true values (Figure 3). However, there were a few exceptions: The most notable ones were teachers (whose size was overestimated), Muslims (whose size was underestimated), and women who gave birth in the past 12 months (whose size was underestimated). On average, across the 22 groups of known size, estimates derived from the meal definition had lower mean squared errors than estimates from the acquaintance definition (2-sided P < 0.001)—a result that was robust to the specific error metric used (Web Figure 3).

Figure 3.

Results from internal consistency checks for the 22 social groups of known size (Table 2) and for the meal tie definition (triangles) and the acquaintance tie definition (squares) of social ties as compared with the true size of each group (circles), Rwanda, 2011. For most of the groups of known size, the internal consistency estimates from both tie definitions are close to the true value. However, the uncertainty intervals—which only capture sampling error—do not include the truth as often as would be expected, a pattern consistent with other scale-up studies (8).

Size estimates for hidden populations and sensitivity analysis

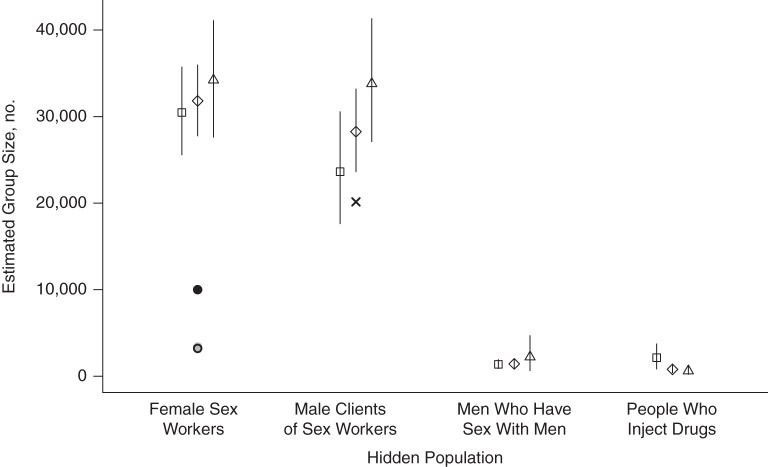
Figure 4 shows the estimated sizes of 4 key populations at risk for HIV infection in Rwanda: male clients of female sex workers, female sex workers, men who have sex with men, and people who inject illicit drugs. As described in more detail in the Discussion, these estimates were consistently higher than earlier estimates in Rwanda, but they were generally lower than international benchmarks.

Figure 4.

Estimated sizes of 4 key hidden populations at risk of human immunodeficiency virus infection, Rwanda, 2011. Estimates are shown for the acquaintance network definition of a social tie (squares); the meal network definition of a social tie (triangles); and both the acquaintance and meal definitions blended together (diamonds). Earlier estimates for Rwanda from a capture-recapture study of female sex workers (gray circle) (45), a mapping study of female sex workers (black circle) (3), and an enumeration study of female sex workers (open circle overlapping gray circle) (46), as well as a direct estimate of male clients of female sex workers (X) (3), are also shown.

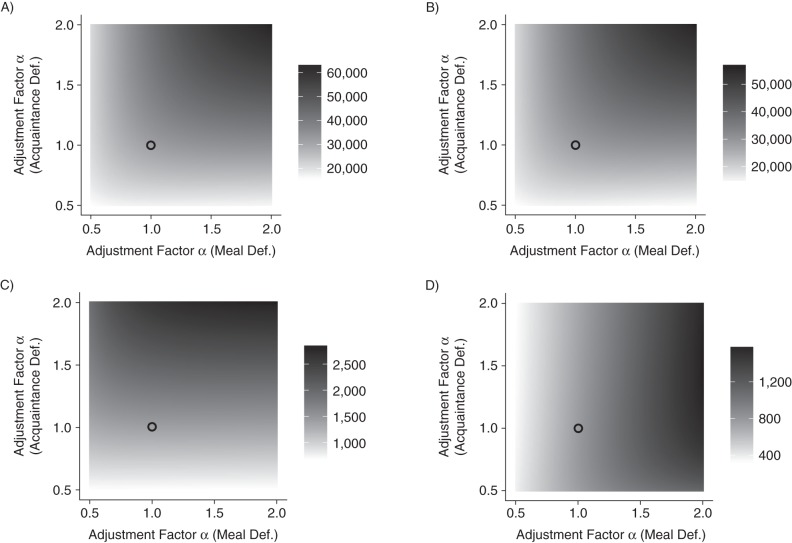
In the absence of empirical evidence about the magnitude of possible biases in the basic scale-up estimator, Figure 4 assumes that the estimates from each tie definition are unbiased (α = 1). In Figure 5, we relax this assumption using our framework for sensitivity analysis to show how the blended estimate depends on the assumed multiplicative bias (α) for each hidden population. For example, if we considered the estimate for the number of female sex workers, and if the meal estimator were unbiased (α = 1) but the acquaintance estimator tended to be too small (α = 1.5), panel A of Figure 5 shows that the blended size estimate should be about 40,000, which is higher than the estimate obtained under the assumption that both arms are unbiased. In general, Figure 5 shows that higher values of α lead to higher estimates. However, the exact nature of the relationship between assumed values for α and size estimates depends on the sampling variance of the estimator from each arm. Web Appendix 2 shows how researchers can use our sensitivity framework to combine our data with any set of assumptions about η_F, φ_F, δ_F, and τ_F to produce adjusted estimates (see Web Tables 1 and 2 for an example).

Figure 5.

Sensitivity of blended estimates of the sizes of 4 key hidden populations at risk of human immunodeficiency virus infection (female sex workers (A), clients of female sex workers (B), men who have sex with men (C), and people who inject illicit drugs (D)), Rwanda, 2011. Adjustment factor values (α) for the estimator from the meal definition of a social tie (x axis) and the estimator for the acquaintance definition of a social tie (y axis) were combined to produce a blended estimate. α can be written as the product of 4 terms related to reporting accuracy and network structure; α satisfies $N_H=\alpha {\hat{N}}_H.$ Areas with darker shading correspond to combinations of α values that lead to higher estimated group sizes. The circle shows the point estimate from Figure 4, which assumes that both the meal and the acquaintance definitions produce unbiased estimates.

DISCUSSION

Findings

Our survey experiment demonstrated that the definition of a social tie which respondents are asked to report about is a potentially critical parameter that researchers can vary. There appears to be a trade-off between quantity and quality of network reports: For the groups of known size, the internal consistency checks revealed that the meal definition outperformed the acquaintance definition that has been used in all previous scale-up studies. These results show that learning about fewer people can, somewhat surprisingly, lead to more accurate estimates. Our study, therefore, makes the clear and falsifiable prediction that future scale-up studies will produce more accurate estimates using stronger definitions of social ties.

We also used our survey to estimate the sizes of 4 populations at risk for HIV infection in Rwanda. Our blended scale-up estimates were consistently higher than earlier estimates from Rwanda made using other methods (Figure 4). For female sex workers, our estimate was higher than 3 earlier estimates—1 made using mapping (3), 1 made using enumeration (45), and 1 using capture-recapture (3). Our estimate for the number of male clients of female sex workers was higher than an earlier direct estimate (3, 45, 46). To our knowledge, there have been no previous estimates of the numbers of people who inject drugs and men who have sex with men in Rwanda. On the other hand, our estimates are comparable to or lower than benchmark estimates from the Joint United Nations Programme on HIV/AIDS (UNAIDS) (47), which were derived from published literature on population size estimates from around the world. Our estimated number of female sex workers was within the range given by the UNAIDS benchmarks. However, our estimates for the number of male clients of female sex workers and the number of injecting drug users were both lower than the UNAIDS benchmarks. There are no UNAIDS benchmarks available for men who have sex with men in Africa. Additional details about these comparisons are presented in Web Appendix 5 (also see Web Tables 4–7 and Web Figure 4).

Finally, we have introduced a framework for sensitivity analysis that enables scale-up researchers to calculate estimates under different assumptions about possible biases. Our framework is derived from first principles, enabling it to account for all of the sources of potential bias, only some of which were previously discussed in the scale-up literature. We have demonstrated the framework in action by assessing the sensitivity of our basic scale-up estimates for the sizes of 4 populations at risk of HIV infection in Rwanda. Web Appendix 2 contains a step-by-step guide to using the framework for sensitivity analysis, which can be applied in other studies regardless of whether a tie definition experiment has been conducted.

Limitations

Our study had several important limitations. The fact that the meal definition worked better than the acquaintance definition on average across the 22 groups of known size in Rwanda does not guarantee that it will work better for hidden populations in Rwanda or hidden populations in other countries.

Further, we do not claim that the meal definition is optimal. In fact, we hope future research explores a wider range of tie definitions with the goal of developing an empirical understanding of the general relationship between tie strength and total survey error. We recommend that future studies explore tie definitions from a parameterized family that is sufficiently flexible for use in many different countries. For example, the meal and acquaintance tie definitions are members of a 2-parameter family, where 1 parameter is an interaction type (e.g., had some contact, shared a meal or drink) and 1 parameter is a time window (e.g., in the past year). By focusing on a parameterized family of tie definitions, it will be possible to compare and combine results from different studies, enabling knowledge about the method to build up as more scale-up studies are conducted.

Empirically, our blended estimates (Figure 4) depended on the assumption that the basic scale-up estimator was unbiased in this setting. However, our framework for sensitivity analysis shows that different plausible assumptions about the bias can lead to a wide range of possible estimates (Figure 5). Therefore, we recommend that in future studies investigators attempt to measure these possible biases directly (e.g., see Salganik et al. (33) and Maghsoudi et al. (48)) so that estimates are less dependent on assumptions.

Conclusion

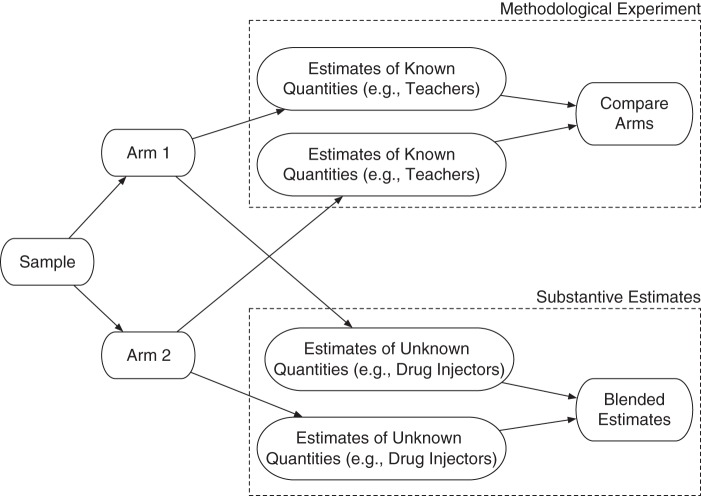
Estimating the sizes of hidden populations such as sex workers and people who inject drugs is a critical problem in many settings. The network scale-up method is a promising approach, and in this paper we show that it is more flexible and potentially more accurate than had been previously realized. Further, the methodology we developed and deployed—a survey experiment with blending (Figure 6)—provides a general template that future researchers can replicate, customize, and extend. If this design becomes standard, future studies will provide both estimates about specific hidden populations and more general insights that will lead to cumulative methodological improvement.

Figure 6.

Structure of a survey experiment with blending. Respondents from the sample are randomly placed in one of 2 arms, and a different variation of the scale-up method (in our case, a different definition of a social tie) is used in each arm. Researchers can learn about which experimental condition performs better by comparing estimates of the known quantities with their actual values. Researchers can produce substantive size estimates for hidden populations by blending the results from each arm together.