Maximum-Likelihood Tree Estimation Using Codon Substitution Models with Multiple Partitions

Abstract

Many protein sequences have distinct domains that evolve with different rates, different selective pressures, or may differ in codon bias. Instead of modeling these differences by more and more complex models of molecular evolution, we present a multipartition approach that allows maximum-likelihood phylogeny inference using different codon models at predefined partitions in the data. Partition models can, but do not have to, share free parameters in the estimation process. We test this approach with simulated data as well as in a phylogenetic study of the origin of the leucin-rich repeat regions in the type III effector proteins of the pythopathogenic bacteria Ralstonia solanacearum. Our study does not only show that a simple two-partition model resolves the phylogeny better than a one-partition model but also gives more evidence supporting the hypothesis of lateral gene transfer events between the bacterial pathogens and its eukaryotic hosts.

Introduction

Phylogeny inference from molecular data became essential in evolutionary biology, bioinformatics, and other fields, such as immunology, evolutionary medicine, and conservation of biodiversity. The evolution of molecular characters over time is typically described using Markov substitution models. Parameters of substitution models and phylogenies can be estimated by maximum likelihood (ML) or Bayesian approach. For protein-coding sequences, codon substitution models should provide the most realistic description of sequences (e.g., Seo and Kishino 2008, 2009; Anisimova and Kosiol 2009). In contrast to nucleotide models, codon models naturally account for the structure of genetic code, alleviating the biases that are usually observed at different codon positions. Unlike amino acid models, codon substitution models explicitly include selective pressure that typically acts on protein-coding regions. Recently, a large variety of codon models with constant or variable selection over sites were implemented for ML phylogeny inference in the CodonPhyML package (Gil et al. 2013).

In theory, more realistic models (with justified number of parameters) should provide basis for more accurate phylogenetic inferences. Indeed, codon models of various degrees of sophistication were proposed, each expanding the capacity of a model by including different biological factors. Here, we explore whether ML phylogeny inference with codon models could be enhanced by allowing for heterogeneity of evolutionary patterns across multiple gene partitions defined a priori based on known or inferred gene structure. Indeed, many proteins have distinct domains which evolve with different rates, different selective pressures and may differ in codon bias (Adzhubei et al. 1996; Fraser 2005). Models with a priori partitions were first proposed and implemented for DNA sequences evolving on a fixed tree (Yang 1994). Codon models with site partitions fitted on a fixed tree were used to study diversifying selection on the antigen recognition domain of human major histocompatibility complex (Yang and Swanson 2002). For a fixed phylogeny, multipartition models can be fitted using the programs baseml and codeml of the PAML package (Yang 1997, 2007). It is also possible to define multiple gene partitions within the Bayesian implementation MrBayes (Ronquist and Huelsenbeck 2003). Nevertheless, due to complexity, models with multiple partitions have not been employed for phylogeny inference, and no ML implementation of codon models with multiple partitions is available to date.

Here, we present a multiple partition approach that allows ML phylogeny inference using different codon models at predefined partitions. To illustrate the new approach, we present a phylogenetic study of the origin of the leucine-rich repeat (LRR) region in the type III effector proteins (GALA-LRRs) of phytopathogenic bacteria Ralstonia solanacearum. Type III effectors act to suppress the extracellular immunity of plants. It has been long known that LRR regions play an important role in the numerous resistance genes (R-genes) of plant genomes. In bacteria however, LRR regions were discovered only recently (Cunnac et al. 2004; Angot et al. 2006).

The LRRs in R. solanacearum are hypothesized to have appeared by a lateral gene transfer (LGT) from a host plant (Kajava et al. 2008), but its exact origin and the mode of evolution are not known. The LRR region of GALA-LRR folds into independent horse-shoe-like structure formed by tandem LRRs. Residues under positive selection in GALA-LRR were detected on the bulging outward side of the horse-shoe domain, and are likely to be involved in binding to the target proteins of the host plant. Consequently, the evolutionary pressures acting on the LRR region of the protein may be distinct to the forces shaping its globular part. To test this, we apply our multipartition approach to all genes that contain LRRs similar to those employed by R. solanacearum. Further, based on the same example, we study how using multipartition codon models can affect phylogenetic inference.

New Approaches

The Multiple Partition Model and Implementation

Our multipartition method for ML phylogeny inference was implemented in the CodonPhyML package (Gil et al. 2013). This allows users to harness the full variety of implemented models, including empirical, parametric, and semiparametric model variants. As the sites in a multiple sequence alignment (MSA) are considered independent, different models for a priori defined site partitions in a MSA can be used.

The ML phylogeny inference chooses the phylogeny and model parameters that maximize the likelihood function, which is achieved by optimizing the log-likelihood. The likelihood is defined as the probability of data, that is, an MSA of n columns $x={\left(x_s\right)}_{s=\mathrm{1...}n}$, given model parameters θ and phylogeny τ:

$$L(\tau ,\theta )=\text{Pr}(x|\tau ,\theta )={\displaystyle \prod _{s=1}^n\text{P}}\text{r}(x_s|\tau ,\theta ).$$

With K site-partitions, different sites in an MSA may be governed by different models, with parameters $\theta ={({\theta }_p)}_{p=\mathrm{1...}K}$, and a site likelihood at site s from partition p is computed using corresponding parameters θ_p:

$$L(\tau ,{\theta }_1,\mathrm{...},{\theta }_p)={\displaystyle \prod _{s=1}^n\text{P}}\text{r}(x_s|\tau ,{\theta }_p).$$

Subsequently, different model combinations can be used for further hypotheses testing without constraining the phylogeny to the one previously inferred with different methods/models. This has not been possible with other existing tools.

In our implementation, models defined for different partitions can have shared parameters. For example, it is possible to define two site partitions each described by different instances of model M0 (Goldman and Yang 1994) with two different free parameters ω (the nonsynonymous to synonymous rate ratio measuring selection on the protein), but with one shared parameter κ (the transition to transversion rate ratio). In the given example, to test whether selective pressure is the same in both regions of the MSA, the null hypothesis hypothesis H₀ “${\omega }_1={\omega }_2$” is contrasted with the alternative hypothesis H₁ “${\omega }_1\ne {\omega }_2$.” If the test is significant, the null is rejected suggesting that the two regions evolve under different selective pressure.

Indeed, for protein-coding genes consisting of multiple domains, this allows for more flexible hypothesis testing than a single-model approach. Likelihood ratio tests (LRT) could be applied to learn whether protein regions evolve differentially and in which aspect. All parameters including the best-fitting topology are then estimated during a single optimization. Despite allowing different substitution models for different site partitions, our approach estimates one single tree for the whole MSA.

The user can define different model configurations by annotating an input MSA (PHYLIP format). This is done using an additional single line with prefix “#=GR mods” followed by a sequence of characters which specify the partition for each column of the MSA (and therefore has the same length as the MSA). Models for different partitions are defined in a separate configuration file.

The multipartition version of CodonPhyML supports two different formats of configuration files: YAML (Ben-Kiki et al. 2001) or Darwin (Gonnet et al. 2000) format. If only one single-model configuration is used, the user can still provide model settings through the command line interface. As soon as more model configurations are needed (Easton and Hardy 1997), command line input is not supported anymore. Using configuration files offers the advantage of serving as documentation to the work process. For a detailed description of the possible parameters, documented example configuration files are distributed with the program.

The Application of Multiple Partition Models to Elucidate the Origin of Bacterial LRRs

Although the LRR region might have been acquired by R. solanacearum through an LGT from a host plant, the host range of R. solanacearum spans greater than 250 plant varieties, and the exact origin of the bacterial LRR is unknown. Clarifying this requires a careful phylogenetic analysis of all bacterial-like LRR domains. Therefore, to glean deeper into the origin and the evolution of bacterial LRRs, we assembled an exhaustive data set of protein-coding genes containing LRRs similar to that found in R. solanacearum. Using HMMER v3 (Finn et al. 2011b), we constructed a profile hidden Markov model (HMM) from the alignment of tandem LRR units detected in R. solanacearum strains from Remigi et al. (2011). This profile HMM was used to search for similar regions in the TREMBL sequences (Boeckmann et al. 2003). Out of the total 1,228 hits, 505 with P < 0.01 were retained for further analysis. Due to high heterogeneity of all assembled gene sequences, the data were subdivided into smaller homologous groups.

This was done using BLASTClust (Dondoshansky and Wolf 2002) with different requirements for sequence similarity (p) and matching sequence length coverage (L) (see supplementary material, Supplementary Material online). Next, we filtered out sequences that included TR regions with less than four sites and clusters with less than four sequences. In the end, the set of clusters with L = 90% and p = 50% included 19 groups with a maximum of 37 sequences and a mean of 9 sequences per group (further denoted as data set L90p50). With more relaxed clustering L = 60% and p = 30% (data set L60p30), almost all sequences clustered in one homologous group with 367 sequences, whereas the remaining sequences (after filtering) fell into one of the other two clusters, each with four sequences.

Guided by the annotations of LRR units, each homologous group was aligned and each column of the LRR region in the MSA was annotated. These annotations were used to define two-partition models for each set of homologous cluster (see supplementary material, Supplementary Material online). Strong negative selection is known to drive the evolution of the non-LRR regions in both bacterial and plant genes, whereas positive selection was detected on some residues of the LRR domain, both in bacteria (Kajava et al. 2008; Remigi et al. 2011) and in plants (Michelmore and Meyers 1998). Thus, here using codon models we explicitly modeled selection pressure at the protein level on these data. For each homologous group, two-partition models were compared with single-partition models. Phylogenies were estimated simultaneously with other parameters for each model. See Materials and Methods for further details of our analyses.

Results and Discussion

Multiple Partition Models Often Improve Fit to Data

Overall, two-model configurations were preferred for the majority of alignments (table 1). For example, codon models with multiple partitions fitted the best for all MSAs in L60p30. In the L90p50 data set, a two model configuration fitted the best for 12 out the total 19 MSAs. In four cases, the single-model configuration was fitting equally well compared with an alternative two-model configuration. For these cases, the best model was the single-partition model to minimize the number of unnecessary parameters. In our data sets, the amount of information in a data set such as the length of the MSA, the number of taxa, or the total number of sites did not bias the model choice (Wilcoxon rank test was not significant at $\alpha =0.01$).

Table 1.

Consensus Results of Both Data Sets.

	L90p50			L60p30
	Tot	Cons	Aic	Tot	Cons	Aic
g1	24	15	9	0	0	0
g2	13	2	2	2	1	1
2	11	0	3	1	0	0
rg2	18	1	5	8	2	3
r2	16	1	4	2	0	0

Note.—The total number (Tot) of model configurations chosen by one of the three model selection methods, the conservative consensus (Con) configuration, and the AICc (Aic) friendly consensus (see Results for details) are given in this table.

This suggests that the patterns of codon evolution tend to be distinct in the tandem LRR regions of the protein-coding genes compared with the remaining part of the protein. Consequently, phylogenies inferred with best-fitting models should also be more accurate at recovering the molecular history.

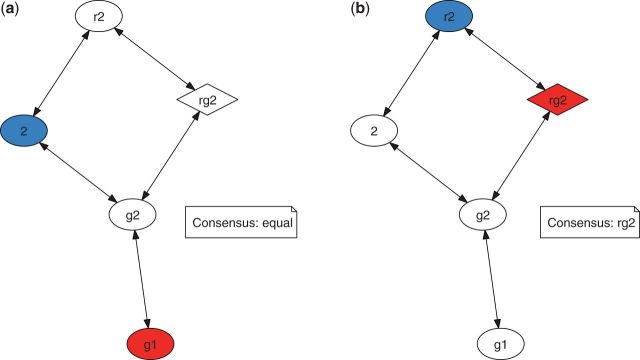
Figure 1 illustrates the results of model selection procedures for the two largest alignments, one from each data sets L90p50 and L60p30. Each node in the graph represents one of the model configurations described in table 2; see the Materials and Methods section for more information. The arrows depict comparisons by the hierarchical LRT (or hLRT) tests (Posada and Crandall 1998). Red and blue nodes indicate the best model according to the forward and the backward hLRTs, respectively. Diamond-shaped nodes mark the best-fitting models according to the corrected Akaike information criterion (AICc) (Hurvich and Tsai 1989).

Fig. 1.

Graphs representing the forward (red) and backward (blue) hLRT tests. Each node represents a model configuration according to table 2. End nodes are colored accordingly. Diamond-shaped nodes are AICc test favorite configurations. (a) refers to the first MSA in the L90p50 data set (length: 2,055 nt), whereas (b) depicts the model selection in the first MSA of the L60p30 data set (length: 45,099 nt).

Table 2.

Model Configurations Used in the Experiments.

g1	One instance of M0; codon frequencies estimated from whole MSA with a F3X4 model
g2	Two instances of M0; codon frequencies estimated from whole MSA
2	Two instances of M0; codon frequencies estimated from either tandem regions or rest of the MSA, respectively (which leads to two different sets of frequencies)
rg2	Two instances of M0; codon frequencies estimated from whole MSA. Different model mutation rates assumed
r2	Two instances of M0; codon frequencies estimated from either tandem regions or rest of the MSA. Different model mutation rates assumed.

In one case (fig. 1a), all three model selection methods resulted in choosing three different model configurations. The conservative consensus approach (see Materials and Methods for more information) suggested model configuration g1 as the best-fitting model. A more liberal approach based on AICc suggested rg2 as the best-fitting model. For the second example alignment (fig. 1b), model configuration rg2 is chosen by AICc, which is consistent with the choice by the forward hLRT. Model rg2 therefore constitutes the consensus configuration.

Fig. 2.

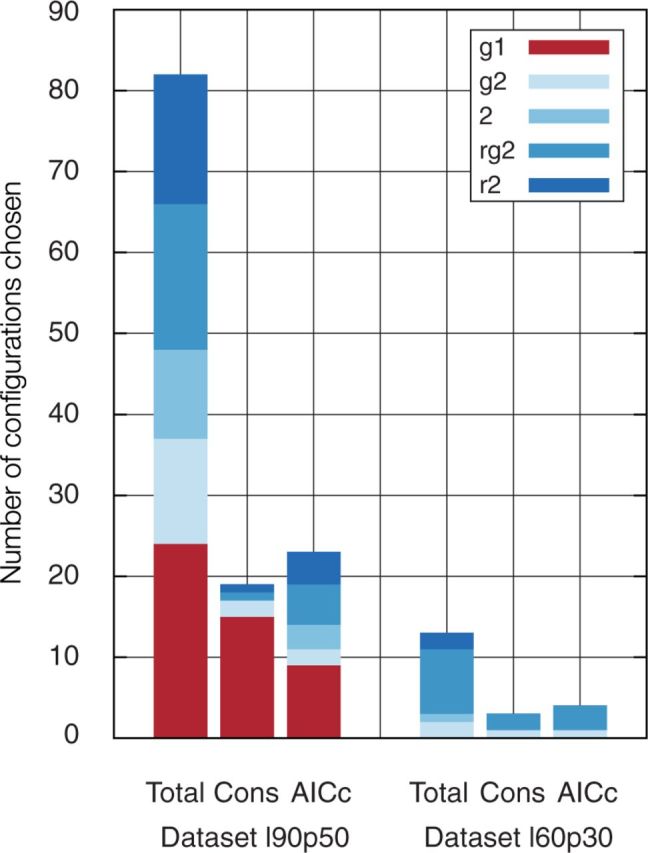
Preferred model configurations in data sets L90p50 and L60p30. Consensus is calculated per MSA, either conservative (if more than one model got chosen, select the configuration with the lowest number of parameters) or liberal (if more than one model got chosen, select the AICc choice). Shown are the total number a given configuration was chosen by either forward hLRT, backward hLRT or AICc (“Total” column), the number a configuration was chosen as conservative consensus (“Cons” column) and the number a configuration was chosen using a liberal consensus (“AICc” column). Note that AICc can choose more than one configurations.

Simulations

If there are two distinct regions in the data in question, does using two-partition models allow us to infer better phylogenies? We simulated data sets, each on four levels of divergence ($0.15,0.3,0.6,0.12$), as described in the Materials and Methods section. We then measured the Robinson–Foulds distance of each of the estimated trees to the true tree of the simulation and counted how many times a given configuration was further from the truth than its competitor. The results are shown in figure 3. Smaller bars are better. An example: In the simulation with divergence 0.015 under a comb tree as the true tree, using the one-partition model led to 23 trees that are more distant from the true tree than the two-partition model, whereas only 14 trees estimated using the two-partition model are more distant from the true tree than the one-partition model.

Fig. 3.

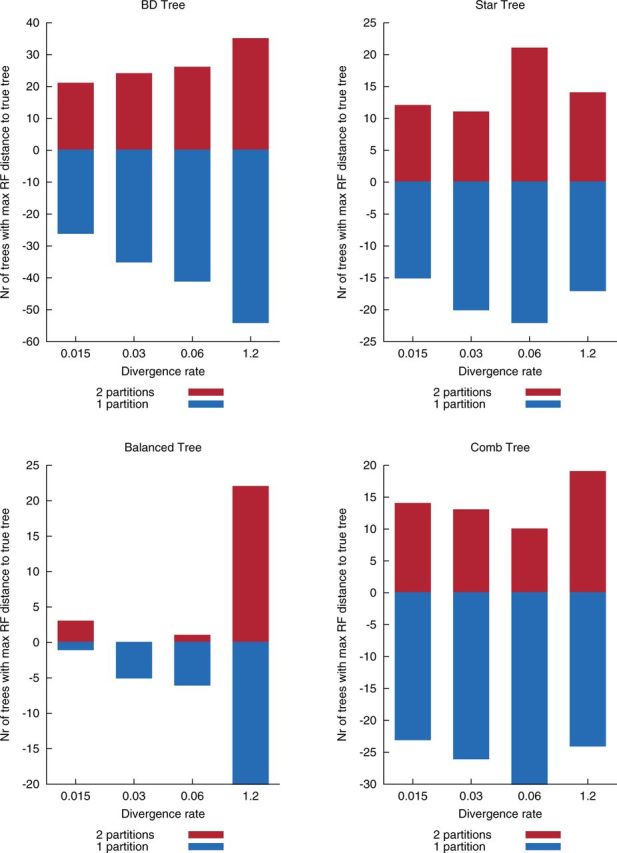
Results on simulated data with different divergence rates and different guide trees. “BD Tree” refers to simulated topologies according to a birth–death process (100 simulations; see Materials and Methods); “Comb tree” (50 simulations), “Balanced tree” (50 simulations), and “Star tree” (100 simulations) refer to well-known artificial topologies. We measure the Robinson–Foulds distance of the estimated trees under a one-partition (blue) or two-partition (red) model to the true tree of the simulation. Displayed are the counts on how many times a certain configuration was further from the true tree than its competitor (smaller bars are better; the sign of the bar is arbitrary).

Topologies estimated under a two-partition model are, on average, in 14 out of 16 simulations as close or closer to the true tree than topologies estimated under a one-partition model. If we pool all absolute numbers, the one-partition model is in 365 cases (30.4%) further from the true tree than the two-partition model, vice versa only in 246 (20.5%) cases (of 1,200 simulation runs in total).

In LRTs applied on all simulations, the two-partition model is always chosen as being the better fitting model.

Phylogenetic Inference for LRR Homologs from R. solanacearum

To gain more insights into the origin and evolution of the bacterial LRRs, we further focused on the phylogenetic analyses of the largest homologous cluster of sequences from the L60p30 data set. The consensus model for this MSA was rg2 which included two instances of M0, global frequencies and a rate parameter (see Materials and Methods for details). ML estimation of a phylogeny for this large MSA under two-partition codon model was expensive in terms of computational resources. Thus, we used a jackknifing procedure, which helped us not only to reduce the computational costs but also to reduce the chance of getting trapped in a local optimum and to provide statistical confidence for estimated trees. By random sampling of 100 sequences from the original MSA, we created a total of 100 jackknifed MSAs. For each of jackknifed MSA, we estimated phylogenies under all model configurations and found that a large subclade of Naegleria gruberi was stable in all replicates. Therefore, we pruned the original MSA for this subclade, reducing the number of taxa in the original topology from 375 down to 250. This smaller data set could then be handled more efficiently.

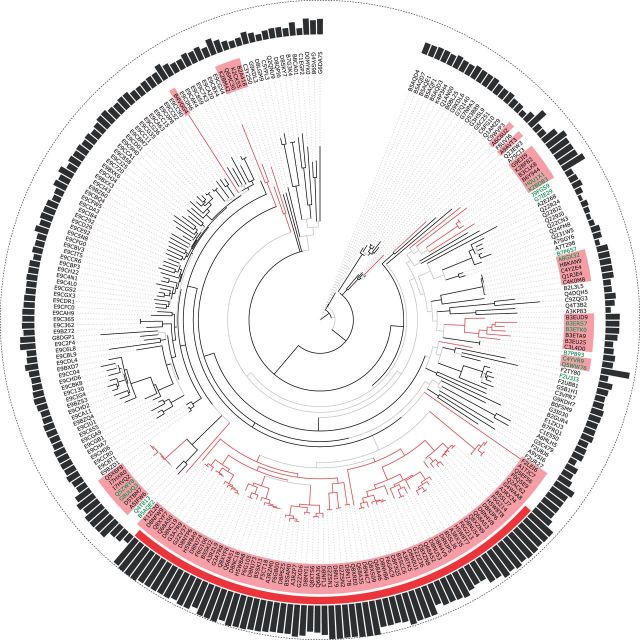
All topologies inferred under the five model configurations are different; table 3 contains the Robinson–Foulds distance of the topologies (Robinson and Foulds 1981). The ML tree under the consensus model for this pruned MSA is shown in figure 4. Sequences marked with light red are bacterial sequences; those additionally marked with a red ribbon belong to a Ralstonia family. The black bars depict the HMM scores of the respective sequence (see Methods for details); the higher the bar, the closer the sequence in question is to the GALA LRR sequence in R. solanacearum. Bacteria-only subclades are drawn in red, branches leading to nonbacterial sequences are black. Branches with approximate Bayes support lower than 0.9 are held in gray. Note that all members of the Ralstonia family can be found in one subtree; this is to be expected and can be interpreted as a confirmation of our approach.

Table 3.

Robinson–Foulds (RF) Distances of Topologies Inferred under Different Model Configurations on First MSA of the L60p30 Data Set.

	g2	rg2	2	r2
g1	0.13	0.22	0.17	0.21
g2		0.21	0.17	0.22
rg2			0.26	0.21
2				0.27

Note.—The RF distance is the number of nontrivial bipartitions present in one of the two trees but not in the other, divided by the number of possible bipartitions.

Fig. 4.

Phylogenetic tree of the first MSA in L60p30 after pruning of the MSA. Bacterial sequences are marked as red; the red ribbon spans the sequences of Ralstonia. HMM scores are shown as black bars; branches with aBayes support lower than 0.9 are held in gray. Labels that also occur in table 4 are written in green.

We can find some pairings of Bacteria and Eukaryota in the tree (see table 4; IDs have been marked green in fig. 4 to be better detectable). Optimally, we would expect the tree—given we root it correctly—to divide between Bacteria and Eukaryota. This is obviously not true for any of the inferred topologies; but inner nodes that divide between Eukaryota and Bacteria are at least candidates for a possible rooting.

Table 4.

Pairings of Eukaryota and Bacteria in Tree 4.

	ID	Score	Name	Desc
1	B7P893	12.8	Ixodes scapularis	Deer tick
	C4YVR9	11.5	Rickettsia	Protobacteria, endosymbiont
	B3ETK0, B3ERS7	15.0	Amoebophilus asiaticus	Ameoba symbiont
2	B7P657	4.4	Ixodes scapularis	Deer tick
	A8GX32	12.2	Rickettsia	Protobacteria, endosymbiont
3	Q4T813	15.0	Tetraodon nigroviridis	Green puffer fish
	B5AQE2	14.2	Gasterosteus aculeatus	Three-spined stickleback
	Q5ZWY8, G8UUQ3	23.8	Legionella pneumophilia	Bacteria
4	J9FGS9	8.0	Oxytricha trifallax	Ciliate protozoan
	G7IE29	9.3	Medicago truncatula	Barrel Medic
	K2BDB3	27.8	—	Uncultured bacterium
	H0U1X1	23.1	Wolbachia pipientis	Arthropod species infecting bacteria
5	Q5WW76	32.0	Legionella pneumophilia	Bacteria
	F2U3J3	15.3	Salpingoeca	Eukaryota

Note.—Sequence IDs of the interesting pair plus those sequences in vicinity in the tree with the highest HMM scores (marked with italic scores), the corresponding HMM scores, and names of the organisms are given in this table.

Some of the pairings might be because of LGT events. For example, Rickettsia are known to be deer tick-transmitted pathogens (see Entries 1 and 2 in table 4) (Spielman et al. 1985).

Conclusion

Using a multipartition model can be an advantage when estimating model parameters, testing hypotheses or building phylogenies. This is especially true if we include prior knowledge about the data, such as the position of especially conserved or variable domains or the existence of tandem repeats (TRs) in the molecular data. Using the modular approach we implemented, our new version of CodonPhyML enables researchers to harness the full potential of a multipartition approach without the need to design completely new models of evolution. Although there is still enough room for new model approaches, our intuitive method allows the user to combine well-known models into new configurations that can be selected and validated by existing methods and pipelines. Tools like HMMER to select a priori partitions have been successfully used in combination with circular HMMs to detect TR regions in sequences (Schaper et al. 2014). Other approaches are discussed, for example, in Heger et al. (2009). A possible future extension with regards to inferring a fixed number of partitions could be the implementation of a Dirichlet process to infer the most probable partitions as discussed in Moore et al. (2014).

Availability

The source code, written in C, to our modified version of CodonPhyML is available at the main page of CodonPhyML, http://codonphyml.sf.net (last accessed April 30, 2015). A tarball named “codonphyml_multi.tgz” can be found in the “Files” section of this page. It includes detailed instructions on how to compile and run the software.

Materials and Methods

Annotation and Alignment of Protein-Coding Genes with LRRs

LRR regions were annotated based on the combination of 1) the profile HMM search using HMMER (Finn et al. 2011a) and 2) the de novo meta-approach for TR detection (Schaper et al. 2012). Table 5 summarizes the statistics obtained with both approaches. Only sequences that had codon information were used for this study. Homologous groups including less than four sequences were excluded from our analysis. To obtain more accurate MSAs of homologous protein sequences with LRR regions, we opted to use more conservative annotations obtained by the approach of Schaper et al. (2012). These annotations helped to guide alignment inference using a tandem-repeat-aware MSA inference program ProGraphMSA+TR by Szalkowski and Anisimova (2013).

Table 5.

Statistics on Different TR Detection Methods on Our Data Set.

	Profile HMM Search (Finn et al. 2011b)	De Novo Meta (Schaper et al. 2012)
(avg #TR)/Protein	7.3 (5.1)	3.6 (4.5)
(avg length TRR)/Protein	120.4 (108.45)	80 (111.5)
(avg length TR)/Protein	7.3 (5)	20.7 (7.9)

Note.—Average number of TRs per protein, average length of tandem repeat region (TRR) per protein, and average length of TR per protein (standard deviations in brackets) are given in this table.

Model Configurations and Model Comparison

In each MSA, we defined two partitions: The LRR region and the remaining sequence. To define the LRR region, we used annotations of LRR units as obtained by HMMER. Each alignment column that included at least one sequence annotated as LRR region has been marked as being a possible LRR region. Five different model configurations were defined for each MSA and have been applied to estimate phylogenies. The most simple codon model M0 assumes constant selection pressure over all sites (M0; Goldman and Yang 1994). Our single-partition model used model M0 on the whole MSA. Four two-partition models utilized two different M0 models in the two partitions of an MSA. Different two-partition model configurations differed by parameters that were shared between the two partitions. Codon frequencies have been estimated empirically (always F3X4) either from the whole MSA or only from the two partitions separately. Mutation rate, ω, and κ parameters could be shared (i.e., be the same) between the partitions or estimated as two independent parameters for the two partitions. All model configurations are listed in table 2. Configuration g1 is the simplest, and configuration r2 is the most complex variant in this set. All optimizations used a starting tree generated by BioNJ (Gascuel 1997), followed by an NNI heuristic search under one of the specified codon models (see Gil et al. [2013] for more information).

After estimating all model parameters (M0 parameters κ and ω, frequencies, tree topology, branch lengths and, in some cases, model mutation rates), we used the hLRT (e.g., Posada and Crandall 1998) to assess the performance of different model configurations. The order in which the hLRTs can be applied is either forward (from the simplest model to the most complex) or backward (from the most complex model to the simplest one). In both cases, a series of LRTs were performed. Each LRT compared two nested model configurations a and b with their maximized likelihoods L_a and L_b and their respective free parameter numbers d_a and d_b. The significance of the test was assessed by comparing the test statistic $2(\log L_a-\log L_b)$ to a ${\chi }^2$ distribution with $d_a-d_b$ degrees of freedom. In our analyses, we used stringent significance level $\alpha =0.01$.

Forward and backward LRT procedures do not necessarily agree on a single best model. As a tie breaker, we also include the AICc (Hurvich and Tsai 1989). For each model configuration a on an MSA with n sites, we calculate an AICc value $2d_a-2\log L_a+\frac{2d_a(d_a+1)}{n-d_a-1}$. Smaller AICc values indicate better model fit. As AICc differences of less than 4 are considered not to be well distinguishable (Burnham and Anderson 2002), we used this as a threshold for our model selection with AICc. For each single data set, all models with AICc no more than 4 points distant from the smallest AICc value were considered equally fitting.

The results of AICc, forward and backward LRT were summarized in one consensus agreement. If the three measures did not agree on a single model, we reported two consensus configurations; first, a conservative approach where we chose the model with the lowest number of parameters, and second the winning configuration by AICc.

Simulated Sequences under Different Topologies

To see whether using two-partition models allows to infer better topologies, we simulated different data sets under different constraints. For each chosen level of divergence ($0.15,0.3,0.6,0.12$), we simulated first two different basic sets of sequences, one under M0 with $\omega =0.5,\kappa =1.6$, the other set under M0 with $\omega =1.5,\kappa =1.6$. Each set contains 100 trees with 100 leaves each and 540 nt at each leaf. The trees emerged from a birth–death process but correspond, that is, the first tree in the first basic set is also used for the first sample in the second set. Next, the two sets have been combined into one data set such that the sequences have been concatenated. This leads to one larger data set of 100 trees with 100 leaves each, using 1,080 nt at each leaf. We then reestimated the topology using codonPhyML in two different configurations; first, using only one instance of M0 for the whole MSA, second, using a two-partition model. This has been done for all four levels of divergence. We next measured the Robinson–Foulds distance of the estimated trees to the true tree and used the distance differences as a measurement of how good the two model configurations estimate the true topology (Robinson and Foulds 1981).

In a second round of simulations, we constructed a comb tree, a perfectly balanced tree, and a near star-like tree (all internal branches with length a, branches connected to leafs with length $100\times a$). For each of these topologies, 50 samples have been simulated, again with 100 taxa using 1,080 nt in total. As before, we simulated two halves of each of the finally used sequences once using M0 using $\omega =0.5$, once under M0 using $\omega =1.5$. To evaluate the results, we compared the Robinson–Foulds distances of the estimated trees to the true trees.

All simulations have been done with ALF (Dalquen et al. 2012).

Supplementary Material

Supplementary materials S1 and S2 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).