A Two-step Estimation Approach for Logistic Varying Coefficient Modeling of Longitudinal Data

Abstract

Varying coefficient models are useful for modeling longitudinal data and have been extensively studied in the past decade. Motivated by commonly encountered dichotomous outcomes in medical and health cohort studies, we propose a two-step method to estimate the regression coefficient functions in a logistic varying coefficient model for a longitudinal binary outcome. The model depicts time-varying covariate effects without imposing stringent parametric assumptions. The proposed estimation is simple and can be conveniently implemented using existing statistical packages such as SAS and R. We study asymptotic properties of the proposed estimators which lead to asymptotic inference and also develop bootstrap inferential procedures to test whether the coefficient functions are indeed time-varying or are equal to zero. The proposed methodology is illustrated with the analysis of a smoking cessation data set. Simulations are used to evaluate the performance of the proposed method compared to an alternative estimation method based on local maximum likelihood.

1 Introduction

Longitudinal data arise frequently from medical and health cohort studies where the subjects are measured repeatedly over time. Our working example is the smoking cessation data described in Shoptaw et al. (2002). Follow-up data was collected on 175 participants for 12 weeks in a clinical trial to evaluate two behavioral methods for optimizing smoking cessation outcomes in methadone maintained cigarette smokers. At each visit, samples of breath were measured for carbon monoxide level and a binary outcome representing smoking status was recorded along with many covariates including age, gender and behavioral treatment. Hence, the data is of the form [{t_ij, X_i(t_ij), Y_i(t_ij)}, i = 1, …, n, j = 1, …, T_i] for n subjects, where T_i denotes the total number of repeated measures, X_i(t_ij) = {X_i1(t_ij), …, X_id(t_ij)}^T and Y_i(t_ij) denote the vector of d covariates and the binary response variable measured at time t_ij for subject i, respectively. Of interest is to assess the potentially time-varying effects of behavioral treatments on the outcomes adjusting for potential risk factors.

Many parametric models have been proposed to analyze longitudinal binary data (Pendergast et al., 1996) including generalized linear mixed models (GLMM) (McCullagh and Nelder, 1989; Breslow and Clayton, 1993). These approaches are typically limited by the stringent assumption of constant covariate effects over time which may not always hold in applications. Furthermore, even if the covariate effects do not change over time, parametric approaches involving a small number of parameters do not work well when there is a large number of repeated measurements, as the pattern of covariate effects over time may not be fully captured by only a few parameters. Logistic varying coefficient models for longitudinal binary data have been proposed to allow regression coefficient functions to change over time,

$$Y_i(t)\mid X_i(t)~\text{Bernoulli}\{{\pi }_i(t)\},log\left\{\frac{{\pi }_i(t)}{1-{\pi }_i(t)}\right\}=X_i{(t)}^{\mathrm{T}}\beta (t),$$ (1)

without assuming any parametric form (Cleveland, Grosse and Shyu, 1991; Hastie and Tibshirani, 1993; Cai, Fan and Li, 2000). In (1), corr{Y_i(s), Y_i′(t)} = γ(s, t)I_(i=i′), where β(t) is a vector of d regression coefficient functions, π_i(t) = Pr{Y_i(t) = 1|X_i(t)}, and γ(s, t) is an unknown bivariate correlation function. In this model, the observations from different subjects are independent and the repeated measurements from the same subject are correlated. The use of this model is two-fold. First, it can be used to check whether or not the effect of a covariate changes over time by plotting the corresponding coefficient function. Second, it provides a useful alternative for analyzing longitudinal binary data when the constant covariate effects assumption is not valid.

Recently several works have been proposed for estimation in generalized varying coefficient models. Cai, Fan and Li (2000) proposed local maximum likelihood and Zhang and Peng (2010) developed simultaneous confidence bands and hypothesis testing for i.i.d data applications. For longitudinal generalized outcomes, Zhang (2004) extended the GLMM model by representing the covariate effects via smooth but otherwise arbitrary functions of time. They use random effects to model the correlation among and within subjects, and use the double penalized quasi-likelihood method for estimation. However as mentioned in the paper, this approach does not perform well for binary outcomes and may require an additional bias correction step. Qu and Li (2006) proposed an efficient estimation procedure for generalized varying coefficient models for longitudinal data via an integrated quadratic inference function and penalized splines approach. This approach can easily take into account correlation within subjects; however it is still parametric in nature although the dimension of the parameter space is high. Şentürk et al. (2013) and Estes et al. (2014) consider extensions of the local maximum likelihood approach of Cai, Fan and Li (2000) for estimation in generalized varying coefficient models for i.i.d. data to modeling longitudinal data. This extension is shown to be useful in applications where follow-up in longitudinal studies are truncated by death. For estimation in a generalized varying coefficient model from unsynchronized longitudinal data where response and predictors may not be collected at the same time points, Şentürk et al. (2013) proposed a nonparametric moments approach, while Cao, Zeng, Fine (2014) proposed kernel weighted estimating equations.

As a novel departure from existing literature, we propose a two-step procedure to estimate the coefficient functions in a logistic varying coefficient model. The first step involves fitting a standard logistic regression at each of the observation time points t_ij. In the second step an estimate of each regression coefficient function is obtained by smoothing the raw estimates from the first step based on a nonparametric regression method. The proposed methodology is applicable when data is observed or can be grouped/binned across a set of common time points for patients, such that 1) there is enough data at each time point to fit a logistic regression model in the first step and 2) the set of observation times are dense in the considered time domain for the smoothing implemented in the second step. A major advantage of the proposal is that our estimators can be easily obtained using existing statistical softwares. We point out that our approach is similar to that used by Fan and Zhang (2000) for varying coefficient models with continuous response, referred to by the authors as the functional linear model. However, there is a fundamental difference between a functional linear model and a logistic varying coefficient model in that the raw estimates are unbiased for the linear model, but biased for the logistic regression model for finite samples. The bias for the latter model has to be handled with care when developing the large sample properties of the proposed two-step (TS) estimators. In addition to establishing the asymptotic properties of the TS estimators leading to asymptotic confidence intervals, we also develop bootstrap inferential procedures to test whether the coefficient functions are indeed time-varying or are equal to zero. While the first hypothesis evaluates whether the logistic varying coefficient model reduces to a parametric form, the second can be used in identifying significant predictors.

This paper is organized as follows. The two-step estimation procedure is described in detail in Section 2. In Section 3, the asymptotic properties of the proposed estimators are studied, and statistical inference procedures are discussed. In Section 4, we apply the proposed method to the smoking cessation data described earlier. In Section 5, we present simulation studies to assess and compare the performance of the proposed TS estimation with the local maximum likelihood (LML) approach of Şentürk et al. (2013) and Estes et al. (2014). Similar to previously published results for continuous outcome (Fan and Zhang, 2000), our simulations show that the proposed TS estimators perform better than those obtained through LML also for longitudinal binary outcome when the varying coefficient functions admit varying degrees of smoothness. This is due to the flexibility of the TS approach in allowing the use of different bandwidths for each varying coefficient function, different from the single global bandwidth used in the LML approach. We conclude with a discussion section and collect technical proofs in an appendix, deferred to supplementary documents.

2 The Proposed Two-step Estimation Procedure

In this section, we derive the proposed two-step estimator for the coefficient function β(t). In the first step, a raw estimate of β(t) at each design time point is obtained by fitting a standard logistic regression. In the second step, a final estimate of β(t) is obtained by smoothing the raw estimates using a nonparametric curve estimation method. Throughout this paper, we let 𝒟 = [{t_ij, X_i(t_ij)}, i = 1, …, n, j = 1, …, T_i], which contains the design time points and the covariate information. The range of time is [0, D] for some specified D. Note that under model (1), we have Cov{Y_i(t), Y_i(t)|𝒟} = Var{Y_i(t)|𝒟} = π_i(t){1 − π_i(t)} and Cov{Y_i(s), Y_i(t)|𝒟} = γ(s, t) [Var{Y_i(s)|𝒟}Var{Y_i(t)|𝒟}]^1/2, where γ(t, t) = 1.

2.1 Step I: Obtaining the Raw Estimates

Let A = {t_j, j = 1, …, T} be the collection of distinct time points among {t_ij, i = 1, …, n, j = 1, …, T_i}. For any t_j ∈ A, let N_j = {i₁, …, i_nj} denote the collection of subject indices of all Y_i(t_ij) observed at t_j, where n_j is the number of subjects observed at t_j. Then, under model (1), we have at the time t_j,

$$Y_i(t_j)\mid X_i(t_j)~\text{Bernoulli}\{{\pi }_i(t_j)\},log\left\{\frac{{\pi }_i(t_j)}{1-{\pi }_i(t_j)}\right\}=X_i{(t_j)}^{\mathrm{T}}\beta (t_j),\text{for}\text{all}i\in N_j.$$ (2)

The raw estimate b(t_j) = {b₁(t_j), …, b_d(t_j)}^T is defined as the maximum likelihood estimate of β(t_j) = {β₁(t_j), …, β_d(t_j)}^T from the standard logistic regression model (2).

2.2 Step II: Refining the Raw Estimates

For the r-th component of the coefficient vector, we obtain a refined estimate by smoothing the raw estimates [{t_j, b_r(t_j)}, j = 1, …, T], r = 1, …, d. For example, the local polynomial smoothing method (Fan and Gijbels, 1996) yields the following linear estimator for the q^th derivative of β(t), which is assumed to be (p + 1)-times continuously differentiable for some p ≥ q:

$$\widehat{{\beta }_r^{(q)}}(t)=\sum _{j=1}^T{\omega }_{q,p+1}(t_j,t)b_r(t_j)\text{for}r=1,\dots ,d,0\le q\le p+1.$$ (3)

The weight functions ω_q,p+1(t_j, t) in (3) are induced by the local polynomial fitting and are defined in the assumptions section given at beginning of the Appendix. Note that the raw estimates of the coefficient functions are defined only at the design time points. However, the refined estimate $\widehat{{\beta }_r^{(q)}}(t)$ are defined for all t ∈ [0, D]. Furthermore, it aggregates the information around time t.

A big advantage of the component-wise smoothing in the second step is that the estimation can adapt to the different degrees of smoothness of the varying coefficient regression functions. The resulting favorable performance of the proposed TS with separate bandwidths for each varying coefficient function over the LML with a single bandwidth for all varying coefficient functions will be studied in the simulation studies. The bandwidths for smoothing in the second step of the proposed TS approach can be chosen by plotting the raw estimates from the first step or by automatic bandwidth selection algorithms. We utilize plots of the raw estimates in the analysis of the smoking cessation data in Section 4 and utilize the rule-of-thumb bandwidth selection criteria of Ruppert, Sheather and Wand (1995) in the simulation studies presented in Section 5. The rule-of-thumb estimator is a ‘plug-in’ bandwidth selection rule, which involves estimation of unknown functionals that appear in formulas for the asymptotically optimal bandwidth (balancing the bias and variance trade-off). Rupert, Sheather and Wand (1995) extend the ‘plug-in’ bandwidth selectors of density estimation to local least squares kernel regression; traditional smoothing bandwidth section rules, such as those based on cross-validation, exhibit very inferior asymptotic and practical performance, on the other hand, plug-in bandwidth selection rules have been shown to perform more reliably, both theoretically and in practice. We refer the reader to Ruppert, Sheather and Wand (1995) for a more detailed discussion of the properties of the rule-of-thumb bandwidth selector and other ‘plug-in’ bandwidths selectors that are equally easy to employ in local least squares kernel regression.

Remark 1

We note that the raw estimate b(t_j) of β(t_j) usually has a finite sample bias that may not be negligible when n_j is small. This bias will be carried over to the refined estimate obtained in the second step and needs to be handled with care when studying the asymptotic properties of the two-step estimator. In practice, one may also run into situations where, for some time point t_j, the sample size n_j is smaller than the number of covariates d. In such a case, it is impossible to fit a logistic regression model at time t_j. In fact, n_j > 10d (10 observation per parameter) may be needed typically in applications for stable regression fits and more observations may be needed when the conditional mean is close to 0 or 1. Similar to the approach by Fan and Zhang (2000) for functional linear models, one could leave b(t_j) missing. This is equivalent to treating observations at these t_j’s as if they were not in the data at all. This potentially reduces the bias compared to including them in the calculation. Another possible solution is to increase the sample size by including observations from the neighbors. For instance, one could include observations at t_j−1 and t_j+1 to fit the logistic regression at t_j. We study the performance of these approaches via simulations. Results summarized in Section 5.1 show that both remedies perform reasonably well in practice for a moderate proportion (10–30%) of time points with smaller sample size (i.e. n_j < 10d) as long as β(t) is smooth and changes slowly in time.

Remark 2

In step 2 we define our estimator (3) by smoothing each component separately without utilizing the covariance structure between different components. One could potentially improve our estimator by incorporating the covariance information that is determined by the correlation function γ(s, t). However, because the bivariate function γ(s, t) is unknown, the efficiency gain could be hard to realize if γ(s, t) is not accurately estimated. We choose to use (3) for its simplicity and computational convenience.

3 Asymptotic Properties and Inference

In this section, we investigate the asymptotic bias, variance and normality of the proposed TS estimators. A bootstrap method is also proposed to construct global confidence bands, which enables one to perform hypothesis testing about the coefficient functions. We assume the outcomes at each time point are missing completely at random hereafter.

3.1 Asymptotic Properties

Denote the response vector and the design matrix for the logistic regression model (2) at t_j by Ỹ_j = {Y_i1(t_j), Y_i2(t_j), ···, Y_inj(t_j)}^T, and X̃_j = {X_i1(t_j), X_i2(t_j), …, X_inj(t_j)}^T respectively. The following lemma gives the asymptotic properties of the raw estimators.

Lemma 1

Assume that condition (A4) in the Appendix (Supplementary documents) holds. Assume further that given 𝒟,

• (N1)The covariates are uniformly bounded, i.e., there exists an M₀ such that |X_ijr| ≤ M₀, for all i, j, and r.
• (N2)Let $I_j={\stackrel{\sim }{X}}_j^{\mathrm{T}}{W}_j{\stackrel{\sim }{X}}_j$ be the Fisher information matrix where W_j = diag[π_i1(t_j){1 − π_i1(t_j)}, …, π_inj(t_j){1 − π_inj(t_j)}] is the covariance matrix of Ỹ_j. Further let λ_1,nj and λ_ℓ,nj be respectively the smallest and the largest eigenvalue of I_j. There exists a random variable M₁ such that, with probability 1, λ_ℓ,nj/λ_1,nj< M₁, for all n_j, j and E(M₁) < ∞.

Let b(t_j) be the raw estimate of β(t_j) defined in Section 2.1. Then

$$\begin{array}{c}E\{b(t_j)-\beta (t_j)\mid \mathcal{D}\}=o\left(n_j^{-1}\right),\mathit{Cov}\{b(t_j)\mid \mathcal{D}\}=I_j^{-1}\{1+o(1)\}\text{and}\\ \mathit{Cov}\{b(t_j),b(t_k)\mid \mathcal{D}\}=I_j^{-1}{I}_{jk}{I}_k^{-1}\gamma (t_j,t_k)\{1+o(1)\},\end{array}$$ (4)

as n_j → ∞ and n_k → ∞, where $I_{jk}={\stackrel{\sim }{X}}_j^{\mathrm{T}}{W}_j^{1/2}{M}_{jk}{W}_k^{1/2}{\stackrel{\sim }{X}}_k$. The n_j ×n_k matrix M_jk is defined as follows: If the a^th entry of Ỹ_j and the b^th entry of Ỹ_k come from the same subject, then the (a, b)^th entry of M_jk is equal to 1, and is 0 otherwise.

Note that

$$\begin{array}{ll}\hfill \mathrm{E}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}& =\sum _{j=1}^T{\omega }_{q,p+1}(t_j,t)\mathrm{E}\{b_r(t_j)\mid \mathcal{D}\},\text{and}\hfill \\ \hfill \text{Var}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}& =\sum _j\sum _k{\omega }_{q,p+1}(t_j,t){\omega }_{q,p+1}(t_k,t)\text{Cov}\{b_r(t_j),b_r(t_k)\mid \mathcal{D}\}.\hfill \end{array}$$ (5)

The following theorem gives the asymptotic bias of $\widehat{{\beta }_r^{(q)}}(t)$.

Theorem 1

Assume that the conditions (A1)–(A6) in the Appendix and the conditions (N1) and (N2) of Lemma 1 hold. Then

$$\begin{array}{l}\mathit{Bias}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}=\frac{q!{\beta }_r^{(p+1)}(t)h^{p-q+1}}{(p+1)!}{B}_{p+1}(K_{q,p+1})\{1+o_p(1)\}+O(1/n_{\wedge })\\ =O(h^{p-q+1})+O(1/n_{\wedge }),\end{array}$$

as T → ∞ and n_∧ = min{n₁, …, n_T} → ∞, for r = 1, …, d and 0 ≤ q ≤ p + 1, where h is the bandwidth for local polynomial smoothing and B_p+1(K_q,p+1) is as defined in the Appendix before the proof of Lemma 1.

We note that the asymptotic bias comes from two sources. The first term is from the smoothing step, which goes to 0 when the bandwidth tends to 0. The second term is from the logistic regression in the first step, since the MLE in ordinary logistic regression is biased. It goes to 0 when the sample sizes go to ∞.

The variance of $\widehat{{\beta }^{(q)}}(t)$ in (5) can be further simplified under more assumptions on the model. First, assume condition (A4) holds and let Ω_j = E[π_i(t_j){1 − π_i(t_j)}X_i(t_j)X_i(t_j)^T], and ${\mathrm{\Omega }}_{jk}=\mathrm{E}[\sqrt{{\pi }_i(t_j)\{1-{\pi }_i(t_j)\}}\sqrt{{\pi }_i(t_k)\{1-{\pi }_i(t_k)\}}{X}_i(t_j)X_i{(t_k)}^{\mathrm{T}}]$. Then, for any given time t_j and β(t_j), $I_j={\stackrel{\sim }{X}}_j^{\mathrm{T}}{W}_j{\stackrel{\sim }{X}}_j={\sum }_{k=1}^{n_j}{\pi }_{i_k}(t_j)\{1-{\pi }_{i_k}(t_j)\}{X}_{i_k}(t_j)X_{i_k}{(t_j)}^{\mathrm{T}}$, where π_ik(t_j){1 − π_ik(t_j)} = {e^{X_ik(t_j)Tβ(t_j)}}/{1 + e^{X_ik(t_j)Tβ(t_j)}}², depends on X_ik(t_j) only. Therefore, I_j is a sum of i.i.d. random matrices with E(I_j)=n_jΩ_j. This fact, combined with Lemma 1, implies that

$$\text{Cov}\{b(t_j),b(t_k)\mid \mathcal{D}\}=I_j^{-1}{I}_{jk}{I}_k^{-1}\gamma (t_j,t_k)\{1+o(1)\}=\gamma (t_j,t_k)\frac{n_{jk}}{n_j{n}_k}{\mathrm{\Omega }}_j^{-1}{\mathrm{\Omega }}_{jk}{\mathrm{\Omega }}_k^{-1}\{1+o_p(1)\}$$

and $\text{Var}\{b(t_j)\mid \mathcal{D}\}=({\mathrm{\Omega }}_j^{-1}/n_j)\{1+o_p(1)\}$, with probability 1, where n_jk is the number of subjects in N_j ∩ N_k. Plugging the above equations into (5) gives

$$\begin{array}{l}\text{Var}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}=\{\sum _{j\ne k}\frac{n_{jk}}{n_j{n}_k}\gamma (t_j,t_k){\omega }_{q,p+1}(t_j,t){\omega }_{q,p+1}(t_k,t){({\mathrm{\Omega }}_j^{-1}{\mathrm{\Omega }}_{jk}{\mathrm{\Omega }}_k^{-1})}^{(rr)}\\ +\sum _j\frac{1}{n_j}{\omega }_{q,p+1}^2(t_j,t){({\mathrm{\Omega }}_j^{-1})}^{(rr)}\}\{1+o_p(1)\},\end{array}$$ (6)

where M^(rr) denotes the (r, r)^th element of a matrix M. In general, we can not simplify the formula in (6) without further assumptions. This is because Ω_j depends on j through β(t_j) and X̃_j, which makes the summation very hard to compute. If the covariates X_i(t_j) and coefficient functions β(t) satisfy conditions (A7) and (A8), that is, they are time-invariant, then Ω_j = Ω_k = Ω_jk = Ω₁. In this case, $\text{Cov}\{b(t_j),b(t_k)\mid \mathcal{D}\}=\gamma (t_j,t_k)\{n_{jk}/(n_j{n}_k)\}{\mathrm{\Omega }}_1^{-1}\{1+o_p(1)\}$ and Cov{b_r(t_j), b_r(t_k)|𝒟} = γ(t_j, t_k){n_jk/(n_jn_k)}ω^(rr){1+o_p(1)} where ${\omega }^{rr}={({\mathrm{\Omega }}_1^{-1})}^{(rr)}$ denotes the (r, r)^th element of ${\mathrm{\Omega }}_1^{-1}$.

We will derive the asymptotic variance for two specific situations: n_ij is either small or large, as in Fan and Zhang (2000). Let I_t = {j : |t_j − t| ≤ h} be the indices of the local neighborhood. In some situations, n_jk may be much smaller than n_j or n_k for all j ≠ k, j, k ∈ I_t and n_j, j ∈ I_t are about the same proportion as n. Results for this situation are summarized in the following theorem.

Theorem 2

Let conditions (A1)–(A8), (N1) and (N2) hold. Assume

$$n_{jk}/(n_j{n}_k)=\{\begin{array}{ll}o\{1/(nT{h}^{2q+1})\},\hfill & j\ne k,\hfill \\ 1/(cn)+o\{1/(nT{h}^{2q+1})\},\hfill & j=k\hfill \end{array}$$

holds uniformly for all j, k ∈ I_t for some constant 0 < c < 1, then when h → 0 and nTh^2q+1 → ∞ as n, T → ∞,

$$\mathit{Var}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}=\frac{{\omega }^{rr}q{!}^2}{{\mathit{cnTh}}^{2q+1}f(t)}V(K_{q,p+1})\{1+o_p(1)\},$$

where V(·) is as defined in the Appendix before the proof of Lemma 1 and f(·) denotes the density of t.

The proof of Theorem 2 is similar to the proof of Theorem 2 of Fan and Zhang (2000) except that γ(t, t) is 1 and therefore is not included in the above result. Recall that they define γ(s, t) as the covariance function of the process, and we define it as the correlation function.

In some other situations, n_j, n_k and n_jk may be about the same as n. An extreme case is a dataset with no missing values, in which n_j = n for all j = 1, …, T. Let γ_α,β(s, t) denote ∂^α+βγ(s, t)/∂s^α∂t^β for any integers α, β = 0, 1, …, p + 1.

Theorem 3

Let conditions (A1)–(A8), (N1) and (N2) hold. Assume n_jk/(n_jn_k) = 1/n + o(1/n) holds uniformly for all j = 1, …, T. Then when h → 0 and n, T → ∞,

$$\mathit{Var}\left\{\widehat{{\beta }_r^{(q)}}(t)\mid \mathcal{D}\right\}=\frac{{\omega }^{rr}}{n}\left\{{\gamma }_{q,q}(t,t)+\frac{2q!{\gamma }_{q,p+1}(t,t)h^{p-q+1}}{(p+1)!}{B}_{p+1}(K_{q,p+1})\right\}+o_p\left(\frac{h^{p-q+1}}{n}\right),$$

where B_p+1(·) is as defined in the Appendix before the proof of Lemma 1.

The proof of Theorem 3 is straight forward by applying Lemma 3 in Fan and Zhang (2000), but with σ²(t) = 0. This lemma is applicable because our γ(s, t) satisfies the requirements of γ₀(s, t) in their paper.

Furthermore, the next theorem gives asymptotic normality of $\widehat{{\beta }_r^{(q)}}(t)$. First, define $b={(b_1^{\mathrm{T}},b_2^{\mathrm{T}},\dots ,b_T^{\mathrm{T}})}^{\mathrm{T}}$ and $\beta ={({\beta }_1^{\mathrm{T}},{\beta }_2^{\mathrm{T}},\dots ,{\beta }_T^{\mathrm{T}})}^{\mathrm{T}}$, to be the vectors of the raw estimators and the true coefficients across time. For r ∈ {1, …, d}, define a T×dT matrix P^(r), whose {k, (k−1)d+r}th elements for k ∈ {1, …, T} are equal to 1, and all other elements are equal to 0. The operator P^(r) extracts the r^th row of b and β, i.e. P^(r)b = {b_r(t₁), …, b_r(t_T)}^T. Define dT × dT block diagonal matrix B̄ = Diag {I₀(β₁)⁻¹, …, I₀(β_T)⁻¹} where I₀(β_j) is the Fisher information matrix for β_j unconditional on 𝒟 for j = 1, …, T, i.e.

$$I_0({\beta }_j)=\mathrm{E}\{{\pi }_{1j}(1-{\pi }_{1j})X_1{(t_j)}^{\mathrm{T}}{X}_1(t_j)\}.$$ (7)

Further let Σ_i be the matrix

$$\left[\begin{array}{ccc}{X}_{i1}{X}_{i1}^{\mathrm{T}}{\pi }_{i1}(1-{\pi }_{i1})& \cdots & \cdots \\ X_{i2}{X}_{i1}^{\mathrm{T}}\sqrt{{\pi }_{i1}(1-{\pi }_{i1})}\sqrt{{\pi }_{i2}(1-{\pi }_{i2})}\gamma (t_1,t_2)& \cdots & \cdots \\ ⋮& \ddots & ⋮\\ X_{iT}{X}_{i1}^{\mathrm{T}}\sqrt{{\pi }_{i1}(1-{\pi }_{i1})}\sqrt{{\pi }_{iT}(1-{\pi }_{iT})}\gamma (t_1,t_T)& \cdots & X_{iT}{X}_{iT}^{\mathrm{T}}{\pi }_{iT}(1-{\pi }_{iT})\end{array}\right]$$

and Σ = E(Σ_i) with respect to [X_ij = {X_i1(t_j), …, X_id(t_j)}^T, j = 1, …, T]. The matrix Σ is well defined because under condition (A4), E(Σ_i) = E(Σ_i′).

Theorem 4

Let conditions (A1)–(A4), (A6), (N1) and (N2) hold. Then conditional on 𝒟, it holds that

$$\sqrt{n}(b-\beta )\stackrel{d}{\to }\overline{B}N(0,\mathrm{\sum }),$$

as T is fixed and n → ∞. For fixed T, let ω_T(t) be the vector of weight functions, ω_T(t) = {ω_q,p+1(t₁, t), …, ω_q,p+1(t_T, t)}^T where $\widehat{{\beta }_r^{(q)}}(t)={\omega }_T(t)P^{(r)}b$ by (3). Then it holds that

$$\sqrt{n}\left\{\widehat{{\beta }_r^{(q)}}(t)-{\omega }_T(t)P^{(r)}\beta \right\}\stackrel{d}{\to }{\omega }_T(t)P^{(r)}\overline{B}N(0,\mathrm{\sum }),$$

as T is fixed and n → ∞. Or equivalently,

$$V_T^{-\frac{1}{2}}\sqrt{n}\left\{\widehat{{\beta }_r^{(q)}}(t)-{\omega }_T(t)P^{(r)}\beta \right\}\stackrel{d}{\to }N(0,I_T),$$

as n → ∞ for fixed T where V_T = ω_T(t)P^(r)B̄Σ{ω_T(t)P^(r)B̄}^T.

Theorem 4 shows that for any fixed T, the distribution of our final estimate $\widehat{{\beta }_r^{(q)}}(t)$ for ${\beta }_r^{(q)}(t)$ is approximately normal for sufficiently large n. However, to construct a confidence interval for ${\beta }_r^{(q)}(t)$, the difference between ω_T(t)P^(r)β and ${\beta }_r^{(q)}(t)$ must go to zero at a rate faster than (V_T/n)^1/2, since

$$V_T^{-\frac{1}{2}}\sqrt{n}\left\{\widehat{{\beta }_r^{(q)}}(t)-{\beta }_r^{(q)}(t)\right\}=V_T^{-\frac{1}{2}}\sqrt{n}\left\{\widehat{{\beta }_r^{(q)}}(t)-{\omega }_T(t)P^{(r)}\beta \right\}+V_T^{-\frac{1}{2}}\sqrt{n}\{{\omega }_T(t)P^{(r)}\beta -{\beta }_r^{(q)}(t)\}.$$

The following proposition gives conditions under which this requirement is satisfied. For simplicity, we only consider the case n_j = n for j = 1, …, T.

Proposition 1

Assume that the conditions in Theorem 4 hold and $\sqrt{n}{h}^{p-q+1}/T\to 0$, then

$$V_T^{-\frac{1}{2}}\sqrt{n}\{{\omega }_T(t)P^{(r)}\beta -{\beta }_r^{(q)}(t)\}=o_p(1)I_T.$$

Remark 3

As an example, lets consider the case p = 1 and q = 0, the local linear smoothing. It is easy to verify that if h ∝ T^ε−1 for ε ∈ (0, 1) and n ∝ T^δ for δ ∈ (0, 6 − 4ε), then n → ∞, h → 0, Th → ∞ and $\sqrt{n}{h}^{p-q+1}/T\to 0$ as T → ∞, which are needed for Theorem 4 and Proposition 1 to hold. For instance, if ε = 4/5, then h = O(T^−1/5). In addition, δ should be between 0 and 2.8, which could be easily satisfied in practice since n is usually much bigger than T.

3.2 Statistical Inference: The Proposed Asymptotic Confidence Intervals and the Bootstrap Confidence Bands

In practice, the variance of $\widehat{{\beta }_r^{(q)}}(t)$ can be estimated using equation (5). Cov{b(t_j), b(t_k)} is estimated by the first term in the second and the third equations of (1) by replacing W_j, W_k and γ(t_j, t_k) with their estimates accordingly. Here we estimate γ(t_j, t_k) by the Pearson’s sample correlation, denoted by γ̂(t_j, t_k), with data {Y_i(t_j), Y_i(t_k)} for all i ∈ N_jk. We estimate W_j by Ŵ_j = diag[π̂_i1(t_j){1 − π̂_i1(t_j)}, …, π̂_inj(t_j){1 − π̂_inj(t_j)}], where π̂_ik(t_j) = {e^{X_ik(t_j)Tβ̂(t_j)}}/{1 + e^{X_ik(t_j)Tβ̂(t_j)}}. Then ${\widehat{I}}_j={\stackrel{\sim }{X}}_j^{\mathrm{T}}{\widehat{W}}_j{\stackrel{\sim }{X}}_j$ and ${\widehat{I}}_{jk}={\stackrel{\sim }{X}}_j^{\mathrm{T}}{\widehat{W}}_j^{\frac{1}{2}}{M}_{jk}{\widehat{W}}_k^{\frac{1}{2}}{\stackrel{\sim }{X}}_k$. In (5), Var{b_r(t_j)} is estimated by the (r, r)^th element of ${\widehat{I}}_j^{-1}$, and Cov{b_r(t_j), b_r(t_k)} by the (r, r)^th element of $\widehat{\gamma }(t_j,t_k){\widehat{I}}_j^{-1}{\widehat{I}}_{jk}{\widehat{I}}_k^{-1}$. Finally, the variance estimator for ${\beta }_r^{(q)}(t)$ is given by

$$\widehat{\text{Var}}\left\{\widehat{{\beta }_r^{(q)}}(t)\right\}=2\sum _{j<k}{\omega }_{q,p+1}(t_j,t){\omega }_{q,p+1}(t_k,t)\widehat{\text{Cov}}\{b_r(t_j),b_r(t_k)\}+\sum _{j=1}^T{\omega }_{q,p+1}^2(t_j,t)\widehat{\text{Var}}\{b_r(t_j)\}.$$ (8)

The asymptotic results suggest that a 95% confidence interval of ${\beta }_r^{(q)}(t)$ be given by $\widehat{{\beta }_r^{(q)}}(t)\pm 1.96{[\widehat{\text{Var}}\{\widehat{{\beta }_r^{(q)}}(t)\}]}^{1/2}$, where the variance estimator is from (8).

Next we propose a global confidence band for the estimated curve $\widehat{{\beta }_r^{(q)}}(t)$, t ∈ [t₁, t_T] via bootstrap. We want to find two curves L(t) and U(t), t ∈ [t₁, t_T], such that, in the nominal confidence level 0.95,

$$\mathrm{P}\{L(t)\le {\beta }_r^{(q)}(t)\le U(t),t\in [t_1,t_T]\}=\mathrm{0.95.}$$ (9)

We consider a confidence band that is symmetric about the estimated curve. Therefore, $\{L(t),U(t)\}=\widehat{{\beta }_r^{(q)}}(t)\pm C_{0.95}{[\widehat{\text{Var}}\{\widehat{{\beta }_r^{(q)}}(t)\}]}^{1/2}$, where C_0.95 is an unknown constant that satisfies equation (9). With the confidence band taking the form above, equation (9) is equivalent to

$$\mathrm{P}\left({sup}_{t\in [t_1,t_T]}\frac{\mid \widehat{{\beta }_r^{(q)}}(t)-{\beta }_r^{(q)}(t)\mid }{\sqrt{\widehat{\text{Var}}\{\widehat{{\beta }_r^{(q)}}(t)\}}}<C_{0.95}\right)=\mathrm{0.95.}$$

We can estimate C_0.95 with a bootstrap 95^th percentile of the distribution of the supremum in the equation above. The algorithm is as following:

1. Resample the subjects with replacement from the original data, say B times. For simplicity, the size of each resample is the same as the original data.

2. For the k^th resample, k ∈ 1, …, B, calculate the value

   $$C^{(k)}={sup}_{t\in [t_1,t_T]}\frac{\mid {\widehat{{\beta }_r^{(q)}}}^{(k)}(t)-\widehat{{\beta }_r^{(q)}}(t)\mid }{\sqrt{\widehat{\text{Var}}\{{\widehat{{\beta }_r^{(q)}}}^{(k)}(t)\}}},$$

   where the superscript k indicates it is for the k^th resample.

3. Estimate C_0.95 by the sample 95^th percentile of the B values C^(k), k = 1, …, B, denoted by $\widehat{C_{0.95}}$.

Therefore, our bootstrap confidence band for ${\beta }_r^{(q)}(t)$, t ∈ [t₁, t_T] is given by $\widehat{{\beta }_r^{(q)}}(t)\pm \widehat{C_{0.95}}{[\widehat{\text{Var}}\{\widehat{{\beta }_r^{(q)}}(t)\}]}^{1/2}$.

Finally, the bootstrap confidence band can be used to test hypotheses about β_r(t). A typical null hypothesis is $H_0:{\beta }_r^{(q)}(t)=f(t)$, for all t ∈ [t₁, t_T], where f(t) is a known function defined in the specific interval. When f(t) ≡ 0, we can test whether the r^th covariate is insignificant throughout this interval, which in turn provides a way of variable selection in modeling. We reject the null hypothesis if the curve f(t) is not completely inside the confidence band.

Another null hypothesis of interest is $H_0:{\beta }_r^{(q)}(t)\equiv C^{\ast }$, for all t ∈ [t₁, t_T], where C^* is an unknown constant. With this null hypothesis, we can test whether the correlation of the r^th covariate with the response variable is time-invariant, which in turn provides a way to simplify a fully nonparametric model into a semiparametric model, or even a fully parametric model. We reject the null hypothesis if there does not exist a horizontal line completely inside the confidence band. Note that this test is expected to be conservative because the significance level is usually less than α. The reason is clear from the testing procedure. When the null hypothesis is true, confidence bands at nominal confidence level 95% for the line f(t) ≡ C^*, for all t ∈ [t₁, t_T], has a probability of 0.95 to cover f(t). For those that do not cover f(t), they may cover another constant line such as f(t) + 0.01. In this case, the test will still accept H₀. This results in an acceptance rate that is higher than 0.95 for H₀, which implies that the significance level is less than 0.05.

4 Application to Smoking Cessation Data

In this section, we illustrate the proposed method using the smoking cessation data described in the Introduction. The main objective of this clinical trial is to evaluate and compare two behavioral methods, relapse prevention (RP) and contingency management (CM), alone and in combination, for optimizing smoking cessation outcomes using nicotine replacement therapy in methadone maintained cigarette smokers. All 175 participants received nicotine transdermal therapy and were randomly assigned to receive one of the four behavioral treatments (none, RP, CM, RP+CM) for a period of 12 weeks. The participants were scheduled to visit back on every Monday, Wednesday and Friday. At every visit, measures were taken, including samples of breath (analyzed for carbon monoxide - CO reading) and urine, and weekly self-reported number of cigarettes smoked. Some participants didn’t complete all the 36 visits, nevertheless many covariates were measured for each participant.

The dichotomous response variable of interest is smoking status determined from the CO reading, where smokers are coded as 1 (smoking status=1) and non-smokers as 0 (smoking status=0). The following subset of covariates are considered in our analysis: gender (2 categories), ethnicity (3 categories), treatment group assignments (4 categories), baseline CO reading, baseline urine opiate result (2 categories dirty or clean), baseline urine cocaine result (2 categories dirty or clean), baseline cotinine reading, age, number of cigarettes smoked per day, number of years smoked, depth of inhalation (3 categories), and number of times making serious attempt to quit. These covariates are all baseline measures, which means they are time-invariant. We treat categorical variables as class variables. That is, each category (except the reference level) has its own coefficient function. Among the 175 participants, only one subject is found to have a 0 (not at all) for the variable INHALE. It is modified to value 1 to reduce the categories to 3 for INHALE. The only two Asian subjects are dropped from the data to reduce the variable ETHNICITY to 3 categories. The rationale for these reductions in categories is that if a category has too few observations, the coefficient function corresponding to this category will have a sample size that is too small for a logistic regression model. This may result in an unstable raw estimator in the first step, and make the final estimator questionable. Hence, there are 17 coefficient functions to be estimated, including the intercept and all non-reference levels of the categorical variables. Using the notation of our model, we have T = 36, n = 173, d = 17 for this example. We utilize local linear regression as the smoothing method in step two where the bandwidths are selected visually by plotting the raw estimates from step one separately for each varying coefficient function. The selected 17 bandwidths were between 12 and 17.

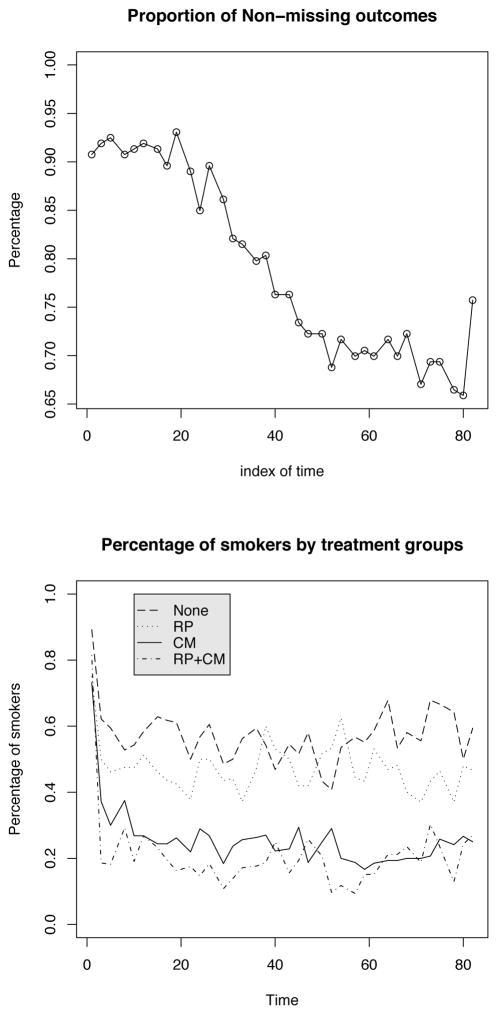
Figure 1 shows the percentage of nonmissing outcomes during each visit of the study. In the first 3 weeks, most individuals (over 90%) are observed at the scheduled visits. In the last several weeks, this percentage drops to about 70%. The main reason for missing data in our data example is patient drop-out. For estimation of the time varying effects at follow-up time point t, the proposed TS algorithm utilizes data on those subjects whose drop-out times (denoted now by R_i for subject i) are greater than t. In other words, in the presence of drop-out, the proposed modeling has a conditional target of inference E{Y_i(t)|X_i(t), R_i > t}, where the model characterizations of the relationship between the response and predictors at time t only pertain to those subjects that have not dropped out of the study at time t. It is important that the interpretation of the model fits be made according to this conditional target of inference. Also note that for the missing data encountered on observations of a subject before their dropout time, the proposed TS estimation algorithm is valid under missing completely at random (MCAR) structures. Please see the Discussion section for further comments on extensions of the proposed methodology to missing at random (MAR) data structures and alternative approaches to handling informative drop-out.

Figure 1.

The Smoking Cessation data. Percentage of nonmissing outcomes during each visit of the study (top plot). Percentage of smokers (determined by CO readings) by 4 treatment groups (bottom plot). Index of time is plotted in days.

Figure 1 also descriptively illustrates the effect of behavioral treatments. It plots the percentage of smokers (smoking status=1) by the 4 treatment groups along the 36 time points. The CM-only and RP+CM groups are significantly below the reference group (“none”), by having almost no overlap. The RP-only group is also below the reference group, but they overlap during the middle of the 12 week period. RP+CM group is also slightly below CM-only group with some overlap. It can be seen that both treatments are helping, but CM is much more effective.

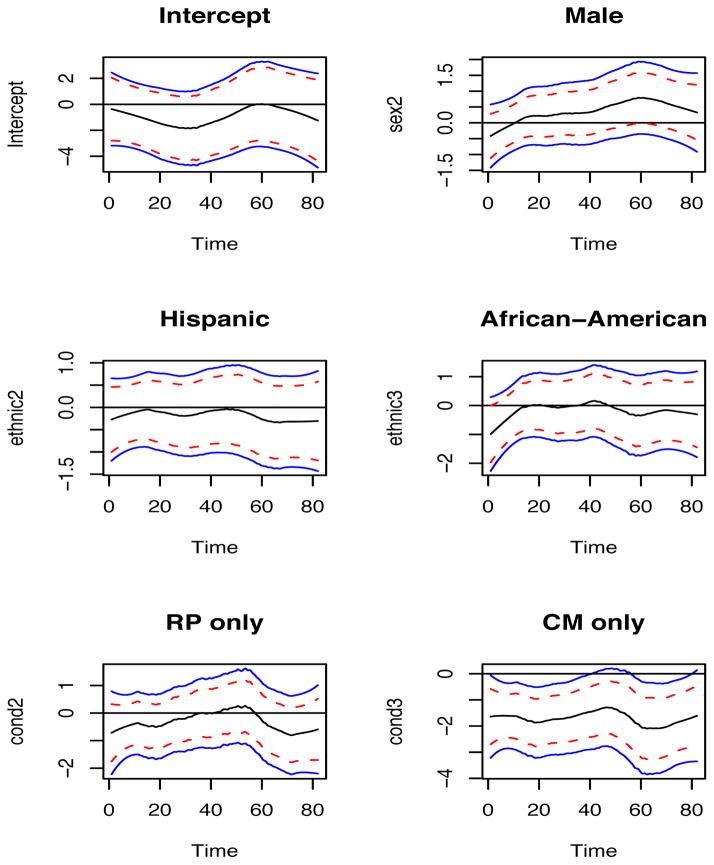
The refined estimators of the coefficient functions, along with their 95% bootstrap confidence bands and 95% point-wise confidence bands for all the covariates are presented in Figures 2–4. Note that the estimated γ(s; t) with correlation values ranging between zero and 0.2 was used in targeting the asymptotic variance of the varying coefficient function estimators leading to the proposed point-wise and bootstrap simultaneous CI’s. It is observed that the treatment effects of CM-only and CM+RP are significantly different from 0. In particular, the 95% bootstrap confidence band of the CM+RP treatment is almost completely below the zero line. This indicates a strong negative effect of the CM+RP treatment on the probability of being a smoker. The estimated curve for RP-only treatment is generally below the zero line, except in the middle. But the 95% bootstrap confidence band covers the entire zero line, indicating that it is not significant. These results are consistent with the findings of Shoptaw et al. (2002) and visual findings from Figure 1.

Figure 2.

The Smoking Cessation data (part 1). Curve estimate (solid line in center), 95% bootstrap confidence band (solid lines) and 95% point-wise confidence intervals (dash lines).

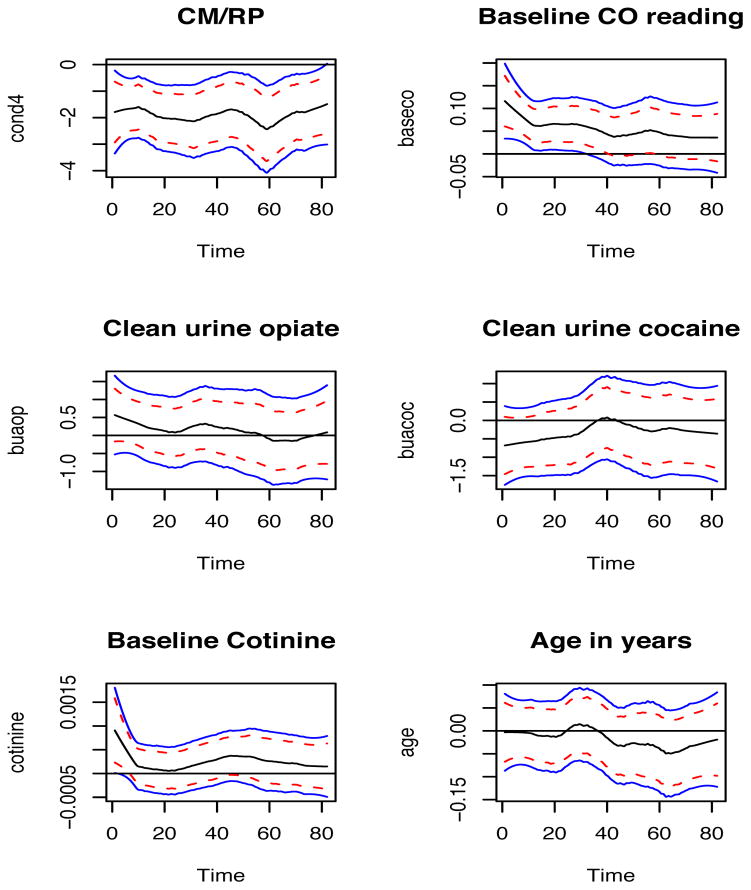
Figure 4.

The Smoking Cessation data (part 3). Curve estimate (solid line in center), 95% bootstrap confidence band (solid lines) and 95% point-wise confidence intervals (dash lines).

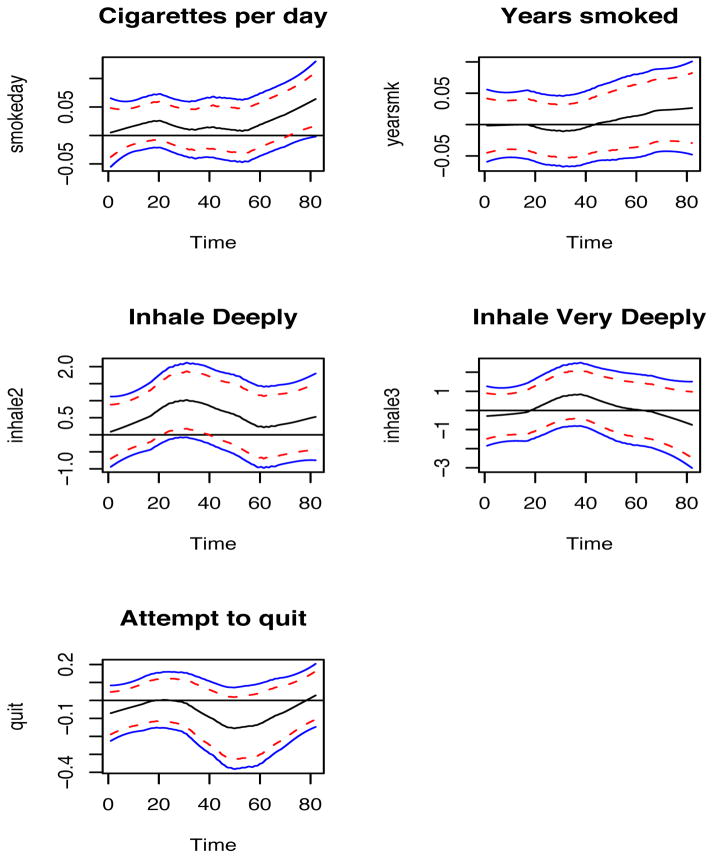
The effect of the baseline CO reading is significant in the first 5 weeks of the study. This is likely because it is more difficult for heavier smokers entering the study to quit smoking, and this effect became weaker and weaker along time until there was no effect. All other covariates are non-significant since the 95% bootstrap confidence bands cover the entire zero line. Similar to the baseline CO reading, the baseline cotinine reading also has a consistently positive effect, although it is not significant. Men have higher probability of being smokers than women, as the estimated curve is mostly above the zero line. There is no difference among the different ethnicities. Age has a slight negative effect. It may reflect a stronger mind to quit smoking among older participants. As expected, cigarettes per day reported at baseline positively predicts smoking. The effect has become stronger at the end of the study, which may indicate a relapse. Number of years smoked has a positive effect only for the second half of the study, also reflecting a relapse. It reflects the fact that it is harder to change long standing behavior patterns. The number of attempts to quit smoking has a negative effect on smoking status. People who are more committed to quit smoking by themselves are less likely to be smokers in the study. Inhaling deeply when smoking has a constant positive relationship on smoking status, compared to inhaling somewhat. Inhaling very deeply has no obvious relationship, possibly because of the small sample size in the group that inhales very deeply (24) compared to those inhaling deeply (110). The relationship between smoking status and clean urine opiate is positive, while the relationship to clean urine cocaine is negative. Intuitively, both should be negative. This result may be due to the collinearity between the two. The Pearson’s sample correlation is 0.266 with p-value 0.0004.

Overall for the smoking cessation data, the proposed two-step method and the logistic varying coefficient modeling were very effective in describing the results. They not only confirm the finding of Shoptaw et al. (2002) in a more general model, but also evaluate the effects of many other covariates and lead to intuitive interpretations. We are also able to study the change of effect along time, which distinguishes varying coefficient models from many others.

5 Simulation Studies

We conduct simulation studies to evaluate the finite sample performance of the proposed methodology including the TS estimation, asymptotic pointwise confidence intervals and the bootstrap confidence bands. We also include comparisons with LML, and time-invariant GLMM of Wolfinger and O’Connell (1993) with a random y-intercept. Smoothing in the TS is carried out via local linear regression. For component-wise bandwidth selection of the proposed TS method, we utilize the automatic rule-of-thumb bandwidth selector of Ruppert, Sheather and Wand (1995), separately for each varying coefficient function. LML maximizes the local likelihood and selects a single global bandwidth for all varying coefficient functions. We utilize leave-one-subject out cross-validation for selection of the global bandwidth similar to Cai, Fan and Li (2000). For more details on the LML method, we refer the readers to Şentürk et al. (2013) and Estes et al. (2014). While all three methods are used for comparisons via integrated mean squared error (IMSE), coverage of the point-wise asymptotic confidence intervals and bootstrap confidence bands and power of the proposed hypothesis testing are also studied.

5.1 Finite Sample Performance Comparisons

Our simulation model contains 3 coefficient functions for the two covariates X₁, X₂, and the y-intercept. The covariate X₁ is a time-invariant discrete uniform variable taking on values in {0.5, 1, 1.5}. The covariate X₂ is generated from a Uniform(0, 0.5) distribution. The sample size is 175 as in the smoking cessation data and results are reported based on 500 Monte Carlo runs. The times {t_j, j = 1, …, 36} are also from the smoking cessation data. We assume the correlation structure among repeated measurements to be AR-1(0.5), that is corr{Y_i(t_j1), Y_i(t_j2)} = 0.5^{|j₁−j₂|}. The algorithm described in Park, Park and Shin (1996) is adopted to generate correlated binary data. The varying coefficient functions are β₀(t) = 2 sin{2π(t − 1)/81}, β₁(t) = {log₁₀(t) − 1}/4, and β₂(t) = 1/(20t) − 2.

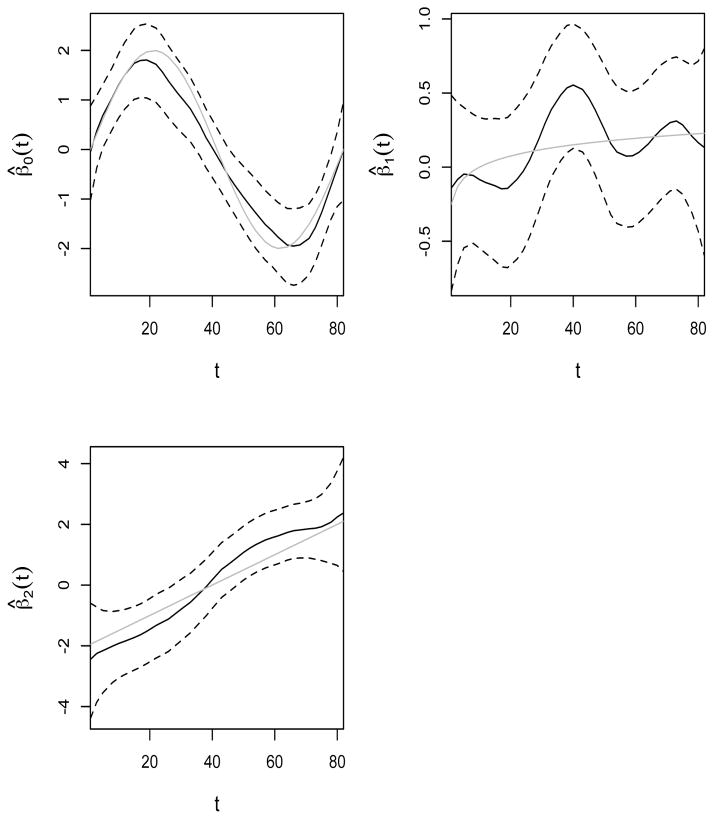
The median of the selected bandwidths across the 500 Monte Carlo runs are (8.5, 15.0, 17.2) for {β₀(t), β₁(t), β₂(t)} for the TS method. The median of the selected global bandwidths for LML is 9. The results are reported in Tables 1 – 3 and in Figure 5. Figure 5 displays the true coefficient functions (solid gray) and their TS estimates (solid black) together with the proposed 95% bootstrap confidence bands (dashed black) from the sample with the median IMSE value among 500 Monte Carlo runs. Note that the true coefficient functions fall inside the bootstrap confidence bands, and that the automatic bandwidth selection may lead to under smoothing at times, as displayed for the estimation of β₁(t). Nevertheless, the TS method, selecting different bandwidths for each coefficient function separately, is more effective in targeting varying coefficient functions of varying degrees of smoothness compared to the LML method with a global bandwidth. This can be observed in the estimated integrated mean square errors (IMSE) reported in Table 1. Since the median global bandwidth selected by LML is 9, LML performs better in estimation of β₀(t) which requires a lower bandwidth, but undersmooths β₁(t) and β₂(t), leading to higher mean IMSE values, compared to the TS method. Note also that when the covariate effects change over time, the time-invariant models such as GLMM have a much larger mean IMSE, compared to TS and LML, due to modeling bias. It can be 26 times as big as the IMSE from TS.

Table 1.

Comparison of the mean estimated integrated mean square error (IMSE) of the proposed two-step approach (TS), local maximum likelihood (LML) and generalized linear mixed model (GLMM) over 500 Monte Carlo runs. Estimated IMSE is taken to be the sum of the estimated MSE across all 36 time points.

	IMSE			IMSE Ratio
	TS	LML	GLMM	LML/TS	GLMM/TS
β0(t)	2.58	2.42	69.62	0.94	26.96
β1(t)	1.29	1.56	0.62	1.21	0.48
β2(t)	7.48	10.37	53.67	1.39	7.18

Table 3.

Coverage rates (in %) of the pointwise confidence intervals at 8 time points.

t	β0(t)		β1(t)		β2(t)
	95%	90%	95%	90%	95%	90%
1	94.4	89.8	93.0	87.2	94.2	88.8
12	93.6	89.4	93.2	87.4	92.6	87.8
24	94.8	87.2	94.0	87.8	94.4	88.2
36	95.0	87.6	95.4	89.6	94.0	90.0
47	94.2	88.0	94.8	89.2	95.2	90.2
59	93.4	87.2	95.6	90.4	94.4	87.2
71	94.6	88.6	95.2	89.8	95.0	89.2
82	96.6	93.0	94.8	88.8	94.4	89.0

Figure 5.

The true varying coefficient functions (solid gray), their estimates (solid black) based on the proposed TS method and 95% bootstrap confidence bands (black dashed) from the run with median IMSE among 500 Monte Carlo runs.

We also conducted a simulation study to assess the performance of the two remedies outlined in the first remark of Section 2.2 for sparse longitudinal designs, namely leaving b(t_j) missing (TS_missing) and increasing the sample size at t_j by including observations from neighboring time points t_j−1 and t_j+1 (TS_merge) for cases with inadequate sample size (n_j) at some of the time points to obtain stable logistic regression fits. Under the current simulation set-up where the conditional mean response ranges between .11 and .9, we need even larger sample sizes than the common rule of thumb of 10d. Preliminary studies yielded that a minimum sample size of n_j = 60 was needed at each time point for stable logistic regression fits in our set-up. Hence we generated data under three scenarios of (11, 20, 30)% or (4, 7, 11) of the time points having small sample sizes ranging between 20 and 30, where the sample size for the rest of the time points ranged between 60 and 80. Time points with smaller sample sizes, sample size at each time point as well as subject id’s observed at each time point were generated randomly in each Monte Carlo run. The estimated mean IMSE values from 500 Monte Carlo runs for LML, and two versions of the TS method, namely TS_missing and TS_merge are given in Table 2. Note that the mean IMSE values are higher in general in Table 2 compared to Table 1 since the simulation involves smaller sample sizes at each time point. Under the sparse longitudinal design set-up where TS is unable to produce stable logistic regression fits in the first step of the algorithm, both remedies are shown to fix this problem in practice reasonably well with TS_merge performing better, for a moderate proportion (10–30%) of time points with smaller sample size (i.e. n_j < 10d). Note that under sparse designs LML is able to merge information from neighboring time points more efficiently than the TS method, through its local weighing scheme via the kernel function. While results from the small sample size at 11% time points case resemble the patterns in the estimated IMSE from Table 1 (namely that LML performs better in estimation of β₀(t) but leads to higher IMSE values for β₁(t) and β₂(t), compared to TS), for larger proportion of time points with smaller sample sizes, LML leads to lower IMSE values. Hence the advantage of TS over LML in effectively targeting varying coefficient functions of varying degrees of smoothness does not extend to sparse longitudinal designs.

Table 2.

Comparison of the mean estimated integrated mean square error (IMSE) of the two versions of the two-step approach (TS), TS_missing and TS_merge as well as the local maximum likelihood (LML) over 500 Monte Carlo runs under a sparse longitudinal design with (11, 20, 30)% of the time points having insufficient sample size for stable logistic fits. Estimated IMSE is taken to be the sum of the estimated MSE across all 36 time points.

	11%			20%			30%
	TSmissing	TSmerge	LML	TSmissing	TSmerge	LML	TSmissing	TSmerge	LML
β0(t)	6.69	6.30	4.85	8.67	7.57	5.74	12.28	8.44	4.90
β1(t)	2.44	2.34	2.46	3.18	2.86	2.79	4.95	3.63	2.58
β2(t)	37.23	35.21	36.28	46.86	42.29	41.12	47.21	41.25	39.79

5.2 Performance of the Proposed Inference Tools

We conduct further simulations to study the performance of the proposed point-wise confidence intervals, bootstrap confidence bands and hypothesis testing described in Section 3.2. Table 3 provides the coverage probabilities of point-wise confidence intervals at nominal levels 95% and 90% at eight time points from the total 36 points. It is observed that the coverage probability of the proposed TS method is reasonably close to the nominal level. In addition Table 4 reports on coverage rates of the proposed bootstrap confidence bands and Tables 5 reports results from a hypotheses testing setup, utilizing the relationship between hypotheses testing and confidence bands (or confidence interval in non-functional situations). Results are reported from 200 Monte Carlo runs where each run is based on 500 bootstrap samples at sample size n = 175. Component-wise bandwidths are selected based on the automatic rule-of-thumb bandwidth selection of Ruppert, Sheather and Wand (1995) in each Monte Carlo run and fits to bootstrap samples utilize the same bandwidths as those selected for the Monte Carlo runs. We use two settings where the first setting is the same as the simulation setup described above and the second setting differs by utilizing time-invariant coefficient functions, β₀(t) = −1, β₁(t) = 0 and β₂(t) = 2.

Table 4.

Coverage rates (in %) of the bootstrap confidence bands based on 200 Monte Carlo runs. 1.96*(standard error) is reported in parenthesis.

Setting	95%			90%
	β0(t)	β1(t)	β2(t)	β0(t)	β1(t)	β2(t)
1	92.5 (3.65)	92.0 (3.76)	89.0 (4.34)	85.0 (4.95)	87.5 (4.58)	80.0 (5.54)
2	94.5 (3.16)	93.0 (3.54)	91.0 (3.97)	85.5 (4.88)	84.5 (5.02)	82.0 (5.32)

Table 5.

The estimated rejection ratio (in %) for H₀(a) : β_r(t) does not change over time and H₀(b) : β_r(t) = 0. The superscript ^* indicates the empirical probability of a Type I error.

Setting	H0	α = 5%			α = 10%
		β0(t)	β1(t)	β2(t)	β0(t)	β1(t)	β2(t)
1	(a)	100	3.5	100	100	9.0	100
	(b)	100	27.5	100	100	43.0	100
2	(a)	1.5*	1.5*	2.5*	4.0*	3.5*	5.5*
	(b)	100	7.0*	100	100	15.5*	100

The coverage rates reported in Table 4 are pretty close to the nominal levels in both settings, where β₂(t) is less covered than β₀(t) and β₁(t). This may be due to the fact that β₂(t), being the most smooth function of the three, may be under smoothed in some runs because of the under smoothing tendency of the automatic bandwidth selectors. Table 5 gives the estimated rejection proportions (in %) for two hypotheses tests: 1. H₀(a) : β_r(t) does not change over time; 2. H₀(b) : β_r(t) = 0, for all t ∈ [t₀, t_T]. The testing procedure is based on the proposed bootstrap confidence bands. In the first setting, the powers for rejecting H₀(a) and H₀(b) are satisfying for β₀(t) and β₂(t) where they are all at 100%. The powers for β₁(t) are much smaller than those for the other two coefficient functions. This is because β₁(t) is much more similar to a constant function, more specifically a constant function at 0. Note also that the powers for rejecting H₀(a) are consistently smaller than those for rejecting H₀(b), since H₀(b) is a special case for H₀(a). For the second setting, reported proportions for H₀(a) at all varying coefficient functions and for H₀(b) at β₁(t) are estimated significance levels since the null hypotheses are true in these cases. For H₀(b), while the significance levels for β₁(t) are close to the nominal levels, the reported values for the other two coefficient functions show that the powers are 1 for rejecting H₀(b) when the constants are other than 0. For H₀(a), the estimated significance levels are consistently less than the nominal level as discussed in Section 3.2. These findings imply that the proposed bootstrap confidence bands are very effective in identifying whether H₀(a) is true and the unknown constant.

6 Discussion

In this paper, we proposed a TS estimation procedure for logistic varying coefficient modeling of longitudinal binary data. The basic idea behind the proposal as well as its implementation are simple. We also evaluated the asymptotic properties of the proposed estimators and found them to be asymptotically unbiased. We established the asymptotic variance under two specific situations and proved that the estimators are asymptotically normal, leading to the proposed asymptotic and finite sample inference procedures. We applied the proposed methodology to smoking cessation data. The main results are consistent with findings from previous studies. Moreover, we evaluated many other covariates and have provided reasonable interpretations of the results. The estimators give intuitively consistent inferences and the bootstrap confidence intervals are effective in identifying significant predictors.

Simulation studies included comparisons of the TS and LML methods. Unlike the LML approach, the proposed TS method is able to target coefficient functions with varying degrees of smoothness, via component-wise bandwidth selections. In addition, the TS method also allows for visual selection of component-wise bandwidths via plotting of the raw varying coefficient function estimates. The efficacy of the proposed bootstrap confidence bands are shown via simulation studies where the implied tests have very high power in many cases. While the first hypothesis of constant coefficient functions tests whether the logistic varying coefficient model reduces to a semi-parametric or a parametric model, the second hypothesis of coefficient functions being equal to zero, allows us to perform model selection.

The proposed methodology can easily be extended to be applicable to other forms of longitudinal data. For example longitudinal categorical data can be modeled in a similar way, as long as an appropriate marginal model (e.g. the proportional odds model of Agresti (2002)) is selected for cross-sectional modeling in the first step. A second extension can be to spatial correlated longitudinal data, such as that encountered in progression detection of glaucoma in the visual field (Gardiner and Crabb, 2002). Spatial correlation can be taken into account in the proposed TS method by applying a higher dimensional smoothing procedure in the second step. We noted that the proposed methodology involves a conditional target of inference in presence of informative drop-out, where inference is restricted to those subjects who have not yet dropped out of the study at a fixed time t. When the interest may be in modeling both drop-out time and a longitudinal outcome, an alternative modeling approach would be the joint modeling of drop-out time and the longitudinal binary outcome. While in our application the main reason for missing data is patient drop-out, in other applications there may be missing data in subjects’ observations before they drop out of the study. The proposed methodology can handle missing completely at random (MCAR) data structures and extensions to missing at random (MAR) data need further research.

Figure 3.

The Smoking Cessation data (part 2). Curve estimate (solid line in center), 95% bootstrap confidence band (solid lines) and 95% point-wise confidence intervals (dash lines).

Highlights.

• Proposed a two-step estimation procedure for a logistic varying coefficient model.

• The method is simple and can be conveniently implemented.

• We provide tools for finite sample and asymptotic inference.

• Methods are illustrated with the analysis of a smoking cessation data set.