Sparse meta-analysis with high-dimensional data

Abstract

Meta-analysis plays an important role in summarizing and synthesizing scientific evidence derived from multiple studies. With high-dimensional data, the incorporation of variable selection into meta-analysis improves model interpretation and prediction. Existing variable selection methods require direct access to raw data, which may not be available in practical situations. We propose a new approach, sparse meta-analysis (SMA), in which variable selection for meta-analysis is based solely on summary statistics and the effect sizes of each covariate are allowed to vary among studies. We show that the SMA enjoys the oracle property if the estimated covariance matrix of the parameter estimators from each study is available. We also show that our approach achieves selection consistency and estimation consistency even when summary statistics include only the variance estimators or no variance/covariance information at all. Simulation studies and applications to high-throughput genomics studies demonstrate the usefulness of our approach.

1. Introduction

Meta-analysis is commonly used in many scientific areas. By combining multiple data sources, one can achieve higher statistical power, more accurate estimation, and greater reproducibility (Noble, 2006). There are over 33 million entries of “meta-analysis” on Google, and the majority of meta-analysis publications have appeared in biostatistical and medical journals.

Traditional meta-analysis methods are designed for low-dimensional datasets. For example, both the fixed-effects model and the random-effects model (DerSimonian and Laird, 1986; Jackson and others, 2010; Chen and others, 2012) are typically used to analyze a single covariate; the former assumes a common value for the parameter of interest, and the latter assumes a probabilistic distribution for the effects of the covariate among studies. Lin and Zeng (2010) extended the fixed-effects model to the case of multiple covariates; however, their model assumes that the number of covariates is relatively small compared with the sample size.

When the number of covariates becomes very large, as in gene expression studies and genome-wide association studies (GWAS), the incorporation of variable selection into meta-analysis improves model interpretation, reduces prediction errors, and provides better prioritization of genomic features for follow-up studies. When raw data are available, existing variable selection methods, such as LASSO (Tibshirani, 1996) and adaptive-LASSO (aLASSO) (Zou, 2006), can be applied to each study, and the selection results can be combined. Other strategies that seek to borrow information that is shared among the studies have also been proposed (Liu and others, 2011; Ma and others, 2011; Chen and Wang, 2013; Tenenhaus and others, 2014).

In practice, raw data are often unavailable because of high cost, logistical difficulties, time constraints, IRB restrictions, and other study policies. Taking GWAS as an example, virtually all meta-analyses to date have been conducted at the summary-statistics level rather than the raw-data level (Lango and others, 2010; Liu and others, 2014). The emergence of big data, such as next-generation sequencing data, makes the collation of raw data even more challenging. A question naturally arises as to whether it is possible to conduct effective variable selection using only summary statistics. In addition, it is unclear how to extract information shared by different studies while allowing heterogeneity among studies. Furthermore, the high-dimensional nature of “-omics” studies makes information extraction and model building highly challenging.

In this article, we propose a new approach, sparse meta-analysis (SMA), in which variable selection for meta-analysis is based solely on summary statistics. To our knowledge, no such method exists in the literature. We show that the SMA estimator is as efficient as using raw data if the estimated covariance matrix of the parameter estimators from each study is available; our approach can achieve selection consistency and estimation consistency even when the summary statistics include only the variance estimators or no variance/covariance information at all.

The SMA can handle both homogeneous and heterogeneous structures of covariate effects; see Figure 1. The former assumes that the effects of each covariate are either all zero or all non-zero across studies, whereas the latter allows the effects of each covariate to be partly zero among studies. Biological evidence shows that genetic variants may exhibit on/off effects due to genetic modifiers, environmental exposures, or epigenetic mechanisms (Zeisel, 2007). Other sources of heterogeneity include differences in the study design, ethnic group, and experimental platform.

Fig. 1.

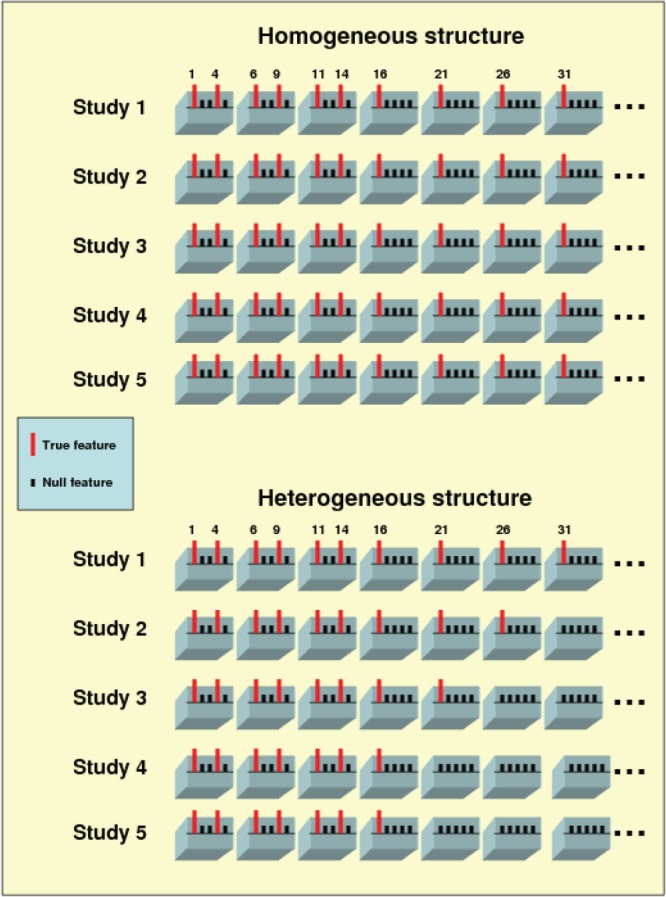
True models under homogeneous and heterogeneous structures. Each block contains five covariates, and the omitted blocks do not harbor any important covariates. In the first structure, a covariate needs to be active (or inactive) in all of the studies, whereas in the second structure, a covariate can be partly active among the studies.

The rest of this article is organized as follows. In Section 2, we describe the SMA approach and its variations that are designed to adapt to different practical situations. We also show that the SMA has desirable theoretical properties. In Section 3, we use extensive simulation studies to demonstrate the superiority of the SMA to alternative approaches. In Section 4, we illustrate the effectiveness of the SMA by performing meta-analysis of multiple GWAS studies on cardiovascular disease. In Section 5, we discuss possible directions for future research.

2. Methods

2.1. Data and models

Suppose that there are 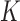independent studies, with 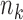subjects in the 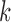th study. The raw data consist of 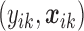, 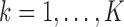; 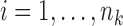, where 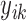is the response for the 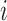th subject in the 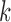th study, and is the corresponding 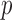-vector of covariates. We assume that the data for the 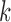th study are generated from a generalized linear model with the 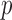-dimensional vector of regression coefficients 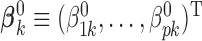. We divide the covariates into two disjoint sets: the important set 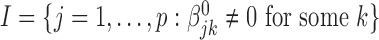, and the unimportant set 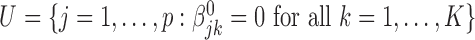. Our major goals are to identify the set 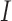correctly and to estimate the effects of the covariates in .

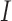In meta-analysis, the available information pertains to the estimators 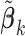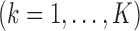, where 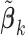is typically the minimizer of some loss function. Often, the variance estimators for individual regression coefficients are also available. In prospectively designed meta-analysis, it is possible to obtain the estimated covariance matrix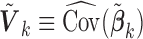 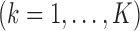. Traditional meta-analysis focuses on one covariate at a time. To jointly analyze several covariates, Lin and Zeng (2010) suggested a multivariate version of the well-known inverse-variance estimator 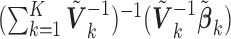, which is essentially the minimizer of 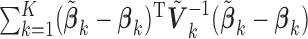under the constraint that 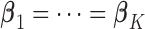. Motivated by this estimator, we propose an approach to perform variable selection in meta-analysis when raw data are not available.

2.2. SMA estimators

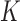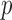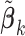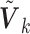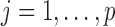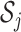We now introduce the SMA approach to variable selection and effect estimation based on summary statistics alone. We allow the sets of summary statistics to be derived from different (but overlapping) subsets of the covariates, such that the dimensions of the 's may be different (likewise for the 's). For , let denote the set of studies which contain the 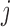th covariate in the summary statistics. In this section, we consider the situation where the covariance matrix estimator 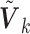is available, say, in a meta-analysis consortium. In Section 2.3, we deal with the cases where the covariance information is not available.

The form of the estimator depends on the structure of the important set :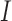

1. Homogeneous structure: for any 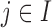, 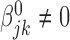for all 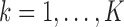; and

2. Heterogeneous structure: for any 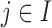, 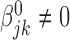for at least one .

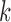The homogeneous structure requires each covariate in 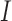to be active in all 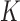studies, whereas the heterogeneous structure allows each covariate in 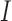to be partly active among the 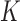studies. The former structure can be viewed as a special case of the latter. If we treat the regression coefficients for a covariate in the 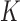studies as a group, then the homogeneous structure assumes sparsity only at the group level, whereas the heterogeneous structure allows additional sparsity at the study level within groups.

For the heterogeneous structure, we propose to minimize the following objective function with respect to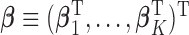

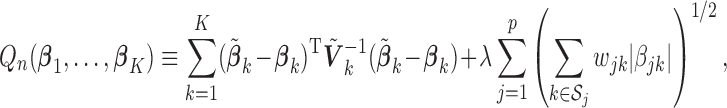(2.1)

where 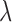is a tuning parameter, and 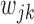is a user-specified penalty weight for 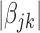. If 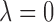and all of the 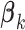are equal, then the minimizer of (2.1) reduces to the aforementioned multivariate inverse-variance estimator (Lin and Zeng, 2010). Our model also has a natural connection with the approach proposed by Wang and Leng (2007), in which the least-square approximation is applied to the original loss function and the applicability of the LASSO penalty is expanded to include various model settings. The form of the penalty term in (2.1) was proposed by Zhou and Zhu (2010) in the context of gene-set analysis for a single dataset. In practice, 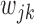can be chosen to be 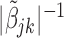. We denote 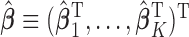as the minimizer of (2.1).

Remark 1. —

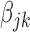
Although (2.1) allows heterogeneity between studies, it is different from performing separate variable selection in individual studies. If we replace the second term in (2.1) by , then there will be separate variable selection in each study. In contrast, the second term in (2.1) is , which treats as a group for each and conducts a group-type selection (with weights).

For the homogeneous structure, we propose to use a common penalty weight for all of the coefficients associated with a given covariate. That is, we minimize

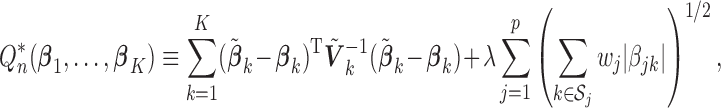(2.2)

where 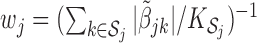for 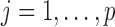, where 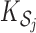is the cardinality of 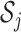. The choice of 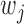(and 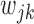) is in a similar spirit to the adaptive LASSO, with stronger predictors receiving less penalty. Note that 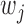is the weight for the penalty term, while 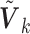serves as the weight for the traditional (un-penalized) meta-analysis. Let 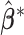denote the minimizer of (2.2).

Remark 2. —

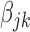
By the construction of the weight , the penalty in (2.2) borrows the strength from the studies with strong signals for the th variable to protect the weak signals, such that tend to be selected or removed simultaneously. Due to the use of the norm inside the penalty, it is possible for very small coefficients to be penalized to 0. However, this has little impact on the utility of the selected model since very small effects contribute little to prediction. We can strictly enforce the all-in/all-out structure by replacing the norm in (2.2) with the norm, although the small estimates induced by the norm may not be desirable.

2.3. SMA estimators with working covariance matrices

In practice, one may only have access to the diagonal elements of 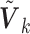, i.e., 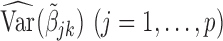, for 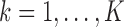. In that case, we extend the SMA to accommodate the working covariance matrix 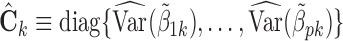. In particular, for the heterogeneous structure, we minimize

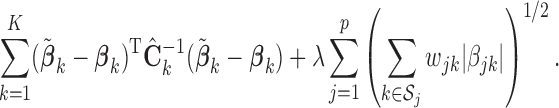(2.3)

We call the solution to (2.3) the SMA-Diag estimator. In some applications, even 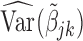may not be available. Then we replace 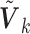with the 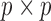matrix 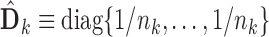and minimize

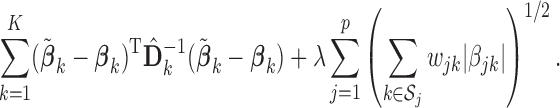(2.4)

We name the solution to (2.4) the SMA-S estimator. The SMA-Diag and SMA-S for the homogeneous structures can be obtained in a similar manner.

The covariance matrix 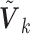is primarily determined by the correlations of the covariates (Hu and others, 2013). The correlations can be estimated from one of the participating studies or from an external panel, such as the Hapmap or the 1000 Genomes data in genomic studies. Thus, when only the diagonal elements of the 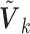are available, one can utilize the correlation matrix from an internal or external source to recover the 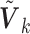. The corresponding versions of the SMA are called the SMA-I and SMA-E, respectively. If the 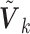's are neither available nor recoverable, then the SMA-Diag may be the only viable tool.

2.4. Algorithms and tuning

We focus on the optimization algorithm to solve (2.1), as the minimizations of (2.2)–(2.4) can be carried out in similar manners. Note that the objective function in (2.1) is not convex in 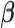and has a complex nonlinear form. First, we derive the following simpler yet equivalent version for the problem

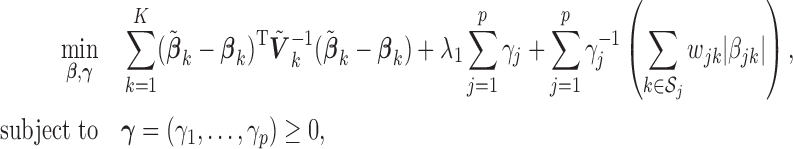(2.5)

where 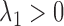is a tuning parameter. The proof for the equivalence of (2.1) and (2.5) is given in supplementary material. There is a one-to-one correspondence between 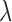and 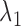. We propose an iterative algorithm to alternately minimize (2.5) with respect to 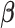(or 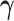), with 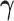(or 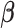) being fixed at their current values. When 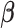is fixed, we obtain a closed-form solution for 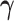. When 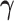is fixed, the minimization problem can be transformed into an adaptive-LASSO problem and solved by the cyclic coordinate descent algorithm (Friedman and others, 2007).

Algorithm:

• Step 1: Initialize 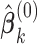by the estimates 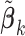for all 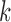. Set .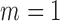

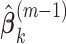
• Step 2: Fix 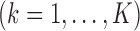at their current values and minimize (2.5) with respect to 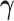. The solution is .

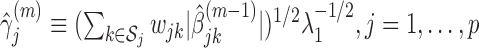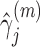
• Step 3: Fix 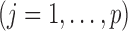at their current values and minimize (2.5) with respect to 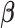. Denote the solution as .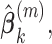

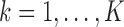• Step 4: Let 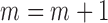, and go to Step 2 until convergence.

The above algorithm clearly shows that the SMA involves a dynamic thresholding process rather than a simple thresholding procedure. The tuning parameter 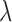controls the trade-off between model sparsity and model fit. Motivated by the work of Wang and Leng (2007), we determine the tuning parameter by a modified information criterion (MIC). Defin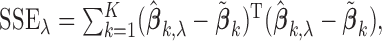e where 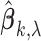is the estimate of 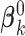under 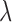. Let 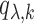be the number of nonzero components of 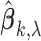. Then, the MIC is defined as

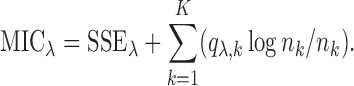The first part of 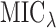measures the overall model fit for the 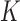studies, whereas the second part measures the model complexity among the 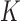studies. It can be shown that the proposed MIC is consistent for model selection (see Section A of supplementary material available at Biostatistics online). When 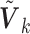is available, we can redefine the 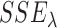by 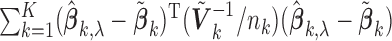to accommodate variance estimates in the MIC.

2.5. Asymptotic properties

We study the asymptotic properties of the SMA estimators in terms of selection and estimation. We show in Section A of supplementary material available at Biostatistics online that, for arbitrary covariance matrices 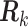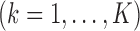, the SMA can achieve both selection consistency and estimation consistency; when 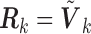, the SMA estimator has the oracle property in that it is asymptotically normal and efficient.

3. Numerical studies

We conducted extensive simulation studies to evaluate the empirical performance of the SMA approach under various scenarios. Specifically, we compared the following methods: (i) the method that utilizes the raw data along with a group penalty, which we call the Raw method; (ii) the SMA; (iii) the SMA-derived methods (i.e., SMA-Diag, SMA-S, SMA-I, and SMA-E); (iv) the aLASSO-U method, which first applies the adaptive-LASSO to each of the 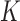studies to obtain 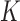models and then takes the union of the 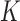models as the final model; (v) the aLASSO-I method, which is the same as the aLASSO-U except that it takes the intersection of the 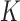models; (vi) the Hard-Thresholding-Union (HT-U) method, which is similar to the aLASSO-U but replaces the aLASSO by hard-thresholding; and (vii) the Hard-Thresholding-Intersection (HT-I) method, which is similar to the aLASSO-I but replaces the aLASSO by hard-thresholding. Methods (iv)–(vii) represent two natural ways of combining variable selection results obtained from individual studies.

To measure the performance of each method, we calculated the estimated model sparsity, defined as 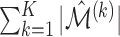, where 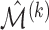denotes the set of selected covariates for the 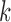th study. We further calculated the correct_0 rate 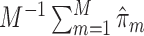and the incorrect_0 rate 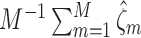, where 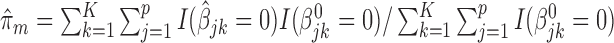, 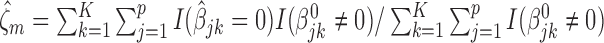for the 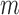th simulation, 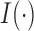is the indicator function, and 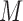is the total number of simulations. Similar criteria were used by Wang (2009). We generated the data from linear regression models and set 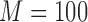. To assess the prediction accuracy, we further simulated 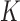datasets, 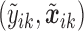for 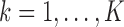and 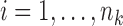, and calculated the prediction error 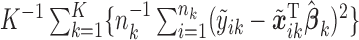. We considered small 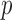, large 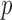, and “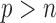,” as well as several other practical situations.

3.1. Small dimensions

We first considered the situation with a small number of covariates. We simulated five studies, each with 50 covariates. The sample sizes for the five studies were 1500, 1400, 1300, 1200, and 1100. The 50 covariates were evenly divided into 10 blocks. To simulate single nucleotide polymorphisms (SNPs), we adopted a simulation scheme in line with Wu and others (2009). For each block, we first simulated a multivariate normal distribution, with mean being the unit vector and covariance matrix following either the compound symmetry or the auto-regressive correlation structure with correlation coefficient 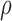; we then trichotomized each covariate into (0, 1, 2) to represent an SNP. For the SMA-I, we used the correlations of the SNPs from the largest study (i.e., the first study) to recover the 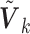; for the SMA-E, we simulated an external panel with 500 subjects.

We first focused on the homogeneous structure, in which five studies share 10 active SNPs (see Figure 1, upper panel). For 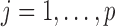, the nonzero coefficients for the 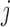th SNP were simulated under the random-effects model, with the values of the coefficients following the 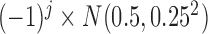distribution. The coefficients fluctuate primarily between 0 and 1 or between 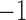and 0. The variance explained by individual SNPs fluctuates around 6% and is 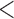1% for 14% of the SNPs (under the auto-regressive structure with 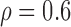). All SNP genotypes were standardized before variable selection.

As shown in Table 1, the performance of the SMA is comparable with that of the Raw method. This is consistent with our theoretical results that the two methods are asymptotically equivalent. The SMA-Diag and SMA-S appear to have reasonable performance, although they are less efficient than the SMA because of the loss of information on the estimated covariance matrix. Both the SMA-I and SMA-E work nearly as well as the SMA. The aLASSO-U and HT-U clearly over-select models, and their parameter estimation errors are always higher than those of the SMA and SMA-derived methods. The prediction errors for the first six methods are close to each other, and the SMA tends to perform slightly better than the aLASSO-U and HT-U. The aLASSO-I and HT-I always under-select models, resulting in grossly inflated estimation errors and prediction errors. The results for the heterogeneous structure show similar patterns (see Table S1a of supplementary material available at Biostatistics online). Indeed, under the heterogeneous structure, the aLASSO-I and HT-I are bound to fail by their design.

Table 1.

Comparison of the SMA with other methods under the homogeneous structure for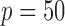

Method		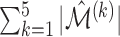Correct_0 (%)	Incorrect_0 (%)		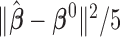Prediction error
Correlation structure: auto-regressive ()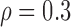
Raw	49.64	99.9	1.0	0.017	1.009
SMA	49.63	99.9	1.0	0.017	1.009
SMA-Diag	49.76	99.9	1.0	0.019	1.010
SMA-S	49.73	99.9	1.1	0.019	1.010
SMA-I	49.65	99.9	1.0	0.018	1.009
SMA-E	49.73	99.9	1.0	0.019	1.010
aLASSO-U	164.55	42.7	0	0.032	1.016
aLASSO-I	43.55	100.0	12.9	0.343	1.415
HT-U	91.00	79.5	0	0.037	1.019
HT-I	40.8	100.0	18.4	0.488	1.680
Correlation structure: auto-regressive ()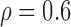
Raw	49.72	99.9	1.0	0.017	1.009
SMA	49.71	99.9	1.0	0.017	1.009
SMA-Diag	50.88	99.4	0.5	0.025	1.013
SMA-S	51.15	99.3	0.5	0.025	1.013
SMA-I	49.81	99.9	0.8	0.018	1.009
SMA-E	49.85	99.8	1.0	0.019	1.010
aLASSO-U	163.25	43.4	0	0.036	1.016
aLASSO-I	43.35	100.0	13.3	0.350	1.443
HT-U	116.85	66.6	0	0.061	1.026
HT-I	40.10	100.0	19.8	0.513	1.713
Correlation structure: compound symmetry ()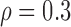
Raw	49.83	99.9	0.7	0.017	1.009
SMA	49.83	99.9	0.7	0.017	1.009
SMA-Diag	49.86	99.9	0.8	0.020	1.010
SMA-S	49.97	99.8	0.8	0.020	1.010
SMA-I	49.78	99.9	0.7	0.018	1.009
SMA-E	49.90	99.9	0.8	0.019	1.010
aLASSO-U	169.05	40.5	0	0.033	1.016
aLASSO-I	43.15	100.0	13.7	0.365	1.509
HT-U	91.15	79.4	0	0.038	1.019
HT-I	40.4	100.0	19.2	0.506	1.707
Correlation structure: compound symmetry ()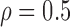
Raw	49.63	99.9	1.0	0.019	1.009
SMA	49.73	99.9	1.0	0.019	1.009
SMA-Diag	50.35	99.6	1.0	0.025	1.012
SMA-S	50.36	99.6	0.9	0.025	1.012
SMA-I	49.84	99.9	0.8	0.020	1.009
SMA-E	49.85	99.8	0.9	0.021	1.010
aLASSO-U	168.55	40.7	0	0.040	1.016
aLASSO-I	42.75	100.0	14.5	0.390	1.487
HT-U	113.2	68.4	0	0.057	1.025
HT-I	39.75	100.0	20.5	0.557	1.732

3.2. Large dimensions

We increased the number of SNPs to 200 and set the sample sizes to 2000, 1900, 1800, 1900, and 2000. For the SMA-E, we simulated an external panel of 1000 subjects. The results are shown in Table 2 and Table S1b of supplementary material available at Biostatistics online. The SMA method continues to perform similarly to the Raw method. In addition, the SMA is able to capture most of the important SNPs, while maintaining a model size that is close to the true model size. The SMA-Diag and SMA-S are less efficient than the SMA but still possess the desirable model sparsity. The SMA-I and SMA-E maintain their model sparsity with quite accurate estimation of parameters. In contrast, the aLASSO-U and HT-U include a large number of noise SNPs, while the aLASSO-I and HT-I tend to miss important SNPs.

Table 2.

Comparison of the SMA with other methods under the homogeneous structure for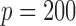

Method		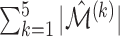Correct_0 (%)	Incorrect_0 (%)		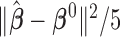Prediction error
Correlation structure: auto-regressive ()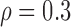
Raw	49.75	100.0	0.8	0.010	1.006
SMA	49.76	100.0	0.8	0.011	1.006
SMA-Diag	50.31	99.9	0.8	0.013	1.008
SMA-S	50.19	99.9	0.7	0.013	1.007
SMA-I	50.26	99.9	0.7	0.013	1.007
SMA-E	51.29	99.8	0.8	0.015	1.008
aLASSO-U	531.40	49.3	0	0.040	1.021
aLASSO-I	44.25	100.0	11.5	0.311	1.441
HT-U	135.25	91.0	0	0.044	1.022
HT-I	40.65	100.0	18.7	0.496	1.649
Correlation structure: auto-regressive ()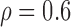
Raw	50.11	99.9	0.7	0.011	1.006
SMA	50.00	100.0	0.8	0.011	1.006
SMA-Diag	52.81	99.7	0.5	0.018	1.010
SMA-S	52.71	99.7	0.5	0.018	1.010
SMA-I	50.21	99.9	0.7	0.013	1.007
SMA-E	51.11	99.8	0.7	0.015	1.008
aLASSO-U	537.20	48.7	0	0.044	1.020
aLASSO-I	44.60	100.0	11.0	0.308	1.415
HT-U	217.60	82.4	0	0.088	1.040
HT-I	40.45	100.0	19.1	0.517	1.767
Correlation structure: compound symmetry ()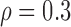
Raw	50.00	100.0	0.8	0.012	1.007
SMA	49.97	100.0	0.8	0.012	1.007
SMA-Diag	50.20	99.9	0.8	0.014	1.008
SMA-S	50.17	99.9	0.8	0.014	1.008
SMA-I	50.09	99.9	0.8	0.013	1.007
SMA-E	51.06	99.9	0.5	0.016	1.008
aLASSO-U	531.35	49.3	0	0.042	1.021
aLASSO-I	44.55	100.0	11.0	0.306	1.407
HT-U	143.95	90.1	0	0.048	1.024
HT-I	40.5	100.0	19.0	0.511	1.698
Correlation structure: compound symmetry ()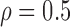
Raw	49.92	100.0	0.7	0.012	1.006
SMA	49.92	100.0	0.8	0.012	1.006
SMA-Diag	51.80	99.8	0.6	0.018	1.010
SMA-S	51.96	99.8	0.6	0.018	1.010
SMA-I	50.19	99.9	0.8	0.015	1.007
SMA-E	51.68	99.8	0.7	0.017	1.008
aLASSO-U	515.00	51.1	0	0.045	1.020
aLASSO-I	43.60	100.0	12.8	0.369	1.467
HT-U	201.85	84.0	0	0.079	1.037
HT-I	40.0	100.0	20.0	0.565	1.779

3.3.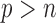

When is greater than , variable selection in meta-analysis becomes extremely challenging. Our SMA is based on summary statistics, but the ordinary least-squares (OLS) estimates cannot be obtained when 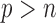. Under such a situation, it is necessary to reduce the dimension from an ultra-high level to a level that is amenable to most variable selection methods. We propose to first conduct marginal screening to reduce the dimension to be smaller than 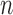and then obtain the summary statistics based on the reduced set of variables. This strategy is in the same vein as the sure independence screening (SIS) of Fan and Lv (2008). Because the SIS theory ensures that all important variables are preserved after the marginal screening, the selection consistency of the SMA with marginal screening is guaranteed. We evaluated the empirical performance in simulation studies. To have a fair comparison, the aLASSO-U, aLASSO-I, HT-U, and HT-I were also conducted after the SIS procedure. We set the sample sizes of the five studies to 600, 500, 600, 500, and 400. The dimension 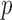was set to 10 000. We first performed the marginal screening on each study to reduce the dimension from 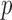to 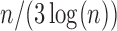and then took a union of the reduced sets of SNPs for subsequent variable selection. As shown in Table 3, the SMA model still has a reasonable model size, with the parameter-estimation error and the prediction error comparable with the Raw method. The aLASSO-U, aLASSO-I, HT-U, and HT-I either lose model sparsity or miss important SNPs, thus resulting in higher estimation errors and prediction errors, as was the case in the previous simulation studies.

Table 3.

Performance of the SMA and other methods with marginal screening under the homogeneous structure for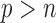

Method		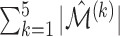Correct_0 (%)	Incorrect_0 (%)		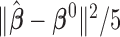Prediction error
Correlation structure: auto-regressive ()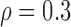
Raw	56.89	98.5	0.9	0.059	1.033
SMA	61.39	97.6	0.7	0.067	1.038
SMA-I	63.34	97.1	1.0	0.143	1.073
SMA-E	58.77	98.0	1.4	0.151	1.078
aLASSO-U	504.40	6.3	0	0.363	1.183
aLASSO-I	42.25	99.7	18.6	0.556	1.865
HT-U	452.30	17.1	0	0.583	1.291
HT-I	37.95	99.9	24.7	0.727	2.246
Correlation structure: auto-regressive ()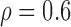
Raw	56.80	98.4	1.3	0.065	1.037
SMA	61.30	97.5	1.0	0.073	1.041
SMA-I	61.55	97.4	1.3	0.143	1.073
SMA-E	57.22	98.2	2.1	0.150	1.075
aLASSO-U	483.15	7.9	0.2	0.362	1.179
aLASSO-I	41.25	99.7	20.2	0.601	1.928
HT-U	441.65	16.6	0.2	0.597	1.288
HT-I	37.6	99.9	25.7	0.782	2.337
Correlation structure: compound symmetry ()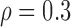
Raw	57.58	98.3	1.5	0.068	1.037
SMA	63.17	97.3	1.2	0.079	1.042
SMA-I	63.91	97.1	1.7	0.168	1.081
SMA-E	57.25	98.4	2.1	0.174	1.083
aLASSO-U	522.9	6.0	0.4	0.400	1.196
aLASSO-I	41.15	99.7	20.5	0.629	2.032
HT-U	464.2	17.7	0.4	0.630	1.309
HT-I	36.55	100.0	27.2	0.818	2.435
Correlation structure: compound symmetry ()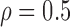
Raw	57.23	98.3	1.9	0.084	1.041
SMA	60.98	97.5	1.9	0.090	1.044
SMA-I	61.86	97.3	2.3	0.172	1.077
SMA-E	57.06	98.3	2.4	0.176	1.078
aLASSO-U	489.35	7.7	1.0	0.394	1.187
aLASSO-I	40.95	99.7	21.4	0.644	1.901
HT-U	452.35	15.4	1.0	0.633	1.301
HT-I	37.45	99.9	25.8	0.759	2.219

Note: 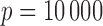and the sample sizes range from 400 to 600. The Correct_0 (%) and Incorrect_0 (%) were based on the dimensions after the SIS procedure. The SMA-E used an external panel of 1000 subjects.

3.4. Other considerations

We also addressed several other issues on sparse meta-analysis, such as a model structure different from the homogeneous and heterogeneous structures, the influence of sparsity on variable selection, different sets of candidate variables among studies, and the influence of screening on variable selection. The interested readers are referred to Section B of supplementary material available at Biostatistics online.

4. Real data analysis

We considered the Multi-Ethnic Study of Atherosclerosis (MESA), the Coronary Artery Risk Development in Young Adults (CARDIA) study, the Cardiovascular Health Study (CHS), the Framingham Heart Study (FHS), and the Atherosclerosis Risk in Communities (ARIC) study. These studies are currently focused on the genetic factors for cardiovascular diseases.

The FHS includes 2066 European Americans; the other four studies include both African Americans and European Americans. Numbers of African Americans and European Americans in the MESA, CARDIA, CHS, and ARIC are 1568 and 2249, 1261 and 1422, 717 and 3824, and 2532 and 8907, respectively. We considered the two race groups separately, thus performing meta-analysis of nine studies: FHS, MESA-A, MESA-E, CARDIA-A, CARDIA-E, CHS-A, CHS-E, ARIC-A, and ARIC-E, where “A” and “E” denote African and European Americans, respectively. The phenotype of interest for our analysis was lipidpc1, which is a continuous variable derived from the principal component analysis of several fasting serum measurements: low-density lipoprotein, high-density lipoprotein, triglycerides, apolipoprotein A1, and apolipoprotein B; lipidpc1 was found to be associated with genetic loci implicated in obesity, atherogeneic dyslipidemia, and glucose metabolism (Avery and others, 2011). We conducted marginal screening (details in Section C of supplementary material available at Biostatistics online) which yielded 276 candidate SNPs for variable selection. The number of SNPs studied herein is in accordance with the SIS theory, as well as practical variable selection in GWAS (Wu and others, 2009). We adjusted the values of lipidpc1 by environmental covariates (i.e., age, gender, and study site), as well as the first 10 eigenvectors from the principal component analysis of the GWAS SNPs to account for the population substructure (Avery and others, 2011). We then applied the SMA and other methods to the adjusted lipidpc1 and the 276 SNPs.

Due to differences in the study population, especially the ethnicity, we adopted the heterogeneous structure. Because the ARIC-A and ARIC-E have appreciably larger sample sizes than the other studies, we used the other seven studies to select important SNPs and used the ARIC-A and ARIC-E to evaluate the prediction accuracy. We compared the Raw, SMA, SMA-Diag, SMA-S, SMA-I, SMA-E, aLASSO-U, and HT-U methods. The aLASSO-I and HT-I methods were omitted because of their inherent incompatibility with the heterogeneous structure. For the SMA-I, the MESA-A and CHS-E were used to recover the covariance matrices for the “-A” group and the “-E” group, respectively. For the SMA-E, the 1000 Genomes data were used (separately for the “-A” and “-E” groups). Table 4 shows the model sizes obtained by the various methods, and Table 5 shows the estimated regression coefficients for some of the selected SNPs in the SMA model. (The results for the Raw model can be found in Table S10 of supplementary material available at Biostatistics online) For the seven studies combined, 164 of the selected SNPs overlap between the SMA and the Raw model. By treating the Raw as the truth, we observed that the SMA's true-positive rate (TPR) and false-positive rate (FPR) are 0.80 and 0.01, respectively. For the SMA-Diag, the TPR and FPR are 0.90 and 0.08, respectively. All the SMA-derived methods achieve sparse models. In contrast, the aLASSO-U and HT-U select much larger models which are difficult to interpret. SNP rs12982656 identified by the SMA and SMA-Diag is located in the INSR (insulin receptor) gene. This gene was found to be associated with triglycerides by the Global Lipids Genetics Consortium (2013) in a study of 188 000 subjects, which is much bigger than ours. The estimated regression coefficients vary across different studies and sometimes shrink to zero among the seven studies. For example, rs2954021 is active only in the European Americans, and rs660240 is active in five studies. The observed pattern of the active SNPs is consistent with the heterogeneous structure. The European American studies seem to share more active SNPs than the African American studies, reflecting the well-known fact that the former population is more homogeneous than the latter. The meta-analysis of multiple studies also captures SNPs that are (partly) missed by the individual aLASSO. For example, we observe that rs4420638 is captured in five studies by the SMA, but only in three studies by the individual aLASSO; likewise, rs6511720 is captured in seven studies by the SMA-Diag, but only in six studies by the individual aLASSO.

Table 4.

Variable selection in seven studies (i.e., FHS, MESA-A, MESA-E, CARDIA-A, CARDIA-E, CHS-A, and CHS-E) followed by prediction in the ARIC-A and ARIC-E studies

	Model sizes
Method	MESA-A	CARDIA-A	CHS-A	MESA-E	CARDIA-E	CHS-E	FHS	Pred-error
Raw	29	37	16	33	32	26	31	2.62
SMA	29	25	26	28	20	28	25	2.63
SMA-Diag	49	52	42	52	38	44	53	2.69
SMA-S	46	56	29	49	53	42	56	2.64
SMA-I	30	22	14	25	15	27	19	2.62
SMA-E	43	39	38	57	35	51	55	2.62
aLASSO-U	258	258	258	258	258	258	258	2.84
HT-U	241	241	241	241	241	241	241	2.78

Table 5.

Estimated regression coefficients for some selected SNPs in the SMA model

SNP	Annotation	Gene	MESA-A	CARDIA-A	CHS-A	MESA-E	CARDIA-E	CHS-E	FHS
rs4420638	Downstream	APOC1	0.03			0.03	0.19	0.26	0.49
rs660240	3UTR	CELSR2	0.24			0.07	0.26	0.22	0.15
rs445925	Upstream	APOC1		0.03	0.17	0.25	0.32	0.31	0.42
rs6511720	Intron	LDLR	0.16	0.23		0.16	0.20	0.28	0.38
rs964184	Downstream	ZPR1	0.08				0.24	0.12	0.15
rs2954021	Intron	LOC105375745				0.03	0.15	0.10	0.07
rs9302635	Intron	DHX38		0.07		0.05	0.02		0.10
rs7254892	Intron	PVRL2		0.49
rs13414987	Downstream	APOB
rs520861	Downstream	TDRD15	0.23	0.25	0.04	0.10	0.10	0.14
rs4803770	Downstream	APOC1		0.10			0.16	0.02
rs2867314	Intron	LUZP1						0.09
rs1367117	Missense	APOB				0.13	0.11	0.17
rs9939224	Intron	CETP							0.23
rs6669785	Intron	LEPR	0.13
rs4148817	Intron	ABCB4	0.10
rs38117588	Intron	Ipcef1						0.08
rs12357364	Intron	RNLS							0.07
rs1544410	Upstream	VDR				0.09
rs4384362	Intron	PDGFD				0.16
rs1002054	Intron	MAPK1IP1L					0.16
rs1470641	Intron	ITPR2		0.18		0.07		0.20
rs3846662	Intron	HMGCR		0.14		0.05	0.05	0.04	0.14
rs12982656	Intron	INSR	0.03			0.17		0.08

Note: Zero estimates are left blank. Annotation is based on dbSNP (http://www.ncbi.nlm.nih.gov/snp).

To investigate the prediction performance, we tested the SNPs selected by the eight methods on the ARIC-A and ARIC-E. We chose the active SNPs from the CARDIA-A and CARDIA-E for prediction, as these two studies are clinically similar to the ARIC studies and have well-balanced sample sizes for the two race groups. We assessed the prediction accuracy by randomly dividing each of the ARIC-A and ARIC-E into two halves, using one half to estimate the regression coefficients (via unpenalized linear regression) and the other half to calculate the prediction error. As shown in Table 4, the SMA, the SMA-Diag, and other SMA-derived methods achieve higher prediction accuracies than the aLASSO-U and HT-U. The larger prediction errors of the aLASSO-U and HT-U methods are likely due to their large model sizes, demonstrating the importance of variable selection when predicting genetic risks.

5. Discussion

Variable selection in meta-analysis is important for improving model interpretability and prediction accuracy. We have developed a class of variable selection methods—the SMA and its variations—that require only summary statistics and thus will greatly broaden the applicability of variable selection in meta-analysis. The proposed methods are particularly useful for prospectively planned meta-analysis, in which the participating studies coordinate with each other to report appropriate summary statistics. We anticipate that our approach will find its applications in the forthcoming era of big data where it is impractical to collect or store all of the raw data.

Our theoretical and numerical studies demonstrate that summary statistics can replace raw data for variable selection in meta-analysis, at least in the asymptotic sense, when full covariance matrices are available. In a similar spirit (although not in the context of variable selection), Lin and Zeng (2010) showed that summary statistics are asymptotically equivalent to raw data for meta-analysis under the fixed-effects model. We conjecture that if the first part of equation (2.1) is replaced by other suitable risk functions, then the asymptotic equivalence between summary statistics and raw data will continue to hold. If the penalty term in equation (2.1) is replaced by other reasonable penalties, such as group LASSO and group SCAD, then the asymptotic equivalence is also expected to hold. Which risk function or penalty term to use should depend on the scientific nature of the problem and the modeling aims of the investigators.

Although the penalty term in (2.1) is similar to that of Zhou and Zhu (2010), our paper deals with a very different problem. Zhou and Zhu (2010) considered group selection for a single dataset, with each group consisting of different variables (e.g., multiple genes in one pathway). In our case, each group corresponds to the same variable in multiple studies. The work of Zhou and Zhu (2010) requires access to raw data. In contrast, our approach is based solely on summary statistics and can even accommodate situations where the covariance information is not available. Because we address a different problem and work with (potentially incomplete) summary statistics instead of raw data, our technical arguments and theoretical results are somewhat different from those of Zhou and Zhu (2010). We have established the oracle property of the SMA and the selection consistency and estimation consistency for arbitrary working covariance matrices.

We have implicitly assumed that 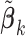is obtained under a multi-variable model. Published studies, however, may report regression coefficients that are estimated with one covariate in the model at a time. If the covariates are approximately uncorrelated, then the regression coefficients from the multi-variable and single-variable models are similar. When the covariance matrix of the covariates is available from one of the participating studies or from an external panel, such as the Hapmap and 1000 Genomes, we can recover the regression coefficients in the multi-variable model by adjusting the regression coefficients estimated from the single-variable models through simple matrix multiplication.

It would be worthwhile to enhance the capability of the SMA to tackle the “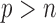” situation. In this article, we adopt the SIS theory to reduce the dimension to a manageable size and then apply the SMA for variable selection. This strategy is practically useful and seems to work well. An alternative approach would be to directly handle the “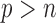” challenge, without implementing any pre-screening procedure. However, such methods are still very limited, and their applications to large datasets (such as those derived from GWAS) may be severely hindered by the excessively large number of variables. Indeed, it is still unclear what kind of summary statistics one can/should collect for data with “.”

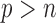Recently, Guan and Stephens (2011) proposed a Bayesian variable selection approach, which was shown to be capable of detecting weak effects in GWAS. In addition, Pickrell (2014) proposed a Bayesian hierarchical model for integrating functional genomic information with GWAS data. It would be worthwhile to extend such Bayesian methods to the setting of variable selection in meta-analysis and make a comparison with the frequentist methods presented in this paper.

In summary, we introduce a novel approach to variable selection in meta-analysis—the SMA—that relies on summary statistics alone. The SMA can be adapted to different practical situations. In addition, the SMA is computationally efficient, as it works directly on summary statistics. Our sensitivity analysis (Table S8 of supplementary material available at Biostatistics online) shows that the SMA approach is not sensitive to data perturbation, indicating that the SMA is numerically stable. As demonstrated in our simulated and empirical data, the SMA has excellent performance and thus provides a valuable new tool for high-dimensional meta-analysis.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by National Institutes of Health grants (R01 CA082659, P01 CA142538, and R37GM047845) and National Science Foundation grants (DBI-1261830 and DMS-1418172).