Effects of Mutations on the Reconfiguration Rate of α-Synuclein

Abstract

It is still poorly understood why α-synuclein, the intrinsically disordered protein involved in Parkinson’s and other neurodegenerative diseases, is so prone to aggregation. Recent work has shown a correlation between the aggregation rate and the rate of diffusional reconfiguration by varying temperature and pH. Here we examine the effects of several point mutations in the sequence on the conformational ensemble and reconfiguration rate. We find that at lower temperatures the PD causing aggregation enhancing mutations slow down and aggregation reducing mutations drastically speed up intramolecular diffusion, as compared to the wild type sequence. However, at higher temperatures, one of three familial mutations that enhance aggregation slows intramolecular diffusion while non-natural mutations that inhibit aggregation speed up intramolecular diffusion. These results support the hypothesis that the first step of aggregation is kinetically controlled by reconfiguration in which the protein chain cannot reconfigure rapidly enough to escape oligomerization. Finally we provide physical and chemical insights into why small point mutations cause these dramatic changes in the conformational ensemble and dynamics.

Graphical abstract

INTRODUCTION

A number of neurological diseases, most notably Parkinson’s disease (PD), seem to result from the aggregation of the 140 residue, intrinsically disordered protein α-synuclein.¹ Recent work has shown that α-synuclein is mostly unstructured in vitro, though not a true random coil, and highly diffusive.^2–9 However, it is still not very well understood why α-synuclein and some of its naturally occurring mutant forms are so very aggregation prone. The process is likely initiated by aggregation prone segments becoming exposed to solvent and enabling them to form intermolecular interactions.¹⁰ Ultimately, the determinant of whether a sequence will aggregate is embedded within the ensemble of unfolded states.¹¹ This ensemble samples different conformations by intramolecular diffusion and it has been shown by a simple model that when such conformational sampling slows down, aggregation competent monomer conformations can easily associate with each other, thus initiating the process of bimolecular association.¹² On the other hand, when reconfiguration is extremely fast, these aggregation competent conformations do not have time to make stabilizing interactions and aggregation is prevented.

In agreement with this model, Ahmad et al. showed that the average size of disordered α-synuclein compacts and intramolecular diffusion slows with increasing temperature.¹³ This nonintuitive result correlates with the propensity to aggregate. Therefore, it is the nature of the conformational ensemble and dynamics of reconfiguration that are in crucial control of aggregation speed. This observation has been used to find small molecule inhibitors that are able to prevent early aggregation of α-synuclein.^14,15 It is possible that point mutations in the amino acid sequence would also affect reconfiguration in a manner that correlates with aggregation propensity.

There have been numerous attempts in vitro to study the effects of aggregation-enhancing, PD-causing, familial mutations^16,17 on wild type α-synuclein by measuring and characterizing the aggregates that appear at later stages of aggregation using conventional methods such as ThT fluorescence, atomic force microscopy, electron microscopy, size exclusion chromatography, and light scattering.^18–22 Each of these mutations is unique in the lag time, formation rate, and/or morphology of fibrils and protofibrils, yet they all accelerate disease. Therefore, understanding how these mutations affect how an oligomeric dimer may form from an unstructured monomer could be useful in exploring the early stages in aggregation, which is difficult to probe using existing methods. A potential application of this technique is to screen natural mutations to identify those that encourage early stage aggregation and increase the risk of PD.^23,24

In this work we attempt to understand the sequence-dependent effect in more detail by examining the effects of point mutations on monomeric α-synuclein. The PD causing A30P mutant was reported to slow down reconfiguration by a factor of 2 at physiological temperatures,¹³ but here we attempt to investigate if the previous measurement reflected a localized effect on the sequence or if it was indeed a global phenomenon. We also test the effect of the other PD causing mutants A53T and E46K on the wildtype sequence of alpha-synuclein. Our measurements show that all the three mutants slow down diffusion of alpha-synuclein at lower temperatures. At higher temperatures, both A53T and E46K have intramolecular diffusion similar to the wild type, which lies in the dangerous regime where aggregation is extremely likely. However, A30P slows down diffusion more than wildtype at higher temperatures, making bimolecular contacts more likely compared to the wildtype and the other two mutants A53T and E46K. This correlates with previously reported studies where A30P was reported to form early stage oligomers faster than wild-type,²⁵ while E46K and A53T were found to accelerate aggregation by enhancing fibrillation.^20,26 To test if early stage aggregation can be correlated with slower diffusion in sequences, we further created two non-natural mutants in different parts of the alpha-synuclein sequence. Both these mutants reportedly inhibit the aggregation of the protein.^23,24 Our measurements show that both these mutants drastically speed up the diffusion of alpha-synuclein. This supports a model in which formation of early stage oligomers such as dimers is a competition between intramolecular reconfiguration and bimolecular diffusion, where faster diffusion enables the sequence to escape from forming bimolecular contacts.

MATERIALS AND METHODS

α-Synuclein Mutation, Expression, and Purification

The α-synuclein plasmid was a kind gift from Gary Pielak (University of North Carolina, Chapel Hill, NC). The α-synuclein mutant containing the tryptophan/cysteine (Trp/Cys) pairs Y39W/A69C (hereafter named WT_39–69) and A69C/F94W (hereafter named WT_69–94) was created using the QuikChange site-directed mutagenesis kit (Stratagene). For mutation studies, a third mutation was then introduced in either the WT_39–69 or WT_69–94, and five such triple mutants were created, namely A30P, A53T, E46K, V74E, and T72P. Each of the mutations was confirmed by DNA sequencing. The mutants were then expressed in E. coli BL21 (DE3) cells and purified by a procedure described previously.^1,2 The monomeric α-synuclein peak obtained using size exclusion was found to be >95% pure as assessed by SDS-PAGE and Coomassie blue staining.

Trp-Cys Contact Quenching Experiments

For each measurement, the respective α-synuclein mutant fractions were thawed and diluted 10× in 25 mM sodium phosphate buffer (pH 7.5), 10 mM TCEP (to prevent disulfide bond formation), 10 mM NaCl and various sucrose concentrations (0, 10, 20, and 30% w/w). The A30P_39–69 was completed with 0 mM NaCl and measured by Ahmad et al.¹³ The final concentration of the mutant proteins was kept fixed at 30 μM for each set of temperature and viscosity measurements. The buffer, sucrose, and TCEP solutions were bubbled with N₂O for 1 h to eliminate oxygen and scavenge solvated electrons created in the UV laser pulse. Triplet lifetime decay kinetics of tryptophan as a result of cysteine quenching was measured with an instrument described previously.²⁷ Briefly, the tryptophan triplet state was excited by a 10 ns laser pulse at 289 nm created from the fourth harmonic of an Nd:YAG laser (Continuum) and a 1-m Raman cell filled with 450 PSI of D₂ gas. The triplet population was probed at 441 nm by a HeCd laser (Kimmon). The probe and the reference beam were measured with silicon detectors and then combined in a differential amplifier (DA 1853A, LeCroy) with an additional stage of a 350-MHz preamplifier (SR445A, Stanford Research Systems). The total gain was 50-fold. All measurements were completed within 30 min, much less than the observed lag times for α-synuclein (~60 h). Variation of solution viscosity was achieved by varying the sucrose concentrations. Each sucrose concentration was measured at six temperatures (0, 10, 15, 20, 30, and 40 C). The viscosity of each sucrose concentrations at each different temperature was measured independently using a cone-cup viscometer (Brookfield engineering).

RESULTS

Choice of Mutations

To employ the Trp-Cys quenching method in this work, the sequence of α-synuclein was modified to contain a Tyr(Y) → Trp(W) mutation at position 39 and an Ala(A) → Cys(C) mutation at position 69, creating a W39/C69 loop on which the Trp-Cys quenching could be measured. Ahmad et al. showed that these mutations did not change the aggregation rate significantly as measured by ThT fluorescence or the CD spectrum.¹³ Thus, we will call the Y39W/A69C mutation hereafter WT_39–69. Two sets of further mutations were chosen in order to investigate the effects on the polypeptide chain dynamics of α-synuclein using the Trp-Cys quenching method on the W39/C69 loop. The first set is the well-known familial mutations, A53T, A30P (previously measured in ref 13), and E46K, which have been found to accelerate PD in humans. In order to investigate the effect of aggregation reducing mutations on α-synuclein, we chose two previously reported fibrillation-defective mutants of α-synuclein, V74E and T72P.^23,24

Trp-Cys Measurements and Data Analysis

The schematic representation of Trp-Cys contact quenching measurement is shown in Figure 1a. To measure intramolecular diffusion, we excite the W39 to a long-lived triplet state, which is quenched upon close contact with C69, almost 400-times more efficiently than with any other amino acid. The observed rate of triplet decay consists of two processes, intramolecular diffusion and irreversible quenching of the triplet by Cys on close contact. In equilibrium, intramolecular diffusion brings the Trp and Cys within the same polypeptide together with a diffusion-limited forward rate k_D+, where it may be quenched with rate q or diffuse away with rate k_D−. The observed rate is given by²⁸

$$k_{\text{obs}}=\frac{k_{\mathrm{D}}+q}{k_{\mathrm{D}-}+q}$$ (1)

Equation 1 can be rewritten as²⁹

$$\frac{1}{k_{\text{obs}}}=\frac{k_{\mathrm{D}-}}{q{k}_{\mathrm{D}+}}+\frac{1}{k_{\mathrm{D}+}}=\frac{1}{k_{\mathrm{R}}\left(T\right)}+\frac{1}{k_{\mathrm{D}+}\left(T,\eta \right)}$$ (2)

We assume the reaction-limited rate k_R depends only on temperature (T) but k_D+ depends on both temperature and viscosity of the solvent (η). Therefore, by making measurements at different viscosities for a constant temperature we can extract both k_R and k_D+ by fitting a plot of 1/k_obs vs η at a given temperature to a line in which the intercept is 1/k_R and the slope is 1/ηk_D+.

Figure 1.

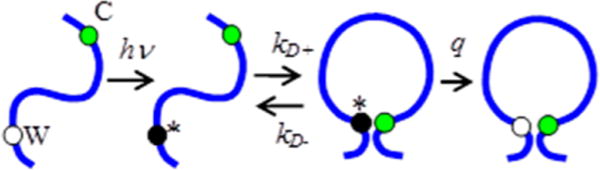
Schematic of Trp-Cys quenching measurement.

Figure S1 shows the plots of 1/k_obs vs η for all the 39–69 sequences. These times are all ~1–10 μs, indicating that the chains are freely diffusing monomers. Stable oligomers would not be freely diffusing, and the lifetimes would be ~40 μs, the natural lifetime of the Trp triplet. For the wildtype and aggregation enhancing mutations, the intercept decreases and slope increases drastically with temperature. The reaction-limited and diffusion-limited rates are plotted in Figure 2a,b. At low temperatures, the reaction-limited rates for A53T and E46K are ~2× lower than those for the wildtype and the A30P is within error, but the diffusion-limited rates are fairly similar to the wildtype. At 30 and 40 °C the intercept approaches zero, 1/k_R ≈ 0 (for some measurements, the fitted value is actually negative but within error of 0). Therefore, in these cases the observed rate is diffusion-limited, k_obs = k_D+. The triangles in Figure 2b plot k_obs for the wildtype and aggregation enhancing mutants at 30 and 40 C. Only A30P is significantly different from the wildtype. For the aggregation-inhibiting mutations (T72P and V74E) the intercepts do not approach zero for any temperature, and the slopes are fairly constant with temperature, displaying behavior seen previously in the cases of unstructured peptides and denatured proteins.^{11,27,29–34} The reaction-limited and diffusion-limited rates for the aggregation-inhibiting mutations are plotted in Figure 3a,b and diverge significantly from the wildtype at T = 30 and 40 °C.

Figure 2.

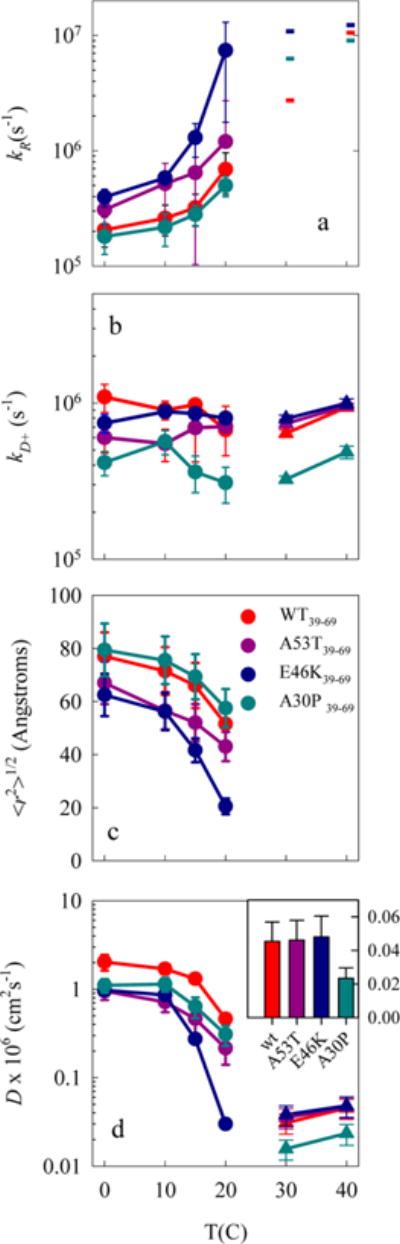
Effect of aggregation-enhancing, PD-causing, familial mutations (A53T, E46K, and A30P). (a) Reaction-limited rates. The dashes at 30 and 40 °C represent the lower limit of the rates. (b) (circles) Diffusion-limited rates, normalized to the viscosity at water at that temperature. Error bars are determined from the linear fits. (triangles) At T = 30 and 40 °C the observed rates are diffusion limited (k_obs ~ k_D+) and the error bars are the standard deviation of multiple measurements. The subscripts in the legend indicate the location of the Trp and Cys. (c) Average root-mean-square distance between the Trp and Cys determined for each reaction-limited rate using eqs 4 and 6. Error bars are determined as the change in distance required to change k_R by the measured error. (d) (circles) Intramolecular diffusion coefficients determined for each diffusion-limited rate using eq 5. The error bars are determined as proportional to the error in k_D+. (triangles) D determined from values in (b) using eq 3 and ⟨r²⟩ = 400 ± 100 Ų. The error bars are the propagated error of k_D+ and ⟨r²⟩. Inset: The diffusion coefficients of the different mutants at 30 °C.

Figure 3.

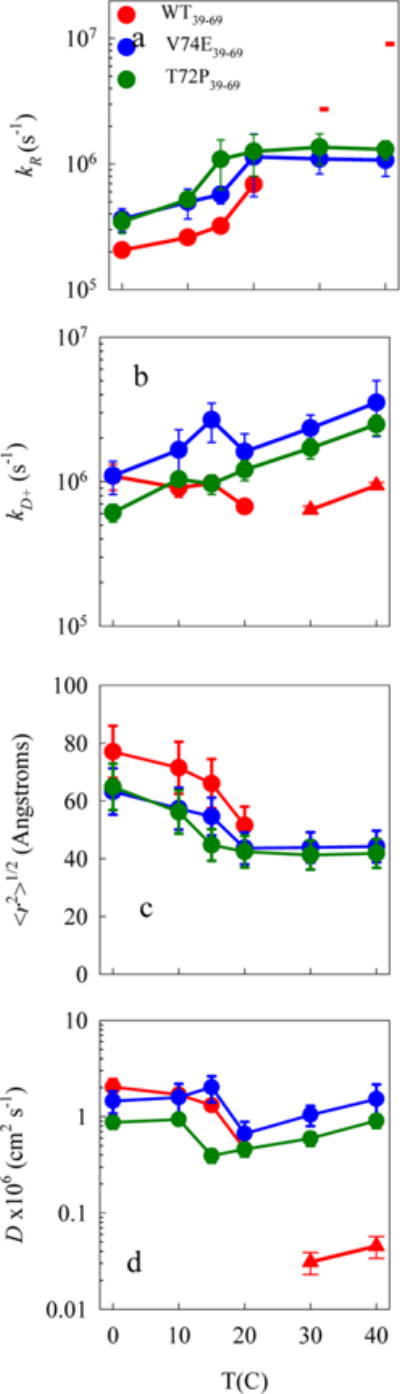
Effect of aggregation reducing mutations (V74E and T72P). (a) Reaction-limited rates. The dashes represent the lower limit of this rate. (b) (circles) Diffusion-limited rates, normalized to the viscosity of water at that temperature. Error bars are determined from the linear fits. (triangles) The observed rates are diffusion limited (k_obs ≈ k_D+), and the error bars are the standard deviation of multiple measurements. The subscripts in the legend indicate the location of the Trp and Cys. (c) Average root-mean-square distance between the Trp and Cys determined for each reaction-limited rate using eqs 4 and 6. Error bars are determined as the change in distance required to change k_R by the measured error. (d) Intramolecular diffusion coefficients determined for each diffusion-limited rate using eq 5. The error bars are determined as proportional to the error in k_D+. (triangles) D determined from values in (b) using eq 3 and ⟨r²⟩ = 400 ± 100 Ų. The error bars are the propagated error of k_D+ and ⟨r²⟩.

To interpret these rates we use a theory by Szabo, Schulten, and Schulten (SSS), which models intramolecular diffusion as diffusion on a 1-dimensional potential of mean force determined by the probability of intrachain distances (P(r)). If the observed rate is diffusion-limited and we assume the intrachain distances are approximated by a Gaussian distribution, the diffusion-limited rate is given by²⁸

$$k_{\mathrm{D}+}=\frac{4\pi D{d}_{\alpha }}{{(2\pi \langle r^2\rangle /3)}^{3/2}}$$ (3)

where d_α = 4 Å, the distance of closest approach, ⟨r²⟩ is the average Trp-Cys distance, squared, and D is the effective intramolecular diffusion coefficient. For the aggregation-enhancing mutations plus wildtype at T ≤ 20 C and the aggregation-inhibiting mutations at all temperatures, the observed rate is not diffusion-limited because diffusion is much faster. In this case we use a more detailed form of SSS theory. The measured reaction-limited (k_R) and diffusion-limited (k_D+) rates are given by²⁹

$$k_{\mathrm{R}}={\displaystyle {\int }_{d_{\alpha }}^{l_{\mathrm{c}}}q\left(r\right)P\left(r\right)\mathrm{d}r}$$ (4)

$$\frac{1}{k_{\mathrm{D}+}}=\frac{1}{k_{\mathrm{R}}^{2}D}{\displaystyle {\int }_{d_{\alpha }}^{l_{\mathrm{c}}}\frac{\mathrm{d}r}{P\left(r\right)}}{\{{\displaystyle {\int }_r^{l_{\mathrm{c}}}\left(q\left(x\right)-k_{\mathrm{R}}\right)}P\left(x\right)\mathrm{d}x\}}^2$$ (5)

where the integration limits are d_α = 4 Å, and l_c, the contour length of the protein. r is the distance between the Trp and Cys, and q(r) = 4.2 × 10⁹ exp(4.0(r − 4.0)) s⁻¹ is the experimentally determined distance-dependent quenching rate.³⁵ This rate for the Trp-Cys system drops off very rapidly beyond 4.0 Å, so the reaction-limited rate is mostly determined by the probability of the shortest distances.³⁵ Very generally, k_R and k_D+ are both inversely proportional to the average volume of the chain and k_D+ is directly proportional to D.

To determine D we assume the probability distribution, P(r), for each mutant and temperature is given by a Gaussian chain model

$$P\left(r\right)=\frac{4\pi r^2}{N}{\left(\frac{3}{2\pi \langle r^2\rangle }\right)}^{3/2}\exp \left(-\frac{3r^2}{2\langle r^2\rangle }\right)$$ (6)

where ⟨r²⟩, the average Trp-Cys distance, is an adjustable parameter, and N is a normalization constant such that ∫P(r) = 1. For each mutant and temperature, ⟨r²⟩ was found such that the calculated k_R from eq 3 matched the measured rate. These distances are plotted in Figures 2c and 3c. In the absence of any mutations the WT_39–69 compacts significantly and its diffusion slows down significantly with temperature.¹³ These values are likely unrealistic because a Gaussian curve is a much broader distribution than expected for a compact chain, but they serve as a rough guide for comparison of the chain size at various temperatures and sequences.

Alternatively, an energy reweighted wormlike chain (WLC) is a more realistic model of the unfolded chain. This model begins with 10 million randomly generated wormlike chains with a persistence length of 4 Å and a backbone excluded diameter of 4 Å. Each of these chains is given an energy determined by the number of close range interactions between residues of similar hydrophobicity.¹¹

$$\begin{array}{l}{E}_{\mathrm{H}}=-{\displaystyle \sum _{|i-j|>1}\frac{e_{i,j}}{|r_i-r_j|}}\\ e_{i,j}=\{\begin{array}{l}0,|h_i-h_j|>0.3\hfill \\ \sigma ,|h_i-h_j|\le 0.3\hfill \end{array}\end{array}$$ (7)

where the hydropathy, h, for each residue in the sequence is given using the Miyazawa-Jernigan scale. We assume that two residues with h values within 30% of each other contribute to hydrophobic or hydrophilic interactions, reducing the free energy of the system and therefore making conformations containing such interactions favorable. We also apply a distance cutoff to E_H such that E_H = 0 for |r_i − r_j| > 6.5 Å. Using the interaction energy E_H, we can reweight the probability distribution P(r) to yield a new distribution Z(r)¹¹

$$\begin{array}{l}Z(r)=N{\displaystyle \int P(r,E_{\mathrm{H}})}\exp (-E_{\mathrm{H}}/kT)\mathrm{d}{E}_{\mathrm{H}}\\ =N{\displaystyle \int P(r,E_{\mathrm{H}})}\mathrm{d}{E}_{\mathrm{H}}\frac{{\displaystyle \int P(r,E_H)\exp (-E_{\mathrm{H}}/kT){\displaystyle \int \mathrm{d}}{E}_{\mathrm{H}}}}{{\displaystyle \int P(r,E_{\mathrm{H}})}\mathrm{d}{E}_{\mathrm{H}}}\\ =NP(r){\langle \exp (-E_{\mathrm{H}}/kT)\rangle }_{\mathrm{R}}\\ \frac{1}{N}={\displaystyle \int P(r){\langle \exp (-E_{\mathrm{H}}/kT)\rangle }_{\mathrm{R}}\mathrm{d}r}\end{array}$$ (8)

The reaction-limited rate is calculated using eq 4 and substituting Z(r) for P(r). The only adjustable parameter in this model is σ, which can be tuned from 0 to ~2.5. This model is sequence specific so, in principle, the different mutants should produce the measured differences in k_R for the same tuning parameter, σ. The model fails on this account and therefore σ is assigned individually for each measurement. Table S1 shows the best values of σ that can be computed and the resulting ⟨r⟩ at 20 and 30 °C.

Using either polymeric model, the intramolecular diffusion constant, D, is determined from eq 5 using the appropriate calculated distribution and the measured k_D+. Figure 4 shows the computed values of D for both models at 20 °C. Although the average Trp-Cys distance is significantly smaller for the reweighted WLC than for the Gaussian chain, the values of D are fairly close. Thus, for purposes of comparing D between different mutants, the Gaussian chain and the reweighted WLC are equivalent. The values of D for the Gaussian chain are plotted in Figures 2d and 3d. For those sequences (WT and aggregation-enhancing mutations) that are diffusion-limited at 30 and 40 °C, we assume ⟨r²⟩^1/2 ≈ 20 Å for all mutants and use eq 3 to calculate D. This value is approximately what is required to achieve k ≈ 10⁷s⁻¹ using eq 4. It is also close to the value of a maximally compact polymer given by Flory, R ≈ l_kN^1/3 ≈ 19 Å, where l_k = 3.8 Å is the single amino acid length and N = 140 is the peptide length.

Figure 4.

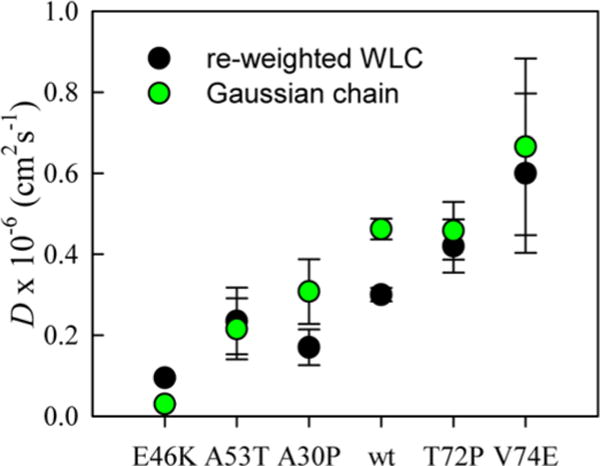
Average intramolecular diffusion coefficient of the W39–C69 loop for each mutant calculated using the Gaussian chain and energy reweighted wormlike chain (WLC) at 20 °C.

At low temperatures (0–15 °C), diffusion is about 2× slower for A30P, A53T, and E46K compared to wildtype, as shown in Figure 2d. Near 20 C, diffusion begins to slow significantly for these sequences, though it appears to occur at a lower temperature for E46K than for the others, resulting in a diffusion coefficient that is ~15× lower than the wildtype. Above 30 C the observed rates for all these sequences become diffusion-limited and we can no longer distinguish differences in chain volume. If we assume ⟨r²⟩ = 400 ± 100 Ų for all these sequences, then diffusion coefficients for A53T and E46K are within error of the wildtype. Only A30P is significantly slower, as illustrated by the inset to Figure 2d.

Figure 3d compares the aggregation-inhibiting mutations. Both V74E and T72P mutations behaved similarly by opening up the polypeptide chain and making it diffuse faster at higher temperatures. At 30 °C the V74E mutation was observed to increase diffusion by at least 25-fold while the T72P mutation by at least 14-fold compared to WT_39–69.

Ahmad et al. also demonstrated that other Trp-Cys loops throughout the sequence showed the same dynamics at pH 7.5. Therefore, we assume the 39W-69C loop is sensitive to the global dynamics of the chain.¹³ To check this assumption we made the A30P and V74E mutations to the WT_69–94 sequence containing the 69C-94W loop. These mutations are plotted in Figure S2 and show similar changes as the mutations discussed above, although the reduction in diffusion coefficient by A30P at 30 °C is smaller in the 69W-94C loop than the 39W-69C loop.

DISCUSSION

α-Synuclein is an intrinsically disordered protein in vitro that adopts an ensemble of conformations that are stabilized by long-range interactions involving the N- and C-termini. A number of SAXS and NMR studies have looked at how these long-range interactions change with the mutants E46K, A30P, and A53T and have produced conflicting reports on whether these mutations compact the chain compared to the wildtype.^19,36–40 CD and other NMR studies show minor differences in the preference for secondary structure between the mutants and the wildtype, but no difference represents a significant population within the broad ensemble that can explain the difference in aggregation behavior of the familial mutants with that of the wild type.^36,38,39 Molecular dynamics simulations have produced similarly conflicting reports.^37,40,41 Therefore, the key factor that drives these mutants to be so much more aggregation prone and pathogenic in nature than the WT and causes early onset of PD is still unknown.

In this work we have investigated how point mutations of the α-synuclein sequence affect the dynamics of the intrinsically disordered protein chain. The aggregation-inhibiting mutations, T72P and V74E, each make the chain more expanded and diffusion faster at T > 20 °C (see Figure 3d), while the aggregation-inducing mutations, A53T and E46K, make the chain slightly more compact and diffusion slower at T ≤ 20 °C but have no measurable effect at T > 20 °C compared to wildtype possibly due to our inability to assess differences in chain size at these temperatures. Ahmad et al.¹³ showed that WT α-synuclein compacts significantly and enters a dangerous regime of aggregation at T > 30 °C wherein it is much more likely to make stable bimolecular contacts, making it significantly aggregation prone at those temperatures.¹³ Our measurements here show that both A53T and E46K preserves the same kind of behavior of the sequence at higher temperatures, while further lowering the diffusion at lower temperatures and making bimolecular contact formation much more likely than the wildtype. The aggregation-inducing mutation A30P does not compact the chain significantly but slows down reconfiguration dynamics at all temperatures, enabling the sequence to make bimolecular contacts more easily than the wildtype under all conditions measured.

It should be noted that the intramolecular diffusion coefficient, D, is not the same as that obtained from classical Brownian diffusion which is entirely governed by the viscosity of the solution. If the chain was freely diffusing, each residue would randomly move as if it was a free amino acid. In reality, the chain constrains the movement of each residue both sterically and by adding some drag to the motion. This produces diffusion on a potential of mean force which is related to P(r). Furthermore, a real chain in water has many attractive and repulsive intramolecular interactions that further constrain diffusion. D as calculated in eq 5 reflects all of these contributions. The effect of these mutations is to change the pattern of intramolecular interactions to bias D compared to the wildtype pattern.

The correlation of diffusion constant with aggregation propensity can be reconciled with a model of aggregation in which the first step of dimerization depends on the speed of reconfiguration dynamics. The details of the model are described in the SI. Briefly, if the rate of diffusive reconfiguration of the monomer chain is much faster than bimolecular diffusion, when two monomers come into contact in an encounter complex, stabilizing interactions cannot be made because each chain reconfigures too quickly. However, if reconfiguration slows to about the rate of bimolecular association, stabilizing interactions can be made to form a stable oligomer. Therefore, if intramolecular diffusion (D) is slower than WT, as seen for A30P, oligomerization will be more rapid, and if diffusion is faster than WT, as observed for T72P and V74E, oligomerization is slower. As shown in the SI, assuming all other rates are the same, the oligomer formation rate scales with D. Note that later steps of oligomerization, fibril conversion and fibril elongation may not depend on reconfiguration because stable intermolecular contacts slow down intramolecular diffusion and may instead be more sensitive to structure of these states, which could also be altered with point mutations. For example, A30P is well-known to form fibrils significantly slower than the wildtype, even though it appears to accelerate Parkinson’s disease.^42,43 It is likely that oligomers are formed faster but the rate of fibril conversion is slower. Conversely, A53T and E46K form fibrils faster than wildtype but do not change reconfiguration significantly compared to that of the wildtype under physiological temperatures.

Dimer formation rates were recently measured directly using single molecule methods. Lv et al.⁴⁴ observed the residence times of fluorescently labeled α-synuclein interacting with unlabeled surface-immobilized α-synuclein. For the wildtype, Lv et al. measured a residence time of ~200 ms, much longer than the reconfiguration times measured here, indicating the encounter complex is quite stable. Furthermore, the aggregation enhancing mutations, A53T and E46K showed only modest (15% and 50%, respectively) increases in residence times, while A30P was 3 times longer than the wildtype, commensurate with our measurements of D. These lifetimes therefore support the model in which the aggregation-enhancing mutations increase time spent in the encounter complex by slowing diffusion. Although we could not measure slower diffusion for A53T and E46K outside of error, these measurements suggest diffusion is indeed slightly slower for these mutants compared to wildtype. Intriguingly Lv et al. also observe a longer lifetime for 10–20% of the dimers, ~3 s. This population could correspond to the final oligomers described in the model.

Our measurements show that a single-point mutation in a 140 residue long chain can affect the largely disordered monomeric ensemble quite significantly by either increasing or decreasing diffusion coefficients by up to 1 order of magnitude. Such differences may very well be the underlying cause of drastic differences between aggregation behaviors of the mutants with that of the wildtype. Hoffmann et al. showed that proteins of different sequences followed different polymer scaling laws and that the scaling exponent varied by mean net charge and mean hydrophobicity.⁴⁵ Unfortunately no coarse sequence determinants such as these precisely capture the observed effects of the single-point mutations measured in this work. Furthermore, wildtype α-synuclein is not a typical unstructured polypeptide. Other unstructured sequences that have been measured typically show only a small increase in k_R and actually an increase in k_D+ with temperature.^11,27,46 Wildtype α-synuclein shows opposite behavior, with a drastic increase in k_R with temperature, wherein the chain compacts significantly, and a decrease in k_D+, implying a dramatic slowdown in diffusion. The temperature-dependent behavior of k_D+ for α-synuclein may indicate that this sequence is on the verge of an anomalous glass transition near physiological temperatures.¹³ It appears E46K is shifting this glass-transition temperature down while T72P and V74E are shifting it up or eliminating the transition entirely.

Most of the mutations have a change in hydrophobicity which could affect the temperature dependence as well. The seminal work by Brandts showed that the free energy of hydration for different residues had different temperature dependencies.⁴⁷ Theoretically, Huang and Chandler showed the temperature of maximum chemical potential depended on the size of the hydrophobic solute.⁴⁸ More recently, Li and Walker directly measured the compaction of hydrophobic homopolymers by single molecule force measurements and showed that different types of hydrophobic groups shifted the temperature dependence of free energy of extension significantly.⁴⁹ Data compiled by Wuttke et al. of the free energy of solvation of all amino acids vs temperature showed that Ala and Pro have similar positive free energies and little temperature dependence, while Thr has a negative free energy and a strong temperature dependence,⁵⁰ which could explain the A53T and T72P results. However, there is no well-developed sequence-specific theory to predict the ensemble changes that we observe here. As we showed above, the reweighted WLC model cannot account for these sequence changes using the same tuning parameter, σ. This makes it a challenge to predict changes in intramolecular diffusion quantitatively.

Two mutations, V74E and E46K involve changes in charge. The net charge of the wildtype sequence at physiological pH is ~−9, so the aggregation-inhibiting mutation makes the net charge more negative (−10) and the aggregation-enhancing mutation makes it less negative (−7). Using the theory of Higgs and Joanny,⁵¹ we calculate that the chain radius of E46K should be 18% smaller than the wildtype, similar to the difference in chain size at 0 C. The radius of V74E should be 8% larger, within our error at 0 °C but much smaller than we estimate at 30–40 °C. Pappu and co-workers have further postulated that there exists a coil-to-globule transition for most intrinsically disordered sequences at high net positive or negative charge, though the charge pattern and hydrophobicity affect where this transition occurs.^52,53 Commensurate with the discussion above, the wildtype sequence may sit on the edge of this transition and simply increasing or decreasing the net charge will push the ensemble into coil or globule states, with bigger changes than estimated by net charge alone. As with hydrophobicity, there is still no sequence-specific theory to predict these effects.

The only mutation that does not significantly alter the conformational ensemble (as detected by k_R) at any temperature is A30P, in agreement with the similar free energies of solvation for Ala and Pro found by Wuttke et al.⁵⁰ However, A30P does have about a 2-fold lower diffusion coefficient than the WT suggesting that proline acts as a stiffer link in the chain than alanine. This may also explain why the effect is bigger for the 39W-69C loop than the 69C-94W loop since the stiffness is essentially a local sequence effect. The same effect can also be seen for T72P. This mutant has practically the same reaction-limited rates at all temperatures as V74E but the diffusion coefficient is ~2-fold slower than V74E. That proline adds stiffness to the chain is not at all surprising. Lapidus et al. showed that polyproline chains as short as 3 residues had no measurable end-to-end contact.²⁸

In conclusion, we have shown that the reconfiguration rates of various mutants of α-synuclein correlates strongly with the propensity to make early bimolecular contacts both in vitro and in vivo, supporting the hypothesis that aggregation is kinetically controlled by intramolecular diffusion. Experimentally, this work is unique in directly measuring reconfiguration dynamics but is relatively poor at describing the entire conformational ensemble, especially at high temperatures when the ensemble is quite compact. Thus, future measurements need to be coupled to other temperature-dependent measurements of specific intramolecular distances, such as single-molecule FRET. A fundamental question that remains incompletely answered is how these small changes to sequence have such a huge effect on dynamics. Future work is needed to produce predictive models of conformation ensembles based on the sequence that is sensitive to single-point mutations.