Quantitative and predictive model of kinetic regulation by E. coli TPP riboswitches

ABSTRACT

Riboswitches are non-coding elements upstream or downstream of mRNAs that, upon binding of a specific ligand, regulate transcription and/or translation initiation in bacteria, or alternative splicing in plants and fungi. We have studied thiamine pyrophosphate (TPP) riboswitches regulating translation of thiM operon and transcription and translation of thiC operon in E. coli, and that of THIC in the plant A. thaliana. For all, we ascertained an induced-fit mechanism involving initial binding of the TPP followed by a conformational change leading to a higher-affinity complex. The experimental values obtained for all kinetic and thermodynamic parameters of TPP binding imply that the regulation by A. thaliana riboswitch is governed by mass-action law, whereas it is of kinetic nature for the two bacterial riboswitches. Kinetic regulation requires that the RNA polymerase pauses after synthesis of each riboswitch aptamer to leave time for TPP binding, but only when its concentration is sufficient. A quantitative model of regulation highlighted how the pausing time has to be linked to the kinetic rates of initial TPP binding to obtain an ON/OFF switch in the correct concentration range of TPP. We verified the existence of these pauses and the model prediction on their duration. Our analysis also led to quantitative estimates of the respective efficiency of kinetic and thermodynamic regulations, which shows that kinetically regulated riboswitches react more sharply to concentration variation of their ligand than thermodynamically regulated riboswitches. This rationalizes the interest of kinetic regulation and confirms empirical observations that were obtained by numerical simulations.

Introduction

Thiamine pyrophosphate (TPP), the active form of thiamine (vitamin B1), is an essential cofactor for many enzymes, particularly in the universally conserved pyruvate dehydrogenase complex involved in the citric acid cycle (or Krebs cycle).¹ As such, cellular TPP concentration has to be tightly regulated. In bacteria, thiamine and TPP are synthesized de novo following a complex pathway^2-4 sketched in Fig. 1 for E. coli. It has long been considered that the regulation of such a pathway was exclusively protein-dependent. However, non-coding leader regions of mRNA, precisely of mRNAs involved in thiamine biosynthesis, were shown to be important in the regulation process. It was hypothesized that TPP could interact directly with the regulatory sequence,⁵ which was shown rapidly to hold true.^6,7 The same scenario had occurred for the interaction of vitamin B12 with the btuB mRNA leader.^8-10 Such RNA regulatory modules found in the 5′-UTR of bacterial mRNAs have been coined riboswitches.⁸ Since then, many other riboswitches have been uncovered,¹¹ comprising riboswitches in the 3′-UTR of plant and fungi mRNAs,¹² and structural aspects as well as their modes of action have been reviewed.^13-16 Globally, a riboswitch is divided into an aptamer domain able to bind its specific ligand and a so-called expression platform. Regulation originates from alternative pairing of sequences in the aptamer domain and in the expression platform depending on the concentration of the ligand (Fig. 2AB).

Figure 1.

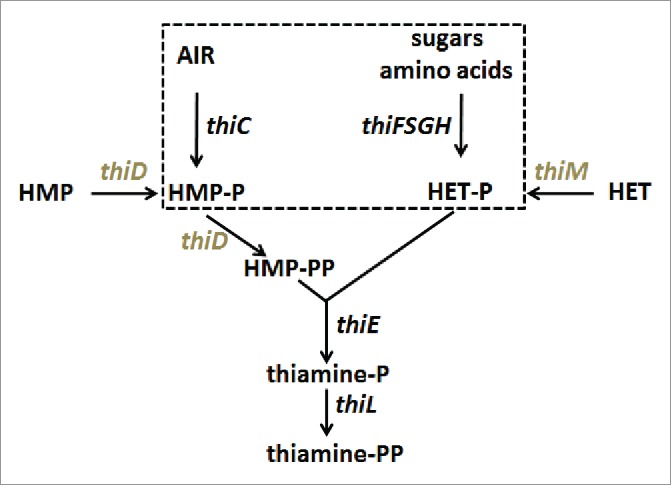
Simplified view of the thiamine biosynthesis pathway in E.coli. Enzymes encoded by the thiC operon (thiC and thiF,S,G,H, dashed box) synthezise the primary substrates hydroxymethylpyrimidine phosphate (HMP-P) and hydroxyethylthiazole phosphate (HETP). AIR: Amino-imidazole ribotide. Note that thiE is in the same operon. Genes in the thiM operon (thiM and thiD in gray) code for kinases that ultimately produce HMP-PP. Adapted from.³

Figure 2.

Organization, regulation mechanisms and secondary structures of E.coli and A.thaliana thiamine pyrophosphate riboswitches. (A) In E.coli, riboswitches are located in the 5′-UTR and control translation (thiM, shown here as an example) and/or transcription (thiC) of the downstream genes. At low TPP concentration, the aptamer (black) is not fully folded and the regulatory sequence (here the Shine-Dalgarno sequence,SD) in the expression platform (EPF, gray) is available for gene expression whereas, at higher concentration, TPP binding induces a sequestering of SD, which prevents initiation of translation see Fig. 8B for thiC. (B) In A.thaliana, the TPP riboswitch is located in the 3′-UTR of the gene THIC. At low TPP concentration, the 5′-strands of helices P4 and P5 pair within intron 2 (In2), which masks the 5′-splice site, leaves the major poly-adenylation site available and produces a short stable transcript. At higher TPP concentration, the riboswitch aptamer folds completely, which permits Intron 2 splicing and removal of the major poly(A) site thus producing a longer unstable transcript (adapted from ¹²). (C) Structure of the ditopic thiamine pyrophosphate with the pyrimidine and pyrophosphate groups interacting at different locations within the RNA (see D). (D) The sequences of the bacterial riboswitch aptamers are the wild type sequences, whereas the sequence of ATthiC is the one used for the crystallographic study.⁵¹ The stem P3 is most variable in plant riboswitches and the retained shortened P3 corresponds to the conserved part.¹² The box labeled ECthiC_mutP1 corresponds to the sequence of a P1-helix variant of ECthiC (see text). The conserved loop sequence UGAGA between P2 and P3 is the binding site for the pyrimidine moiety of the TPP and the conserved internal loop between P4 and P5 is the pyrophosphate binding site.

An important aspect concerning the mechanism of action of a riboswitch is whether it is acting thermodynamically, or kinetically. In the first case, the dissociation constant of its specific ligand fits with the cellular concentration of the ligand to be maintained and the mass action law governs the riboswitch response. In the second case, the dissociation constant is too low, i.e. the affinity is too high, for a thermodynamic control since the riboswitch would always be saturated by its ligand and, therefore, would never act as a switch. The riboswitch, then, has to proceed by a kinetic mechanism.^17,18 This aspect is particularly important for transcription regulators, because a decision has to be taken ‘on the fly’ after synthesis of the aptamer sequence, but before the RNA polymerase has reached the critical point after which it cannot be halted anymore. In this particular case of TPP riboswitches, crude measurements of TPP in cells ^19,20 allowed us to derive that, depending on the growing media in use, the TPP concentration lies roughly in the range 3-150 µM. In addition, the ${\mathit{K}}_d$ values of TPP as a cofactor of different bacterial enzymes range from 0.27 to 9 µM with a mean value of 3 µM (SD-1). One may thus consider that riboswitch-mediated regulation, be it of kinetic or thermodynamic nature, has to switch from the OFF to the ON state in response to a concentration of free TPP decreasing (roughly) below the micromolar range.

We have considered in this work three structurally-related, but functionally different TPP riboswitches, two in E. coli and one in A. thaliana (Fig. 2). E. coli thiM riboswitch regulates translation of the thiM operon^6,21 (Fig. 1A), whereas genetic control of the thiC operon by E. coli thiC riboswitch appears to occur both at the level of translation and transcription.⁶ For the latter, however, no clear sequence signatures that could explain these properties are apparent.⁶ A. thaliana THIC riboswitch regulates 3′-UTR processing with alternative splicing events depending upon the TPP concentration ¹² (from now on ECthiC, ECthiM and ATthiC will stand respectively for E. coli thiC, E. coli thiM and A. thaliana thiC). One major difference between these prokaryotic and plant riboswitches is that, in line with their respective functions, ECthiC and ECthiM are in the 5′-UTR, whereas ATthiC is in the 3′-UTR. Also, the expression platform is downstream of the aptamer in ECthiC and ECthiM, whereas it is upstream of the aptamer in ATthiC (Fig. 2AB).

Our goal was to compare their kinetics of folding and, particularly, to fully understand the regulatory mechanism. For that, we have used extensively hydroxyl-radical (^•OH) footprinting (with an efficient processing method), which confirmed that the ditopic TPP (Fig. 2C) interacts first within the RNA mostly through its pyrimidine moiety and not through its pyrophosphate. We also used our recently developed kinetic method (kinITC) based on Isothermal Titration Calorimetry (ITC)²² in conjunction with Surface Plasmon Resonance (SPR). We verified that these TPP riboswitches follow a pure ‘induced-fit’ mechanism involving a first binding step followed by complete RNA folding. Based upon the firmly established kinetic model, kinITC yielded the full set of thermodynamic and kinetic parameters for the two E. coli riboswitches, which showed that they are kinetically regulated. A quantitative model linked these experimentally determined parameters to the dependence of ECthiC- and ECthiM-mediated regulation on TPP concentration. This yielded a regulation curve with a typical sigmoid shape indicating a switch at a TPP concentration in the expected micromolar range. In contrast, the plant riboswitch is thermodynamically regulated and showed considerable dependence of its kinetics of folding upon temperature, which suggests that it could also act as a thermosensor.

Results

Hydroxyl-radical footprinting results: kinetic aspects

Hydroxyl-radical-footprinting experiments were performed on ATthiC and on ECthiC_mutP1 related to ECthiC (Fig. 2D). The results showed that ATthiC folds very slowly at room temperature since 30 min were necessary at 25°C to achieve its folding after TPP addition at 2 µM concentration (Fig. 3). Importantly, this slow folding was not due to the low TPP concentration used in this experiment as confirmed by ^•OH experiments at higher TPP concentrations (not shown) and by kinetic ITC experiments at high TPP concentrations (Fig. SD-2A). This means that, around 25°C, ATthiC is intrinsically a slow folder irrespective of the TPP concentration above 0.1 µM (see conclusion of SD-9). In comparison, ECthiC_mutP1 achieved its folding at 27°C in less than 10 s (Fig. SD-3ABC). The overall folding process of ATthiC showed unambiguously a fast component characterized by a ‘short time’ (8 ± 2)s and a slow component characterized by a ‘long time’ (700 ± 140)s (Fig. 3A). Such a behavior is the mark of a kinetic mechanism in two steps, as a single kinetic step with a large excess of ligand (justifying 1^st-order approximation) would only show one single exponential time.

Figure 3.

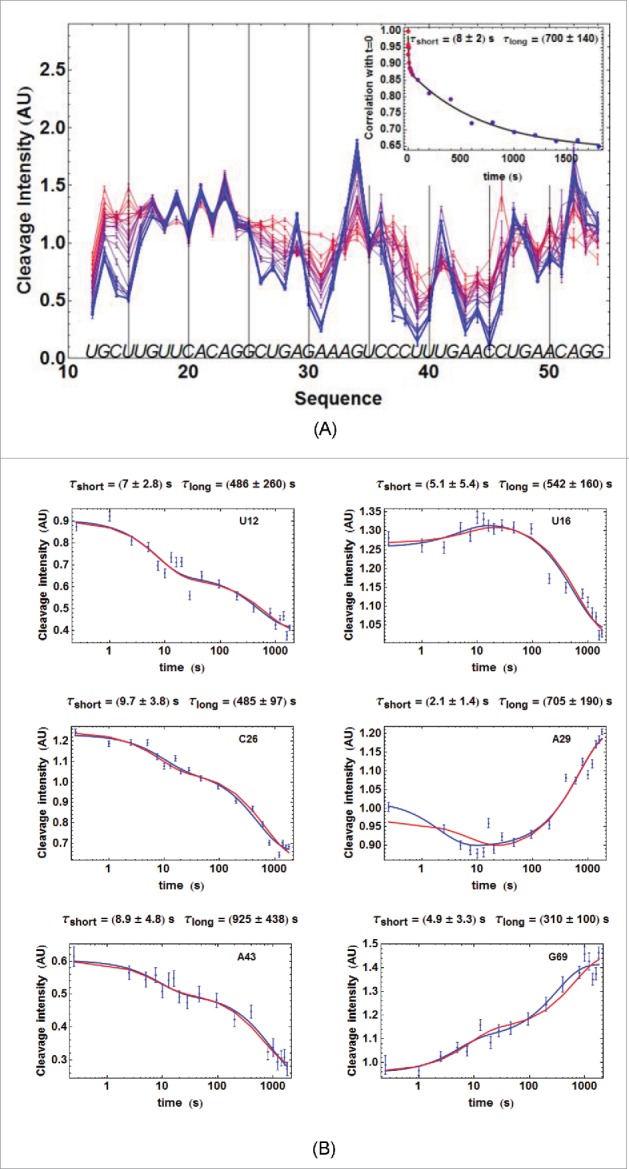
For figure legend, see next page.Figure 3. (figure previous page) Kinetics of ATthiC cleavage from ^•OH footprinting. (A) Each color corresponds to a particular time after TPP addition from t = 0 (pure red), to t = 30 min (pure blue). The times were 0, 1, 2.5, 5, 7.5, 10, 13, 16, 20, 28, 46, 95, 200, 400, 800, 1000, 1200, 1400, 1600 and 1800 s. Conditions: TPP 2 µM, magnesium acetate 2 mM, sodium cacodylate buffer 5 mM, pH 6.5, 25 °C. The fact that no cleavage variation was observed from G17 to G24, which was not imposed in the processing, is a good indication of the quality of the overall quantification procedure since these residues form a quickly folded apical loop not susceptible to be influenced by TPP binding. Cleavage curves for selected residues are shown in Fig. 3B. A typical gel is shown in Fig. SD-3D. The inset shows the correlation of each cleavage curve with the cleavage curve for t = 0 as a function of time, which highlights the biphasic character of the kinetics. (For this correlation curve, the experimental data in the main figure, limited to the residue range U12-G54, were supplemented with other data to cover the wider residue range U12-G69).The solid curve is from a bi-exponential fit; the resulting times τ_short and τ_long from the fit correspond well with those obtained for individual cleavage curves in Fig. 3B. (B) Kinetics of ^•OH cleavage for selected residues of ATthiC. The experimental points are those for six particular residues (U12, U16, C26, A29, A43 and G69) from Fig. 3A and from other data (not shown). A few experimental points were flagged as outliers and suppressed (e.g., t = 1 s for A29 and A43). The two kinds of fit mentioned in the text are shown: in blue, the simple bi-exponential fit (equation 4) and, in red, the fit making use of kinetic model #1 proved to be the correct one in the following (see Fig. SD-10 for an assessment of the quality of fit). The times ${\tau }_{short}$ and ${\tau }_{long}$ reported for each residue result from the bi-exponential fit and are related to $k_{fast}$ and $k_{slow}$ in equation (4) by ${\displaystyle k_{fast} =1/{\tau }_{short} }$ and ${\displaystyle k_{slow} =1/{\tau }_{long}}$.

Two extreme kinetic models are possible. Kinetic model #1 (‘induced fit’) implies that the TPP ligand (L) binds to the incompletely folded RNA (R₀) to yield the bound species R₁ subsequently folded fully into R₂ according to the two steps:

$${\mathit{R}}_0+\mathit{L}\underset{{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}}{\overset{{\mathit{k}}_{\mathit{o}\mathit{n}}}{\to \leftarrow }}{\mathit{R}}_1$$ (1a)

$${\mathit{R}}_1\underset{{\mathit{k}}_{\mathit{U}}}{\overset{{\mathit{k}}_{\mathit{F}}}{\to \leftarrow }}{\mathit{R}}_2$$ (1b)

Alternatively, kinetic model #2 (‘conformational selection’) implies that the essential folding step occurs first and TPP binding in a second step, according to:

$${\mathit{R}}_0\underset{{\mathit{k}}_{\mathit{U}}}{\overset{{\mathit{k}}_{\mathit{F}}}{\to \leftarrow }}{\mathit{R}}_1$$ (2a)

$${\mathit{R}}_1+\mathit{L}\underset{{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}}{\overset{{\mathit{k}}_{\mathit{o}\mathit{n}}}{\to \leftarrow }}{\mathit{R}}_2$$ (2b)

In both cases, ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}\mathit{ }}$ and ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{U}}\mathit{ }}$ stand, respectively, for ‘folding’ and ‘unfolding’ and one may define the dissociation constant ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{d}}={\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}/{\mathit{k}}_{\mathit{o}\mathit{n}}\mathit{ }}$ and the equilibrium constant ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{F}}={\mathit{k}}_{\mathit{F}}/{\mathit{k}}_{\mathit{U}}.}$ It is extremely important to emphasize that ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{d}}\mathit{ }}$ corresponds to the dissociation constant, either of the initial step (model ##1), or of the final step (model #2), and not to the overall dissociation constant (noted ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$ in the following). Whatever the kinetic model, the two terms are related by ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{d}}(\text{overall})={\mathit{K}}_{\mathit{d}}/{\mathit{K}}_{\mathit{F}}.}$ Keeping in mind this difference between ${\displaystyle {\mathit{K}}_{\mathit{d}}\mathit{ }}$ and ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$ is crucial for correct understanding and for a valid comparison with previous works that reported on ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$^23-25 For example, for ECthiM, we obtained at 30°C ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$= 19 nM, but ${\displaystyle {\mathit{K}}_{\mathit{d}}}$= 0.45 µM with ${\displaystyle {\mathit{K}}_{\mathit{F}}}$ = 23.3. Thermodynamically, the two models cannot be discriminated since ${\displaystyle \mathit{ }\mathit{\Delta }\mathit{H}(\text{overall})=\mathit{\Delta }{\mathit{H}}_{\mathit{B}\mathit{i}\mathit{n}\mathit{d}\mathit{i}\mathit{n}\mathit{g}}+\mathit{\Delta }{\mathit{H}}_{\mathit{F}\mathit{o}\mathit{l}\mathit{d}\mathit{i}\mathit{n}\mathit{g}}}$ and ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{d}}(\text{overall})={\mathit{K}}_{\mathit{d}}/{\mathit{K}}_{\mathit{F}}\mathit{ }}$ are equally verified in the two situations. However, the two models can be discriminated kinetically. The mathematical basis for this discrimination is explained in Materials and Methods.

Finally, it is of interest of coming back on the large difference in folding kinetics observed for ATthiC and ECthiC_mutP1. Such a large difference was surprising for highly similar RNAs. Since it has been reported that a C2′-endo / C3′-endo conformational switch of a single residue could be rate-limiting in RNA folding,²⁶ we examined whether such a critical residue could explain the slow folding of ATthiC. We considered U35 as a candidate because (i) it is both in a C2′-endo and bulgedout conformation in the crystal structure of ATthiC, (ii) it has no counterpart neither in ECthiC nor in ECthiC_mutP1 and (iii), its counterpart U36 in ECthiM is in a different environment as it is flanked on 3′ by a non-canonical A37-G9 base pair, whereas U35 in ATthiC is flanked on 5′ by a non-canonical G34-G11 base pair. Surprisingly, ITC showed that a ΔU35 sequence was unable to bind TPP. We can thus only conclude that, in the context of the ATthiC sequence, U35 is crucial for shaping a TPP-binding competent riboswitch. Identifying the sequence determinants of ATthiC slow folding would deserve a full study.

Disclosing the kinetic mechanism / assessing our methodology

There is now direct evidence from single-molecule fluorescence energy transfer (smFRET) experiments on ECthiM ²⁷ that the TPP interacts with a pre-organized riboswitch aptamer following the induced-fit mechanism of kinetic model #1 (equations 1ab). Model #1 was also shown to agree with the results from a single-molecule study of ATthiC with optical tweezers.²⁸ Furthermore, TPP riboswitches are commonly considered as belonging to class II riboswitches (i.e., those achieving complete folding after binding of their ligand).²⁹ Nevertheless, given the crucial importance of this for the kinetic regulation theory that follows, and also in view of assessing our methodology, we examined this aspect in great details. For that, we performed a comparison of our results obtained with ^•OH footprinting, kinITC and SPR. We also included in the comparison results from a fluorescence study.²³ The rationale is that the correct kinetic model has to be consistent with different techniques monitoring different parameters. We considered in this comparison ATthiC (^•OH footprinting, SPR), the slightly modified sequence ECthiC_mutP1 for which numerous results were already available (^•OH footprinting, kinITC, SPR) and ECthiM (kinITC, fluorescence). A part of the results for ECthiC_mutP1 were presented in ²² to describe the method kinITC. Here, the kinITC study was extended to ECthiC and ECthiM.

First, we compared the ^•OH footprinting results for ATthiC showing clear biphasic kinetics (Fig. 3) with SPR results. For that, we attempted to process the SPR experimental curves with both kinetic models. Importantly, it was impossible to fit the experimental curves with model #2, whereas model #1 yielded a good result with the following values for all kinetic parameters (at 25°C): ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}=}$ (3.26 ± 0.16)×10⁴ M⁻¹s⁻¹, ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}=}$(1.09 ± 0.02) × 10⁻³s⁻¹, ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}=}$(0.39 ± 0.03)×10⁻³s⁻¹ and ${\displaystyle {\mathit{k}}_{\mathit{U}}=}$(1.30 ± 0.08) × 10⁻³ s⁻¹ (thus ${\displaystyle {\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}=}$(1.7 ± 0.1)×10⁻³s⁻¹) (Fig. SD-4A). From these values, the corresponding short and long times could be derived from equations 5a,b (Material & Methods) on ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}}$ and ${\displaystyle {\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}}$, which yielded $\mathit{}{\mathit{\tau }}_{\mathit{s}\mathit{h}\mathit{o}\mathit{r}\mathit{t}}={\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}^{-1}=$ 15 s and $\mathit{}{\mathit{\tau }}_{\mathit{l}\mathit{o}\mathit{n}\mathit{g}}={\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}^{-1}=$ 595 s, in reasonable agreement with the fully independent ^•OH experimental results (Fig. 3A). To go beyond these partial results, we took advantage of the slow folding of ATthiC yielding well-resolved ^•OH cleavage curves (Fig. 3B) to make use of the second processing method with kinetic model ##1, which allowed us obtaining ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}}$ and ${\displaystyle {\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}}$ in a way completely independent from SPR (see SD-10 about the fact that only the sum ${\displaystyle {\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}}$ and not ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}}$ and ${\displaystyle {\mathit{k}}_{\mathit{U}}}$ separately, could be determined). We imposed in this search the value of ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$ obtained independently, which constrained the kinetic parameters of equations (1a,b) to verify ${\displaystyle \mathit{ }({\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}/{\mathit{k}}_{\mathit{o}\mathit{n}})({\mathit{k}}_{\mathit{U}}/{\mathit{k}}_{\mathit{F}})={\mathit{K}}_{\mathit{d}}(\text{overall}).}$ Since ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$ was obtained by SPR and ITC, we used both estimates. The results are in Table 1, which shows that model #1 led to good agreement between the two techniques despite their great difference, and despite the very small number of really free parameters used for extracting kinetic results from the ^•OH cleavage curves. Particular examples of the joint fit of all cleavage curves are in Fig. 3B.

Table 1.

Comparison of SPR and ^•OH results on ATthiC for model #1. The indicated values of ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$(from SPR or ITC) were used to constrain the search of the kinetic parameters with the ^•OH cleavage curves (see text). The value for ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\text{ITC\hspace{0.17em}}=0.35\text{\hspace{0.17em}µM}}$ is the value estimated at 25°C for the major RNA species representing ca. 95 % of the active RNA: Fig. SD-17A,C.

	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}\left({\text{M}}^{\text{−1}}{\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}\left({\text{s}}^{\text{−1}}\right)}$
SPR	${\displaystyle \left(3.26\pm 0.16\right)\times {10}^4}$	$\left(1.7\pm 0.1\right)\times {10}^{-3}$
•OH with ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\text{SPR}\mathit{ }=0.1\text{\hspace{0.17em}µM\hspace{0.17em}}}$	${\displaystyle \left(3.5\pm 2\right)\times {10}^4}$	$\left(2.6\pm 0.6\right)\times {10}^{-3}$
•OH with ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\text{ITC\hspace{0.17em}}=0.35\text{\hspace{0.17em}µM}}$	${\displaystyle \left(1.7\pm 0.9\right)\times {10}^4}$	$\left(3.9\pm 1.1\right)\times {10}^{-3}$

For ECthiC_mutP1, we compared the SPR and kinITC results reported in.²² However, in²² the SPR data were processed with a classical single-step mechanism whereas the kinITC data were processed with model #1 only. Here, we reprocessed with our own programs all these data with models #1 and #2. At variance with ATthiC, the SPR data could be fitted almost equally well with both models (Fig. SD-4BC). However, only model #1 yielded very good agreement with the kinITC results for the values of ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},\mathit{ }{\mathit{k}}_{\mathit{F}}}$ and ${\displaystyle {\mathit{k}}_{\mathit{U}}}$ (Table 2). Both kinetic models led to the same disagreement on ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}}$(see legend of Table 2).

Table 2.

Confrontation of the two models with SPR and kinITC results on ECthiC_mutP1. The values from SPR were obtained at 25°C, and those from kinITC were calculated for 25°C from the results obtained at 20, 27, 30, 34 and 37°C. Only model #1 led to excellent agreement for ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},{\mathit{k}}_{\mathit{F}}\text{\hspace{0.17em}and\hspace{0.17em}}{\mathit{k}}_{\mathit{U}}}$ from the two techniques, whereas model #2 led to serious disagreement for ${\displaystyle {\mathit{k}}_{\mathit{F}}}$ and considerable disagreement for ${\displaystyle {\mathit{k}}_{\mathit{U}}.}$ As already mentioned in ²² for model #1, both kinetic models and both techniques disagree on ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}}$ by a factor of 6. However, only kinITC is in agreement with the very well determined value of ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$ obtained by ITC after independent measurements at five temperatures.

Model #1	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}\left({\text{M}}^{\text{−1}}{\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}\left({\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}\left({\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{U}}\left({\text{s}}^{\text{−1}}\right)}$
SPR	${\displaystyle \left(1.28\pm 0.03\right)\times {10}^5}$	0.16 ± 0.025	1.8 ± 0.26	$\left(3\pm 0.5\right)\times {10}^{-3}$
kinITC	${\displaystyle \left(0.26\pm 0.02\right)\times {10}^5}$	0.09 ± 0.006	1.1 ± 0.1	$\left(3.7\pm 0.5\right)\times {10}^{-3}$
Model #2	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}\left({\text{M}}^{\text{−1}}{\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}\left({\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{F}}\left({\text{s}}^{\text{−1}}\right)}$	${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{U}}\left({\text{s}}^{\text{−1}}\right)}$
SPR	${\displaystyle \left(1.39\pm 0.03\right)\times {10}^5}$	$\left(2.4\pm 0.1\right)\times {10}^{-4}$	1.5 ± 0.35	$\left(2.9\pm 0.7\right)\times {10}^{-2}$
kinITC	${\displaystyle \left(9.4\pm 4.4\right)\times {10}^5}$	$\left(3\pm 1.6\right)\times {10}^{-4}$	0.32 ± 0.08	17 ± 3

In this work we also submitted ECthiC and ECthiM to kinITC with the experimental protocol described in ²² for ECthiC_mutP1. The fit of all injection curves with model #1 is shown in Fig. SD-5AD, all numerical results are in SD-6AB, the evolution with the temperature of all thermodynamic and kinetic parameters are reported in Fig. 4 for ECthiM and in Fig. SD-7 for ECthiC. We could compare our new results on ECthiM with those from an independent fluorescence study that was performed by considering 2-aminopurine (2AP) substitution for adenine at seven positions in the aptamer.²³ This allowed Lang et al. to obtain, for each modified position, the slow component of the kinetics of 2AP disturbance (at 25°C) upon TPP addition at various concentrations (their Table 1). These raw experimental results yielded a set of seven ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{b}\mathit{s}}}$ values with a mean value ${\displaystyle <{\mathit{k}}_{\mathit{o}\mathit{b}\mathit{s}}>=}$8.7×10⁴ M⁻¹s⁻¹ and a standard deviation of 4.4×10⁴ M⁻¹s⁻¹. From the analysis exposed in SD-9, ${\displaystyle <{\mathit{k}}_{\mathit{o}\mathit{b}\mathit{s}}>}$ should be comparable to ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}}$ for model #1 (equation S9.1), whereas it should be comparable to $\mathit{}{\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{k}}_{\mathit{F}}/\left({\mathit{k}}_{\mathit{F}}+\mathit{}{\mathit{k}}_{\mathit{U}}\right)$ for model #2 (equation S9.2). The results at 25°C of the kinITC experiments yielded ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}=}$(6.4 ± 2) × 10⁴ M⁻¹s⁻¹ with model #1 and $\mathit{}{\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{k}}_{\mathit{F}}/\left({\mathit{k}}_{\mathit{F}}+\mathit{}{\mathit{k}}_{\mathit{U}}\right)\approx$2.8 × 10⁴ M⁻¹s⁻¹ with model #2 (the error was not estimated). By comparison to ${\displaystyle <{\mathit{k}}_{\mathit{o}\mathit{b}\mathit{s}}>=}$8.7×10⁴ M⁻¹s⁻¹, model #1 is again favored. We have no independent experiments to be compared with those for ECthiC.

Figure 4.

Thermodynamic and kinetic results from kinITC for ECthiM. (A) Thermodynamic results. The evolution with the temperature of the thermodynamic parameters of all steps in equations 1a,b was obtained with kinITC used with model #1. The figures for ΔG and ΔS refer to the complete reaction involving TPP binding and RNA folding. The figure for ΔH collects ΔH_Binding, ΔH_Folding (dashed curve) and ΔH_ITC = ΔH_Binding + ΔH_Folding shown in blue with the individual values obtained by normal use of ITC at five different temperatures (blue dots). Note the extremum of K_d reached at the temperature where ΔH_Binding = 0 in agreement with the Van't Hoff equation linking K_d(binding) and ΔH_Binding. This extremum is here a maximum because $\mathit{}\mathit{\Delta }{\text{C}}_{\text{P}}\left(\text{Binding}\right)=\partial \mathit{\Delta }{\mathit{H}}_{\text{Binding}}/\partial \mathit{T}$ is positive. The injection curves of the kinITC experiments at different temperatures and their fit are shown in Fig. SD-5C. (B) Kinetic results. The evolution with the temperature of all kinetic parameters in equations 1a,b was obtained with kinITC used with model #1. The activation energies and $\mathit{}\mathit{\Delta }{\text{H}}_{\text{on}}^{‡}\text{and}\mathit{}\mathit{\Delta }{\text{H}}_{\text{U}}^{‡}$ were obtained as adjustable parameters in kinITC, and $\mathit{}{\text{ΔH}}_{\text{on}}^{‡}$and $\mathit{}{\text{ΔH}}_{\text{U}}^{‡}$ were deduced from $\mathit{}\mathit{\Delta }{\text{H}}_{\text{Binding}}^0=\mathit{}\mathit{\Delta }{\text{H}}_{\text{on}}^{‡}–\mathit{}\mathit{\Delta }{\text{H}}_{\text{off}}^{‡}$ and $\mathit{}\mathit{\Delta }{\text{H}}_{\text{Folding}}^0=\mathit{}\mathit{\Delta }{\text{H}}_{\text{F}}^{‡}–\mathit{}\mathit{\Delta }{\text{H}}_{\text{U}}^{‡}$, respectively.

In conclusion, all our experimental results on ECthiC_mutP1, ECthiM and ATthiC, as well as the fluorescence²³ and smFRET ²⁷ experiments on ECthiM, and the optical-tweezer experiments on ATthiC,²⁸ are unambiguously in favor of kinetic model #1, which is thus the assumed model in the following.

kinITC results shed light on the kinetic regulation by E.coli riboswitches

The kinetic mechanism being now firmly established we can discuss the results obtained from kinITC with model #1. As a consequence of the ability of kinITC to dissect the overall process into its two components, TPP binding and RNA folding, the global enthalpic term measured by ITC could be split into ${\displaystyle \mathit{\Delta }{\mathit{H}}_{\text{Binding}}}$ and ${\displaystyle \mathit{\Delta }{\mathit{H}}_{\text{Folding}}}$. It appears that ${\displaystyle \left|\mathit{\Delta }{\mathit{H}}_{\text{Binding}}\right|}$ for ECthiM never becomes large (it has a null value at 32°C), whereas ${\displaystyle \mathit{\Delta }{\mathit{H}}_{\text{Folding}}}$ becomes more and more negative as the temperature increases (Fig. 4A). Globally, the same features were also observed for ECthiC in this work (Fig. 5A) and for ECthiC_mutP1in,²² which adds support to these observations.

Figure 5.

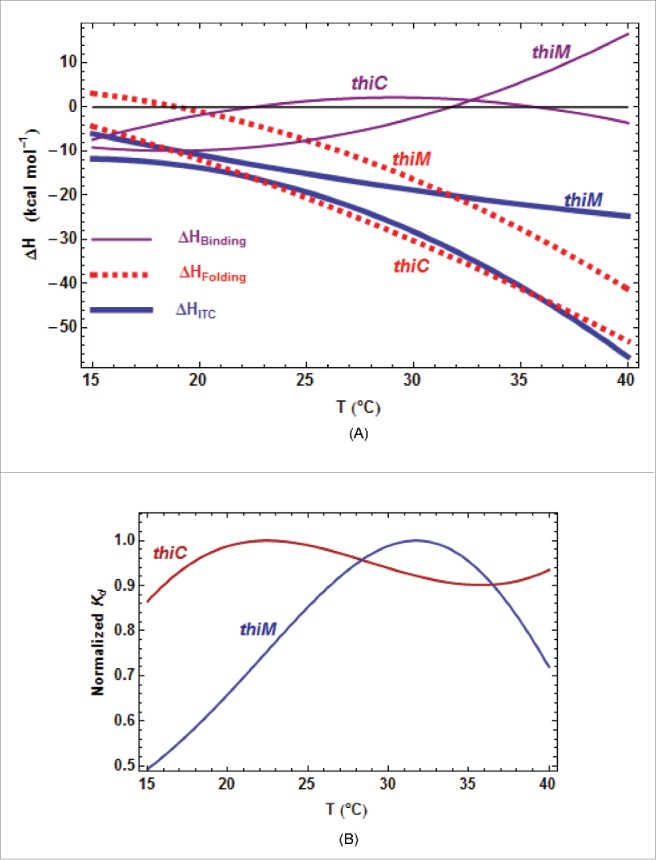
Comparison of the thermodynamic parameters for E. coli riboswitches. A. Comparison of all ΔH terms from kinITC. The three curves are related by ΔH_ITC= ΔH_Binding+ ΔH_Folding. The pattern is similar for the two E. coli riboswitches: the two ΔH_Binding curves cross ΔH_Binding= 0 at nearby temperatures and the two ΔH_Folding curves are quasi parallel. B. Quasi absence of temperature variation for ${\displaystyle {\mathit{K}}_{\mathit{d}}.}$ Each ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ curve has been normalized to a unit value at its maximum (0.93 µM for ECthiC and 0.45 µM for ECthiM). ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ is almost constant for ECthiC and varies at most twofold for ECthiM in a broad temperature range in comparison of ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }}$ which varies tenfold for ECthiM (Fig. 4A) and more than thirtyfold for ECthiC (Fig. SD-7A).

First, that ${\displaystyle \mathit{\Delta }{\mathit{H}}_{\text{Folding}}}$ becomes more negative when the temperature increases is consistent with the fact that, upon TPP-triggered folding (implying stabilization), the RNA releases most of the heat stored as thermal agitation during its progressive destabilization in absence of TPP. Second, as a consequence of the van ‘t Hoff equation linking the ${\displaystyle \mathit{\Delta }\mathit{H}}$ and the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ of an equilibrium $(\partial \mathit{ln}{\mathit{K}}_{\mathit{d}}/\partial (1/\mathit{T})=\mathit{\Delta }\mathit{H}\text{/R,}$ with R the gas constant), a null value of ${\displaystyle \mathit{\Delta }\mathit{H}}$ at some temperature implies that the corresponding ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ is extremum at that temperature and, in turn, varies little around that temperature. This feature is clearly visible for ECthiC and ECthiM (Fig. 5B) as previously noticed for ECthiC_mutP1.²² This fact has implications of strong significance because the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ for the initial step appears to be tuned for the TPP concentration to be regulated (${\displaystyle {\mathit{K}}_{\mathit{d}}}$ = 0.9 µM for ECthiC and 0.45 µM for ECthiM at 30°C, see tables SD-6AB). On the contrary, ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})\mathit{ }={\mathit{K}}_{\mathit{d}}/{\mathit{K}}_{\mathit{F}}}$ is not only strongly variable with the temperature, but is also much too low at all temperatures (less, or much less than 0.2 µM for ECthiC (Fig. SD-7A), and less than 0.06 µM for ECthiM (Fig. 4A) to be at the basis of a classical thermodynamic regulation. Therefore, these two riboswitches ensure a regulation of kinetic nature and their ability to detect a low TPP concentration appears to be correlated to the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ for the initial step, not to ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall}).}$

Primary and secondary (late) sites of TPP interaction

Beyond yielding classical kinetic information (through the parameters ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}}}$ and ${\displaystyle {\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}}$), the second processing method of ^•OH footprinting results (see Material and Methods and SD-10) makes use of the firmly established kinetic model, which eventually yields three coefficients ${\displaystyle {\mathit{\alpha }}_0^{\mathit{n}},{\mathit{\alpha }}_1^{\mathit{n}},{\mathit{\alpha }}_2^{\mathit{n}}}$ for each residue. These coefficients represent the propensity of the n^th residue to be cleaved in, respectively, the species ${\displaystyle {\mathit{R}}_0,{\mathit{R}}_1,{\mathit{R}}_{2\mathit{ }}}$ (equations 1a,b). If a particular residue is sensing early TPP binding, its cleavage propensity is expected to change between the initial state ${\displaystyle {\mathit{R}}_0}$ and the intermediate state ${\displaystyle {\mathit{R}}_1}$. This implies that ${\displaystyle \left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)}$ should be significantly different from 0. We have represented the evolution along the sequence of this difference normalized by its e.s.d, viz. ${\displaystyle \left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)/\mathit{\sigma }\left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)}$, which shows remarkably well that the primary binding of TPP occurs via its pyrimidine ring into the conserved loop sequence UGAGA between P2 and P3 (Fig. 2D, Fig. 6AB). This is particularly clear for ATthiC, which does not show any primary binding in the P4/P5 junction where the pyrophosphate moiety eventually interacts, whereas EcthiC_mutP1 shows slight primary binding in the P4/P5 junction (Fig. SD-11A). These results fit well with those obtained by chemical probing in³⁰ and with a study that showed that thiamine (corresponding to TPP deprived of pyrophosphate) can bind like TPP within the pyrimidine binding pocket without any contact with the (disordered) pyrophosphate-binding pocket.³¹ Analogous conclusions derive from crystal structures of ECthiM bound to TPP, TMP and pyrithiamine also deprived of pyrophosphate.³² Therefore, this confirms that prior pyrophosphate binding is not necessary for pyrimidine binding and this also shows (at least for ECthiM studied in^31,32) that the pyrophosphate-binding pocket becomes ordered only upon interaction with the pyrophosphate. Also adding support to our results is the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ value of 1.5 µM reported for thiamine/ECthiM interaction,³³ which is close to ${\displaystyle {\mathit{K}}_{\mathit{d}}}$= 0.45 µM obtained with kinITC (SD-6B) for the initial binding step of TPP comparable to thiamine binding.

Figure 6.

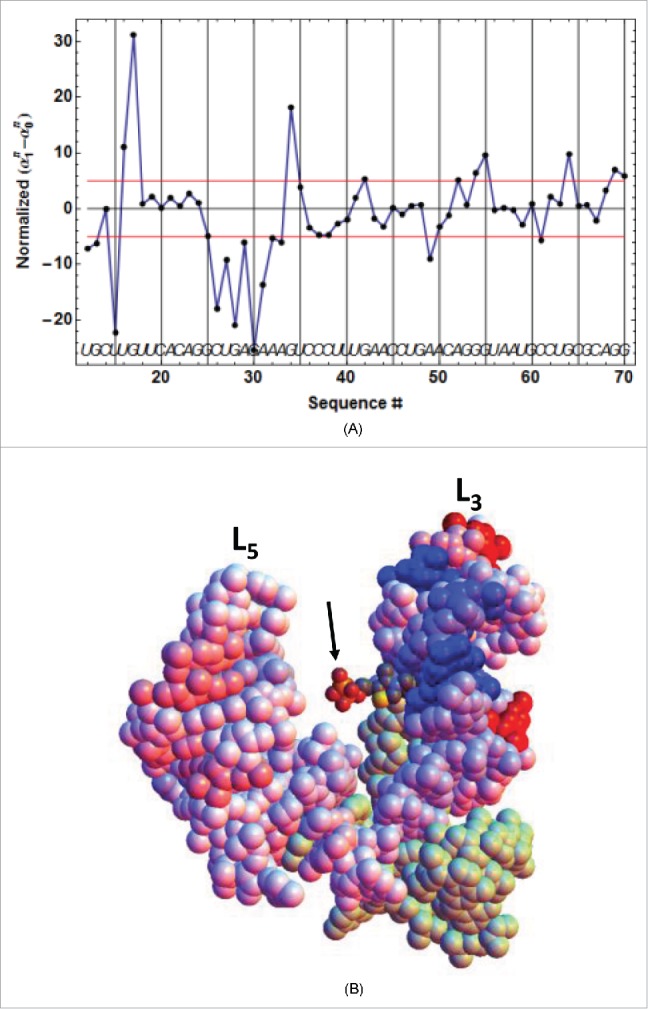
Primary TPP/RNA interaction for ATthiC. (A) The evolution along the sequence of the normalized difference ${\displaystyle \left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)/\mathit{\sigma }\left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)}$ (see text) is shown. A large negative (resp. positive) value of the difference is the mark of early protection against cleavage (resp early enhanced cleavage) after TPP addition. The red lines mark the positive and negative limits at a 5σ threshold. B. The closed riboswitch from the crystal structure has been opened to visualize the primary interaction of the TPP with the RNA; only the pyrophosphate of the TPP is visible (arrow). The loops L5 and L3 are labeled (Fig. 2D). The colors evolve from pure blue to pure red for, respectively, the most negative and most positive values of the normalized difference ${\displaystyle \left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)/\mathit{\sigma }\left({\mathit{\alpha }}_1^{\mathit{n}}-{\mathit{\alpha }}_0^{\mathit{n}}\right)}$ shown in Fig. 6A. The greenish color corresponds to the 5′-end and 3′-end residues for which no accurate results were obtained. All significantly negative values (pure blue), as well as the highest positive values (pure red), are exclusively located around the interaction site of the TPPpyrimidine moiety.

The same analysis performed with ${\displaystyle \left({\mathit{\alpha }}_2^{\mathit{n}}-{\mathit{\alpha }}_1^{\mathit{n}}\right)/\mathit{\sigma }\left({\mathit{\alpha }}_2^{\mathit{n}}-{\mathit{\alpha }}_1^{\mathit{n}}\right)}$ highlighted the secondary (or late) TPP interaction occurring during the second kinetic step (Fig. SD-11BC). Particularly striking is the protection of C14 and C26 in P3 by the closing of the apical loop L5, and the protection of G60 by the formation of a close contact with the TPP. Altogether, these results are perfectly consistent with kinetic model ##1.

Determination of ON/OFF-state probabilities for kinetically-regulated riboswitches

As a major consequence of the previous results, we developed a quantitative model of kinetic regulation. For that, we sought to express, as a function of the ligand concentration and of all relevant kinetic parameters, the probabilities ${\displaystyle {\mathit{P}}_{\text{ON}}}$ and ${\displaystyle {\mathit{P}}_{\text{OFF}}=1-{\mathit{P}}_{\text{ON}}}$ for a kinetically-regulated riboswitch to be in the ON- and OFF-state, respectively. These considerations extend those in ¹⁷ where the binding of the ligand to an adenine riboswitch was modeled satisfactorily with one kinetic step. Here, we take in consideration the two-step mechanism of model ##1. Negative regulation (corresponding to the OFF-state) results from the formation of the species ${\displaystyle {\mathit{R}}_2\mathit{ }}$(equation 1b) due to stable binding of TPP to the newly synthesized aptamer, importantly before the polymerase has reached a point where it cannot be halted anymore for transcription regulation, or within the time left for the ribosome to bind to the Shine-Dalgarno sequence for translation regulation. If we note ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ (noted ${\displaystyle \mathit{\Delta }{\mathit{t}}_{\mathit{R}\mathit{N}\mathit{A}\mathit{P}}}$ in ¹⁷) the average time necessary for the polymerase to reach such a critical switching point, the probability ${\displaystyle {\mathit{P}}_{\text{OFF}}}$ is thus equal to the probability of formation of the species ${\displaystyle {\mathit{R}}_2\mathit{ }}$ after ${\displaystyle {\mathit{t}}_{\mathit{S}}}$. This probability is nothing else than the molar fraction of ${\displaystyle {\mathit{R}}_2\mathit{ }}$ formed at ${\displaystyle \mathit{t}={\mathit{t}}_{\mathit{S}}}$ with ${\displaystyle {\mathit{R}}_1\mathit{ }={\mathit{R}}_2\mathit{ }=0}$ at ${\displaystyle \mathit{t}=0.}$ From equation (4) in Materials and Methods, it is thus obtained:

$${\mathit{P}}_{\text{ON}}\mathit{}=1-{\tilde{\mathit{R}}}_2-{\mathit{f}}_2\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}\mathit{}{\mathit{t}}_{\mathit{S}})-{\mathit{s}}_2\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\mathit{}{\mathit{t}}_{\mathit{S}})$$ (3)

with ${\tilde{\mathit{R}}}_2={\mathit{K}}_{\mathit{F}}{\left(1+{\mathit{K}}_{\mathit{F}}+{\mathit{K}}_{\mathit{d}}/{\mathit{L}}_{\text{tot}}\right)}^{-1}$ being the fraction of ${\displaystyle {\mathit{R}}_2\mathit{ }}$ at equilibrium (equation S8.3c in SD-8),${\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}$ and ${\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}$ being given by equation (5a) and the coefficients ${\displaystyle {\mathit{f}}_2}$ and ${\displaystyle {\mathit{s}}_2}$ by equations S8.5. The dependence of ${\displaystyle {\mathit{P}}_{\text{ON}}}$ on the logarithm of ${\displaystyle {\mathit{L}}_{\text{tot}}}$ shows the characteristic sigmoid shape of a ‘logistic function’ (Fig. 7). However, equation (3) is not a ‘general-purpose’ equation involving adjustable parameters; instead it makes an explicit link to, and only to, the ligand concentration ${\displaystyle {\mathit{L}}_{\text{tot}}}$ and the measurable kinetic parameters ${\displaystyle {\mathit{t}}_{\mathit{S}},{\mathit{k}}_{\mathit{o}\mathit{n}},{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},{\mathit{k}}_{\mathit{F}},{\mathit{k}}_{\mathit{U}}}$(since all parameters ${\tilde{\mathit{R}}}_2,{\mathit{f}}_2,{\mathit{s}}_2,{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}$ and ${\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}$ in equation (3) can be calculated from ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}},{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},{\mathit{k}}_{\mathit{F}},{\mathit{k}}_{\mathit{U}}}$ and ${\displaystyle {\mathit{L}}_{\text{tot}}}$). One may thus expect legitimately that the position of the inflection point of the sigmoid curve, which only depends on these measurable parameters, should correspond to the expected TPP concentration of the ON/OFF switching point. We will see that this is indeed the case.

Figure 7.

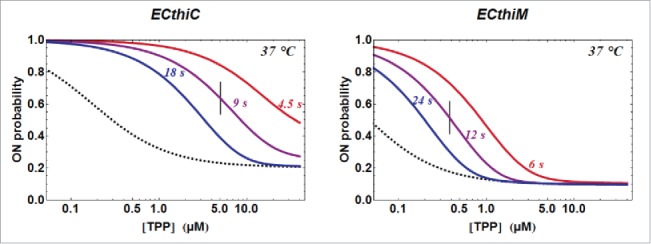
TPP concentration dependence of the kinetic regulation by ECthiC and ECthiM. The dependence of ${\displaystyle {\mathit{P}}_{\text{ON}}}$ on the TPP concentration from equation (3) is shown (solid curves) for a common temperature (37°C) and for three values of ${\displaystyle {\mathit{t}}_{\text{S}}}$. The value for each middle curve (9 s for ECthiC and 12 s for ECthiM ) corresponds to the experimental pausing time observed at 37°C with NusA. The vertical bar on each middle curve marks the inflection point where the regulation efficiency is maximum. The two other curves corresponding to half and twice the pausing time are shown to illustrate the effect of this parameter on the regulation. The black dashed curves correspond to ${\displaystyle {\mathit{P}}_{\text{ON}}}$ that would be obtained if each riboswitch was thermodynamically, and not kinetically controlled, which emphasizes the strong kinetic character of the regulation.

From equation (3), it is clear that an increase of ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ would shift progressively the regulation from a dominant kinetic regime to a purely thermodynamic regime corresponding to ${\mathit{P}}_{\text{ON}}\mathit{}=1-{\tilde{\mathit{R}}}_2$, which is illustrated in Fig. 7 with three values of ${\displaystyle {\mathit{t}}_{\mathit{S}}.}$ The kinetic parameters ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}},{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},{\mathit{k}}_{\mathit{F}},{\mathit{k}}_{\mathit{U}}}$ being determined (at a given temperature) for a particular riboswitch, only ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ can thus influence the ligand concentration of the ON/OFF switch. As we have seen (introduction), this switch has to occur when the TPP concentration lies broadly in the micromolar range, which is precisely the order of magnitude of the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ values of the initial step obtained by kinITC. Interestingly, equation (3) gives deep insight into a condition ensuring that this ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ value would be the TPP concentration around which the ON/OFF switch occurs. (This obviously does not mean that the switch has to occur exactly at the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$, but that the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ value defines a range of concentration for the switch). At variance with the usual and practical definition of the ON/OFF switch corresponding to the ligand concentration at half-maximum response, we define it as the inflection point of the sigmoid curves where the variation of ligand concentration has the greatest effect (Fig. 7). We think this is the appropriate definition since it corresponds to an intrinsic property not biased by the responses at high and low ligand concentrations. On a practical ground, however, the two definitions are more or less equivalent. The full mathematical expressions (equations 3 and 5a,b) are too involved to be used directly for the determination of the inflection point. However, as explained in SD-8 (equation S8.5c et seq.), the term ${\mathit{f}}_2\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}\mathit{}{\mathit{t}}_{\mathit{S}})$ becomes rapidly negligible in comparison of ${\mathit{s}}_2\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\mathit{}{\mathit{t}}_{\mathit{S}}),$ which greatly simplifies the problem. An analysis based upon carefully checked approximations (detailed in SD-12) showed that the inflection point of the regulation curve lies at a TPP concentration very close to ${({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{t}}_{\mathit{S}})}^{-1},$ which corresponds to ${\mathit{K}}_{\mathit{d}}={({\mathit{k}}_{\mathit{o}\mathit{n}}/{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}})}^{-1}$ if ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ is equal to ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}.$ This theoretical conclusion was perfectly confirmed by numerical calculations (Fig. SD-12A,C). The major result of this study, therefore, is that the overall time ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ left for ligand binding has to be roughly of the order of ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}$ to obtain a regulation in the right range of TPP concentration, which is a strong prediction of our quantitative model. There is an apparent contradiction with one conclusion in¹⁷ stating instead that ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ has to be significantly smaller, or much less, than ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}.$ The contradiction disappears when considering the different meaning of ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}}$ in¹⁷ and in this work (see SD-13). Before examining the validity of this prediction we consider other consequences of the model.

A kinetic regulation is more efficient than a thermodynamic regulation

A ‘kinetic regulation efficiency’ (KRE) can be defined by the steepness of the response to concentration variation of the ligand. Such steepness can be quantified by considering the slope ${\displaystyle \left|\mathit{d}{\mathit{P}}_{\mathit{O}\mathit{N}}/\mathit{d}\left(\mathit{l}\mathit{o}\mathit{g}10{\mathit{L}}_{\text{tot}}\right)\right|}$ at the inflection point (Fig. SD-12C). Interestingly, the exposed model allows estimating this slope (SD-14), which shows that this KRE is very close to ${\displaystyle \mathit{l}\mathit{n}\left(10\right){\mathit{e}}^{-(1+1/{\mathit{K}}_{\mathit{F}})}}$ for any riboswitch ensuring a kinetic regulation according to model ##1. In addition, if ${\displaystyle {\mathit{K}}_{\mathit{F}}\gg 1,}$ the index is close to the universal maximum value ${\text{KRE}}_{\text{max}}=\mathit{ln}\left(10\right){\mathit{e}}^{-1}\approx \mathrm{0.847.}$ In general, one thus has $\text{KRE }\approx {\text{ KRE}}_{\text{max}}{\mathit{e}}^{-1/{\mathit{K}}_{\mathit{F}}}.$ When ${\displaystyle {\mathit{K}}_{\mathit{F}}\gg 1,}$ this implies that a 4-fold increase of the ligand concentration around the switching point makes ${\displaystyle {\mathit{P}}_{\text{ON}}}$ drop by ca. 1/2 (from ∼0.65 to ∼0.15).

For a classical thermodynamic regulation based upon mass action law, a ‘thermodynamic regulation efficiency’ (TRE) index can also be estimated from ${\displaystyle \left|\mathit{d}{\mathit{P}}_{\mathit{O}\mathit{N}}/\mathit{d}\left(\mathit{l}\mathit{o}\mathit{g}10{\mathit{L}}_{\text{tot}}\right)\right|}$ (see SD-14), which also yields a universal value ${\displaystyle \text{\hspace{0.17em}TRE}=\mathit{l}\mathit{n}\left(10\right)/4\approx 0.576}$. This universality is in agreement with the analysis in³⁴ for thermodynamically regulated riboswitches. (It is interesting to compare our ‘ideal’ value ${\displaystyle \text{\hspace{0.17em}TRE}\approx 0.576}$ with the results obtained in ³⁴ by numerical simulations. From Fig. 2C in,³⁴ we derived the lower value ${\displaystyle \text{\hspace{0.17em}TRE}\approx 0.45}$, which fits with a decrease of efficiency resulting from mRNA degradation taken into account in the simulations). According to our results, a ‘kinetic regulation’ is thus intrinsically more efficient than a ‘thermodynamic regulation’ since ${\text{KRE}}_{\text{max}}\text{ / TRE}=4{\mathit{e}}^{-1}\approx \mathrm{1.47.}$ More precisely, with a ‘thermodynamic regulation’, a 4-fold increase of the ligand concentration from ${\displaystyle {\mathit{L}}_{\text{tot}}\approx {\mathit{K}}_{\mathit{d}}/2}$ to ${\displaystyle {\mathit{L}}_{\text{tot}}\approx 2{\mathit{K}}_{\mathit{d}}}$ makes ${\displaystyle {\mathit{P}}_{\text{ON}}}$ drop by 1/3 only (from 2/3 to 1/3), and not by 1/2 as with a ‘kinetic regulation’. To recover the same drop of ${\displaystyle {\mathit{P}}_{\text{ON}}}$ by 1/2, a thermodynamic regulation requires a 9-fold increase of the ligand concentration from ${\displaystyle {\mathit{L}}_{\text{tot}}={\mathit{K}}_{\mathit{d}}/3}$ to ${\displaystyle {\mathit{L}}_{\text{tot}}=3{\mathit{K}}_{\mathit{d}}}$. In conclusion, a kinetic regulation produces a steeper response than a thermodynamic regulation, which leads to a more accurately defined concentration of the ON/OFF switch. This rationalizes the interest of a kinetic regulation. Noteworthy, analogous conclusions were reached empirically after numerical simulations in.¹⁷

RNA polymerase pauses and kinetic regulation

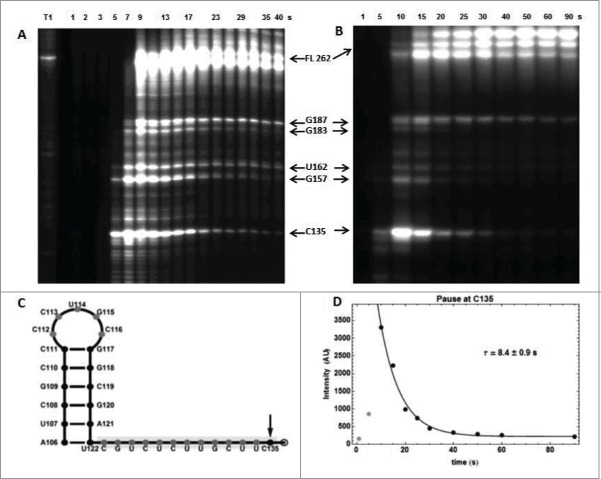
The fact that the RNA polymerase pauses at critical locations is at the basis of riboswitch-mediated kinetic regulation.^17,18,35-37 Indeed, a kinetic regulation results from these pauses leaving the appropriate time to the ligand for binding to the riboswitch aptamer, but only when its concentration is high enough. We thus first verified the existence of pauses for the 2 E. coli riboswitches (Fig. SD-15B), next we determined the pausing times and, finally, we compared these results with the predictions of our kinetic-regulation model.

For ECthiC, we observed a strong pause site at C₁₃₅ downstream of the aptamer domain (Fig. 8A-B). That it can be seen as a programmed pausing site is corroborated by the existence of a stable hairpin-loop (A₁₀₆-U₁₂₂) upstream of the pause site (Fig. 8C), thus forming a canonical transcription pausing site.³⁸ From the exponential decrease of the intensity of the corresponding band on gel we derived an average pausing time of the polymerase at C₁₃₅ of (5.8 ± 0.3) s at 30°C (Fig. 8A) and (5.2 ± 0.4) s at 37°C (not shown). Since the protein NusA is known to increase the pausing time,^39,40 the analysis was repeated with E. coli NusA, which yielded the enhanced value (8.4 ± 0.9) s at 37°C (Fig. 8B, D). These pausing times should be increased slightly to take into account the time necessary for the polymerase to reach the pausing site from the end of the aptamer, say ca. 2 s (this is not critical). With ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}=}$ (22 ± 7)×10³ M⁻¹ s⁻¹ obtained from kinITC at 37°C and from the previous theoretical analysis on the determination of ON/OFF-state probabilities, one derives with ${\displaystyle {\mathit{t}}_{\mathit{S}}}$∼8+2 = 10 s that the ON/OFF switch takes place around a TPP concentration equal to ${\left({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{t}}_{\mathit{S}}\right)}^{-1}=$ (6.1 ± 2.4) µM without NusA and to (4.5 ± 2.) µM with NusA. It is interesting to compare the observed pausing time (∼8+2 = 10 s with NusA) with the theoretical value ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}\approx$(52 ± 5) s ensuring that the regulation would take place around a TPP concentration equal to the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ of the initial step (i.e. 0.85 µM). The value of the ratio ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}/\left(\text{pausing time}\right)\approx 5.2$ simply means that the regulation takes place at a concentration roughly 5 times above the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$.

Figure 8.

RNA polymerase pause sites observed during ECthiC template transcription. (A) Transcription kinetics without nusA (see SD-15AB). Transcription times are indicated on top of the gel. Pause sites positions are indicated on the right (FL: full length transcript). The leftmost lane is an RNAse-T1 ladder. Significant pausing is visible at upstream positions of C135. Transcription was performed at 30°C. (B) Transcription kinetics with NusA (0.3 µM). Pausing at C135 is now prominent as compared to A. Transcription experiment was performed at 37°C. (C) Sequence upstream of the pausing site at C135. The footprint of the polymerase is indicated by the gray rectangle. The hairpin structure forms a class I pause site according to.³⁹ (D) Kinetic analysis of pausing at C135. The exponential time τ = 8.4 s corresponds to the average pausing time. The points corresponding to 1 and 5 s (in gray) were not used in the fit.

For ECthiM, we observed 2 strong pauses at the close sites C₁₅₃ and G₁₅₉, and 2 weaker pauses at G₁₀₇ and at G₁₂₈ of the AUG codon (Fig. SD-16). Pausing was already mentioned in the same region of the ECthiM expression platform,⁴¹ but we could not make a detailed comparison of our results with those in.⁴¹ With several consecutive pause sites contributing to the overall pausing time ${\displaystyle {\mathit{t}}_{\mathit{S}}}$, the observed kinetics of pausing at the 3′-pause-site is also affected by the incoming flux of RNA polymerase from the upstream pause-sites. Therefore, the observed pausing time ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ at G₁₅₉, including the effect of the upstream pausing sites, is the relevant pausing time for the kinetic regulation mechanism. As for ECthiC, upon addition of NusA at 37°C, the pausing time increased, but marginally from (8.2 ± 1.9) s to (10 ± 1.2) s. With the value ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}=}$(22 ± 6.6) × 10⁴ M⁻¹s⁻¹ obtained with kinITC at 37 °C (Fig. 4B) and ${\displaystyle {\mathit{t}}_{\mathit{S}}\approx 10+2=12\text{\hspace{0.17em}s,\hspace{0.17em}}}$ one derives that the regulation takes place around a TPP concentration equal to ${\left({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{t}}_{\mathit{S}}\right)}^{-1}=$ (0.38 ± 0.2) µM. Finally, we can compare the observed pausing times at 37 °C (∼12 s) with the theoretical value ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}.$ With ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}}$ at 37 °C from kinITC, it is obtained ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}^{-1}=$(11.6 ± 1) s. Here, the agreement with the observed pausing time is excellent, which means that the regulation takes place around a TPP concentration very close to the ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ of the initial step (i.e., 0.4 µM).

It may thus be emphasized that the kinetic-regulation model, only supplemented with experimental values from kinITC (that is without any adjustable parameters), yielded the order of magnitude for the pausing time of the RNA polymerase for ECthiC, and an accurate value of it for ECthiM. Furthermore, the switching TPP concentration deduced from the model is around 4.5 µM for ECthiC and around 0.4 µM for ECthiM (at 37°C). Again, there is good agreement between the predictions of the model and the expected range of TPP concentration where the ON/OFF switch has to take place (see Introduction and SD-1).

ATthiC is under thermodynamic control

Although we could not obtain for ATthiC the rich amount of information that was obtained with kinITC for ECthiC and ECthiM, we nevertheless obtained with SPR all kinetic parameters at 25°C, which yielded ${\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}}=1.1\times {10}^{-3}{\text{s}}^{\text{−1}}$ and ${\mathit{k}}_{\mathit{F}}+\mathit{}{\mathit{k}}_{\mathit{U}}=1.7\times {10}^{-3}{\text{s}}^{\text{−1}}$ (Fig. SD-4A). According to the considerations in SD-9, these close values imply that the separation between the linear and saturation regimes for ${\displaystyle {\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\left({\mathit{L}}_0\right)}$ is close to ${\displaystyle 2\left({\mathit{k}}_{\mathit{F}}+\mathit{ }{\mathit{k}}_{\mathit{U}}\right)/{\mathit{k}}_{\mathit{o}\mathit{n}}\approx 0.1\text{\hspace{0.17em}\hspace{0.17em}µM,\hspace{0.17em}}}$ well below the usual TPP concentration. As a consequence,${\displaystyle {\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}}$ is almost independent of the TPP concentration since it is close to its asymptotic value ${\displaystyle {\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{U}}}$ and no kinetic regulation is possible (at least around 25°C). This is in agreement with the fact that ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$ obtained by ITC (Fig. SD-17A) varies from less than 0.3 µM below 20°C to more than 1 µM above 35°C (Fig. SD-17B). Such values of ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$ are much higher than those for ECthiC and ECthiM and appear to be well tuned for a thermodynamic regulation. Therefore, the regulation by ATthiC is under classical thermodynamic control around a TPP concentration equal to ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall}).}$ The absence of a kinetic regulation is not surprising for a 3′-UTR riboswitch that neither affects early transcription arrest, nor translation inhibition.^12,42 Admittedly, the latter conclusion is based upon the ${\displaystyle {\mathit{K}}_{\mathit{d}}(\text{overall})}$ values valid for ca. 95 % of the RNA population (see SD-17A and SD17C).

ITC experiments in the Single Injection Mode (SIM) allowed us obtaining raw kinetic information at different temperatures for ATthiC (Fig. SD-2A). The major result is that the kinetics of complete riboswitch folding/closing is extremely temperature-dependent with an overall activation energy of (44.7 ± 1.7) kcal mol⁻¹ at 26 °C and (32 ± 1.7) kcal mol⁻¹ at 37 °C (the Arrhenius plot is significantly curved: Fig. SD-2B). As a consequence, the TPP-triggered folding takes 3 min at 37 °C, more than 4 min at 34 °C, and almost 30 min at 26 °C (the latter value being in perfect agreement with ^•OH results obtained at a much lower TPP concentration: see Fig. 3). An extrapolation from 26 °C making use of the activation energy at 26 °C (a conservative hypothesis) indicates that complete folding would take at least ∼10 hours at 15 °C and ∼6 days at 5 °C. Therefore, ATthiC appears to be ‘frozen’ at low temperatures commonly experienced by plants like A. thaliana. Altogether, these kinetic considerations suggest that ATthiC riboswitch might act as a thermosensor too. Since ATthiC regulates alternative splicing, it is of interest to mention that, FLM, a set of transcription factor genes involved in the regulation of flowering in A. thaliana, has been shown to be subject to temperature-dependent alternative splicing.⁴³ This, at least, corroborates the need for such a functionality in A. thaliana and supports the suggestion that ATthiC might regulate alternative splicing in a temperature-dependent way too.

Discussion

We have clearly established that the 3 TPP riboswitches examined in this work function according to an induced-fit mechanism. However, the regulation by the 2 E. coli riboswitches is kinetically controlled, whereas the regulation by A. thaliana riboswitch is thermodynamically controlled. We have developed an efficient and predictive model linking all kinetic parameters of the induced-fit mechanism to the kinetic regulation. An interesting result from this model is that any kinetically controlled riboswitch of that kind may ensure its regulation activity around a specific ligand concentration, but always with the same, or almost the same, ‘kinetic regulation efficiency’. ECthiC and ECthiM, for example, regulate the TPP concentration around significantly different values, respectively ∼5 µM and ∼0.5 µM (at 37 °C), but equal relative variations of the concentration around each specific value would induce almost the same effect on the regulation. This means that ECthiC appears to be specialized for a TPP high-concentration range 1.5-15 µM, and ECthiM for a low-concentration range 0.2-1.5 µM. Such results are of interest for the understanding of a complex regulation network with several riboswitches (as this is the case for the TPP regulation network in E. coli ³). In particular, the tuning of each riboswitch to a specific concentration range of the ligand is likely related to its position within the TPP biosynthetic network. Examination of Fig. 1 shows that the production of HMP-PP by thiD (thiM operon) is an obligatory step that can only occur after all steps depending on the thiC operon. One may thus speculate that, when the TPP concentration is decreasing, the OFF-to-ON switch of ECthiC occurs likely before that of ECthiM, i.e. at a higher TPP concentration. We note that this is in agreement with our results (∼4.5 µM for ECthiC vs. ∼0.5 µM for ECthiM). Interestingly, such a variability of the ON/OFF switch ligand concentration is well documented for S-adenosyl-methionine (SAM) riboswitches for which the SAM concentration at half-maximum response was found to vary from 0.35 µM to 4 µM for 8 related riboswiches, with 2 ‘outliers’ responding around 15 and 40 µM.⁴⁴

Kinetic regulation by riboswitches is based on a well-defined lapse of time ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ left for ligand binding to the riboswitch aptamer. This can be decomposed into ${\displaystyle {\mathit{t}}_{\mathit{S}}={\mathit{t}}_{\text{pol}}+{\mathit{t}}_{\text{pause}}}$ with ${\displaystyle {\mathit{t}}_{\mathit{p}\mathit{o}\mathit{l}}}$ the time necessary to polymerize at normal speed the intervening sequence from the end of the aptamer up to the decision point, and ${\displaystyle {\mathit{t}}_{\text{pause}}}$ the RNA-polymerase pausing time at specific loci. For ECthiC and ECthiM, as well as for the cases reported in ^17,18,35-37, ${\displaystyle {\mathit{t}}_{\text{pause}}}$ makes the major contribution to ${\displaystyle {\mathit{t}}_{\mathit{S}}}$. We arrived for example at ${\displaystyle {\mathit{t}}_{\mathit{p}\mathit{o}\mathit{l}}\approx 2\text{\hspace{0.17em}s\hspace{0.17em}}}$ and ${\displaystyle {\mathit{t}}_{\text{pause}}\approx 8\text{\hspace{0.17em}s\hspace{0.17em}}}$ for ECthiC, and ${\displaystyle {\mathit{t}}_{\mathit{p}\mathit{o}\mathit{l}}\approx 2\text{\hspace{0.17em}s\hspace{0.17em}}}$ and ${\displaystyle {\mathit{t}}_{\text{pause}}\approx 10\text{\hspace{0.17em}s\hspace{0.17em}}}$ for ECthiM. However, there is a priori no reason as to why ${\displaystyle {\mathit{t}}_{\mathit{S}}={\mathit{t}}_{\text{pause}}+{\mathit{t}}_{\text{pol}}}$ could not be obtained with ${\displaystyle {\mathit{t}}_{\text{pol}}>{\mathit{t}}_{\text{pause}}}$, and even with ${\displaystyle {\mathit{t}}_{\text{pause}}=0}$. Since ${({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{t}}_{\mathit{S}})}^{-1}$ determines the ligand concentration ${\displaystyle {\mathit{L}}_{\mathit{S}}}$ of the ON/OFF switch (hence ${\mathit{t}}_{\mathit{S}}={({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{L}}_{\mathit{S}})}^{-1}$), a likely limitation of a putative pause-free kinetic regulation is on the upper limit of ${\mathit{t}}_{\mathit{S}}={({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{L}}_{\mathit{S}})}^{-1}$ for not having to synthesize an unreasonably long intervening sequence to achieve regulation. For example, on the basis of a transcription rate of ∼50 nt s⁻¹, it would be necessary to synthesize as much as 450-500 nt for ECthiC and 550-600 nt for ECthiM to reproduce the values of ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ observed with pausing, respectively 10 and 12 s. However, it would suffice that ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}}}$ and ${\displaystyle {\mathit{L}}_{\mathit{S}}}$ be each greater merely by a factor of 2 to lower ${\displaystyle {\mathit{t}}_{\mathit{S}}={\mathit{t}}_{\text{pol}},}$ and hence the length to be transcribed, by a factor of 4. One may thus envision the possibility of a kinetic regulation without significant pause(s) of the RNA polymerase.

The variability of the important parameter ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ is a versatile way of dictating the ligand concentration of the ON/OFF switch. It can manifest itself among different riboswitches because of the variability of their sequence to be transcribed or, for a given riboswitch, because of the variability of the expression, or availability, of factors like NusA and NusG.⁴⁵ Of course, a significant stochastic variability of ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ is also to be expected, which would be particularly significant for low-copy number mRNAs. We think that further analysis on these different topics will require studying the collective behavior of the full TPP biosynthetic network comprising several genes being controlled by TPP riboswitches.³ In particular, to be realistic, such network simulations require taking into account other parameters than those bearing merely on riboswitch functioning, e.g. mRNA and protein degradation, as performed in.³⁴ We have taken steps toward that goal. We note that our model of kinetic regulation by ECthiC and ECthiM cannot be compared to the numerical simulations in³⁴ that were based on model ##2 (conformational change before ligand binding), whereas our experimental results implied to use model #1.

Finally, it is of interest of addressing the important question of new antibiotics development. Indeed, finding TPP analogs that, on one hand, could turn off the expression of genes involved in the biosynthesis of TPP but that, on the other hand, could not be used as cofactors of crucial enzymes would be a valuable route to fight pathogenic bacteria.^46-49 The success of such a strategy depends on the ability of such analogs to lure the regulation mechanism to the point that gene expression is switched off even though the TPP concentration is becoming too low. Our results on kinetic regulation imply that the in-cell concentration ${\displaystyle {\mathit{L}}_{\text{A}}}$ of the TPP analog has to be of the order of, or above ${({\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{t}}_{\mathit{S}})}^{-1}$ or, put differently, ${\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{L}}_{\text{A}}>{\mathit{t}}_{\mathit{s}}^{-1}$. This means roughly ${\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{L}}_{\text{A}}>0.1{\mathit{s}}^{-1}$ at 37 °C for ECthiC and ECthiM if one considers the approximate value ${\displaystyle {\mathit{t}}_{\mathit{S}}\approx 10\mathit{s}}$ for both. Since kinetic parameters are involved, one should keep in mind the possibility of a significant influence of the temperature on this criterion. Of course, these considerations on TPP riboswitches can be extended to all other kinetically-regulated riboswitches. They indicate how the relevant parameters ${\displaystyle {\mathit{k}}_{\mathit{o}\mathit{n}},}$${\displaystyle {\mathit{L}}_{\text{A}}}$ and ${\displaystyle {\mathit{t}}_{\mathit{S}}}$ provide us, at least in theory, with an objective criterion for a successful hijacking of kinetic regulation for therapeutic purpose. In practice, this obviously cannot replace the assessment of candidate molecules by monitoring directly the expression of the targeted genes, as mentioned in.⁴⁸

Materials and methods

RNA preparation

The aptamer domains of ECthiC and ECthiM genes were cloned in pRZ plasmid ⁵⁰ under the control of the T7 RNA polymerase promoter. For ECthiC, a mutated form in helix P1 (noted ECthiC_mutP1), prepared initially for crystallization experiments, had already been used for ^•OH footprinting experiments, as well as for kinITC and SPR experiments.²² Here, we prepared the wt sequence (ECthiC) for new kinITC experiments. The aptamer domain of ATthiC was cloned in pUC19 plasmid.⁵¹ Linearized plasmids were used for in vitro run-off transcription by T7 RNA polymerase according to usual protocols. The RNA products were further purified on DNA Pac100 column (Dionex, Thermo Fischer Science) and relevant fractions were extensively washed with water and concentrated on Centricon 10K (Millipore). For ^•OH footprinting experiments, RNA was 5′dephosphorylated using Fast AP enzyme from Fermentas (Thermo Fischer Scientific), then ³²P 5′-radiolabelled when required, according to usual protocols using Polynucleotide kinase (New England Biolabs) and ATP-γ³²P (Hartmann, Germany). The labeled RNA was gel purified, eluted, precipitated and resuspended in water.

RNA solutions in water, at 60 nM and 60 µM for footprinting and ITC experiments respectively, were heated at 90°C for 4 min and let stand for 40 min at room temperature. Ten-fold concentrated buffer (sodium cacodylate pH 6.5, 0.5 M; potassium acetate 1 M; magnesium acetate 50 mM) was then added and the mixture was incubated for 40 min at room temperature.

Hydroxyl-radical footprinting experiments

We used a Kintek RQF-3 quench flow apparatus with the protocol described in.⁵² Final concentrations are indicated in the following. Briefly, the renatured RNA (30 nM) was rapidly mixed with a solution containing TPP (from 2 to 60 µM) and 0.3 % H₂O₂ (Sigma). The RNA/TPP mixture was incubated for various times (from 15 ms to ca. 100 s for ECthiC_mutP1, but from 15 ms to 1800 s for ATthiC) before addition of Fe-EDTA (6 mM-6.6 mM) to generate hydroxyl radicals (^•OH). The probing reaction (in 30 µl) was rapidly quenched after 15 ms with 600 µl of ethanol and the RNA was resuspended in gel-loading solution. The cleavage products were resolved on 10% polyacrylamide gels in denaturing conditions. Gels were dried, exposed on imaging plates and scanned on a Bioimage Analyzer (Fuji Photo Film Co, Ltd).

ITC experiments

Experiments were performed at various temperatures on an ITC₂₀₀ apparatus (Microcal, GE-Healhtcare Northampton MA, USA). Renatured RNA was loaded in the cell (from 20 to 60 µM) and the TPP in the syringe (buffer used: sodium cacodylate pH 6.5, 50 mM; potassium acetate 100 mM; magnesium acetate 5 mM). To obtain thermodynamic information ITC was used in the classical multiple-injection mode. Experimental data processing was performed with our own methods and programs. We have taken steps for their introduction into the program AFFINImeter (S4SD, Santiago de Compostela, Spain). We also made use of kinITC ²² to obtain complete kinetic information (see below). Raw kinetic information was also obtained for ATthiC through experiments in the single-injection mode (at different temperatures).

SPR experiments

SPR experiments with ATthiC were performed on a Biacore 2000 instrument using Research Grade CM5 sensor chips (GE Healthcare). RNA constructs were prepared and experiments conditions were conducted as described for ECthiC_mutP1 in²² (same buffer as for the ITC experiments). Experimental data were acquired in single-cycle mode⁵³ and processed with our own program, either with the 2-step ‘induced-fit’ model #1, or conformational selection model #2. The equations necessary for this processing are described in the following. The theoretical SPR signal in Resonance Units (RU) was considered to be proportional to ${\displaystyle \mathit{ }{\mathit{R}}_1\left(\mathit{t}\right)+{\mathit{R}}_2\left(\mathit{t}\right)}$ for model ##1, and to ${\displaystyle {\mathit{R}}_2\left(\mathit{t}\right)}$ for model ##2 (equations 1a-b, 2b). The kinetic parameters were derived from a joint fit of 2 experimental data sets.

In vitro transcription by E. coli RNA-polymerase

DNA templates were first synthesized by PCR. Under the control of the T7A1 promoter, the sequences contain the full length riboswitch (ECthiC or ECthiM) and the first 60 nucleotides of the downstream gene (thiC or thiM) (SD-15A). In vitro singleround transcription experiments were performed at 37°C in buffer (30 µl) containing 40 mM Tris HCl (pH 7.5), 150 mM KCl, 10 mM MgCl2, 0.01 % Triton X-100. DNA templates (100 nM final concentration) were first incubated for 10 min with E. coli RNA polymerase (Epicentre) (100 nM final concentration), GTP, ATP, UTP (25 µM final concentration) and [α³²P]GTP (Hartmann Analytic, Germany) (33 nM, 6000 Ci mmol⁻¹). Fifteen microliters of this labeling mix were added to 15 µl of elongation mix containing 0.1 mg ml⁻¹ heparin (Sigma) and the 4 NTP (0.5 mM final concentration) in the same buffer. Protein NusA from E. coli (0.3 µM final concentration) was added in the elongation mix when needed. The reaction was quenched with 150 µl of ethanol and Na-acetate 0.3 M, precipitated and the radioactive products were analyzed on 6 or 10% denaturing polyacrylamide gels. Gels were dried, exposed on imaging plates and scanned on a Bioimager Analyzer (Fuji Photo Film Co, Ltd). Images were processed with our own programs.

Quantification of hydroxyl radical footprinting experiments

We have developed our own program for gel quantification. Basically, the method in use is the same as that described in,^54,55 but has several specificities linked to automation (unpublished). The overall quality of our procedure is illustrated in Fig. SD-3E showing excellent correlation between the cleavage patterns obtained with the ATthiC riboswitch aptamer and its prediction from the crystal structure.⁵¹

Differentiating the kinetic models

The two possible kinetic models correspond to equations 1a,b (model #1) and 2a,b (model #2). The results obtained with kinITC were in favor of model #1 for ECthiC, but not sufficiently for a definite conclusion, and they did not significantly differentiate the 2 models for ECthiM. For ATthiC, kinITC turned out to be inapplicable in part due to ATthiC being a slow folding RNA below 30°C (hence a weak heat-power producer), which implied using too high RNA concentration to obtain sufficient signal-to-noise ratio. Furthermore, ITC revealed the existence of a minor RNA species undetected by the other methods (see SD-17A,C), which also contributed to the inapplicability of kinITC with ATthiC. We thus considered other methods to obtain a clearcut answer.

Although kinITC alone did not allow differentiating the 2 models convincingly for ECthiC and ECthiM, the kinetic parameters obtained with each model were quite different and we confronted the 2 sets of results with fully independent observations, either from our own experiments using ^•OH footprinting and Surface Plasmon Resonance (SPR), or from published fluorescence-based experiments.²³ The basis of the method is as follows.

We need to describe how the concentrations of the 3 RNA species (${\displaystyle {\mathit{R}}_0,{\mathit{R}}_1,{\mathit{R}}_2}$ in equations 1-2) evolve after any perturbation, for example in our experimental systems after addition of TPP or, in vivo, immediately after synthesis of the aptamer in presence of TPP. In both cases the system evolves from an initial state (${\displaystyle \mathit{t}=0}$) with no TPP bound to the RNA, to the equilibrium state where the different concentrations of ${\displaystyle {\mathit{R}}_0,{\mathit{R}}_1,{\mathit{R}}_2}$ are defined by the equilibrium constants ${\displaystyle {\mathit{K}}_{\mathit{d}}}$ and ${\displaystyle {\mathit{K}}_{\mathit{F}}}$. In situations where TPP is in large excess (${\displaystyle {\mathit{L}}_{\text{tot}}\gg {\mathit{R}}_{\text{tot}}}$,${\displaystyle \mathit{ }{\mathit{L}}_{\text{tot}}\mathit{ }}$ and ${\displaystyle {\mathit{R}}_{\text{tot}}\mathit{ }}$ being the total TPP and RNA concentrations), as in ^•OH footprinting experiments, the kinetic equations describing the evolution of the concentrations can be linearized by assuming that ${\displaystyle \mathit{L}\left(\mathit{t}\right)\approx {\mathit{L}}_{\text{tot}}}$ remains constant, which corresponds to pseudo first-order kinetics (equations S8.1a,b in SD-8). In SPR experiments, the latter assumption is still valid due to continuous injection of TPP even though the bulk concentration of TPP may not be in large excess relative to the RNA. In vivo, the concentrations of the concerned mRNAs lie in the nanomolar, or high nanomolar range, that is well below the TPP concentration, and the same assumption ${\displaystyle \mathit{L}\left(\mathit{t}\right)\approx }$ constant is valid (of course, the TPP concentration is not constant during the life cycle of a cell, but its variation is on a longer time-scale than that necessary for the functioning of a riboswitch). As a consequence of this first-order approximation, classical calculations (see SD-8) show that the variations of the RNA concentrations from this initial state to equilibrium are given by:

$${\mathit{R}}_{\mathit{i}}(\mathit{t})={\tilde{\mathit{R}}}_{\mathit{i}}+{\mathit{f}}_{\mathit{i}}\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}\mathit{}\mathit{t})+{\mathit{s}}_{\mathit{i}}\mathit{e}\mathit{x}\mathit{p}(-{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\mathit{}\mathit{t})$$ (4)

with i = 0,1,2, ${\displaystyle {\tilde{\mathit{R}}}_{\mathit{i}}}$ the concentration of the i^th RNA species at equilibrium (i.e., that can be calculated from ${\displaystyle {\mathit{L}}_{\text{tot}}}$ and the equilibrium constants ${\displaystyle \mathit{ }{\mathit{K}}_{\mathit{d}},{\mathit{K}}_{\mathit{F}}}$ only: See equation S8.3b in SD-8), ${\displaystyle {\mathit{f}}_{\mathit{i}},{\mathit{s}}_{\mathit{i}}}$ being time independent coefficients specific for the species ${\displaystyle {\mathit{R}}_{\mathit{i}},}$ and ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}},\mathit{ }{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}}$ (${\displaystyle {\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}<\mathit{ }{\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}}$) being kinetic parameters governing, respectively, a ‘slow’ and a ‘fast’ component of concentration variations during the return to equilibrium. Importantly, all these parameters depend only on ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{o}\mathit{n}},\mathit{ }{\mathit{k}}_{\mathit{o}\mathit{f}\mathit{f}},{\mathit{k}}_{\mathit{F}},{\mathit{k}}_{\mathit{U}}}$(equations 1, 2) and on ${\displaystyle {\mathit{L}}_{\text{tot}}.}$ Note also that the appearance of a ‘slow’ and a ‘fast’ component and, thus, of 2 distinct time scales (${\text{τ}}_{\mathit{s}\mathit{h}\mathit{o}\mathit{r}\mathit{t}}={\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}^{-1}$ and ${\text{τ}}_{\mathit{l}\mathit{o}\mathit{n}\mathit{g}}={\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}^{-1}$), results naturally from the mathematical treatment of a 2-step mechanism in the frame of first-order approximation. The expressions for ${\displaystyle {\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\mathit{ }}$ and ${\displaystyle {\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}\mathit{ }}$ can be obtained as (see,⁵⁶ pp. 118-119 and SD-8 for full details):

$${\mathit{k}}_{\hspace{0.17em}\mathit{f}\mathit{a}\mathit{s}\mathit{t}\hspace{0.17em}\mathit{}\text{or}\hspace{0.17em}\mathit{}\mathit{s}\mathit{l}\mathit{o}\mathit{w}}=\frac{1}{2}\left[{\mathit{k}}_{\mathit{U}}+{\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{o}\mathit{n}}\left({\mathit{L}}_{\text{tot}}+{\mathit{K}}_{\mathit{d}}\right)\right]\left(1\pm \sqrt{1-\frac{4{\mathit{k}}_{\mathit{o}\mathit{n}}{\mathit{k}}_{\mathit{U}}\mathit{}{\mathit{K}}_{\text{model}}}{{\left[{\mathit{k}}_{\mathit{U}}+{\mathit{k}}_{\mathit{F}}+{\mathit{k}}_{\mathit{o}\mathit{n}}\left({\mathit{L}}_{\text{tot}}+{\mathit{K}}_{\mathit{d}}\right)\right]}^2}}\right)$$ (5a)

${\displaystyle {\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}\mathit{ }}$ and ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\mathit{ }}$ corresponding, respectively, to the plus and minus sign within the parenthesis, and the term ${\displaystyle {\mathit{K}}_{\text{model}}}$ being model-dependent according to:

$$\mathit{}{\mathit{K}}_{\hspace{0.17em}\text{model}\mathit{}\#\text{1}}={\mathit{K}}_{\mathit{d}}+\left(1+{\mathit{K}}_{\mathit{F}}\right){\mathit{L}}_{\text{tot}}$$ (5b)

$$\mathit{}{\mathit{K}}_{\hspace{0.17em}\text{model}\mathit{}\#\text{2}}={\mathit{K}}_{\mathit{d}}+{\mathit{K}}_{\mathit{F}}\left({\mathit{L}}_{\text{tot}}+{\mathit{K}}_{\mathit{d}}\right)$$ (5c)

To get insight into a reaction mechanism it is common to monitor the kinetic effects resulting from the variation of ${\displaystyle \mathit{ }{\mathit{L}}_{\text{tot}}}$. However, without using a particular experimental setup able to record short-time variations (or by voluntarily disregarding badly resolved short-time variations), only the slow kinetic component will show up (or will be used) in the experimental data, which explains the importance of the function ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}({\mathit{L}}_{\text{tot}})}$ (see SD-9 for a detailed discussion on ${\displaystyle \mathit{ }{\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}\left({\mathit{L}}_{\text{tot}}\right)}$). Equations (4 and 5a-c) will be of great importance for establishing a quantitative model of kinetic regulation. These are also at the basis of the processing of ^•OH footprinting data to obtain information both on the primary site of TPP interaction and on the kinetics of TPP binding (see below ‘Quantification of the kinetic curves from hydroxyl radical footprinting’). Equations (4, 5a-c) were also used to process the successive SPR binding curves acquired with increasing TPP concentrations by considering a 2-step mechanism.

Quantification of the kinetic curves from hydroxyl-radical footprinting

We used 2 different methods for processing the kinetic curves from ^•OH footprinting experiments with ECthiC_mutP1 and ATthiC. These methods were particularly adapted to ATthiC due to its slow folding. The first method relied on a bi-exponential fit of each cleavage curve separately. Such a fit is justified by equation (4) since the evolution of all RNA concentrations, and thus of the cleavage of each species can be described by an equation of this type. This method allows obtaining values of $\mathit{}{\mathit{\tau }}_{\mathit{s}\mathit{h}\mathit{o}\mathit{r}\mathit{t}}={\mathit{k}}_{\mathit{f}\mathit{a}\mathit{s}\mathit{t}}^{-1}$ and $\mathit{}{\mathit{\tau }}_{\mathit{l}\mathit{o}\mathit{n}\mathit{g}}={\mathit{k}}_{\mathit{s}\mathit{l}\mathit{o}\mathit{w}}^{-1}$ for each residue showing a clear cleavage signal. The second method sought to obtain more detailed information, both on the primary and secondary (or early and late) sites of TPP binding and on the kinetics of interaction. The essence of the method has been described in.⁵⁷ It consists in fitting the kinetic cleavage curves of all residues (apart for the badly resolved 5′ and 3′ ends) by considering the evolution of the concentrations of the different RNA species following equation (4). The great difference with the previous method is that a global fit of all cleavage curves is performed at once, and not a separate fit for each curve. The great interest of this method is of yielding information on the cleavage propensity of each residue in all species ${\displaystyle {\mathit{R}}_0,{\mathit{R}}_1,{\mathit{R}}_2}$. All details are in SD-10.

Thermodynamic and kinetic information obtained with kinITC

The kinITC method has been described elsewhere.²² We only recall here (i) that kinITC works by fitting simultaneously the complete shapes of all injection curves of several ITC experiments performed at different temperatures and (ii) that kinITC results are not obtained as discrete numerical values at these different temperatures but, instead, as explicit mathematical functions of the variation with the temperature of all thermodynamic and kinetic quantities. Importantly, kinITC is a model-dependent method that requires proposing a well-established kinetic description of the reaction(s) taking place after mixing of the reagents. Although related to the method described in,⁵⁸ it is more general, firstly because it does not disregard the short-time part of the injection curves potentially conveying information on a possible fast component and, secondly, because it can cope with situations involving 2 kinetic steps (equations 1a-b or 2a-b) to obtain thermodynamic and kinetic information about these 2 steps. This feature, unique to kinITC, was particularly important for the major result of this work about the kinetic regulation mechanism of such TPP riboswitches. Note that, in all ITC experiments, the TPP concentration is variable and a first-order approximation is inapplicable, which implies that the exact non-linear differential equations describing the kinetics of the reaction have to be integrated in kinITC processing.

For ECthiC and ECthiM, we used the method described for ECthiC_mutP1 in.²² The temperatures were (20.2, 27, 27.3, 30, 34°C) for ECthiC and (18, 26, 30, 34, 37°C) for ECthiM. For each temperature, the initial RNA concentrations in the measurement cell were respectively: (24, 24, 21, 21, 21 µM) for ECthiC and (19.3, 18.8, 18.8, 18.8, 16.3 µM) for ECthiM, and the TPP concentrations in the syringe were 200 µM for ECthiC and (200, 200, 200, 200, 160 µM) for ECthiM.

Programming

Computer programs used in this work for gel processing, kinetic processing of ^•OH footprinting data, for SPR and kinITC experiments, as well as for illustrations (apart when indicated differently), were written with the Mathematica language from Wolfram Res. The symbolic capabilities of Mathematica were also of great interest throughout this work.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Acknowledgments

We thank Bianca Sclavi (ENS, Cachan), Véronique Hubscher (IPCMS, Strasbourg), Nicolas Humbert (Faculté de pharmacie, Illkirch) and Philippe Wolff in our team for much appreciated help in several occasions. We also thank an anonymous referee for a suggestion about the search for new antibiotics from TPP analogs.

Funding

This work was supported in part by the ‘Agence Nationale de la Recherche’ (ANR PCV08_324694).