Abstract
Remodelling of soft biological tissue is characterized by interacting biochemical and biomechanical events, which change the tissue's microstructure, and, consequently, its macroscopic mechanical properties. Remodelling is a well-defined stage of the healing process, and aims at recovering or repairing the injured extracellular matrix. Like other physiological processes, remodelling is thought to be driven by homeostasis, i.e. it tends to re-establish the properties of the uninjured tissue. However, homeostasis may never be reached, such that remodelling may also appear as a continuous pathological transformation of diseased tissues during aneurysm expansion, for example. A simple constitutive model for soft biological tissues that regards remodelling as homeostatic-driven turnover is developed. Specifically, the recoverable effective tissue damage, whose rate is the sum of a mechanical damage rate and a healing rate, serves as a scalar internal thermodynamic variable. In order to integrate the biochemical and biomechanical aspects of remodelling, the healing rate is, on the one hand, driven by mechanical stimuli, but, on the other hand, subjected to simple metabolic constraints. The proposed model is formulated in accordance with continuum damage mechanics within an open-system thermodynamics framework. The numerical implementation in an in-house finite-element code is described, particularized for Ogden hyperelasticity. Numerical examples illustrate the basic constitutive characteristics of the model and demonstrate its potential in representing aspects of remodelling of soft tissues. Simulation results are verified for their plausibility, but also validated against reported experimental data.
Keywords: constitutive modelling, soft tissue, healing, remodelling, repair, damage
1. Background
Living matter has the ability to adapt and evolve in response to disease, external loads and environmental stimuli or aggressions. In particular, tissues are capable of healing in order to arrest the extent of the damage caused by injury or disease and, ultimately, restore the tissue's original function. The repair of soft tissues is known to be driven by a complex sequence of events involving cellular processes as well as biochemical and biomechanical factors [1,2]. The exact role of many of these factors is not completely understood yet. Nonetheless, from a physiological point of view, the healing process is classified into four distinct but overlapping phases: haemostasis, inflammation, proliferation and remodelling [3,4].
Following an injury, the loss of structural integrity in the tissue immediately activates the coagulation cascade that results in a platelet-rich fibrin clot (haemostasis phase). Within 1–3 days after injury, neutrophils and macrophages are attracted to the wound site to phagocytose bacteria and debris, preventing wound infection (inflammation phase). Cytokines are also released, which stimulate angiogenesis and enhance the production of fibroblasts. The ensuing fibroblast proliferation and migration results in the synthesis and deposition of collagen in the extracellular matrix (ECM), that leads to the formation of granulation tissue (proliferation phase). This phase can last up to several weeks. In skin wounds, epithelialization and wound retraction is also observed [5]. The final stage (remodelling phase) lasts from weeks to years and consists of a continuous synthesis and degradation of collagen as the ECM is remodelled, and the granulation tissue becomes the scar tissue. As this matrix turnover takes place, its composition shifts and reorganizes: the newly formed blood vessels regress, the ‘flaws' (such as fat cells and inflammatory pockets) are removed, and the collagen fibres become increasingly organized. Over time, and under adequate biochemical and biomechanical conditions, the remodelled tissue approaches the characteristics of the original undamaged tissue. However, the completely healed scar tissue often does not fully recover the characteristics of the uninjured tissue it replaces [1]. In addition, homeostasis may never be reached, such that remodelling may also appear as a continuous pathological transformation of diseased tissues during aneurysm expansion for example [6].
The mathematical modelling of wound healing has been widely addressed since the development of the first models in the 1990s [7–9]. These models focus on the underlying cellular and biochemical mechanisms to define and simulate dermal wound contraction [10–12] and angiogenesis [13–15] from a continuum-based approach. The inflammation and proliferation phases have also been modelled using a discrete or a hybrid discrete/continuum approach [16–18] and, more recently, a systems-biology multi-scale and multi-field approach has been proposed [19]. The reader is referred to the works by Tepole & Kuhl [20] and Valero et al. [21] for a comprehensive review of mathematical and computational dermal wound healing models.
On the other hand, the remodelling phenomena, understood as a change in the properties of the tissue, have also been extensively addressed. In general, it is treated together with growth and not necessarily in the biological context of the above-described tissue healing process [22–25]. Many of these models aim at characterizing collagen fibre reorientation through evolving structural tensors [26–31]. A different approach characterizes growth and remodelling as a continual turnover of tissue constituents by means of a constrained mixture theory [32–35], or, more recently, a mechanistic microstructural theory [36].
Over the past few years, advancements in the field resulted in sophisticated models with cellular [37,38] and molecular [39] processes being the driving forces of remodelling. In this sense, much effort is directed towards representing remodelling in vascular tissue [40–43], with a particular focus on the pathological remodelling observed in aortic aneurysm tissue [44–46]. The mathematical modelling of the inflammation, proliferation and remodelling phases in ligament tissue has also been addressed [47,48].
Numerous studies, both in animal models and in patients, have shown that mechanical loading has a significant impact on the speed and efficiency of healing [49–52]. However, the optimal loading regime remains unclear, and the detailed mechanobiogical mechanisms involved are not fully understood. Computational approaches have been widely used in bone healing mechanobiological modelling to enable predictions of bone healing and improve the understanding of both mechanical and biological mechanisms at play [53,54]. In order to apply this approach to soft tissue healing, a continuum constitutive model is required that can represent both the changing soft tissue mechanics during healing and the proposed biophysical stimuli for the cells involved.
This work introduces a novel constitutive model that captures the continuous turnover of tissue observed in the remodelling phase that ultimately leads to the recovery of injured tissue. This homeostatic-driven turnover remodelling (HTR) model is capable of modelling the last stage in the above-described healing process, but can also capture the pathological remodelling of tissue observed in certain diseases [55], such as the abdominal aortic aneurysm (AAA) [56].
The proposed HTR model is consistent with an open-system thermodynamics framework [57]. It is formulated in accordance with the principles of continuum damage mechanics (CDM), following ideas proposed in bone remodelling by Doblaré & García [58]. Consequently, damage is assimilated to an apparent density that evolves in response to mechanical loading. In the present formulation, however, damage (and its repair) can be physically associated with the injury (and healing) observed in live tissues. Thus, the granulation tissue formed in the proliferation phase is akin to a damaged material in CDM, characterized by microfissures and voids that result in a loss of stiffness and strength. Then, through remodelling, the ‘flaws' in the granulation tissue are removed (healed) and it becomes increasingly organized, approaching the original characteristics of the ECM material. This process is comparable to a reversal of damage in a CDM framework, in which the load-carrying capacity of the tissue is gradually recovered.
The HTR model describes the overall change in material behaviour at tissue level of healing/remodelling tissues. Healing in this model is not only driven by mechanical loading, but also by biological stimuli. In particular, the underlying metabolism in healing tissues is represented by phenomenological parameters.
The thermodynamic basis and derivation of the HTR constitutive model is developed in §2. The damage evolution and healing rate equations are also outlined in this section as are the details of the numerical implementation in an in-house finite-element (FE) software [59]. Additional information for this numerical implementation is detailed in appendix A. Section 3 includes several examples with the aim of illustrating the basic constitutive characteristics of the model and validate it with experimental data from the literature. The characteristics of the model, in addition to its advantages and shortcomings, are discussed in §4. Finally, conclusions are addressed in §5.
2. A constitutive model for homeostatic-driven turnover remodelling
Soft tissue is known to be highly deformable, yet experience negligible volume changes, and exhibit a characteristic J-shaped nonlinear response [60]. For many applications, its behaviour can be described by means of decoupled quasi-incompressible hyperelastic models [61–63], with damage affecting solely the deviatoric term [64–68]. Albeit their limitations, discussed in §4, these simplifying hypotheses are also assumed in this work.
The HTR model captures the homeostatic-driven turnover remodelling of soft tissues, i.e. the last phase of tissue healing. The model is developed within the framework of CDM and is based on the thermodynamics of irreversible processes with internal state variables [69–72].
Unlike inert materials, tissues have an underlying metabolism, which is essential to the growth, healing and remodelling processes characteristic of living organisms. From a continuum mechanics standpoint, this metabolism introduces energy into the system, allowing for the ‘recovery’ of the energy dissipated during damage and, thus, permitting a ‘reversal’ of the damage produced in the material. Consequently, the total specific Helmholtz free energy density introduced into the system is the sum of the initial strain energy Ψini contained in the tissue and the strain energy 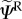 introduced by the metabolism such that
introduced by the metabolism such that
| 2.1 |
Here, the energies are given with respect to the density in the reference configuration, and the tilde indicates the deviatoric or volume-preserving part of the free energy. The subscript ‘vol’ refers to the volumetric part.
The recovery energy 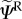 reverses the damage in the tissue such that the internal damage variable is no longer accumulative in nature, i.e. as in classic CDM models. Specifically, we postulate the deviatoric part of the specific Helmholtz free energy density to be of the form
reverses the damage in the tissue such that the internal damage variable is no longer accumulative in nature, i.e. as in classic CDM models. Specifically, we postulate the deviatoric part of the specific Helmholtz free energy density to be of the form
| 2.2 |
where 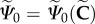 is the original (undamaged) hyperelastic specific Helmholtz free energy density given in terms of the deviatoric part of the right Cauchy–Green strain tensor,
is the original (undamaged) hyperelastic specific Helmholtz free energy density given in terms of the deviatoric part of the right Cauchy–Green strain tensor, 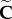 . The effective damage Deff is the internal (recoverable) damage variable, which only affects the deviatoric part of the tissue's strain energy. Its rate is given by
. The effective damage Deff is the internal (recoverable) damage variable, which only affects the deviatoric part of the tissue's strain energy. Its rate is given by
| 2.3 |
where 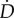 is the rate of
is the rate of  , an explicit Kachanov-like mechanical damage variable, and
, an explicit Kachanov-like mechanical damage variable, and 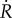 is the rate of R, the repair or healing term. From a CDM point of view, D may be associated with the microvoids and small fissures that appear and extend as damage initiates and evolves. D = 0 corresponds to a compact material with no voids or fissures, whereas D = 1 is a completely damaged material whose amount of voids and fissures is such that it can no longer carry any load. The healing term R represents the reversal or ‘filling’ of these microvoids and small fissures such that the original load-carrying capacity of the material is recovered. Then, R = 1 corresponds to a mass deposition equivalent to the original undamaged material stiffness and, thus, coincides with a recovery energy
is the rate of R, the repair or healing term. From a CDM point of view, D may be associated with the microvoids and small fissures that appear and extend as damage initiates and evolves. D = 0 corresponds to a compact material with no voids or fissures, whereas D = 1 is a completely damaged material whose amount of voids and fissures is such that it can no longer carry any load. The healing term R represents the reversal or ‘filling’ of these microvoids and small fissures such that the original load-carrying capacity of the material is recovered. Then, R = 1 corresponds to a mass deposition equivalent to the original undamaged material stiffness and, thus, coincides with a recovery energy 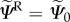 , i.e. the initial pre-injury strain energy. Hence, the healing term can be defined in terms of the specific strain energy densities as
, i.e. the initial pre-injury strain energy. Hence, the healing term can be defined in terms of the specific strain energy densities as 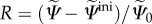 .
.
Ideally, the original properties of the uninjured tissue should be recovered at the end of the healing process such that the healed tissue is indistinguishable from the pre-injured tissue. In practice, some healed tissues are softer than their corresponding healthy uninjured tissue [1,73,74], whereas others become stiffer, often loosing functionality. The latter is the case of fibrotic scar tissue [75–77], which has been associated with pathological conditions caused by an aberrant ECM production that results from perturbed homeostasis in the tissue [55]. In this work, the former case will be addressed and, thus, 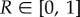 is assumed, i.e. at most, the original properties can be recovered. The full recovery (R = 1) corresponds to a successful restoration of the tissue's homeostatic state.
is assumed, i.e. at most, the original properties can be recovered. The full recovery (R = 1) corresponds to a successful restoration of the tissue's homeostatic state.
The evolution of both D and R will be defined in more detail in §§2.2 and 2.3, respectively. However, because R will be seen to implicitly depend on the tissue damage, it is anticipated that 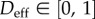 .
.
2.1. Thermodynamic basis and constitutive equation
The Clausius–Duhem inequality in terms of specific free energy density, considering the simplifying arguments introduced by Simo [78], is 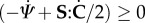 , where S is the second Piola–Kirchhoff stress tensor. This expression, deduced in the framework of classic CDM, does not account for the energy introduced into the system to allow for the reversal of damage. To account for the entropy entering the system, a term analogous to the one described in the free-energy-based Clausius–Duhem inequality for open systems proposed by Kuhl & Steinmann [57] is added, resulting in
, where S is the second Piola–Kirchhoff stress tensor. This expression, deduced in the framework of classic CDM, does not account for the energy introduced into the system to allow for the reversal of damage. To account for the entropy entering the system, a term analogous to the one described in the free-energy-based Clausius–Duhem inequality for open systems proposed by Kuhl & Steinmann [57] is added, resulting in
| 2.4 |
Here, 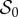 is the density of entropy source and θ is the absolute temperature. We assume the entropy is introduced into the system exclusively through an internal source, the system's metabolism. Hence, the entropy flux
is the density of entropy source and θ is the absolute temperature. We assume the entropy is introduced into the system exclusively through an internal source, the system's metabolism. Hence, the entropy flux 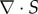 defined by Kuhl & Steinmann [57] is null here.
defined by Kuhl & Steinmann [57] is null here.
Introducing now (2.1) and (2.2), and considering that the inequality must hold true for any strain increment, leads to the constitutive equation
| 2.5 |
Thereby, the dissipation inequality
| 2.6 |
must be satisfied. A density of entropy source 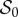 of the type typically found in the context of biomechanics [57] is considered,
of the type typically found in the context of biomechanics [57] is considered, 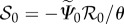 , with a normalized mass source
, with a normalized mass source 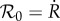 . Here,
. Here, 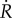 is the healing rate introduced in (2.3), i.e. the normalized rate at which strain energy is introduced into the system to allow for damage reversal. Then, the dissipation inequality (2.6) becomes
is the healing rate introduced in (2.3), i.e. the normalized rate at which strain energy is introduced into the system to allow for damage reversal. Then, the dissipation inequality (2.6) becomes
| 2.7 |
Introducing (2.3), this expression is reduced to the classic mechanical dissipation owing to damage, given in the reference configuration, 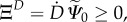 which must be non-negative at any time.
which must be non-negative at any time.
2.2. Mechanical damage evolution
Following CDM theory, the stress level determines the damage D in the tissue. The linear and exponential softening laws used in the generalized damage model described in Comellas et al. [79] are considered for the evolution of the variable D:
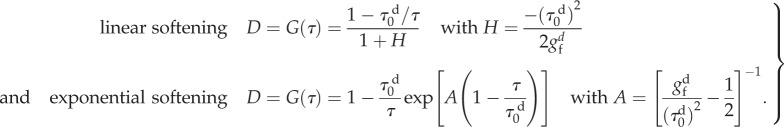 |
Here, the initial damage threshold 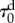 and the fracture energy
and the fracture energy 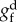 are material properties per unit spatial volume that can be identified from passive in vitro tests and
are material properties per unit spatial volume that can be identified from passive in vitro tests and 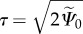 denotes the Simo & Ju energetic norm [70].
denotes the Simo & Ju energetic norm [70].
2.3. Healing rate
The evolution of the repair or healing variable R is defined in accordance with the biochemical and biomechanical observations of healing soft tissue. It is inferred from the description of the phases of the healing process that damage is a trigger of this process, but healing only occurs when the metabolism allows for it (figure 1). In addition, in many cases, the mechanical properties of the completely healed tissue remain inferior to uninjured tissue [1,73,74]. Based on this experimental evidence, the healing rate,
| 2.9 |
is proposed. Here,  represents the Macaulay brackets [80],
represents the Macaulay brackets [80], 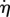 is a function that regulates how fast healing occurs (introduces a time scale) and ξ defines the percentage of stiffness that is not recovered at the end of the healing process. Note the implicit character of the healing rate, because Deff is a function of R. In addition, because Deff is also a function of D, the healing rate is also implicitly dependent on the mechanical loading of the tissue.
is a function that regulates how fast healing occurs (introduces a time scale) and ξ defines the percentage of stiffness that is not recovered at the end of the healing process. Note the implicit character of the healing rate, because Deff is a function of R. In addition, because Deff is also a function of D, the healing rate is also implicitly dependent on the mechanical loading of the tissue.
Figure 1.
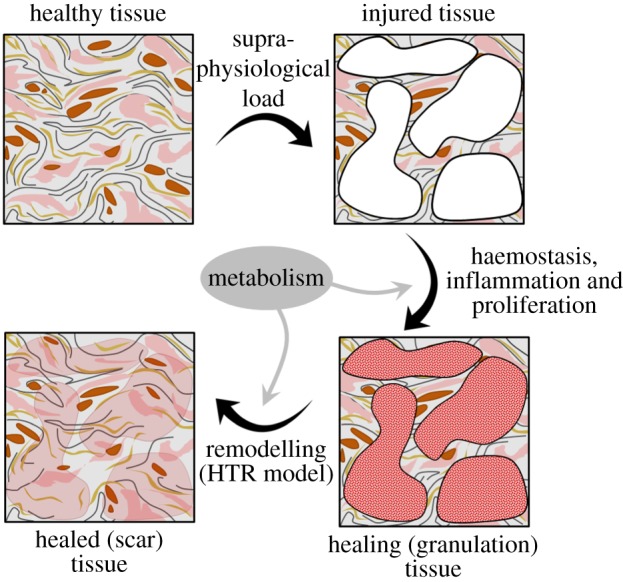
Interpretation of the healing process in a CDM framework and contribution of the HTR model in this context. (Online version in colour.)
The irreversible stiffness loss parameter 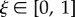 is a given value that dictates the amount of stiffness lost, with respect to the uninjured tissue's stiffness, at the end of the healing process. In other words, ξ establishes the remnant effective damage that is not recovered in the completely healed tissue. For example, ξ = 0.2 indicates that, after complete healing, the tissue will have recovered 80% of its original stiffness, namely there will remain a Deff = 0.2.
is a given value that dictates the amount of stiffness lost, with respect to the uninjured tissue's stiffness, at the end of the healing process. In other words, ξ establishes the remnant effective damage that is not recovered in the completely healed tissue. For example, ξ = 0.2 indicates that, after complete healing, the tissue will have recovered 80% of its original stiffness, namely there will remain a Deff = 0.2.
The function 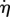 regulates the healing speed, which is directly related to the system's metabolism or biological availability. Here, the biological availability is understood as the complete set of internal biochemical elements (proteins, enzymes, growth factors, etc.) necessary for healing to take place [81]. Owing to lack of experimental data and for the sake of simplicity, a constant healing rate has been defined,
regulates the healing speed, which is directly related to the system's metabolism or biological availability. Here, the biological availability is understood as the complete set of internal biochemical elements (proteins, enzymes, growth factors, etc.) necessary for healing to take place [81]. Owing to lack of experimental data and for the sake of simplicity, a constant healing rate has been defined, 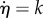 . The healing rate parameter k is a given value that determines the healing time scale and is measured in [time]−1.
. The healing rate parameter k is a given value that determines the healing time scale and is measured in [time]−1.
Thus, the healing rate function 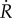 proposed here complies with the basic biomechanical conditions that under absence of injury (Deff = 0) or in the case of no biological availability (k = 0 days−1) healing will not occur.
proposed here complies with the basic biomechanical conditions that under absence of injury (Deff = 0) or in the case of no biological availability (k = 0 days−1) healing will not occur.
2.4. Numerical implementation
The proposed HTR constitutive model has been implemented in the in-house FE software PLCd [59]. The code, developed in Fortran, uses the direct sparse solver Pardiso [82] and a full Newton algorithm to solve nonlinear finite strain three-dimensional solid mechanics problems. The HTR model has been implemented in a total Lagrangian framework at Gauss point level of a Q1P0 mixed u/p FE formulation [83,84]. The Ogden model has been chosen owing to its ability to reproduce the stress–stretch J-curve characteristic of soft biological tissues, such that the deviatoric strain energy reads
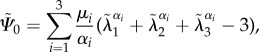 |
2.10 |
where 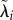 are the principal deviatoric stretches, μi are (constant) shear moduli and αi are dimensionless constants. The material parameters must satisfy the consistency condition
are the principal deviatoric stretches, μi are (constant) shear moduli and αi are dimensionless constants. The material parameters must satisfy the consistency condition
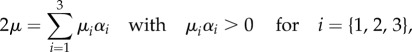 |
2.11 |
where μ is the referential shear modulus of the material. The volumetric strain energy,
| 2.12 |
is used. Here, κ is the bulk modulus and J is the Jacobian determinant of the deformation gradient tensor F. Note that the bulk modulus acts as a numerical penalizer in the mixed FE formulation such that J → 1 is satisfied on the element level.
Consequently, the corresponding volumetric and deviatoric parts of the second Piola–Kirchhoff stress in (2.5) read
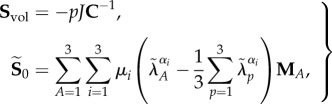 |
2.13 |
with the hydrostatic pressure 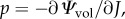 and
and 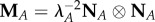 , NA being the eigenvector of the right Cauchy–Green deformation tensor.
, NA being the eigenvector of the right Cauchy–Green deformation tensor.
Details regarding the numerical implementation of the HTR model are schematized in table 1, and the required tangent constitutive tensor is derived in appendix A. The numerical implementation introduces an auxiliary mechanical damage variable, 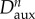 , to be able to detect the cases in which there is an (elastic) unloading on the tissue. This is due to the fact that the mechanical damage variable is updated at the end of each increment with the computed effective damage value (
, to be able to detect the cases in which there is an (elastic) unloading on the tissue. This is due to the fact that the mechanical damage variable is updated at the end of each increment with the computed effective damage value (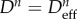 ) so that at the end of the healing process, when Deff = ξ is recovered, there is no stored history of accumulated mechanical damage. This is in accordance with the definition of the HTR model's internal variable Deff (2.3) in terms of rates.
) so that at the end of the healing process, when Deff = ξ is recovered, there is no stored history of accumulated mechanical damage. This is in accordance with the definition of the HTR model's internal variable Deff (2.3) in terms of rates.
Table 1.
Numerical implementation at Gauss point level of the constitutive model for homeostatic-driven turnover remodelling in the in-house FE code PLCd [59].
| initialization at t = 0 and n = 0 |
effective damage, 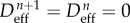 and mechanical damage, and mechanical damage, 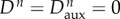
|
maximum reached value of the damage threshold stress, 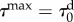
|
| algorithm at each load increment n |
given: deformation gradient tensor F, elemental pressure p and material properties: μi, αi, 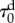 , , 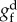 , k and ξ , k and ξ
|
determine the right Cauchy–Green tensor 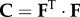 , its invariants , its invariants 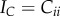 and and 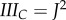 , principal stretches , principal stretches 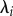 and its deviatoric parts and its deviatoric parts 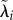 . . |
compute the volumetric and deviatoric parts of the predictor hyperelastic stress, 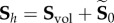 , from (2.13) and the corresponding tangent constitutive tensor (see appendix A) , from (2.13) and the corresponding tangent constitutive tensor (see appendix A) |
determine the undamaged deviatoric part of the Helmholtz free energy 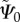 from (2.10), and compute the present damage threshold, from (2.10), and compute the present damage threshold, 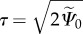 [70] [70] |
IF 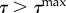 THEN (damage progresses) THEN (damage progresses) |
compute the mechanical damage increment, 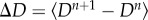 , with Dn+1 from (2.8). Obtain , with Dn+1 from (2.8). Obtain 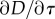 as in appendix A as in appendix A |
IF 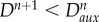 THEN (elastic unloading) THEN (elastic unloading) |
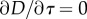
|
| END |
update auxiliary damage variable from previous step 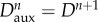
|
| ELSE (no further damage) |
assign ΔD = 0 and 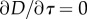
|
| END |
| evaluate the effective damage and the derivative of the healing variable: |
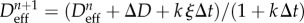 and and 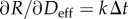
|
IF 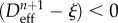 THEN (no further healing) THEN (no further healing) |
assign 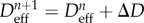 and and 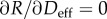
|
| END |
update the maximum reached value of the damage threshold for current 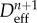 : impose : impose 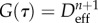 in (2.8) and isolate in (2.8) and isolate 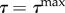
|
update the internal variables 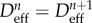 and and 
|
| compute the stress state for the present load step from (2.5): |
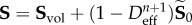 |
| compute the corresponding tangent constitutive tensor (see appendix A): |
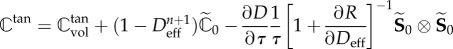 |
It becomes clear from the numerical algorithm that the computed value of Deff may decrease only when there is active healing, which occurs for 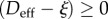 . Hence, this variable is automatically bounded from below by
. Hence, this variable is automatically bounded from below by 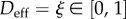 , 0 being the lowest possible value that the effective damage may take. Because
, 0 being the lowest possible value that the effective damage may take. Because 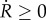 (as defined in (2.9)) and the mechanical damage rate
(as defined in (2.9)) and the mechanical damage rate 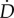 is necessarily non-negative (as deduced from (2.7)), Deff only increases when the mechanical damage progresses (ΔD > 0) which, at most, will produce a value D = 1. As a result, Deff is automatically bounded from above by 1. Although R is not required, because Deff is computed in terms of the implicit function defined for the healing rate
is necessarily non-negative (as deduced from (2.7)), Deff only increases when the mechanical damage progresses (ΔD > 0) which, at most, will produce a value D = 1. As a result, Deff is automatically bounded from above by 1. Although R is not required, because Deff is computed in terms of the implicit function defined for the healing rate 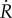 , it could be calculated at the end of each load increment as
, it could be calculated at the end of each load increment as 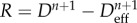 and, considering the aforementioned bounds of Deff and D, it would be seen to satisfy
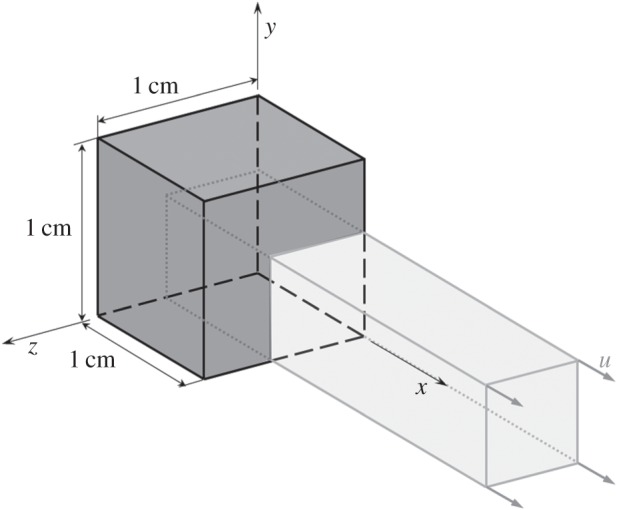
and, considering the aforementioned bounds of Deff and D, it would be seen to satisfy 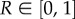 .
.
3. Validation examples
The main characteristics of the HTR model are illustrated by means of a simple uniaxial tensile test example. Then, data on ligament healing taken from the literature are used to validate the model. Finally, an AAA is numerically reproduced under different healing conditions to demonstrate the applicability of the model in reproducing experimental set-ups and the capability of the formulation to analyse geometrically complex models.
3.1. Homogeneous uniaxial tension
An eight-noded cubic element with 1 cm length sides is subjected to a displacement-driven pure tensile load applied in steps of 0.1 mm, as shown in figure 2. Each load step corresponds to a time increment of 0.05 days. Two sets of hyperelastic and damage material properties have been considered (listed in table 2), one reproduces a neo-Hookean-like behaviour and the other, an Ogden-like one. A penalizer value 109 times the maximum value of the shear moduli has been considered for the bulk modulus κ in all cases.
Figure 2.
Prescribed displacements applied on an eight-noded hexahedral linear element with a single pressure integration point (Q1P0) used in the homogeneous uniaxial tensile test example.
Table 2.
Hyperelastic and damage material parameters used in the homogeneous uniaxial tensile test example. The fracture energy per unit area is computed as: 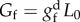 , where L0 is the localization or characteristic length in the reference configuration [85,86].
, where L0 is the localization or characteristic length in the reference configuration [85,86].
| parameter | value |
|---|---|
| Ogden material behaviour | |
| μ1 | 4 kPa |
| μ2 | 370 kPa |
| μ3 | −5 kPa |
| α1 | 6.4 |
| α2 | 1.9 |
| α3 | −4.2 |
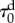 |
1.16 kPa1/2 |
| Gf | 20 N cm−1 |
| neo-Hookean material behaviour | |
| μ1 | 1.5 MPa |
| α1 | 2.0 |
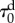 |
322.8 kPa1/2 |
| Gf | 40 N cm−1 |
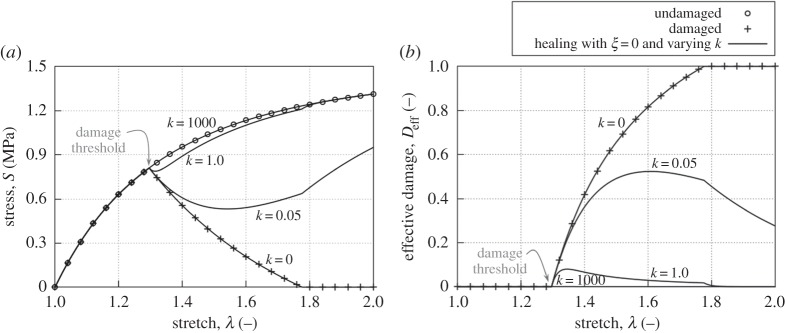
In the first set of examples (figure 3), an irreversible stiffness loss parameter ξ = 0 has been used, such that the initial stiffness properties will be completely recovered by healing. The healing rate parameter k changed between 0 and 1000 days−1. A high healing rate (k = 1000 days−1 in figure 3) is undistinguishable from the hyperelastic model, because healing immediately compensates for the damage produced. This can be understood as a representation of the continuous turnover known to occur in living tissues. In addition, a null healing rate (k = 0 days−1 in figure 3) results in a passive damage response, i.e. accumulation of damage in an inert material.
Figure 3.
Second Piola–Kirchhoff stress versus stretch (a) and effective damage versus stretch (b) responses of the homogeneous uniaxial tensile test example using the neo-Hookean material parameters (table 2) with linear damage for an irreversible stiffness loss parameter ξ = 0 and varying values of the healing rate parameter k (values given in days−1).
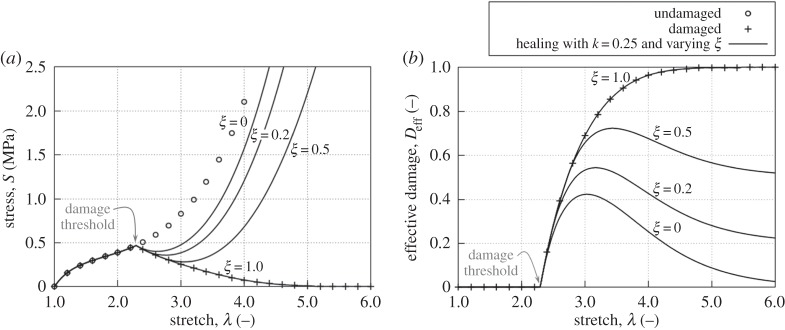
The next set of examples (figure 4) show the effect of varying the parameter ξ, which dictates the final effective damage in the completely healed tissue. As expected, for a value ξ = 1.0, a behaviour analogous to the passive damage model is obtained, because no stiffness can be recovered and damage continuously accumulates.
Figure 4.
Second Piola–Kirchhoff stress versus stretch (a) and effective damage versus stretch (b) responses of the homogeneous uniaxial tensile test example using the Ogden material parameters (table 2) with exponential damage for a healing rate parameter k = 0.25 days−1 and varying values of the irreversible stiffness loss parameter ξ.
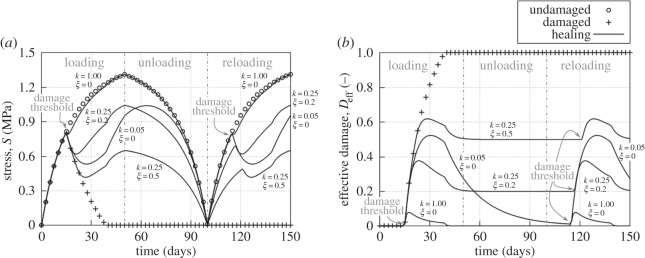
Finally, a loading–unloading–reloading case is reproduced for different values of the healing variables (figure 5) to illustrate how healing may continue while unloading takes place, such that damage progression and recovery (healing) may or may not occur simultaneously.
Figure 5.
Second Piola–Kirchhoff stress versus time (a) and effective damage versus time (b) responses of the homogeneous uniaxial tensile loading–unloading–reloading test example using the neo-Hookean material parameters (table 2) with linear damage for varying values of the healing rate parameter k (values given in days−1) and irreversible stiffness loss parameter ξ.
3.2. Healing ligament
Quantitative experimental data on healing are difficult to find in the literature and, when available, are not always in a form that can be readily used and reproduced to validate numerical models. As one of the rare examples, the experimental work by Abramowitch et al. [87] on healing medial collateral ligaments (MCL) in goat knees provides excellent data to validate the HTR model. In their experiments, the MCL is surgically sectioned, and the free ends of the ligament are realigned but not sutured, leaving a gap of about 0.5 cm between the free ends [87,88]. The wound is then closed, and the animals are allowed to recover for six weeks, after which they are humanely euthanized and their knees are prepared for testing. Typical tensile stress–strain curves are provided for the healed ligament and a healthy (uninjured) ligament used as control (see grey lines in figure 6). Because there are no specific geometry and boundary conditions associated with these curves, the data have been used to calibrate material properties with the cubic element of the previous set of examples (figure 2). However, the length of the element sides has been reduced to 0.5 cm to match the experimental data provided.
Figure 6.
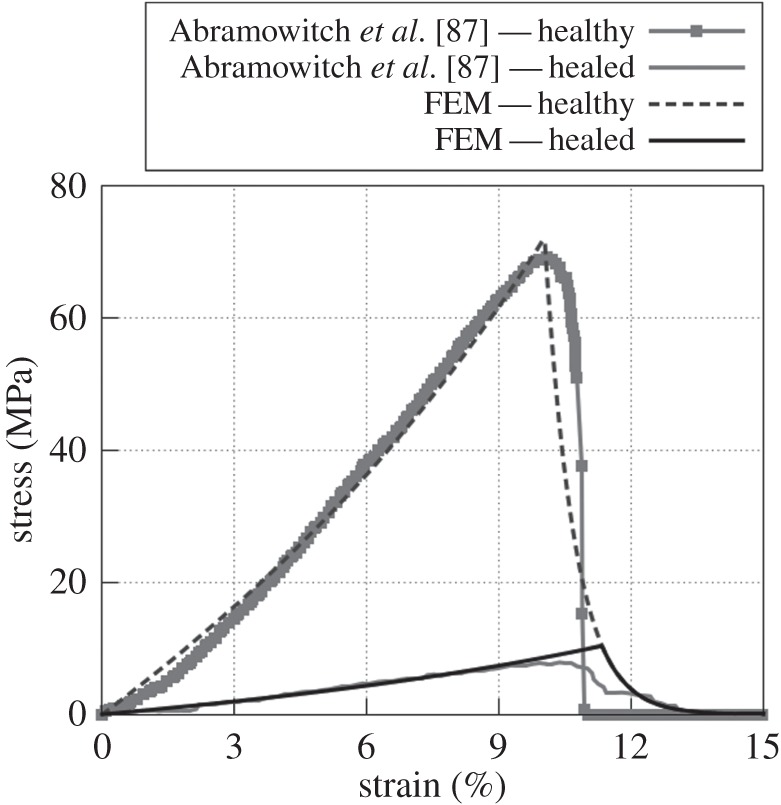
Cauchy stress versus engineering strain responses to uniaxial loading of a healthy and a six week healed MCL tissue following a surgical sectioning. FE results (solid black lines) were obtained using the material properties given in table 3. The grey curves illustrate the response from the experimental data in Abramowitch et al. [87].
A uniaxial tensile loading is reproduced in order to estimate the Ogden and damage material properties that fit best the healthy stress–strain curve. These material properties are then used in a simulation with a forced initial damage Deff = 1, in which no load is applied but healing is allowed to progress for six weeks. An irreversible stiffness loss parameter ξ = 0.65 has been considered, because MCL scar tissue is known to regain at most 30–40% of its normal stiffness [73]. The healing rate parameter k is adjusted such that, after a six week healing period, the stress–strain curve obtained for uniaxial tensile loading fits the experimental data. Table 3 summarizes the material parameters used in this numerical example, and figure 6 compares the numerical results with the experimental data. The set of parameters used was achieved by a manual trial and error approach and is not unique nor satisfies the minimum of an objective function. A penalizer value κ = 106 Pa has been considered as the bulk modulus.
Table 3.
Material parameters, estimated from experimental data [87], used in the MCL healing example (figure 6). The fracture energy per unit area is computed as: 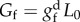 , where L0 is the localization or characteristic length in the reference configuration [85,86].
, where L0 is the localization or characteristic length in the reference configuration [85,86].
| parameter | value |
|---|---|
| μ1 | 1.3 MPa |
| μ2 | 50 MPa |
| μ3 | 22 MPa |
| α1 | 13.7 |
| α2 | 0.7 |
| α3 | 12.8 |
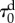 |
2.43 kPa1/2 |
| Gf | 17 N mm−1 |
| k | 0.01 days−1 |
| ξ | 0.65 |
3.3. Remodelling abdominal aortic aneurysm
An AAA is a permanent localized dilatation of the abdominal aorta which, if left untreated, progresses over time and can eventually rupture, leading to death. AAA rupture is a multifactorial process that involves interacting biomechanical, biochemical, cellular and proteolytic aspects. An irreversible remodelling is known to occur in the connective tissue of an aneurysm's aortic wall, characterized by a progressive imbalance between the synthesis and degradation of collagen and elastin in the ECM.
The degradation of elastin is linked to a decreased load-bearing capacity of the wall tissue, which leads to the initial arterial dilatation. A compensatory increase in collagen synthesis, associated with the overall hardening of the aortic tissue, is observed in the latter stages of AAA evolution. Beyond a certain threshold, however, the aneurysm becomes at high risk of rupture. It is believed that this final progression to rupture involves the proteolytic degradation of the tissue's collagen fibres. The reader is referred to [6,45,89,90] and references therein for further details on the many factors involved in the progression and rupture of AAAs, some of which are not completely understood yet.
The proteolytic degradation of elastin described above may be regarded, from a macroscopic point of view, as a degradation of the tissue's properties. Thus, the HTR model has the potential to characterize this particular factor in the complex evolution of AAAs, linking the pathological arterial dilatation observed in the initial stages of AAA formation to the ‘healing’ capacity of the tissue.
A three-dimensional reconstruction of an AAA was obtained through segmentation of computer-tomography images (A4research, VASCOPS GmbH [91]) and meshed using 4707 hexahedral Q1P0 elements. A single element was included across the wall thickness with an approximately constant value of 1.5 mm throughout the aneurysm. Therefore, bending effects are neglected in the simulation. The model is fully fixed at the top slice and allowed vertical displacements at the bottom one. A blood pressure of 100 mmHg (13.33 kPa) is applied in 200 load increments on the inner surface of the wall by means of a deformation-dependent follower pressure load on the face of each element. Material properties were estimated from the experimental tensile test data available in Gasser [92] using a single element (figure 2). A penalizer value κ = 1012 Pa has been considered as the bulk modulus. The set of parameters used (listed in table 4) was achieved by a manual trial and error approach and is not unique nor satisfies the minimum of an objective function. The corresponding constitutive response is plotted in figure 7. The distal and proximal extents of the aneurysm are excluded from damage evolution, i.e. assigned the purely hyperelastic response shown in figure 7.
Table 4.
Ogden and damage material parameters, estimated from experimental data [92], used in the remodelling AAA example. The fracture energy per unit area is computed as: 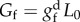 , where L0 is the localization or characteristic length in the reference configuration [85,86].
, where L0 is the localization or characteristic length in the reference configuration [85,86].
| parameter | value |
|---|---|
| μ1 | 1.0 kPa |
| μ2 | 2.1 kPa |
| μ3 | 3.6 kPa |
| α1 | 12.3 |
| α2 | 10.4 |
| α3 | 10.9 |
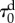 |
169.8 Pa1/2 |
| Gf | 45 N m−1 |
Figure 7.
First Piola–Kirchhoff stress versus stretch responses to uniaxial loading of an AAA tissue. The FE results (black lines) were obtained using the material properties given in table 4. The grey dots illustrate the response from the experimental data provided in Gasser [92].
The example was studied with two different values of the healing rate parameter k, and an irreversible stiffness loss parameter ξ = 0 was assumed in both cases. Under non-pathological conditions, the aortic wall is continuously remodelling and, thus, for a high healing rate its behaviour should be that of a healthy tissue. Figure 8 shows the deformed shape of the same AAA at identical loading and boundary conditions but considering two different healing rate parameters: k = 0.01 (high rate) and k = 0.002 years−1 (low rate). The high healing rate resulted in deformations comparable to a sole hyperelastic simulation, because damage is healed quasi-simultaneously. However, for the low healing rate, the simulation failed at a blood pressure of 71.5 mmHg (9.53 kPa). At this loading value, a high damage concentration localizes in a narrow band of elements (figure 9), which leads to structural instability and numerical failure in the following load step.
Figure 8.
Deformed shape of an AAA considering the material properties given in table 4 and subjected to a blood pressure of 71.5 mmHg (9.53 kPa). Two different healing rate parameters k have been considered in addition to an irreversible stiffness loss parameter ξ = 0. The distal and proximal extents were excluded from damage and assigned a hyperelastic material behaviour. (Online version in colour.)
Figure 9.
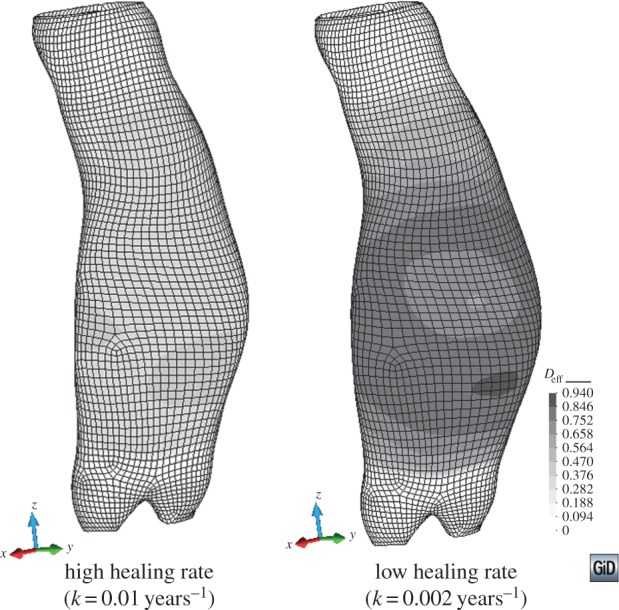
Effective damage distribution in an AAA considering the material properties given in table 4 and subjected to a blood pressure of 71.5 mmHg (9.53 kPa). Two different healing rate parameters k have been considered in addition to an irreversible stiffness loss parameter ξ = 0. The distal and proximal extents were excluded from damage and assigned a hyperelastic material behaviour. (Online version in colour.)
4. Discussion
The effective damage Deff (2.3) drives healing in the HTR model. This variable is a direct representation of the tissue's state because it dictates the stiffness of the healing tissue, which can be measured through experimental tests. In contrast with previous remodelling models (see §1), the present description does not attempt to capture the realignment of collagen or the processes taking place at cellular or microscopic level. Instead, it is a phenomenological model that aims to describe the overall change in material behaviour (stiffness) at tissue level of a healing tissue.
The driving internal variable Deff accounts for both mechanical and biological stimuli. Mechanical loading induces damage in the tissue as D is a function of the stress. The injury produces a biological response such that, if the metabolism allows for it, then healing occurs and the effective damage in the tissue is reversed (figure 1). The metabolism's action is quantified through the two healing parameters, k and ξ. Then, a healed tissue that has completely recovered the original properties is undistinguishable from the original tissue. The model is able to capture this, as seen in figure 5 for the uniaxial tensile loading–unloading–reloading case with k = 1.00 days−1; ξ = 0.0, where the reloading curve is exactly the same as the first loading curve.
In contrast, when the healed tissue does not recover the original properties (ξ > 0), it is assumed to have a remnant damage such that it is permanently softer than the initial pre-injured tissue. This is observed in figure 5 for the cases with k = 0.25 days−1; ξ = 0.2 and k = 0.25 days−1; ξ = 0.5. In both cases, the reloading curves have a lower stiffness in their initial elastic portion than the corresponding portion in the loading curves. Note how a healed scar tissue that suffers additional injury will heal back to the first scar tissue properties, i.e. the stiffness loss is not accumulative over successive injuries in the same tissue.
The issue arises, then, whether this (new) healed material should maintain the updated damage threshold corresponding to the remnant damage value. An alternative would be to redefine the healed tissue as a completely new material by eliminating the remnant damage and affecting the hyperelastic (and, possibly, the damage) material properties instead. Then, the same effect would be achieved (lower stiffness), but the material would be considered simply as new and ‘undamaged’. In this case, if ξ > 0, an additional injury would result in a further reduction of stiffness in the scar tissue. This approach entails certain difficulties, namely the calculation of the new material properties owing to the nonlinear nature of the Ogden material definition. In addition, the idea of keeping a remnant damage seems to fit well with the concept of a healed tissue that has not recovered completely from injury. That is, the ECM in the healing tissue tends to reorganize and remodel towards the original configuration but does not quite achieve it. Hence, the denomination of the model as homeostatic-driven turnover remodelling.
The pathological remodelling that is known to result in fibrotic scars, which are stiffer than the original pre-injured tissue, could be accounted for by introducing negative values of the irreversible stiffness loss parameter ξ. In this way, the ‘healed’ tissue would have a final negative value of the effective damage variable, resulting in a final material behaviour stiffer than the original pre-injured one. The HTR model would no longer be homeostatic-driven and would require substantial modifications to ensure that the ‘extra’ stiffening only occurs as a result of injury. This could probably be addressed by defining a variable value of ξ in terms of the present damage in the tissue. Furthermore, the fulfilment of the Clausius–Duhem inequality (2.4) could no longer be possible, because the energy introduced into the system to remodel the tissue would be larger than the energy dissipated owing to damage.
An interesting feature of the HTR model is that there exist two completely different scales for the generation of the mechanical stimulus that produces damage (load step) and the effectivization of the biochemical part of the healing process (time step). Hence, the evolution of the mechanical damage D is dictated solely by the loading pattern imposed in the numerical simulation. Yet, the healing variable R is driven by both the load increment and the time step considered for that load increment. Then, the healing rate can be sped up or slowed down to match experimental observations independently of the loading speed imposed. Owing to this characteristic, the mechanical damage loses its physical meaning. In particular, a high value of D may be computed for a given load but, if the healing rate is high enough, the effective damage Deff could be, in fact, practically null. As a result, a tissue can be completely healed, even when the value of D is significant. This ties in well with the fact that, in the HTR model, Deff is the variable that describes the actual state of the tissue, as stated at the beginning of this section.
In this regard, a value Deff = 1 corresponds to a newly formed granulation tissue, whereas Deff = 0 corresponds to a healed scar tissue that has recovered the properties of the original uninjured tissue. This is in accordance with the simplifying hypothesis introduced in §2, namely that tissue behaviour is reproduced with a quasi-incompressible hyperelastic model, with damage affecting only the deviatoric term. The quasi-incompressible behaviour in tissues is attributed to the high volume fraction of water present in most soft tissues [22]. For supra-physiological loadings, the injury produced could potentially introduce changes in the water content of the tissue, resulting in a compressible material. In some cases, the adequacy of the quasi-incompressibility hypothesis in soft tissues subjected to physiological loading has also been debated [93,94]. The possibility of cavitational damage arising in soft tissues has also been put forth [95]. Nonetheless, the HTR model accounts for remodelling from the granulation tissue obtained in the proliferative phase of the healing process to the scar tissue resulting at the end of the remodelling phase (figure 1). Hence, a complete damage Deff = 0 does not correspond to vacuum or inexistent tissue, but to a newly formed granulation tissue. Albeit the granulation tissue has barely any resistance to loading, it may be considered to have a fixed content of water and, thus, certain quasi-incompressibility. This would correspond to the volumetric part of the specific strain energy density, not affected by damage.
Healing is influenced by many factors such as age, severity of injury and location of the injury, among others [1,4], and the healing parameters ξ and k should account for this. At present, they are constant throughout the healing process and manually adjusted. It would be interesting to automatically adjust their value at the moment of injury, although this would require a comprehensive database quantifying the influence of the above factors on the value of the parameters. Unfortunately, the type of data required to produce this type of study is not abundant in the literature. On the other hand, the healing rate function 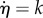 could be made variable through the healing process. This would allow accounting for the regression of the blood vessels, i.e. the reduction of biological availability, observed in the final phase of soft tissue healing. For example, the healing rate function could be coupled to a convection/diffusion system such that the biochemical contribution to the healing rate would change as healing occurs, allowing for an adaptive biological availability distribution.
could be made variable through the healing process. This would allow accounting for the regression of the blood vessels, i.e. the reduction of biological availability, observed in the final phase of soft tissue healing. For example, the healing rate function could be coupled to a convection/diffusion system such that the biochemical contribution to the healing rate would change as healing occurs, allowing for an adaptive biological availability distribution.
Further improvements to the HTR model include coupling it to a continuum growth model [96] to account for the tissue growth seen in hypertrophic scars. This is relatively straightforward for a volumetric growth model based on the multiplicative decomposition of the deformation gradient tensor, 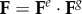 . Here,
. Here,  corresponds to the elastic part and
corresponds to the elastic part and 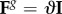 to the incompatible growth part. The evolution of the growth stretch
to the incompatible growth part. The evolution of the growth stretch 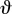 may be defined in terms of the mechanical loading and a function that accounts for the biological availability [81,97]. Then, the coupling of the HTR model to such a growth model would simply require determining first the behaviour owing to growth and, then, computing the healing effect on the updated grown configuration.
may be defined in terms of the mechanical loading and a function that accounts for the biological availability [81,97]. Then, the coupling of the HTR model to such a growth model would simply require determining first the behaviour owing to growth and, then, computing the healing effect on the updated grown configuration.
Nonetheless, the present HTR model is capable of reproducing experimental data on healing (figure 6) and has potential to reproduce certain characteristics of pathological remodelling, as has been exemplified in an AAA dilatation case (figures 8 and 9). This example aims at demonstrating a possible application of the HTR model to a complex three-dimensional problem. In this case, the model is shown to capture the degradation of the aortic wall's structural properties owing to the pathological remodelling in the initial stages of AAA disease.
The low healing rate case in this example reproduces the abnormal dilatation of an AAA, where the elastin degradation results in larger deformations and reduced load-bearing capacity. On the other hand, the results for the high healing rate case are comparable to a tissue with a higher structural integrity, more akin to a healthy tissue.
The present model only addresses the dilatation of the aortic wall, linked to the progressive degradation of elastin in the ECM. It does not include other known factors that contribute to the evolution and rupture of AAAs such as growth in the abdominal wall tissue, changes in phenotypes and chemomechanical responses of the cells composing said tissue, or the effect of thrombus development and maturation of the AAA, among others [45]. Even so, the inclusion of the HTR model in a general model for AAAs that accounts for the aforementioned factors could potentially contribute to better understand the complex processes involved in the evolution of AAAs.
In particular, the proteolytic degradation of the tissue's collagen fibres that has been linked to the final progression to rupture in AAA disease could be reproduced with the same HTR model. However, it would require a separate material characterization and time-scale application than that of the elastin degradation presented in the example. Introducing a modification similar to the one previously proposed for the case of fibrotic scars, the hardening effect observed in the latter stages of AAA evolution, previous to the final progression to rupture, might also be captured.
Finally, the structural instability encountered in the low healing rate case of the AAA example is attributable to the numerical limitations of the generalized damage model [79]. From a numerical point of view, in problems with negligible healing effects the HTR model is limited by stress-locking owing to the smeared approach of the damage formulation. This has been widely addressed in the literature [83,84], and a known solution to the problem is to use higher-order FE formulations. Otherwise, the HTR formulation is robust and, in any case, thermodynamically consistent.
5. Conclusion
A constitutive model for homeostatic-driven turnover remodelling in soft tissues has been presented and discussed. This model captures the stiffness recovery that occurs as a consequence of the ECM turnover observed in both the last phase of healing in tissues and the pathological remodelling of certain tissues. During remodelling, the tissue composition shifts and reorganizes, approaching the characteristics of the original undamaged material. Thus, healing is understood as a recovery or reversal of damage in the tissue, which is driven by both mechanical and biochemical stimuli. Set in a CDM framework, the driving internal variable of the HTR model is the effective damage, whose rate is the sum of a Kachanov-like mechanical damage rate and a healing rate. The former is purely driven by mechanical loading, as observed in the proposed damage softening laws. The latter is defined as an implicit healing rate, which depends on the effective damage and two healing material parameters that account for the biochemical aspects of the healing process. The model is formulated in accordance with open-system thermodynamics to account for the energy introduced into the system by the metabolism.
Numerical implementation of the HTR model is straightforward and may be particularized for any hyperelastic model. The formulation is flexible and versatile, because both the damage softening laws and the healing rate can be easily changed or modified to fit particular biological observations. However, the advantage of the phenomenological evolution laws proposed here is that they require few (damage and healing) material parameters, which is especially useful when fitting experimental data. In addition, a physical meaning can be attributed to these parameters, conferring a more functional character to the model.
Albeit the HTR model's simplicity, it has the potential to represent the active properties of complex tissues. Usage of this model in conjunction with mixture theory [98] would allow the inclusion of fibrous components and, in this way, introduce anisotropy in the overall behaviour of the tissue. Furthermore, coupling with formulations which model other biomechanical aspects such as tissue growth and necrosis [99] could result in a powerful numerical tool to represent live soft tissue behaviour.
Acknowledgements
We thank the anonymous reviewer whose insightful comments on an earlier version of the manuscript helped to improve the arguments, clarity and presentation of our work.
Appendix A. Derivation of the tangent constitutive tensor
The tangent constitutive tensor, required in the numerical implementation of the proposed HTR constitutive model, is given by
| A1 |
The volumetric part of the tensor, introducing 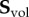 from (2.13), results in
from (2.13), results in
| A2 |
and the deviatoric part, considering (2.5) and (2.13), is
| A3 |
Here, 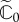 corresponds to the material elasticity tensor of the undamaged material,
corresponds to the material elasticity tensor of the undamaged material, 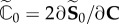 , and the derivative of Deff is
, and the derivative of Deff is
| A4 |
Rearranging terms and isolating the derivative of Deff, yields
| A5 |
Now, considering the Simo & Ju criterion [70] as the energetic norm, 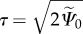 , produces
, produces
| A6 |
Introducing this expression into (A 5) and, then, into (A 3) results in
| A7 |
The derivative of the mechanical damage variable with respect to τ for the linear and exponential softening laws (2.8) considered is [79]
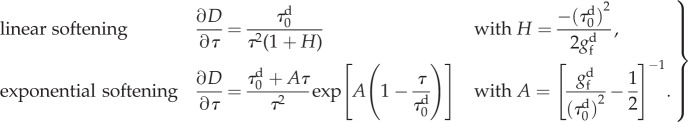 |
The derivative of the healing variable with respect to Deff, taking into account the healing rate defined in (2.9), is given by
| A9 |
where t* denotes the present time. The Leibniz integral rule allows introducing the derivative into the integral and, eliminating the Macaulay brackets, the expression results in
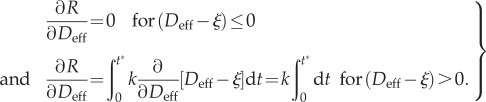 |
A10 |
Data accessibility
The PLCd source code containing the numerical implementation of the model is available at http://www.cimne.com/PLCd.
Authors' contributions
S.O. and F.J.B. conceived and designed the study. E.C. and T.C.G. developed the theoretical model formulation with the collaboration of S.O. and F.J.B. E.C. implemented the computational model, performed the numerical simulations and drafted the manuscript. F.J.B. collaborated in the numerical simulations and T.C.G. helped draft the manuscript. All authors revised and approved the manuscript for publication.
Competing interests
We declare we have no competing interests.
Funding
This work was partially supported by the European Research Council under the Advanced grant ERC-2012-AdG 320815 COMP-DES-MAT ‘Advanced tools for computational design of engineering materials'. E.C. gratefully acknowledges the support of the Universitat Politècnica de Catalunya (BarcelonaTECH) through an FPI-UPC scholarship.
References
- 1.Frank C, Shrive N, Hiraoka H, Nakamura N, Kaneda Y, Hart D. 1999. Optimisation of the biology of soft tissue repair. J. Sci. Med. Sport 2, 190–210. ( 10.1016/S1440-2440(99)80173-X) [DOI] [PubMed] [Google Scholar]
- 2.Gurtner GC, Werner S, Barrandon Y, Longaker MT. 2008. Wound repair and regeneration. Nature 453, 314–321. ( 10.1038/nature07039) [DOI] [PubMed] [Google Scholar]
- 3.Enoch S, Leaper DJ. 2008. Basic science of wound healing. Surgery (Oxford) 26, 31–37. ( 10.1016/j.mpsur.2007.11.005) [DOI] [Google Scholar]
- 4.Young A, McNaught C-E. 2011. The physiology of wound healing. Surgery (Oxford) 29, 475–479. ( 10.1016/j.mpsur.2011.06.011) [DOI] [Google Scholar]
- 5.Williamson D, Harding K. 2004. Wound healing. Medicine 32, 4–7. ( 10.1383/medc.32.12.4.55399) [DOI] [Google Scholar]
- 6.Choke E, Cockerill G, Wilson WRW, Sayed S, Dawson J, Loftus I, Thompson MM. 2005. A review of biological factors implicated in abdominal aortic aneurysm rupture. Eur. J. Vasc. Endovasc. 30, 227–244. ( 10.1016/j.ejvs.2005.03.009) [DOI] [PubMed] [Google Scholar]
- 7.Sherratt JA, Murray JD. 1990. Models of epidermal wound healing. Proc. R. Soc. Lond. B 241, 29–36. ( 10.1098/rspb.1990.0061) [DOI] [PubMed] [Google Scholar]
- 8.Tranquillo RT, Murray JD. 1992. Continuum model of fibroblast-driven wound contraction: inflammation-mediation. J. Theor. Biol. 158, 135–172. ( 10.1016/S0022-5193(05)80715-5) [DOI] [PubMed] [Google Scholar]
- 9.Pettet GJ, Byrne HM, Mcelwain DLS, Norbury J. 1996. A model of wound-healing angiogenesis in soft tissue. Math. Biosci. 136, 35–63. ( 10.1016/0025-5564(96)00044-2) [DOI] [PubMed] [Google Scholar]
- 10.Javierre E, Moreo P, Doblaré M, García-Aznar JM. 2009. Numerical modeling of a mechano-chemical theory for wound contraction analysis. Int. J. Solids Struct. 46, 3597–3606. ( 10.1016/j.ijsolstr.2009.06.010) [DOI] [Google Scholar]
- 11.Murphy KE, Hall CL, Maini PK, McCue SW, McElwain DLS. 2012. A fibrocontractive mechanochemical model of dermal wound closure incorporating realistic growth factor kinetics. Bull. Math. Biol. 74, 1143–1170. ( 10.1007/s11538-011-9712-y) [DOI] [PubMed] [Google Scholar]
- 12.Valero C, Javierre E, García-Aznar JM, Gómez-Benito MJ. 2014. A cell-regulatory mechanism involving feedback between contraction and tissue formation guides wound healing progression. PLoS ONE 9, e92774 ( 10.1371/journal.pone.0092774) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schugart RC, Friedman A, Zhao R, Sen CK. 2008. Wound angiogenesis as a function of tissue oxygen tension: a mathematical model. Proc. Natl Acad. Sci. USA 105, 2628–2633. ( 10.1073/pnas.0711642105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Flegg JA, Byrne HM, McElwain DLS. 2010. Mathematical model of hyperbaric oxygen therapy applied to chronic diabetic wounds. Bull. Math. Biol. 72, 1867–1891. ( 10.1007/s11538-010-9514-7) [DOI] [PubMed] [Google Scholar]
- 15.Valero C, Javierre E, García-Aznar JM, Gómez-Benito MJ, Menzel A. 2015. Modeling of anisotropic wound healing. J. Mech. Phys. Solids 79, 80–91. ( 10.1016/j.jmps.2015.03.009) [DOI] [Google Scholar]
- 16.Callaghan T, Khain E, Sander LM, Ziff RM. 2006. A stochastic model for wound healing. J. Stat. Phys. 122, 909–924. ( 10.1007/s10955-006-9022-1) [DOI] [Google Scholar]
- 17.McDougall S, Dallon J, Sherratt J, Maini P. 2006. Fibroblast migration and collagen deposition during dermal wound healing: mathematical modelling and clinical implications. Phil. Trans. R. Soc. A 364, 1385–1405. ( 10.1098/rsta.2006.1773) [DOI] [PubMed] [Google Scholar]
- 18.Cumming BD, McElwain DLS, Upton Z. 2010. A mathematical model of wound healing and subsequent scarring. J. R. Soc. Interface 7, 19–34. ( 10.1098/rsif.2008.0536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tepole AB, Kuhl E. 2014. Computational modeling of chemo-bio-mechanical coupling: a systems-biology approach toward wound healing. Comput. Methods Biomech. Biomed. Eng. 19, 13–30. ( 10.1080/10255842.2014.980821) [DOI] [PubMed] [Google Scholar]
- 20.Tepole AB, Kuhl E. 2013. Systems-based approaches toward wound healing. Pediatr. Res. 73, 553–563. ( 10.1038/pr.2013.3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Valero C, Javierre E, García-Aznar JM, Menzel A, Gómez-Benito MJ. 2015. Challenges in the modeling of wound healing mechanisms in soft biological tissues. Ann. Biomed. Eng. 43, 1654–1665. ( 10.1007/s10439-014-1200-8) [DOI] [PubMed] [Google Scholar]
- 22.Humphrey JD. 2003. Review paper: continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A 459, 3–46. ( 10.1098/rspa.2002.1060) [DOI] [Google Scholar]
- 23.Ambrosi D, et al. 2011. Perspectives on biological growth and remodeling. J. Mech. Phys. Solids 59, 863–883. ( 10.1016/j.jmps.2010.12.011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ateshian GA, Humphrey JD. 2012. Continuum mixture models of biological growth and remodeling: past successes and future opportunities. Annu. Rev. Biomed. Eng. 14, 97–111. ( 10.1146/annurev-bioeng-071910-124726) [DOI] [PubMed] [Google Scholar]
- 25.Menzel A, Kuhl E. 2012. Frontiers in growth and remodeling. Mech. Res. Commun. 42, 1–14. ( 10.1016/j.mechrescom.2012.02.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Driessen NJB, Peters GWM, Huyghe JM, Bouten CVC, Baaijens FPT. 2003. Remodelling of continuously distributed collagen fibres in soft connective tissues. J. Biomech. 36, 1151–1158. ( 10.1016/S0021-9290(03)00082-4) [DOI] [PubMed] [Google Scholar]
- 27.Kuhl E, Garikipati K, Arruda EM, Grosh K. 2005. Remodeling of biological tissue: mechanically induced reorientation of a transversely isotropic chain network. J. Mech. Phys. Solids 53, 1552–1573. ( 10.1016/j.jmps.2005.03.002) [DOI] [Google Scholar]
- 28.Garikipati K, Olberding JE, Narayanan H, Arruda EM, Grosh K, Calve S. 2006. Biological remodelling: stationary energy, configurational change, internal variables and dissipation. J. Mech. Phys. Solids 54, 1493–1515. ( 10.1016/j.jmps.2005.11.011) [DOI] [Google Scholar]
- 29.Menzel A. 2007. A fibre reorientation model for orthotropic multiplicative growth. Configurational driving stresses, kinematics-based reorientation, and algorithmic aspects. Biomech. Model. Mechanobiol. 6, 303–320. ( 10.1007/s10237-006-0061-y) [DOI] [PubMed] [Google Scholar]
- 30.Kroon M. 2010. A continuum mechanics framework and a constitutive model for remodelling of collagen gels and collagenous tissues. J. Mech. Phys. Solids 58, 918–933. ( 10.1016/j.jmps.2010.03.005) [DOI] [Google Scholar]
- 31.Sáez P, Peña E, Doblaré M, Martínez MA. 2013. Hierarchical micro-adaptation of biological structures by mechanical stimuli. Int. J. Solids Struct. 50, 2353–2370. ( 10.1016/j.ijsolstr.2013.03.029) [DOI] [Google Scholar]
- 32.Humphrey JD, Rajagopal KR. 2002. A constrained mixture model for growth and remodelling of soft tissues. Math. Models Methods Appl. Sci. 12, 407–430. ( 10.1142/S0218202502001714) [DOI] [Google Scholar]
- 33.Ateshian GA. 2007. On the theory of reactive mixtures for modeling biological growth. Biomech. Model. Mechanobiol. 6, 423–445. ( 10.1007/s10237-006-0070-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rao IJ. 2011. Modeling of growth and remodeling in soft biological tissues with multiple constituents. Mech. Res. Commun. 38, 24–28. ( 10.1016/j.mechrescom.2010.11.003) [DOI] [Google Scholar]
- 35.Myers K, Ateshian GA. 2014. Interstitial growth and remodeling of biological tissues: tissue composition as state variables. J. Mech. Behav. Biomed. Mater. 29, 544–556. ( 10.1016/j.jmbbm.2013.03.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lanir Y. 2014. Mechanistic micro-structural theory of soft tissues growth and remodeling: tissues with unidirectional fibers. Biomech. Model. Mechanobiol. 14, 245–266. ( 10.1007/s10237-014-0600-x) [DOI] [PubMed] [Google Scholar]
- 37.Loerakker S, Obbink-Huizer C, Baaijens FPT. 2014. A physically motivated constitutive model for cell-mediated compaction and collagen remodeling in soft tissues. Biomech. Model. Mechanobiol. 13, 985–1001. ( 10.1007/s10237-013-0549-1) [DOI] [PubMed] [Google Scholar]
- 38.Heck TAM, Wilson W, Foolen J, Cilingir AC, Ito K, van Donkelaar CC. 2015. A tissue adaptation model based on strain-dependent collagen degradation and contact-guided cell traction. J. Biomech. 48, 823–831. ( 10.1016/j.jbiomech.2014.12.023) [DOI] [PubMed] [Google Scholar]
- 39.Ateshian GA, Nims RJ, Maas S, Weiss JA. 2014. Computational modeling of chemical reactions and interstitial growth and remodeling involving charged solutes and solid-bound molecules. Biomech. Model. Mechanobiol. 13, 1105–1120. ( 10.1007/s10237-014-0560-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hariton I, de Botton G, Gasser TC, Holzapfel GA. 2007. Stress-driven collagen fiber remodeling in arterial walls. Biomech. Model. Mechanobiol. 6, 163–175. ( 10.1007/s10237-006-0049-7) [DOI] [PubMed] [Google Scholar]
- 41.Baaijens F, Bouten C, Driessen N. 2010. Modeling collagen remodeling. J. Biomech. 43, 166–175. ( 10.1016/j.jbiomech.2009.09.022) [DOI] [PubMed] [Google Scholar]
- 42.Sáez P, Peña E, Martínez MA, Kuhl E. 2013. Mathematical modeling of collagen turnover in biological tissue. J. Math. Biol. 67, 1765–1793. ( 10.1007/s00285-012-0613-y) [DOI] [PubMed] [Google Scholar]
- 43.Valentn A, Humphrey JD, Holzapfel GA. 2013. A finite element-based constrained mixture implementation for arterial growth, remodeling, and adaptation: theory and numerical verification. Int. J. Numer. Methods Biomed. Eng. 29, 822–849. ( 10.1002/cnm.2555) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Watton PN, Hill NA, Heil M. 2004. A mathematical model for the growth of the abdominal aortic aneurysm. Biomech. Model. Mechanobiol. 3, 98–113. ( 10.1007/s10237-004-0052-9) [DOI] [PubMed] [Google Scholar]
- 45.Humphrey JD, Holzapfel GA. 2012. Mechanics, mechanobiology, and modeling of human abdominal aorta and aneurysms. J. Biomech. 45, 805–814. ( 10.1016/j.jbiomech.2011.11.021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Martufi G, Gasser TC. 2012. Turnover of fibrillar collagen in soft biological tissue with application to the expansion of abdominal aortic aneurysms. J. R. Soc. Interface 9, 3366–3377. ( 10.1098/rsif.2012.0416) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sandoval RPC, Garzón-Alvarado DA, Martínez AMR. 2012. A mathematical model of the process of ligament repair: effect of cold therapy and mechanical stress. J. Theor. Biol. 302, 53–61. ( 10.1016/j.jtbi.2012.01.035) [DOI] [PubMed] [Google Scholar]
- 48.Garzón-Alvarado DA, Cárdenas Sandoval RP, Vanegas Acosta JC. 2012. A mathematical model of medial collateral ligament repair: migration, fibroblast proliferation and collagen formation. Comput. Methods Biomech. Biomed. Eng. 15, 571–583. ( 10.1080/10255842.2010.550887) [DOI] [PubMed] [Google Scholar]
- 49.Eliasson P, Andersson T, Aspenberg P. 2009. Rat Achilles tendon healing: mechanical loading and gene expression. J. Appl. Physiol. 107, 399–407. ( 10.1152/japplphysiol.91563.2008) [DOI] [PubMed] [Google Scholar]
- 50.Killian ML, Cavinatto L, Galatz LM, Thomopoulos S. 2012. The role of mechanobiology in tendon healing. J. Shoulder Elbow Surg. 21, 228–237. ( 10.1016/j.jse.2011.11.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schepull T, Kvist J, Andersson C, Aspenberg P. 2007. Mechanical properties during healing of Achilles tendon ruptures to predict final outcome: a pilot Roentgen stereophotogrammetric analysis in 10 patients. BMC Musculoskelet. Disord. 8, 116 ( 10.1186/1471-2474-8-116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wang JH-C, Guo Q, Li B. 2012. Tendon biomechanics and mechanobiology—a minireview of basic concepts and recent advancements. J. Hand Ther. 25, 133–140. ( 10.1016/j.jht.2011.07.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Isaksson H. 2012. Recent advances in mechanobiological modeling of bone regeneration. Mech. Res. Commun. 42, 22–31. ( 10.1016/j.mechrescom.2011.11.006) [DOI] [Google Scholar]
- 54.Anderson DD, Thomas TP, Campos Marin A, Elkins JM, Lack WD, Lacroix D. 2014. Computational techniques for the assessment of fracture repair. Injury 45, S23–S31. ( 10.1016/j.injury.2014.04.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cox TR, Erler JT. 2011. Remodeling and homeostasis of the extracellular matrix: implications for fibrotic diseases and cancer. Dis. Model. Mech. 4, 165–178. ( 10.1242/dmm.004077) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Didangelos A, Yin X, Mandal K, Saje A, Smith A, Xu Q, Jahangiri M, Mayr M. 2011. Extracellular matrix composition and remodeling in human abdominal aortic aneurysms: a proteomics approach. Mol. Cell. Proteomics 10, M111008128. ( 10.1074/mcp.M111.008128) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kuhl E, Steinmann P. 2003. Mass- and volume-specific views on thermodynamics for open systems. Proc. R. Soc. Lond. A 459, 2547–2568. ( 10.1098/rspa.2003.1119) [DOI] [Google Scholar]
- 58.Doblaré M, García JM. 2002. Anisotropic bone remodelling model based on a continuum damage-repair theory. J. Biomech. 35, 1–17. ( 10.1016/S0021-9290(01)00178-6) [DOI] [PubMed] [Google Scholar]
- 59.PLCd research group. PLCd: non-linear thermo-mechanic finite element code for research-oriented applications. Free access code developed at CIMNE. See http://www.cimne.com/PLCd. [Google Scholar]
- 60.Fung YC. 1993. Biomechanics: mechanical properties of living tissues, 2nd edn New York, NY: Springer. [Google Scholar]
- 61.Simo JC, Taylor RL. 1991. Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Comput. Methods Appl. Mech. Eng. 85, 273–310. ( 10.1016/0045-7825(91)90100-K) [DOI] [Google Scholar]
- 62.Gasser TC, Ogden RW, Holzapfel GA. 2006. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35. ( 10.1098/rsif.2005.0073) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Limbert G, Middleton J, Laizans J, Dobelis M, Knets I. 2006. A transversely isotropic hyperelastic constitutive model of the PDL. Analytical and computational aspects. Comput. Methods Biomech. Biomed. Eng. 6, 337–345. ( 10.1080/10255840310001637572) [DOI] [PubMed] [Google Scholar]
- 64.Calvo B, Peña E, Martínez MA, Doblaré M. 2007. An uncoupled directional damage model for fibred biological soft tissues. Formulation and computational aspects. Int. J. Numer. Methods Biomed. Eng. 69, 2036–2057. ( 10.1002/nme.1825) [DOI] [Google Scholar]
- 65.Peña E. 2011. Damage functions of the internal variables for soft biological fibred tissues. Mech. Res. Commun. 38, 610–615. (doi:0.1016/j.mechrescom.2011.09.002) [Google Scholar]
- 66.Balzani D, Brinkhues S, Holzapfel GA. 2012. Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls. Comput. Methods Appl. Mech. Eng. 213–216, 139–151. ( 10.1016/j.cma.2011.11.015) [DOI] [Google Scholar]
- 67.Martins P, Peña E, Natal Jorge RM, Santos A, Santos L, Mascarenhas T, Calvo B. 2012. Mechanical characterization and constitutive modelling of the damage process in rectus sheath. J. Mech. Behav. Biomed. Mater. 8, 111–122. ( 10.1016/j.jmbbm.2011.12.005) [DOI] [PubMed] [Google Scholar]
- 68.Blanco S, Polindara CA, Goicolea JM. 2015. A regularised continuum damage model based on the mesoscopic scale for soft tissue. Int. J. Solids Struct. 58, 20–33. ( 10.1016/j.ijsolstr.2014.12.013) [DOI] [Google Scholar]
- 69.Kachanov LM. 1986. Introduction to continuum damage mechanics. Mechanics of Elastic Stability, vol. 10. Dordrecht, The Netherlands: Springer; ( 10.1007/978-94-017-1957-5) [DOI] [Google Scholar]
- 70.Simo JC, Ju JW. 1987. Strain- and stress-based continuum damage models—I. Formulation. Int. J. Solids Struct. 23, 821–840. ( 10.1016/0020-7683(87)90083-7) [DOI] [Google Scholar]
- 71.Chaboche JL. 1988. Continuum damage mechanics: part I—general concepts. J. Appl. Mech. 55, 59–64. ( 10.1115/1.3173661) [DOI] [Google Scholar]
- 72.Lemaitre J. 1996. A course on damage mechanics. Berlin, Germany: Springer. [Google Scholar]
- 73.Frank CB, Hart DA, Shrive NG. 1999. Molecular biology and biomechanics of normal and healing ligaments—a review. Osteoarthr. Cartil. 7, 130–140. ( 10.1053/joca.1998.0168) [DOI] [PubMed] [Google Scholar]
- 74.Woo SL-Y, Abramowitch SD, Kilger R, Liang R. 2006. Biomechanics of knee ligaments: injury, healing, and repair. J. Biomech. 39, 1–20. ( 10.1016/j.jbiomech.2004.10.025) [DOI] [PubMed] [Google Scholar]
- 75.Clark JA, Cheng JCY, Leung KS. 1996. Mechanical properties of normal skin and hypertrophic scars. Burns 22, 443–446. ( 10.1016/0305-4179(96)00038-1) [DOI] [PubMed] [Google Scholar]
- 76.Corr DT, Gallant-Behm CL, Shrive NG, Hart DA. 2009. Biomechanical behavior of scar tissue and uninjured skin in a porcine model. Wound Repair Regen. 17, 250–259. ( 10.1111/j.1524-475X.2009.00463.x) [DOI] [PubMed] [Google Scholar]
- 77.Hinz B. 2009. Tissue stiffness, latent TGF-β1 activation, and mechanical signal transduction: implications for the pathogenesis and treatment of fibrosis. Curr. Rheumatol. Rep. 11, 120–126. ( 10.1007/s11926-009-0017-1) [DOI] [PubMed] [Google Scholar]
- 78.Simo JC. 1987. On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects. Comput. Methods Appl. Mech. Eng. 60, 153–173. ( 10.1016/0045-7825(87)90107-1) [DOI] [Google Scholar]
- 79.Comellas E, Bellomo FJ, Oller S. 2015. A generalized finite-strain damage model for quasi-incompressible hyperelasticity using hybrid formulation. Int. J. Numer. Methods Biomed. Eng. 105, 781–800. ( 10.1002/nme.5118) [DOI] [Google Scholar]
- 80.Oller S. 2014. Nonlinear dynamics of structures. Berlin, Germany: Springer; ( 10.1007/978-3-319-05194-9) [DOI] [Google Scholar]
- 81.Bellomo FJ, Oller S, Armero F, Nallim LG. 2011. A general constitutive model for vascular tissue considering stress driven growth and biological availability. Comput. Model. Eng. Sci. 80, 1–21. ( 10.3970/cmes.2011.080.001) [DOI] [Google Scholar]
- 82.Schenk O, Gärtner K. 2004. Solving unsymmetric sparse systems of linear equations with PARDISO. Fut. Gen. Comput. Syst. 20, 475–487. ( 10.1016/j.future.2003.07.011) [DOI] [Google Scholar]
- 83.Crisfield MA. 1991. Non-linear finite element analysis of solids and structures. London, UK: John Wiley and Sons. [Google Scholar]
- 84.Bathe K-J. 1996. Finite element procedures. Upper Saddle River, NJ: Prentice Hall. [Google Scholar]
- 85.Oliver J. 1989. A consistent characteristic length for smeared cracking models. Int. J. Numer. Methods Eng. 28, 461–474. ( 10.1002/nme.1620280214) [DOI] [Google Scholar]
- 86.Oliver J, Cervera M, Oller S, Lubliner J. 1990. Isotropic damage models and smeared crack analysis of concrete. In Proc. SCI-C Computer Aided Analysis and Design of Concrete Structures, Zell am See, Austria, 4–6 April 1990, pp. 945–957.
- 87.Abramowitch SD, Yagi M, Tsuda E, Woo SL-Y. 2003. The healing medial collateral ligament following a combined anterior cruciate and medial collateral ligament injury—a biomechanical study in a goat model. J. Orthop. Res. 21, 1124–1130. ( 10.1016/S0736-0266(03)00080-9) [DOI] [PubMed] [Google Scholar]
- 88.Scheffler SU, Clineff TD, Papageorgiou CD, Debski RE, Ma CB, Woo SL-Y. 2001. Structure and function of the healing medial collateral ligament in a goat model. Ann. Biomed. Eng. 29, 173–180. ( 10.1114/1.1349701) [DOI] [PubMed] [Google Scholar]
- 89.Vorp DA. 2007. Biomechanics of abdominal aortic aneurysm. J. Biomech. 40, 1887–1902. ( 10.1016/j.jbiomech.2006.09.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Martufi G, Gasser TC. 2013. Review: the role of biomechanical modeling in the rupture risk assessment for abdominal aortic aneurysms. J. Biomech. Eng. 135, 021010 ( 10.1115/1.4023254) [DOI] [PubMed] [Google Scholar]
- 91.Auer M, Gasser TC. 2010. Reconstruction and finite element mesh generation of abdominal aortic aneurysms from computerized tomography angiography data with minimal user interactions. IEEE Trans. Med. Imaging 29, 1022–1028. ( 10.1109/TMI.2009.2039579) [DOI] [PubMed] [Google Scholar]
- 92.Gasser TC. 2011. An irreversible constitutive model for fibrous soft biological tissue: a 3-D microfiber approach with demonstrative application to abdominal aortic aneurysms. Acta Biomater. 7, 2457–2466. ( 10.1016/j.actbio.2011.02.015) [DOI] [PubMed] [Google Scholar]
- 93.Ní Annaidh A, Destrade M, Gilchrist MD, Murphy JG. 2013. Deficiencies in numerical models of anisotropic nonlinearly elastic materials. Biomech. Model. Mechanobiol. 12, 781–791. ( 10.1007/s10237-012-0442-3) [DOI] [PubMed] [Google Scholar]
- 94.Pierrat B, Murphy JG, MacManus DB, Gilchrist MD. 2015. Finite element implementation of a new model of slight compressibility for transversely isotropic materials. Comput. Methods Biomech. Biomed. Eng. 19, 745–758. ( 10.1080/10255842.2015.1061513) [DOI] [PubMed] [Google Scholar]
- 95.Horgan CO, Murphy JG. 2011. Simple shearing of soft biological tissues. Proc. R. Soc. A 467, 760–777. ( 10.1098/rspa.2010.0288) [DOI] [Google Scholar]
- 96.Kuhl E. 2014. Growing matter: a review of growth in living systems. J. Mech. Behav. Biomed. Mater. 29, 529–543. ( 10.1016/j.jmbbm.2013.10.009) [DOI] [PubMed] [Google Scholar]
- 97.Oller S, Bellomo FJ, Armero F, Nallim LG. 2010. A stress driven growth model for soft tissue considering biological availability. IOP Conf. Ser. Mater. Sci. Eng. 10, 012121 ( 10.1088/1757-899X/10/1/012121) [DOI] [Google Scholar]
- 98.Comellas E, Valdez SI, Oller S, Botello S. 2015. Optimization method for the determination of material parameters in damaged composite structures. Compos. Struct. 122, 417–424. ( 10.1016/j.compstruct.2014.12.014) [DOI] [Google Scholar]
- 99.Bellomo FJ, Armero F, Nallim LG, Oller S. 2012. A constitutive model for tissue adaptation: necrosis and stress driven growth. Mech. Res. Commun. 42, 51–59. ( 10.1016/j.mechrescom.2011.11.007) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The PLCd source code containing the numerical implementation of the model is available at http://www.cimne.com/PLCd.