Abstract
Pathologies of the optic nerve and orbit impact millions of Americans and quantitative assessment of the orbital structures on 3-D imaging would provide objective markers to enhance diagnostic accuracy, improve timely intervention and eventually preserve visual function. Recent studies have shown that the multi-atlas methodology is suitable for identifying orbital structures, but challenges arise in the identification of the individual extraocular rectus muscles that control eye movement. This is increasingly problematic in diseased eyes, where these muscles often appear to fuse at the back of the orbit (at the resolution of clinical computed tomography imaging) due to inflammation or crowding. We propose the use of Kalman filters to track the muscles in three-dimensions to refine multi-atlas segmentation and resolve ambiguity due to imaging resolution, noise, and artifacts. The purpose of our study is to investigate a method of automatically generating orbital metrics from CT imaging and demonstrate the utility of the approach by correlating structural metrics of the eye orbit with clinical data and visual function measures in subjects with thyroid eye disease. The pilot study demonstrates that automatically calculated orbital metrics are strongly correlated with several clinical characteristics. Moreover, the superior, inferior, medial and lateral rectus muscles obtained using Kalman filters are each correlated with different categories of functional deficit. These findings serve as foundation for further investigation in the use of CT imaging in the study, analysis and diagnosis of ocular diseases, specifically thyroid eye disease.
Keywords: Multi-Atlas Segmentation, Computed Tomography, Thyroid Eye Disease, Kalman filters
1. INTRODUCTION
Pathologies of the optic nerve and orbit, such as glaucoma, thyroid eye disease, multiple sclerosis, and optic neuritis impact millions of Americans. Successful treatment of these pathologies is sensitive to the early diagnosis. However, current diagnostic techniques are dependent on variable clinical presentations between patients and subjective clinical testing. A quantitative assessment of the orbital structures would provide objective markers to enhance diagnostic accuracy, improve timely intervention and, eventually, preserve visual function. Modern image processing and machine learning methods allow for the development of automated pipelines for large-scale analysis of these diseases. The primary task of such a pipeline is the automated identification of anatomical structures in the visual system, such as the optic nerve, extraocular rectal muscles, eye globe, and orbital fat, and automated computation of structural metrics to correlate with clinical characteristics. We have created a large-scale image processing and data analytics database on Pathologies of the Human Eye, Orbit, and The Optic Nerve (PHOTON) to better understand early disease stages, enable timely intervention, and improve disease management. PHOTON is a collection of electronic medical records and medical imaging spanning 8 major cohorts of 25 individual diseases. As a pilot study on this database, we study thyroid eye disease using statistical label fusion methods and Kalman filters to identify orbital structures of interest and investigate correlations between these structures and eye functionality.
Presently, computed tomography (CT) imaging is the modality of choice in evaluating the orbit for evidence of thyroid eye disease[1]. In CT, the intensity of a pixel depends on the density of the tissue with respect to water. Therefore, distinct structures such as globe, nerve, muscle, and fat can be identified with a high accuracy. Extraocular muscle, bone, fat, and orbital volume indices are among the metrics used in previous study[2–15] as objective findings used to aide in early diagnosis.
Our novel analysis pipeline builds off multi-atlas segmentation methods. Briefly, a human expert labels the anatomical structures of interest in a set of representative training images (i.e., the atlases). The structures are identified in each target image by registering the training atlas and assigning a label to each voxel in the target image by statistical voting. Recent studies have shown that the multi-atlas methodology is suitable for identifying orbital structures [16–19]. However, challenges arise in the identification of the individual extraocular muscles that control eye movement. This is increasingly problematic in diseased eyes, where the muscles often appear to fuse (at the resolution of clinical CT) at the back of the orbit due to inflammation. We propose the use of Kalman filters to track the muscles in three-dimensions and identify individual extraocular rectus muscles. The purpose of our study is to investigate a method of automatically generating orbital metrics from CT imaging and correlating these to known clinical characteristics.
2. METHODOLOGY
2.1 Data
Subjects were selected based on both having met clinical criteria for thyroid eye disease and undergoing CT imaging as part of their regular clinical care. A total of 258 scans were acquired from 102 subjects, of which 24 (23.5%) were male. Variable CT imaging protocols (head, orbital, maxillofacial, etc.) were acquired and the highest resolution scan without severe orbital artifact and with a field of view including the full optic nerves was manually selected. Clinical characteristics including demographic information, ocular mobility, visual acuity, color vision, and visual field testing were recorded. Institutional Review Board approval for this retrospective study was obtained at Vanderbilt University.
Visual disability was assessed with the American Medical Association Functional Vision Score (FVS) which “provides criteria for evaluating permanent impairment of the visual system as it affects an individual’s ability to perform activities of daily living” as a percentage of disability relative to a healthy control[20]. The FVS is characterized by four sub-scores: an individual assessment of visual acuity in each eye, Visual Acuity Score (VAS); a composite of visual acuity over both eyes, Functional Acuity Score (FAS); individual assessment of field perception in each eye, Visual Field Score (VFS); and the composite of field perception over both eyes, Functional Field Score (FFS).
2.2 Multi-atlas segmentation
The selected CT image for each patient was loaded into eXtensible Neuroimaging Archive Toolkit [21, 22] and automatically segmented using a previously described multi-atlas segmentation pipeline which uses non-local STAPLE, a label fusion algorithm, to identify the optic nerves (including surrounding CSF sheaths), chiasm, rectus muscles, globes, and orbital bony structures [16, 23]. Briefly, segmentation followed a multi-atlas labeling framework[24] in which a set of manually labeled example scans were non-rigidly registered to each patient’s scan and statistical fusion was used to combine the labels from each of the examples to estimate the structure for each point in the target scan. Figure 1 (a) shows axial view of an input CT scan and 1 (b) shows the result of the multi-atlas segmentation pipeline.
Figure 1.
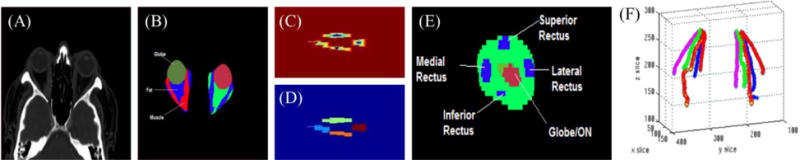
Muscle tracking using Kalman filters: (A) Input CT scan (B) output of label fusion (C) distance transform with imposed maxima (D) measured muscle pieces (E) Coronal view of muscles with respect to landmark (F) the resultant five Kalman filters, for each eye, tracking the muscles. Note that the muscles are well-separated in the front of the orbit (B), but as we approach the back of the orbit there is no longer a clean boundary between them due to inflammation and crowding. The measured positions at each slice are given by a watershed calculation as shown in (C) and segmented in (D). A distance function is calculated over slice z wherein the value of each pixel is given by the distance to its nearest non-zero pixel as shown in (C), creating a contour where there is a maxima at the center of each of the four muscles. At each slice, the algorithm examines the top, bottom, right, and left quadrants for each of the four muscles as see in (E). In total, ten Kalman filters (5 for each eye) are used to track the muscles (F), which results in the 3-D tracks shown in (F).
2.3 Kalman Filters
We use Kalman filters to identify the Superior Rectus Muscle, Inferior Rectus Muscle, Lateral Rectus Muscle and Medial Rectus Muscle from the muscle labels obtained from the multi-atlas segmentation pipeline shown in Figure 1(b). For each image volume, we start at a coronal slice at the center of the globe, where the muscles are well-separated, and use Kalman filters to track each muscle in the z-plane (anterior-posterior). The globe and the optic nerve pass through the center of the orbit and can be used as landmarks at each coronal slice to help identify the muscle positions. Five Kalman filters are defined for each of the four muscles and the landmarks. To keep the model simple, the centroids of the structures are used for tracking. Therefore, the state of system is the centroid of the two-dimensional slice in the coronal plane. The predicted state at slice z, given state z−1 is
| (1) |
where ε is the process error defined by covariance R. That is, the process expects the muscle/nerve structure to be in the same position within a margin of error. Note that the control vector is eliminated as the tracking “moves” in the z-plane at a constant rate. At each step, the measured positions are given by a watershed calculation on the distance transform of a coronal slice, as seen in Figures 1 (c) and (d). The predicted muscle positions of the previous step are used to impose a maxima on the distance transform. The current predicted position of each filter is then given by,
| (2) |
where δ is the measurement error defined by covariance Q.
For each image volume, a region of interest is selected as the set of all the coronal slices containing muscle, globe, and the optic nerve. A Kalman filter is initiated for the centroids of globe and optic nerve, which are used as landmarks to identify the initial muscle positions.
Initial labels for the rectus muscles are assigned based on their relative position to the landmark filter. Once the algorithm finds the first slice containing a rectus muscle, it initiates a Kalman filter for the muscle at that slice. The Kalman filter is then used to track that specific rectus muscle until the end of the orbit. The predicted mean , and variance of the state at each position are given by,
| (3) |
| (4) |
Here, A is the identity matrix and R is the process error covariance. The Kalman gain K is given by,
| (5) |
This yields a predicted position μz and variance σ:
| (6) |
| (7) |
where, C is the identity matrix and Q is the measurement covariance.
2.4 Automated Structural Metric Calculation
Following multi-atlas segmentation and extraction of individual rectus muscles using Kalman filters, we compute descriptive features from the segmentation of the orbital anatomy for each patient to assess correlations between functional or clinical data and structural measures. These features included the (1) volume, maximum diameter, and average diameter for the superior, inferior, medial, and lateral rectus muscles and total rectus muscle volume[10, 25–27]; (2) Barrett index[8]; (4) volume and diameter of the globe[11, 27–29]; (5) orbital volume; (6) volume crowding index[12]; (7) orbital angle; (8) degree of proptosis; and (9) length, volume, average area, and maximum diameter of the optic nerve[30, 31]. All metrics were performed bilaterally, which resulted in 24 measures for each eye.
3. RESULTS
Kalman filters provide a convenient mechanism to distinguish between individual rectus muscles in eye orbits segmented in the multi-atlas framework. Error covariance values for the process and the measurement are determined heuristically as follows:
| (8) |
| (9) |
Figure 2 shows representative final segmented images in two-dimensional and three-dimensional views. To assess the utility of this approach we compute geometrical metrics based on the identified orbital structures and see how they correlate with the subject’s clinical data which is routinely used in the diagnosis of ocular disease[9, 10], such as visual disability scores, ocular motility, hertel score, color vision and neuropathy.
Figure 2.
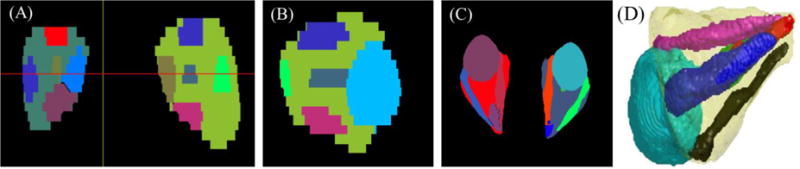
Representative segmentation in different views: (A) Coronal, (B) sagittal, (C) axial, and (D) 3-dimensional.
In this pilot study, we compute the correlation between structural metrics from the segmentations and clinical data using a Spearman correlation. The results of univariate correlations for orbital metrics (including orbital volume, volumetric crowding index[15], and proptosis) and optic nerve metrics (include length, cross sectional area, volume, and diameter) are shown in Table 1. Similarly, the correlations for clinical characteristics with muscle metrics are shown in Table 2. Notice from Table 1 that Hertel measurements demonstrated strong correlation with nearly all optic nerve and orbital metrics. Additional findings included a strong correlation between visual acuity and volumetric crowding index and between smoking and degree of proptosis.
Table 1.
Spearman rho correlations of orbital and optic nerve metrics with clinical characteristics
| Visual Acuity | Color Vision Score | Smoking (no, current, former) | Motility Defect (No, Yes) | Hertel Score | Optic neuropathy (No, Yes) | Best Corrected Visual Acuity | Visual Acuity Score | Functional Acuity Score | Visual Field Score | Functional Field Score | Functional Vision Score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrett Index | −0.02 | −0.06 | 0.08 | 0.20 | −0.04 | 0.04 | 0.11 | −0.14 | −0.13 | −0.05 | 0.02 | −0.09 |
| Globe Volume | −0.15 | 0.06 | −0.09 | 0.11 | −0.06 | −0.16 | 0.22 | −0.16 | −0.01 | 0.00 | −0.07 | −0.02 |
| Globe Diameter | −0.15 | 0.06 | −0.09 | 0.11 | −0.06 | −0.16 | 0.22 | −0.16 | −0.01 | 0.00 | −0.07 | −0.02 |
| ON Length | 0.06 | −0.11 | 0.06 | 0.05 | 0.16 | −0.02 | −0.13 | 0.09 | 0.10 | 0.10 | 0.18 | 0.13 |
| ON Length Traditional | 0.09 | −0.11 | 0.09 | −0.01 | 0.27 | −0.04 | −0.18 | 0.12 | 0.10 | 0.06 | 0.15 | 0.12 |
| ON Volume | −0.04 | 0.01 | 0.01 | 0.03 | −0.14 | −0.08 | 0.27 | −0.25 | −0.16 | −0.09 | 0.03 | −0.09 |
| ON Avg Area | −0.05 | −0.04 | −0.06 | 0.01 | −0.21 | −0.09 | 0.29 | −0.24 | −0.18 | −0.13 | 0.02 | −0.11 |
| ON Max Diameter | 0.00 | −0.03 | −0.07 | 0.07 | −0.20 | −0.11 | 0.18 | −0.12 | −0.09 | −0.11 | 0.02 | −0.07 |
| Orbital Volume | 0.02 | −0.14 | 0.12 | 0.17 | 0.28 | −0.04 | 0.02 | −0.06 | −0.05 | 0.15 | 0.01 | −0.06 |
| Volumetric Crowding Index | −0.16 | 0.04 | −0.10 | 0.01 | −0.24 | −0.07 | 0.19 | −0.18 | −0.11 | −0.10 | 0.06 | −0.08 |
| Proptosis | 0.01 | 0.11 | 0.18 | 0.03 | 0.21 | 0.07 | −0.09 | 0.10 | 0.06 | 0.09 | −0.04 | 0.01 |
| Angle | −0.11 | −0.02 | −0.03 | 0.06 | 0.14 | 0.03 | 0.12 | −0.11 | −0.08 | −0.14 | −0.11 | −0.12 |
Note that yellow highlights indicate a p value less than 0.1, and green indicate p value less than 0.05
Table 2.
Spearman rho correlations of muscle metrics with clinical characteristics.
| Visual Acuity | Color Vision Score | Smoking (no, current, former) | Motility Defect (No, Yes) | Hertel Score | Optic neuropathy (No, Yes) | Best Corrected Visual Acuity | Visual Acuity Score | Functional Acuity Score | Visual Field Score | Functional Field Score | Functional Vision Score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Superior Muscle Volume | −0.07 | −0.18 | 0.01 | 0.11 | −0.13 | −0.04 | 0.18 | −0.17 | −0.15 | −0.04 | −0.09 | −0.14 |
| Inferior Muscle Volume | −0.01 | −0.04 | 0.11 | 0.17 | −0.03 | −0.09 | 0.02 | −0.05 | −0.03 | −0.05 | 0.07 | 0.01 |
| Lateral Muscle Volume | −0.07 | −0.07 | 0.11 | 0.15 | 0.06 | −0.01 | 0.00 | −0.06 | −0.05 | −0.07 | −0.07 | −0.01 |
| Medial Muscle Volume | −0.07 | −0.10 | 0.05 | 0.12 | 0.04 | −0.02 | 0.10 | −0.17 | −0.18 | −0.11 | −0.04 | −0.16 |
| Superior Muscle Diameter Avg | −0.11 | −0.11 | 0.02 | 0.16 | −0.02 | 0.03 | 0.21 | −0.19 | −0.18 | −0.02 | −0.12 | −0.18 |
| Inferior Muscle Diameter Avg | −0.12 | −0.08 | 0.11 | 0.20 | 0.05 | −0.04 | 0.00 | 0.00 | 0.02 | −0.05 | 0.07 | 0.09 |
| Lateral Muscle Diameter Avg | −0.05 | −0.07 | 0.09 | 0.19 | 0.06 | −0.02 | 0.02 | −0.07 | −0.09 | −0.04 | −0.06 | −0.03 |
| Medial Muscle Diameter Avg | −0.11 | −0.10 | 0.05 | 0.11 | 0.02 | 0.03 | 0.15 | −0.21 | −0.21 | −0.14 | −0.07 | −0.18 |
| Superior Muscle Diameter Max | −0.12 | −0.20 | −0.01 | 0.14 | 0.01 | 0.09 | 0.17 | −0.16 | −0.15 | 0.02 | −0.08 | −0.15 |
| Inferior Muscle Diameter Max | −0.11 | −0.18 | 0.15 | 0.26 | 0.11 | 0.00 | −0.01 | −0.04 | −0.14 | −0.02 | 0.00 | −0.08 |
| Lateral Muscle Diameter Max | −0.08 | −0.11 | 0.13 | 0.17 | 0.08 | 0.02 | 0.09 | −0.14 | −0.15 | −0.03 | −0.10 | −0.10 |
| Medial Muscle Diameter Max | −0.09 | −0.14 | 0.02 | 0.08 | 0.02 | −0.04 | 0.11 | −0.14 | −0.10 | −0.12 | 0.02 | −0.07 |
| Total Muscle Volume | −0.08 | −0.10 | 0.06 | 0.16 | 0.02 | −0.03 | 0.08 | −0.12 | −0.10 | −0.05 | −0.04 | −0.06 |
Note that yellow highlights indicate a p value less than 0.1, and green indicate p value less than 0.05.
Several extraocular muscle metrics including average diameter, maximum diameter, and muscle volume of the superior rectus, inferior rectus, and lateral rectus demonstrated strong correlation (p-value <0.05) with the presence of ocular motility deficit. On the other hand, medial rectus muscle demonstrated only a mild correlation with motility deficit. Color vision measurements demonstrated strong correlation (p-value <0.05) with inferior rectus, medial rectus, and superior rectus muscle maximum diameters while demonstrating a mild correlation (p-value = 0.056) with the lateral rectus maximum diameter. Additional findings included a strong correlation between visual acuity and superior rectus maximum diameter.
4. DISCUSSION
Identifying the individual ocular structures has significant advantages for the diagnosis, analysis and study of ocular diseases. Traditional methods of orbital segmentation are manual and tedious, or cannot capture the 3-D structure of orbital anatomy. In this study, we have shown the significant structural-functional correlations of the orbital structures such as muscles, the optic nerve, and eye globe with visual function and other clinical data. Further, we highlight the importance of studying each muscle separately by establishing that they have varying degrees of predictive power. We demonstrate that Kalman filters provide a simple, yet fast and efficient solution to improving muscle segmentation in diseased eye. The strong correlation demonstrated by several clinical characteristics with the automatically obtained orbital metrics serves as foundation for further investigation. In future study, machine learning methods can be employed to find latent features in these structures and robust models of disease and treatment can be built based on these algorithms.
Acknowledgments
This project was supported by NIH 5R21EY024036 (Landman) and the National Center for Research Resources, Grant UL1 RR024975-01 (now at the National Center for Advancing Translational Sciences, Grant 2 UL1 TR000445-06). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. Supported in part by an unrestricted grant to the Vanderbilt Eye Institute and Physician Scientist Award from Research to Prevent Blindness, New York, NY. This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN.
References
- 1.Müller-Forell W, Kahaly GJ. Neuroimaging of Graves’ orbitopathy. Best Practice & Research Clinical Endocrinology & Metabolism. 2012;26(3):259–271. doi: 10.1016/j.beem.2011.11.009. [DOI] [PubMed] [Google Scholar]
- 2.Kennerdell JS, Rosenbaum AE, El-Hoshy MH. APical optic nerve compression of dysthyroid optic neuropathy on computed tomography. Archives of Ophthalmology. 1981;99(5):807–809. doi: 10.1001/archopht.1981.03930010807002. [DOI] [PubMed] [Google Scholar]
- 3.Feldon SE, Weiner JM. Clinical significance of extraocular muscle volumes in graves; ophthalmopathy: A quantitative computed tomography study. Archives of Ophthalmology. 1982;100(8):1266–1269. doi: 10.1001/archopht.1982.01030040244006. [DOI] [PubMed] [Google Scholar]
- 4.Feldon SE, et al. Quantitative computed tomography of graves' ophthalmopathy: Extraocular muscle and orbital fat in development of optic neuropathy. Archives of Ophthalmology. 1985;103(2):213–215. doi: 10.1001/archopht.1985.01050020065021. [DOI] [PubMed] [Google Scholar]
- 5.Barrett L, et al. Optic nerve dysfunction in thyroid eye disease: CT. Radiology. 1988;167(2):503–507. doi: 10.1148/radiology.167.2.3357962. [DOI] [PubMed] [Google Scholar]
- 6.Hallin ES, Feldon SE. Graves’ ophthalmopathy: I. Simple CT estimates of extraocular muscle volume. British Journal of Ophthalmology. 1988;72(9):674–677. doi: 10.1136/bjo.72.9.674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Giaconi JA, et al. CT Scan Evidence of Dysthyroid Optic Neuropathy. Ophthalmic Plastic & Reconstructive Surgery. 2002;18(3):177–182. doi: 10.1097/00002341-200205000-00005. [DOI] [PubMed] [Google Scholar]
- 8.Monteiro MLR, et al. Diagnostic ability of barrett’s index to detect dysthyroid optic neuropathy using multidetector computed tomography. Clinics. 2008;63:301–306. doi: 10.1590/S1807-59322008000300003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chan LL, et al. Graves ophthalmopathy: the bony orbit in optic neuropathy, its apical angular capacity, and impact on prediction of risk. AJNR American journal of neuroradiology. 2009;30(3):597–602. doi: 10.3174/ajnr.A1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Weis E, et al. Clinical and soft-tissue computed tomographic predictors of dysthyroid optic neuropathy: Refinement of the constellation of findings at presentation. Archives of Ophthalmology. 2011;129(10):1332–1336. doi: 10.1001/archophthalmol.2011.276. [DOI] [PubMed] [Google Scholar]
- 11.Weis E, et al. Quantitative Computed Tomographic Predictors of Compressive Optic Neuropathy in Patients with Thyroid Orbitopathy: A Volumetric Analysis. Ophthalmology. 2012;119(10):2174–2178. doi: 10.1016/j.ophtha.2012.04.021. [DOI] [PubMed] [Google Scholar]
- 12.Gonçalves ACP, et al. Quantification of orbital apex crowding for screening of dysthyroid optic neuropathy using multidetector CT. AJNR. American journal of neuroradiology. 2012;33(8):1602–1607. doi: 10.3174/ajnr.A3029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Al-Bakri M, et al. Orbital Volumetry in Graves’ Orbitopathy: Muscle and Fat Involvement in relation to Dysthyroid Optic Neuropathy. ISRN ophthalmology. 2014;2014:435276. doi: 10.1155/2014/435276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lima BdR, Perry JD. Superior Ophthalmic Vein Enlargement and Increased Muscle Index in Dysthyroid Optic Neuropathy. Ophthalmic Plastic & Reconstructive Surgery. 2013;29(3):147–149. doi: 10.1097/IOP.0b013e3182831bd8. [DOI] [PubMed] [Google Scholar]
- 15.Gonçalves ACP, et al. Predicting dysthyroid optic neuropathy using computed tomography volumetric analyses of orbital structures. Clinics. 2012;67:891–896. doi: 10.6061/clinics/2012(08)06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Harrigan RL, et al. Robust optic nerve segmentation on clinically acquired computed tomography. Journal of Medical Imaging. 2014;1(3):034006–034006. doi: 10.1117/1.JMI.1.3.034006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gensheimer M, et al. Automatic delineation of the optic nerves and chiasm on CT images. 2007 [Google Scholar]
- 18.Isambert A, et al. Evaluation of an atlas-based automatic segmentation software for the delineation of brain organs at risk in a radiation therapy clinical context. Radiotherapy and Oncology. 2008;87(1):93–99. doi: 10.1016/j.radonc.2007.11.030. [DOI] [PubMed] [Google Scholar]
- 19.Heckemann RA, et al. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- 20.Rondinelli RD, et al. Guides to the evaluation of permanent impairment. American Medical Association; 2008. [Google Scholar]
- 21.Harrigan RL, et al. Vanderbilt University Institute of Imaging Science Center for Computational Imaging XNAT: A multimodal data archive and processing environment. NeuroImage. doi: 10.1016/j.neuroimage.2015.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marcus D, et al. The extensible neuroimaging archive toolkit. Neuroinformatics. 2007;5(1):11–33. doi: 10.1385/ni:5:1:11. [DOI] [PubMed] [Google Scholar]
- 23.Panda S, et al. Robust optic nerve segmentation on clinically acquired CT. 2014 doi: 10.1117/12.2043715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Asman AJ, Landman BA. Non-local statistical label fusion for multi-atlas segmentation. Medical Image Analysis. 2013;17(2):194–208. doi: 10.1016/j.media.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hallin ES, Feldon SE. Graves’ ophthalmopathy: II. Correlation of clinical signs with measures derived from computed tomography. The British journal of ophthalmology. 1988;72(9):678–682. doi: 10.1136/bjo.72.9.678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ozgen A, Ariyurek M. Normative measurements of orbital structures using CT. AJR American journal of roentgenology. 1998;170(4):1093–1096. doi: 10.2214/ajr.170.4.9530066. [DOI] [PubMed] [Google Scholar]
- 27.Szucs-Farkas Z, et al. Using morphologic parameters of extraocular muscles for diagnosis and follow-up of Graves’ ophthalmopathy: diameters, areas, or volumes? AJR American journal of roentgenology. 2002;179(4):1005–1010. doi: 10.2214/ajr.179.4.1791005. [DOI] [PubMed] [Google Scholar]
- 28.Tian S, et al. MRI measurements of normal extraocular muscles and other orbital structures. Graefe’s Archive for Clinical and Experimental Ophthalmology. 2000;238(5):393–404. doi: 10.1007/s004170050370. [DOI] [PubMed] [Google Scholar]
- 29.Pearce E, Bridge H. Is orbital volume associated with eyeball and visual cortex volume in humans? Annals of Human Biology. 2013;40(6):531–540. doi: 10.3109/03014460.2013.815272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rubin PAD, et al. Orbital computed tomographic characteristics of globe subluxation in thyroid orbitopathy. Ophthalmology. 1998;105(11):2061–2064. doi: 10.1016/S0161-6420(98)91125-3. [DOI] [PubMed] [Google Scholar]
- 31.Peyster RG, et al. High-resolution CT of lesions of the optic nerve. AJR American journal of roentgenology. 1983;140(5):869–874. doi: 10.2214/ajr.140.5.869. [DOI] [PubMed] [Google Scholar]


