Filling-enforced quantum band insulators in spin-orbit coupled crystals

Quantum effects produce a band insulator with fewer electrons than permitted in any classical picture.

Abstract

An early triumph of quantum mechanics was the explanation of metallic and insulating behavior based on the filling of electronic bands. A complementary, classical picture of insulators depicts electrons as occupying localized and symmetric Wannier orbitals that resemble atomic orbitals. We report the theoretical discovery of band insulators for which electron filling forbids such an atomic description. We refer to them as filling-enforced quantum band insulators (feQBIs) because their wave functions are associated with an essential degree of quantum entanglement. Like topological insulators, which also do not admit an atomic description, feQBIs need spin-orbit coupling for their realization. However, they do not necessarily support gapless surface states. Instead, the band topology is reflected in the insulating behavior at an unconventional filling. We present tight binding models of feQBIs and show that they only occur in certain nonsymmorphic, body-centered cubic crystals.

INTRODUCTION

Consider a system of noninteracting electrons. When does a band insulator arise? There are two approaches to answering this question. The first approach is a position-space description in which the immobility of electrons is rationalized by localizing them either to atoms or bonding orbitals, corresponding to ionic and covalent compounds. The second approach emphasizes the quantum mechanical wave nature of electrons and analyzes the situation from a momentum-space perspective, in which the insulating behavior arises when all states below a band gap are filled.

The two pictures do not have to agree, as exemplified by the existence of Chern insulators (1, 2) and topological insulators (TIs) (3, 4). Nonetheless, it is generally believed that by tuning parameters in the Hamiltonian while preserving symmetries, any nontrivial band insulator can be deformed into a reference atomic insulator (AI) through an intervening phase transition (3).

Here, we argue that the aforementioned common belief concerning band insulators does not necessarily hold in the presence of time reversal (TR) and certain space group (SG) symmetries. We establish theoretically that in systems with spin-orbit coupling (SOC), there are filling-enforced quantum band insulators (feQBIs) realized at electron fillings ν for which no reference AI with the same symmetries can exist. Existence of feQBIs can be exposed by analyzing the possible insulator fillings in position- and momentum-space.

RESULTS

Atomic versus band insulators

First, consider the position-space approach. We could imagine localizing electrons at specific points in space, corresponding to the limiting case of an AI. To ensure TR symmetry, the total spin per point has to be integer, and hence, we must localize electrons in pairs. The points must also form an SG-symmetric lattice. Note that in a symmetric “valence bond” state, the electron positions can be smoothly deformed to the center of mass of each valence bond, which reduces to the above point-like picture (Supplementary Materials). The electron fillings consistent with an AI can then be determined by analyzing the possible number of lattice points in such lattices. For any SG, this can be inferred from the tabulated crystallographic information known as “Wyckoff positions” (5) (Supplementary Materials). In particular, for each SG, there is a minimum filling ${\mathrm{\nu }}_{\text{min}}^{\text{AI}}$ for which AIs become possible.

The second approach is to consider band structures in momentum space. The minimal filling for forming a band insulator, ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}$, is the smallest number of connected bands isolatable from all other bands. This can be analyzed using the momentum-space representations of the SG (6). While Kramers degeneracy ensures ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}$ is even, further band degeneracies can be forced by the SG, raising the minimum filling ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}\text{to be greater than} 2$. In particular, the class of free electron problems contains AIs, and hence for any SG ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}\le {\mathrm{\nu }}_{\text{min}}^{\text{AI}}$. Do ${\mathrm{\nu }}_{\text{min}}^{\text{AI}}$ and ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}$ always agree? Here, we answer this question in the negative: There exist SGs for which TR-symmetric band insulators can appear at a filling smaller than that required for any AI, provided that SOC is nonnegligible. A band insulator realized at such “subatomic” filling is necessarily nonatomic, and hence the name feQBI. While feQBIs may seem superficially similar to Mott insulators, which also appear at nonatomic filling, they do not require interactions.

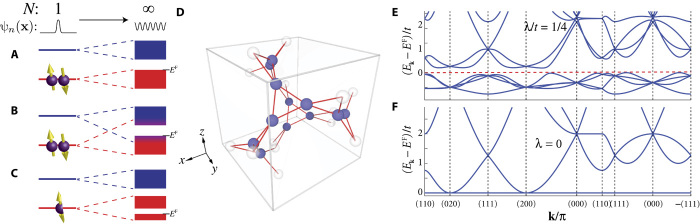
Before turning to examples of feQBIs, we emphasize their quantum nature. If electrons behaved classically, like the atomic cores, they would be forced to occupy well-defined positions in space. In this picture, systems with nonatomic fillings cannot respect all symmetries. Thanks to quantum interference, however, electrons can evade such dilemma by remaining insulating despite being delocalized (Fig. 1, A to C).

Fig. 1. Filling-enforced quantum band insulators.

(A to C) Schematic band diagrams. Starting from a “primitive motif,” one can generate a crystal by repeating it according to the SG symmetries. Depending on the nature of the material, the motif can correspond to atoms, molecules, or bonding orbitals. Band theory accounts for how the electronic levels evolve when the number of motifs N is varied from 1 to ∞, during which the single-particle electronic wave function ${\mathrm{\psi }}_{\mathit{n}}(\overrightarrow{\mathit{x}})$ evolves from localized to delocalized. (A) In a strict AI, the set of filled bands, as indicated by the Fermi energy E^F, has a natural correspondence to the filled electronic level of a single motif and therefore admits an equally valid classical, localized representation. (B) For a general band insulator (including all previously known quantum band insulators), a set of electronic levels are fully filled in the single-motif limit, although the filled bands do not have a simple correspondence with them. (C) feQBIs are crystals in which no symmetry-respecting choice of motif will have fully filled local energy levels, but nonetheless, a band insulator is made possible by quantum mechanical interference of the electron waves. (D) Nearest-neighbor hyperkagome lattice considered in Eq. 1 for SG No. 199. Blue spheres correspond to sites assigned to the displayed conventional cubic unit cell, which has twice the volume of a primitive unit cell. Transparent spheres represent sites in adjacent cells. (E and F) Example band structures for the tight-binding model in Eq. 1 with filling ν = 4. The lattice constant is set to 1. With spin-orbit coupling in (E), the system is insulating and forms an feQBI. When spin-orbit coupling is switched off in (F), the lowest four bands are completely flat and touch the upper bands at $\overrightarrow{\mathit{k}}=(0,0,2\mathrm{\pi })$, rendering the system semimetallic.

Example of an feQBI

We now provide an explicit example of feQBIs, which was found by a systematic study of all 230 SGs. An interesting observation is that for almost all SGs, one can see from their Wyckoff positions that the number of sites required to form an SG-symmetric lattice is always an integer multiple of the minimum number, implying ${\mathrm{\nu }}^{\text{AI}}\in {\mathrm{\nu }}_{\text{min}}^{\text{AI}}\mathbf{\mathbb{N}}$. However, there are four exceptions: SG Nos. 199, 214, 220, and 230 (Table 1). We term such SGs as “Wyckoff-mismatched.”

Table 1. feQBIs in the four Wyckoff-mismatched SGs.

“Wyckoff multiplicities” denotes the number of lattice points per primitive unit cell required to form an SG symmetric lattice corresponding to one of the Wyckoff positions. ν^AI and ν^Band respectively denote the electron fillings consistent with atomic and band insulators, and their discrepancy corresponds to feQBIs.

Space group	Wyckoff multiplicities (5)	νAI	νBand
No. 199 (I 213)	4, 6, 12	4ℕ\{4}	4ℕ
No. 214 (I 4132)	4, 4, 6, 6, 8, 12, 12, 12, 24	4ℕ\{4}	4ℕ
No. 220 (I $\overline{4}$ 3d)	6, 6, 8, 12, 24	4ℕ\{4, 8, 20}	4ℕ\{4}
No. 230 (I a $\overline{3}$ d)	8, 8, 12, 12, 16, 24, 24, 48	8ℕ\{8}	8ℕ

The simplest of the four Wyckoff-mismatched SGs is No. 199, which allows for AIs whenever ν ∈ 4ℕ except for ν = 4, giving ${\mathrm{\nu }}_{\text{min}}^{\text{AI}}=8$. Yet, we discovered that feQBI is indeed possible at ν = 4 (Supplementary Materials), that is, ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}=4<{\mathrm{\nu }}_{\text{min}}^{\text{AI}}=8$. For concreteness, we construct below a simple feQBI tight-binding model. Consider the SG-symmetric lattice generated by the point ${\overrightarrow{\mathit{r}}}^1=(1/8,1,1/4)$, which takes the hyperkagome structure with six sites in each primitive unit cell (Fig. 1D). We consider an s-orbital on each site and denote the electron operators by ${\mathit{f}}_{\overrightarrow{\mathit{x}}}^{\mathit{l}\mathit{s}†}$, where $\overrightarrow{\mathit{x}}$ and l respectively label the unit cells and the sites within, and s = ↑, ↓ corresponds to up and down spin quantized along the crystalline z axis. Note that the choice of the site label l is not unique, and our convention is discussed in the Supplementary Materials.

The SG-symmetric tight-binding Hamiltonian can be constructed by applying all the symmetries in the SG to a single term h₀, that is

$$\mathit{H}={\displaystyle \sum _{\mathit{g}\in \text{SG}}}\widehat{\mathit{g}}{\mathit{h}}_0{\widehat{\mathit{g}}}^{-1}; {\mathit{h}}_0={\mathit{f}}_{\overrightarrow{\mathit{x}}}^{4\mathit{s}\prime †}(\mathit{t}{\mathrm{\delta }}_{\mathit{s}\prime \mathit{s}}+\mathit{i}\mathrm{\lambda }{({\mathrm{\sigma }}^{\mathit{z}})}_{\mathit{s}\prime \mathit{s}}){\mathit{f}}_{\overrightarrow{\mathit{x}}}^{1\mathit{s}}+ \text{h.c.}$$ (1)

where “h.c.” denotes Hermitian conjugate, repeated indices are summed over, and the sum over g ∈ SG includes all terms generated under SG symmetries. Note that λ is a SOC term, and H is TR-symmetric when the parameters t and λ are real. h₀ corresponds to a nearest-neighbor hopping term; for simplicity, we have not included all the symmetry-allowed terms. A detailed tabulation of the various terms in the Hamiltonian is provided in table S5.

As shown in Fig. 1E, when λ/t = 1/4, the system is a band insulator at filling $\mathrm{\nu }=4<8={\mathrm{\nu }}_{\text{min}}^{\text{AI}}$. This simple observation alone establishes the existence of feQBIs.

Before proceeding, we note the following points. Without SOC (λ = 0), the system at ν = 4 is semimetallic (Fig. 1F). This is in fact the manifestation of a more general result: No feQBI is allowed when spin-rotation invariance is restored (7). The lower four bands are also completely flat because Eq. 1 describes a nearest-neighbor tight-binding model defined on the frustrated hyperkagome lattice. In contrast to the flat bands of the kagome lattice, for example, here they cannot correspond to localized, SG symmetric orbitals because of the non-atomic filling.

Entanglement spectrum of the “spin-orbital entanglement cut”

In the following, we argue that the quantum mechanical nature of feQBIs can be diagnosed through quantum entanglement, the defining feature of quantum mechanics. Imagine dividing the system in position space into two halves and grouping the degrees of freedom into A and Ā. One can resolve the ground state wave function into a tensor product of basis states on A and Ā as $|\mathrm{\Psi }\rangle ={\displaystyle \sum _{\mathrm{\alpha }}}{\mathit{e}}^{-{\mathcal{E}}_{\mathrm{\alpha }}/2}|{\mathit{A}}_{\mathrm{\alpha }}\rangle \otimes |{\overline{\mathit{A}}}_{\mathrm{\alpha }}\rangle$. The coefficients $\mathcal{E}$_α in this expansion are termed the entanglement spectrum. A simple product state of well-localized orbitals, as for a strict AI, will only have a single finite ${\mathcal{E}}_{\mathrm{\alpha }}$, indicating the absence of entanglement. In contrast, for quantum band insulators, a symmetric, localized AI picture is forbidden, and the entanglement spectrum must look qualitatively different to encode the irremovability of quantum entanglement. Indeed, it is known that the entanglement spectrum of a TI is gapless, reflecting the irremovable entanglement.

The irremovability of entanglement is more subtle for feQBIs, which are protected by body-centered cubic, nonsymmorphic SG symmetries that will be broken at any naïve spatial cut. Hence, we need a new approach to probe their irremovable entanglement. To this end, we devise a novel “spin-orbital entanglement cut” (SE cut) that preserves all symmetries and differentiates unequivocally AIs from feQBIs. More concretely, we let subsystem A = ⇑ be the collection of spin “up” electrons (Fig. 2A), chosen in a way to respect both TR and SG symmetries (Supplementary Materials).

Fig. 2. SE cut and entanglement spectrum.

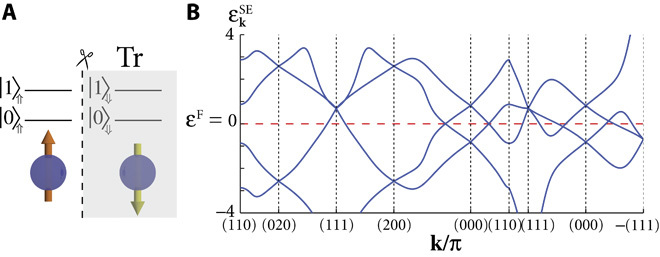
(A) Schematic of the SE cut in which the occupancy of one spin species (say ⇓) is traced over. (B) Example SE cut spectrum for the feQBI model of SG No. 199. As detailed in the Supplementary Materials, the entanglement band structure inherits little group representations from the physical bands, and TR symmetry is realized in a “particle-hole” manner. These together force an unavoidable gaplessness about ε^F (dashed line).

For free fermion problems, the entanglement spectrum {${\mathcal{E}}_{\mathrm{\alpha }}$} is constructible from the single-particle version {ε_α} (8–11). In particular, the SE cut respects translation invariance, and hence, the “entanglement bands” ${\mathrm{\epsilon }}_{\overrightarrow{\mathit{k}}}^{\text{SE}}$ are defined on the entire three-dimensional (3D) Brillouin zone. Generally, ${\mathrm{\epsilon }}_{\overrightarrow{\mathit{k}}}^{\text{SE}}$ inherits symmetry representations from the physical bands, although TR is now realized as a unitary, particle-hole like symmetry on the entanglement spectrum. For an AI, the spin-orbital entanglement gap about the “entanglement Fermi level” ε^F = 0 can be deformed to infinity. However, as shown in Fig. 2B, for the ν = 4 feQBI in SG No. 199, SG and TR symmetries together force an entanglement band to cross ε^F between (π, π, π) and − (π, π, π) (Supplementary Materials). This translates into a symmetry-protected gaplessness of the entanglement Hamiltonian and implies that the feQBI has irremovable spin-orbital entanglement.

DISCUSSION

Considering that we have focused on SG No. 199 to illustrate the existence and novelty of feQBIs, it is natural to ask if feQBIs can exist in systems with other SG symmetries. We have performed a comprehensive study, and the results will be presented elsewhere (7). Here, we note that when the system has spin-rotation invariance, ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}={\mathrm{\nu }}_{\text{min}}^{\text{AI}}$ for all SGs; however, with SOC ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}={\mathrm{\nu }}_{\text{min}}^{\text{AI}}$ for all but the four Wyckoff-mismatched SGs: Nos. 199, 214, 220, and 230. These four SGs admit feQBIs at ${\mathrm{\nu }}_{\text{min}}^{\text{Band}}$ = 4, 4, 8, and 8, respectively. It appears that feQBI arises from the interplay between Wyckoff-mismatch and the spin-1/2 nature of electrons. Understanding this link is an interesting problem we leave for future investigation.

What are the physical manifestations of an feQBI? TIs, for example, have protected surface states. We note that whereas protected surface states may occur in feQBIs, they are not necessary. For example, the feQBI model in Eq. 1 with λ/t = 1/4 and filling ν = 4 happens to also be a strong TI and, therefore, has gapless surface states. However, other feQBI examples can be shown to have trivial strong and weak indices. Because the Wyckoff-mismatched SGs all have SG symmetries that are broken by the existence of any surface, the existence of gapless surface states is not mandated by the topological bulk, as explicitly demonstrated in the Supplementary Materials. Therefore, finding physical bulk signatures of feQBIs is an important open question. As suggested by the irremovable spin-orbital entanglement demonstrated here, feQBIs may also show interesting signatures in probes such as spin- and angle-resolved photoemission spectroscopy. Understanding the physical manifestation of feQBIs in various spin-resolved probes is therefore an important direction for future investigations.

We further remark that feQBIs can be distinguished from Mott insulators at the same filling—the latter will necessarily feature local moment physics at intermediate temperature scales, having either a symmetry-breaking ground state or exotic excitations at low energies. In contrast, feQBIs can arise even in weakly correlated systems where such signatures will be absent.

Recently, various studies on the interplay between nonsymmorphic symmetries and topological phases of noninteracting electrons have emerged (12–15). We note here that feQBI is intrinsically different from the topological nonsymmorphic crystalline phases already studied in the literature. In particular, several studies (12–14) investigate bulk band topology by the stability of the surface gapless modes, whereas Varjas et al.’s study (15) focuses on the quantized magnetoelectric response of a system with a single glide plane symmetry. In contrast, the nontrivial nature of feQBIs is established using the full set of SG and TR symmetries, instead of studying the consequences of a single nonsymmorphic symmetry operation (13–15) or the surface symmetries (12). Most importantly, feQBIs are signaled by the electron filling, which has no analog in these previous works. An interesting open question is to identify the topological invariants classifying feQBIs within the K-theory framework (16).

We close by discussing possible material realizations. As indicated here, one should consider a system with significant SOC in SG No. 199 or 214 with ν = 4 (disregarding core electrons tightly bounded to atoms) or in SG No. 220 or 230 with ν = 8. In addition, the energy bands relevant near the Fermi energy should contain the correct symmetry representations needed (Supplementary Materials). Here, we point out that the celebrated spin-liquid candidate (17) Na₄Ir₃O₈ features significant SOC and crystallizes in SG No. 213 with a hyperkagome structure (18), the simple-cubic version of the Wyckoff-mismatched SG No. 214. Its hole-doped cousin Na₃Ir₃O₈ (19) comes even closer to providing the required ingredients. In its synthesized form, the iridium atoms sit at the symmetric-lattice generated by (1/8, y, y + 1/4) with the parameter y = −0.113 (19). By changing the parameter to y = 0 (and altering the other atom positions; see the Supplementary Materials), the symmetry can be increased from SG No. 213 to 214 and the electron filling is effectively ν = 4, giving rise to an feQBI in certain parameter regions. Although the above scenario relies on a hypothetical structure of Na₃Ir₃O₈, it illustrates the setting for which feQBIs can be realized. An important future direction is to identify realistic material realizations.

MATERIALS AND METHODS

Irremovable spin-orbital entanglement of feQBI in SG No. 199

The entanglement spectrum is determined from the single-particle entanglement Hamiltonian h^SE = log(C⁻¹ − 1) (8–11), where ${\mathit{C}}_{\mathit{i}\mathit{j}}=\langle \mathrm{\Psi }|{\mathit{f}}_{\mathit{i}}^{†}{\mathit{f}}_{\mathit{j}}|\mathrm{\Psi }\rangle$ is the correlation matrix and i and j are restricted to degrees of freedom in A = ⇑. Note that C is nothing but the projector onto occupied bands further projected onto A. In contrast to a spatial cut, which introduces a boundary, h^SE behaves like a local Hamiltonian throughout the entire bulk. ${\mathrm{\epsilon }}_{\overrightarrow{\mathit{k}}}^{\text{SE}}$ therefore inherits symmetry representations from the physical bands. In particular, at momenta (π, π, π) and −(π, π, π), the four bands split into a pair of 3D and 1D symmetry representations. In addition, TR is realized as a unitary, particle-hole like symmetry on the entanglement Hamiltonian, which forces an entanglement band to cross ε^F = 0 along (π, π, π) to −(π, π, π) (Supplementary Materials).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501782/DC1

Electron filling in AIs

Symmetries of SG No. 199

feQBI tight-binding examples

Hypothetical structure for spin-orbit coupled hyperkagome material Na₃Ir₃O₈

Discussions on the SE cut

Fig. S1. Reproduction of Fig. 1D with different viewing conditions and extra annotation.

Fig. S2. Energy and entanglement band structure for an alternative feQBI example for SG No. 199.

Fig. S3. Plot of band gap for the hyperkagome model in eq. S3 at filling ν = 4.

Fig. S4. Plot of surface band structure against the surface crystal momentum ${\overrightarrow{\mathit{k}}}_{||}$ for the model in eq. S3.

Table S1. List of symmetry elements for SG No. 199.

Table S2. Spin-quantization axes corresponding to the SG symmetric spin texture.

Table S3. Symmetry eigenvalues of the irreducible little group representations at high-symmetry momenta.

Table S4. Transformation of tight-binding sites under the symmetry elements.

Table S5. A full list of terms in the feQBI tight-binding example given in the text.

Table S6. Terms in an alternative eight-band feQBI tight-binding example.

Table S7. Measured structure of Na₃Ir₃O₈ by Takayama et al. (19).

Table S8. “Symmetry-enriched” hypothetical structure of Na₃Ir₃O₈ in SG No. 214.