A Bayesian Hierarchical Framework for Modeling Brain Connectivity for Neuroimaging Data

Summary

We propose a novel Bayesian hierarchical model for brain imaging data that unifies voxel level (the most localized unit of measure) and region level brain connectivity analyses, and yields population level inferences. Functional connectivity generally refers to associations in brain activity between distinct locations. The first level of our model summarizes brain connectivity for cross-region voxel pairs using a two component mixture model consisting of connected and non-connected voxels. We use the proportion of connected voxel pairs to define a new measure of connectivity strength, which reflects the breadth of between-region connectivity. Furthermore, we evaluate the impact of clinical covariates on connectivity between region-pairs at a population level. We perform parameter estimation using Markov chain Monte Carlo (MCMC) techniques, which can be executed quickly relative to the number of model parameters. We apply our method to resting-state functional magnetic resonance imaging (fMRI) data from 32 subjects with major depression and simulated data to demonstrate the properties of our method.

1. Introduction

Functional brain connectivity refers to associations between neural processing units from distinct brain locations. Specific patterns of connectivity may be linked to corresponding actions, emotions, cognition, or resting-state (reflecting default mode of neural processing). Disruptions to these connectivity patterns are often associated with psychiatric and neurological disorders. Functional magnetic resonance imaging (fMRI) enables the assessment of functional connectivity by calculating the temporal coherence of neural activity measures arising from spatially distinct regions of the brain. There are several connectivity metrics available to measure the coherence of the temporal profiles. Examples include Pearson correlation; spectral coherence, which measures the coherence between the two temporal profiles in the frequency domain and mutual information, which measures the mutual dependence between the random variables giving rise to the observed two time series (Sun et al., 2004). Modeling connectivity directly on fMRI time series often leads to a prohibitive computational burden, and thus most methods first calculate the connectivity metrics, then model these summaries to draw statistical inferences across subjects (Turk-Browne, 2013; Zatorre, 2013).

There are numerous intrinsic challenges to evaluating functional connectivity in the brain. Typical neuroimaging data in standard 2mm Montreal Neuroimaging Institute (MNI) space usually include roughly 300,000 voxels within the brain (on a regular lattice of 91×109×91 voxels). Therefore, there are more than 40 billion voxel pairs for a single whole brain connectivity analysis. It is desirable for connectivity analysis to provide spatially detailed inferences between all voxel pairs (Turk-Browne, 2013). However, such ultra-high dimensionality poses a formidable computational load. Zalesky et al., 2010 summarized the numbers of regions (or voxels) used for analysis in recent highly cited functional connectivity studies. A common strategy is to choose a small set of seed voxels among all voxels and calculate the associations between each seed voxel and all of the remaining voxels (Cordes et al., 2001). A second approach is to define regions of interest (ROIs) using an existing anatomical parcellation of the brain, for example automated anatomical labeling (AAL) or the Brodmann brain atlas (Tzourio-Mazoyer et al., 2002; Garey, 1994) and to quantify connectivity at the region level rather than voxel level (Greicius et al., 2003; Zalesky et al., 2012b). This approach usually first summarizes the temporal profiles of all voxels within each region by taking averages (or similar dimension reduction) and then estimating the connectivity by using the regional summaries. In addition, independent component analysis (ICA) has been applied to assess connectivity by separating spatially independent sources of signals (Calhoun et al., 2001).

Recently, there has been a focus on the application of graph theory metrics to depict complex brain networks (Bullmore and Sporns, 2009; Simpson et al., 2013; Bowman et al., 2014). Graph theory metrics reflect important topological properties of brain networks. For example, the “small-worldness” property indicates that most neural units (voxels) are often directly connected to neighbors (e.g. high positive Pearson correlation), but distant units can be connected through only a small number of steps via highly connected nodes (‘hub’ nodes) (Achard et al., 2005). The “small-worldness” property is common in highly organized networks such as the internet, vehicle traffic, and social networks. Nevertheless, those metrics usually only function as summary statistics rather than as motifs for establishing brain connectivity.

The seed voxel approach is simple for computation, but it is inherently limited in scope as it ignores functional connections other than the ones associated with the seeds. The region based method neglects the variations within regions, which may lead to substantial bias and information loss, and these problems are exacerbated as the size of an ROI increases. Moreover, region-based methods lack detail on the particular voxels that are connected between pairs of regions. ICA is often conducted on the voxel level where detected components may be difficult to interpret and may span multiple brain regions. Bayesian modeling has been applied to estimate localized brain activity with corresponding group/task differences and to perform region level connectivity analysis using task-induced fMRI data (Bowman et al., 2008; Patel et al., 2006; Xue et al., 2015). In summary, most existing statistical methods for brain connectivity analysis are conducted either on the region level or on the voxel level alone. There is an unmet need to develop analytical methods to unify connectivity analyses at these two levels of spatial units. We provide a new statistical framework that unifies voxel and region level connectivity analyses.

We propose a novel Bayesian hierarchical model for inferring brain connectivity. We use Pearson correlation, which is the most widely used connectivity metric in the neuroimaging community as the input data for our method (Zalesky et al., 2012a; Zatorre, 2013; Greicius et al., 2003). The base level of our framework assumes that the connections between voxel pairs from two brain regions follow a mixture distribution with two modes reflecting connected and non-connected voxel pairs (i.e. high and low connectivity metrics). The assumption follows naturally from the “small-worldness” property of brain networks, since two distant ROIs may be well connected through a small proportion of efficiently connected nodes (represented by the mixture component with higher connectivity metric values). The rest of the nodes in these two regions may not have direct across-region connections, but they could communicate via those efficiently connected voxels(connected component). Our model utilizes the connectivity information from all cross-region voxel pairs. From parameters in our mixture model, we introduce a new statistic called connectivity breadth, which reflects a measure of connectivity strength. We adjust for an individual’s covariate effects such as age, gender, and psychiatric conditions in a generalized linear model (GLM).

The hierarchical Bayesian model unifies voxel level and region level connectivity by recognizing the distribution of voxel connectivity between regions, which allows us to fully utilize rich voxel level connectivity information while keeping the more interpretable region level connectivity findings. At the voxel level, our model provides inferences to identify voxels (within a region) acting as ‘hubs’ by exhibiting many connections to another region. In addition, our model identifies cross-region voxel pairs that exhibit strong connectivity. Thus, two regions may be functionally connected via a hub in at least one of the regions or by two high-traffic ports directly linking the regions. Our method could have important applications, for example to reveal differences in connectivity properties (or other potential biomarkers) between patients with Parkinson’s disease and healthy controls. We estimate the parameters from our model using Markov chain Monte Carlo (MCMC) methods and draw inferences based on the joint posterior probability distribution for all of the parameters.

2. Motivating Example

There is currently a major focus in the neuroimaging literature on resting-state functional connectivity, which examines connectivity properties during an undirected mental state without the explicit performance of tasks. We consider resting-state fMRI data from 32 patients with major depressive disorder (MDD) participating in a depression treatment biomarker study (Dunlop et al., 2012). The sample includes 12 males and 20 females ages 24 to 57 years. We have data from baseline fMRI scans acquired prior to treatment randomization, a baseline 17 item Hamilton Depression Rating Scale (HAM-D17), and covariates age and gender. The patient cohort was divided into two groups based on the HAM-D17 score, as suggested by Maruish (1999) and Schutte and John (1995). The resulting classification includes 11 mildly depressed subjects, with HAM-D17 greater than 15 and less than 18, and 21 severely depressed subjects with HAM-D17 18 or above. For each subject, 150 fMRI volumes were obtained in 7.5 minutes during a resting-state, in which subjects are left to think for themselves while visually focusing on a cross displayed on a monitor in the scanner. We performed standard data preprocessing steps, including motion correction to offset subject movement in the scanner, slice timing correction to adjust for the fact that each 3D scan representing a single time point is actually acquired as a series of 2D slices over time, normalization to adopt a common reference space across subjects, and spatial smoothing. Also, we apply de-trending and demeaning steps to remove low frequency trends unrelated to neural processing (e.g. due to scanner hardware) and to adjust for spatial variation in brain tissue properties that may affect the fMRI signal. Pre-whitening is performed to remove the temporal correlation of the time course at each voxel.

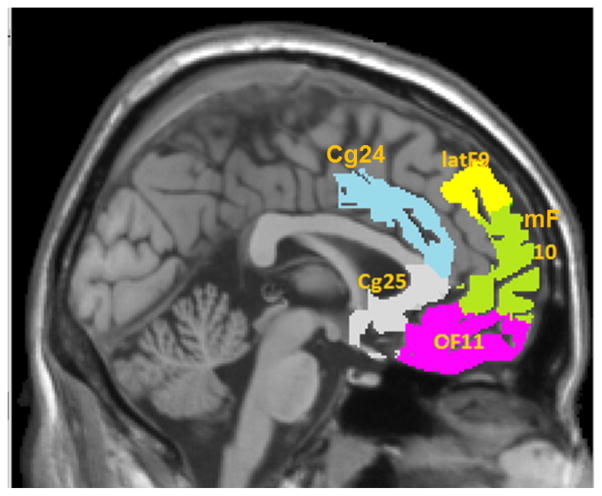
Models of depression emphasize dysfunctional interactions among specific cortical and limbic brain areas. Particularly, the interactions between subdivisions of frontal cortex and cingulate gyrus have been repeatedly reported in depression studies by using multiple complementary imaging methods (Seminowicz et al., 2004; Mayberg et al., 2005; Greicius et al., 2007; and Fox et al., 2012). We focus on the interactions between some of those reported ROIs (based on the Brodmann atlas) in the prefrontal cortex (PFC) including medial frontal cortex (mF10), orbital frontal cortex (OF11), and lateral prefrontal cortex (latF9); subgenual cingulate cortex (Cg25) and anterior cingulate (Cg24). We show these regions of interest in Figure 1. The goal is to assess functional connections between the five ROIs and to make inferences about how depression severity influences them.

Figure 1.

Sagittal view of the brain with selected regions of interest (ROI). Region sizes are given as the number of voxels in 4mm, space and the ROI centers are given in Talarach space. This figure appears in color in the electronic version of this article.

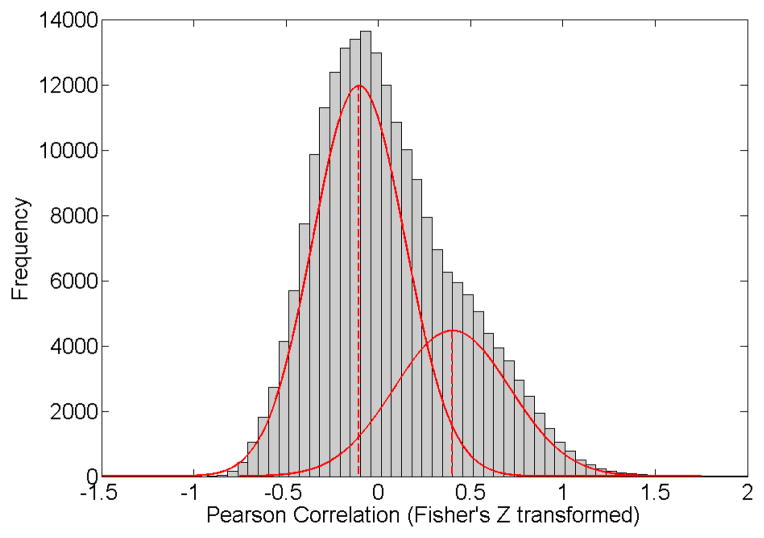
Exploring the distribution of voxel-level functional connections (using correlations for example) between ROIs, we note the appearance of a mixture distribution with two components: a larger component of relatively weakly connected voxel pairs and a smaller component of more strongly connected voxel pairs (see Figure 2). Moreover, each subject has a different number of connected voxel pairs. The size of the connected component represents the connectivity breadth, and reflects aspects of the the “small-worldness” property. Therefore, we develop a method to study such connectivity breadth and to identify what factors may influence this connectivity breadth.

Figure 2.

Histograms of voxel pair functional connections (correlation via Fisher’s transformation) for two example subjects. The histograms demonstrate asymmetry due to the highly connected component in the right tail (the two components demonstrated in the figure are estimated by Gaussian mixture model). The two modes center at −0.1 and 0.8.

3. Methods

We formulate a model that builds on the calculated voxel-level functional connections within ROIs and between ROIs. ROIs are labeled as g = 1, …, G, where we may set G as high as 116 for the AAL map and 48 for the Brodmann map (for our data example G = 5). We use z_ig̈v̈ to denote connectivity (here, we consider correlations with a Fisher transformation) between the cross-region pair of voxels v and v′ denoted by v̈; for regions g (v ∈ g)and g′ (v′ ∈ g′), labeled by g̈; and for subject i (i = 1, …, n). Throughout, we use the two-dot notation to indicate pairs of voxels or regions. For a region pair g̈, the total number of voxel pairs is V_g̈. Thus, if regions g and g′ include V_g and V_g′ voxels respectively, then V_g̈ = V_g×V_g′.

3.1 Bayesian Hierarchical Model

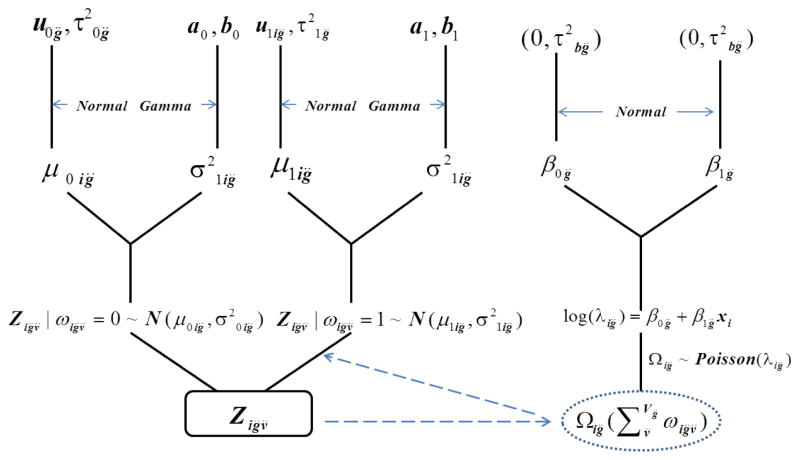
We use a Bayesian hierarchical framework to jointly model functional connections between pairs of voxels and pairs of ROIs along with clinical covariate effects while tracking the variability at each level (see Figure 3).

Figure 3.

Diagram of the Bayesian hierarchical model. From the bottom to top are voxel pair data (observed and augmented), region level parameters, and hyperpriors.

3.1.1 Distribution for connectivity

The first level of our model specifies functional links between ROIs for each subject via a distribution of connections from cross-region voxel pairs. A driving heuristic is that according to the “small-worldness” property of brain networks, two regions can be efficiently connected through only a small proportion of connected voxels, and this property is also borne out by descriptive assessments of our data. In the two component mixture model, we limit our attention to only non-negative correlations, following a strong precedent in the neuroimaging literature, which facilitates interpretations. (Weissenbacher et al., 2009; Fox et al., 2009).

At the first level, we assume that z_ig̈v̈ follows a mixture distribution with two modes representing connected and non-connected voxel pairs. The two components vary around means μ_0ig̈ (non-connected) and μ_1ig̈ (connected), with the variances ${\sigma }_{0i\ddot{g}}^2$ and ${\sigma }_{1i\ddot{g}}^2$ respectively. We set μ_1ig̈ > μ_0ig̈ to aid identifiability. Specifically, the model is given by

$$\begin{array}{l}{z}_{i\ddot{g}\ddot{v}}\mid {\omega }_{i\ddot{g}\ddot{v}},{\mu }_{0i\ddot{g}},{\sigma }_{0i\ddot{g}}^2{\mu }_{1i\ddot{g}},{\sigma }_{1i\ddot{g}}^2~{\omega }_{i\ddot{g}\ddot{v}}\mathrm{N}({\mu }_{1i\ddot{g}},{\sigma }_{1i\ddot{g}}^2)+(1-{\omega }_{i\ddot{g}\ddot{v}})\mathrm{N}({\mu }_{0i\ddot{g}},{\sigma }_{0i\ddot{g}}^2),\\ {\omega }_{i\ddot{g}\ddot{v}}\mid {\pi }_{i\ddot{g}}~\text{Bernoulli}({\pi }_{i\ddot{g}}),\text{and}\text{correspondingly}\sum _{\ddot{v}}^{V_{\ddot{g}}}{\omega }_{i\ddot{g}\ddot{v}}={\mathrm{\Omega }}_{i\ddot{g}}\mid {\lambda }_{i\ddot{g}}~\text{Poisson}({\lambda }_{i\ddot{g}}),\end{array}$$ (1)

where λ_ig̈ = V_g̈π_ig̈.

The latent indicator variable ω_ig̈v̈ classifies a voxel pair as either connected or non-connected. Our interest lies in detecting connectivity breadth between ROIs, which is represented by the average number of connected voxel pairs λ_ig̈ = V_g̈π_ig̈. Note that ω_ig̈v̈ in line 2 may be correlated with ω_ig̈v̈′, and then the indicator variables of all cross-region voxel pairs are a set of dependent Bernoulli trials (connected 1 or not connected 0). Moreover, we let the marginal sum ${\mathrm{\Omega }}_{i\ddot{g}\ddot{v}}={\sum }_{\ddot{v}}^{V_{\ddot{g}}}{\omega }_{i\ddot{g}\ddot{v}}$ follow a Poisson distribution and link the hyperprior parameters with λ_ig̈ because i) the information of parameters from Bernoulli distribution and Poisson distribution are almost equivalent (λ_ig̈ = V_g̈π_ig̈) and ii) Ω_ig̈v̈ is more sensible and computationally convenient for group level inferences. It has been shown that the Poisson distribution has a bounded approximation for the sum of dependent Bernoulli trials (Chen, 1975). The approximation should be very close in our application since V_g̈ is on the order of hundreds of thousands in many cases. Therefore, using independent or dependent correlation structure between all voxel pairs ω_ig̈v̈ does not impact the marginal parameter estimation of λ_ig̈. Our approximation is analogous to the areal/lattice spatial data analysis in disease mapping, where each incident (dependent on each other) follows Bernoulli distribution yet within an area (e.g. county) the marginal sum incident count is often used as an outcome variable for association analysis.

Why two component mixture?

We adopt the two component mixture model reflecting that voxels exhibit connectivity or not, rather than specifying a finite mixture model with k > 2 or an infinite mixture model. Our formulation mirrors the use of two component mixtures in other massive hypothesis testing settings, e.g. local fdr (Efron, 2004; George and McCulloch, 1993; Do et al., 2005; Müller et al., 2007). The common target is to identify the true positive elements from a mixture model consisting of a dominating null distribution and a small number of positive events (here, functional connections). Whereas the local fdr method tends to focus on control rates at specific z values or events, we are interested in the sum of latent indicator variables Ω_ig̈. Marginally, $E({\mathrm{\Omega }}_{i\ddot{g}})={\sum }_{\ddot{v}}^{V_{\ddot{g}}}\int P(z_{i\ddot{g}\ddot{v}})f(z_{i\ddot{g}\ddot{v}})\mathrm{d}{z}_{i\ddot{g}\ddot{v}}=V_{\ddot{g}}{\pi }_{i\ddot{g}}={\lambda }_{i\ddot{g}}$, where f(z_ig̈v̈) = π_ig̈f₁(z_ig̈v̈) + (1 − π_ig̈)f₀(z_ig̈v̈), f₀ and f₁ represent the probability density functions associated with the null and positive components, and P(z_ig̈v̈) is the probability of “true positive”, which is identical to 1 − fdr. The marginal variable Ω_ig̈ is subject to less variance and is invariant to the choice of distributions for f₀ and f₁.

In addition, the conceptualization as a two component mixture mitigates the cross-subject identifiablility issues. If each subject includes k (k > 2) components, we ought to ensure that not only all components (with different center parameters) are identifiable, but also that the components can be matched across subjects for group-level inferences. The matching procedure pose challenges with respect to numerical optimization.

3.1.2 Prior specifications

The second level of the hierarchical model in (2) expresses a prior belief that each subject’s mixture component means μ_0ig̈ and μ_1ig̈ arise from normal distributions with means u_0g̈ and u_1ig̈ and variances ${\tau }_{0\ddot{g}}^2$ and ${\tau }_{1i\ddot{g}}^2$ respectively. We anticipate that the mean parameter u_1ig̈ for the cross-region voxel pairs from the connected component will be relatively large. Thus, we empirically inform u_1ig̈ by calculating the mode of voxel pair functional connections within an ROI at geometric distances up to 30 mm for each subject, which seems to represent a reasonable starting point since voxel pairs within anatomically-defined regions generally exhibit high association.

$$\begin{array}{l}{\mu }_{0i\ddot{g}}\mid u_{0\ddot{g}},{\tau }_{0\ddot{g}}^2~N(u_{0\ddot{g}},{\tau }_{0\ddot{g}}^2),\\ {\mu }_{1i\ddot{g}}\mid u_{1i\ddot{g}},{\tau }_{1\ddot{g}}^2~N(u_{1i\ddot{g}},{\tau }_{1\ddot{g}}^2),\\ {\sigma }_{0i\ddot{g}}^{-2}~\text{Gamma}(a_0,b_0),\\ {\sigma }_{1i\ddot{g}}^{-2}~\text{Gamma}(a_1,b_1),\\ \mathit{log}({\lambda }_{i\ddot{g}})={\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i,\text{where}{\lambda }_{i\ddot{g}}=E({\mathrm{\Omega }}_{i\ddot{g}}\mid {\beta }_{\ddot{g}0},{\beta }_{\ddot{g}}),\end{array}$$ (2)

We inform the mode of u_0g̈ by using the mode of voxel pair functional connections between ROIs across all subjects which is close to zero. The variances ${\tau }_{0\ddot{g}}^2$ and ${\tau }_{1\ddot{g}}^2$ reflect the confidence of the prior mean specification, and we set ${\tau }_{0\ddot{g}}^2$ and ${\tau }_{1\ddot{g}}^2$ as a relatively small value as the mean priors are informative. For the first level variance parameters ${\sigma }_{0i\ddot{g}}^2$ and ${\sigma }_{1i\ddot{g}}^2$, we assume Gamma distributions with hyperprior parameters a₀ = 0.1, b₀ = 0.005, a₁ = 0.1, b₁ = 0.005, reflecting vague priors.

We model the region pair mean connectivity breadth λ_g̈ through a GLM with a log link to accommodate the Poisson distribution. The parameters β_g̈ of the GLM capture covariate effects such as disease status, age, and treatment group. The priors for β_g̈ are set vaguely enough to let the large amount of observed data weigh heavily in determining the posterior distribution, specifically using

$${\beta }_{\ddot{g}0}~\mathrm{N}(0,{\tau }_{0b}^2),{\beta }_{\ddot{g}}~\mathrm{N}(0,{\tau }_b^2).$$ (3)

3.2 Estimation and posterior inference

We apply MCMC algorithms to estimate the parameters in our hierarchical probability model. The priors for the main effects β in the GLM are not conjugate, so we use a Gibbs sampler with Metropolis updates where needed for posterior sampling. The full conditional distributions are given by the following:

$$\begin{array}{l}{\omega }_{i\ddot{g}\ddot{v}}~\text{Bernoulli}\left(\frac{{\pi }_{i\ddot{g}}\mathrm{N}(z_{i\ddot{g}\ddot{v}}\mid {\mu }_{1i\ddot{g}},{\sigma }_{1i\ddot{g}}^2)}{{\pi }_{i\ddot{g}}\mathrm{N}(z_{i\ddot{g}\ddot{v}}\mid {\mu }_{1i\ddot{g}},{\sigma }_{1i\ddot{g}}^2)+(1-{\pi }_{i\ddot{g}})\mathrm{N}(z_{i\ddot{g}\ddot{v}}\mid {\mu }_{0i\ddot{g}},{\sigma }_{0i\ddot{g}}^2)}\right)\\ {\mu }_{0i\ddot{g}}~\text{Normal}\left({\mathrm{\Psi }}_{0i\ddot{g}}\{{\tau }_{0i\ddot{g}}^{-2}{u}_{0\ddot{g}}+(V_{\ddot{g}}-{\mathrm{\Omega }}_{i\ddot{g}}){\sigma }_{0i\ddot{g}}^{-2}{\overline{z}}_{0i\ddot{g}}\},{\mathrm{\Psi }}_{0i\ddot{g}}\right)\\ {\mu }_{1i\ddot{g}}~\text{Normal}\left({\mathrm{\Psi }}_{1i\ddot{g}}\{{\tau }_{1i\ddot{g}}^{-2}{u}_{1i\ddot{g}}+{\mathrm{\Omega }}_{i\ddot{g}}{\sigma }_{1i\ddot{g}}^{-2}{\overline{z}}_{1i\ddot{g}}\},{\mathrm{\Psi }}_{1i\ddot{g}}\right)\\ {\sigma }_{0i\ddot{g}}^{-2}~\text{Gamma}\left\{a_0+(V_{\ddot{g}}-{\mathrm{\Omega }}_{i\ddot{g}})/2,{\left(\frac{1}{b_0}+\frac{1}{2}\sum _{\forall {\omega }_{i\ddot{g}\ddot{v}}=0}{(z_{i\ddot{g}\ddot{v}}-{\mu }_{0i\ddot{g}})}^2\right)}^{-1}\right\}\\ {\sigma }_{1i\ddot{g}}^{-2}~\text{Gamma}\left\{a_1+({\mathrm{\Omega }}_{i\ddot{g}})/2,{\left(\frac{1}{b_1}+\frac{1}{2}\sum _{\forall {\omega }_{i\ddot{g}\ddot{v}}=1}{(z_{i\ddot{g}\ddot{v}}-{\mu }_{1i\ddot{g}})}^2\right)}^{-1}\right\}\\ {\beta }_{\ddot{g}0}\propto \prod _i^n{e}^{({\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i){\mathrm{\Omega }}_{i\ddot{g}}}\mathit{exp}(-e^{({\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i)})\mathrm{N}({\beta }_{\ddot{g}0}\mid 0,{\tau }_{0b}^2)\\ {\beta }_{\ddot{g}}\propto \prod _i^n{e}^{({\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i){\mathrm{\Omega }}_{i\ddot{g}}}\mathit{exp}(-e^{({\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i)})\mathrm{N}({\beta }_{\ddot{g}}\mid 0,{\tau }_b^2),\end{array}$$ (4)

where ${\mathrm{\Psi }}_{0i\ddot{g}}=\left((V_{\ddot{g}}-{\mathrm{\Omega }}_{1\ddot{g}}){\sigma }_{0i\ddot{g}}^2+{\tau }_{0i\ddot{g}}^2\right),{\mathrm{\Psi }}_{1i\ddot{g}}=\left({\mathrm{\Omega }}_{i\ddot{g}}{\sigma }_{1i\ddot{g}}^{-2}+{\tau }_{1i\ddot{g}}^{-2}\right)$, z̄_1ig̈ is the mean for all cross-region voxel pairs v̈ from the connected component, i.e. ω_ig̈v̈ = 1, z̄_0ig̈ is the mean for all v̈ of ω_ig̈v̈ = 0, and π_ig̈ = e^{β_g̈0+ β_g̈x_i}/V_g̈.

When implementing the MCMC procedure, we first sample the latent indicator variable, then sample the four parameters of the Gaussian mixture model. In formula 4 line 1, each latent indicator variable ω_ig̈v̈ for the corresponding voxel pair v̈ is conditional on the region level parameter π_ig̈, which is equivalent to λ_ig̈/V_g̈. λ_ig̈ is determined by β_g̈ (along with the subject covariates) and β_g̈0, and both β_g̈ and β_g̈0 are sampled by incorporating ${\mathrm{\Omega }}_{i\ddot{g}}={\sum }_{\ddot{v}}^{V_{\ddot{g}}}{\omega }_{i\ddot{g}\ddot{v}}$ (see the last two lines of formula 4). Note that Ω_ig̈ is updated by taking the summation of updated ω_ig̈v̈ rather than sampled directly from Poi(λ_ig̈). Therefore, similar to other mixture model settings, our sampling scheme includes an implicit constraint that each ω_ig̈v̈ is dependent on [ω_ig̈v̈′, ω_ig̈v̈″, …] because the update of π_ig̈ (λ_ig̈/V_g̈) depends on connections of all voxel pairs between a region pair i.e. π_ig̈ = λ_ig̈/V_g̈ = g⁻¹(β_g̈0, β_g̈) and the updates of β_g̈0 and β_g̈ are both dependent on Ω_ig̈ (the sum of [ω_ig̈v̈, ω_ig̈v̈′, ω_ig̈v̈″, …]).

At the second level, the GLM parameters are updated through Metropolis steps with input of Ω_ig̈ following a Poisson (log link). We favor a Poisson distribution, rather than a Binomial, because with Ω_ig̈ and V_g̈ being on the order of thousands and millions, respectively, the ratio function of the Metropolis step may easily generate zeros in the denominator if the logit link is used. In addition, since the number of voxel pairs V_g̈ is often large, the inferences for π_ig̈ can be directly computed as λ_g̈/V_g̈ from the posterior simulations. The ratios of βs in the Metropolis step can be expressed as:

$$r_{\beta }=exp\{\sum _i^n[{\mathrm{\Omega }}_{i\ddot{g}}({\beta }_{i\ddot{g}}^{\prime }-{\beta }_{i\ddot{g}})+\mathit{exp}(-{\eta }_{i\ddot{g}}^{\prime })-\mathit{exp}(-{\eta }_{i\ddot{g}})]+\mathit{log}(p_0({\beta }_{i\ddot{g}}^{\prime }\mid 0,{\tau }_b^2))-\mathit{log}(p_0({\beta }_{i\ddot{g}}\mid 0,{\tau }_b^2))\},$$

where β′ are proposed values, p₀ indicates the prior distribution, and we accordingly obtain η_ig̈ from η_ig̈ = β_g̈0 + β_g̈x_i. The proposed value will be accepted with probability min(1, r_β). All other parameters can be sampled from known distributions through the Gibbs sampler as shown in (4).

Implementation of our Bayesian model takes samples from the joint posterior distribution for all of the model parameters, which enables statistical inferences regarding connectivity and brain network properties. First, we can make inferences about voxel-level connectivity for each subject. For example, we can target inferences pertaining to the probability of a cross region voxel pair being connected, say P_ig̈(v̈), by calculating the proportion of ω_ig̈(v̈) equaling one. Secondly, we can identify which voxels operate as hubs, with a hub defined here as a voxel that connects with numerous cross-region voxels. Thirdly, we can determine which specific pairs of voxels are highly connected to each other. We can also make inferences about region-level connectivity. For example, we can draw inference about the connectivity breadth of a region pair by calculating the posterior probability of e^{β_g̈0 + β_g̈x_i}. Relevant to our upcoming data analysis, our modeling framework yields inferences at the population level, and we can investigate the impact of covariate effects such as age, disease groups, and treatment responses on connectivity breadth between ROIs.

4. Results

We apply our Bayesian hierarchical model to resting-state fMRI data from the depression study and empirically evaluate our model using simulated data. We compare our method with the region average method which is the most commonly used group-wise region level analysis approach under the predefined brain ROI atlases.

4.1 MDD Study Using Resting-state fMRI Data

In the MDD study, our goal is to explore the neural circuits associated with medial and lateral regions of prefrontal cortex (e.g. latF9, mF10, OF11) and effective subdivisions of the anterior Cingulate Cg25 and Cg24 as described in section 2. We employ the commonly used Pearson correlation coefficient as a measure of the temporal coherence between fMRI time series from distinct voxels and further apply the Fisher normalizing transformation. As demonstrated in Figure 2, the functional connections appear to follow a mixture distribution. We apply our Bayesian hierarchical model to the transformed correlation metrics to investigate functional connectivity. For illustration, we highlight results for the region pair mF10 and Cg25.

Inferences for voxel pair connectivity

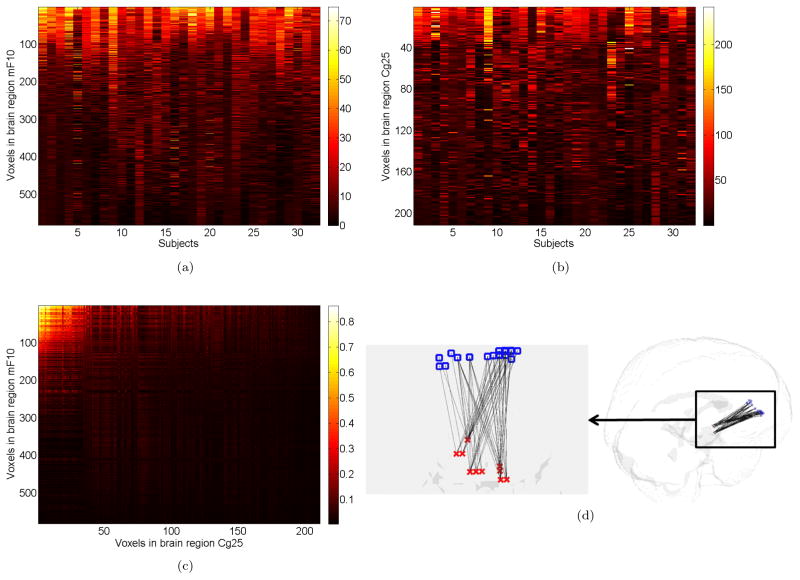
After applying our Bayesian model, we estimate the probability of functional connectivity between each cross-region voxel pair. Then, we identify voxels in one brain region that are highly connected to voxels in the other region, representing hubs at the population level. In Figure 4a, each row represents a voxel in mF10, each column represents a subject, and the intensity indicates the corresponding number of functionally connected voxels in Cg25. For convenience, we have ordered the voxels in mF10 according to the number of functionally connected voxels (across subjects), with the most highly connected voxels appearing at the top and with the least connected voxels appearing at the bottom. We note that there are several mF10 voxels that are highly connected to region Cg25 across all 32 subjects, while most voxels are weakly connected. These highly connected voxels serve as “hubs” connecting the two regions since they reveal coherent activity with many other voxels. Reciprocally, Figure 4b shows the voxels in Cg25 connected to mF10. Specifically, we consider the voxels that are cumulatively connected to roughly 30% or more of the voxels in the other region. For example, in considering hubs linking voxels in mF10 to those in Cg25, we identify voxels with degree > 60 (the degree of a voxel equals to the number of its connected voxels) and voxels in Cg25 with degree > 150. The joint posterior distribution also allows also allow us to identify particular voxel pairs connecting the two regions. Figure 4c shows the highly connected voxel pairs between the two regions, and Figure 4d illustrates locations of the functionally connected voxel pairs linking regions mF10 and Cg25. The posterior also yields inferences to identify highly connected voxels for each subject, and note from Figure 4 that connections between voxels vary across subjects. Our framework has particular utility in reforming models of depression relevant to focal neuromodulation where targeting of discrete pathways may be critical (Mayberg et al., 2005; Gutman et al., 2009; and Fox et al., 2012).

Figure 4.

Voxel pair connectivity inferences:(a) the heatmap intensity reflects the number of functionally connected voxels in Cg25 to each voxel (row) of brain region mF10 across subjects (columns). (b) shows the number of functionally connected voxels in mF10 to each voxel (row) in Cg25 across 32 Subjects. The regional voxels (rows) in (a) and (b) are ordered such that the voxel with the most connections is listed first and the voxel with the least connections is listed last. Note that some voxels in mF10 and Cg25 consistently show a large number of connections to voxels in the other region across the 32 subjects. These highly connected voxels serves as neural processing hubs since they reveal coherent activity with many other voxels. (c) is a heatmap showing voxel pairs that are highly connected between mF10 and Cg25 and the intensity is the average posterior probability that a cross-region voxel pair is connected (averaged across subjects). (d)right is a 3D plot showing voxel pairs connected with high probabilities (P_g̈(v̈) > 0.9 for across subject average) falling in regions Mf10 and Cg25. The squares and crosses represent the voxels in mF10 and Cg25 respectively. (d) left is enlarged and rotated for better visualization of links between voxels. This figure appears in color in the electronic version of this article.

Inferences for region pair connectivity

At the region level, we summarize the breadth of functional connectivity, stratified by different depression severity groups, by counting the number of the functionally connected voxel pairs. In Table 1, we note that the region pairs mF10 and Cg25, OF11 and Cg25, and Cg24 and Cg25 are relatively highly connected, but not latF9 and Cg25C. There are marked differences in connectivity breadth between mildly and severely depressed patients for mF10 and Cg25 (7.5%), latF9 and Cg25 (6%), and OF11 and Cg25 (10%) with more severely depressed patients having increased functional connections. These findings may reveal that with increased depression severity, the brain locations for emotion processing interact more with the prefrontal cortex neural units. There is very little difference, however, in extent of functional connections between groups for Cg24 and Cg25 (2% difference), with severely depressed patients exhibiting slightly reduced connectivity breadth.

Table 1.

Patient group comparisons for breadth of connectivity between specified regions (entries represent number of connected voxel pairs.)

Parameters	Median (πg̈ %)	std	25 pct	75 pct	Mode	Difference(CI)	% Difference
Cg25 & mF10 (122,591 voxel pairs)
(Mildly depressed exp(β0+β1))	36526 (29.8)	143	36466	36526	36600	2879	7.5 %
(Severely depressed expβ0)	39423(32.1)	155	39325	39422	39437	(2705,3084)
Cg25 & latF9 (119,426 voxel pairs)
(Mildly depressed exp(β0+β1))	8654 (7.2)	26	8334	8921	8688	488	6 %
(Severely depressed expβ0)	9124(7.6)	31	8968	9306	9132	(440,518)
Cg25 & OF11 (214,376 voxel pairs)
(Mildly depressed exp(β0+β1))	45632 (21.3)	318	45273	45987	45686	4729	10 %
(Severely depressed expβ0)	50361 (23.5)	387	50186	50626	50357	(4461,4891)
Cg25 & Cg24 (32,705 voxel pairs)
(Mildly depressed exp(β0+β1))	10162 (31.1)	71	10083	10239	10168	−149	−2 %
(Severely depressed expβ0)	10013 (30.5)	68	9972	10045	10018	(−120,−171)

For comparison, we apply a commonly used approach that calculates correlations between the regional temporal profiles obtained as an average of all temporal profiles in mF10 and Cg25 for all subjects. There is no difference between the two groups with t test p value at 0.57 (Supplementary Figure 2). We further address differences between our proposed method and the regional representative approach in a simulation study. We conclude that our model is able to reveal the subtle difference driven by the relatively few connected voxel pairs, and accordingly to detect the group difference. Overall, we find that that cg25 and frontal cortices appeared hyper-connected in more depressed subjects, which is consistent with previous research findings about the frontal-limbic circuitry (Greicius et al., 2007; Greicius, 2008; Zeng et al., 2012). Besides the similar region-level connectivity findings above, we provide additional voxel level inferences that previous methods do not permit (e.g. Figure 4 results); for instance we can identify those highly-connected voxel pairs that effectively connect a pair of regions.

We check our MCMC runs to ensure the stability of the results and the convergence of the chains. However, the massive number of voxel pairs prevents formal use of MCMC convergence tools for all model parameters. We monitor the trace plots for all region level parameters and for parameters corresponding to select voxel pairs. For each MCMC, we sample 20,000 iterations in total and set the first 500 iterations as burn-in. The resulting Markov chain converges within 500 burn-in samples (Supplementary Figure 1).

4.2 Simulation Study

We conduct a simulation study to further examine properties of our proposed connectivity modeling framework. We generate resting-state fMRI time series based on one region pair with sizes of a 7×7×7 voxel cube and a 5×5×5 voxel cube, from 20 subjects (10 controls and 10 cases). Therefore, for each subject we simulate 7³ +5³ = 468 fMRI time series, which allows us to calculate the connectivity metrics of V_g̈ = 7³ ×5³ = 42875 between-region voxel pairs. First, we randomly generate the numbers of connected cross-region voxel pairs using Poisson distributions with mean parameter:

$${\mathrm{\Omega }}_{i\ddot{g}}=\mathit{exp}({\beta }_{\ddot{g}0}+{\beta }_{\ddot{g}}{x}_i).$$

We use β_g̈0 = 8 and β_g̈1 = 0.9 to indicate that the controls have more breadth in connectivity than cases do. Second, we construct the correlation matrix R (468 × 468) for all voxels in the two regions, which determines the correlations between the fMRI time series. We set each group with different Rs since we use different Ω_ig̈ and V_g̈ − Ω_ig̈ to indicate the numbers of highly correlated (e.g. correlation coefficient=0.6) and uncorrelated (e.g. correlation coefficient=0) between-region voxel pairs for each group. For the within region voxel pairs, we use correlations on the geometric distances between voxels so that voxels close to each other are more highly correlated and distant voxel pairs are less correlated. We slightly adjust R to ensure that it is positive definite. Based on different Rs of case and control groups, we generate 468 resting-state fMRI time series for each of the 20 subjects by using multivariate normal distribution with mean zero and covariane of R (Supplementary Figure 3 demonstrates the resting-state fMRI time series for 10 voxels in one subject). We assume that the pre-whitening has been performed, so there is no temporal autocorrelation within each voxel. We also apply different variance parameters of multivariate normal distribution (power magnitude) of the BOLD signal and band filtering to remove the low and high frequency components. The tuning of these simulation parameters does little change to the resulting distribution of correlation (connectivity metric) which is the input our of method.

Based on the simulated resting-state fMRI time series, we calculate correlation coefficients of the between region voxel pairs for each subject (see histograms in Supplementary Figure 4), where the controls have a larger component of connected voxel pairs. Our main goal is to detect a group effect and to check the number of voxel pairs that are determined to be connected for each subject. We apply our proposed hierarchical Bayesian framework to the simulated data.

Based on trace plots of parameters for the group effects from our MCMC samples of 20,000 iterations (Supplementary Figure 5), we note that the chains converge after around 300 iterations and henceforth tightly vary around the true values. The results shown in Table 2 reveal that our model captures the group effect accurately. Thus, this simulation supports that the proposed method and estimation algorithm can detect differential connectivity breadth when they exist. The small bias of βs may come from the false negative classification of the mixture model due to the heavy inclination of the predominant null component.

Table 2.

Summaries of distributions of posteriors in the simulation study with posterior median, standard deviation credible interval, and Ω̄₀ and Ω̄₁ represent the group average number of connected voxel pairs in cases and controls respectively.

Parameters	Median	std	25 pct	75 pct	Mode
Ω̄0	2785	12.38	2591	2889	2781
Ω̄1	6778	15.32	6691	7153	6776
β0 (8)	7.95	0.022	7.91	8.01	7.97
β1 (0.9)	0.89	0.009	0.88	0.90	0.89

As a comparison, we use the the regional representative method described in the analysis of our depression data, to detect the connectivity difference between the two groups. We first calculate the regional temporal profiles for each subject using the the average all of the fMRI time series in each region. Then, we measure the correlation coefficients between the two regional fMRI time series for each subject. We conduct a t-test to assess the null hypothesis that the two regions have the same connectivity between the two groups, and the result shows non-significant difference with p = 0.673. We note that our method detects the informative group difference that the region representative method fails to identify. Our method also provides richer information about voxel level connectivity. There are many methods that quantify connectivity, in a general sense, between pairs of ROIs across different clinical groups. However, as we limit our attention to compare connectivity between one pair of ROIs, we only compare our approach with the region representative method.

5. Discussion

Our proposed method is the first model that is able to use all available voxel pair connectivity information, while also capturing connectivity between region pairs. Given the massive number of voxel pairs across the entire brain (tens of billions), it is imperative for any voxel level approach to reduce the number of pairs considered, and we do so by focusing on particular ROIs. Another attribute of our model is that it naturally lends itself to network graph theoretical properties characterizing brain connectivity. Our Bayesian model yields inferences on numerous quantities reflecting brain connectivity. Our model enables the examination of covariate effects, and we illustrate this by considering how depression severity impacts the extent of brain connectivity. Estimation of regional brain connectivity is robust to potential bias due to imperfect image registration because the posterior inferences are not dependent on the specific locations of voxel pairs between a region pair but only on the marginal connectivity between a region pair. At the voxel level, we may also detect inter-region “hub” voxels as those that are connected to many other voxels with high probabilities, and the voxel pair connectivity pathways that connect the two regions with high probabilities across subjects. The relative size of the connected component, i.e. the proportion of connected voxel pairs, could arguably be affected by the physical distance between the pair of ROIs, e.g. yielding increased connectivity breadth between two adjacent regions. However, increased connectivity breadth between adjacent (or relatively close) regions arguably may have a valid neurophysiological basis. Regardless, the influence of distance should have little bearing on our statistical inferences, for instance the between group comparisons, since all subjects share the identical spatial adjacency information.

The mixture model in the first level determines the number of connected voxel pairs in a fashion that is similar to local fdr, rather than choosing hard cutoff points, which improves the accuracy. Although we choose Gaussian distributions for both components of the mixture model (which seems to work well for our data example), we could adopt more flexible distributions (e.g. a gamma distribution for the skewed connected component). Both the MDD study and our simulation study results indicate that the MCMC parameter estimation is satisfactory, and the trace plots of the chains behave normally. Although there are numerous voxel pairs per subject and many subjects are included, the computational load is manageable. All the programming including MCMC and imaging processing was implemented in MATLAB. With a sample size of 20 subjects and more than 40,000 voxel pairs, the MCMC procedure takes around 6 minutes for the simulation study and on average 15 minutes for the example data to run for one region pair on an Intel i7 3.4 GHz CPU and 24G memory PC. When modeling a larger number of region pairs, we would leverage the appropriate parallelization algorithms for faster implementation. It will cost approximately 60 hours to calculate all region pairs of the Brodmann atlas in 2mm standard space by using parallel computing.

In this article, our model does not explicitly account for the correlation between different pairs of voxel connections. In contrast to activity analyses, where spatial correlations are more readily addressed (Bowman et al., 2008; Derado et al., 2010), connectivity studies typically consider the association between time courses of two brain units as input data. Thus, the dependence structure between two connectivity metrics may rely on the spatial information of four nodes. Numerous complexities are involved in modeling this spatial dependence structure, and the commonly used assumptions for spatial dependence (e.g. second-order stationarity) may need to be cautiously tested and verified. Thus, while accounting for the spatial dependence structure between connections of brain areas (including region level and voxel level) is certainly an important consideration, the topic will require in depth investigation in future work. Our proposed model is also applicable to other functional connectivity metrics (e.g. mutual information and spectral coherence), and other brain connectivity measures such as structural connectivity from DTI data.