Abstract
The estimation of treatment effects on medical costs is complicated by the need to account for informative censoring, skewness and the effects of confounders. Since medical costs are often collected from observational claims data, we investigate propensity score (PS) methods such as covariate adjustment, stratification and inverse probability weighting taking into account informative censoring of the cost outcome. We compare these more commonly used methods to doubly robust estimation (DR). We then use a machine learning approach called Super-Learner (SL) to choose among conventional cost models to estimate regression parameters in the DR approach and to choose among various model specifications for PS estimation. Our simulation studies show that when the PS model is correctly specified, weighting and DR perform well. When the PS model is misspecified, the combined approach of DR with SL can still provide unbiased estimates. SL is especially useful when the underlying cost distribution comes from a mixture of different distributions or when the true PS model is unknown. We apply these approaches to a cost analysis of two bladder cancer treatments, cystectomy versus bladder preservation therapy, using SEER-Medicare data.
Keywords: propensity scores, doubly robust estimation, cost estimation, observational studies, super learner
1. Introduction
Proper medical cost estimation is imperative to health economics evaluation and decision-making. Policy makers are often most interested in the average effect treatment effect (ATE) on total costs. Since medical costs are often collected from claims data which are susceptible to confounding, appropriate estimation of the ATE from observational data demands attention. These methods must also account for other complicating features of cost data including informative censoring and skewness.
The primary focus of earlier studies of cost estimation has been on methods for dealing with their distributional skewness. Historically, researchers have used natural logarithm transformed costs in ordinary least square regression (OLS) or used generalized linear models (GLM) with a log link. However, Manning and Mullahy [1] showed that OLS estimators can be biased under heteroscadasticity and GLM estimators can yield imprecise estimates if the log-scale error is heavy-tailed. Others have suggested using median regression since the median is less sensitive to skewness and outliers [2]. Several studies [3–5] have evaluated additional approaches such as OLS, OLS for log cost, standard gamma, standard GLM, generalized gamma, median regression, exponential models with log link, and the weibull model. Dodd et al. [3] found the generalized gamma model to be the most robust cost model. Recent works [6, 7] have focused on two part models and Bayesian approaches to accommodate structural zeros and end of life costs.
An important feature of medical costs is censoring, which often occurs if the study terminates after a fixed follow-up period. Even though survival time is non-informatively censored due to end-of-study censoring, cost is not. Censoring in cost is informative since the rate of cost accrual over time may vary greatly among patients. To address this issue, Lin et al.[8] introduced two estimators of mean cost by partitioning study period into subintervals and assuming censoring occurs only at the boundaries of these subintervals. Bang and Tsiatis [9] improved on Lin et al.'s work and proposed two popular methods: the simple weighted method and the partitioned method, to estimate mean medical cost under informative censoring. The simple weighted method averages subjects with complete cost information weighted by the inverse of the probability of not being censored. The partitioned estimator builds on the same weighting idea but also makes use of cost history information and is therefore more efficient. Properties of these methods have been widely studied [10–12]. Lin [13, 14] and Baser et al. [15] have since extended these methods to linear regression and general linear models to incorporate the effect of covariates. Several studies [16, 17] have also applied these techniques to median regression to handle censored cost data.
Heath care cost information is often collected from observational sources, such as Medicare, necessitating the need to adjust for potential confounders. The propensity score (PS), first introduced by Rosenbaum and Rubin [18] is commonly employed to adjust for confounding in observational studies [19]. Propensity scores are often used in covariate adjustment, matching, stratification and weighting [20, 21]. Covariate adjustment of the PS is easily implemented but is sensitive to the assumption that the relationship between the propensity score and the outcome has been correctly modeled [22]. Stratification based on PS is also often used as it greatly simplifies implementation over standard methods; Rubin and Rosenbaum [23] demonstrated that stratification based on the quintiles of the PS eliminates approximately 90% of bias due to measured confounders. More recently, inverse probability of treatment weighting (IPTW) [20] has become the method of choice. The normalized version of IPTW has been proposed [24, 25] which belongs to a broader class of weighted estimators described by Robins [26]. Several studies [21, 27] compared the relative performance of these methods. Covariate adjustment using PS and IPTW has been shown to be more sensitive to whether the PS has been accurately estimated [22, 28].
In this study, we investigate doubly robust (DR) estimation of cost and compare it to more conventional propensity score based approaches. DR estimation combines outcome regression (regression model) with weighting by PS (PS model) such that it is robust to misspecification of one (but not both) of these models [29, 30]. Lunceford and Davidian [21] demonstrated that the DR estimator performs better than stratification and IPTW. The doubly robust property is appealing but can still lead to biased estimates if both the regression model and the PS model are misspecified [31]. When using the DR method, the biggest challenge is to accurately model cost in the regression model. Given the heterogeneous nature of cost distributions and the many possible choices of cost models described above, we propose using an ensemble machine learning approach that relies on V-fold cross validation called Super Learner (SL) [32]. Using SL, we can incorporate various potential cost models and obtain asymptotically optimal prediction. Moreover, although logistic regression is the most commonly used method for estimating the PS; we can use SL to obtain PS estimates from other potential non-parametric PS models or PS models with different functional forms.
The goal of this study is to develop appropriate PS methods for estimating skewed and censored cost data. In the current literature, Basu et al. [33] have discussed several methods for estimating the ATE on health care costs. Anstrom and Tsiatis [34] have proposed on normalized IPTW for censored cost. We extend this literature by considering PS methods on censored cost. We begin by reviewing some of the existing cost estimation methods and then examine PS covariate adjustment, stratification and weighted approaches. We follow by discuss DR and the application of SL in cost estimation. We provide results from simulation studies that compare the performance of these estimators, and we also highlight the effect of PS mis-specification on treatment effect estimation and demonstrate the merits of SL. Finally, we apply these PS approaches to a cost analysis of two competing bladder cancer treatments, cystectomy versus bladder preservation therapy, using costs derived from SEER-Medicare data.
2. Cost estimation - existing methods
Cost estimation has been a great interest in the health economics literature. In this section we give some brief background on existing methods. We are interested in estimation cost up to time L. We define Yi(u) to be the known accumulated cost up to time u and Yi is the total cost that subject i accrues up to L. Let ti and Ci denote an individual's survival time and censoring time in the duration of interest respectively. Hence the random variable t is bounded by L. L can be considered as a large number such as 100 if we are interested in life time cost. The observables are given by:
We only observe Yi for the uncensored subjects. For censored subjects, their cost is still accruing hence their total cost Yi is unknown. in standard survival analysis we say censoring is non-informative if t⫫C. In total cost estimation Y is not non-informatively censored since Y(t)⫫Y(C) does not hold. In practice, a patient with high cost at the time of censoring, Y(C), is also likely to have high cost at the time of event Y(t) as that patients may likely have higher cost accrual rate. Hence, censoring of cost is not non-informative and standard survival techniques do not apply. Now, let K(u) = Pr(C ≥ u) be the probability of not being censored at time u. K(u) can be estimated from either parametric or non-parametric models. For instance, we can assume a parametric survival model such as an exponential or weibull and estimate K(u) based on maximal likelihood methods. Another approach is to use the Kaplan-Meier estimates K̂(u), based on the data (T, 1 – δ).
Economists and policy makers are often most interested in E(Y). We describe two popular existing methods to estimate E(Y) assuming individual cost history data are not recorded, i.e. only cost at event or censoring time Yi(Ti) is observed while Yi(u), u < Ti is unobserved. To estimate mean total cost E(Y), Lin et al. [8] proposed to partition the study period (0, L) into K subintervals and then “sum up” the cost contribution from subjects who died in each interval. Their method assumes that censoring only occurs at the boundaries of the subintervals. To overcome this limitation, Bang and Tsiatis [9] propose using cost information from uncensored subjects and then weighting each complete cost observation by the inverse of the probability of not being censored, which is evaluated at the time of the subject's death:
This weighted estimator is unbiased as . This estimator is also shown to be consistent regardless of the censoring pattern [9]. Intuitively, a subject that is observed to die at Ti represents subjects who would have been observed if there were no censoring.
Lin[13] also applied the same weighting technique to model the linear relationship between total cost and other covariates X as Y = β′X, when total cost is subjected to informative censoring. If there were no censoring, the least square normal equation can be simply written as . However, to account for censoring, Lin applied the same weighting idea and modified the above equation as follows:
This weighting method can also be applied to other regression models such as GLM or median regression as discussed by Lin [14] and Bang and Tsiatis[17].
3. Propensity score approaches
Cost information is often collected from observational databases which are subjected to confounding, here we develop propensity score approach to modeling censored cost data. Let Z be an indicator of the treatment exposure: Z = 1 if treated, Z = 0 if control. We adopt the counterfactual framework described by Rubin [35] and define to be the total cost of subject i if he were in the control group. Similarly, is the total cost if the patient had received treatment. Also, let and denote the survival time if the patient were in the control and treatment group respectively.
Although we are most interested in total cost Y, we want to consider both Y and survival time t as Y is dependent on t. We extend the usual assumption of strong ignorability to include both time and total cost as follows
| (1) |
We also modify the assumption of non-informative censoring to state:
| (2) |
In other words, we assume censoring time to be independent of potential failure time and cost outcomes as well of other confounders conditional on covariates and treatment assignment. This assumption is valid for end-of-study and other administrative censoring commonly seen in cost studies; and was first formally introduced by Anstrom and Tsiatis [34].
Moreover, let μ be the average causal treatment effect on cost adjusted for covariates X. We use μ1 and μ0 to represent E(Y(1)) and E(Y(0)) respectively. Therefore μ can be defined as:
| (3) |
Further, Kz(u) = P(C ≥ u|Z = z) and must be estimated separately for the treatment and control groups since they may have different survival trajectories. For simplicity, we use K̂(u) to denote the treatment-specific estimated probability of being uncensored at time u, K̂z(u).
Our goal is to estimate μ from observational data utilizing propensity score methods. We extend popular propensity score approaches to handle censored cost data. We also provide general step-by-step guidelines for the proposed methods. First, we need to estimate propensity scores e(X) = Pr(Z = 1|X). It is routine to estimate propensity scores from (Z, X) using a logistic regression model:
| (4) |
For simplicity, we write ei = e(Xi, β) and eβ = ∂ei/∂β. Moreover, β can be estimated using the maximum likelihood method by solving:
| (5) |
Estimated propensity scores êi can be predicted from the logistic regression model in Equation 4.
3.1. Covariate Adjustment
In the covariate adjustment approach, the outcome variables Y is regressed on Z along with the estimated propensity score ê, and any additional covariates (subset of X). Using an extension of the OLS model described by Lin [13], we impose the simple weights to account for censoring in costs. The choice of regression model depends on the nature of the outcome Y. Here we present three popular options:
Normal model
The simplest method is a standard linear regression, which assumes that the total cost Y follows a normal distribution, something unlikely to happen in practice. We regress Y on Z and ê weighted by :
| (6) |
Hence,
| (7) |
Lognormal model
This is similar to the linear regression model, except the outcome is transformed using the natural logarithm. This is a popular approach in health economics, as cost is transformed to reduce its skewness. The main shortcoming of this approach is that the analysis does not result in a model for μ in the original scale. Re-transformation to the original scale of interest is problematic [1] especially in the presence of heteroscedasticity. Nevertheless, log transformation of the response variable followed by OLS is still common. Assuming log-scale errors that are normally distributed with mean zero and common variance σ2, we regress log(Y) on Z and ê weighted by .
| (8) |
Hence,
| (9) |
Gamma model
The gamma distribution has a raw-scale variance function that is proportional to the square of the raw-scale mean function (Equation 10), an attribute common to many health applications. To implement this, we regress Y on Z and ê in a GLM model weighted by , and specify the variance family to be gamma.
| (10) |
| (11) |
Hence,
| (12) |
The variance of from covariance adjustment methods can be obtained in several ways. Analytically, the estimated variance of equals the variance of estimated from Equation 6. The variances of and can be derived using the delta method on Equation 8 and Equation 10. We can also use non-parametric bootstrapping to estimate the variances of , and .
3.2. Stratification
In stratification, subjects are first ranked and stratified into S mutually exclusive subsets based on êi. If balance between treatment groups is achieved within each stratum, we can estimate μ by a weighted sum of the difference of sample means of Yi across strata. Simple weights are imposed to account for informative censoring:
| (13) |
where Qs is the sth sample quantile of ê, nzs is the total number of subjects with Zi = z. Here, K̂s0(Ti) denotes the estimated probability of uncensoring for treated subjects in stratum s and K̂s1(Ti) the estimated probability of uncensoring for control subjects in stratum s. Within each stratum, subjects have roughly similar values of the propensity scores. Loosely speaking, we treat S strata as S different independent groups. Therefore, K̂(Ti) needs to be estimated separately for subjects in stratum s and treatment group z.
Notice that δi may be correlated with Zi since subjects on treatment may live longer; hence we are less likely to observe their complete cost information and δi is more likely to be zero. However, consistency of is still valid. Consistency follows from the fact that is bounded, total cost is bounded (see Appendix 1 of Bang and Tsiatis [9] for details) and the unbiasedness property of stratification method [21].
Lunceford and Davidian [21] recommended approximating the empirical variance by treating as the average of S independent, within-stratum, treatment effect estimates. If we further assume independence of δi and Zi, we have
where and are the sample variance of Yi for treated and control subjects in stratum s weighted by δi/K̂(Ti). In real life settings, it is unlikely that δi is independent of Zi. Hence, the formula above only serves as a “quick and dirty” variance estimate. In this case, it is preferably to obtain the variance of via bootstrapping [36].
3.3. Weighted approaches
Weighted estimators were first introduced by Horvitz and Thompson [37] and were extended to propensity scores by Rosenbaum [20]. There are many different weight choices; the most popular being the inverse probability of treatment weights (IPTW). IPTW are defined as , so that a subject's weight is equal to the inverse of the probability of receiving the treatment the subject was actually given. Again, simple weights are applied to account for informative censoring.
| (14) |
Another popular weight choice is the normalized version of IPTW [24, 25], which follows from and the estimating equations , .
| (15) |
As above δi may be correlated with Zi but the consistency of is still valid. Consistency of and can also be demonstrated using M estimation.
The variance of and can be obtained in several ways. One option is to use non-parametric bootstrapping. In addition, Anstrom and Tsiatis [34] derived the analytic form for the variance of when K(Ti) is estimated using the KM method. Similar methods can be used to derive the analytic variance of . If K(Ti) is estimated using parametric models, we can use M-estimation to derive in Equation 14 and 15. Here we give the sketch of the derivation when survival time ti follows an exponential distribution exp(λ):
λ can be estimated using the maximal likelihood . And thus . Together with Equation 5 and Equation 14 we have the following estimating equations:
| (16) |
Using the general framework described by Stefanski and Boos [38], var(θ) = A(θ)−1B(θ)[A(θ)−1]T where θ = (μ, β, λ)T. Hence Var(μ) is the top left corner entry of var(θ).
where , and .
where , , , and . The components of all of the above expressions can be estimated from the observed data.
4. Doubly Robust Estimation
Doubly Robust (DR) estimation incorporates outcome regression (regression model) and weighting by PS (PS model), and it is robust to misspecification of one (but not both) of these models. There are many forms of DR estimators; here we follow the general procedure described by Robins et al. [26]. DR estimator has the smallest large sample variance among the class of weighted estimators and is locally semi parametric efficient. First, we estimate the regression model for the treated group (Y ~ X for Z = 1) and obtain predicted values for the entire sample: m̂1(Xi). We then do the same for the control subjects and obtain predicted values for the entire sample: m̂0(Xi). In other words, m0(Xi) and m1(Xi) are the postulated models for the true regressions E(Y|Z = 0, X) and E(Y|Z = 1, X). Note that simple weights are applied to the regression models to account for informative censoring. The DR estimator of is given by:
| (17) |
Similar to section 2.2, the regression models m1(X) and m0(X) can be modeled in several ways:
Normal model:
| (18) |
Lognormal model:
| (19) |
Gamma model:
| (20) |
The doubly robust estimates are consistent if the propensity score model or the regression model m1(X) = E(Y|Z = 1, X) and m0(X) = E(Y|Z = 0, X) are correctly specified. To see this, consider . By the Law of Large Numbers, estimates:
Hence for to be unbiased, we need the second term to be zero. This condition is satisfied when the propensity score model is correctly specified: so . When the regression model m1(X) is correctly specified, so . Hence, the DR estimator is unbiased if either the propensity score model or the regression model is correctly specified. The doubly robust procedure has benefits over standard estimation but can result in biased estimates if both the regression model and PS model are misspecified [31].
5. Super-Learning
The Super-learner algorithm [32] is an ensemble machine learning approach based on V-fold cross validation. It allows one to specify several candidate prediction models and use them to produce an asymptotically optimal combination. Specifically, data are split into blocks and then each of the candidate algorithms are fitted on the training set and outcomes are predicted using the validation set. The loss function is calculated within each validation set, and averaging across validation sets provides the estimated cross validated risk score for each method The SL algorithm finds the optimal weighted combination of all the methods. Van der Laan et al. [32] proved asymptotic efficiency of the SL algorithm. Further, it is guaranteed to perform at least as well as the best estimators from the candidate models. This machine learning algorithm is available as an R package called Super Learner (https://cran.rproject.org/web/packages/SuperLearner/SuperLearner.pdf) and as a SAS macro [39]
In DR estimation, our primary concern is whether the cost regression models m1(X) and m0(X) are correctly specified. Given the heterogeneous nature of costs, there is no one-size-fits-all regression model. In machine learning literature, it is common to combine predictions from multiple models or multiple parametric and non-parametric predictive algorithms. Hence, one intuitive solution to accommodate the complex features of cost distribution is to employ SL to obtain the optimal prediction from common cost models.
Super-learner methods can also be applied when we are uncertain about model specification in the propensity model. Untill now, we have assumed the propensity score model to be correctly specified; but this is unlikely to be true in practice. If the correct subset and functional forms of covariates are unknown, we can include all combinations of potential subsets, interactions and quadratic forms of covariates and use SL to find the optimal estimates. Recent studies have proposed to use tree-based methods [40], random forests [41] and neural networks for estimating the PS. These can be included as candidate PS models, allowing SL to obtain optimal PS estimates from a wide variety of candidate algorithms [42].
6. Simulation studies
Using simulation studies, we evaluate the performances of all methods discussed in Section 2, 3 and 4 under various settings, including different survival models, cost models, and censoring distributions. We report the bias, the coverage probability of the resulting 95% confidence interval and the mean square error ratio (MSER) which is the ratio of MSE of each approach with reference to MSE of DR with SL in regression models.
We based choices of our simulation parameters on data from our bladder cancer study (Section 7). We simulated three covariates X = {X1, X2, X3}. Since most covariates in our empirical example were categorical, we simulated X1 and X2 as binary with success probabilities of 0.5 and 0.25 respectively. X3 followed a normal distribution with standard deviation 1 and mean 0. Using these covariates, we then defined treatment choice Z using a logit index model where D ~ Bernoulli(p) and
| (21) |
The coefficients were fixed so that approximately 30% of the population received treatment, to mirror our bladder cancer data. The sample sizes were set to be 1000 and 5000, typical sizes for observational studies.
We drew failure times from weibull and exponential distributions where . For weibull failure times, we set k = 2.5 and λ = 3.2 + 2Z + 1.2X1 + 1.4X2 – 0.6X3. For exponential failure times, k = 1 and λ = exp(–Z – 0.8X1 – 1.2X2 – 0.6X3). Censoring times were independently simulated from uniform distribution U(0, 20) and U(0, 12) for light and moderate censoring. The probability of censoring was approximately 20% for light censoring and 35% for moderate censoring, respectively. The latter scenario was similar to our bladder cancer example. Observed time was defined as the lesser of survival time and censoring time.
As medical costs are often complex and can come from very different distributions, we generated total medical costs from normal, lognormal and gamma distributions according to the parametrization shown below. The mixed distribution was a weighted average of the normal, lognormal and gamma cases.
Propensity scores were estimated using a logistic regression model assuming correct model specification according to Equation 21. We then applied PS covariates adjustment with normal, lognormal and gamma models, stratification, IPTW, normalized IPTW, DR with normal, lognormal and gamma regression models and DR using SL for regression models to estimate μ. Jiang and Zhou [36] showed that using bootstrap methods to estimate CI of mean cost work well. Bang and Tsiatis [9] also showed that bootstrap estimates of variance for mean cost are consistent with the analytically derived asymptotic variance estimates. In our analysis, there are several sources of variation for . For example, when using the DR estimator, we have variation from the PS model, KM model, regression models and the final DR estimation model. This greatly complicates analytic variance estimation but can be easily dealt with by using non-parametric bootstrapping. We used a bootstrap estimate with bias-corrected and accelerated (BCa) correction [43] to construct 95% CI confidence intervals of . Lastly, we included the naive regression method where total cost is regressed on the main effects of covariates in a linear model to recognize the consequences of analyses that do not properly account for confounding, skewness and censoring.
We simulated each scenario 500 times and summarize results by the empirical percentage bias (%bias), coverage probability of the 95% confidence interval (Coverage) and MSE ratio based on BCa standard errors (MSER). Note that for subjects with large observation time, if the estimated probability of censored K̂(ti) was zero, mini K̂(ti) in the specific treatment or treatment-stratum group was used instead to avoid the issue of the denominator of being zero. Thus, all empirical estimations of μ were under-estimations. The extent of under-estimation depends on the censoring proportion and method used.
6.1. Simulation results
Results of the simulation with various censoring and cost settings and sample size of 1000 appear in Table 1. The naive estimator ignoring censoring and confounders is biased under all settings. As anticipated, the PS covariate adjustment performs well when the correct model is specified, but exhibits bias when mis-specified. For example, when cost follows gamma distribution, covariate adjustment with gamma model yields 0.35% bias while the lognormal model had 18.74% bias under light censoring. If cost comes from a mixture of normal, lognormal and the gamma distributions, covariate adjustment methods perform poorly since the true relationship between outcome and PS is unknown. Of the covariate adjustment models, the gamma model is the most robust, with the smallest biases for misspecifed cost distributions, a finding consistent with Dodd et al.[3] and Basu et al. [4]. The PS stratification estimator has large biases and worst MSE among all PS methods. Note that stratification is most susceptible to under-estimation of μ. Since we need to calculate stratum and treatment specific K̂(u), K̂(u) is more likely to be zero for observations with large observation time T.
Table 1.
%Bias, coverage and relative efficiency for estimated treatment effect on cost
| normal | lognormal | gamma | mixed | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| light censoring | %bias | Coverage | MSER | %bias | Coverage | MSER | %bias | Coverage | MSER | %bias | Coverage | MSER |
| naive regression | −40.56 | 0.09 | 125.14 | −34.32 | 0.04 | 42.32 | −30.23 | 0.04 | 4.15 | −34.31 | 0.05 | 29.36 |
| covariates adjustmt: normal | 0.11 | 0.94 | 2.34 | −12.81 | 0.52 | 12.65 | −7.86 | 0.84 | 0.83 | −14.15 | 0.41 | 5.79 |
| covariates adjustmt: lognormal | 1.82 | 0.36 | 3.66 | −1.48 | 0.95 | 2.80 | 18.74 | 0.74 | 2.43 | −15.67 | 0.17 | 6.43 |
| covariates adjustmt: gamma | 0.35 | 0.95 | 2.36 | 2.62 | 0.94 | 1.19 | 0.35 | 0.96 | 0.62 | −11.45 | 0.49 | 3.90 |
| stratification | −1.43 | 0.84 | 10.33 | −8.99 | 0.85 | 5.84 | −3.30 | 0.90 | 1.15 | −4.73 | 0.89 | 3.23 |
| IPTW | −0.81 | 0.99 | 49.38 | −2.72 | 0.90 | 8.18 | −0.74 | 0.92 | 1.74 | −0.38 | 0.95 | 6.80 |
| IPTW: normalized | 0.13 | 0.94 | 39.94 | −0.03 | 0.90 | 7.26 | −0.09 | 0.90 | 1.61 | −0.08 | 0.93 | 5.75 |
| DR: normal | 0.02 | 0.97 | 1.00 | 0.83 | 0.92 | 1.85 | −0.36 | 0.91 | 1.00 | 0.44 | 0.95 | 1.34 |
| DR: lognormal | −0.02 | 0.96 | 1.08 | 0.36 | 0.94 | 1.01 | −0.42 | 0.92 | 1.04 | 0.03 | 0.97 | 1.03 |
| DR: gamma | −0.02 | 0.96 | 1.07 | 0.91 | 0.94 | 1.00 | −0.36 | 0.92 | 1.00 | 0.04 | 0.94 | 1.00 |
| DR: SL in regression model | 0.01 | 0.97 | 1 (ref) | 0.96 | 0.96 | 1 (ref) | 0.07 | 0.94 | 1 (ref) | 0.01 | 0.93 | 1 (ref) |
| moderate censoring | ||||||||||||
| naive regression | −67.59 | 0.04 | 188.13 | −25.61 | 0.03 | 35.21 | −44.57 | 0.02 | 5.59 | −47.69 | 0.08 | 32.93 |
| covariates adjustmt: normal | 0.56 | 0.92 | 2.92 | −12.18 | 0.69 | 7.10 | −8.12 | 0.87 | 0.76 | −14.69 | 0.48 | 4.14 |
| covariates adjustmt: lognormal | 2.33 | 0.52 | 4.14 | −1.49 | 0.97 | 4.47 | 33.36 | 0.59 | 3.76 | −13.47 | 0.51 | 3.43 |
| covariates adjustmt: gamma | 0.78 | 0.94 | 2.95 | 2.55 | 0.93 | 1.07 | 0.52 | 0.96 | 0.59 | −11.78 | 0.60 | 2.86 |
| stratification | −24.97 | 0.85 | 54.56 | −2.66 | 0.92 | 7.05 | −12.30 | 0.82 | 1.80 | −14.08 | 0.78 | 6.05 |
| IPTW | −1.68 | 0.90 | 92.04 | 2.14 | 0.96 | 10.49 | −6.58 | 0.90 | 2.36 | −5.51 | 0.90 | 8.49 |
| IPTW: normalized | 0.73 | 0.90 | 86.74 | 2.10 | 0.95 | 10.08 | −1.27 | 0.89 | 2.24 | −1.33 | 0.88 | 8.14 |
| DR: normal | −0.70 | 0.92 | 1.00 | 1.93 | 0.94 | 1.82 | −1.32 | 0.95 | 1.01 | −1.90 | 0.94 | 1.30 |
| DR: lognormal | −0.82 | 0.94 | 1.08 | 2.01 | 0.95 | 1.00 | −2.17 | 0.95 | 1.04 | −1.86 | 0.94 | 1.03 |
| DR: gamma | −0.79 | 0.94 | 1.08 | 2.01 | 0.95 | 0.98 | −1.15 | 0.96 | 1.01 | −1.72 | 0.94 | 1.00 |
| DR: SL in regression model | −0.73 | 0.96 | 1 (ref) | 1.81 | 0.97 | 1 (ref) | −1.12 | 0.97 | 1 (ref) | −1.41 | 0.95 | 1 (ref) |
IPTW estimators yield bias ranging from −0.38% to −6.58%. The normalized IPTW estimator has smaller bias than the typical IPTW, consistent with findings from Lunceford and Davidian [21]. Estimates from DR methods had very small bias, even when the regression model is mis-specified. Since the PS is correctly modeled, DR estimators should be unbiased due to their doubly robust property as demonstrated here. Correct regression model specification in DR has very small effect on bias and coverage since PS model is already correct. Nevertheless, using SL for the regression model results in small bias and MSE among all DR models. Simulations with a sample size of 5000 (data not shown) produce similar results in terms of bias and coverage, but have smaller MSE. As expected, the larger sample size increases overall estimation efficiency.
6.2. Misspecified PS
Next, we explore the case of PS misspecification when the correct model is unknown. We use the same simulation procedure as above changing Equation 21 to
| (22) |
In the simulated data, we estimated PS according to the correct model in Equation 22, and also a misspecified PS model with only main effects of X1, X2 and X3. Finally, we used SL to estimate PS using all possible combinations of the second order polynomials of X and the two way interactions among them. Table 2 shows the results for weibull survival time, light censoring, sample size of 1000, gamma and mixed cost models.
Table 2.
%Bias, coverage and relative efficiency for estimated treatment effect on cost under different PS estimation methods
| Correct PS | Misspecified PS | SL PS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| gamma model | %bias | Coverage | MSER | %bias | Coverage | MSER | %bias | Coverage | MSER |
| naive regression | −9.52 | 0.67 | 5.81 | ||||||
| covariates adjustmt: normal | 6.66 | 0.92 | 5.18 | 7.50 | 0.88 | 7.80 | 5.01 | 0.92 | 3.85 |
| covariates adjustmt: lognormal | −21.98 | 0.22 | 1.35 | −22.67 | 0.12 | 2.04 | −22.19 | 0.72 | 1.26 |
| covariates adjustmt: gamma | 0.30 | 0.94 | 2.07 | 4.13 | 0.94 | 3.12 | 0.30 | 0.96 | 1.53 |
| stratification | 2.85 | 0.91 | 10.54 | 32.58 | 0.77 | 20.65 | 1.77 | 0.94 | 5.94 |
| IPTW | 0.76 | 0.96 | 14.25 | 46.71 | 0.28 | 21.48 | 0.62 | 0.93 | 8.95 |
| IPTW: normalized | −0.36 | 0.94 | 1.83 | 8.88 | 0.90 | 2.76 | 0.21 | 0.92 | 1.58 |
| DR: normal | 0.61 | 0.94 | 1.46 | 0.75 | 0.93 | 1.31 | 0.30 | 0.94 | 1.07 |
| DR: lognormal | −0.71 | 0.94 | 1.45 | 8.91 | 0.89 | 1.05 | 0.38 | 0.96 | 0.93 |
| DR: gamma | 0.29 | 0.93 | 1.53 | 0.19 | 0.93 | 0.94 | 0.09 | 0.95 | 0.90 |
| DR: SL in regression model | 0.48 | 0.92 | 1 (ref) | 3.10 | 0.94 | 1 (ref) | 0.02 | 0.90 | 1 (ref) |
| mixed | |||||||||
| naive regression | −48.82 | 0.29 | 6.70 | ||||||
| covariates adjustmt: normal | 44.45 | 0.54 | 1.74 | 45.15 | 0.54 | 2.27 | 42.34 | 0.60 | 2.21 |
| covariates adjustmt: lognormal | −16.81 | 0.85 | 2.54 | −26.51 | 0.85 | 5.09 | −19.18 | 0.83 | 4.21 |
| covariates adjustmt: gamma | 23.84 | 0.79 | 1.46 | 15.84 | 0.79 | 1.84 | 21.56 | 0.84 | 1.71 |
| stratification | 12.64 | 0.91 | 5.49 | 15.47 | 0.77 | 16.84 | 9.25 | 0.95 | 3.57 |
| IPTW | 8.57 | 0.97 | 9.47 | 10.57 | 0.97 | 23.13 | 4.23 | 0.92 | 6.00 |
| IPTW: normalized | −1.00 | 0.94 | 1.10 | −2.00 | 0.94 | 1.88 | −0.80 | 0.92 | 1.05 |
| DR: normal | −1.81 | 0.96 | 1.74 | −8.07 | 0.96 | 1.03 | −1.21 | 0.95 | 1.06 |
| DR: lognormal | −2.00 | 0.97 | 3.85 | −6.77 | 0.98 | 1.86 | −1.24 | 0.96 | 1.07 |
| DR: gamma | −2.07 | 0.97 | 1.82 | −1.93 | 0.95 | 0.97 | −0.34 | 0.95 | 1.05 |
| DR: SL in regression model | −0.18 | 0.98 | 1 (ref) | −5.72 | 0.97 | 1 (ref) | −0.02 | 0.97 | 1 (ref) |
When the PS model is mis-specified, estimates from PS covariate adjustment are biased (4.13% to 45.15%). Estimates from IPTW methods are also highly biased (−2.00% to 46.71%) when PS model is mis-specified, in line with Rubin [28]. When the regression models in DR are correctly established, DR estimators have very small bias. However, when both the regression model and the PS model are wrong, as anticipated we see some bias (0.75% to 8.91%). Overall, PS misspecification affects all of the estimators discussed, especially those that are sensitive to PS. The only method that is robust to PS misspecification is DR, provided the regression model is correctly established.
When SL is used to estimate PS, we see significant improvement of performance across all estimators. In most cases, using SL in PS estimation yields less bias and better coverage than when the correct PS model is used. Hence, we recommend using SL when the correct PS model is unknown. When true cost comes from a mixture of normal, lognormal and gamma distributions, SL in DR can provide the best regression model estimates. In real life settings, it is highly likely that cost comes from a mixture of different distributions and the correct PS model is unknown. In this case, using SL with DR and PS estimation provides added flexibility which improves estimates substantially.
7. Costs of Bladder Cancer Therapies
Bladder cancer affects more than 70,000 people annually in the United States and accounts for almost 5% of the total cancer-related costs to Medicare. The guideline recommended treatment for bladder cancer is radical cystectomy (RC) which involves surgical removal of the bladder. Bladder preservation therapy (BPT) is a less aggressive, non-surgical alternative that involves radiation and chemotherapy. Recent studies have shown that BPT may improve quality of life over RC [44]. We have applied our method to compare the life-time cost of RC and BPT using a cohort of patients derived from SEER-Medicare registry.
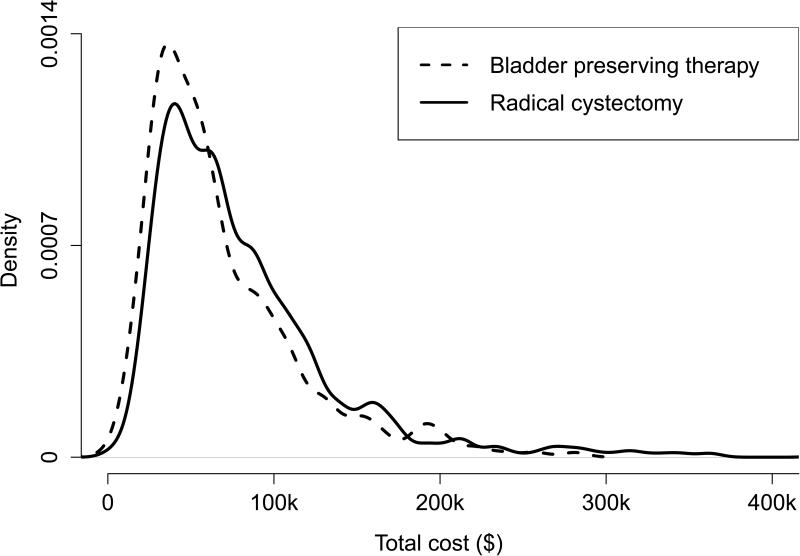
We included stage II/III bladder cancer patients diagnosed between 1995 and 2005. See Bekelman et al.[45] for a detailed description of inclusion/exclusion criterion. 32% of the study cohort were censored at the end of the study. Payment data were extracted from Carrier Claims file, the Outpatient file, and the Medicare Provider Analysis and Review Record. We adjusted all costs to year 2000 dollars using the Medicare Economics Index [46]. The final cohort sample size was 1860; 422 had BPT and 1438 had RC. The mean uncensored costs were $68,800 for BPT patients and $83,040 for RC patients. Total treatment cost were highly right skewed (Figure 1) with a maximum observed cost of $511,200. The average observation time was 3.93 years.
Figure 1.
Cost density plot of Bladder preserving therapy and Radical cystectomy.
In this study, both treatment assignment and total cost may have been affected by covariates such as stage, grade, race, marital status, comorbidities, median income at the census tract level and community size. Hence, we estimated PS using a logistic regression model that was adjusted for all of these potential confounders. We then estimated the difference in total cost between BPT and RC using the approaches described above including: PS covariates adjustment with normal, lognormal and gamma models, stratification, IPTWs, DR with normal, lognormal and gamma regression models and DR using SL in regression model. Naive linear regression ignoring censoring and non-random treatment assignment was used as a reference. Approximate confidence intervals for the treatment effect on cost were constructed using non-parametric bootstrapping with BCa correction.
From Table 3, BPT was estimated to be $7,412 cheaper than RC using naive regression. Difference in cost estimated from various propensity score methods ranged from −$10,661 to −$20,937, differed significantly from the naive regression method. Failure to account for censoring and the effect of confounders could lead to biased estimates. Furthermore, covariate adjustment, stratification and weighting methods could be sensitive to the choice of PS model estimation. Unsurprisingly, we saw large variation in treatment effect estimates from these models. DR models yielded more consistent treatment effect estimates; BPT was estimated to be −$12,144 to −$14,117 cheaper than RC. Using SL in regression model in DR gave slight different estimations (−$14,163). SL in regression model in DR is likely to be the closest to the true cost estimate as evidenced from the simulation study. Lastly, all CIs did not cross zero, indicating that BPT was significantly less costly than RC.
Table 3.
Estimated mean cost difference for bladder preserving therapy and radical cyccwetomy
| Regular PS Model | SL PS Model | |||
|---|---|---|---|---|
| Estimates | 95% CI | Estimates | 95% CI | |
| naive regression | −7,412 | (−13,545, −1,279) | - | - |
| covariates adjustment normal | −12,423 | (−22,235, −3,047) | −11,448 | (−23,237, −2,689) |
| covariates adjustment lognormal | −13,877 | (−25,729, −3,323) | −13,033 | (−26,674, −3,092) |
| covariates adjustment gamma | −12,482 | (−22,171, −2,400) | −11,599 | (−24,943, −3,579) |
| stratification | −17,678 | (−28,542, −9,685) | −15,416 | (−26,876, −787) |
| IPTW | −20,937 | (−34,244, −7,171) | −22,473 | (−30,633, −8,446) |
| IPTW: normalized weights | −10,661 | (−21,073, −1,078) | −11,951 | (−21,469, −607) |
| DR: normal | −12,163 | (−23,285, −764) | −12,312 | (−23,458, −104) |
| DR: lognormal | −14,117 | (−25,070, −3,444) | −14,086 | (−24,449, −3,333) |
| DR: gamma | −12,144 | (−22,920, −172) | −12,179 | (−23,745, −235) |
| DR: SL mean model | −14,163 | (−24,216, −3,941) | −14,086 | (−26,876, −787) |
Next we applied SL in propensity score model to obtain the estimated PS. We specify several potential propensity score models with different covariates functional forms: the basic logistic model where all covariates were included, also a model including all two way interactions between covariates, adding square terms of all covariates and a backwards stepwise selection algorithm with cut-off p-value of 0.1. SL was used to find the optimal combination of predications from these candidate models. We then use this estimated PS to find the differences in cost between BPT and RC.
From Table 3, the SL PS models provided similar estimates from the regular PS models. One possible explanation is all covariates were categorical, hence there was little variation in PS due to limited covariate patterns. Interaction and quadratic terms might not have a huge impact on PS estimation for the same reason. SL PS model would be more useful when we have little understanding of the true PS model. Nevertheless, SL PS showed that the estimates of cost differences were between −$11,448 and −$22,473, and 95% CIs strongly suggest the differences in cost between BPT and RC were significant.
All of the approaches discussed above demonstrate that BPT substantially decreases the total medical cost compared to the standard treatment RC. However, we observed significant variations in the ATE estimations and large range in the CIs. From our simulation studies, we believe DR with SL in both regression model and PS model provides the best estimate. Hence, our findings indicate that BPT was $14,086 ($787, $26,876) cheaper than RC.
8. Discussion
In this study, we explored propensity score based approaches for estimating the treatment effect on censored costs in an observational study. We extended covariate adjustment, stratification, weighting and doubly robust methods to handle censored medical cost. We also utilized a machine learning algorithm, Super Learner, to better estimate PS and the regression models in DR. Our simulation studies showed that when PS is correctly modeled, stratification and weighting yield unbiased estimates. Covariate adjustment is sensitive to the choice of outcome model, while DR is more robust to misspecification. When the correct PS model is unknown, misspecification could result in biased estimates of the treatment effect even when using DR methods. SL mitigates this bias by producing optimal regression models and PS estimates. In addition, one may consider tree-based methods, random forests and neural networks. These methods can be easily incorporated into SL to obtain optimal PS estimation from both fully parametric and non parametric models.
We note that in this study, we only used total cost data and ignored cost history data which may be available from claims data. Bang and Tsiatis[9] have proposed partitioned estimators making use of cost history data which they showed to be more efficient than the simple weighted approach we employed. It is unclear what the effect of partitioned estimators would have on PS-based estimation and is worthy of future work.
We have shown that the variance of the IPTW estimator can be obtained analytically. However, multi-parameter or non-parametric survival models add substantial complexity to analyzing variance estimates due to the complex interaction between censoring and propensity scores.
As in any observational study, unobserved or hidden bias may be of concern. We suggest that in addition to a propensity score based analysis of censored cost data, one should conduct a carefully planned sensitivity analysis to assess the effect of an unmeasured confounder on the treatment effect [47].
Acknowledgment
Dr. Bekelman was supported by K07-CA163616. Dr. Handorf was supported by NIH grant P30-CA06927. We used the linked SEER-Medicare database and acknowledge the efforts of the Applied Research Program; National Cancer Institute; Office of Research, Development and Information; Centers for Medicare and Medicaid Services; Information Management Services; and SEER program tumor registries in the creation of the SEER-Medicare database.
References
- 1.Manning WG, Mullahy J. Estimating log models : to transform or not to transform? Journal of Health Economics. 2001;20:461–494. doi: 10.1016/s0167-6296(01)00086-8. [DOI] [PubMed] [Google Scholar]
- 2.Manning WG, Basu A, Mullahy J. Generalized modeling approaches to risk adjustment of skewed outcomes data. Journal of Health Economics. 2005;24(3):465–488. doi: 10.1016/j.jhealeco.2004.09.011. [DOI] [PubMed] [Google Scholar]
- 3.Dodd S, Bassi A, Mrcp KB, Williamson P. A comparison of multivariable regression models to analyse cost data. Journal of Evaluation in Clinical Practice. 2006;12(1):76–86. doi: 10.1111/j.1365-2753.2006.00610.x. [DOI] [PubMed] [Google Scholar]
- 4.Basu A, Manning WG, Mullahy J. Comparing alternative models: log vs cox proportional hazard? Health Economics. 2004;13(8):749–766. doi: 10.1002/hec.852. [DOI] [PubMed] [Google Scholar]
- 5.Basu A, Rathouz PJ. Estimating marginal and incremental effects on health outcomes using flexible link and variance function models. Biostatistics. 2005;6(1):93–109. doi: 10.1093/biostatistics/kxh020. [DOI] [PubMed] [Google Scholar]
- 6.Tian L, Huang J. A two-part model for censored medical cost data. Statistics in Medicine. 2007;26:4273–4292. doi: 10.1002/sim.2847. doi:10.1002/sim. [DOI] [PubMed] [Google Scholar]
- 7.Basu A, Manning WG. Estimating lifetime or episode-of-illness costs under censoring. Health Economics. 2010;19:1010–1028. doi: 10.1002/hec.1640. [DOI] [PubMed] [Google Scholar]
- 8.Lin DY, Feuer EJ, Etzioni R, Wax Y. Estimating medical costs from incomplete follow-up data. Biometrics. 1997;53(2):419–434. [PubMed] [Google Scholar]
- 9.Bang H, Tsiatis A. Estimating medical costs with censored data. Biometrika. 2000;87(2):329–343. [Google Scholar]
- 10.Zhao H, Bang H, Wang H, Pfeifer PE. On the equivalence of some medical cost estimators with censored data. Statistics in Medicine. 2007;26:4520–4530. doi: 10.1002/sim.2882. doi:10.1002/sim. [DOI] [PubMed] [Google Scholar]
- 11.Zhao H, Cheng Y, Bang H. Some insight on censored cost estimators. Statistics in Medicine. 2011;30(19):2381–2388. doi: 10.1002/sim.4295. doi:10.1002/sim.4295.Some. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Raikou M, McGuire A. Estimating medical care costs under conditions of censoring. Journal of Health Economics. 2004;23(3):443–470. doi: 10.1016/j.jhealeco.2003.07.002. [DOI] [PubMed] [Google Scholar]
- 13.Lin D. Linear regression analysis of censored medical costs. Biostatistics. 2000;1(1):35–47. doi: 10.1093/biostatistics/1.1.35. [DOI] [PubMed] [Google Scholar]
- 14.Lin D. Regression analysis of incomplete medical cost data. Statistics in Medicine. 2003;22(7):1181–1200. doi: 10.1002/sim.1377. [DOI] [PubMed] [Google Scholar]
- 15.Baser O, Gardiner JC, Bradley CJ, Given CW. Estimation from censored medical cost data. Biometrical Journal. Jul;(3):351–363. doi:10.1002/bimj.200210036. [Google Scholar]
- 16.Ying Z, Jung S, Wei L. Survival analysis with median regression models. Journal of the American Statistical Association. 1995;90(429):178–184. [Google Scholar]
- 17.Bang H, Tsiatis A. Median regression with censored cost data. Biometrics. 2002;58(3):643–649. doi: 10.1111/j.0006-341x.2002.00643.x. [DOI] [PubMed] [Google Scholar]
- 18.Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- 19.Austin PC. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate Behavioral Research. 2011;46(3):399–424. doi: 10.1080/00273171.2011.568786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rosenbaum PR. Model-based direct adjustment. Journal of the American Statistical Association. 1987;82(398):387–394. [Google Scholar]
- 21.Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine. 2004;23(19):2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- 22.Austin PC, Mamdani MM. A comparison of propensity score methods: a case-study estimating the effectiveness of post-ami statin use. Statistics in Medicine. 2006;25(12):2084–2106. doi: 10.1002/sim.2328. [DOI] [PubMed] [Google Scholar]
- 23.Rubin DB, Rosenbaum PR. Reducing bias in observational studies using score on the propensity subolassification. The American Economic Review. 1984;79(387):516–524. [Google Scholar]
- 24.Hirano BYK, Imbens GW, Ridder G. Efficient estimation of average treatment effects using the estimated propensity score. Econometrica. 2003;71(4):1161–1189. [Google Scholar]
- 25.Busso M, DiNardo J, McCrary J. New evidence on the finite sample properties of propensity score reweighting and matching estimators. Review of Economics and Statistics. 2014;96(5):885–897. [Google Scholar]
- 26.Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some of regression coefficients estimation regressors are not always observed. Journal of the American Statistical Association. 1994;89(427):846–866. [Google Scholar]
- 27.Austin PC, Grootendorst P, Anderson GM. A comparison of the ability of different propensity score models to balance measured variables between treated and untreated subjects: a monte carlo study. Statistics in Medicine. 2007;26(4):734–753. doi: 10.1002/sim.2580. [DOI] [PubMed] [Google Scholar]
- 28.Rubin DB. On principles for modeling propensity scores in medical research. Pharmacoepidemiology and Drug Safety. 2004;13(April):855–857. doi: 10.1002/pds.968. doi:10.1002/pds.968. [DOI] [PubMed] [Google Scholar]
- 29.Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61(December):962–972. doi: 10.1111/j.1541-0420.2005.00377.x. doi:10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- 30.Tsiatis AA, Davidian M. Comment: Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science: a review journal of the Institute of Mathematical Statistics. 2007;22(4):569. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Funk MJ, Westreich D, Wiesen C, Stürmer T, Brookhart MA, Davidian M. Doubly robust estimation of causal effects. American Journal of Epidemiology. 2011;173(7):761–767. doi: 10.1093/aje/kwq439. doi:10.1093/aje/kwq439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Van der Laan MJ, Polley EC, Hubbard AE. Super learner. Statistical Applications in Genetics and Molecular Biology. 2007;6(1) doi: 10.2202/1544-6115.1309. [DOI] [PubMed] [Google Scholar]
- 33.Basu A, Polsky D, Manning WG. Estimating treatment effects on healthcare costs under exogeneity: is there a ‘magic bullet’? Health Services and Outcomes Research Methodology. 2011;11(1-2):1–26. doi: 10.1007/s10742-011-0072-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Anstrom KJ, Tsiatis AA. Utilizing propensity scores to estimate causal treatment effects with censored time-lagged data. Biometrics. 2001;57(4):1207–1218. doi: 10.1111/j.0006-341x.2001.01207.x. [DOI] [PubMed] [Google Scholar]
- 35.Rubin D. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- 36.Jiang H, Zhou XH. Bootstrap confidence intervals for medical costs with censored observations. Statistics in Medicine. 2004;23(21):3365–3376. doi: 10.1002/sim.1556. [DOI] [PubMed] [Google Scholar]
- 37.Horvitz D, Thompson D. A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association. 1952;47(260):663–685. [Google Scholar]
- 38.Stefanski L, Boos D. The calculus of m-estimation. The American Statistician. 2002;56:29–38. [Google Scholar]
- 39.Brooks JC. PhD Thesis. University of California; Berkeley: 2012. Super learner and targeted maximum likelihood estimation for longitudinal data structures with applications to atrial fibrillation. [Google Scholar]
- 40.Setoguchi S, Schneeweiss S, Brookhard M, Glynn R, Cook F. Nih public access. Pharmacoepidemiology and Drug Safety. 2009;27(6):417–428. doi:10.1055/s-0029-1237430. [Google Scholar]
- 41.Lee BK, Lessler J, Stuart Ea. Improving propensity score weighting using machine learning. Statistics in Medicine. 2010;29(3):337–346. doi: 10.1002/sim.3782. doi:10.1002/sim.3782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gruber S, Logan RW, Jarrín I, Monge S, Hernán MA. Ensemble learning of inverse probability weights for marginal structural modeling in large observational datasets. Statistics in Medicine. 2015;34(1):106–117. doi: 10.1002/sim.6322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Efron B. Better bootstrap confidence intervals. Journal of the American statistical Association. 1987;82(397):171–185. [Google Scholar]
- 44.Efstathiou JA, Spiegel DY, Shipley WU, Heney NM, Kaufman DS, Niemierko A, Coen JJ, Skowronski RY, Paly JJ, McGovern FJ, et al. Long-term outcomes of selective bladder preservation by combined-modality therapy for invasive bladder cancer: the mgh experience. European Urology. 2012;61(4):705–711. doi: 10.1016/j.eururo.2011.11.010. [DOI] [PubMed] [Google Scholar]
- 45.Bekelman JE, Handorf EA, Guzzo T, Pollack CE, Christodouleas J, Resnick MJ, Swisher-McClure S, Vaughn D, Ten Have T, Polsky D, et al. Radical cystectomy versus bladder-preserving therapy for muscle-invasive urothelial carcinoma: examining confounding and misclassification biasin cancer observational comparative effectiveness research. Value in Health. 2013;16(4):610–618. doi: 10.1016/j.jval.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Centers for Medicare and Medicaid. Medicare economic index 2010 URL http://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/MedicareProgramRatesStats/Downloads/mktbskt-summary.pdf.
- 47.Handorf Ea, Bekelman JE, Heitjan DF, Mitra N. Evaluating costs with unmeasured confounding: A sensitivity analysis for the treatment effect. Annals of Applied Statistics. 2013;7(4):2062–2080. doi: 10.1214/13-AOAS665. doi:10.1214/13-AOAS665. [DOI] [PMC free article] [PubMed] [Google Scholar]