Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Apr 26.
Published in final edited form as: ACS Nano. 2016 Apr 15;10(4):4644–4651. doi: 10.1021/acsnano.6b00940

Water Mediates Recognition of DNA Sequence via Ionic Current Blockade in a Biological Nanopore

Swati Bhattacharya †,§, Jejoong Yoo †,‡,§, Aleksei Aksimentiev †,¶,✉
PMCID: PMC4849127  NIHMSID: NIHMS779919  PMID: 27054820

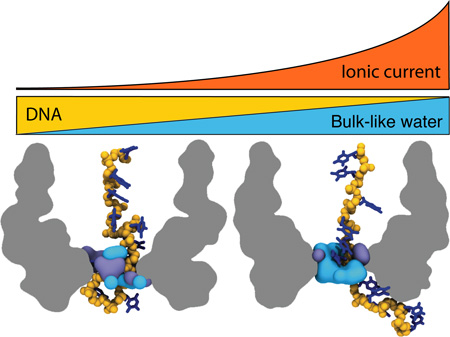
Abstract

Electric field-driven translocation of DNA strands through biological nanopores has been shown to produce blockades of the nanopore ionic current that depend on the nucleotide composition of the strands. Coupling a biological nanopore MspA to a DNA processing enzyme has made DNA sequencing via measurement of ionic current blockades possible. Nevertheless, the physical mechanism enabling the DNA sequence readout has remained undetermined. Here, we report the results of all-atom molecular dynamics simulations that elucidated the physical mechanism of ionic current blockades in the biological nanopore MspA. We find that the amount of water displaced from the nanopore by the DNA strand determines the nanopore ionic current, whereas the steric and base-stacking properties of the DNA nucleotides determine the amount of water displaced. Unexpectedly, we find the effective force on DNA in MspA to undergo large fluctuations, which may produce insertion errors in the DNA sequence readout.

Graphical abstract

graphic file with name nihms779919f6.jpg

The dramatic reduction of DNA sequencing costs has enabled new scientific discoveries and holds promise for spectacular advances in medical practice.1 The nanopore method of sequencing DNA promises further reductions of the sequencing costs by offering very long sequence reads from unlabeled DNA.2 Coupling an engineered biological nanopore to a DNA processing enzyme has made nanopore sequencing by measuring ionic current feasible,3–9 however, the microscopic mechanism of sequence detection has remained unknown.

In a typical experimental system, a single MspA nanopore10 is embedded in a lipid bilayer membrane and a DNA strand threaded through the nanopore, Figure 1a. A phi29 polymerase is attached to the junction of single- and double-stranded DNA at the rim of the MspA nanopore. An electric field is applied across the membrane via electrodes immersed in the electrolyte solution on both sides of the membrane, generating ionic current through the nanopore. In the process of DNA synthesis, the DNA polymerase pulls the DNA strand through the pore constriction in discrete steps, against the force of the applied electric field.7 The DNA sequence is inferred by measuring the ionic current owing through the nanopore and using a look-up table to associate a particular current level with the sequence of DNA nucleotides in the nanopore.8

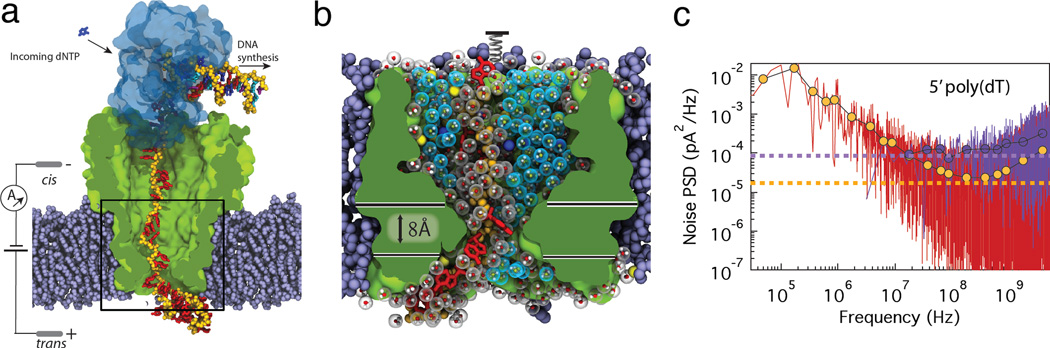
Figure 1. Molecular dynamics simulations of blockade currents in MspA.

Figure 1

Open in a new tab

(a) All-atom model of MspA (green) suspended in a lipid bilayer membrane (purple spheres). A phi29 polymerase (blue semitransparent surface) is bound to the junction of single- and double-stranded DNA (the DNA backbone is shown using yellow spheres). Water and ions are not shown. The black rectangle indicates approximate dimensions of the reduced-length system shown in panel b. (b) Minimal simulation system containing a reduced-length MspA channel, a fragment of DNA strand, potassium and chloride ions (blue and yellow spheres, respectively), and water. Individual water molecules are shown as molecular bonds enclosed by a semi-transparent sphere. Blue and grey spheres represent bulk and structured water molecules, respectively. Structural water molecules are defined as those located within 2.5 Å of any protein or DNA atom. The horizontal lines define the constriction region of MspA used in subsequent analysis. (c) Power spectral density of the ionic current obtained from the simulations of the minimal MspA system containing a 5′-poly(dT) strand (red) and the open pore (no DNA) minimal MspA system (purple). For each system, a theoretical noise oor is shown as a horizontal dashed line. The symbols show the block-average values of the respective PSDs.

Empirical data so far have shown no simple relation between the sequence of DNA (or RNA) nucleotides in the nanopore constriction and the nanopore ionic current.11–14 In the case of MspA, the current is affected by at least three adjacent nucleotides and depends on the global orientation of the DNA strand in the nanopore.12 Defying simple geometric arguments, larger nucleotides adenine (A) and guanine (G) can block the current less than smaller cytosine (C), thymine (T) or uracil (U).15–18 The current blockades are not additive; knowing the blockade current for all DNA homopolymers does not permit prediction of the blockade current for a heterogeneous sequence.8, 12 Here, we use a special-purpose supercomputer system19 to determine the microscopic mechanism by which the sequence of DNA nucleotides affects the ionic current owing through the biological nanopore, MspA.

Results and Discussion

To determine the microscopic origin of the sequence dependence of the ionic current blockades we obtained multiple molecular dynamics (MD) trajectories of the MspA nanopore system. Our exploratory simulations of the full-length MspA-DNA-phi29 system (Supplementary Methods 1, Supplementary Figure 1 and Supplementary Movie 1) showed that the conformation of the DNA strand in the pore constriction is not affected by the motion of the DNA polymerase at the rim of MspA. This observation allowed us to make efficient use of the special purpose supercomputer system19 by constructing a minimal simulation system containing a single copy of a truncated MspA nanopore (residues 75 to 120), a DNA strand, lipids and 1 M KCl solution, Figure 1b. To mimic the action of a DNA polymerase, a terminal nucleotide of the DNA strand was restrained using a harmonic potential, which also directly reported the effective force applied to the DNA strand in the nanopore. We have previously shown that truncation of the MspA pore does not considerably alter the distribution of the electrostatic potential inside MspA,20 Supplementary Figure 2; similar reduced models have been used in MD studies of alpha-hemolysin systems.21, 22 Six homopolymer systems were simulated in continuous 10–30 µs runs under a transmembrane bias of 180 mV. The ionic currents were computed by measuring average displacements of the ions23 in the 8-Å section of the MspA constriction, Figure 1b.

Like in any experimental measurement of the nanopore ionic current, our simulated ionic current recordings are subject to noise. In our computational experiments, possible sources of noise include thermal motion of ions, stochastic variation of the number of ions in the nanopore (counting noise) and conformational fluctuation of the DNA and the channel. Figure 1c plots the noise power spectral density (PSD) of the simulated ionic current for the minimal MspA system with and without DNA. In the absence of DNA (the open pore case), the noise PSD does not considerably depend on the frequency and remains close to the theoretical noise floor 4kBT/R,24–27 where R is the electrical resistance. In the presence of DNA, 1/f noise develops for frequencies less than 108 Hz, which, as we show below, is associated with the conformational fluctuations of the DNA strand. The PSD curve levels off around 105 Hz. Note that typical experimental PSDs feature the 1/f dependence that extends to much lower frequencies,24–27 indicating the effect of noise sources absent in our MD simulations.

Figure 2a–c (center panels) and Supplementary Figure 3 plot the ionic current traces obtained for homopolymers of T, A and C nucleotides for the 5′-trans and 3′-trans orientations of the strand, respectively. The traces show considerable fluctuations of the current at the microsecond timescale, which we attribute to the structural dynamics of DNA in the nanopore, see Supplementary Movies 2–7. The all-point histograms of the simulated ionic current traces, Figure 2a–c (right panels), are asymmetric; their shapes (but not the average current values) depend on the current block-averaging interval, becoming more compact as thermal fluctuations are averaged out, Supplementary Figure 4 and Supplementary Note 1.

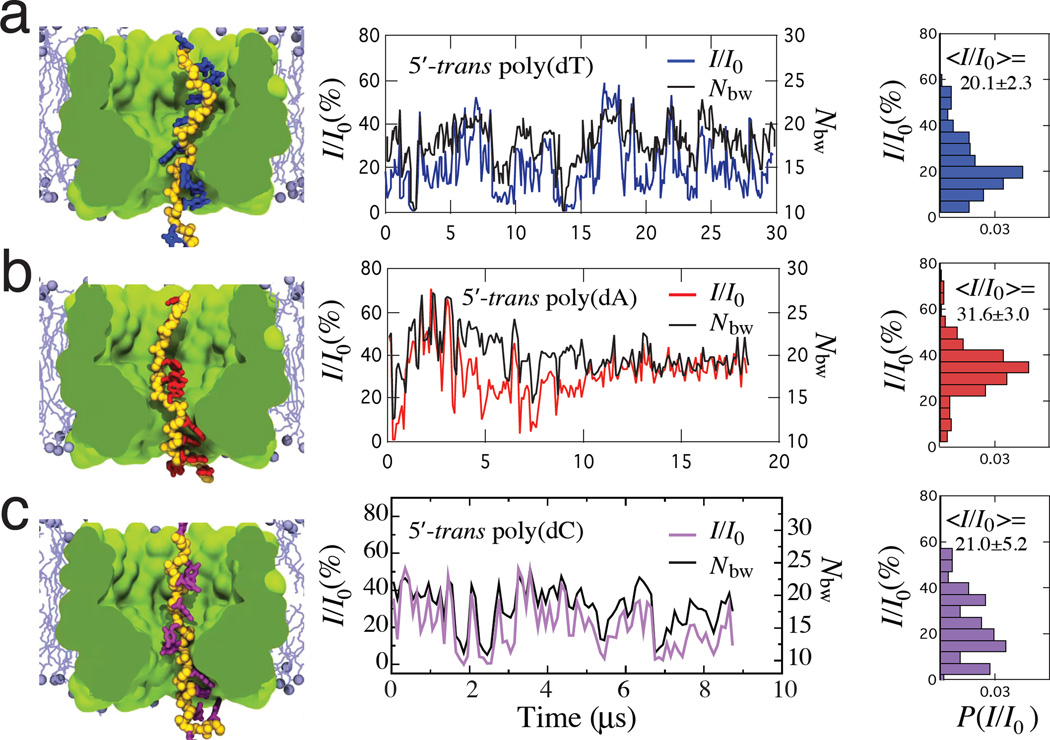
Figure 2. Simulated ionic current blockade traces.

Figure 2

Open in a new tab

(a) (Left) A representative conformation of a thymine homopolymer. (Center) Blockade current (color) and the number of bulk-like water molecules (black) in the MspA constriction versus simulation time for the minimal systems containing a thymine homopolymer threaded through MspA in the 5′-trans orientation of the strand. Each data point shows a 100 ns block-average of the 100 ps-sampled MD trajectory, see Supplementary Note 1. (Right) Normalized histograms of the blockade current traces for thymine homopolymer. The histograms were built using 100 ns block-averages of the 100 ps-sampled current. Supplementary Figure 3 shows the ionic current traces for the 3′-trans systems. Supplementary Movies 2–7 illustrate the six MD trajectories. (b,c) Same as in panel a but for adenine and cytosine homopolymers threaded through MspA in the 5′-trans orientation of the strand.

Despite considerable fluctuations, the average values of the blockade currents could be determined for five out of six homopolymers; the 3′-trans poly(dA) trace did not converge within the simulation time scale. In qualitative agreement with experiment,12 the blockade current for 5′-poly(dA), 31.6±3.0%, is greater than that for 5′-poly(dT), 20.1±2.3%, whereas the blockade current for 3′-poly(dT), 21.5 ± 0.9%, is greater than that for 3′-poly(dC), 16.7 ± 0.9%. The error was estimated by splitting the simulation trajectories into 5-µs intervals, Supplementary Figure 5. Similar blockade currents were measured in the ensemble simulations of DNA homopolymers, Supplementary Table 1, where sixteen replicas of each DNA homopolymer systems were simulated for 400–900 ns each starting from a unique microscopic conformation20 (Supplementary Methods 2, Supplementary Figure 6). As our simulations employed a reduced-length model of the MspA nanopore, the simulated blockade currents are higher than the experimental ones (Supplementary Note 2).

The number of water molecules in the MspA constriction was found to strongly correlate with the ionic current owing through MspA. For the analysis of our MD trajectories, we selected an 8-Å section of the MspA nanopore centered on the pore constriction (residues 90 and 91), Figure 1b. For our subsequent analysis we refer to water molecules residing within the first solvation shell of MspA or DNA, i.e., waters molecules located within 2.5 Å of protein or DNA atoms, Supplementary Figure 7, as structured water28 and all other water molecules as bulk-like water. The black traces in Figure 2a–c (center panels) show the number of bulk-like water molecules in the pore constriction. In all systems studied, we found a strong correlation between the number of bulk-like water molecules (Nbw) and the blockade current I/I0. Including water molecules that were in direct contact with the protein or DNA (structured water) reduced but did not eliminate the correlation, Supplementary Table 2. The correlation decreased with the block averaging interval, Supplementary Figure 4, and was very weak in the absence of DNA, Supplementary Figure 8.

Approximating the volume of the MspA constrictions as a cylinder of uniform conductivity, one could expect the ionic current to linearly depend on the number of water molecules, Supplementary Note 3. In contrast, the complex shape of the volume occupied by the bulk-like water molecules in the constriction of MspA, Figure 3a, makes the dependence of the nanopore ionic current I on the number of bulk-like water molecules Nbw superlinear: I~Nbw1.6, Figure 3b. At low water count (Nbw = 10 or 17 in Figure 3a), the bulk-like water does not form a stable continuous passage through the constriction. At higher water counts (Nbw = 21 or 25 in Figure 3a), a continuous passage exists, but its diameter is considerably smaller than that of a cylinder containing the same number of water molecules. It appears that the amount of water that can be displaced along the ion path through the nanopore determines the ion conductance. Supplementary Movie 8 illustrates typical behavior of bulk and structured water molecules during an ion permeation event.

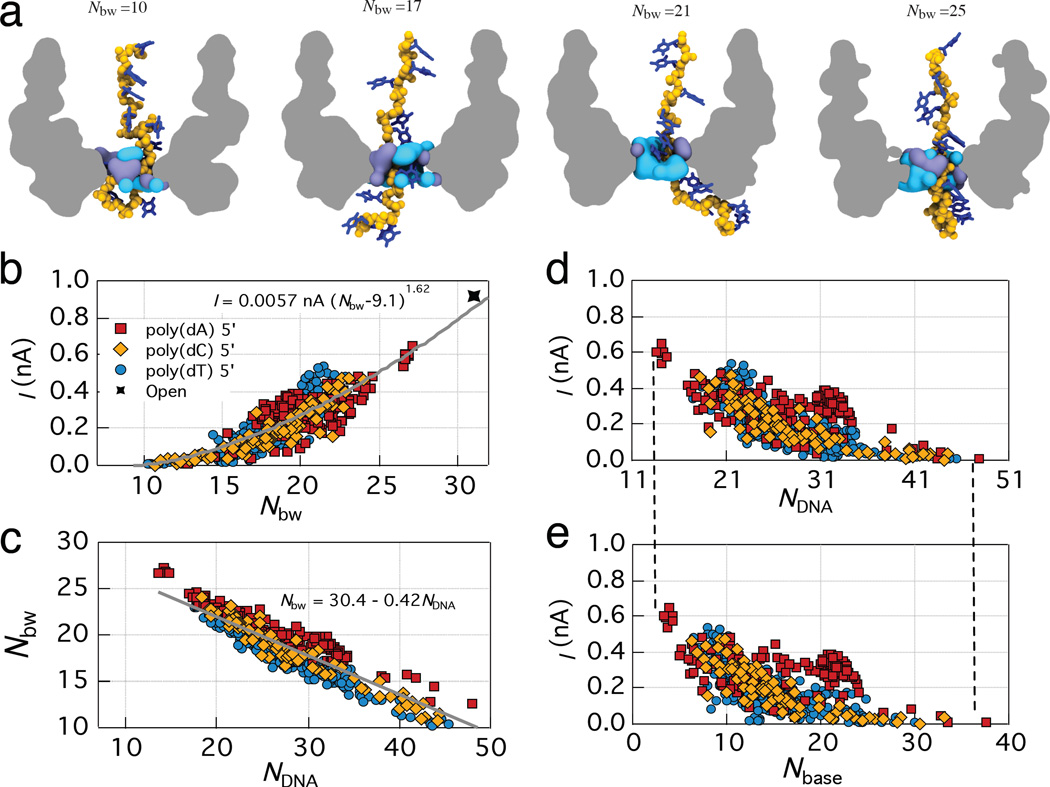
Figure 3. Microscopic mechanism of the ionic current blockades.

Figure 3

Open in a new tab

(a) Instantaneous volumes occupied by bulk-like water (light blue) and structured water (purple) in the MspA constriction. The number of water molecules in the bulk-like water volume is indicated in each snapshot. An outline of the MspA channel and the poly(dT) strand are shown for reference. (b) Ionic current versus the number of bulk-like water molecules in the constriction of MspA for the 5′-trans DNA homopolymer systems. The gray line shows a power-law fit to the data. Supplementary Table 2 lists parameters of the fit for individual trajectories. All data points in panels b–e show 100 ns block averages of the 100 ps-sampled data from the respective MD trajectories. (c) The number of bulk-like water molecules versus the number of non-hydrogen DNA atoms in the constriction of MspA. The gray line shows a linear fit to the data. (d,e) The ionic current versus the number of non-hydrogen atoms of DNA nucleotides (d) or DNA bases (e) in the constriction of MspA. The vertical dashed lines are guides for the eyes.

The presence of DNA nucleotides affects the nanopore ionic current by altering the number of bulk-like water molecules in the MspA constriction. The amount of water displaced by DNA from the constriction depends linearly on the number of DNA atoms, Figure 3c, indicating the absence of pockets of vacuum that can form in narrow hydrophobic cavities.29 Among all atoms that constitute a DNA strand, the atoms that comprise the nucleobases cause the difference in ionic current blockades produced by the DNA homopolymers. In-deed, the dependence of the ionic current on the number of non-hydrogen atoms of the entire DNA stand, Figure 3d, closely follows the dependence of the current on the number of non-hydrogen atoms comprising only the nucleobases, Figure 3e. The PSDs of the number of bulk-like water molecules and non-hydrogen atoms of DNA nucleotides, Supplementary Figure 9, exhibit the 1/f dependence on the sampling frequency similar to that of the ionic current, Figure 1c, indicating that the 1/f noise in the simulated ionic current is produced by the changes in the DNA conformation.

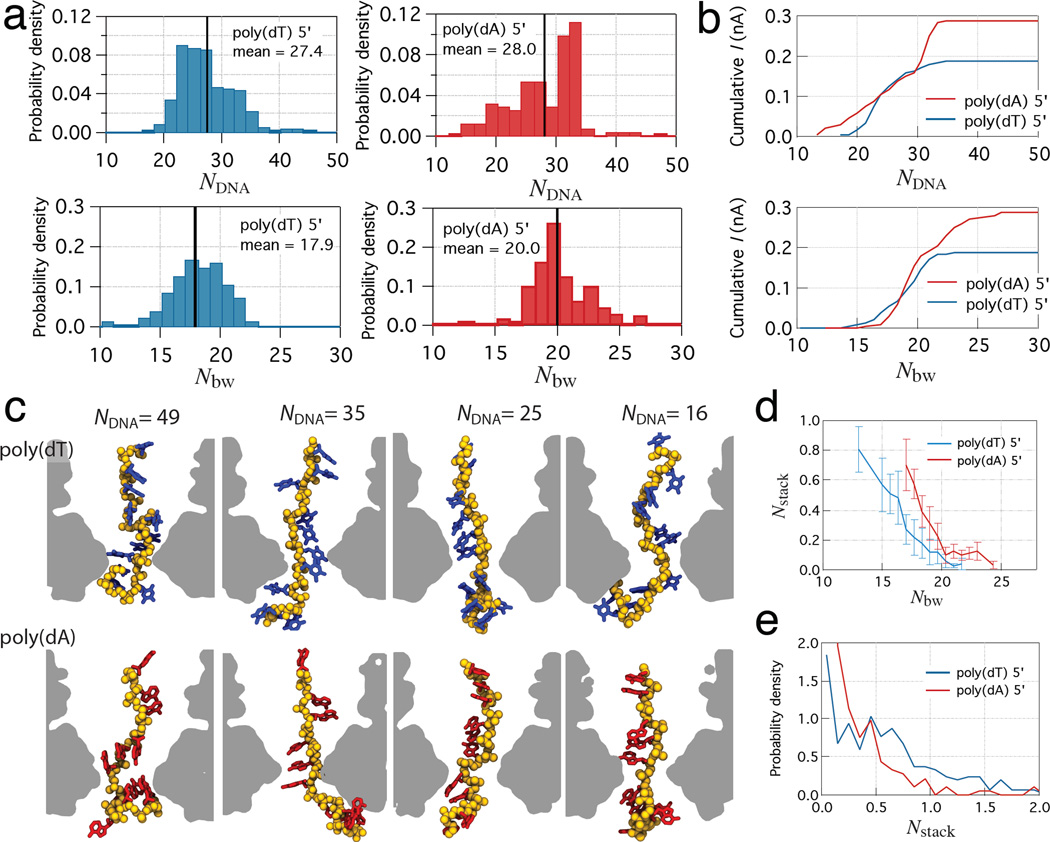
The sequence specificity of the ionic current blockades originates from the statistical differences in the ensemble of conformations that DNA strands adopt in the constriction of MspA. The probability of observing a given number of DNA atoms and a given number of bulk-like water molecules in the MspA constriction differ considerably between the 5′-poly(dA) and 5′-poly(dT) systems, the former has a higher probability in the low DNA atom / high bulk-like water count range, Figure 4a,b. Supplementary Figure 10 shows equivalent data for the 3′-poly(dT) and 3′-poly(dC) systems. Because the dependence of the ionic current on the number of bulk-like water molecules is superlinear (Figure 3b), considerably higher currents are observed in the 5′-poly(dA) system, which is characterized by more frequent high-water-count microscopic states. The high number of DNA atoms (low current) is observed when nucleotides stack and jam the constriction whereas the low number of DNA atoms (high current) is associated with a broken base-stacking pattern, Figure 4c. The number of base-stacked nucleotides in the MspA constriction is anti-correlated with the number of bulk-like water molecules, Figure 4d. The probability of observing base-stacking in the 5′-poly(dT) system is higher than in 5′-poly(dA), Figure 4e, opposite to the behavior observed in bulk solution.30 Thus, steric constraints of the MspA nanopore alter the propensity of DNA nucleotides to form a base-stacking pattern, modulating the number of bulk-like water molecules in the MspA constriction and thereby the nanopore ionic current.

Figure 4. The sequence specificity of ionic current blockades.

Figure 4

Open in a new tab

(a) The normalized probability of observing a given number of non-hydrogen atoms of DNA nucleotides (top) and a given number of bulk-like water molecules (bottom) for 5′-poly(dT) (left) and 5-poly(dA) (right) systems. Vertical black lines indicate the mean values. (b) Cumulative ionic currents as a function of NDNA (left) and Nbw (right). The cumulative ionic currents were computed by integration of the probability density functions weighted by the mean ionic current in each bin. (c) Representative conformations of thymine and adenine homopolymers each having 49, 35, 25, and 16 non-hydrogen atoms in the MspA constriction. Broken base-stacking reduces the number of DNA atoms in the MspA constriction, increases the number of bulk-like water molecules and therefore increases the ionic current. (d) The number of base stacks in the constriction versus the number of bulk-like water molecules. Bins with fewer than five data points were ignored. Error bars indicate standard deviation of data points in each bin. (e) Normalized probability of observing a given number of base-stacked conformations among nucleotides in the constriction of MspA.

Despite being subject to a restraining harmonic potential mimicking the action of a DNA polymerase, the DNA strands were found to undergo large-amplitude collective motion in the MspA constriction, Figure 5a,b. Although the nucleotides maintained, on average, a constant distance from the nanopore constriction throughout the simulations, they could transiently move through the constriction by as many as two nucleotides in either direction, Figure 5c. The relatively stiff restraints applied to the anchor atoms in our simulations may have reduced the amplitude of the collective motion in comparison to a full-length MspA system. In the case of a heterogeneous sequence DNA strand, such longitudinal displacements move DNA nucleotides in and out of the sensing volume of the nanopore, producing “sequence flickering” noise that complicates determination of the DNA sequence. Indeed, a single nucleotide substitution was experimentally found to affect the average blockade current of at least three neighboring nucleotides.8, 9 Limited by the timescale of our simulations, such large displacements precluded determination of the average ionic current for systems containing DNA strands of mixed nucleotide sequence. However, even for a mixed-sequence DNA strand, the number of bulk-like water molecules in the MspA constriction was found to exhibit strong correlation with the blockade current, Supplementary Figure 11.

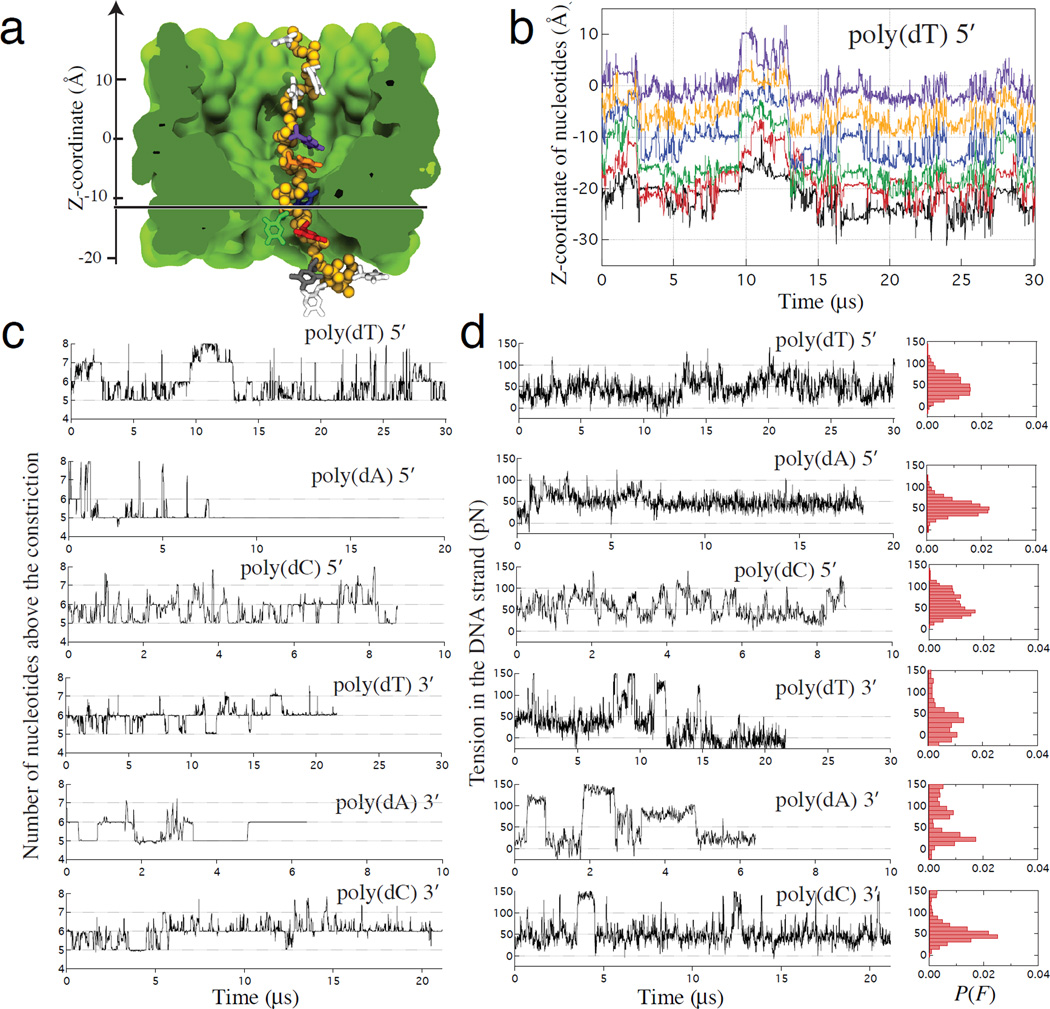
Figure 5. Stochastic displacement of nucleotides and the effective force.

Figure 5

Open in a new tab

(a) A typical simulation system containing MspA (green) and a DNA strand attached to a harmonic spring. Extension of the spring reports the effective force applied to DNA. The backbone of DNA is shown as yellow spheres, the DNA bases are individually colored. Lipids, water and ions are not shown. The horizontal line indicates the plane passing through the middle of the MspA constriction. (b) Centers of mass of DNA nucleotides versus simulation time in a representative MD trajectory. The color of the lines corresponds to the color of nucleotides shown in panel a. The z coordinate is defined in panel a. The dashed line indicates the location of the middle plane of the MspA constriction. For clarity, data are shown only for six nucleotides nearest to the constriction. (c) The number of nucleotides above the middle plane of the constriction versus simulation time for six homopolymer systems. (d) The force experienced by the harmonic spring attached to the uppermost nucleotide. Spontaneous, collective displacements of DNA nucleotides are associated with large fluctuations of the effective force applied to DNA. Normalized histograms summarize force distributions for each simulation system. In this figure, all data points represent 10-ns block averages of MD trajectories sampled at 100 ps. Because our simulations employed a reduced-length MspA system, the simulated values of the effective force can be up to 30% higher than the experimentally measured ones at the same transmembrane bias, Supplementary Note 4.

The large-amplitude displacements of the nucleotides in the MspA constriction anti-correlate with the fluctuations of the effective force applied by the DNA on the restraining anchor that mimics the presence of a DNA polymerase, Figure 5d and Supplementary Figure 12. In some simulations, the effective force transiently increased from a baseline value of approximately 30 pN (Supplementary Note 4, Supplementary Figures 13 and 14) by two- or even three-fold for a period of several microseconds, facilitated by simultaneous binding of a DNA phosphate group to three amine groups of Asp90 and Asp91 residues, Supplementary Figure 14. As the probability of a DNA polymerase backstepping exponentially increases with the effective force, even short lived but high magnitude fluctuations in the effective force can considerably increase the backstepping probability.

Conclusions

The results of our MD simulations indicate that the sequence of DNA nucleotides modulates the ionic current blockade in MspA via a steric exclusion effect. Previously, the steric exclusion effect was invoked to explain the magnitude of the ionic current blockades in solid-state 31 and biological32 nanopores. In the case of ionic current blockades produced by DNA strands in MspA, their sequence dependence could not be, at first look, rationalized by the steric exclusion effects as, for example, larger nucleotides were found to block the current less than the smaller nucleotides. Furthermore, the dense packing of DNA nucleotides in the pore constriction can, potentially, modulate the ionic current via several different mechanisms, for example, by imposing electrostatic barriers to ion permeation or creating pockets of vacuum (common to small hydrophobic nanopores) that block the passage of ions.

The key difference between the naïve volume exclusion argument and the mechanism elucidated by this study is in explicit consideration of the packing geometry of the DNA nucleotides within the pore constriction afforded by the all-atom MD approach. The diameter of the MspA pore is just right to alter the conformations of DNA nucleotides in a non-trivial manner, reflecting the competition of steric and base-stacking interactions. The volume accessible to ion transport, Figure 3a, changes non-linearly with the number of DNA atoms, Figure 3b, amplifying the excluded volume effect. Analysis of our explicit solvent all-atom trajectories provides no evidence to support either the electrostatic barrier or the vacuum pockets mechanisms.

Our simulations have also found the DNA strands to undergo large-amplitude displacements through the pore constriction despite being anchored to the enzyme. Such large-amplitude displacements broaden the effective sensing volume of the MspA pore to at least four nucleotides and produce large fluctuations of tension in the DNA strand. Modifications to the MspA structure that reduce the amplitude of the DNA displacements will lower the fluctuations of tension in the DNA strand and, possibly, the rate of insertion errors in nanopore sequence recordings.7, 8 The same modifications would sharpen the effective sensing volume of the MspA pore, improving the resolution of the DNA sequence readout.

Methods

Initial atomic coordinates of the MspA porin were obtained from the Protein Data Bank (entry 1UUN).10 Eight R96 residues were reverted to alanines in accordance with the sequence of wild type MspA. Twenty-four aspartate residues were replaced by asparagines to create the D90N/D91N/D93N mutant used in experiment.33 A reduced model of the MspA nanopore was constructed by eliminating the vestibule part of the channel. The truncated nanopore, containing residues 75 to 120, was merged with an 8 nm × 8 nm patch of 2-oleoyl-1-pamlitoyl-sn-glyecro-3-phosphocholine bilayer. All lipid molecules overlapping with the nanopore were removed. The remaining bilayer contained 60 lipid molecules. Using the phantom-pore method34 a DNA strand was placed inside the MspA with its backbone approximately aligned with the nanopore axis. Two systems were constructed having either the 5′ or 3′ end of the DNA strand at the trans end of the pore. The systems were immersed in a volume of water molecules. DNA fragments extending outside the solvation box were removed producing a continuous 11- or 12-nucleotide strand for the 5′-trans and 3′-trans systems, respectively. The nucleotide sequence of the strands was adjusted to produce three systems containing thymine, adenine and cytosine homopolymers for each orientation of the DNA strand and one mixed sequence 5′-TTTAAATTTTT-3′ system. K+ and Cl− ions were added at random positions corresponding to a concentration of 1 M. Additional charges neutralized the system. The final system consisted of about 25,000 atoms.

Following 2,000 steps of energy minimization, each system was equilibrated for 3 ns in the constant number of particles, pressure and temperature ensemble maintained by the Nosé-Hoover Langevin piston pressure control35 in NAMD2.36 All production simulations of the minimal MspA systems were performed using the D.E. Shaw Research supercomputer Anton,19 the Nosé-Hoover NVT integrator37 and a k-Gaussian Split Ewald method.38 All simulations employed periodic boundary conditions and the CHARMM36 parameter set.39 All bonds involving hydrogen atoms were constrained using an implementation of M-SHAKE.40 A multistage r-RESPA scheme41 was used for integration of the equations of motion using a 2-fs timestep for bonded and short-ranged non-bonded interactions and 6-fs time step for long-range non-bonded interactions. The temperature was set at 295 K.

All production simulations were carried out in the constant number of particles, volume and temperature ensemble under a constant external electric field applied normal to the membrane, producing a 180 mV transmembrane bias.23 The ionic currents were calculated as described previously.23 In all systems, the C1′ atom of the terminal nucleotide at the cis side of the membrane was restrained using harmonic potentials with the spring constants of 174 and 695 pN/nm within and normal to the plane of the membrane, respectively. To maintain the structural integrity of the nanopore, all Cα atoms of the protein were restrained to their crystallographic coordinates using harmonic potentials with spring constants of 695 pN/nm.

Supplementary Material

Supporting Information

Acknowledgments

This work was supported in part through grants from the National Institutes of Health (R01-HG005115 and R01-HG007406) and the National Science Foundation (DMR-0955959 and PHY-1430124). Computer time was provided via Teragrid/XSEDE allocation MCA05S028, the Department of Energy INCITE program and the National Resource for Biomedical Supercomputing at the DESRES supercomputer Anton at the Pittsburgh Supercomputing Center (PSCA00052).

Footnotes

Supporting Information Available

Simulation and analysis of the full-length MspA system, ionic current blockades in the 3′-trans MspA systems, discussions on the effect of block averaging interval and convergence, data from ensemble simulations, a note on the relationship between simulated and experimental ionic currents, analysis on water distribution, additional correlation analysis, a note on the cylindrical model system, additional analysis on the 1/f noise, microscopic mechanisms of the ionic current blockades, discussions on the correlation between displacement of ssDNA and the force on the anchor, analysis on electro-osmotic effect and transient binding of DNA to the channel, and movies illustrating the key MD trajectories. This material is available free of charge via the Internet at http://pubs.acs.org/.

References

  • 1.Metzker ML. Sequencing Technologies — the Next Generation. Nat. Rev. Genet. 2010;11:31–46. doi: 10.1038/nrg2626. [DOI] [PubMed] [Google Scholar]
  • 2.Branton D, Deamer DW, Marziali A, Bayley H, Benner SA, Butler T, Di Ventra M, Garaj S, Hibbs A, Huang X, Jovanovich SB, Krstic PS, Lindsay S, Ling XS, Mastrangelo CH, Meller A, Oliver JS, Pershin YV, Ramsey JM, Riehn R, et al. The Potential and Challenges of Nanopore Sequencing. Nat. Biotech. 2008;26:1146–1153. doi: 10.1038/nbt.1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Benner S, Chen R, Wilson N, Abu-Shumays R, Hurt N, Lieberman K, Deamer DW, Dunbar W, Akeson M. Sequence-Specific Detection of Individual DNA Polymerase Complexes in Real Time Using a Nanopore. Nat. Nanotech. 2007;2:718–724. doi: 10.1038/nnano.2007.344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Cockroft SL, Chu J, Amorin M, Ghadiri MR. A Single-Molecule Nanopore Device Detects DNA Polymerase Activity with Single-Nucleotide Resolution. J. Am. Chem. Soc. 2008;130:818–820. doi: 10.1021/ja077082c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Olasagasti F, Lieberman KR, Benner S, Cherf GM, Dahl JM, Deamer DW, Akeson M. Replication of Individual DNA Molecules Under Electronic Control Using a Protein Nanopore. Nat. Nanotech. 2010;5:798–806. doi: 10.1038/nnano.2010.177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Chu J, Gonzalez-Lopez M, Cockroft SL, Amorin M, Ghadiri MR. Real-Time Monitoring of DNA Polymerase Function and Stepwise Single-Nucleotide DNA Strand Translocation through a Protein Nanopore. Angew. Chem. Int. Ed. 2010;49:10106–10109. doi: 10.1002/anie.201005460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Cherf GM, Lieberman KR, Rashid H, Lam CE, Karplus K, Akeson M. Automated Forward and Reverse Ratcheting of DNA in a Nanopore at 5-Å Precision. Nat. Biotech. 2012;30:344–348. doi: 10.1038/nbt.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Manrao EA, Derrington IM, Laszlo AH, Langford KW, Hopper MK, Gillgren N, Pavlenok M, Niederweis M, Gundlach JH. Reading DNA at Single-Nucleotide Resolution with a Mutant MspA Nanopore and Phi29 DNA Polymerase. Nat. Biotech. 2012;30:349–353. doi: 10.1038/nbt.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Laszlo AH, Derrington IM, Ross BC, Brinkerhoff H, Adey A, Nova IC, Craig JM, Langford KW, Samson JM, Daza R, Doering K, Shendure J, Gundlach JH. Decoding Long Nanopore Sequencing Reads of Natural DNA. Nat. Biotech. 2014;32:829–833. doi: 10.1038/nbt.2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Faller M, Niederweis M, Schultz GE. The Structure of a Mycobacterial Outer Membrane Channel. Science. 2004;303:1189–1192. doi: 10.1126/science.1094114. [DOI] [PubMed] [Google Scholar]
  • 11.Derrington IM, Butler TZ, Collins MD, Manrao E, Pavlenok M, Niederweis M, Gundlach JH. Nanopore DNA Sequencing with MspA. Proc. Natl. Acad. Sci. U.S.A. 2010;107:16060. doi: 10.1073/pnas.1001831107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Manrao EA, Derrington IM, Pavlenok M, Niederweis M, Gundlach JH. Nucleotide Discrimination with DNA Immobilized in the MspA Nanopore. PLoS ONE. 2011;6:e25723. doi: 10.1371/journal.pone.0025723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Stoddart D, Maglia G, Mikhailova E, Heron AJ, Bayley H. Multiple Base-Recognition Sites in a Biological Nanopore: Two Heads are Better than One. Angew. Chem. Int. Ed. 2010;122:566–569. doi: 10.1002/anie.200905483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Howorka S, Siwy ZS. Nanopore Analytics: Sensing of Single Molecules. Chem. Soc. Rev. 2009;38:2360–2384. doi: 10.1039/b813796j. [DOI] [PubMed] [Google Scholar]
  • 15.Kasianowicz JJ, Brandin E, Branton D, Deamer DW. Characterization of Individual Polynucleotide Molecules Using a Membrane Channel. Proc. Natl. Acad. Sci. U.S.A. 1996;93:13770–13773. doi: 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Akeson M, Branton D, Kasianowicz JJ, Brandin E, Deamer DW. Microsecond Time-Scale Discrimination Among polycytidylic Acid, Polyadenylic Acid, and Polyuridylic Acid as Homopolymers or as Segments Within Single RNA Molecules. Biophys. J. 1999;77:3227–3233. doi: 10.1016/S0006-3495(99)77153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Meller A, Nivon L, Brandin E, Golovchenko J, Branton D. Rapid Nanopore Discrimination Between Single Polynucleotide Molecules. Proc. Natl. Acad. Sci. U.S.A. 2000;97:1079–1084. doi: 10.1073/pnas.97.3.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Purnell RF, Mehta KK, Schmidt JJ. Nucleotide Identification and Orientation Discrimination of DNA Homopolymers Immobilized in a Protein Nanopore. Nano Lett. 2008;8:3029–3034. doi: 10.1021/nl802312f. [DOI] [PubMed] [Google Scholar]
  • 19.Shaw DE, Chao JC, Eastwood MP, Gagliardo J, Grossman JPP, Ho CR, Lerardi DJ, Kolossváry I, Klepeis JL, Layman T, McLeavey C, Deneroff MM, Moraes MA, Mueller R, Priest EC, Shan Y, Spengler J, Theobald M, Towles B, Wang SC, et al. Anton, a Special-Purpose Machine for Molecular Dynamics Simulation. Comm. ACM. 2008;51:91. [Google Scholar]
  • 20.Bhattacharya S, Derrington IM, Pavlenok M, Niederweis M, Gundlach JH, Aksimentiev A. Molecular Dynamics Study of MspA Arginine Mutants Predicts Slow DNA Translocations and Ion Current Blockades Indicative of DNA Sequence. ACS Nano. 2012;6:6960–6968. doi: 10.1021/nn3019943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Bond PJ, Guy AT, Heron AJ, Bayley H, Khalid S. Molecular Dynamics Simulations of DNA within a Nanopore : Arginine-Phosphate Tethering and a Binding / Sliding Mechanism for Translocation. Biochemistry. 2011;50:3777–3783. doi: 10.1021/bi101404n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Biase PMD, Solano CJF, Markosyan S, Czapla L, Noskov SY. BROMOC-D: Brownian Dynamics/Monte-Carlo Program Suite to Study Ion and DNA Permeation in Nanopores. J. Chem. Theory Comput. 2012;8:2540–2551. doi: 10.1021/ct3004244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Aksimentiev A, Schulten K. Imaging α-Hemolysin with Molecular Dynamics: Ionic Conductance, Osmotic Permeability and the Electrostatic Potential Map. Biophys. J. 2005;88:3745–3761. doi: 10.1529/biophysj.104.058727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Tabard-Cossa V, Trivedi D, Wiggin M, Jetha NN, Marziali A. Noise Analysis and Reduction in Solid-State Nanopores. Nanotech. 2007;18:305505. [Google Scholar]
  • 25.Uram JD, Ke K, Mayer M. Noise and Bandwidth of Current Recordings from Submicrometer Pores and Nanopores. ACS Nano. 2008;2:857–872. doi: 10.1021/nn700322m. [DOI] [PubMed] [Google Scholar]
  • 26.Smeets RMM, Keyser UF, Dekker NH, Dekker C. Noise in Solid-State Nanopores. Proc. Natl. Acad. Sci. U.S.A. 2008;105:417–421. doi: 10.1073/pnas.0705349105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Rosenstein JK, Wanunu M, Merchant CA, Drndic M, Shepard KL. Integrated Nanopore Sensing Platform with Sub-Microsecond Temporal Resolution. Nat. Methods. 2012;9:487–492. doi: 10.1038/nmeth.1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid-Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
  • 29.Hummer G, Rasaiah JC, Noworyta JP. Water Conduction Through the Hydrophobic Channel of a Carbon Nanotube. Nature. 2001;414:188–190. doi: 10.1038/35102535. [DOI] [PubMed] [Google Scholar]
  • 30.Aalberts DP, Parman JM, Goddard NL. Single-Strand Stacking Free Energy from DNA Beacon Kinetics. Biophys. J. 2003;84:3212–3217. doi: 10.1016/S0006-3495(03)70045-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Smeets RMM, Keyser UF, Krapf D, Wu M-Y, Dekker NH, Dekker C. Salt-Dependence of Ion Transport and DNA Translocation Through Solid-State Nanopores. Nano Lett. 2006;6:89–95. doi: 10.1021/nl052107w. [DOI] [PubMed] [Google Scholar]
  • 32.Reiner JE, Kasianowicz JJ, Nablo BJ, Robertson JWF. Theory for Polymer Analysis Using Nanopore-based Single-Molecule Mass Spectrometry. Proc. Natl. Acad. Sci. U.S.A. 2010;107:12080–12085. doi: 10.1073/pnas.1002194107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Butler TZ, Pavlenok M, Derrington IM, Niederweis M, Gundlach JH. Single-Molecule DNA Detection with an Engineered MspA Protein Nanopore. Proc. Natl. Acad. Sci. U.S.A. 2008;105:20647–20652. doi: 10.1073/pnas.0807514106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Mathé J, Aksimentiev A, Nelson DR, Schulten K, Meller A. Orientation Discrimination of Single Stranded DNA Inside the α-Hemolysin Membrane Channel. Proc. Natl. Acad. Sci. U.S.A. 2005;102:12377–12382. doi: 10.1073/pnas.0502947102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Martyna GJ, Tobias DJ, Klein ML. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994;101:4177–4189. [Google Scholar]
  • 36.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Hoover WG. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
  • 38.Shan Y, Klepeis JL, Eastwood MP, Dror RO, Shaw DE. Gaussian Split Ewald: A fast Ewald Mesh Method for Molecular Simulation. J. Chem. Phys. 2005;122:054101. doi: 10.1063/1.1839571. [DOI] [PubMed] [Google Scholar]
  • 39.Hart K, Foloppe N, Baker CM, Denning EJ, Nilsson L, MacKerell AD., Jr Optimization of the CHARMM Additive Force Field for DNA: Improved Treatment of the BI/BII Conformational Equilibrium. J. Chem. Theory Comput. 2012;8:348–362. doi: 10.1021/ct200723y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Kräutler V, van Gunsteren WF, Hünenberger PH. A Fast SHAKE Algorithm to Solve Distance Constraint Equations for Small Molecules in Molecular Dynamics Simulations. J. Comput. Chem. 2001;22:501–508. [Google Scholar]
  • 41.Tuckerman M, Berne BJ, Martyna GJ. Reversible Multiple Time Scale Molecular Dynamics. J. Chem. Phys. 1992;97:1990–2001. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
NIHMS779919-supplement-Supporting_Information.pdf (50.4MB, pdf)

RESOURCES