The Strehler-Mildvan Correlation from the Perspective of a Two-process Vitality Model

Abstract

The Strehler and Mildvan (SM) general theory of aging and mortality provided a mechanism based explanation for the Gompertz law and predicted a log-linear relationship between the two Gompertz coefficients, known as the SM correlation. While the SM correlation was validated in developed countries before the second half of the 20^th century, the recent breakdown of the correlation pattern in these countries prompted demographers to conclude that the SM theory needs to be reassessed. In this work, we utilized a newly developed two-process vitality model to explain the SM correlation and its breakdown in terms of asynchronous trends in the acute (extrinsic) and chronic (intrinsic) mortality factors. We proposed that the mortality change in the first period was largely determined by the elimination of immediate hazards to death, whereas the mortality change in the second period was primarily driven by the slowdown of the deterioration rate of intrinsic survival capacity.

Introduction

Strehler and Mildvan (1960) proposed a biological explanation to the well-established Gompertz law (μ(x) = ae^bx, where μ(x) is the mortality rate at age x) (Gompertz 1825), known as the Strehler and Mildvan (SM) general theory of aging and mortality. The theory used an analogy to chemical kinetics (Golubev 2009) to explain the exponentially increasing shape of the Gompertz law as resulting from the interaction between the internal energy reserves of the organism and the external energy demands from environmental insults. An essential finding from the theory is the SM correlation in which the Gompertz coefficients are negatively correlated, i.e., log a is a linear function of b. This regularity implies that in spite of continuous improvements in the longevity for humans, the evolution of mortality curves should follow certain patterns (Yashin et al. 2001a). A series of early studies (Riggs 1990; Riggs and Millecchia 1992; Prieto et al. 1996) empirically confirmed the stably negative relationship between the Gompertz parameters in the earlier decades of the 20^th century. However, a break in relationship for recent data from industrialized countries, such as Sweden, Japan and France (Yashin et al. 2001a, 2002), challenges the concept of aging and mortality that stems from the SM theory as well as the interpretation of coefficients of models that are based on the rate in mortality, e.g., the Gompertz model.

In this work, we demonstrate that the correlation between log a and b can be readily explained in a two-process vitality framework developed by Li and Anderson (2013). In terms of the new structure, the observed pattern of correlation of Gompertz coefficients is the consequence of the asynchronous trends over years in an intrinsic aging process, producing intrinsic mortality, and an extrinsic challenge process, producing extrinsic mortality. Moreover, we show that the age-specific adult mortality pattern over history is more complex than what can be characterized by a two-parameter Gompertz model. The two-process vitality model, which is based on four parameters, is the minimum needed to capture the major patterns of adult mortality observed over history. This new framework provides a flexible perspective for describing the relationship between the physiological and demographic patterns of aging that can be applied to a wide range of areas, such as longevity projection and assessing the sex/race differences in mortality.

The SM theory and the SM correlation

We begin with a brief introduction of the SM theory that derives from hidden processes. Organisms are assumed to start with an initial survival capacity, termed V, declining linearly with age x as V(x) = V₀(1 − Bx), where B indicates the fraction of vitality loss per unit time. Over life, animals experience random external challenges or insults with a mean frequency K. Challenges have random magnitudes, exponentially distributed with an average magnitude D that expresses the average deleteriousness of the environment. Death occurs when the magnitude of a challenge exceeds the remaining vitality. These assumptions produce the exponentially increasing mortality pattern with age, i.e., the Gompertz law. A detailed review of the SM theory can be found in Finkelstein (2012).

The SM correlation derived from the theory describes a negative log-linear relationship between the two Gompertz coefficients:

$$\text{log }a=\text{log }K-b/B$$ (1)

which, when substituted into the Gompertz law, expresses morality in terms of the mean frequency of the random extrinsic challenges and the rate of loss of vitality as

$$\text{log }\mu (x)=\text{log }K+b(x-1/B)=\text{log }K+B/D(x-1/B)$$ (2)

where a = K exp(−1/D) and b = B/D, and B and D are normalized by V₀. Eq. (2) imposes strong regularity on mortality, such that given the assumptions of the SM theory, no matter how human longevity changes over time, the shape of the mortality curves conform to a fixed relationship. To be specific, when K and B are constant, i.e., both the challenge frequency and the fraction of vitality loss per unit time are stable over time, all mortality curves in log scale must intersect at one point (1/B, log K) (Riggs and Millecchia 1992; Yashin et al. 2001a, 2002). With this restriction, as log a declines and b increases, the survival function defined as $l(x)=\text{exp}(-\underset{0}{\overset{x}{\int }}\mu (t)dt)$ becomes more and more rectangular over time known as the rectangularization of the survival curve (Wilmoth and Horiuchi 1999; Yashin et al. 2001b). Fig. 1 in Yashin et al.’s paper (2001a) illustrates how mortality and survival patterns should change under the SM theory.

The SM theory has been applied to analyze population mortality data by obtaining both the vitality loss fraction B that is considered to reflect the genetic influence on survival and the environmental parameters K and D = B/b that are considered to reflect the extrinsic conditions (Riggs 1990; Riggs and Millecchia 1992; Prieto et al. 1996; Zheng et al. 2011). However, a problem exists because eq. (2) is a linear function with 2 degrees of freedom but is defined by 3 parameters (K, b and B) or (K, D and B), and thus it is impossible to specify all the parameters for a single mortality curve. In order to estimate the parameters, Strehler and Mildvan (1960) developed several methods that postulated different restrictions on eq. (2) or a series of mortality curves. The resulting estimates vary among these methods and are highly dependent on the specific assumptions.

However, all the estimation methods, as well as the SM theory itself, fundamentally rely on the validity of SM correlation pattern implied by eq. (2). Although a series of experimental studies (Riggs 1990; Riggs and Millecchia 1992; Prieto et al. 1996) suggest a stable negative relationship between the Gompertz coefficients in the first half of the 20^th century, the pattern tends to break after 1950 for many industrialized countries (Wilmoth and Horiuchi 1999; Yashin et al. 2001a, 2002; Golubev 2004).

The first sign of deviation from the SM correlation pattern was demonstrated by Myers and Manton (1984) who found “the tail of the survival curve of the U.S. population tended to increase with years” in the second half of the 20^th century. In effect, the mortality trajectories in recent years do not cross the supposedly single intersection point (1/B, log K), but tend to become parallel at old ages. Similar findings were confirmed by other studies (Gavrilov and Gavrilova 1991; Manton and Tolley 1991; Kannisto 1994; Jeune and Vaupel 1995; Horiuchi and Wilmoth 1997, 1998; Wilmoth and Horiuchi 1999; Wilmoth et al. 2000; Robine 2001). In spite of using different terminologies and emphasizing different demographic phenomena, these studies all pointed to the tendency of derectangularization of survival curves and a corresponding breakdown of the SM correlation pattern. Yashin et al. (2001a, 2002) summarized the information and demonstrated the instability of SM correlation in a plot of Gompertz log a vs. b (Fig. 3–6 in Yashin et al. 2001a).

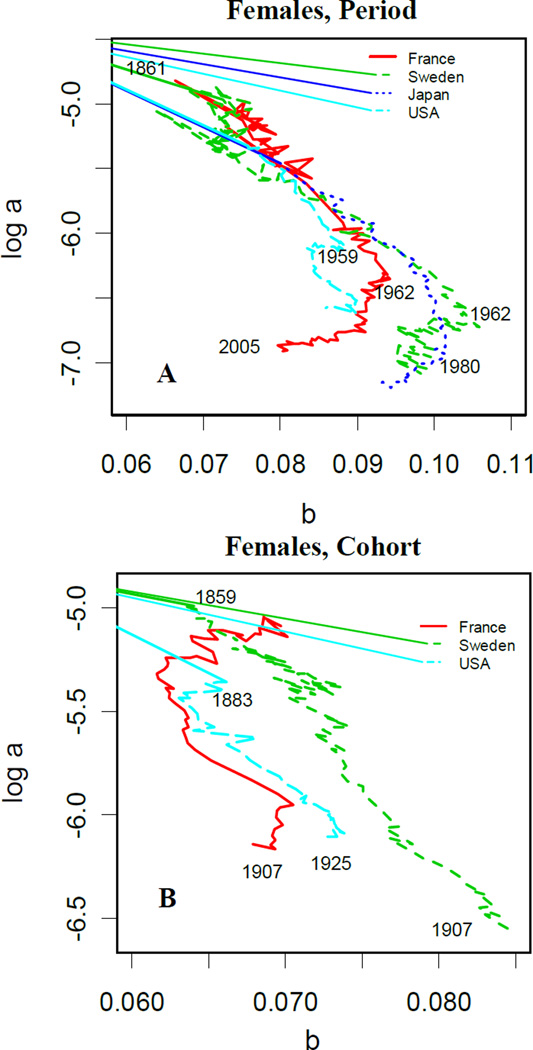
Following the Yashin et al. analysis (2001a), Fig. 1 illustrates the estimated Gompertz log a against b for adult mortality (age 40–80) from France, Japan, Sweden and the U.S.. Until the second half of the 20^th century, period data as predicted by the SM theory have a negative linear relationship with curves going from top-left to bottom-right. Thereafter, “hooks” emerge and the curves flatten for France, Sweden and the U.S. around 1960s and for Japan around 1980. For cohort data, the countries have complex patterns in which the slope changes sign multiple times over the years of data. In summary, the SM correlation breaks down for the years where the curves change slope and flatten.

Figure 1.

(A) Female Period: patterns of SM correlation in France (1861–2005), Sweden (1861–2005), Japan (1950–2000) and the US (1938–2005); (B) Female Cohort: patterns of SM correlation in France (1859–1917), Sweden (1821–1915) and the US (1883–1927).

Note: For consistency with other studies (see Fig. 3 and Fig. 5 in Yashin et al. (2001a)), we used mortality for ages between 40 and 80.

Source: Human Mortality Database (2011).

While the SM theory establishes an attractive connection between the intrinsic (organism specific) and extrinsic (environmental) forces that shape mortality patterns, its deterministic structure is inadequate to characterize the interaction between the internal physiological aging processes of individuals and environmental challenges. More importantly, the effect of the intrinsic vitality decline is only revealed indirectly through its interaction with extrinsic challenges, which makes it difficult to disentangle the two processes. Specifically, in the SM framework, the three process parameters B, K, and D are not independent of each other and rely on additional constraints to specify the relationship. Therefore, assuming that the basic intrinsic-extrinsic division is reasonable, the irregular patterns of the SM correlation in recent decades are likely caused by changes in the relationships of the three parameters over time. The essential message here is that the simple relationship inferred by the SM model is violated, which compelled Yashin et al. (2001a, 2002) to call for development of new concepts in the theory of mortality and the relationship between the physiological and demographic patterns of aging.

The compensation law of mortality and the Gompertz-Makeham model

Another way of interpreting the SM correlation is known as the compensation law of mortality (Gavrilov and Gavrilova 1991), according to which the negative log-linear relationship between the two Gompertz coefficients suggests that a reduction in the level of mortality (i.e. a) is always compensated by an increase of the relative rate of mortality growth (i.e. b). That is, a higher survival capacity endorsed in younger ages results in a faster aging rate in older ages. The compensation law of mortality arrives in the same form of eq. (1) and the parameter 1/B and K are separately defined as the species-specific life span and the species-specific mortality (Gavrilov and Gavrilova 1991). Both the compensation law of mortality and the SM correlation identified the negative relationship between the Gompertz parameter a and b, although the former law inferred the correlation based on the Gompertz-Makeham (GM) model, while the latter did not adjust the so-called age-invariant background mortality (Gavrilov and Gavrilova 1991; Strulik and Vollmer 2013).

The GM model is an extension to the Gompertz model by adding a constant mortality term (M) known as the background mortality giving (Makeham 1860)

$$\mu (x)=M+a{e}^{bx}.$$ (3)

For mortality data over a long historical period, the GM model was shown to significantly improve the model fit over the simple Gompertz form especially between age 30 and 90. Such observations lead Gavrilov and Gavrilova (1991) to conclude that ignoring background mortality could generate an artificial dependency between the Gompertz coefficients, which coincides with the real correlation pattern. Therefore, they recommended to use the Makeham-adjusted Gompertz coefficients to derive the compensate law of mortality or the equivalent SM correlation.

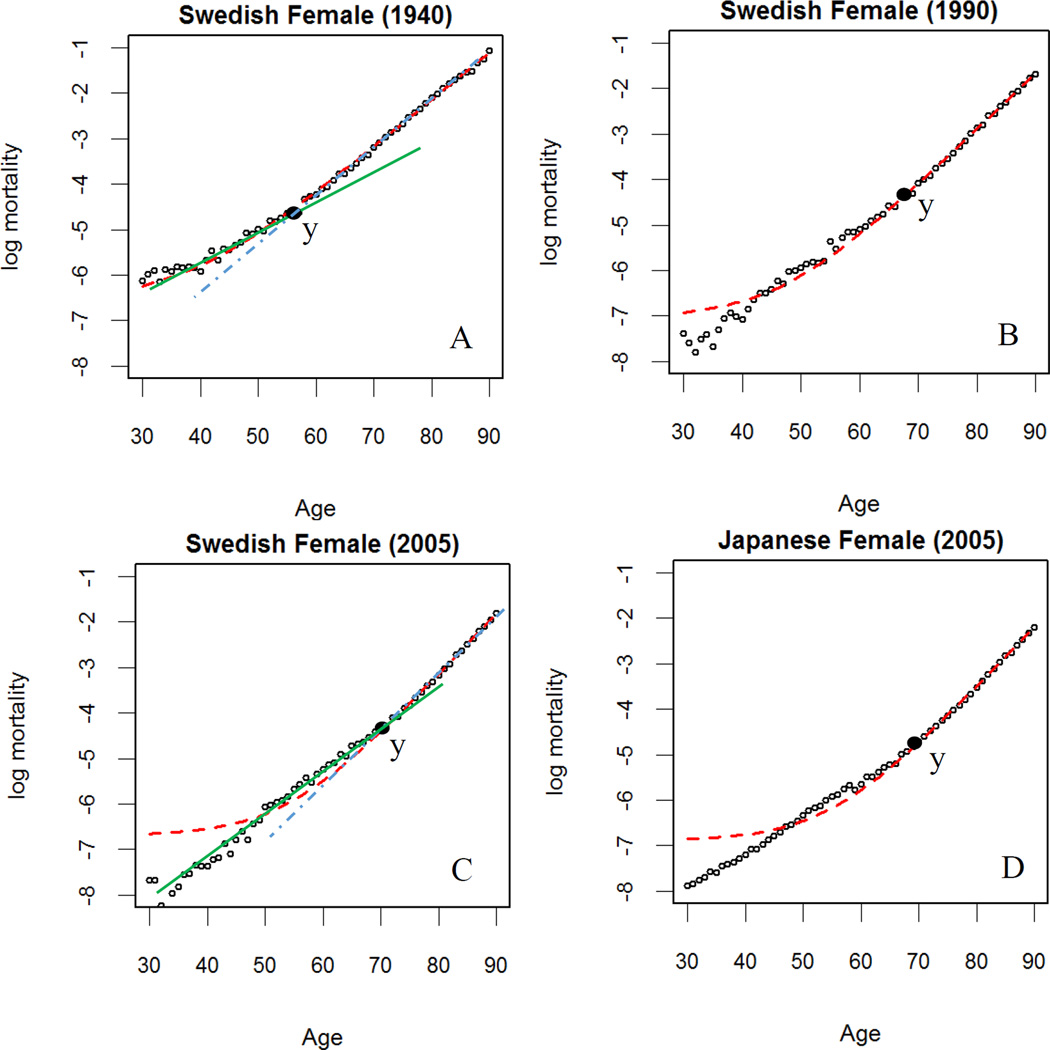
While it is generally assumed that the GM model is always superior to the Gompertz model, few studies have statistically examined this hypothesis, in particular, using data of recent decades. To our knowledge, only one study briefly mentioned a consistent deviation observed from the fit of a GM type model to data from the second half of the 20^th century (Bongaarts 2005). In Fig. 2, we illustrate the fit of the GM model to early and late period mortality data between age 30 and 90 based on the conventional weighted least square method with exposure as the weights (using “nls” function in R). We also tried other algorithms such as the built-in function “fitGM” in the R package “fmsb” and the results were very similar. As expected, the GM model fits well period mortality data prior to year 1950s, i.e., year 1940 in Fig.2. Nevertheless, discrepancies between the model fit and the true data emerge after year 1950, i.e. year 2005 in Fig. 2. Specifically, the GM model tends to overestimate mortality between age 30 and 50 and underestimate mortality between age 50 and 70. Such deviations become more significant in the recent years and are consistently observed in developed countries such as Sweden and Japan as shown in Fig. 2.

Figure 2.

Gompertz-Makeham model fit to selected period mortality data. (A): Swedish Female, 1940; (B) Swedish Female, 1990; (C) Swedish Female, 2005; (D): Japanese Female, 2005.

Note: The data (○) is fit with the GM model () using conventional weighted least-squares methods. A piecewise linear model that transitions between the middle-age () and old-age () linear segments at age y was demonstrated in (A) and (C).

Source: As for Figure 1.

The GM deviations can be explained as a mismatch of the nonlinear properties of the GM model and the piecewise linear nature of log mortality curves. As is illustrated in Fig. 2 (A) and (C), log mortality curves, to a first approximation, can be described by two straight-line segments, one fitting the middle-age portion of data and a second fitting the old-age portion (Milne 2007). The intersection point where the two lines meet (y in Fig. 2) has shifted to older ages with time (Fig 2: e.g. age 58 in 1940 and age 70 in 2005). Fitting log mortality data, the GM model tends to fit the old-age linear piece because the GM model becomes linear at old age. However, the model is highly curved at younger ages so to fit the middle-age segment it underestimates mortality between 50 and 70 and overestimated mortality below 50. In effect, in order to fit the mortality pattern in old age, the GM model has to raise artificially the value of the background mortality, which results in a poor fit to early-age mortality. For further discussion of the mortality increase in early old age see Li et al. (2013) who, using a two process vitality model, analyze the transition in terms of a shift from extrinsic to intrinsic mortality processes.

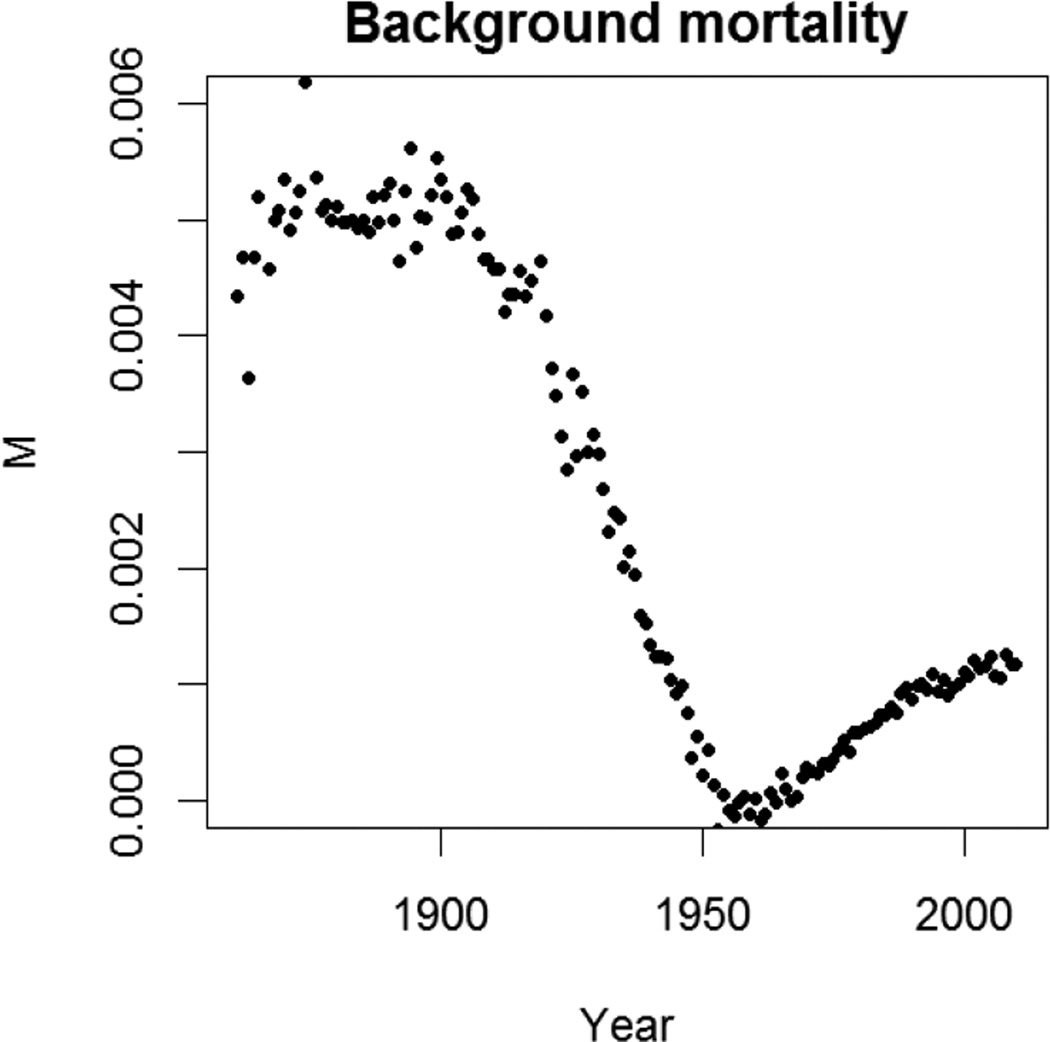
While the background mortality (M) in the GM model might be expected to decline over centuries because improvements in public health and increase in longevity, Fig. 3 illustrates this is not the case. A dramatic decline of M to the first half of the 20^th century corresponds to the overall mortality reduction across all ages. However, a surprisingly increase in M from about 1955 is unlikely to reflect a real increase in background mortality. Rather we suggest it indicates the underlying mortality dynamics have changed such that the GM deviations from the actual pattern of mortality have been increasing. Note that there is certainly another fitting algorithm to force the GM model to fit the younger-age mortality and suppresses the increase in M, but in doing so it would result in bias in fitting the older-age mortality (Bongaarts 2005). In either case, the GM model cannot generate unbiased estimation for mortality from recent period.

Figure 3.

Gompertz-Makeham background mortality (M) derived by weighted least-squares of fitting period data for Swedish females between ages 30 and 90.

Source: As for Figure 1.

Because the GM model fails to characterize the mortality trajectory in recent decades, and in particular, fails to capture the critical change of mortality shape between age 40 and 80, we suggest that exploring the breakdown of the SM correlation based on the GM model adds additional complexity to interpreting the changing dynamics of mortality. To ensure a consistent and viable assessment of the SM correlation across time, we therefore use the Gompertz model to explore the SM correlation and restrict the data analyses between age 40 and 80, the age interval in which the impact of the background mortality is minimized and the slope of the log mortality rate with age mortality is approximately constant.

We also note that the failure of the GM model in fitting mortality data and the breakdown of the SM correlation both occur after the second half of the 20^th century. Both phenomena likely reflect a common and fundamental change of the underlying mortality dynamics. We now explore this change by describing the breakdown of the SM pattern in terms of a shift of intrinsic and extrinsic mortality processes characterized through a vitality model.

The two-process vitality model

Yashin et al. (2001a) concluded that changes in the SM correlation pattern with time indicate changes in the frequency of extrinsic challenges K and changes in the rate of loss of vitality B. We agree with this essential conclusion but suggest that the underlying mechanisms involve additional dimensions that the Gompertz and GM models cannot reveal. We propose that to understand the historical SM pattern we require a model that explicitly identifies the minimum number of dimensions needed to characterize mortality. We further propose that at its most reduced form mortality involves intrinsic and extrinsic processes and at a minimum characterization of each process requires one dimension quantifying some measure of the process magnitude and one dimension characterizing the process frequency. Thus, at a minimum a model of mortality requires four dimensions; two characterizing extrinsic and intrinsic magnitudes and two characterizing their frequencies. At this point we do not specify the mathematical forms of these processes nor do we suggest that a four dimensional model is sufficient, only that it represents a minimum number of independent dimensions for the most reduced model of mortality.

The vitality model developed by (Anderson 2000) and expanded by (Li and Anderson 2013) into a full two-process framework (also referred to as “two-mortality model” in (Li et al. 2013)) meets our criteria for exploring the SM correlations and the historical changes in braking the correlation over the second half of the 20^th century. Specifically, this new framework considers mortality resulting from: 1) stochastic depletion of intrinsic survival capacity, i.e. vitality, and 2) extrinsic challenges exceeding vitality. We describe the model here and demonstrate that the breakdown of the SM correlation in the recent decades is a natural consequence of independent changes in the extrinsic and intrinsic processes over decades.

Intrinsic mortality

In the original SM model, the intrinsic process is modeled as a linearly declining function of the organism’s vitality in which deaths results when an external challenge exceeds the available vitality. In our model, death occurs from extrinsic challenges but also as the end point of the organism’s gradual loss of vitality. For evidence on the biological basis of intrinsic death see (Anderson et al. 2008). Additionally, in demography, Mitnitski and colleagues (Mitnitski et al. 2004; Mitnitski et al. 2005; Rockwood and Mitnitski 2006, 2007) demonstrated that the frail index, constructed as “a proportion of all potential deficits (symptoms, signs, laboratory abnormalities, disabilities) expressed in a given individual”, had a limit independent of age (0.65±0.05). In terms of vitality, their findings suggest a minimum value of survival capacity (i.e., the inverse of deficits accumulation) below which survival is unlikely and thus supports our notion of intrinsic mortality when vitality drops below a threshold. From a utility point of view, the inclusion of intrinsic mortality along with the more traditional extrinsic mortality allows for a quantitative estimate of the direct role of senescence in mortality.

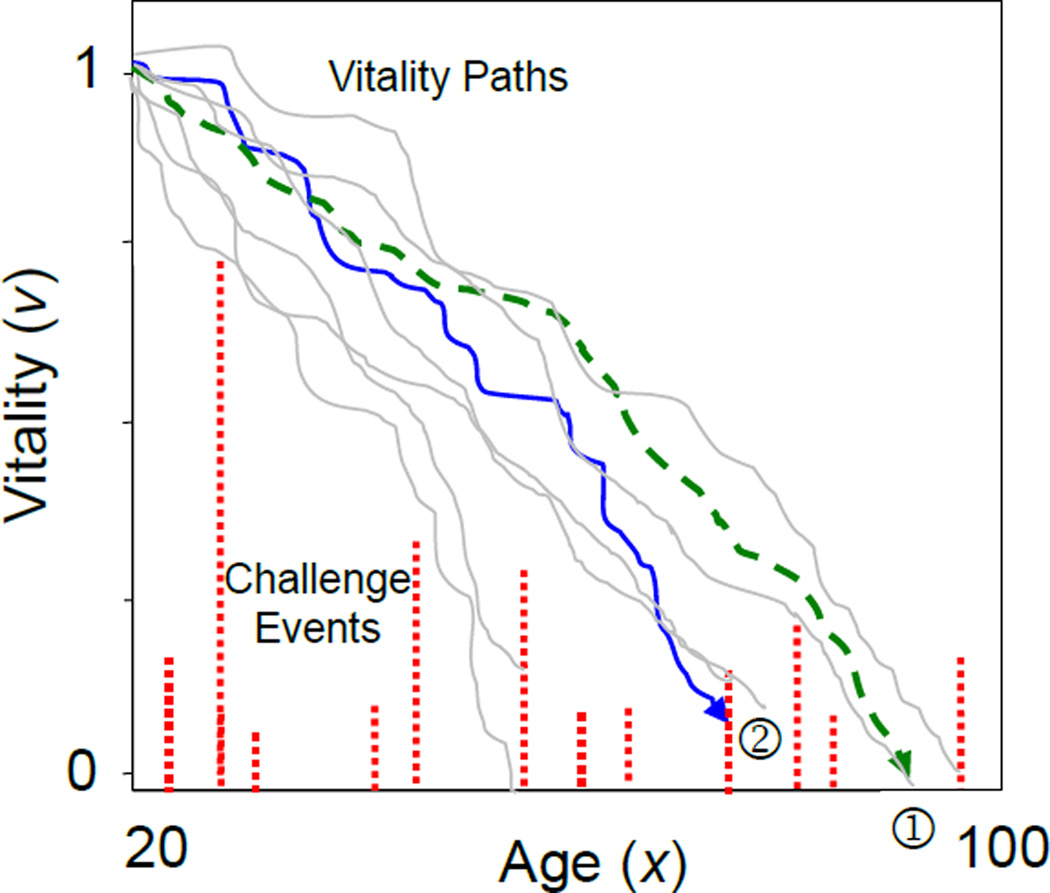
We represent the stochastic loss of vitality leading up to intrinsic mortality in terms of a Markovian process (Anderson 2000; Aalen and Gjessing 2001; Weitz and Fraser 2001; Anderson et al. 2008; Li and Anderson 2009). Each individual begins with an initial vitality, ν₀, that stochastically declines with age and results in death when its vitality reaches zero (Fig. 4①). The random trajectory of vitality, ν_x, between ν₀ and 0 is described by the Wiener process with drift:

$${\nu }_x={\nu }_{x-1}-r+s{W}_x\hspace{1em}\hspace{1em}x=1,2,3\dots$$ (4)

where W_x is a standard Wiener process modeled from a unit normal distribution N[0,1]. When eq. (4) is standardized to the initial vitality then r is the deterministic fraction of vitality lost in a unit increment of time and s is the intensity of the random contribution to the rate of vitality loss. In this case, each normalized vitality trajectory starts from a single point ν₀ = 1 and the actual differences in the initial values are reflected in the spread term s. To be specific, s demonstrates the average combined variation in survival capacity from both inherent (initial) and acquired (evolving) sources per unit time. Without the presence of extrinsic mortality, the distribution of the time to death from intrinsic processes is the inverse Gaussian function (Cox and Miller 1965) describing the first-passage time of vitality in eq. (4) to the zero boundary.

Figure 4.

The two-process vitality model illustrated.

Note: Vitality declines stochastically from an initial value of 1. Intrinsic mortality results when adult vitality is exhausted, ①, and extrinsic mortality occurs when a random challenge exceeds the remaining vitality, ② (Reproduced from Fig. 1 of Li and Anderson (2013)).

Extrinsic mortality

Extrinsic mortality is usually considered as death that is “relatively preventable and treatable”, including “mortality mainly from infections and accidents” (Shryock and Siegel 1975). We construct the extrinsic death process following the SM theory in which extrinsic mortality results when a random exterior event challenges the survival capacity of the organism. While in the SM theory the survival capacity is deterministic, we numerically model the stochastic trajectory of vitality through eq. (4) such that survival capacity is a stochastic variable. The interaction between the intrinsic aging process and the extrinsic challenge process resulting in death also has biological support. For instance, aging-related degeneration in the immune system has been widely documented (Goidl et al. 1976; McElhaney et al. 1992). Older adults are more susceptible to fatal infectious diseases and neoplasia due to the senescence-related failure in immune functions (Miller 1996).

To express the extrinsic mortality rate at age x ≥ 0, let a random point process Y_x with mean frequency of challenges λ represent an extrinsic challenge, e.g. natural disaster or infection. For each challenge, a variable Z_x with a cumulative distribution function φ(z) denotes the challenge magnitude. Assume that death from an extrinsic cause occurs when the challenge magnitude Z_x exceeds the current vitality level ν_x, i.e., death occurs when Pr[Z_x > ν_x] (Fig.4②). Further consider that Y_x is a history-independent Poisson process (Finkelstein 2007) and challenge magnitudes are exponentially distributed with a scale parameter β, such that most challenges are small and the probability of large events declines relative to their magnitude as in the SM theory. The conditional extrinsic mortality rate is

$$m_e(x|{\nu }_x)=\lambda \text{Pr}[Z_x>{\nu }_x]=\lambda (1-\phi ({\nu }_x))=\lambda e^{-{\nu }_x/\beta }$$ (5)

where ν_x is a realization of the vitality process at x and λ and β indicate the challenge frequency and the average challenge magnitude respectively. The population-level extrinsic mortality rate can be obtained by integrating eq. (5) over vitality states ν_x > 0.

Total Mortality

In this new model, mortality has two sources: an extrinsic killing expressed by instantaneous challenges to the survival capacity and an intrinsic killing expressed as chronic wearing out of the survival capacity to an absorption boundary. Close form solutions are possible for intrinsic mortality when every challenge kills (Anderson 2000) or extrinsic death is ignored (Weitz and Fraser 2001) and for extrinsic mortality when the intrinsic process is linear (Strehler and Mildvan 1960). However, when the two processes interact stochastically, as assumed above, the age-dependent distribution of vitality in the population has no analytical solution, because challenges preferentially eliminate low-vitality individuals modifying the distribution derived from the Wiener process. In this case, the total mortality rate can either be approximated as was done by Li and Anderson (2013) or be calculated numerically using microsimulation. Here to maintain the interaction of processes and explore the consequences of the system, we use microsimulation that derives the average macro-level characteristics from large sample simulations at the individual level (Manton et al. 2009).

The simulation procedure is as follows. We first simulate vitality trajectories of a population of 10,000 individuals using eq. (4). For each individual, a Poisson process, with rate parameter λ, generates a vector of random challenge times where the magnitude of each challenge is drawn from an exponentially distributed random processes scaled by parameter β. Mortality occurs in the age interval [x − 1, x] if the individual’s vitality becomes zero or negative through the intrinsic loss process, or if a random challenge occurs with a magnitude exceeding the individual’s vitality ν_x−1. In either case, the individual’s vitality trajectory is removed and the time to death recorded. Combining the mortality times of all individuals, we construct the population life table by calculating the age-specific survival rate, mortality rate and expected life span (Preston et al. 2001).

The mortality curves generated by microsimulation are determined by 4 parameters: r and s characterize the intrinsic process in terms of the average intrinsic degeneration rate and the variation in the rate, while λ and β determine the extrinsic challenge frequency and challenge magnitude respectively. It is worth noting that, in principle, extrinsic challenges that do not result in mortality could incrementally alter the vitality of a survivor. In this model, we ignore this process but assume the effect is subsumed into the Wiener process.

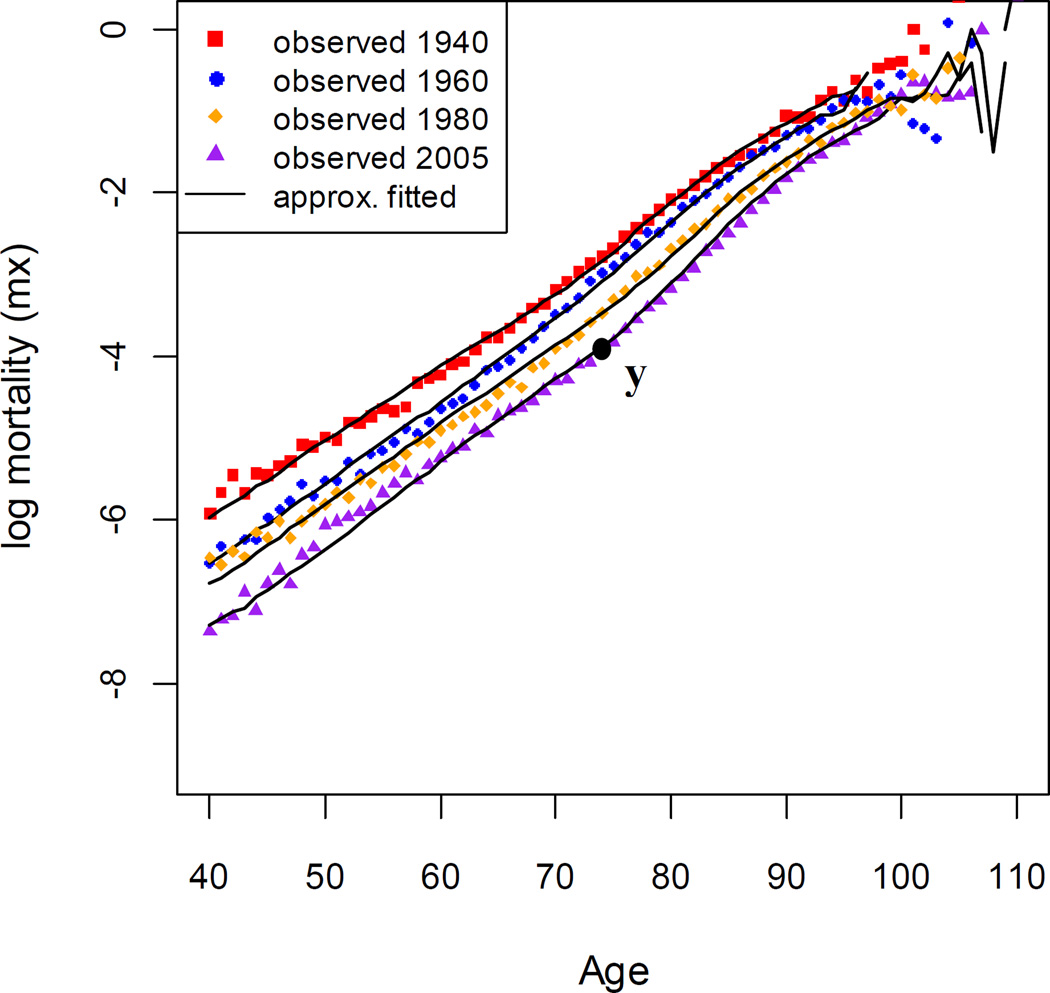
Fig.5 illustrates that the two-process vitality framework captures adult mortality patterns of Swedish female (age 40–110) obtained from the Human Mortality Database (2011) for period years 1940, 1960, 1980 and 2005. Because the choice of age span influences the correlation of the Gompertz coefficients, we start at age 40 to ensure the consistency with early studies (Yashin et al. 2001a, 2002). The lines were generated from microsimulation with prescribed parameter values that match the trend of the data. The nearly linear increase in log mortality rate with age in middle lifespan results from the interactions between the intrinsic degeneration and extrinsic challenges. The mortality plateaus at very old age are a result of the properties of the Wiener process (Aalen and Gjessing 2001; Weitz and Fraser 2001; Li and Anderson 2009, 2013). Notably, the model also captures the acceleration in the log mortality pattern beginning at old age (e.g. at point y of the 2005 mortality curve in Fig.5)(Li et al. 2013). Of particular importance here, Fig. 5 illustrates that the two-process vitality model readily tracks the observed mortality patterns across late 20^th century when the SM correlation breaks down.

Figure 5.

The approximated fit of the two-process vitality model to selected period mortality curves of Swedish females (40–110).

Note: The approximated parameter values are 1940 (r = 0.0177, s = 0.0112, λ = 0.155, β = 0.202), 1960 (r = 0.0175, s = 0.011, λ = 0.152, β = 0.171), 1980 (r = 0.0164, s = 0.0102, λ = 0.142, β = 0.172), and 2005 (r = 0.0161, s = 0.010, λ = 0.12, β = 0.157).

Source: As for Figure 1.

Explaining the SM correlation patterns

To explain the SM correlation in terms of the two-process model, first note that the deterministic rates of loss of vitality in the two models are equivalent, so r = B. Second, note that the models formulate the extrinsic challenges in the same way, so the representative magnitudes and mean frequencies are equivalent, i.e. D = β and K = λ. Thus, in the notation of the two-process vitality model, the SM correlation defined by eq. (1) is simply

$$\mathrm{log }a=\mathrm{log }\lambda -b/r.$$ (6)

That is, the log-linear relationship between a and b is preserved if λ and r are constant in the same way that the SM theory requires K and B to be constant (Finkelstein 2012). In both the two-process vitality model and SM theory, the mid-20^th century breakdown of the log-linear relationship involves the parameters not being constant. However, the explicit linkage of parameters in the SM framework makes it difficult to explain how the parameters need to change to produce the breakdown. In contrast, in the two-process vitality model, λ and r are formed by independent processes that result in distinct forms of mortality (Li and Anderson 2013). Thus, evoking two largely distinct mortality processes compared to one process allows for more flexibility in attributing the causes of the SM correlation and its breakdown.

To illustrate the SM correlation pattern and its breakdown in terms of the two-process model, we fit the Gompertz model to survival curves simulated with the two-process model (Section 4.3). In this manner for each set of r, s, λ and β, we derived the corresponding log a and b measures. It is then straightforward to illustrate what combinations of parameters generate and break the log-linear relationship of Gompertz parameters.

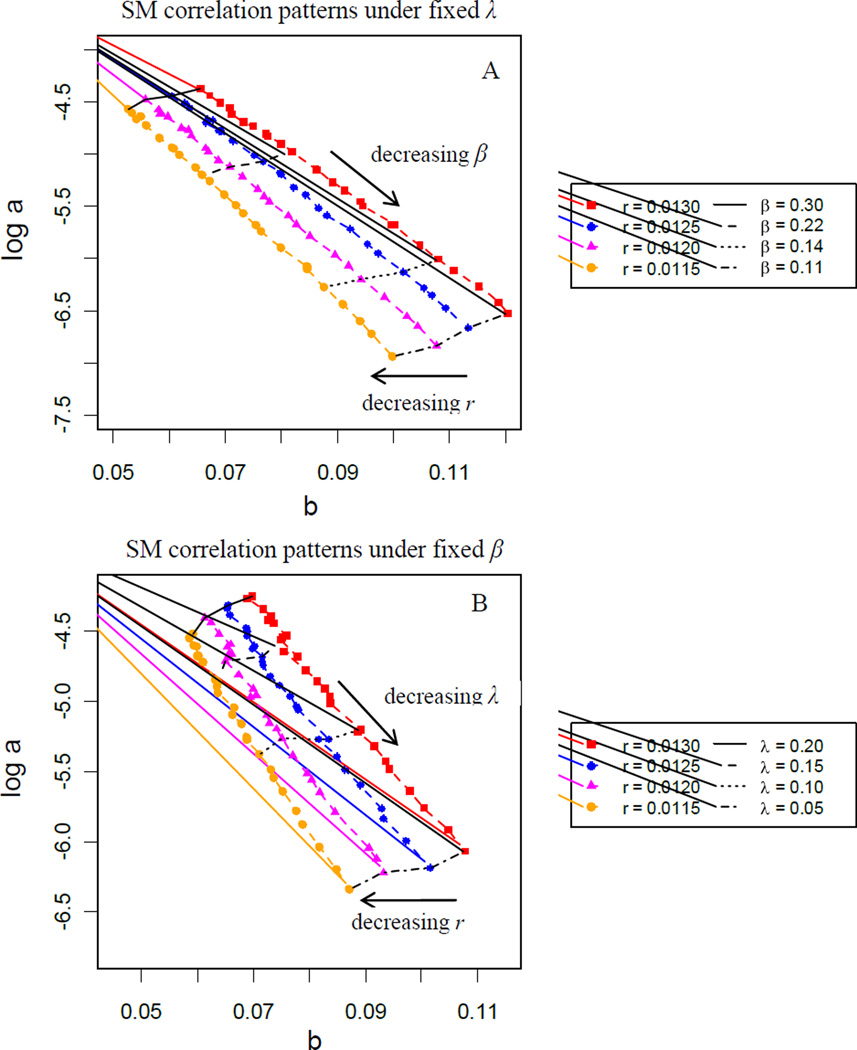
Fig. 6 illustrates the Gompertz coefficient correlations (log a vs. b) estimated from mortality curves generated from the two-process vitality model. The parameters (r, s, λ and β) used in simulating mortality trajectories are typical for adult mortality period data (age 40–110). The log a vs. b patterns are readily generated by fixing λ but varying r and β (Fig. 6A) or fixing β but varying r and λ (Fig. 6B). For both patterns, points forming each line tending from upper left to lower right are estimated by survival curves generated with a fixed r. The points forming each horizontal line, tending right to left, are estimated from survival curves generated by fixing λ (plot A) or β (plot B) and decreasing r. Together, the plots illustrate how log a and b change as r, λ and β change. As r decreases, b decreases but log a is relatively unchanged, while as either λ or β decrease, b increases and log a becomes more negative. In both plots, s is fixed because it has little impact on the patterns.

Figure 6.

Simulated SM correlation patterns.

Note: (A) Mortality curves are all simulated under fixed challenge frequency term λ = 0.12; (B) Mortality curves are all simulated under fixed challenge average magnitude term β = 0.125. For both (A) and (B), curves all have the same background variance structure in vitality: s = 0.01.

Now consider the SM correlations in developed countries (France, Sweden, Japan and the USA) in terms of variations in r, λ and β. A stable negative linear pattern of the Gompertz coefficients from about 1860 to 1960 in period survival data (Fig. 1A) reflects changes in the extrinsic parameters λ or β dominating changes in the intrinsic parameter r. The reversal and flattening in the log a vs. b curve since mid-20^th century reflects a reversal in which changes in the intrinsic parameter r dominate changes in extrinsic parameters λ or β. Thus, in terms of the two-process vitality model, up through the first half of the 20^th century, improvements in the environment reduced the average challenge frequency, magnitude or both. The break in the linear trend about 1960, and the subsequent bending backwards of the pattern, reflects a gradual shift from the dominance of improvements in environmental conditions to improvements in intrinsic accumulated health.

In the case of cohort data (Fig. 1B), the complex pattern suggests multiple change in the dominance of intrinsic and extrinsic processes over cohort years. The differences in the cohort and period results reflect differences in how the intrinsic and environmental factors change over time but disentangling these changes is difficult and beyond the scope of our paper. For a further discussion of cohort and period effects in the model see Li and Anderson (2013).

Theoretically, the SM theory fails to explain the correlation patterns because it attributes all mortality to one process: environmental challenges exceeding the available vitality. Because it does not expresses mortality independent of environmental challenges it does not differentiate changes in survival resulting from improvement in chronic aging-related process from improvement in acute environmental process. From this aspect, including two mortality processes alleviates these restrictions.

The shape of mortality

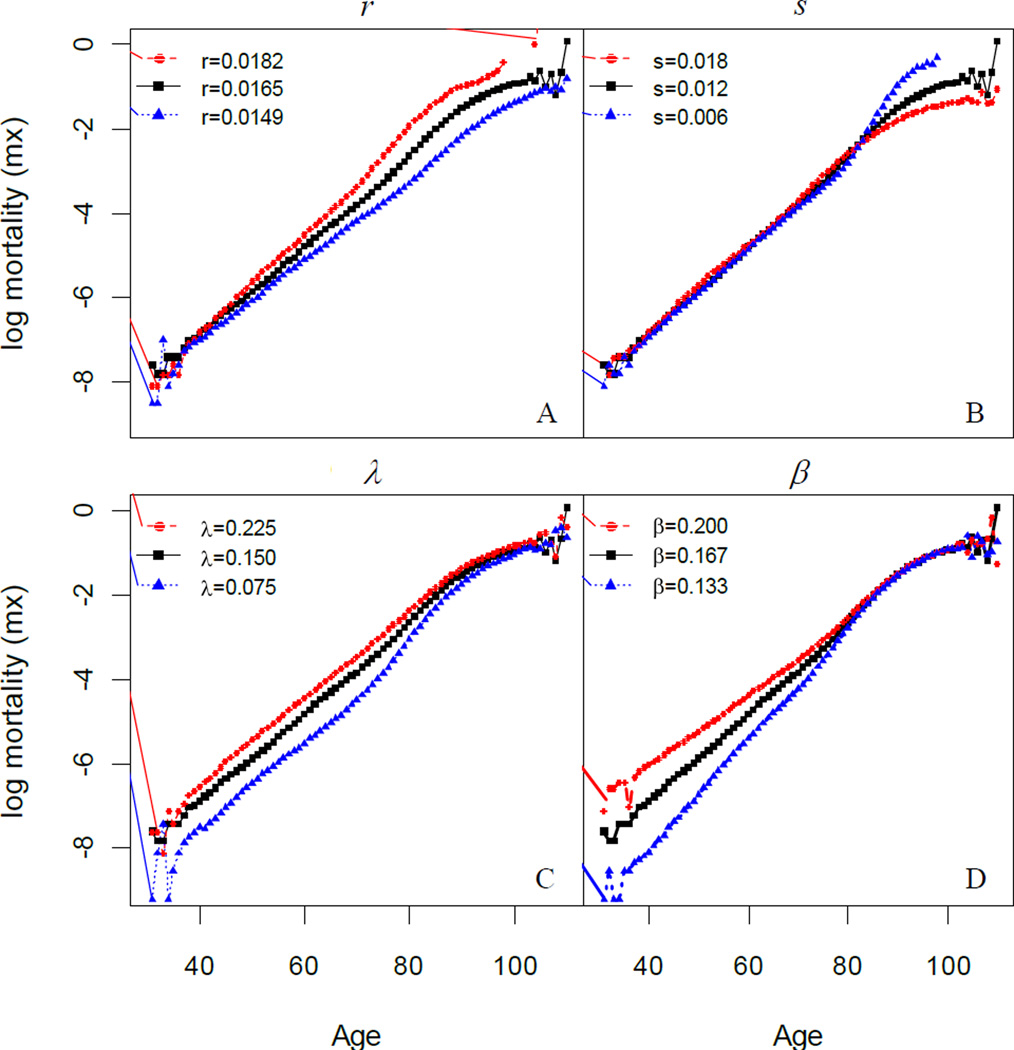
To explore further the complex effect of temporal changes in mortality processes on mortality curves we present simulated plots, generated as described in Section 4.3, summarizing how parameters in the two-process vitality model affect the shape of log-mortality (Fig.7). Each plot depicts the impact on log mortality of three different values of one model parameter with the other parameters constant.

Figure 7.

Simulated patterns of log mortality under varying values of the two-process vitality model parameters. Note: (A) r changes while s, λ, and β are fixed at 0.012, 0.150 and 0.167 respectively; (B) s changes while r, λ, and β are fixed at 0.0165, 0.150 and 0.167 respectively; (C) λ changes while r, s, and β are fixed at 0.0165, 0.012 and 0.167 respectively; (D) β changes while r, s, and λ are fixed at 0.0165, 0.012 and 0.150 respectively.

Demonstrated by Fig.7, all four parameters affect the shape of log-mortality with age but in distinctive ways. The intrinsic parameters r and s primarily affect the mortality patterns at old age, in particular, the characteristics of mortality plateaus. Smaller values of r, which indicate slower rates of intrinsic deterioration, decrease the age of the onset of the plateau, i.e. the age (~ 80) at which the slope of log morality begins to decelerate (Fig. 7A). Smaller values of s increase the asymptotic height of the plateau (Fig. 7B). Neither intrinsic parameter significantly affects early age mortality. In contrast, the extrinsic parameters mostly affect early ages where the log mortality relationship with age is linear. Increases in λ tend to raise the intercept of the relationship (Fig. 7C) while increases in β tend to raise the intercept and lower the slope of the relationship (Fig. 7D). At old age, the effects of both extrinsic parameters are small and the mortality curves quickly converge.

The effects of the model parameters on log-mortality depicted in Fig. 7 helps to further understand the SM patterns revealed in Fig. 6. Applying the Gompertz model (linear fit) to the log-mortality curves between age 40–80, the change in r significantly alters the Gompertz slope b but not the intercept a. Therefore, a decrease in r decreases b, which results in points in the log a vs. b plot shifting left (Fig. 6). For the case of extrinsic parameters, a decline in λ (Fig. 7C) or β (Fig. 7D) significantly reduces the intercept a and because of the convergence of mortality trajectories at old age, the slope b correspondingly increases. This trend occurring, across a series of years, would produce a sequence of points in a log a vs. b plot trending from the top-left to bottom-right as in Fig. 6 and as was observed for the log a vs. b from the 19^th to the mid-20^th century (Fig. 1A). Note that the parameter s which measures the intrinsic heterogeneity has little impact on the log-mortality curve prior to age 80 and thus does not affect the SM correlation pattern.

The change in the empirical patterns of mortality revealed in Fig. 5 also agrees with the change demonstrated in Fig. 7. Comparing the log-mortality curve between period year 1940 and 1960, the difference between the two curves diminishes with age, which corresponds to the change when β is reduced; and the almost parallel shift in the curve until very old age from 1980 to 2005 may suggest reductions in both r and λ.

Discussion

Understanding why human mortality patterns have changed over history has been the subject of many studies (Horiuchi and Wilmoth 1997; Wilmoth and Horiuchi 1999; Tuljapurkar et al. 2000; Bongaarts 2005) and is important for assessing the impacts of public health programs as well as for developing more accurate projections of future patterns of mortality. An important change in the pattern of mortality occurred in mid-20^th century when survival curves began a distinct derectangularization and shift to the right. Of particular interest to demographers, this mid-century change broke, what was assumed to be, a quasi-universal demographic law fixing the relationship between the Gompertz model coefficients (Yashin et al. 2001a, 2002; Finkelstein 2012).

The SM general theory of aging and mortality, as the first important mechanism-based justification for the Gompertz law, is well recognized in the demography literature. Although some generalizations were proposed to the framework such as including a Makeham term to improve the model fit, historically the SM theory well described the mortality pattern, at least between middle and early-old age. Therefore, the theory as well as the correlation it defined was considered as a universal law and widely applied to many studies. However, the evidence exhibited in this study and others (Yashin et al. 2001a, 2002) clearly suggests that the SM framework, in its original form, is no longer suitable for analyzing contemporary mortality data. Because there appears no superior alternative model, modifying the SM framework seems a more feasible option, not only because of the historical influence of the theory, but also due to the belief on the necessity of using a single framework to quantifying the human mortality change. Such belief stems from the fact that the biological processes underlying human mortality and aging have not changed dramatically in the past 100 years (Yashin et al. 2002). Thus, the most parsimonous revision of the model framework is to realistically increase its flexibility to capture the recent changes in mortality patterns.

Several approaches to revising the SM theory have been proposed. Zheng et al. (2011) analyzed the patterns in 42 countries and suggested retaining the general SM theory but admitting heterogeneity in the coefficients across demographic groups, in particular the rate of decline in vitality (B in the SM theory or r in the two-process vitality model) and the amount of deleteriousness (D in the SM theory or β in the two-process vitality model). Finkelstein (2012) explored deviations from the SM theory with models including a gamma-Gompertz frailty model and a vitality-independent model that diminishes the frequency of late-life challenges (Gompertz a parameter) by medical interventions. In our paper we explain the change in the SM correlations by drawing on earlier work (Li and Anderson 2013) that builds on the SM theory by adding a second mortality process and a fourth dimension. The resulting model captures heterogeneity in the rate of loss of survival capacity and includes intrinsic mortality from physiological wear in addition to the extrinsic or acute mortality of the SM theory. The new framework removes the interdependence of the Gompertz parameters and allows a single coherent framework in which to understand historical patterns of mortality. It retains the basic structure of the SM theory, which is broadly recognized in literature, while becoming more flexible in adapting to the current mortality change. In such a way, the new framework bridges the understanding of the mortality dynamics in the past to the possible utility of predicting change in the future.

Within the two-process vitality framework, we explain the change in period mortality of developed countries in the first half of the 20^th century as the result of improvements in environmental conditions including medical achievements that eliminated many infectious diseases, modern technologies that prevented natural disasters and increasing health knowledge that reduced acute risk. Additionally, the framework attributes further reductions in mortality and the corresponding increase in longevity in the second half of the 20^th century to reductions in chronic health risks. While it is unlikely that the intrinsic improvements have a significant genetic contribution, it is possible that they involve physiological responses to advanced living standards, better nutrition and healthier daily behaviors that together reduce the rate of intrinsic vitality loss and delay the onset of organ malfunction and chronic diseases. Intrinsic improvements could also be due to the medical interventions and life-saving technologies, such as replacement surgery that, in extending the life capacity, is equivalent to reducing the rate of physiological decay (Finkelstein 2012; Strulik and Vollmer 2013).

We suggest that the two-process vitality framework, with its natural and intuitive characterization of complex temporal trends in mortality across centuries and in particular over the past half century as demonstrated in this paper and elsewhere (Li and Anderson 2013), provides a basis for studying other demographic problems. First, partitioning of mortality into a slowing varying chronic accumulative process and a rapidly varying acute challenge process can quantitatively characterize genetic, behavioral and environmental contributions to mortality and longevity over different historical periods. Second, the framework, with appropriate extrapolations of the four parameters, should be ideal for projecting mortality and longevity contingent on a population’s physiological status and future patterns of environmental conditions, such as climate, health resource, disease prevalence, and social-economic patterns. Moreover, cross species and cross-habitat comparisons of patterns of intrinsic and extrinsic mortality should illuminate underlying biological and environmental mechanisms. For instance, varying lifespans within or between some species may be the result of differing rates of predation, not differences in the rates of ageing. However, successful applications rely on good analytical approximations of the framework. For example, Li and Anderson (2013) addressed the problem of estimating model parameters by imposing constraints of the extrinsic processes. The potential applications and their challenges will be explored in future work.

While significant challenges are anticipated, the framework is also quite flexible. For example, age-dependent extrinsic challenges can be represented by expressing the challenge frequency parameter λ as a non-homogeneous Poisson process (Finkelstein 2008). Furthermore, other intrinsic process forms can be explored in place of the Wiener process decay to a boundary. Vitality dynamics might be expressed as a stochastic equilibrium processes such as the Ornstein-Uhlenbeck process (Borgan et al. 2008), or as a stationary random processes as that underlying the stress-strength model in reliability theory (Finkelstein and Cha 2013). While these and other stochastic forms are possible their usefulness ultimately rests on their biological realism and empirical support.

In summary, the two-process vitality framework is a simple approximation to the multi-dimensional processes that determine the moment of death. While it is invariably inadequate when higher levels of specificity of mortality are required, we suggest it is the de minimis increment needed to extend the Gompertz framework to meet the challenges in understanding historical and future patterns of mortality.