Improving cardiomyocyte model fidelity and utility via dynamic electrophysiology protocols and optimization algorithms

Abstract

Mathematical models of cardiac electrophysiology are instrumental in determining mechanisms of cardiac arrhythmias. However, the foundation of a realistic multiscale heart model is only as strong as the underlying cell model. While there have been myriad advances in the improvement of cellular‐level models, the identification of model parameters, such as ion channel conductances and rate constants, remains a challenging problem. The primary limitations to this process include: (1) such parameters are usually estimated from data recorded using standard electrophysiology voltage‐clamp protocols that have not been developed with model building in mind, and (2) model parameters are typically tuned manually to subjectively match a desired output. Over the last decade, methods aimed at overcoming these disadvantages have emerged. These approaches include the use of optimization or fitting tools for parameter estimation and incorporating more extensive data for output matching. Here, we review recent advances in parameter estimation for cardiomyocyte models, focusing on the use of more complex electrophysiology protocols and global search heuristics. We also discuss future applications of such parameter identification, including development of cell‐specific and patient‐specific mathematical models to investigate arrhythmia mechanisms and predict therapy strategies.

Introduction

A prominent contribution of George R. Mines, published just over 100 years ago in this journal, was the conceptualization of reentrant activation of cardiac tissue as a mechanism underlying arrhythmias (Mines, 1913; Aguilar & Nattel, 2016). A century later, despite this fundamental insight, sudden cardiac death due to ventricular arrhythmias remains one of the leading causes of mortality in the developed world.

Over the past several decades, the proteins that are altered in congenital and acquired arrhythmia disorders have been largely identified and characterized. Only a few of these basic‐science advances, however, have been translated into successful new therapies for arrhythmia treatment or prevention. One contributing factor to this gap may lie in the complex dependencies and interactions between the many different proteins and molecules underlying electrical activity in the heart. Complex systems, such as the cardiac myocyte, often exhibit emergent properties that are not easily predicted from the characteristics of the individual parts. Therefore, although malfunction in virtually any of the individual components involved in generation of the heartbeat may increase arrhythmia risk, mechanistic and quantitative linking of such individual component malfunction to arrhythmogenesis is daunting.

Because of this complexity, mathematical modelling can be an important means of illuminating both normal and pathophysiological cardiac electrophysiology. Mathematical models of electrophysiological dynamics in cardiac myocytes, consisting of coupled, non‐linear differential equations, have been developed with increasing complexity and specificity for more than 50 years (Noble et al. 2012). These models have inarguably helped increase our understanding of cellular electrophysiology and cardiac arrhythmias (Roberts et al. 2012). In addition to simulating the effects of pharmacological agents, models can be employed in, e.g., predicting the impact of specific genetic variations, and simulating arrhythmogenesis at the tissue level.

Many of the mathematical models used to investigate cardiac physiology and arrhythmia mechanisms, however, suffer from important limitations. For example, the rate dependence of the action potential is inaccurate for several human atrial and ventricular models and models may not exhibit expected arrhythmia‐relevant dynamics such as early afterdepolarizations and repolarization alternans (O'Hara et al. 2011; Gonzales et al. 2014). In addition, models generally present the behaviour of average or typical cells and may not accurately reproduce electrophysiological properties of particular, individual myocytes. In this review, we discuss how limitations inherent to the traditional model development process results in suboptimally parameterized models and discuss recent advances towards improved model generation.

Limitations to cardiac ionic model development process

Although ionic cardiomyocyte models have undergone tremendous development over the last decades, in particular by more thoroughly representing the ensemble of cardiac ionic currents and by improving treatments of intracellular calcium handling, the process through which models are developed remains relatively unchanged. Models are constructed by assembling equations for individual currents into a composite cell model. These formulations are most often based on current data obtained from whole‐cell voltage‐clamp experiments, which ideally would be designed to estimate values for all of the steady‐state and kinetic parameters of the Hodgkin–Huxley formalism, in addition to the maximal conductance.

Well‐known shortcomings intrinsic to the voltage‐clamp process as it relates to modelling include: (1) insufficient separation of activation and inactivation processes (Lee et al. 2006), (2) non‐selective pharmacological ion channel blockers, and (3) non‐physiological solutions. Additionally, modellers often must make do with data that were not obtained for the specific purpose of building a model and therefore are incomplete (ten Tusscher et al. 2004; O'Hara et al. 2011). For example, time constants may be obtained only at a few voltage values, whereas a model requires values over the full physiological range. Further, experimental studies may purposefully select cells that have larger currents in order to more easily characterize kinetics and activation/inactivation processes, thus creating a bias towards larger conductance values (Courtemanche et al. 1998).

Inter‐laboratory variations and data inconsistency

For a number of reasons, including varying experimental specialization required for quantification of different ionic components, data and formulations for individual currents are typically obtained from voltage‐clamp experiments performed in several different laboratories. Distinctions in experimental protocols introduce inter‐laboratory variations in many factors that directly influence cellular electrophysiology, including temperature, composition of solutions, and enzymatic digestion isolation procedure (Fig. 1; Niederer et al. 2009; Fink et al. 2011). Different laboratories may also favour or have primary access to subjects of certain characteristics such as sex, age and breed.

Figure 1. Limitations to cardiac myocyte ionic model development .

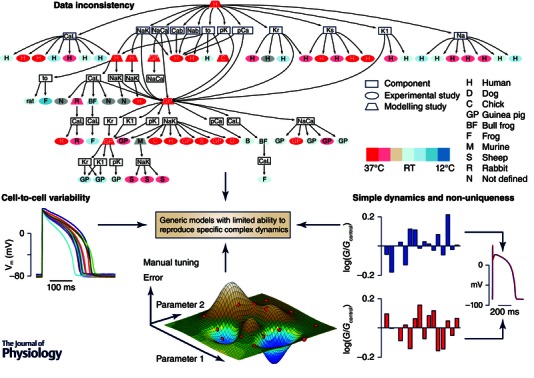
Top: experimental and species variability is illustrated for a human ventricular myocyte model (the ten Tusscher et al. 2004 model). Different ionic components originate from previous modelling or experimental studies using data from a variety of species obtained at a range of temperatures. Reproduced from Niederer et al. (2009) with permission. Left: cell‐to‐cell variability in action potential for 14 myocytes isolated from the guinea pig left ventricle (following the protocol in Groenendaal et al. 2015). Bottom: manual tuning of parameters provides only poor coverage of the model parameter space (red dots represent parameter combinations tested) and may not find the best solution (the dark blue well). Right: two different sets of conductance parameters (represented by blue and red) give rise to overlapping action potentials, emphasizing that simple dynamics cause non‐uniqueness. Reproduced from Sarkar & Sobie (2010).

Besides the inconsistencies stemming from lab‐to‐lab variability, models often contain a source of divergence because data are not always available for all the relevant currents for the particular species and cell‐type of choice. In these cases, modellers make do with what they deem is best back‐up. One might expect such lack of data to be particularly pronounced for human models, for which a careful analysis of data sources was first carried out (Fig. 1; Niederer et al. 2009), but murine models exposed to the same analysis also show considerable re‐use of off‐species data (Niederer & Smith, 2012).

Lab‐to‐lab inconsistencies also occur in the compound data used to validate and/or develop models, such as action potential recordings. As an example of how inter‐lab variability in output data can directly affect model development, consider the two widely used human atrial myocyte models due to Courtemanche et al. (Courtemanche et al. 1998) and Nygren et al. (Nygren et al. 1998). As the two models are contemporary, they were developed based on the same available literature and contain the same currents, although with some differences in their formulations. Even so, the models produce very different outputs, with, most prominently, contrasting baseline action potentials: the Courtemanche et al. model produces a spike‐and‐dome morphology whereas the Nygren et al. model generates a triangular one. These differences have been ascribed to choices made by the developers in order to match the model to the morphology most frequently observed in their own labs (Nygren et al. 2001). For both models, conductance parameters were adjusted to generate the desired action potential morphology, and indeed, modifying parameters can cause the Courtemanche et al. model to instead produce a triangular action potential and the Nygren et al. model to switch to a spike‐and‐dome morphology (Nygren et al. 2001; Syed et al. 2005; Cherry et al. 2008). With the ability to estimate multiple cell‐specific conductances and produce cell‐specific models as discussed in this review, it may now be possible to directly test this idea: do human atrial myocytes exhibiting the spike‐and‐dome morphology have conductances similar to those of the Courtemanche et al. model and do myocytes with the triangular morphology have conductances comparable to those of the Nygren et al. model? If not, the discrepancy may stem from the dissimilar calcium dynamics employed by the models (Cherry et al. 2008) and/or the inconsistency in the choices for data use where human atrial data were not available: the Courtemanche et al. model then relied on a guinea pig ventricular model, whereas the Nygren et al. model used a rabbit atrial model.

Cell‐to‐cell variability

While inter‐laboratory variations can, in theory, be minimized, the electrical activity of individual cardiomyocytes will inherently vary due to population heterogeneity, i.e. inter‐heart variability. It is also well known, from tissue and whole‐heart experiments, that even within individual hearts, intrinsic gradients in ion channel densities cause variations in action potential morphology of many cell types, including sinoatrial, atrial and ventricular (Fig. 1). These large‐scale gradients cover apex‐to‐base, transmurally across the ventricular wall, left versus right atrium or ventricle, and across the sinoatrial node region (Schram et al. 2002). However, even in cells isolated from the same region of the heart, action potential characteristics and currents vary (Bénardeau et al. 1996; Groenendaal et al. 2015).

Mathematical cardiomyocyte models typically do not take into account cell‐to‐cell variability in ionic conductances and electrical activity, but instead use average data to formulate a ‘representative’ cell. This is problematic for several reasons:

1. an average cell may not exist if individual cells from the same region rely to varying extents on different ionic currents as demonstrated in some neuronal systems, e.g. in the crustacean stomato‐gastric ganglion (Schulz et al. 2006);

2. the process of averaging individual model parameters can induce a bias towards larger values and cause mismatch between model output and targeted experimental data (Zhou et al. 2009);

3. the accuracy with which an average cell model can predict responses to perturbations such as pharmacological agents for a particular cell is unclear.

Manual tuning

Given these impediments to the process of model development, it is not surprising that model parameters often need adjustment when assembling the individual current formulations into a composite model. This tuning is usually done manually, varying one parameter at a time, until the model is thought to reproduce the experimental target data, such as an action potential, well enough by some subjective measure. The process seems simpler when manually adjusting a single parameter to a particular output, e.g. sodium current conductance to action potential upstroke velocity or delayed rectifier conductances to action potential duration (Nygren et al. 1998; Courtemanche et al. 1998; ten Tusscher et al. 2004; O'Hara et al. 2011) – steps rationalized by inherent inaccuracies in voltage‐clamp recordings of these currents. However, the mapping between conductances and action potential parameters is not unique, as each action potential feature is generally determined by a combination of a few key ionic current parameters (Sarkar & Sobie, 2010; Britton et al. 2013).

The optimal parameter values for a model are those that give the smallest discrepancy or error between model output and target data. This error is a function of the model parameters (the error function). In addition to being laborious and time consuming, manual parameter tuning is suboptimal as the approach explores only a small fraction of the many possible parameter combinations and therefore will almost certainly not result in the best possible fit to the target data. This idea is illustrated in Fig. 1, where sparse sampling of the combination of the two parameters (i.e. a two‐dimensional parameter space) results in not locating the best solution, identified as the lowest peak of the error function.

The method of manual tuning is also problematic from a physiological point of view as tuning currents individually neglects the possibility of inter‐current dependencies due to channel co‐regulation. Consequently, a hand‐tuned model may therefore not adhere to the underlying physiology. Since arrhythmogenesis occurs through an interaction between different cellular components, ideally a model should be fitted to data capturing relevant interactions in whole‐cell dynamics.

Simplistic target data

Although hand tuning is not expected to find the optimal model fit, it does generate models that closely recreate the targets they were meant to match. However, these are often dynamically simple objectives, such as a single action potential. Because of the many parameters incorporated into modern ionic cardiomyocyte models, different combinations of parameters may generate simple outputs that are very similar (Fig. 1; Dokos & Lovell, 2004; Sarkar & Sobie, 2010; Zaniboni et al. 2010; Groenendaal et al. 2015). It is possible that different individuals or different cells employ distinct parameter combinations as these may each be ‘good enough’ for each cell to perform its functional role (Marder, 2011; Sarkar et al. 2012; Weiss et al. 2012). Therefore, on a population scale, a range of combinations may be representative, but on the scale of the individual myocyte they proffer false alternatives to the particular combination present in that cell. While such a model may recreate existing data well, it would not be expected to be able to accurately predict the effects of perturbations as different ionic current combinations change basic characteristics such as excitability, current sensitivity and rate dependence (Zaniboni et al. 2010). For example, if a particular myocyte relies on a large rapid delayed rectifier potassium current (I _Kr) and on little of the slow delayed rectifier (I _Ks) for normal repolarization, a model generating a similar baseline action potential using a combination of large I _Ks and little I _Kr would be expected to underestimate the effects of I _Kr block (Weiss et al. 2012). Similarly, due to the intrinsically different kinetics of ion channels, models with different parameter combinations would be expected to behave differently during the often fast and irregular excitation patterns associated with arrhythmias.

As we will discuss below, fitting a model to more complex data can help eliminate the incorrect solutions and better constrain parameters. Importantly, this can help overcome the limitation that models tuned to reproduce only simple dynamics may fail to accurately predict more complex dynamics relevant to arrhythmogenesis.

Parameter estimation and optimization

Brief overview of common methods

In general, optimization works by finding the global minimum of the error function in the potentially high‐dimensional parameter space of the model. Different approaches are available to solve optimization problems. Gradient descent methods rely on computing local gradients of the error function to determine a path to a minimum. Special manoeuvres are required to ensure that the global, rather than a local, minimum is eventually found (e.g. Dokos & Lovell, 2004). A fundamentally different methodology, genetic algorithms test many different parameter combinations in the process of guiding an initial, random population of parameter sets toward a best parameter set using ideas from evolutionary biology. Gradient descent methods and genetic algorithms have been used in several studies to optimize parameters in cardiac cell models (e.g. Dokos & Lovell, 2004; Syed et al. 2005; Bot et al. 2012; Guo et al. 2013; Kaur et al. 2014; Groenendaal et al. 2015), rather than adjusting post hoc and by hand. Other techniques used for these or similar types of optimization problems include simulated annealing (Vanier & Bower, 1999) and particle swarm optimization (Weber et al. 2008; Chen et al. 2012). Linear regression presents a simpler alternative to these optimization techniques, using local searches to infer parameter values based on correlations between parameters and biomarkers such as action potential duration and calcium transient amplitude (Sarkar & Sobie, 2010).

There has been no direct comparison or benchmarking of these methods for parameter estimation in cardiac cell models. We expect the answer to the question of which method is best to be problem‐specific and particular to the number of parameters to be estimated, the complexity of the objective, and the characteristics of the error function (Vanier & Bower, 1999).

Search algorithms themselves have intrinsic parameters whose settings affect their speed and ability to find the global minimum. The optimal settings of such parameters may also be problem‐specific and may even vary throughout a given optimization. Optimization thus does not automate parameterization in the process of developing improved models, as it still requires investigator‐based choices and intuitions.

Choice of parameters to be estimated

In general, optimization is computationally expensive. The difficulty and the computational cost of an optimization problem increases tremendously with the number of parameters, as the addition of each parameter adds another dimension to the parameter space, and because more data are required to constrain more parameters. Therefore, many parameter estimation problems have concentrated on optimizing simplified models with fewer parameters (Bueno‐Orovio et al. 2008; Weber et al. 2008; Abed et al. 2013; Guo et al. 2013) or, for biophysically detailed models which can contain hundreds of parameters, have focused on either identifying kinetic and steady‐state parameters for a single current only (Fink & Noble, 2009; Zhou et al. 2009) or determining maximal conductances only (Syed et al. 2005). We have done the latter in previous work (Bot et al. 2012; Groenendaal et al. 2015), based on the assumption that ion channel kinetics are preserved among (healthy) subjects while conductances vary as a result of differences in expression levels. Conductance parameters are intrinsically easier to estimate as they, unlike kinetic parameters, are voltage independent.

In addition to deciding which parameters to estimate, modellers have to choose an allowed search range for each parameter. Constraining these ranges based on a priori knowledge can help reduce computations.

Example: single action potential fitting by genetic algorithm

As an example of an optimization, we show here the estimation of conductance parameters in a guinea pig ventricular myocyte model using a genetic algorithm (Fig. 2; Groenendaal et al. 2015). This example represents an in silico test case, assessing the ability of the optimization method to recover the known model parameters.

Figure 2. Progression of genetic algorithm parameter estimation .

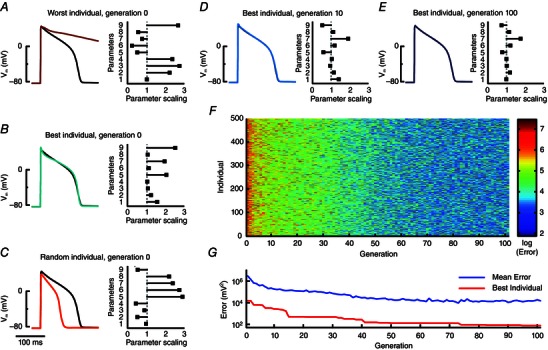
A–C, the genetic algorithm is initialized with 500 random individuals, i.e. model instantiations, in generation 0. Models are paced and a single action potential is recorded as its phenotype. The fitness of each individual is calculated inversely as an error (sum of squared differences) between model output and target objective action potential. Left columns show action potentials generated by three different generation 0 model instantiations (traces are coloured according to their error and colour bar in F) compared to the baseline model (black). Right column bar graphs indicate the scaling of the nine model parameters for each individual, with a scaling of 1 representing the original model value. Parameters 1–9 correspond to maximal conductance of the sodium current, the L‐type calcium current, the T‐type calcium current, the inwardly rectifying potassium current, I _Kr, I _Ks, the plateau potassium current, the sarcolemmal calcium pump current, and the maximal flux of the sarcoplasmic reticulum Ca²⁺‐ATPase, respectively. D–G, with progression through the generations, individual action potentials become more similar to the optimization objective and errors decrease accordingly. At generation 100, the overall best individual and the original model are indistinguishable by eye, although the bar graph indicates differences among the parameters (E). Reprinted from Groenendaal et al. (2015).

We used an initial, random population of 500 individuals, or model instantiations, each characterized by a genotype (a set of parameters), a phenotype (model output, here a single action potential), and fitness (the inverse of the error between model output and target). The evolution of this population occurs in discrete steps, termed generations. From the first generation, individuals with higher fitness are selected, in our set‐up through pair‐wise tournaments, where the most fit of two individuals continues to a mating pool. Individuals in the mating pool produce the offspring for the next generation through randomized parameter swapping and parameter modification (i.e. computational correlates of crossover and mutation). Repeating this process, here through 100 generations, results in a more fit population (Fig. 2 E–G), in which the best individual produces a phenotype that closely replicates the objective (Fig. 2 E). Notice, however, that this match is obtained despite a discrepancy between the genotype of the individual and that of the objective (Fig. 2 E), emphasizing the point that simple target data are insufficient to estimate parameter combinations in these models.

Although the action potential of the optimized model is indistinguishable by eye from its target in this example, the error has not dropped all the way to zero as it ideally should. A larger population size, an increased number of generations, and more diversity through crossover and mutations can help reduce the error (at the cost of raised computation times), but genetic algorithms are not guaranteed to find the global minimum. For practical purposes, fits to within the intrinsic, experimentally observed, beat‐to‐beat variation, or within the limits of measurement noise, are generally considered sufficient.

Use of complex objectives in optimization

Addition of more data to the target objective presents a key strategy to better constrain parameters and help overcome the limitation that multiple parameter combinations may generate the same single action potential. Different approaches to generating more elaborate objectives include (1) developing more complex pacing or voltage‐clamp protocols that probe the cell in dynamically richer ways; and (2) incorporating measurements of multiple variables, such as transmembrane potential, ionic current, and membrane resistance. Complex objectives can be used in conjunction with various search methods, including genetic algorithms. Different types of data may make up a single objective, potentially with different relative weights for the individual components (Groenendaal et al. 2015), or can be implemented as a multiple objective optimization (Druckmann et al. 2007; Kaur et al. 2014). If the protocol generating the objective data is both capable of uniquely defining the model parameters of choice and sufficiently concise that it can be implemented on individual cells (i.e. without significant damage to the cell as can occur with long protocols), then this strategy can be used to generate cell‐specific models, which can overcome the twin shortcomings of data inconsistency and cell‐to‐cell variability.

Pacing‐based protocols

As the rate dependence of the cardiac action potential is of direct relevance to arrhythmogenesis, the approach of fitting to data obtained at multiple pacing rates is pertinent. This has been done for both simplified, phenomenological models (Bueno‐Orovio et al. 2008; Weber et al. 2008; Guo et al. 2013) and biophysically based ionic models (Syed et al. 2005). For example, Syed et al. (2005) demonstrated that fitting a model to experimentally recorded action potentials obtained during 2 Hz pacing only, resulted in inaccurate predictions of action potential dynamics during 1 Hz pacing. However, consistent with the principle that dynamically richer training data improve the fit, fitting to data obtained at four different pacing rates resulted in a more robust parameter estimation.

As recording data from multiple pacing rates can be time consuming, a more efficient way of probing the rate‐dependent action‐potential dynamics is by using a sequence of irregular pacing intervals (Guo et al. 2013; Groenendaal et al. 2015). Such a sequence may also closely resemble arrhythmia‐relevant dynamics such as the irregular excitations associated with fibrillation. When estimating conductances in an ionic model using a genetic algorithm, we found that fitting to a sequence of randomly timed action potentials yielded models much better at predicting novel irregular dynamics than did models fitted to a single action potential (Fig. 3). This increase in predictive power was associated with a more accurate estimation of several conductance parameters, in particular those of I _Kr and I _Ks (Fig. 3). When optimizing using a single action potential only, plausible solutions exist that have too little I _Kr and too much I _Ks. However, due to their differences in kinetics, the stochastic pacing protocol enables an untangling of their otherwise compensatory effects resulting in more accurate estimation.

Figure 3. Complex objectives improve parameter estimation and predictive power .

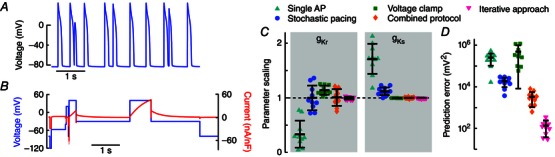
A, irregular sequence of action potentials due to stochastic pacing. B, multi‐segment voltage‐clamp protocol and resulting current response. C, improvements in the in silico, genetic algorithm‐based, parameter estimation of I _Kr and I _Ks conductances by enhancing the optimization objective, from a single action potential (cyan triangles), stochastic stimulation (blue circles), or multi‐segment voltage clamp (green squares), to the combined stochastic pacing and voltage‐clamp protocol (orange diamonds). A parameter scaling of 1 indicates the baseline value to be recovered. Symbols indicate the best solution from each of 10 individual runs, differing due to the random nature of the genetic algorithm. Error bars give mean ± standard deviation. D, the ability of the optimized models to predict novel dynamics is calculated as the error in response to a novel stochastic pacing sequence (‘Prediction error’). Predictive ability is improved when using the stochastic pacing over the single action potential. The prediction error is large for the voltage‐clamp protocol alone, which does not train models according to membrane potential. Adding the voltage‐clamp protocol to the stochastic pacing protocol gives better predictions compared to stochastic stimulation alone. A second application of the genetic algorithm, allowing only fine, local, parameter changes (‘Iterative approach’, magenta triangles) results in improved parameter estimation and predictive power. Reproduced from Groenendaal et al. (2015).

Complex voltage‐clamp protocols

The strategy of generating complex and efficient voltage‐clamp protocols has shown its merits in several studies aimed at developing improved models of individual currents, typically many‐parameter Markov models to enable more precise simulations of pharmacological current inhibition (Fink & Noble, 2009; Zhou et al. 2009). Clamping to wave‐like, artificial voltage series, in addition to a single action potential, leads to more precise estimation of many currents in an ionic model (Dokos & Lovell, 2004).

Another voltage‐clamp strategy is to develop a multi‐segment protocol, where each part is designed to emphasize a different, individual current (Groenendaal et al. 2015). This approach should force optimized models to fit individual currents accurately, as only models that fit each isolated current will match the total voltage‐clamp current well. We have found that this strategy of current separation without pharmacological blockage works well for the currents that are indeed well isolated during the protocol (e.g. I _Ks; Fig. 3), but that it is difficult to design voltage‐clamp sequences that effectively isolate all major currents. When used in combination with a stochastic pacing sequence to generate a target objective, this approach can generate precise estimates of the isolated current conductances and result in models with strong predictive power (Fig. 3).

Membrane resistance and calcium transients

In optimization problems, more precise parameter estimation is typically gained when including information about additional variables rather than entering longer recordings of the same variable. For cardiomyocyte physiology, several variables other than transmembrane voltage and individual currents are crucial to normal and pathological function and are therefore important for a model to reproduce. Membrane resistance, for example, controls the voltage response to a current perturbation, e.g. current flowing through gap junctions from neighbouring cells. Models do not necessarily reproduce physiological resistances but can be adjusted (Nygren et al. 1998; Courtemanche et al. 1998) or optimized (Kaur et al. 2014) to do so.

The intracellular calcium concentration is perhaps the most obvious candidate variable for addition to an optimization problem, due to its importance for contractility, intracellular regulation, and to the fact that it is routinely measured experimentally. Further, several of the examples in which different parameter combinations resulted in similar action potentials had divergent calcium transients (Dokos & Lovell, 2004; Sarkar & Sobie, 2010), suggesting that addition of calcium data would help constrain parameters. In particular, additional optimizing to calcium data would be expected to estimate more precisely the parameters directly regulating [Ca²⁺]_i (e.g. sodium–calcium exchange current and sarcoplasmic reticulum Ca²⁺‐ATPase activity (SERCA) flux; Fink et al. 2011; Groenendaal et al. 2015).

Protocols to improve tissue models

Many mathematical models are developed for the purpose of simulating arrhythmias in virtual tissues and therefore need to accurately reproduce tissue features. Conduction velocity and its restitution are key characteristics of tissue dynamics that can be included in optimizations to help constrain parameters and ensure accurate propagation speed (Bueno‐Orovio et al. 2008; Weber et al. 2008). The process of fitting conduction velocity may take into account tissue‐wide or local conductivities (Camara et al. 2011).

When coupled together to form a virtual tissue, myocyte dynamics may behave differently from the uncoupled cell model constituent (Clayton et al. 2011; Kaur et al. 2014). One way to address this problem is to optimize tissue models to data from tissue recordings (Abed et al. 2013), but this process is computationally demanding for complex models. Therefore, there is a need for rigorous ways to parameterize cellular models so that they exhibit appropriate behaviour in tissue. Inclusion of membrane resistance in the optimization as discussed above, may be a first step towards this goal.

Towards patient‐specific modelling of cardiac electrophysiology

Model optimization presents methods to study both cellular and subject‐level variability. By generating cell‐specific models, we can begin to answer questions regarding cellular heterogeneity, both in terms of global heterogeneity due to intra‐cardiac ionic gradients and small‐scale heterogeneity due to stochastic gene expression. A key question, for example, is how variations in ionic currents contribute to functional differences in action potential and calcium transient waveforms (Sarkar et al. 2012). Simulations of cell‐specific models can also generate new, experimentally testable, predictions specific to an individual cell regarding the response to an intervention such as a particular pacing sequence or drug application.

To be able to quantify, compare and contrast intra‐heart and inter‐subject heterogeneity, these analyses should be applied to large populations of cells. Indeed, such analyses may present a first step towards generating subject‐specific ventricular models, as the intra‐ventricle variation is particularly large with apex–base, transmural and left–right contributions. Development of subject‐specific (animal or human) models may be useful as means to investigate sources underlying inter‐subject variability as well as its functional consequences. This includes, e.g., genetic variations that can make a person more prone to early or delayed afterdepolarizations and ventricular arrhythmias, as well as complex pathologies such as heart failure that slowly change the electrophysiological substrate. Models of individuals in such patient groups can be helpful in making precise predictions and risk stratification on, e.g., vulnerability to arrhythmias upon different challenges or effects of different treatment strategies (Lerma, 2016).

One area of cardiology where patient‐specific modelling may be particularly impactful in the near future is atrial fibrillation. Because atrial fibrillation progresses (deleteriously) with time and has many different comorbidities and variants, the atrial anatomy and arrhythmogenic substrate can vary significantly among patients. Recent years have seen rapid progress in the development of personalized atrial model structures based on medical images (Dössel et al. 2012; Trayanova, 2014). Simulations with such models have replicated clinical electrocardiogram features including P‐wave duration and excitation patterns (Krueger et al. 2013; Gonzales et al. 2014), and have also demonstrated how fibre discontinuities or fibrotic lesions can steady reentrant waves (Gonzales et al. 2014; McDowell et al. 2015), providing plausible mechanisms for the stable rotors seen in many atrial fibrillation patients in clinical investigations (Swarup et al. 2014) (see also Zaman et al. 2016 and Haïssaguerre et al. 2016 in this issue of The Journal of Physiology for discussions on fibrillation mechanisms). As discussed in yet another article in this issue (Jacquemet, 2016), model utilizations have focused on simulating radio‐frequency ablation treatment of atrial fibrillation, with the aim of providing a basis for generation of personalized clinical ablation strategies, including decisions on whether atrial fibrillation is terminable in a given patient and where to best place minimal ablation lesions.

Although atrial structure is of particular importance to atrial fibrillation dynamics due to the anatomical complexity of the atria, we postulate that personalized atrial models stand to gain significant improvement by the addition of patient‐specific electrophysiological cellular models – inter‐subject differences in cellular electrophysiology have been seen clinically using, e.g., monophasic action potential (MAP) catheters (Kim et al. 2002; Krummen et al. 2012) and experimentally in isolated human atrial myocytes (Sánchez et al. 2014). To date, patient specificity in the ionics of personalized atrial models has been limited to groupings between control versus chronic atrial fibrillation and adjustments based on extracellular electrolyte concentrations (Krueger et al. 2013). Efforts to personalize cellular models could include optimization using in situ clinical MAP duration restitution data and ex vivo data such as transmembrane voltage or current recordings in cells isolated from tissue biopsies in patients undergoing surgery. An obvious limitation to these recordings is the lack of sampling of the spatial heterogeneity in electrophysiology (Aslanidi et al. 2011). Also, cellular electrophysiology may change on a short time‐scale in situ due to changes in nervous tone because of the sensitivity of atrial myocytes to levels of both acetylcholine and β‐adrenergic agonists. Therefore, accurate model optimization may require rapid fitting, which is currently possible only when estimating relatively few parameters (Bot et al. 2012).

In addition to informing treatment decisions for individual patients, e.g. regarding an ablation procedure or pharmacological intervention, patient‐specific models may also give insights into basic mechanisms underlying arrhythmias. For example, more accurate models of the human atria may enable us to answer the question of how the novel treatment strategy ‘focal impulse and rotor modulation’ (FIRM) ablation successfully terminates atrial fibrillation in many patients (Narayan et al. 2012), instead of lesions merely anchoring and stabilizing activation waves into an anatomical reentry as that described by Mines (Mines, 1913; Gonzales et al. 2014).

Conclusions

The traditional disjoint method of developing mathematical models of cardiac myocyte electrophysiology suffers from several inherent problems. In recent years, a number of studies have demonstrated the benefits of applying automated optimization methods to cardiac myocyte model parameterization. Because multiple parameter combinations can reproduce simple dynamics such as a single cardiac action potential, these methods only come to full fruition when used in conjunction with more complex target data, such as multiple variables or dynamically rich perturbations. These methodologies can be used to generate cell‐specific and tissue‐specific models in order to address issues such as inter‐subject heterogeneity in baseline electrophysiology and in response to therapeutic interventions.

In addition to generating more accurate models, new information can be gained directly from optimization results. For one, the outcome of an optimization may be analysed in terms of parameter sensitivity. For example, multiple runs of a genetic algorithm result in a distribution of values for each parameter to be estimated (as in Fig. 3). The widths of these distributions are related to the sensitivity of the model to the parameters, with narrow ranges indicating high sensitivity and a broad range suggesting that a parameter has little influence on the target. Secondly, analysing correlations between the estimated parameters can help illuminate under what conditions different parameter combinations result in similar behaviours. To date, little has been done in terms of exploiting this information rigorously and fully, although such analyses could provide important new hypotheses for cellular dynamics and variability.

Additional information

Competing interests

None declared.

Funding

This work was supported by funding from the National Institutes of Health grants R01EB016407 (to D.J.C.), R21HL122564, and P50GM071558 (to E.A.S.).

Biographies

Trine Krogh‐Madsen is an Assistant Research Professor in the Department of Medicine and at the Institute for Computational Biomedicine at Weill Cornell Medical College, New York. She received an MSc degree in applied physics from The Technical University of Denmark and a PhD degree in physiology from McGill University. Her research is in the area of computational cardiac electrophysiology.

Eric Sobie is an Associate Professor in the Department of Pharmacology and Systems Therapeutics at Mount Sinai School of Medicine in New York City. He holds a BSE degree from Duke University and a PhD from The Johns Hopkins University, both in biomedical engineering. His research focuses on gaining a greater quantitative understanding of cardiac physiology and pathophysiology by combining experimental studies and simulations performed with mathematical models.

David Christini received a BS degree in electrical engineering from the Pennsylvania State University and MS and PhD degrees in biomedical engineering from Boston University. He is a Professor in the Departments of Medicine and Physiology and Biophysics, Weill Cornell Medical College, New York. He uses computational and experimental methods to study cellular‐ to organ‐level cardiac electrophysiological dynamics, with an emphasis on understanding the mechanisms underlying arrhythmia initiation and in developing new arrhythmia therapies.