Imaging Extracellular Matrix Remodeling In Vitro by Diffusion-Sensitive Optical Coherence Tomography

Abstract

The mammary gland extracellular matrix (ECM) is comprised of biopolymers, primarily collagen I, that are created and maintained by stromal fibroblasts. ECM remodeling by fibroblasts results in changes in ECM fiber spacing (pores) that have been shown to play a critical role in the aggressiveness of breast cancer. However, minimally invasive methods to measure the spatial distribution of ECM pore areas within tissues and in vitro 3D culture models are currently lacking. We introduce diffusion-sensitive optical coherence tomography (DS-OCT) to image the nanoscale porosity of ECM by sensing weakly constrained diffusion of gold nanorods (GNRs). DS-OCT combines the principles of low-coherence interferometry and heterodyne dynamic light scattering. By collecting co- and cross-polarized light backscattered from GNRs within tissue culture, the ensemble-averaged translational self-diffusion rate, D_T, of GNRs is resolved within ∼3 coherence volumes (10 × 5 μm, x × z). As GNRs are slowed by intermittent collisions with ECM fibers, D_T is sensitive to ECM porosity on the size scale of their hydrodynamic diameter (∼46 nm). Here, we validate the utility of DS-OCT using pure collagen I gels and 3D mammary fibroblast cultures seeded in collagen/Matrigel, and associate differences in artificial ECM pore areas with gel concentration and cell seed density. Across all samples, D_T was highly correlated with pore area obtained by scanning electron microscopy (R² = 0.968). We also demonstrate that DS-OCT can accurately map the spatial heterogeneity of layered samples. Importantly, DS-OCT of 3D mammary fibroblast cultures revealed the impact of fibroblast remodeling, where the spatial heterogeneity of matrix porosity was found to increase with cell density. This provides an unprecedented view into nanoscale changes in artificial ECM porosity over effective pore diameters ranging from ∼43 to 360 nm using a micron-scale optical imaging technique. In combination with the topical deposition of GNRs, the minimally invasive nature of DS-OCT makes this a promising technology for studying tissue remodeling processes.

Introduction

The extracellular matrix (ECM) is made up of a connective fibrous network of macromolecules, including collagen, secreted primarily by fibroblasts. It is a porous mesh that provides structural support for cells while allowing for the diffusion of nutrients from blood to cells within the tissue (1). The architecture of the ECM can be described by its fibers (diameter, composition, tortuosity, cross-linking, and density) and by its pores (size, anisotropy, and permeability), properties that are interrelated and ultimately dictate its micromechanical properties. Importantly, the ECM interacts dynamically with the growth and proliferation of cells, where homeostasis is vital for maintaining healthy cellular behavior, with implications ranging from wound healing to organ function (2). This homeostasis breaks down during tumorigenesis, where ECM remodeling within the microenvironment results in mechanical signaling to cells that further drives cancer progression (2, 3). At the same time, changes in ECM architecture are strongly associated with breast carcinoma (4, 5). Thus, methods are critically needed for rapid and minimally invasive assessment of ECM remodeling processes, both for fundamental studies and for translational technologies to improve cancer diagnosis and therapy.

Here, we report a minimally invasive imaging method, which we apply to study artificial ECM remodeling in 3D tissue cultures based on an optical coherence tomography (OCT) platform. We demonstrate the technique in a model of mammary fibroblast remodeling, a mechanism that is known to play a critical role in breast cancer progression (4). Fibroblasts create the structural collagen comprising the ECM, are a source of proteases necessary to break down the ECM, promote ECM remodeling in wound healing (4, 6), and play a critical role in maintaining ECM homeostasis. In malignant breast tissue, fibroblasts display an altered phenotype, characterized by secretory profiles (7) that promote cancer aggressiveness (8). The phenotype of mammary fibroblasts is well preserved in artificial tissue, making mammary fibroblasts ideal for studying ECM remodeling as it relates to tumorigenesis in breast cancer (9). Furthermore, mammary fibroblasts grown in 3D matrices, compared to 2D cultures, better recapitulate many features of the in vivo microenvironment (10). However, it is important to note that artificial ECM lacks the necessary components and structure to fully emulate in vivo tissue, and that the work presented here provides an initial validation of this new imaging technique in models that may be relevant to studying breast cancer.

There are several currently available methods for studying the micromechanical properties and architecture of the ECM. Immunofluorescence techniques are available to image ECM fibers of specific composition (11), whereas multiphoton microscopy is invaluable for imaging fibrillar collagen (11, 12, 13). Nanoindentation via an atomic force microscope has been used to measure micromechanical properties of tissue with high spatial resolution (∼15 μm) (14). Particle-tracking microrheology has been used to measure ECM rigidity (15). Although the above techniques have greatly advanced our knowledge of tissue micromechanical properties, they either cannot assess live samples or are limited in imaging speed and penetration depth. Here, we propose a method that uses gold nanorods (GNRs) conjugated with polyethylene glycol (PEG) as diffusion probes (16) to sense the nanoporosity of the ECM combined with depth-resolved imaging via OCT to ∼600 μm in depth in 3D cultures. OCT uses the principle of coherence gating to reject multiply scattered light (17), offering greater imaging depth in optically turbid samples compared to scanning confocal microscopy.

Our proposed method incorporates the principles of heterodyne dynamic light scattering (DLS) with OCT. Previously, coherence-gated DLS has been used to spatially resolve the Brownian diffusion coefficient of particle ensembles (18). Spectral-domain OCT, which offers an imaging-speed advantage over the traditional time-domain OCT method, has been shown to rapidly measure Brownian motion to provide 2D imaging of particle diffusion (19). More recently, we showed that GNRs are particularly favorable as diffusion probes in OCT based on their longitudinal plasmon resonance mode tuned to the central wavelength of the OCT system (20); the combination of their small size and large optical cross section results in more rapid and intense speckle fluctuations in OCT. We have also demonstrated that the translational diffusion rate (D_T) of GNRs of the dimensions used here (∼84 × 24 nm) is sensitive to the effective pore size of semidilute polymer solutions (16). When GNRs are put into solution with polymers that have an entanglement length approximately equal to the hydrodynamic diameter of the GNRs, the GNR self-diffusion is weakly constrained (0.1 × D_T,solvent < D_T < D_T,solvent) via intermittent collisions with macromolecules. For the first time, to our knowledge, we employ here the principle of weakly constrained diffusion to reveal the heterogeneity in artificial ECM in 3D cultures by resolving the particle-averaged GNR diffusion in two dimensions. We developed an ensemble imaging mode with OCT, dubbed diffusion-sensitive OCT (DS-OCT), to collect M-mode (depth, z, versus time) scans in a sequence of transverse steps (in x) to reconstruct a cross-sectional image (x-z) of D_T. Furthermore, we use polarization-sensitive OCT measurements to distinguish between speckle fluctuations from optically anisotropic scatterers (GNRs) and isotropic scatterers (cells). In this way, freely diffusing GNRs, weakly constrained by the matrix pore size, are detected via the unique polarization-dependent scattering signal that is recognizable against light scattered from tissue.

We hypothesized that DS-OCT can quantify artificial ECM nanoporosity in 3D tissue culture by restricting GNR Brownian motion; this has a basis in previous observations of restricted diffusion of macromolecules in collagen gels (21). In our previous work, we showed a negative correlation between GNR D_T and collagen concentration (16). Here, we validate the dependence of D_T on collagen pore area using scanning electron microscopy (SEM). We then demonstrate the ability of our proposed method to spatially resolve nanopore heterogeneity in layered collagen samples and artificial ECM subjected to fibroblast cell remodeling. Importantly, GNRs are topically applied to 3D cultures, allowing for cells to continue to grow and interact with their mechanical environment with no evidence of disturbance by the nanoprobes; PEGylated GNRs have been shown to lack cellular uptake (22). Furthermore, DS-OCT employs low-power, near-infrared light to monitor GNRs, minimizing effects such as localized heating or photobleaching that could impact measurements. By eliminating the need to alter or deform the gel, we avoid potential external mechanical stimuli to cells. Thus, DS-OCT represents a way to measure matrix porosity, independent of cellular compliance.

Interestingly, DS-OCT probes the matrix pores, which is complementary to existing imaging methods that contrast the fibers. During the progression of breast cancer, ECM architecture is dramatically altered (5, 23). These alterations all contribute to stiffening of the ECM, which has been shown to further drive cancer progression (2, 3). Although these mechanical properties have been investigated in great detail, the specific role of pore area in ECM remodeling is less known, with conflicting reports on the role porosity plays in migration. Recent studies have suggested that porosity directly relates to tumor invasiveness (24, 25). Other studies have shown porosity to be an indirect measure of matrix elasticity (which is known to influence migration) (26), whereas still others have shown little correlation between porosity and migration (27). By elucidating the heterogeneity of porosity during artificial ECM remodeling, DS-OCT may complement current methods of mechanical measurement and provide a future tool for addressing disparities in recent reports on the role of porosity in tumor invasion. By first validating measurements in controllable collagen matrices and then demonstrating the ability of DS-OCT to sense artificial matrix remodeling by mammary fibroblasts, this work takes the first steps toward establishing DS-OCT as a tool for studying porosity.

Materials and Methods

Preparation of GNRs

GNRs were prepared using previously published methods for large-scale synthesis (28). Conjugation with PEG (0.8–1 kDa molecular weight; Sigma Aldrich, St. Louis, MO) is known to improve the biocompatibility of GNRs (29). GNR size distributions, found using transmission electron microscopy, measured 84.3 ± 9.5 nm × 23.9 ± 4.8 nm, with estimated PEG thickness of ∼0.48 nm (16) and a hydrodynamic diameter of 48.8 ± 7.6 nm. To minimize the incidence of GNR-GNR collisions during measurements, GNR concentrations in all studies were 6.8–11 × 10⁷ GNRs/μL, corresponding to ∼15–24 GNRs per coherence volume.

Preparation of collagen samples

Collagen samples were prepared using high-concentration rat tail collagen I (BD Biosciences, Bedford, MA). Samples were diluted to final concentrations of 2, 5, and 8 mg/mL by mixing with a neutralizing alkaline saline solution at different ratios, according to the protocol provided by the manufacturer. GNRs were premixed into this solution before the final addition of liquid-phase collagen, resulting in a final number density of 6.8 × 10⁷ GNRs/μL. A volume of 300 μL of each sample was then pipetted into 1-cm-diameter 48-well plates and incubated at 37°C in a high-humidity atmosphere containing 5% CO₂ for 30 min. Samples were maintained at 40°C in normal atmosphere for an additional 2 h before imaging to ensure complete gelation. Layered samples were prepared by pipetting a small volume (<100 μL) of either 2 or 8 mg/mL liquid-phase collagen with premixed GNRs into a tilted well plate. After gelation, the second layer of collagen, at either 8 or 2 mg/mL concentration, respectively, was deposited such that the top layer was level with (or slightly below) the tallest point on the rising edge of the bottom layer. This was allowed to incubate for an additional 30 min and then was maintained at 40°C in normal atmosphere for an additional 2 h.

Preparation of reduction mammoplasty fibroblast 3D cultures

First, hTERT-immortalized reduction mammoplasty fibroblast (RMF) three-dimensional (3D) cell cultures were prepared in artificial ECM with varying seed densities to quantify fibroblast-induced matrix remodeling and the corresponding changes in GNR diffusion. Before seeding into a 3D matrix, RMF cells were grown to confluence on a 2D culture that was incubated as described above. RMFs were seeded into artificial ECM comprised of a 1:1 ratio of collagen (1.0 mg/mL final concentration; Corning, Corning, NY) and Matrigel (Fisher Scientific, Pittsburg, PA), with seed densities of 0, 100, 300, and 500 cells/μL, to a total volume of 360 μL using a protocol described previously (16). The cultures were incubated for 48 h. Then, GNRs were suspended in 180 μL RPMI culture media to a concentration of 3.4 × 10⁸ GNRs/μL before being topically applied to each culture (replacing the existing media). Cultures were incubated overnight to allow for GNRs to evenly distribute throughout each culture, reaching an average target concentration of 1.1 × 10⁸ GNRs/μL (∼24 GNRs per coherence volume) before imaging.

A second set of RMF 3D cultures was prepared to study spatial heterogeneity in artificial ECM remodeling using DS-OCT. In comparison to the method above, lower seed densities (0, 50, and 100 cells/μL) with a longer culture time (11 days) were used in an effort to enhance artificial ECM heterogeneity while avoiding overpopulation. Otherwise, samples were prepared for DS-OCT imaging as described above. It is important to note that the total volume of gel in culture was observed to remain constant for all RMF conditions; this was ensured by gentle handling to prevent gels from separating from culture-well walls under internal tensional forces applied by RMFs. This ensures that pore area measurements offer a direct comparison of changes due to ECM remodeling rather than contraction of the gel.

DS-OCT imaging

A custom polarization-sensitive, spectral-domain OCT system was used to provide DS imaging. The system consists of an 800 nm Ti:Sapphire laser source with a bandwidth of 120 nm, and details of the system are described in (20). Briefly, linearly polarized light (H) was directed into a free-space Michelson interferometer, and the co- and cross-polarized output light was directed into a custom spectrometer, where it was imaged onto the first and second halves of a 4096 pixel line-scan camera sampled at an A-line rate of 25 kHz. Co- and cross-polarized signals are defined as light scattered from the sample with either the same (HH) or orthogonal (HV) polarization states, respectively, as that of the input signal. The spectral interferograms were converted into depth-dependent complex analytic signals, ${\tilde{S}}_{\text{HH}}\left(z\right)$ and ${\tilde{S}}_{\text{HV}}\left(z\right)$, using a previously described dispersion compensation method (30). The imaging depth of the OCT system was 2.08 mm in air, resulting in a maximum physical imaging depth of 1.55 mm in the water-based cultures used in this study. The axial and lateral in-water resolutions of the system were measured to be 3.0 and 10 μm, respectively. B-mode (i.e., cross-sectional, x versus z) HV-OCT images were created from the magnitude of ${\tilde{S}}_{\text{HV}}\left(z\right)$ and collected into 1000 × 1024 pixels (2 × 1.55 mm in x and z) by scanning the beam laterally. Since GNRs were the only optically anisotropic scatterers in the examined samples, HV-OCT images predominantly contrast GNRs, providing context for the relative GNR distribution, in comparison to DS-OCT images collected in the same sample.

We introduce DS-OCT, a new method of ensemble (M + B modes) imaging to spatially resolve the GNR diffusion rate in 2D, D_T(x,z). DS-OCT employs a previously established technique for depth-resolving D_T(z) from a single M-scan (z versus t) (16), and implements successive lateral stepping (in x) to construct a cross-sectional view of D_T. Each DS-OCT image was constructed from an ensemble of 100 M-scans collected at increments of 20 μm in x, where each M-scan was comprised of 4000 A-lines collected at 25 kHz and 38 μs exposure time. The total DS-OCT imaging time was as little as 28 s. D_T was subsequently calculated from rows (intensity fluctuations in t) of each M-scan, as described previously (16). Briefly, the complex analytic signals, ${\tilde{S}}_{\text{HH}}\left(z\right)$ and ${\tilde{S}}_{\text{HV}}\left(z\right)$, were obtained from each A-line as above, and the normalized, temporal autocorrelation within each M-scan ($g_{\text{HH}}\left(\tau ;z\right)$ and $g_{\text{HV}}\left(\tau ;z\right)$) was computed. The isotropic autocorrelation, $g_{\text{ISO}}\left(\tau ;x,z\right),$ was calculated from a linear combination of $g_{\text{HH}}\left(\tau ;z\right)$ and $g_{\text{HV}}\left(\tau ;z\right),$ according to standard DLS methods (31), for each M-scan collected at each position x. An average of $g_{\text{ISO}}$ over 3 pixel depths (z) was computed to suppress noise. Finally, each DS-OCT image pixel was represented by $D_{\text{T}}$ computed from $g_{\text{ISO}}$ according to

$$g_{\text{ISO}}\left(\tau ;x,z\right)=e^{-q^2{D}_{\text{T}}\left(x,z\right)\tau },$$ (1)

where q = 4πn/λ₀ (with n being the refractive index of the medium and λ₀ the central wavelength of the system). The model of Eq. 1 was fitted to $g_{\text{ISO}}$ for $\tau \le {\tau }_{1/e},$ which was then used to compute D_T(x,z).

We devised two tests to ensure that diffusion measurements represented diffusion of GNR ensembles, and to avoid potential image artifacts (i.e., motions from cells). D_T(x,z) values were rejected if the signal failed either of the following conditions:

$$\frac{3.25}{f}<{\tau }_{\text{ISO}}<\frac{n_{\text{A}}}{10.75f}$$ (2)

and

$$\frac{{\tau }_{\text{ISO}}}{{\tau }_{\text{HV}}}>5,$$ (3)

where f is the A-line sampling rate, n_A is the number of A-lines in the M-mode image, and ${\tau }_{\text{ISO}}$ and ${\tau }_{\text{HV}}$ are the isotropic and cross-polarized normalized autocorrelation 1/e decay constants, respectively. Equation 2 ensures that the fitted decay time, ${\tau }_{\text{ISO}}$, is within the dynamic range of the OCT system by ensuring that ${\tau }_{\text{ISO}}$ is sufficiently long compared to the sampling rate but short compared to the total image acquisition time. The multipliers of 3.25 and 10.75 were estimated from Monte Carlo simulations of the OCT measurements to ensure <5% error in the resultant D_T value. This corresponds to an effective $D_{\text{T}}$ dynamic range of 0.13−14.88 μm²/s, which we find is sufficient to describe the pore areas used in this study. The second test, represented by Eq. 3, ensures sufficient difference in the isotropic and cross-polarized decay constants to indicate that the signal arises from the GNRs. This can be understood by the fact that the wavelengths used in our study are at the longitudinal plasmon resonance of the GNRs, such that the polarizability components are α_|| ≫ α_⊥. In this approximation, ${\tau }_{\text{ISO}}\text{/}{\tau }_{\text{HV}}=6D_{\text{R}}\text{/}{q}^2{D}_{\text{T}},$ where D_R is the rotational diffusion rate. According to Stokes-Einstein models of diffusion, this term scales as ${\left(\lambda \text{/}L\right)}^2,$ where L is the length of the GNR. Given the small size of GNRs compared to the wavelength $\left(L<<\lambda \right),$ we find that the D_R term is dominant and that ${\tau }_{\text{ISO}}/{\tau }_{\text{HV}}\approx 9$ (16). In comparison, more isotropic scatterers, like cells and collagen (α_|| ≈ α_⊥), will tend to be weighted by their larger light-scattering components $\left(L\approx \lambda \right)$. This causes the D_T decay mode to be more dominant; in the limit where $q^2{D}_{\text{T}}>>6D_{\text{R}}$ and α_|| = α_⊥, ${\tau }_{\text{ISO}}/{\tau }_{\text{HV}}=1.$ Thus, anisotropic optical scatterers (GNRs) give rise to large decay-constant anisotropy, whereas isotropic scatterers exhibit similar values of ${\tau }_{\text{ISO}}$ and ${\tau }_{\text{HV}}.$ These predictions are consistent with our experimental observations that samples without GNRs exhibit ${\tau }_{\text{ISO}}/{\tau }_{\text{HV}}$ values of ∼1, in comparison to >5 for samples with GNRs, as shown in Fig. S1 in the Supporting Material. It is also important to recognize that as GNRs become constrained by the polymer mesh, their diffusion may become nonhydrodynamic, and the ${\tau }_{\text{ISO}}/{\tau }_{\text{HV}}$ ratio may change (32); thus, we chose our cutoff value of 5 primarily to exclude the background medium of cells and collagen without placing specific constraints on the value from GNRs.

For comparison across different experimental conditions and sample types (collagen versus ECM), spatially averaged GNR diffusion values, D_T,avg, were found. For these measurements, M-scans comprising 12,000 A-lines were collected at 25 kHz (38 μs exposure time) at random locations across each sample. The larger number of A-lines allowed for a longer measurement time to determine the experimental range of ${\tau }_{\text{ISO}}$ for these samples, which allowed us to minimize the number of A-lines (n_A in Eq. 1) without data loss for the subsequent DS-OCT measurements.

SEM

Field emission SEM was performed to study matrix porosity on the artificial ECM and collagen samples after GNR diffusion measurements. Gels were briefly washed in phosphate-buffered saline, followed by in a solution of 2% paraformaldehyde, 2.5% glutaraldehyde, and 0.15 M sodium phosphate buffer with a pH of 7.4. The samples were stored in the fixative for several days at 4°C before processing for SEM. The gels were sliced vertically and washed gently three times with 0.15 M sodium phosphate buffer, pH 7.4, to remove surface debris. To stabilize the collagen fibrils and decrease shrinkage, the gel slices were postfixed in 1% osmium tetroxide in phosphate buffer for 30 min, followed by subsequent treatment with 1% tannic acid for 20 min and 1% osmium tetroxide in water for 10 min (33). The samples were then dehydrated in ethanol (30%, 50%, 75%, 90%, 100%, and 100%), transferred to a Samdri-795 critical point dryer, and dried using carbon dioxide as the transitional solvent (Tousimis Research Corporation, Rockville, MD). Slices were mounted on aluminum planchets with double-sided carbon adhesive and coated with 10 nm of gold-palladium alloy (60 Au:40 Pd, Hummer X Sputter Coater, Anatech USA, Union City, CA). Images (n ≥ 2 for each condition) were acquired using a Zeiss Supra 25 FESEM operating at 5 kV, with working distance of ∼5 mm, a 20 μm aperture (Carl Zeiss Microscopy, Peabody, MA) at 10K magnification. Each image used for analysis is an en face 2D view of the matrix cross section.

SEM image processing

A custom Matlab (version R2015a) script was used to autosegment nanopores from SEM images and to quantify the distribution of pore areas. Because SEM images captured fibers at multiple planes, in and out of focus, the pixel intensity histograms varied across samples. We noted that there was a consistent high-pixel-intensity mode representing pixels comprising the in-focus fibers, with the high-intensity edge of this mode following a normal distribution (see Fig. S2). The half-width of this distribution was defined as the pixel intensity for which the mode decayed to peak counts/e² on the high-intensity edge. This was then used to extrapolate the location of the low-intensity edge, defining the pixel intensity threshold used to separate the in-focus fibers from the pores. Although each SEM image captured fibers at multiple depths, this allowed us to consistently define the 2D plane of interest at the depth of focus. Connected pore regions within each image were found and pore areas were tabulated from the number of pixels in each region, with each pixel size corresponding to 31.25 nm. Histograms of the resulting pore-area distributions were constructed with 50 bins, equally spaced, for pore areas within the range 978−362,500 nm². Pore areas >362,500 nm² were rejected from analysis due to a population size at these areas that was inadequate for rigorous statistical analysis. Normalized pore-area probability distributions were calculated using the equation

$$P_i=\frac{n_i{A}_i}{{\sum }_{i=1}^{50}{n}_i},$$ (4)

where i is the bin index, P is the normalized probability, n_i is the number of pores within the bin, and A is the central pore area of the bin. For the collagen data, histogram scatter plots were plotted against smoothed curves generated using a locally weighted second-order polynomial regression model via the “loess” Matlab function. Because GNRs move via a random diffusion process, on average, the amount of time spent within each pore is expected to be proportional to the pore area. Thus, the pore-area centroid, C, represents the time-averaged pore area encountered by diffusing GNRs, which was calculated according to $C={\sum }_{i=1}^{50}{P}_i{A}_i.$ The standard deviation (SD) was calculated using $\text{SD}=\sqrt{\left(n/n-1\right){\sum }_{i=1}^{50}{P}_i{\left(A_i-C\right)}^2},$ where n is the number of bins used in constructing the histogram distributions. A Welch’s t-test using C and SD was used to determine the statistical significance between the pore areas measured for each condition.

The alignment of collagen fibers by RMFs was assessed by comparing angular histograms constructed using a custom Matlab script. The segmented in-focus fiber images were analyzed by finding all pixel groups comprised of a linear structural element (30 × 1 pixels in size, corresponding to ∼938 × 31 nm) using the “strel” Matlab function, and counting the number of pixels within these groups. This process was repeated for angles swept across 360° in 1° increments. The resulting histogram reports the number of linearly connected pixels at all angles. The angular histograms shown (see Fig. 3) have been smoothed for visualization.

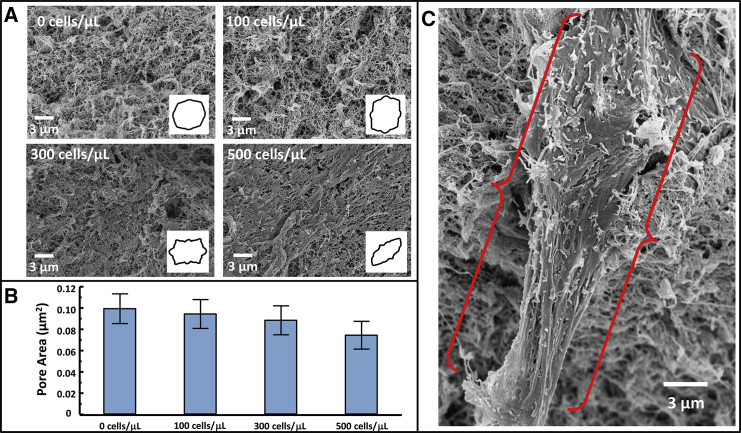
Figure 3.

Analysis of ECM porosity with increasing RMF seed density. (A) Representative SEM images showing the effects of artificial ECM remodeling as RMF density increases, with inset angular histograms showing the degree to which collagen is aligned in each image. (B) Pore-area centroids showing a decrease in overall pore area with increasing RMF seed density, with error bars representing the probability-weighted standard deviation of the pore areas measured (p < 0.01 for all comparisons) (C) RMF cell protruding from artificial ECM. The fibroblast cell is framed by the red brackets. To see this figure in color, go online.

Results and Discussion

The GNR diffusion rate in collagen decreases as collagen pore area decreases

Although we previously reported the decrease of the GNR translational diffusion rate, D_T, with collagen concentration (16), in this article, we quantify, for the first time (to our knowledge), the relationship between D_T and the nanoporosity of the medium. Homogenous collagen gels of varying density were imaged with HV-OCT, DS-OCT, and SEM. First, HV-OCT images in Fig. 1 A indicate that there are no discernible differences in the intensity of cross-polarized, backscattered light across the three densities of collagen, confirming that the GNR density is the same within each sample. The HV-OCT signal declines with depth due to the attenuation of incident light by the GNRs. The corresponding DS-OCT images in the same cross section show spatially resolved D_T measurements represented by a heat map, with regions lacking a GNR signature (i.e., pixels failing the tests of Eqs. 2 and 3, as described in Materials and Methods) represented by blue. These images demonstrate the relative homogeneity in D_T throughout each sample and exhibit an overall decrease in D_T across each condition with increasing collagen density. Interestingly, the D_T values are more stable in depth than the cross-polarized signal in the HV-OCT images, as shown in Fig. S3, demonstrating that the diffusion measurements are robust against changes in the signal intensity. The images did, however, exhibit a slight layer (14−55 μm in thickness) of lower D_T near the top of each of the samples, which we attribute to evaporation of interstitial fluid at the air-gel interface. The corresponding SEM images qualitatively show the decrease in collagen pore size with concentration in these samples.

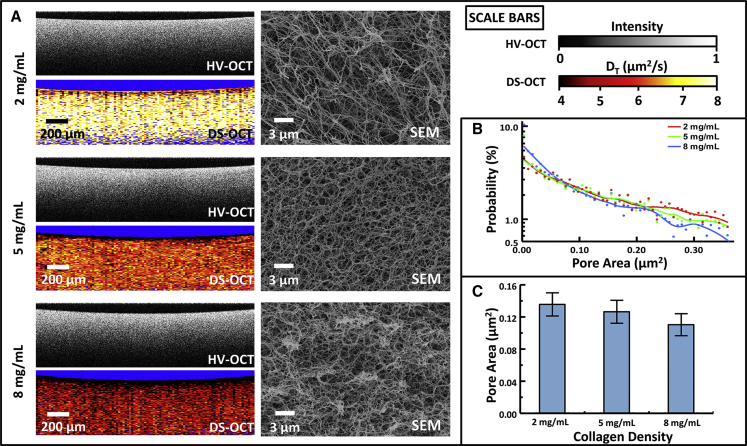
Figure 1.

Analysis of nanoporosity in homogenous collagen gels with densities of 2, 5, and 8 mg/mL. (A) HV-OCT images showing the distribution of GNRs, DS-OCT images showing the corresponding GNR translational diffusion rates (D_T), and corresponding SEM images revealing a decrease in ECM nanoporosity with increasing collagen density. (B) Log-linear plot of probability distributions of pore areas at each collagen concentration, with lines representing a smoothed average of each. (C) Pore-area centroid values, calculated from probability distributions, decrease with increasing collagen density. Error bars represent the probability-weighted standard deviation of the pore areas measured (p < 0.01 for all comparisons).

To quantify the SEM data, Fig. 1 B shows the probability distribution of pore areas for each collagen concentration. The trend lines show that the percentage of smaller pores is greater at the highest collagen density (8 mg/mL) compared to the lower-density gels, and the highest-density gel shows a more rapidly declining trend, indicating fewer, comparatively larger pores. The pore-area distribution measured for the 5 mg/mL collagen predictably fell between those for the higher and lower concentrations. From these probability density functions, the centroid of each pore-area distribution was found and is plotted in Fig. 1 C. The centroids, representing the time-averaged pore area encountered by a GNR, exhibit a significant decrease in size as the density of collagen increases. Considering the wide distribution of pore areas, our pore-area centroid measurements are reasonably consistent with previously reported estimated pore areas in collagen I based on an effective medium model; a pore width of ∼500 nm is reported for 2 mg/mL collagen (21), corresponding to a circular area of 0.2 μm², compared to our measured pore area of 0.14 μm² at the same concentration. Thus, the SEM pore-area analysis shows that D_T is directly proportional to measured areas, with diffusion decreasing as pores become smaller. Furthermore, we estimate that GNRs free in solution would travel between 43 and 260 nm over the time it takes for OCT signal fluctuations in collagen to decorrelate $\left(\tau ={\tau }_{1/e}\right)$. It is interesting to note that the centroid pore areas in collagen correspond to an effective diameter of ∼400 nm, which is consistent with the picture that GNRs are weakly constrained by the collagen fibers while remaining sensitive to changes in pore width.

Sensing heterogeneity in collagen nanoporosity using DS-OCT

Multilayered samples comprised of varying concentrations of collagen were prepared (as shown in the top row of Fig. 2) to demonstrate the ability of DS-OCT to spatially resolve the heterogeneous nanoporosity of a 3D matrix. HV-OCT images (Fig. 2, middle row) confirm that there is a constant distribution of GNRs across high-density (HD, 8 mg/mL) and low-density (LD, 2 mg/mL) layers, but they do not provide information on the changing collagen concentration within the images. In comparison, the corresponding DS-OCT images (Fig. 2, bottom row) clearly discriminate between the different densities, as represented by the transition from dark red to yellow pixels, representing low to high GNR diffusion rates, corresponding to the changes in nanoporosity established in Fig. 1. Interestingly, HD layered over LD collagen did not yield results exactly as predicted. A valley or gap region is apparent between the two layers (blue arrow) that exhibits a D_T value higher than what would be found in either HD or LD collagen; the value of D_T in this region is similar to that in cell media, i.e., ∼9 ± 1 μm²/s compared to 8.88 ± 1.02 μm²/s in cell media. We attribute this finding to the existence of a liquid region void of collagen gel that is caused by the high surface tension of HD collagen in its liquid phase as it was topically deposited onto the LD collagen layer below. This resulted in the denser HD collagen settling to the bottom left of the sample, leaving a void consisting only of liquid.

Figure 2.

HV- and DS-OCT imaging of HD and LD collagen layers. (Top) Cartoon illustrating the ideal geometry of the deposited collagen layers. (Middle) HV-OCT images showing an even distribution of GNRs and little discrimination between collagen layers. (Bottom) DS-OCT images show clear demarcation between collagen layers. A region of increased GNR diffusion rates (blue arrow) is attributed to a liquid void, and another region of decreased GNR diffusion rates (yellow arrow) indicates possible osmotic transfer of fluid from regions of lower collagen density to higher density.

Another anomaly in the DS-OCT images can be seen in the lower-right image in Fig. 2, where a region with D_T lower than that expected is observed where the layer of LD collagen thins near the top of the sample (yellow arrow). This is attributed to osmotic forces, where the finite volume of fluid available for transfer from the LD to the HD layer may locally dehydrate the LD collagen. Overall, the LD-over-HD condition exhibits a slower GNR diffusion rate in the LD layer and a faster GNR diffusion rate in the HD layer compared to those found in the homogenous samples of the same concentration. Similarly, in the HD-over-LD condition, HD collagen exhibits D_T values higher than those in homogeneous samples, with values in LD collagen similar to those for the homogenous counterpart. These observations lend further credence to the suggestion that osmotic forces act to equilibrate interstitial fluid concentration across the LD-HD boundary, thus reducing the contrast between nanoporosity measurements across the boundary. If the sources of these image anomalies are indeed due to osmotic or other effects that modify the pore size, it suggests that they are not artifacts of the DS-OCT method; the DS-OCT artifact that we would have expected to observe would be an increase in apparent D_T with imaging depth due to increased multiple light scattering (34), which was not observed here. Other authors have described the osmotic forces contributing to collagen swelling (35); similar osmotic forces may have dynamically changed the porosity throughout these samples.

Associating pore area with GNR diffusion rate in 3D culture undergoing ECM remodeling

We previously reported that the GNR diffusion rate is sensitive to changes in artificial ECM mechanics under varying RMF seed densities (16). However, directly connecting D_T to measurements of the pore area was beyond the scope of that study. To validate that GNR diffusion measurements are sensitive to changing nanoporosity in artificial ECM, as they are in collagen, SEM was performed on RMF cultures prepared in artificial ECM (collagen/Matrigel) over a range of cell seed densities. Representative SEM images in Fig. 3 A show the varying porosity and collagen alignment as a function of RMF seed density, with inset angular histograms showing the degree to which collagen was aligned for each image. The graph in Fig. 3 B reports the pore areas measured for these conditions. These results show that for increasing cell seed density, ECM pores become smaller and ECM fibers become more aligned, suggesting that this model exhibits the effects of remodeling by RMF cells.

It has been shown that as fibroblasts grow and migrate, collagen coaligns with external forces from fixed points (i.e., tethering of collagen to a well wall in a 3D matrix) (36). It has been shown that this alignment is a direct response to fibroblasts straining the matrix as they grow and migrate (37). Thus, we attribute our observations of collagen fiber alignment to strain applied by RMF cells. This is also consistent with our observations that artificial ECM gels remained attached to culture well walls throughout the timescale of our experiments; others have shown that wall detachment results in collapse of the matrix and no collagen alignment (38). Interestingly, computer modeling has shown that strain-associated collagen fiber alignment results in increased fiber spacing (39). In contrast, our observations show a decrease of pore size with alignment, whereas the cultures do not change in volume (no wall detachment). We thus explain our findings by the secretion of new ECM by RMFs to fill the voids left between bundled collagen fibers, as seen during wound healing (6). We also note that gels were palpably stiffer for increasing cell seed densities, as seen by previous investigators (40). Gel stiffness is determined by a combination of strain, fiber density, and cellular compliance, whereas the increased stiffness in our experiments may be attributed to both increasing strain and fiber density. Importantly, fibroblast-induced mechanical changes are implicated in stromal-epithelial cell signaling that leads to increased epithelial cell malignancy (41, 42). In terms of real ECM structure, it has been shown that collagen aligns around tumors, providing a pathway through which cancer cells can travel, potentially increasing malignancy (43). Although our results show that DS-OCT is sensitive to changing porosity in aligned artificial ECM, further studies need to be conducted to determine the influence of cancer-associated ECM alignment on DS-OCT measurements. In this study, we show that weakly constrained GNR diffusion measurements are predominantly sensitive to artificial ECM pore areas, complementing current techniques used to disentangle ECM properties associated with cancer progression.

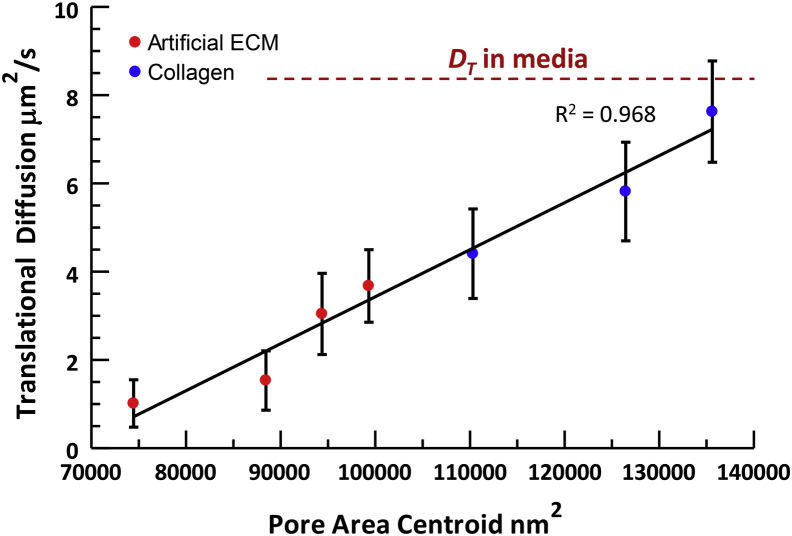
The translational GNR diffusion rate, D_T,avg, was measured at each RMF culture condition before assessment by SEM, as described above. D_T,avg represents a spatial average of GNR diffusion measurements across random locations void of cells (with locations containing cells rejected according to the conditions described by Eqs. 2 and 3, as described in Materials and Methods). Fig. 4 shows a plot of D_T,avg, both in artificial ECM with RMF and in pure collagen, versus measured pore-area centroids. These combined data show a consistently increasing trend in GNR diffusion for increasing pore areas across two different types of matrix. The apparent continuity between data in pure collagen and those in 3D RMF culture suggests that GNR diffusion is sensitive primarily to pore size related to matrix composition, with little to no interaction with cells. However, spatially averaged measurements provide limited information on heterogeneity in the ECM structure, which is revealed by DS-OCT imaging, as desribed in the next section.

Figure 4.

Spatially averaged GNR diffusion measurements in artificial ECM remodeled by fibroblasts and in collagen of varying concentrations show that D_T,avg is positively correlated with nanopore area across all samples, with R² = 0.968 of a linear regression. Error bars represent the standard deviation of D_T,avg, with n ≥ 125 measurements obtained for each data point. To see this figure in color, go online.

Visualizing ECM remodeling with DS-OCT

Although the above measurements showed that increasing RMF seed densities resulted in lower pore areas on average, DS-OCT is capable of capturing the spatial heterogeneity of artificial ECM remodeling by fibroblasts. Here, we show the spatial pattern of that remodeling as a function of RMF seed density, as revealed by DS-OCT (Fig. 5). First, HV-OCT images provide little information on ECM heterogeneity throughout the tissue, although they confirm a relatively constant distribution of GNRs within the 3D culture. Our previous findings demonstrate that PEGylated GNRs do not enter cells (22) and that 3D RMF cultures exhibit regions of low intensity in HV-OCT images that are attributed to locations of the cells that are void of GNRs (16). In this study, we did not observe morphological changes to fibroblasts that would indicate disturbance of the cells by the GNRs. Also, we observed minimal voids in HV-OCT and only occasional evidence of cells in the DS-OCT images (e.g., Fig. 5, green arrow). We attribute this difference to lower cell densities, which was confirmed by histology of replicate 3D cultures cut along the same cross-sectional plane as in OCT (Fig. S4). Despite the lower RMF densities, the effects of remodeling by RMF cells extend sufficiently throughout the culture volume to be observed within any random cross section sampled by DS-OCT.

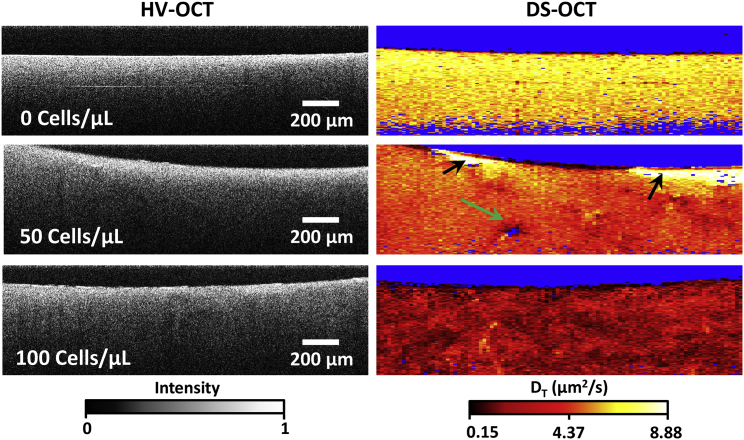
Figure 5.

DS-OCT imaging of 3D cultures seeded with varying densities of RMF reveal nanoscale pore-size changes in ECM due to remodeling. (Left) HV-OCT images showing relative GNR density throughout each sample. (Right) Corresponding DS-OCT images show increasing restructuring and heterogeneity of the artificial ECM with increasing RMF seed density. The green arrow indicates a region void of GNRs, which is attributed to the presence of an RMF cell, and the black arrows point to sites of ECM degradation evident with DS-OCT that are not observable in the HV-OCT image.

DS-OCT of 3D RMF cultures, shown in the right column in Fig. 5, provides a spatially resolved picture of ECM nanoporosity throughout the sample. To demonstrate the reproducibility of these results, we present the results of additional trials using RMF cells with the seed densities shown here in Fig. S5. The color-map scale of D_T was extended to include the larger range of D_T observed in these samples, and we note that the low end of the range is now close to the low end of our system dynamic range (0.13−14.88 μm²/s). Interestingly, we observe that D_T displays increasing heterogeneity with RMF seed density, suggesting that we are observing a pattern of remodeling within the 2D DS-OCT cross section by RMFs, throughout the 3D matrix, that act locally on their microenvironment. Anomalous regions with high GNR diffusion rates near the top of one of the samples (Fig. 5, black arrows) are taken to be liquid areas lacking ECM. In addition to providing insight into the heterogeneity of ECM nanoporosity, DS-OCT shows an overall decrease in GNR diffusion rate for the 100 cell/μL condition (∼2.4 μm²/s) as compared to the 50 cell/μL condition (∼4.5 μm²/s) and the control (∼6.4 μm²/s), suggesting that the entire network of ECM is affected by localized strain caused by RMFs and increased collagen secretion. Interestingly, D_T,avg in the control here was markedly higher than in the control in the study above (∼3.7 μm²/s). We attribute this to swelling of the gel over the increased 9 day incubation period. We also note that D_T,avg in the 100 cell/μL condition was similar to that seen in the study above. Both of these trends over the increased incubation period correspond to previously observed results in RMF cultures with the same seed densities (16).

Fibroblasts remodel the ECM by applying tension to the fibers, increasing the ECM density through protein fiber secretion, and/or degrading ECM fibers via protease secretion. The effects of tension propagate throughout the culture and have been reportedly seen at distances up to 10 times the length of the cell (∼100 μm) (44), which is within the detectible range of DS-OCT. In this study, the heterogeneity in D_T, and thus measured porosity, may be evidence of RMF cells straining the ECM as they apply tension on the fibers (45, 46). The heterogeneity can also partially be attributed to collagen secretion (as seen in Fig. 3 C), which may decrease pore size in the vicinity of the cells. Thus, DS-OCT provides a minimally invasive tool with which to study ECM remodeling with little to no impact on cell behavior.

Conclusions

In this article, we present a novel approach (to our knowledge) for quantitative imaging of artificial ECM nanoporosity in a 3D in vitro tissue model of fibroblast-associated remodeling in the mammary gland. DS-OCT allows for sensing nanoporosity of a fibrous protein matrix, demonstrated here over a pore-area range of 1,400–100,000 nm², based on measured decorrelation times, within a cross-sectional view up to a penetration depth of ∼0.6 mm in 3D tissue cultures. DS-OCT uses a fundamentally microscopic-resolution imaging modality (OCT) to elucidate nanoscopic features via weakly constrained diffusion of GNRs. The fact that DS-OCT measures pore areas may have relevance not only to the migration of cancer cells and tumorigenesis (24, 25), but to the motion of macromolecules and drug vectors as well (47). Interestingly, DS-OCT is complementary to existing multiphoton or confocal microscopy techniques, where ECM fibers are quantified instead of pores. We also note that ECM fibers observed via light microscopy appear coarser than with SEM, likely due to differences in resolution between the two techniques; thus, DS-OCT has the potential to provide new information on a smaller size scale compared to that of traditional microscopies. For the first time, we established a direct link between D_T measurements and pore areas obtained by SEM, showing a consistent positive correlation across both pure collagen I and RMF-remodeled collagen/Matrigel samples. Measurements in layered collagen samples validate that DS-OCT can accurately quantify the spatial heterogeneity of nanoporosity, distinguishing clearly between layered densities.

RMF cells seeded into a 3D matrix of artificial ECM were used here to recapitulate cell forces and secretions that are seen in the ECM of breast tissue as it relates to tissue remodeling during tumorigenesis. Decreasing GNR diffusion throughout the artificial ECM of RMFs for increasing seed densities demonstrates the ability of GNRs to sense stromal cell-induced pore area changes with minimal invasiveness, providing a tool with which to quantify nanoporosity throughout artificial tissue without disturbing cells. This minimally invasive method of sensing nanoporosity in remodeled ECM provides a unique opportunity to directly monitor nanoscale pore-area changes when studying cell cultures. Further improvement in DS-OCT imaging time may be accomplished by high-frame-rate parallel OCT imaging (48) to obviate the need for lateral scanning. One great appeal of DS-OCT is that additional cellular imaging can be conducted in parallel with nanoporosity analysis, for example, by combining DS-OCT with previous methods using OCT to monitor mammary organoids in vitro (22, 49). Employment of this method in tumor organoid models may lead to new connections between cellular function, growth, and migration, in direct relation to artificial ECM nanostructure. Now that we have established a quantitative relationship between D_T and artificial ECM pore size, future studies can apply DS-OCT to reveal remodeling processes in real ECM ex vivo.

Author Contributions

R.L.B. conducted the experiments and processed the data; R.L.B. and A.L.O. developed algorithms used in the data processing; R.L.B., P.C.-H., and R.S. created the samples used in experiments; B.S.C. fabricated the GNRs used in this study; R.L.B., P.C.-H., R.S., J.B.T., M.A.T, and A.L.O. participated in the design of the research; and R.L.B and A.L.O. wrote the article, with comments from all authors.

Editor: David Piston.