Abstract
When a system has more than one stable state, how can the stability of these states be compared? This deceptively simple question has important consequences for ecosystems, because systems with alternative stable states can undergo dramatic regime shifts. The probability, frequency, duration, and dynamics of these shifts will all depend on the relative stability of the stable states. Unfortunately, the concept of “stability” in ecology has suffered from substantial confusion and this is particularly problematic for systems where stochastic perturbations can cause shifts between coexisting alternative stable states. A useful way to visualize stable states in stochastic systems is with a ball‐in‐cup‐diagram, in which the state of the system is represented as the position of a ball rolling on a surface, and the random perturbations can push the ball from one basin of attraction to another. The surface is determined by a potential function, which provides a natural stability metric. Systems amenable to this representation, called gradient systems, are quite rare, however. As a result, the potential function is not widely used and other approaches based on linear stability analysis have become standard. Linear stability analysis is designed for local analysis of deterministic systems and, as we show, can produce a highly misleading picture of how the system will behave under continual, stochastic perturbations. In this paper, we show how the potential function can be generalized so that it can be applied broadly, employing a concept from stochastic analysis called the quasi‐potential. Using three classic ecological models, we demonstrate that the quasi‐potential provides a useful way to quantify stability in stochastic systems. We show that the quasi‐potential framework helps clarify long‐standing confusion about stability in stochastic ecological systems, and we argue that ecologists should adopt it as a practical tool for analyzing these systems.
Keywords: alternative stable states, Freidlin‐Wentzell, Hamilton‐Jacobi, quasi‐potential, regime shifts, resilience, stochastic differential equations, stochastic dynamics
Introduction
Researchers have long been fascinated by the possibility for ecosystems to have more than one stable state (May 1977, Beisner et al. 2003). Such ecosystems have been observed in both natural (van de Koppel et al. 2001) and experimental (Chase 2003) settings. Systems with multiple (i.e., alternative) stable states can can abruptly shift from one stable state to another, sometimes with catastrophic consequences (Scheffer and Carpenter 2003), so understanding their properties is crucially important.
Unfortunately, the understanding of alternative stable states has been significantly hampered by ambiguity about the term “stable.” Grimm and Wissel (1997) note that stability is “one of the most nebulous terms in the whole of ecology,” and they catalog 163 different definitions. Much of this confusion arises when researchers attempt to apply tools designed for the analysis of deterministic models to stochastic models. Fortunately, there is a well‐developed mathematical framework, the Freidlin‐Wentzell quasi‐potential (Freidlin and Wentzell 2012), that provides a rigorous yet natural way to understand alternative stable states in stochastic systems. In this paper, we explain how this tool can clarify much of the confusion about stability in ecological systems by translating intuitive concepts into quantifiable mathematical properties. Through three examples, we show how the quasi‐potential serves as a useful metric of stability, and allows for effective stability comparison between alternative stable states. The results from quasi‐potential analysis often contrast with those from standard stability analysis, and our examples explore these discrepancies. Furthermore, the quasi‐potential allows for stability to be quantified on a continuum that corresponds well with the system's dynamics, and it can be applied to any system state, regardless of whether that state is a deterministic equilibrium. Using the quasi‐potential, a system can be decomposed into orthogonal components, and we explain how this decomposition can be interpreted ecologically. Finally, the quasi‐potential offers insight into the most probable paths a system will take in transitioning from one state to another.
Holling's foundational work on resilience and stability anticipated the quasi‐potential's basic essence (Holling 1973); later, Tuljapurkar and Semura (1979) made the insight that Holling's intuitive ideas were connected to the mathematical work of Freidlin and Wentzell (1970). At that time, numerical methods were insufficient to allow for general, practical computation of quasi‐potentials (see Ludwig 1975), so Tuljapurkar and Semura's insight did not receive the recognition it deserved. In subsequent decades, the flurry of research on alternative stable states largely overlooked this insight. Recently, the quasi‐potential has been embraced by researchers analyzing models in other areas of biology, although it often appears under other names, and is disconnected from the Freidlin‐Wentzell formulation (but see Zhou et al. 2012). These applications include gene regulatory networks (Zhou et al. 2012, Lv et al. 2014), neural networks (Yan et al. 2013), and evolution (Wang et al. 2011, Zhang et al. 2012). Very recently, it has been applied to a predator‐prey system (Xu et al. 2014), and with countless other possibilities for application, we argue that the quasi‐potential is poised to become a major quantitative tool in ecology.
This paper makes three novel contributions to the field of ecology. First, it shows how the quasi‐potential can clarify the confusing tangle of stability concepts that confront ecologists. Second, it demonstrates how the quasi‐potential can be used to quantify stability in systems with alternative stable states, and how the results can be different from and often more useful than deterministic methods. Finally, it shows how a new numerical algorithm for the computation of quasi‐potentials (Cameron 2012) can be expanded for application to systems with multiple stables states, and highlights the utility of the quasi‐potential for understanding such systems.
We use three well‐established ecological models to illustrate these ideas. First, we show how traditional linear stability analysis fails to capture the salient features of a stochastic lake eutrophication model, and explain how the system's potential function provides more useful analytic insights. Next, we move to higher‐dimensional systems, where potential functions rarely exist. We explore a consumer‐resource model with alternative stable states that does not have a potential function. We explain how the quasi‐ potential is defined, and show its usefulness in analyzing this model. Finally, we explore another consumer‐resource model with a stable limit cycle to demonstrate how the quasi‐potential is useful when stable states are more complicated than point equilibria. We conclude by discussing the quasi‐potential as a unifying framework for existing notions of stability in stochastic systems.
Example 1: Lake Eutrophication
Lake ecosystems are among the most well‐studied examples of alternative stable states in ecology. A foundational model by Carpenter et al. (1999) successfully describes the coexistence of a eutrophic state, corresponding to high phosphorous concentration, and an oligotrophic state, corresponding to low phosphorous concentration. Later work by Guttal and Jayaprakash (2007) showed how stochasticity can cause this system to switch between the two stable states, and we will use their model as a starting point for exploring the quantification of stochastic stability.
The underlying deterministic model (i.e., the “deterministic skeleton") describes how the nutrient (phosphorous) concentration x changes over time:
| (1) |
c is the nutrient inflow rate and s is the nutrient loss rate (due to sedimentation, outflow, and sequestration in benthic plants). The last term represents nutrient recycling. r is the maximum recycling rate, is the half‐saturation constant, and q specifies the shape of the sigmoidal recycling curve. At s = 1, r = 1, , q = 8, and c = 0.53 (as in Guttal and Jayaprakash 2007), the system has alternative stable states: a low phosphorous oligotrophic state, , and a high phosphorous eutrophic state, , separated by an unstable equilibrium (a saddle), .
The standard technique for studying systems like this one, is linear stability analysis. The eigenvalue of the linearized system at is , so it is an unstable equilibrium. The eigenvalues corresponding to and are and , respectively, so both and are stable equilibria. The more negative the eigenvalue, the faster the return to the equilibrium following a small perturbation; so the linear analysis indicates that the oligotrophic state is more stable than the eutrophic state.
Ball‐in‐cup
An alternative approach to quantifying stability, and one that is fundamental to the theory of alternative stable states, is the “ball‐in‐cup" heuristic (Beisner et al. 2003). In this framework, the state of the system is represented by the position of a ball rolling on a surface. The ball rolls downhill, but is also subject to continual, stochastically varying perturbations. In the absence of perturbations, the ball will roll to the bottom of a valley. Such locations correspond to stable equilibria of the deterministic skeleton of the system ( and in our example); a system with alternative stable states has more than one valley. The “cup” is the area surrounding an equilibrium that is attracted to it; this is called its domain (or basin) of attraction.
The ball‐in‐cup framework is not just a useful metaphor – it can also yield a mathematical description. For the lake system, define
| (2) |
(ξ is a dummy variable for integration), so that the differential equation becomes: . The dynamics of this system turn out to be equivalent to a ball‐in‐cup system with surface specified by the function U. In analogy with the physics of the ball‐in‐cup metaphor, U is called the “potential function” or simply the “potential.” For the lake system, this surface has local minima at and as shown in Fig. 1a.
Figure 1.
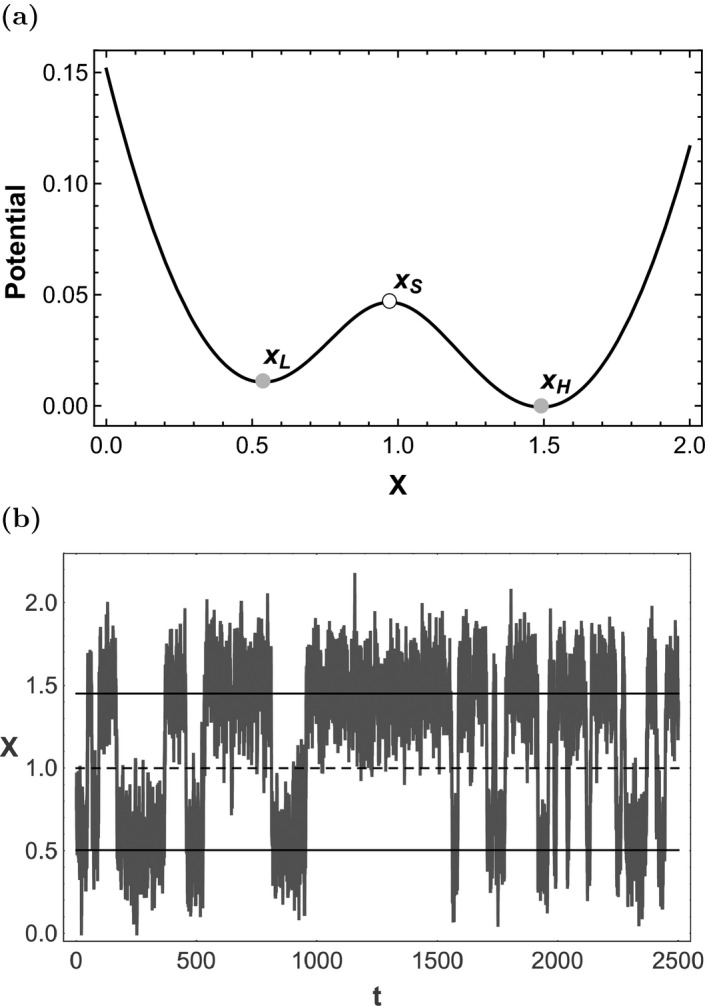
Lake eutrophication model (example 1). (a) The potential function for Eq. (1). The horizontal axis is the scaled nutrient (phosphorous) concentration and the vertical axis is the (dimensionless) potential. Gray disks are stable equilibria, and the white disk is an unstable (saddle) equilibrium. The dynamics of the system can be represented as a ball rolling on the surface specified by the potential function. Note that the basin around is deeper than that around . (b) A realization of Eq. (3), which models nutrient concentration, x, as a function of time, t. Variables are scaled, so the units are dimensionless. Integration was performed with the Euler‐Maruyama method and Δt = 0.005. The solid lines corresponds to stable equilibria (lower) and (higher) for the deterministic skeleton. The dashed line corresponds to the the saddle point of the deterministic skeleton. Note that the realization spends more time near than near .
When random perturbations are present, the ball can be jostled from one basin of attraction to another. Note that stochasticity lies at the heart of the theory of alternative stable states. In a purely deterministic system, the ball would roll to an equilibrium and stay there. The presence or absence of other stable states would be irrelevant, because the ball would have no way of visiting them. Perhaps the surface could change over time, so that the basin of attraction occupied by the ball ceases to be a basin, and the ball rolls out to a different stable state. This situation corresponds to a bifurcation of the system's deterministic skeleton; the ball's transition requires the destruction of a stable state. In this paper, we are interested in how systems can transition between coexisting alternative stable states. Perturbations are required for the system to undergo these transitions; therefore, we argue that the appropriate framework for an alternative stable state model is a stochastic one. Furthermore, real ecological systems are always subject to random perturbations. In order to apply the ball‐in‐cup heuristic to a perturbed system, we next demonstrate an approach to incorporating stochasticity into model (1).
Stochastic differential equation model
If the nutrient concentration varies randomly over time, the lake can shift from one stable state to the other. To study this scenario, we translate the original deterministic model into a stochastic differential equation. A brief explanation of stochastic differential equation models is provided in Appendix S1: Section S1, and more extensive accounts can be found in textbooks (e.g. Allen 2007). Here, we give an informal description of the major concepts, and use discrete‐time analogies to avoid overly technical mathematical terminology.
To emphasize that nutrient concentration is now a stochastic process, and not just a deterministic function of time, we switch notation from x(t) to X(t). For each t > 0, x(t) is a number, but X(t) is a random variable, which can take on any of a set of possible values according to probabilistic rules. A realization of the stochastic process is a deterministic function of time associated with a specific set of random events; this can be thought of as an observed time series, or the result of a single simulation run.
In the original model (1), the external input of nutrients occurs at a constant rate c. In a small time interval dt, the external input is c dt. In reality, this input is likely to vary randomly; this is commonly modeled by adding a Gaussian white noise process, dW(t) (“noise” is used synonymously with “stochastic” or “random”). At each t > 0, dW(t) is a normally distributed random variable with mean zero and variance dt. Since the values are independent of t, this is simply written as dW. The white noise process we describe here has no temporal autocorrelation, and its frequency spectrum is uniform – the descriptor “white” is used in analogy with white light. The accumulated change obtained by adding dW over time yields a Wiener process, also known as Brownian motion. White noise is a useful starting point, but many applications require other types of noise; for example, colored noise might be used instead when perturbations are autocorrelated (e.g. Sharma et al. 2014). A discussion about generalizing the framework in this paper to different noise types is included in the Limitations and Generalizations section.
If the constant input rate c is perturbed by a Gaussian white noise process with intensity σ (analogous to the standard deviation in discrete time systems), then the external input in a small interval dt is c dt + σ dW. The change in nutrient concentration over this time interval is given by
| (3) |
Again using Eq. (2) to define the potential, this system can equivalently be written as
| (4) |
In terms of the ball‐in‐cup heuristic, the shape of the surface is specified by the potential function U, and this is independent of σ. The noise intensity σ only contributes to the movement of the ball on this surface, as determined by the last term in Eq. (4).
We have described this model in terms of change over discrete time intervals, but it is also valid in the continuous time limit, dt→0. For continuous time, which will be the focus of the rest of this paper, (3) is called a stochastic differential equation. The notation in the stochastic differential equation dX = … is different than the deterministic differential equation notation , because the former must be defined using integral equations (the realizations of W(t) are not differentiable anywhere, so , and hence , would not make sense. We use the Itô integration scheme to define stochastic differential equations in this paper; see Appendix S1: Section S1).
Utility of the potential for understanding the stochastic lake eutrophication model
One approach to understanding the stochastic lake eutrophication model is to calculate realizations (i.e. simulations) of (3) for particular values of σ. This approach is limited, because it requires setting a particular σ; we will see later that the potential function provides a more general way of studying system dynamics. A realization with σ = 0.2 is shown in Fig. 1b. All simulations in this paper were done with Mathematica, and the code is available as a supplementary file. The realization in Fig. 1b, which is typical of realizations for this system with σ = 0.2, switches between the two stable states. It spends more time near than ; this suggests that the eutrophic (higher phosphorous) state is more stable than the oligotrophic (lower phosphorous) state for this set of parameter values. Note that this behavior is in contrast to the results of the linear stability analysis of the deterministic skeleton. It is, however, in agreement with what the potential function tells us about the system, as we will demonstrate below.
For (3), we find that , , and . Note that it is the relative, not the absolute, values of the potential function that are important, so the minimum value of the potential can be set at 0. , so the potential function indicates that the eutrophic state is more stable than the oligotrophic state. This corresponds to the intuitive notion that we obtained from examining realizations like the one in Fig. 1b, but it contradicts the results from the linear stability analysis. This discrepancy arises because the linear stability analysis considers only an infinitesimal neighborhood of an equilibrium. In the presence of continuous stochastic perturbations, the system will leave such an infinitesimal neighborhood, and the linear analysis of the skeleton breaks down. The linear analysis provides information about the curvature of the potential surface at the bottom of basins of attraction, but this information is purely local, in that it does not take into account the larger geometry of the surface. Therefore, the potential function provides a more appropriate measure of stability for analyzing alternative stable states than linear stability analysis.
The potential function also relates to other important features of the stochastic system. The probability density function, p(x, t), associated with the random variable X in (3) describes the probability that X(t) = x. It is the solution to the Fokker‐Planck equation:
| (5) |
The steady‐state solution, , is given by
| (6) |
where is a normalization constant. This equation shows that the steady‐state probability density is maximized at the values of x that minimize U, confirming that the minima (valleys) in U correspond to the most likely system states.
The potential can be used to gain insight about the time it takes the system to switch between alternative stable states. If is the expected time it takes a trajectory starting at to reach , (i.e., the mean first passage time), then (Kramers 1940):
| (7) |
Swapping for yields a comparable expression for the expected time to reach from . The asymptotic notation describes the error of the approximation as σ→0. The expected time for a trajectory to leave a basin of attraction around one of the stable states is thus largely dependent on the depth of that basin – the difference between peak U (which occurs at the saddle equilibrium, ) and the value of U at the stable equilibrium.
The eigenvalue obtained in linear stability analysis describes the curvature of the potential at an equilibrium, equal to the second derivative of U; it determines the prefactor that multiplies the exponential function in Eq. (7). For a fixed valley depth, increased curvature is associated with decreased mean first passage time. For instance, note that . As becomes more stable in the deterministic sense (i.e., as becomes more negative), the curvature at increases, and the mean first passage time decreases (similar statements hold for ). At first glance, this seems counterintuitive – increasing stability is associated with decreased escape time – but it makes sense because, for a fixed valley depth, increased curvature decreases the horizontal distance between equilibria.
Knowledge about the potential function thus provides information about the steady‐state probability distribution, mean first passage times, and transition frequencies, motivating its use as a stability metric (Wang et al. 2011, Zhou et al. 2012). The potential function is especially useful because it does not depend on the noise intensity σ (in contrast to the steady‐state probability distribution and mean first passage times; see Appendix S1: Section S4).
Example 2: Consumer and Resource with Alternative Stable States
If the potential is so good at quantifying biologically‐relevant model behaviors, why isn't it routinely applied in ecology? Unfortunately, in most cases, there will not exist a function U that satisfies the mathematical definition of a potential (see Appendix S1: Section S2). Systems that have such a function are called “gradient systems.” One‐dimensional systems are always gradient systems, but systems with more than a single state variable almost never are. For non‐gradient systems, we cannot use a potential function to quantify stability, as we did in the first example. It is for this reason that ecologists typically rely on approaches like linear stability analysis instead; although these approaches give more limited biological insights, they are more widely applicable mathematically. In what follows, we show how to generalize the potential for non‐gradient systems, thus allowing us to apply the many desirable features of potential analysis to a much broader range of ecological systems.
For an ecological example of a two‐dimensional non‐gradient system, we turn to a model of phytoplankton and zooplankton populations. Let R be the phytoplankton (resource) population density and C the zooplankton (consumer) population density. Using the deterministic skeleton of a standard plankton consumer‐resource model (Steele and Henderson 1981, Collie and Spencer 1994), we obtain the stochastic differential equations
| (8) |
Here and are independent Wiener processes. The resource has logistic growth in the absence of consumers, with maximum growth rate α and carrying capacity β. Consumption of resources is represented by a sigmoidal Type III functional response. δ is the maximum consumption rate, and κ controls how quickly the consumption rate saturates. γ determines the conversion from resources to consumers. The consumers have a quadratic mortality term with coefficient μ, which represents the negative impacts of intraspecific competition. and are the noise intensities for the resource and consumer populations, respectively.
The additive form of the stochastic terms in this model represent random inputs and losses of resources and consumers. In situations where inherent growth parameters (e.g., α or γ) are stochastic, other forms of stochasticity would be appropriate. We will deal with additive noise here; the more general case is considered in Appendix S1: Section S6.
We will analyze (8) with parameters set at α = 1.54, β = 10.14, γ = 0.476, δ = κ = 1, and μ = 0.112509. A phase plot of the deterministic skeleton is shown in Fig. 2a. The deterministic skeleton of this system has five equilibria: , , , , .
Figure 2.
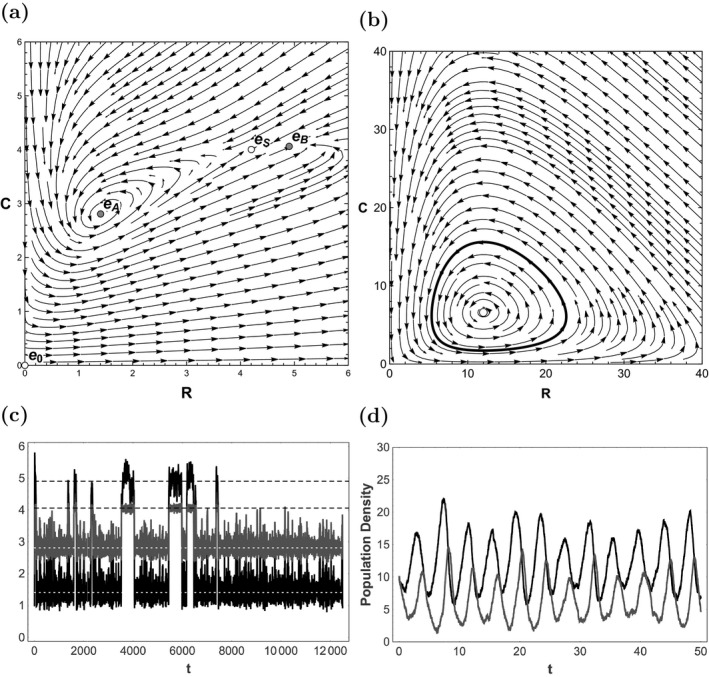
(a) Stream plot for the deterministic skeleton of the consumer‐resource model in example 2. Unstable equilibria are white disks and stable equilibria are gray disks. The unstable equilibrium is not shown, but would appear on the x‐axis to the right of where the graph is truncated. Variables are scaled, so the units are dimensionless. Lines and arrows show the direction of trajectories for Eq. (8) in the absence of noise. (b) Similar stream plot for the deterministic skeleton of the consumer‐resource model in example 3. The white disk is an unstable equilibrium and the gray line is a stable limit cycle. (c) A realization of Eq. (8) for example 2. Integration was performed with the Euler‐Maruyama method and Δt = 0.025. Resource population density is black and consumer population density is gray. The dotted white lines correspond to the equilibrium , and the dashed black lines to the equilibrium . (d) A realization of Eq. (15) for example 3, with σ = 0.8. Integration was performed with the Euler‐Maruyama method and . Resource population density is black and consumer population density is gray.
A linear stability analysis shows that is an unstable equilibrium and is a saddle point. and are stable equilibria, and is a saddle point that lies between them. Equilibria and their stability are summarized in Fig. 2a.
The eigenvalues of the Jacobian are −0.047 ± 0.458i at and −0.377 and −0.093 at . For the real part of the eigenvalue with largest real part is −0.047, and for it is −0.093; therefore, the stability analysis concludes that is more stable, because this value is more negative than it is for .
A realization of the stochastic system (, Fig. 2c) shows switching between the two stable states. It is typical of most realizations we generated, in that it spends more time near (dotted white lines) than (dashed black lines). This realization, which had initial condition , spent 87% of its time in the basin of attraction corresponding to . Intuitively, it seems that should be classified as more stable than , but as in Example 1, this is not what was obtained via the standard linear stability analysis.
Recall that realizations are of limited utility for stability analysis, because each value of σ will produce different dynamics and different steady‐state probability distributions (see Appendix S1: Section S4 and Fig. S1). The potential is defined independently of σ, and hence would be ideal for providing more general insights than σ‐specific realizations. Of course, we do not have a potential function U for this or any other non‐gradient system and hence cannot compare and . Instead, we turn to the Freidlin‐Wentzell quasi‐potential, which generalizes the notion of a potential.
Generalizing the Potential
For higher‐dimensional models, we need to introduce a bit of new notation. We can write an n‐dimensional system of stochastic differential equations with additive noise as
| (9) |
is a column vector of state variables and is a column vector of n independent Wiener processes. We use the lowercase notation to indicate a point in phase space (as opposed to a stochastic process). f is the deterministic skeleton of the system. It is a vector field: for every point x, f(x) specifies the direction that a deterministic trajectory will move. σ is the noise intensity. More general ways of incorporating noise are considered in Appendix S1: Section S6.
Following the same general approach as in example 1, the Fokker‐Planck equation for a two dimensional version of (9), with , and , is
| (10) |
In the gradient case in Example 1, the steady‐state solution of the Fokker‐Planck equation was of the form (6) (replacing x with x and obtaining Z via integration over the positive quadrant). Here, there is no function U to play that role, but using the same general approach, assume that there is a function V(x) such that
| (11) |
where k is a constant. When noise intensity is small, we can obtain an approximation for V (using asymptotic expansion; see Appendix S1: Section S4). This approximation, denoted by , satisfies
| (12) |
where the gradient operator ∇ takes a scalar function ψ as an input, and returns a vector, , that is the multi‐dimensional analogue of the derivative. Intuitively, if one thinks of ψ(x) as specifying the height of a landscape at a particular point x, then −∇ψ(x) points in direction of the steepest descent (as water would flow).
Equation (2) is the static Hamilton‐Jacobi equation. Interestingly, has key properties that make it a useful analog of a potential in a gradient system. First, is independent of the noise intensity σ, just as the potential function U was in the gradient case. Second, if x(t) is trajectory of the deterministic skeleton of (9), then
| (13) |
and only where . Thus is a Lyapunov function for the deterministic system, which is an important feature for the ball‐in‐cup metaphor. If specifies an two‐dimensional surface, then, in the absence of perturbations, trajectories will always move “downhill.” Again, this parallels the role that U played in the gradient systems. Third, we can interpret the relationship between f and the surface . f is the deterministic skeleton that causes trajectories to move across the landscape, and is the component of f that causes trajectories to move downhill. The remaining component of f, which we denote by Q and call the “circulatory” component, is defined as
| (14) |
satisfies the Hamilton‐Jacobi equation, so , hence and Q are perpendicular at every point. This motivates the label “circulatory” – in the absence of other forces, Q would cause trajectories to circulate around level sets of .
The function generalizes the potential function to non‐gradient systems and extends to n‐dimensional systems. Interestingly, is a scalar multiple of a function called the Freidlin‐Wentzell quasi‐potential. The quasi‐potential has extremely important properties, which we explore in the next section before applying all of these ideas to example 2.
The Freidlin‐Wentzell Quasi‐Potential
Freidlin and Wentzell (2012) analyzed stochastic differential equations using a large deviation principle, which is an asymptotic law determining the probabilities of different trajectories. These concepts can be best interpreted by imagining the state of the system (the position of the ball, or the current combination of population densities) being randomly perturbed within a “force field” imposed by the deterministic skeleton. Suppose the system starts at the stable state and travels to another state x. To complete this journey, the populations will need to do some “work” against the force field (i.e., they need to go “uphill”); this work is provided by random perturbations. Trajectories that require the least amount of work (require the least extreme stochastic perturbations) are the most likely. Suppose that θ(t) specifies a path, parameterized by t, that goes from the stable equilibrium to another state θ(T)=x. T is total time it takes the populations to move along this path from to x. The amount of work required for the populations to follow a given path can be quantified by a functional called the action (see Appendix S1: Section S2 for details).
In order to determine the amount of work it takes to get to some state x, one must minimize the action over all possible paths from to x, and all path durations T > 0. The minimum action is called the quasi‐potential, denoted . The quasi‐potential depends on the starting point ; when there are multiple stable states, the corresponding quasi‐potentials can be stitched together to obtain a global quasi‐potential, Φ(x) (Roy and Nauman 1995); see further details in Appendix S1: Section S3. Φ is related to by (Appendix S1: Section S5). In this paper, we use instead of Φ, because agrees with the true potential in gradient systems. The multiple of 2 in the relationship is an inconvenient result of the Freidlin‐Wentzell definition. Conceptually, these two functions measure the same properties, and computing one immediately yields the other.
The quasi‐potential can be calculated by solving the static Hamilton‐Jacobi Eq. (12). This is a numerically difficult task, however; standard finite difference and finite element methods typically break down when applied to this kind of non‐linear partial differential equation. Ordered upwind methods (Sethian and Vladimirsky 2001) are an innovative approach that circumvent the problems encountered by traditional methods. The basic idea is to create an expanding front of points where the solution is known, and march outward by considering and accepting solution values at adjacent points in ascending order. For use in systems of the form (9), the standard ordered upwind method was enhanced by Cameron (2012). Cameron's algorithm allows for efficient computation of the quasi‐potential. It forms the basis for QPot, a freely‐available R package we have developed (Moore et al. 2015) that includes a full set of tools for analyzing two‐dimensional autonomous stochastic differential equations (Moore et al., arXiv:1510.07992). To calculate the quasi‐potential, users simply input the deterministic skeleton of the system, the domain, and the mesh size (although many other options are available). Computation time for the ordered upwind method depends on the model and mesh size; example 2 took <10 min on a fairly average personal computer.
The Freidlin‐Wentzell construction of the quasi‐potential provides a mathematically rigorous justification for the Wentzel‐Kramers‐Brillouin (WKB) ansatz, which can be used to approximate mean first passage times in the small noise limit (Bressloff and Newby 2014). The WKB method has been applied to calculate expected extinction times for several specific models in population dynamics and epidemiology (Roozen 1989, van Herwaarden and Grasman 1995, Meerson and Sasorov 2009, Ovaskainen and Meerson 2010).
Example 2 Continued
We generated solutions to the static Hamilton‐Jacobi equation for the system (8) using base points and , and then matched them into a global quasi‐potential by enforcing continuity at and setting the minimum to 0. We divided this function by two to obtain . The ordered upwind method was implemented using Cameron's algorithm (Cameron 2012). Mathematica was used for data processing and graphics generation, and the code is available as a supplementary file.
For the consumer‐resource system (8), the resulting surface for and a corresponding contour plot are shown in Fig. 3a, b. We find that , , . The relative values of can be used to make calculations regarding first passage times and calculate transition rates between and . The most fundamental observation, however, is that , which indicates that is more stable than . This contrasts with the linear stability analysis, but agrees with the qualitative picture obtained from realizations of the system. As in example 1, analyzing the system through the lens of a potential (or quasi‐potential) function yields a completely different conclusion than the deterministic analysis, and one that aligns much more clearly with the simulated dynamics we observe. Furthermore, and are closer to each other than they are to . This indicates that and have similar stabilities, and it encourages us to move beyond the dichotomous classification of equilibria as either stable or unstable, which is often applied in linear stability analysis. The stable vs. unstable dichotomy classifies and as alike, and as different. The quasi‐potential shows that it is and that are alike, and that is different. By quantifying stability on a useful continuum, the quasi‐potential offers a more nuanced perspective.
Figure 3.
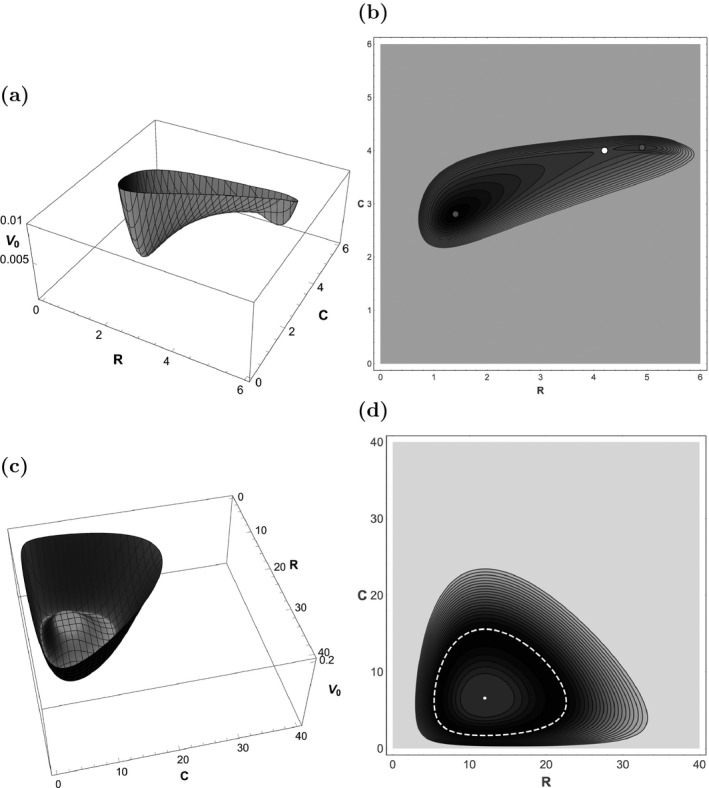
(a) The quasi‐potential function for the consumer‐resource model, Eq. (8). Variables are scaled, so the units are dimensionless. Note that the quasi‐potential surface is much deeper around than . The quasi‐potential is truncated at 0.02 for display purposes; it continues to increase in the regions outside the plot. (b) Contour plot for the same model. The white disk is the saddle point . The gray disks are the stable equilibria and . (c) The quasi‐potential function for Eq. (15). (d) Contour plot for the same model. The white disk is an unstable equilibrium, and the white dashed line is a stable limit cycle.
also provides a useful way to decompose the deterministic skeleton of Eq. (8) into physically interpretable parts, . This decomposition is shown in Fig. 4a, B. represents the part of the system that moves the system towards stable states, while Q represents the part that causes consumer‐resource cycling.
Figure 4.

(a) and (b) are the orthogonal decomposition of the deterministic skeleton of the system (8). (a) The “downhill" component, . (b) The “circulatory" component, Q. Gray disks are stable equilibria. The white disk is an unstable equilibrium. (c) and (d) are the orthogonal decomposition of the deterministic skeleton of the system (8). The thick gray line is a stable limit cycle.
Example 3: Predator and Prey With A Limit Cycle
The quasi‐potential allows for stability analysis of attractors that are more complicated than equilibrium points. As discussed in Cameron (2012) and Freidlin and Wentzell (2012) and explained in Appendix S1: Section S2, the quasi‐potential can be defined for compact sets, such as limit cycles. As an example of a non‐gradient system with a limit cycle, consider a stochastic version of the Rosenzweig‐MacArthur predator‐prey model (e.g. Logan and Wolesensky 2009):
| (15) |
Here R is the resource density, C is the consumer density, and and are independent Wiener processes. Consumption of resources is represented by a Type II functional response; otherwise the resource dynamics are the same as in example 2. In the absence of resources, the consumer density decreases at an exponential rate determined by μ. and are the noise intensity for the resource and consumer densities, respectively. We present the analysis of this model with α = 1.5, β = 45, γ = 5, δ = 10, κ = 18, and μ = 4.
Figure 2b shows a stream plot of the system's deterministic skeleton, and Fig. 2d shows a realization with noise intensities over time interval [0, 50]. This choice of noise intensity and time scale was made to illustrate clear population cycles with amplitude shifts.
Surface and contour plots of for system (15) are shown in Fig. 3c, d. Recall that provides a decomposition of the deterministic system into a “downhill” force and a “circulatory” force, as shown in Fig. 4c, d. In this case, causes trajectories to be attracted to the limit cycle's trough. The circulatory component causes trajectories to cycle in this trough. This decomposition harkens back to Holling (1973), who made the following observation about dynamical systems: “There are two components that are important: one that concerns the cyclic behavior and its frequency and amplitude, and one that concerns the configuration of forces caused by the positive and negative feedback relations.” The latter is described by the gradient of , the former by the circulatory component. Therefore, we see that the Freidlin‐Wentzell approach provides a systematic way to distinguish between the two concepts identified by Holling.
In this example, we cannot contrast the quasi‐potential results with the traditional linear stability analysis, because the latter only applies to equilibrium points.
Limitations and Generalizations
In this paper, we have focused on applying the quasi‐potential framework to stochastic differential equations models that share several characteristics: (1) time is continuous; (2) state variables are continuous; (3) noise is additive and the noise intensity is the same for both state variables; (4) noise is a direct perturbation to the state variables (as opposed to a perturbation to parameter values); (5) noise is white (as opposed to colored); and (6) noise occurs continually with low intensity (as opposed to occurring as discrete, abrupt events). For models with discrete state variables, different approaches in large deviation theory are needed (Wainrib 2013). However, our approach can be adapted to work in systems that deviate from several of the other characteristics. For instance, characteristic 1 is not a limitation of the quasi‐potential framework; Kifer (1990) describes how analogous concepts can be applied to discrete‐time Markov chains (Kifer 1990, Faure and Schreiber 2014). Variable transformations (see Appendix S1: Section S6) can be used to compute quasi‐potentials for systems that deviate from characteristic 3 (e.g. those with noise terms of unequal intensity (), noise that scales with population density (demographic stochasticity; ), or multiplicative environmental stochasticity () (Hakoyama and Iwasa 2000)). Perturbations to parameters rather than state variables can be accommodated by explicitly modeling the parameter as a state variable with its own differential equation (Allen 2007). A similar approach can be applied to models with colored noise (i.e., models that do not have characteristic 5). The noise process itself can be explicitly modeled as a state variable with its own differential equation (e.g., an Ornstein‐Uhlenbeck process). Unfortunately, increasing the dimensionality of the state space in these ways makes the process of numerically calculating the quasi‐potential even more challenging. Given the pace of development of numerical techniques (Cameron 2012), however, it is conceivable that solving such systems will soon be more practical.
Characteristic 6, which states that noise occurs continually with low intensity, is central to the quasi‐potential framework. The expressions relating the quasi‐potential to steady‐state probability distributions and mean first passage times are based on the assumption that the noise intensity is very small. As a rule of thumb, these approximations are only useful when is much less than , where is the difference in the quasi‐potential between the stable equilibrium and the saddle. In Appendix S1: Section S8, we provide details on how mean first passage time scales with noise intensity, and present a numerical examination of these concepts applied to example 2. For systems that experience extreme events and external shocks (e.g., natural disasters, extreme climactic conditions, invasive species introductions, etc.), the quasi‐potential no longer provides complete information. If a shock directly impacts the state variable (e.g., if the lake system in example 1 were to receive a massive pulse of phosphorous run‐off), the ball in the ball‐in‐cup diagram would experience a large, instantaneous horizontal displacement (perhaps skipping over intervening valleys and hills). If the system reverts to deterministic dynamics, or stochastic dynamics with lower‐intensity perturbations after the shock, the quasi‐potential will still be useful for describing the system's response after the shock. In the presence of large shocks, though, the quasi‐potential loses its ability to make probabilistic predictions. If a shock impacts the state variable indirectly (e.g., if an invasive species entered the lake and fundamentally altered the phosphorous cycling), the shape of the quasi‐potential surface would change dramatically. The interaction between a dynamically changing quasi‐potential surface and state‐variable noise would be difficult to analyze using the methods presented here.
The three examples in this article show that the quasi‐potential often provides a more informative stability metric than traditional linear analysis. Linear stability is much easier to measure in the field, though. This can be done by slightly perturbing a system and measuring the time it takes to return to equilibrium. Before the quasi‐potential can be calculated, a model must be fit to observed data and validated. This limitation is also shared by other methods for analyzing systems with alternative stable states, which depend explicitly (e.g., Boettiger and Hastings 2012) or implicitly (e.g., Dakos et al. 2008) on underlying models. Fortunately, carefully controlled experiments (Dai et al. 2012) and advances in model‐fitting (Ives et al. 2008) point toward a promising future for the empirical study of shifts between alternative stable states through models.
A Path Through the Quagmire of Stability Concepts
Systems with alternative stable states are only interesting when perturbations can cause shifts between states; when these stochastic perturbations are continual and random, as in most ecological systems, stochastic models are appropriate. When state and time variables are continuous, stochastic differential equations like (9) are the best option. The three examples presented in this paper show that the quasi‐potential provides a useful way to study such stochastic differential equation models. In particular, it provides a way to quantify the relative stability of alternative stable states.
Unfortunately, many notions of stability were developed for a deterministic context, and these can be misleading when applied to stochastic systems (as in examples 1 and 2). Our goal is not to add to the existing tangle of stability definitions (Grimm and Wissel 1997), but rather to provide a clarifying mathematical interpretation. Many existing definitions can be related to the ball‐in‐cup heuristic, and the quasi‐potential shows that this metaphor has a useful and rigorous mathematical meaning. The translation between mathematical model and potential surface is easy in gradient systems (in particular, for one‐dimensional systems, which are always gradient systems). The translation for more general systems is less obvious, but the quasi‐potential fills that need.
Figure 5a is a ball‐in‐cup diagram of the potential for a one‐dimensional system that helps to illustrate several important concepts associated with stability. These concepts are equally relevant for higher dimensional systems, where the ball rolls on a multi‐dimensional surface specified by (half the Freidlin‐Wentzell quasi‐potential) instead of a curve.
Figure 5.
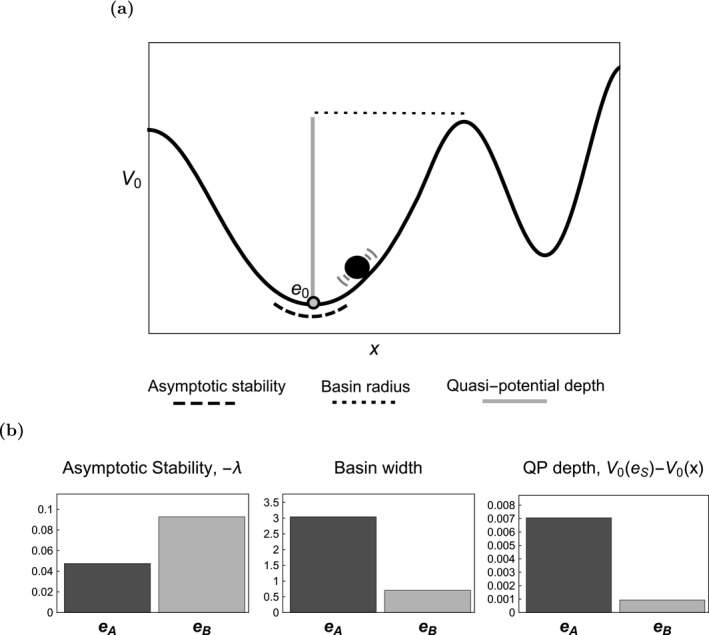
(a) A schematic diagram of the relationship between various concepts of stability, as related to the quasi‐potential and . (b) A comparison of three different metrics of stability for the system (8).
One metric of stability for an equilibrium is the curvature of at (dashed black line in Fig. 5a). The greater the curvature, the more difficult it is to perturb the system away from , and in this sense, the more stable is. In one dimension, the curvature at is , which is minus the eigenvalue obtained in linear stability analysis. In higher dimensions, the eigenvalues are again directly related to curvature, now along different planar sections of (see Appendix S1: Section S7). Thus, measuring the curvature of at is equivalent to determining asymptotic stability through linear stability analysis.
Asymptotic stability has a long history in ecology (May 1973. The primary problem with this metric is that it is purely local – once a trajectory is perturbed outside of a tiny neighborhood of an equilibrium, nonlinear effects can come into play and the approximation is no longer informative. Furthermore, this approach views perturbations as being isolated one‐time events. With this view, a system is displaced, and then the dynamics proceed deterministically without further perturbation. In reality, perturbations often take place on a continual basis. Indeed, as noted by Ives (1995), “To apply generally to ecological communities, stability needs to be defined for stochastic systems in which environmental perturbations are continuous and equilibrium densities are never achieved.” Likewise, Neubert and Caswell (1997) write, “real ecosystems are seldom if ever subject to single, temporally isolated perturbations. Nevertheless, our analyses, together with most theoretical and experimental studies of resilience, ignore the effects of continual stochastic disturbances in the hope that the deterministic results will shed light on the stochastic case.”
A second metric of stability of an equilibrium is the minimum distance between and the boundary of its domain of attraction (dotted line in Fig. 5a). The width of the basin of attraction measures the magnitude of perturbation that a system can sustain and still be guaranteed to return to . One problem with this metric is that, like asymptotic stability, it views perturbations as singular, isolated events. For this metric, it is only the boundary of basins of attraction that matter, not the shape or height of . If perturbations happen continuously, the shape and height of the are important. Nonetheless, this basin width metric can be extremely useful.
A third metric of stability is the height of (gray line in Fig. 5a). Holling (1973) anticipated this concept, and called it resilience, which he explained with ball‐in‐cup diagrams. He defines one aspect of resilience, writing: “the height of the lowest point of the basin of attraction … will be a measure of how much the forces have to be changed before all trajectories move to extinction of one or more of the state variables.” Holling had no way of defining the surface, and so could not actually quantify notions like “height”; the quasi‐potential solves this problem. Holling's identification of the difference between asymptotic stability and this definition of resilience (basin height) is hugely important, and it has major consequences for the analysis of alternative stable states.
This third metric is perhaps the most useful of the three we have explored. Unlike the first two metrics, it is appropriate for use in systems that undergo continuous stochastic perturbations. As we saw in the examples in this paper, it can be used to compute mean first passage times, and is directly related to steady‐state probability densities.
These three metrics of stability can yield conflicting information about alternative stable states. Figure 5b shows these three metrics for the equilibria and from example 2. Note that the basin width metric and the quasi‐potential metric show that is more stable than , but the asymptotic stability metric shows the reverse.
Appendix S1: Section S9 demonstrates that the equilibria in a multi‐stable system can exhibit any combination of the three stability metrics. That is, one equilibrium can be classified as most stable according to the first metric, but not the second or third; or by the first and second, but not the third; etc.
Resilience is a concept closely related to stability, and like stability, it is defined in different ways by different authors. In a large review of the ecological literature, Myers‐Smith et al. (2012) found that resilience was used in many ambiguous and contradictory ways. Some authors, like Holling (1973) view stability and resilience as distinct properties; others, like Harrison (1979) define resilience as a single aspect of stability. Pimm (1984) and Neubert and Caswell (1997) define resilience as essentially the asymptotic stability metric, while Harrison (1979), Peterson et al. (1998), and Gunderson (2000) define it as essentially the basin width metric. Ives and Carpenter (2007) defines Holling's resilience using the dominant eigenvalue of the saddle that separates alternative stable states; like the asymptotic stability metric, this is the result of applying a local analysis to the deterministic skeleton of a system.
Hodgson et al. (2015) argue that resilience cannot be quantified by a single metric, and use a potential function to illustrate the different components of resilience, which include latitude (the width of the basin of attraction) and elasticity (the asymptotic stability metric). The quasi‐potential framework aids this clarification about resilience by extending it to multi‐dimensional systems.
The quasi‐potential is also useful for understanding several other concepts related to stability. Reactivity (Neubert and Caswell 1997) differs from asymptotic stability, in that it quantifies the immediate (as opposed to long‐term) growth or decay of perturbations. In the quasi‐potential framework, reactivity is related to the circulatory component of the vector field. In the neighborhood of asymptotically stable equilibria with high reactivity, the circulatory component of the vector field will carry trajectories away from the equilibrium before bringing them back.
Harrison (1979) defined resistance as the ability of a system to avoid displacement during a time of stress. The stress is quantified in terms of an environmental parameter distinct from the state variables, and hence the interpretation of resistance depends on the parameter under examination. Resistance is best viewed as a measure of how dramatically changes due to environmental parameter changes.
Finally, Harrison defined persistence as the ability of a system to stay in a given range when continual perturbations are applied. He notes that this is the property that is most biologically useful, and that stochastic differential equations are the best mathematical modeling tool to assess it. Unlike his definitions of resilience and resistance, this definition views the dynamics of the system as stochastic and subject to continual perturbations. He was unable to venture far with the mathematical analysis for this definition, but the quasi‐potential provides a way forward. Mathematically, persistence can be defined as the first passage time for a system to leave a specified domain, which is directly related to the quasi‐potential. Thus Harrison's persistence is another manifestation of the quasi‐potential.
Despite the confusing array of stability concepts currently used in ecology, we believe that the quasi‐potential concept provides hope for clarity. The three metrics associated with the quasi‐potential show how many of these concepts are deeply related (Fig. 5a, b). The mathematics developed by Freidlin and Wentzell (2012), coupled with numerical advances by Cameron (2012), make the quasi‐potential a practical and accessible tool for ecologists to study alternative stable states. This paper's goal is to demonstrate the utility of the quasi‐potential, and to properly position it in terms of existing ecological ideas.
Supporting information
Acknowledgments
This work was supported by a Complex Systems Scholar grant to K.C.A. from the James S. McDonnell Foundation. Special thanks to M.K. Cameron for assistance with implementing the quasi‐potential analysis and for providing C code. C. Boettiger and an anonymous reviewer provided valuable feedback that improved the quality of this paper. We thank S. Catella, K. Dixon, C. Moore, C. Stieha, A. Barbaro, A. Alsenafi, R. Snyder, J. Burns, and the rest of the CWRU ecology group for helpful discussions on earlier versions of this manuscript.
Corresponding Editor: B. E. Kendall.
Literature Cited
- Allen, E. J. 2007. Modeling with Ito stochastic differential equations, vol. 22 of Mathematical modelling: theory and applications. Springer, Dordrecht, The Netherlands. [Google Scholar]
- Beisner, B. E. , Haydon D. T., and Cuddington K.. 2003. Alternative stable states in ecology. Frontiers in Ecology and the Environment 1:376–382. [Google Scholar]
- Boettiger, C. , and Hastings A.. 2012. Quantifying limits to detection of early warning for critical transitions. Journal of the Royal Society Interface 9:2527–2539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressloff, P. C. , and Newby J. M.. 2014. Path integrals and large deviations in stochastic hybrid systems. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 89:042701–15. [DOI] [PubMed] [Google Scholar]
- Cameron, M. K. 2012. Finding the quasipotential for nongradient SDEs. Physica D: Nonlinear Phenomena 241:1532–1550. [Google Scholar]
- Carpenter, S. R. , Ludwig D., and Brock W. A.. 1999. Management of eutrophication for lakes subject to potentially irreversible change. Ecological Applications 9:751–771. [Google Scholar]
- Chase, J. M. 2003. Experimental evidence for alternative stable equilibria in a benthic pond food web. Ecology Letters 6:733–741. [Google Scholar]
- Collie, J. S. , and Spencer P. D.. 1994. Modeling predator‐prey dynamics in a fluctuating environment. Canadian Journal of Fisheries and Aquatic Sciences 51:2665–2672. [Google Scholar]
- Dai, L. , Vorselen D., Korolev K. S., and Gore J.. 2012. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336:1175–1177. [DOI] [PubMed] [Google Scholar]
- Dakos, V. , Scheffer M., Van E. H. Nes, V. Brovkin, V. Petoukhov, and Held H.. 2008. Slowing down as an early warning signal for abrupt climate change. Proceedings of the National Academy of Sciences of the United States of America 105:14308–14312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faure, M. , and Schreiber S. J.. 2014. Quasi‐stationary distributions for randomly perturbed dynamical systems. The Annals of Applied Probability 24:553–598. [Google Scholar]
- Freidlin, M. I. , and Wentzell A. D.. 1970. On small random perturbations of dynamical systems. Russian Mathematical Surveys 25:1. [Google Scholar]
- Freidlin, M. I. , and Wentzell A. D.. 2012. Random perturbations of dynamical systems, vol. 260 of Grundlehren der mathematischen Wissenschaften. Springer, Berlin. [Google Scholar]
- Grimm, V. , and Wissel C.. 1997. Babel, or the ecological stability discussions: an inventory and analysis of terminology and a guide for avoiding confusion. Oecologia 109:323–334. [DOI] [PubMed] [Google Scholar]
- Gunderson, L. H. 2000. Ecological resilience‐in theory and application. Annual Review of Ecology and Systematics 425‐439. [Google Scholar]
- Guttal, V. , and Jayaprakash C.. 2007. Impact of noise on bistable ecological systems. Ecological Modelling 201:420–428. [Google Scholar]
- Hakoyama, H. , and Iwasa Y.. 2000. Extinction risk of a density‐dependent population estimated from a time series of population size. Journal of Theoretical Biology 204:337–359. [DOI] [PubMed] [Google Scholar]
- Harrison, G. W. 1979. Stability under environmental stress: resistance, resilience, persistence, and variability. American Naturalist 113:659–669. [Google Scholar]
- Hodgson, D. , McDonald J. L., and Hosken D. J.. 2015. What do you mean, ‘resilient’? Trends in Ecology & Evolution 30:503–506. [DOI] [PubMed] [Google Scholar]
- Holling, C. S. 1973. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics 4:1–23. [Google Scholar]
- Ives, A. R. 1995. Measuring resilience in stochastic systems. Ecological Monographs 65:217–233. [Google Scholar]
- Ives, A. , and Carpenter S. R.. 2007. Stability and diversity of ecosystems. Science 317:58–62. [DOI] [PubMed] [Google Scholar]
- Ives, A. , Einarsson Á., Jansen V., and Gardarsson A.. 2008. High‐amplitude fluctuations and alternative dynamical states of midges in Lake Myvatn. Nature 452:84–87. [DOI] [PubMed] [Google Scholar]
- Kifer, Y. 1990. A discrete‐time version of the Wentzell‐Friedlin theory. The Annals of Probability 18:1676‐1692. [Google Scholar]
- Kramers, H. A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica VII:284–304. [Google Scholar]
- Logan, J. D. , and Wolesensky W.. 2009. Mathematical methods in biology. Pure and applied mathematics: a wiley series of texts, monographs and tracts. Wiley, Hoboken, New Jersey. [Google Scholar]
- Ludwig, D. 1975. Persistence of dynamical systems under random perturbations. SIAM Review 17:605–640. [Google Scholar]
- Lv, C. , Li X., Li F., and Li T.. 2014. Constructing the energy landscape for genetic switching system driven by intrinsic noise. PLoS ONE 9:e88167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- May, R. M. 1973. Stability in randomly fluctuating versus deterministic environments. American Naturalist 107(957):621–650. [Google Scholar]
- May, R. M. 1977. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 269:471–477. [Google Scholar]
- Meerson, B. , and Sasorov P. V. 2009. WKB theory of epidemic fade‐out in stochastic populations. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 80:041130 [DOI] [PubMed] [Google Scholar]
- Moore, C. M. , Stieha C. R., Nolting B. C., Cameron M. K., and Abbott K. C.. 2015. QPot: Quasi‐potential analysis for stochastic differential equations. https://cran.r-project.org/web/packages/QPot/index.html.
- Moore, C. M. , Stieha C. R., Nolting B. C., Cameron M. K., and Abbott K. C.. 2015. QPot: An R package for stochastic differential equation quasi‐potential analysis. eprint arXiv:1510.07992.
- Myers‐Smith, I. H. , Trefry S. A., and Swarbrick V. J.. 2012. Resilience: easy to use but hard to define. Ideas in Ecology and Evolution 5:44‐53. [Google Scholar]
- Neubert, M. G. , and Caswell H.. 1997. Alternatives to resilience for measuring the responses of ecological systems to perturbations. Ecology 78:653–665. [Google Scholar]
- Ovaskainen, O. , and Meerson B.. 2010. Stochastic models of population extinction. Trends in Ecology & Evolution 25:643–652. [DOI] [PubMed] [Google Scholar]
- Peterson, G. , Allen C. R., and Holling C. S.. 1998. Ecological resilience, biodiversity, and scale. Ecosystems 1:6–18. [Google Scholar]
- Pimm, S. L. 1984. The complexity and stability of ecosystems. Nature 307:321–326. [Google Scholar]
- Roozen, H. 1989. An asymptotic solution to a two‐dimensional exit problem arising in population dynamics. SIAM Journal on Applied Mathematics 49:1793–1810. [Google Scholar]
- Roy, R. , and Nauman E.. 1995. Noise‐induced effects on a non‐linear oscillator. Journal of Sound and Vibration 183:269–295. [Google Scholar]
- Scheffer, M. , and Carpenter S. R.. 2003. Catastrophic regime shifts in ecosystems: linking theory to observation. Trends in Ecology & Evolution 18:648–656. [Google Scholar]
- Sethian, J. A. , and Vladimirsky A.. 2001. Ordered upwind methods for static Hamilton‐Jacobi equations. Proceedings of the National Academy of Sciences of the United States of America 98:11069–11074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma, Y. , Abbott K. C., Dutta P. S., and Gupta A. K.. 2014. Stochasticity and bistability in insect outbreak dynamics. Theoretical Ecology 8:163‐174. [Google Scholar]
- Steele, J. H. , and Henderson E. W.. 1981. A simple plankton model. American Naturalist 117:676–691. [Google Scholar]
- Tuljapurkar, S. D. , and Semura J. S.. 1979. Stochastic instability and Liapunov stability. Journal of Mathematical Biology 8:133–145. [Google Scholar]
- van de Koppel, J. , Herman P. M., Thoolen P., and Heip C. H.. 2001. Do alternate stable states occur in natural ecosystems? Evidence from a tidal flat. Ecology 82:3449–3461. [Google Scholar]
- van Herwaarden, O. A. , and Grasman J.. 1995. Stochastic epidemics: major outbreaks and the duration of the endemic period. Journal of Mathematical Biology 33:581–601. [DOI] [PubMed] [Google Scholar]
- Wainrib, G. 2013. A brief introduction to large deviations theory Pages 57–72 in Bachar Mostafa, Batzel Jerry, and Ditlevsen Susanne, editors. Stochastic biomathematical models. Springer, Berlin. [Google Scholar]
- Wang, J. , Zhang K., Xu L., and Wang E.. 2011. Quantifying the Waddington landscape and biological paths for development and differentiation. Proceedings of the National Academy of Sciences of the United States of America 108:8257–8262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, L. , Zhang F., Zhang K., Wang E., and Wang J.. 2014. The potential and flux landscape theory of ecology. PLoS ONE 9:e86746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan, H. , Zhao L., Hu L., Wang X., Wang E., and Wang J.. 2013. Nonequilibrium landscape theory of neural networks. Proceedings of the National Academy of Sciences of the United States of America 110:E4185–E4194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, F. , Xu L., Zhang K., Wang E., and Wang J.. 2012. The potential and flux landscape theory of evolution. The Journal of Chemical Physics 137:065102 [DOI] [PubMed] [Google Scholar]
- Zhou, J. X. , Aliyu M. D. S., Aurell E., and Huang S.. 2012. Quasi‐potential landscape in complex multi‐stable systems. Journal of the Royal Society Interface 9:3539–3553. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


