GLOBAL SOLUTIONS TO FOLDED CONCAVE PENALIZED NONCONVEX LEARNING

Abstract

This paper is concerned with solving nonconvex learning problems with folded concave penalty. Despite that their global solutions entail desirable statistical properties, there lack optimization techniques that guarantee global optimality in a general setting. In this paper, we show that a class of nonconvex learning problems are equivalent to general quadratic programs. This equivalence facilitates us in developing mixed integer linear programming reformulations, which admit finite algorithms that find a provably global optimal solution. We refer to this reformulation-based technique as the mixed integer programming-based global optimization (MIPGO). To our knowledge, this is the first global optimization scheme with a theoretical guarantee for folded concave penalized nonconvex learning with the SCAD penalty (Fan and Li, 2001) and the MCP penalty (Zhang, 2010). Numerical results indicate a significant outperformance of MIPGO over the state-of-the-art solution scheme, local linear approximation, and other alternative solution techniques in literature in terms of solution quality.

1. Introduction

Sparse recovery is of great interest in high-dimensional statistical learning. Among the most investigated sparse recovery techniques are LASSO and the nonconvex penalty methods, especially folded concave penalty techniques (see Fan, Xue and Zou, 2014, for a general definition). Although LASSO is a popular tool primarily because its global optimal solution is efficiently computable, recent theoretical and numerical studies reveal that this technique requires a critical irrepresentable condition to ensure statistical performance. In comparison, the folded concave penalty methods require less theoretical regularity and entail better statistical properties (Zou, 2006; Meinshausen and Bühlmann, 2006; Fan, Xue and Zou, 2014). In particular, Zhang and Zhang (2012) showed that the global solutions to the folded concave penalized learning problems lead to a desirable recovery performance. However, these penalties cause the learning problems to be nonconvex and render the local solutions to be nonunique in general.

Current solution schemes in literature focus on solving a nonconvex learning problem locally. Fan and Li (2001) proposed a local quadratic approximation (LQA) method, which was further analyzed by using majorization minimization algorithm-based techniques in Hunter and Li (2005). Mazumder et al. (2011) and Breheny and Huang (2011) developed different versions of coordinate descent algorithms. Zou and Li (2008) proposed a local linear approximation (LLA) algorithm and Zhang (2010) proposed a PLUS algorithm. Kim, Choi, and Oh (2008) developed the ConCave Convex procedure (CCCP). To justify the use of local algorithms, conditions were imposed for the uniqueness of a local solution (Zhang, 2010; Zhang and Zhang, 2012); or, even if multiple local minima exist, the strong oracle property can be attained by LLA with wisely (but fairly efficiently) chosen initial solutions (Fan, Xue and Zou, 2014). Huang and Zhang (2012) showed that a multistage framework that subsumes the LLA can improve the solution quality stage by stage under some conditions. Wang, Kim and Li (2013) proved that calibrated CCCP produces a consistent solution path which contains the oracle estimator with probability approaching one. Loh and Wainwright (2015) established conditions for all local optima to lie within statistical precision of the true parameter vector, and proposed to employ the gradient method for composite objective function minimization by Nesterov (2007) to solve for one of the local solutions. Wang, Liu and Zhang (2014) incorporated the gradient method by Nesterov (2007) into a novel approximate regularization path following algorithm, which was shown to converge linearly to a solution with an oracle statistical property. Nonetheless, none of the above algorithms theoretically ensure global optimality.

In this paper, we seek to solve folded concave penalized nonconvex learning problems in a direct and generic way: to derive a reasonably efficient solution scheme with a provable guarantee on global optimality. Denote by n the sample size, and by d the problem dimension. Then the folded concave penalized learning problem of our discussion is formulated as following:

$$\underset{\beta \in \mathrm{\Lambda }}{min}\mathcal{L}(\beta ):=\mathbb{L}(\beta )+n\sum _{i=1}^d{P}_{\lambda }(\mid {\beta }_i\mid ),$$ (1.1)

where P_λ(·) : ℝ → ℝ is a penalty function with tuning parameter λ. Our proposed procedure is directly applicable for settings allowing β_i to have different λ_i or different penalty. For ease of presentation and without loss of generality, we assume P_λ(·) is the same for all coefficients. Function 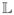(·) : ℝ^d → ℝ is defined as a quadratic function, $\mathbb{L}(\beta ):=\frac{1}{2}{\beta }^{\top }Q\beta +q^{\top }\beta$, which is an abstract representation of a proper (quadratic) statistical loss function with Q ∈ ℝ^d×d and q ∈ ℝ^d denoting matrices from data samples. Denote by Λ := {β ∈ ℝ^d : 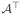β ≤ b} the feasible region defined by a set of linear constraints with 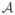∈ ℝ^d×m and b ∈ ℝ^m for some proper m : 0 ≤ m < d. Assume throughout the paper that Q is symmetric, 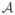is full rank, and Λ is non-empty. Notice that under this assumption, the loss function does not have to be convex. We instead stipulate that problem (1.1) is well defined, i.e., there exists a finite global solution to (1.1). To ensure the well-definedness, it suffices to assume that the statistical loss function 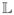(β) is bounded from below on Λ. As we will discussed in Section 2.1, penalized linear regression (least squares), penalized quantile regression, penalized linear support vector machine, penalized corrected linear regression and penalized semiparametric elliptical design regression can all be written in the unified form of (1.1). Thus, the problem setting in this paper is general enough to cover some new applications that are not addressed in Fan, Xue and Zou (2014). Specifically, the discussions in Fan, Xue and Zou (2014) covered sparse linear regression, sparse logistic regression, sparse precision matrix estimation, and sparse quantile regression. All these estimation problems intrinsically have convex loss functions. Wang, Liu and Zhang (2014) and Loh and Wainwright (2015) considered problems with less regularity by allowing the loss functions to be nonconvex. Their proposed approaches are, therefore, applicable to corrected linear regression and semiparametric elliptical design regression. Nonetheless, both works assumed different versions of restricted strong convexity. (See Section 4 for more discussions about restricted strong convexity.) In contrast, our analysis does not make assumptions of convexity, nor of any form of restricted strong convexity, on the statistical loss function. Moreover, the penalized support vector machine problem has been addressed in none of the above literature.

We assume P_λ(·) to be either one of the two mainstream folded concave penalties: (i) smoothly clipped absolute deviation (SCAD) penalty (Fan and Li, 2001), and (ii) minimax concave penalty (MCP, Zhang, 2010). Notice that both SCAD and MCP are nonconvex and nonsmooth. To facilitate our analysis and computation, we reformulate (1.1) into three well-known mathematical programs: firstly, a general quadratic program; secondly, a linear program with complementarity constraints; and finally, a mixed integer (linear) program (MIP). With these reformulations, we are able to formally state the worst-case complexity of computing a global optimum to folded concave penalized nonconvex learning problems. More importantly, with the MIP reformulation, the global optimal solution to folded concave penalized nonconvex learning problems can be numerically solved with a provable guarantee. This reformulation-based solution technique is referred to as the MIP-based global optimization (MIPGO).

In this paper, we make the following major contributions:

1. We first establish a connection between folded concave penalized nonconvex learning and quadratic programming. This connection enables us to analyze the complexity of solving the problem globally.

2. We provide an MIPGO scheme (namely, the MIP reformulations) to SCAD and MCP penalized nonconvex learning, and further prove that MIPGO ensures global optimality.

To our best knowledge, MIPGO probably is the first solution scheme that theoretically ascertains global optimality. In terms of both statistical learning and optimization, a global optimization technique to folded concave penalized nonconvex learning is desirable. Zhang and Zhang (2012) provided a rigorous statement on the statistical properties of a global solution, while the existing solution techniques in literature cannot ensure a local minimal solution. Furthermore, the proposed MIP reformulation enables global optimization techniques to be applied directly to solving the original nonconvex learning problem instead of approximating with surrogate subproblems such as local linear or local quadratic approximations. Therefore, the objective of the MIP reformulation also measures the (in-sample) estimation quality. Due to the critical role of binary variables in mathematical programming, an MIP has been well studied in literature. Although an MIP is theoretically intractable, the computational and algorithmic advances in the last decade have made an MIP of larger problem scales fairly efficiently computable (Bertsimas et al., 2011). MIP solvers can further exploit the advances in computer architectures, e.g., algorithm parallelization, for additional computational power.

To test the proposed solution scheme, we conduct a series of numerical experiments comparing MIPGO with different existing approaches in literature. Involved in the comparison are a local optimization scheme (Loh and Wainwright, 2015), approximate path following algorithm (Wang, Liu and Zhang, 2014), LLA (Wang, Kim and Li, 2013; Fan, Xue and Zou, 2014), and two different versions of coordinate descent algorithms (Mazumder et al., 2011; Breheny and Huang, 2011). Our numerical results show that MIPGO can outperform all these alternative algorithms in terms of solution quality.

The rest of the paper is organized as follows. In Section 2, we introduce our setting, present some illustrative examples, and derive reformulations of nonconvex learning with the SCAD penalty and the MCP in the form of general quadratic programs. Section 3 formally states the complexity of approximating a global optimal solution and then derives MIPGO. Sections 4 and 5 numerically compare MIPGO with the techniques as perWang, Liu and Zhang (2014) and Loh and Wainwright (2015) and with LLA, respectively. Section 6 presents a more comprehensive numerical comparison with several existing local schemes. Section 7 concludes the paper. Some technical proofs are given in Section 8, and more technical proofs are given in the online supplement of this paper.

2. Setting, Example and Folded Concave Penalty Reformulation

It is worth noting that the abstract form (1.1) evidently subsumes a class of nonconvex learning problems with different statistical loss functions. Before we pursue further, let us provide a few examples of the loss functions that satisfy our assumptions to illustrate the generality of our statistical setting. Suppose that {(x_t, y_t) : t = 1, …, n} ⊂ ℝ^d × ℝ is a random sample of size n. Let y = (y₁, …, y_n)^T be the n × 1 response vector, and X = (x₁, …, x_n)^T, the n × d design matrix. Denote throughout this paper by || · ||₂ the ℓ₂ norm and by | · | the ℓ₁ norm.

2.1. Examples

1. The ℓ₂ loss for the least squares problem, formulated as ${\mathbb{L}}_2(\beta ):=\frac{1}{2}{\sum }_{t=1}^n{(y_t-x_t^{\top }\beta )}^2=\frac{1}{2}{\Vert y-X\beta \Vert }_2^2$. It is easy to derive that the ℓ₂-loss can be written in the form of the loss function as in (1.1).

2. The ℓ₁ loss, formulated as ${\mathbb{L}}_1(\beta ):={\sum }_{t=1}^n\mid y_t-x_t^{\top }\beta \mid =\mid y-X\beta \mid$. In this case, we can instantiate the abstract form (1.1) into

   $$\underset{\beta \in {ℝ}^d,\psi \in {ℝ}^n}{min}\left\{{\mathbf{1}}^{\top }\psi +n\sum _{i=1}^d{P}_{\lambda }(\mid {\beta }_i\mid ):-\psi \le y-X\beta \le \psi \right\},$$

   where 1 denotes the all-ones vector with a proper dimension.

3. The quantile loss function in a quantile regression problem, defined as

   $${\mathbb{L}}_{\tau }(\beta ):=\sum _{t=1}^n{\rho }_{\tau }(y_t-x_t^{\top }\beta )=\sum _{t=1}^n(y_t-x_t^{\top }\beta )\{\tau -\mathbb{I}(y_t<x_t^{\top }\beta )\},$$
   where, for any given τ ∈ (0, 1), we have ρ_τ(u) := u{τ − 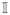(u < 0)}. This problem with a penalty term can be written in the form of (1.1) as

   $$\underset{\beta \in {ℝ}^d,\psi \in {ℝ}^n}{min}{\mathbf{1}}^{\top }[(y-X\beta )\tau +\psi ]+n\sum _{i=1}^d{P}_{\lambda }(\mid {\beta }_i\mid ),s.t.\psi \ge X\beta -y;\psi \ge 0.$$
4. The hinge loss function of a linear support vector machine classifier, which is formulated as ${\mathbb{L}}_{\mathit{SVM}}={\sum }_{t=1}^n{[1-y_t{x}_t^{\top }\beta ]}_{+}$. Here, it is further assumed that y_t ∈ {−1, +1}, which is the class label, for all t = 1, …, n. The corresponding instantiation of the abstract form (1.1) in this case can be written as

   $$\underset{\beta \in {ℝ}^d,\psi \in {ℝ}^n}{min}{\mathbf{1}}^{\top }\psi +n\sum _{i=1}^d{P}_{\lambda }(\mid {\beta }_i\mid ),s.t.{\psi }_t\ge 1-y_t{x}_t^{\top }\beta ;{\psi }_t\ge 0\forall t=1,\dots ,n.$$

5. Corrected linear regression and semiparametric elliptical design regression with a nonconvex penalty. According to Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) both regression problems can be written as general quadratic functions and, therefore, they are special cases of (1.1) given that both problems are well defined.

2.2. Equivalence of Nonconvex Learning with Folded Concave Penalty to a General Quadratic Program

In this section, we provide equivalent reformulations of the nonconvex learning problems into a widely investigated form of mathematical programs, general quadratic programs. We will concentrate on two commonly-used penalties: the SCAD penalty and the MCP.

Specifically, given a > 1 and λ > 0, the SCAD penalty (Fan and Li, 2001) is defined as:

$$P_{\mathit{SCAD},\lambda }(\theta ):={\int }_0^{\theta }\lambda \left\{\mathbb{I}(t\le \lambda )+\frac{{(a\lambda -t)}_{+}}{(a-1)\lambda }\mathbb{I}(t>\lambda )\right\}dt,$$ (2.1)

where 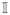(·) is the indicator function, and (b)₊ denotes the positive part of b.

Given a > 0 and λ > 0, the MCP (Zhang, 2010) is defined as:

$$P_{\mathit{MCP},\lambda }(\theta ):={\int }_0^{\theta }\frac{{(a\lambda -t)}_{+}}{a}dt.$$ (2.2)

We first provide the reformulation of (1.1) with SCAD penalty to a general quadratic program in Proposition 2.1, whose proof will be given in the online supplement. Let 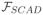(·, ·) : ℝ^d × ℝ^d → ℝ be defined as

$${\mathcal{F}}_{\mathit{SCAD}}(\beta ,g)=\frac{1}{2}{\beta }^{\top }Q\beta +q^{\top }\beta +n\sum _{i=1}^d\left\{(\mid {\beta }_i\mid -a\lambda )·g_i+\frac{1}{2}(a-1)·g_i^2\right\},$$

where β = (β_i) ∈ ℝ^d and g = (g_i) ∈ ℝ^d.

Proposition 2.1

Let P_λ(·) = P_{SCAD, λ}(·).

1. The minimization problem (1.1) is equivalent to the following program

   $$\underset{\beta \in \mathrm{\Lambda },g\in {[0,\lambda ]}^d}{min}{\mathcal{F}}_{\mathit{SCAD}}(\beta ,g).$$ (2.3)

2. The first derivative of the SCAD penalty can be rewritten as $P_{\lambda }^{\prime }(\theta )={\text{argmin}}_{\kappa \in [0,\lambda ]}\{(\theta -a\lambda )·\kappa +\frac{1}{2}(a-1)·{\kappa }^2\}$ for any θ ≥ 0.

To further simplify the formulation, we next show that program (2.3), as an immediate result of Proposition 2.1, is equivalent to a general quadratic program.

Corollary 2.2

Program (2.3) is equivalent to

$$\underset{\beta ,g,h\in {ℝ}^d}{min}\frac{1}{2}({\beta }^{\top }Q\beta +n(a-1)g^{\top }g+2n{g}^{\top }h)+q^{\top }\beta -na\lambda {\mathbf{1}}^{\top }gs.t.\beta \in \mathrm{\Lambda };h\ge \beta ;h\ge -\beta ;0\le g\le \lambda .$$ (2.4)

Proof

The proof is completed by invoking Proposition 2.1 and the non-negativity of g.

The above reformulation facilitates our analysis by connecting the non-convex learning problem with a general quadratic program. The latter has been heavily investigated in literature. Interested readers are referred to Vavasis (1991) for an excellent summary on computational issues in solving a nonconvex quadratic program.

Following the same argument for the SCAD penalty, we have similar findings for (1.1) with the MCP. The reformulation of (1.1) with the MCP is given in the following proposition, whose proof will be given in the online supplement. Let 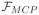(·, ·) : ℝ^d × ℝ^d → ℝ be defined as

$${\mathcal{F}}_{\mathit{MCP}}(\beta ,g):=\frac{1}{2}{\beta }^{\top }Q\beta +q^{\top }\beta +n\sum _{i=1}^d\left\{\frac{1}{2a}{g}_i^2-\left(\frac{1}{a}{g}_i-\lambda \right)\mid {\beta }_i\mid \right\}.$$

Proposition 2.3

Let P_λ(·) = P_MCP,λ(·).

1. The model (1.1) is equivalent to the following program

   $$\underset{\beta \in \mathrm{\Lambda },g\in {[0,a\lambda ]}^d}{min}{\mathcal{F}}_{\mathit{MCP}}(\beta ,g).$$ (2.5)
2. For any θ ≥ 0, the first derivative of the MCP can be rewritten as $P_{\lambda }^{\prime }(\theta )=\frac{a\lambda -g^{\ast }(\theta )}{a}$ where g^*(·) : ℝ₊ → ℝ is defined as

   $$g^{\ast }(\theta ):=\underset{\kappa \in [0,a\lambda ]}{\text{argmin}}\left\{\frac{1}{2a}{\kappa }^2-\left(\frac{1}{a}\kappa -\lambda \right)\theta \right\}.$$

Immediately from the above theorem is an equivalence between MCP penalized nonconvex learning and the following nonconvex quadratic program.

Corollary 2.4

The program (2.5) is equivalent to

$$\underset{\beta ,g,h\in {ℝ}^d}{min}\frac{1}{2}\left({\beta }^{\top }Q\beta +\frac{n}{a}{g}^{\top }g-\frac{2n}{a}{g}^{\top }h\right)+n\lambda {\mathbf{1}}^{\top }h+q^{\top }\beta s.t.\beta \in \mathrm{\Lambda };h\ge \beta ;h\ge -\beta ;0\le g\le a\lambda .$$ (2.6)

Proof

This is a direct result of Proposition 2.3 by noting the non-negativity of g.

With the above reformulations we are able to provide our complexity analysis and devise our promised solution scheme.

3. Global Optimization Techniques

This section is concerned with global optimization of (1.1) with the SCAD penalty and the MCP. We will first establish the complexity of approximating an ε-suboptimal solution in Section 3.1 and then provide the promised MIPGO method in Section 3.2. Note that, since the proposed reformulation di3erentiates between solving nonconvex learning with the SCAD penalty and solving nonconvex learning with the MCP, we will use MIPGO-SCAD or MIPGO-MCP to rule out the possible ambiguity occasionally.

3.1. Complexity of Globally Solving Folded Concave Penalized Nonconvex Learning

In Section 2, we have shown the equivalence between (1.1) and a quadratic program in both the SCAD and MCP cases. Such equivalence allows us to immediately apply existing results for quadratic programs to the complexity analysis of (1.1). We first introduce the concept of ε-approximate of global optimum that will be used Theorem 3.1(c). Assume that (1.1) has finite global optimal solutions. Denote by β^* ∈ Λ a finite, globally optimal solution to (1.1). Following Vavasis (1992), we call ${\beta }_{\epsilon }^{\ast }$ to be an ε-approximate solution if there exists another feasible solution β̄ ∈ Λ such that

$$\mathcal{L}({\beta }_{\epsilon }^{\ast })-\mathcal{L}({\beta }^{\ast })\le \epsilon [\mathcal{L}(\overline{\beta })-\mathcal{L}({\beta }^{\ast })]$$ (3.1)

Theorem 3.1

1. Denote by I_d×d ∈ ℝ^d×d an identity matrix, and by

   $${\mathcal{H}}_1:=\left[\begin{array}{ccc}Q& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& n(a-1)I_{d\times d}& n{I}_{d\times d}\\ \mathbf{0}& n{I}_{d\times d}& \mathbf{0}\end{array}\right]$$ (3.2)

   the Hessian matrix of (2.4). Let 1 < a < ∞, then 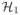has at least one negative eigenvalue (i.e., 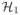is not positive semidefinite).

2. Denote by

   $${\mathcal{H}}_2:=\left[\begin{array}{ccc}Q& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& n/a{I}_{d\times d}& -n/a{I}_{d\times d}\\ \mathbf{0}& -n/a{I}_{d\times d}& \mathbf{0}\end{array}\right].$$ (3.3)

   the Hessian matrix of (2.6). Let 0 < a < ∞, then 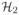has at least one negative eigenvalue.

3. Assume that (1.1) has finite global optimal solutions. Problem (1.1) admits an algorithm with complexity of $O({\lceil 3d(3d+1)/\sqrt{\epsilon }\rceil }^{r}l)$ to attain an ε-approximate of global optimum, where l denotes the worst-case complexity of solving a convex quadratic program with 3d variables, and r is the number of negative eigenvalues of 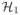for the SCAD penalty, and the number of negative eigenvalues of 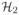for the MCP.

Proof

Consider an arbitrary symmetric matrix Θ. Throughout this proof, Θ ⪰ 0 means that Θ is positive semidefinite.

Notice 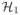⪰ 0 only if

$${\mathcal{B}}_1:=\left[\begin{array}{cc}n(a-1)I_{d\times d}& n{I}_{d\times d}\\ n{I}_{d\times d}& \mathbf{0}\end{array}\right]\succcurlyeq 0.$$ (3.4)

Since 1 < a < ∞, we have n(a−1)I_d×d ≻ 0. By Schur complement condition, the positive semidefiniteness of 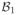requires that −n(a − 1)⁻¹ ≥ 0, which contradicts with the assumption 1 < a < ∞. Therefore, 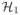is not positive semidefinite. This completes the proof of (a).

In order to show (b), similarly, we have 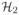⪰ 0 only if

$${\mathcal{B}}_2:=\left[\begin{array}{cc}n/a{I}_{d\times d}& -n/a{I}_{d\times d}\\ -n/a{I}_{d\times d}& \mathbf{0}\end{array}\right]\succcurlyeq 0$$ (3.5)

Since 0 < a < ∞, we have n/aI_d×d ≻ 0. By Schur complement condition, the positive semidefiniteness of 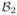requires that −n/a ≥ 0, which contradicts with the assumption 0 < a < ∞. Therefore, 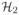is not positive semidefinite, which means 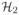has at least one negative eigenvalue. This completes the proof for part (b).

Part (c) can be shown immediately from Theorem 2 in Vavasis (1992), and from the equivalence between (1.1) and the quadratic program (2.4) for the SCAD case, and that between (1.1) and (2.6) for the MCP case.

In Theorem 3.1(c), the complexity result for attaining such a solution is shown in an abstract manner and no practically implementable algorithm has been proposed to solve a nonconvex quadratic program in general, or to solve (2.4) or (2.6) in particular.

Pardalos (1991) provided an example for a nonconvex quadratic program with 2^r local solutions. Therefore, by the equivalence between (2.4) (or (2.6)) for SCAD (or MCP) and (1.1), the latter may also have 2^r local solutions in some bad (not necessarily the worst) cases.

3.2. Mixed Integer Programming-based Global Optimization Technique

Now we are ready to provide the proposed MIPGO, which essentially is a reformulation of nonconvex learning with the SCAD penalty or the MCP into an MIP problem. Our reformulation is inspired by Vandenbussche and Nemhauser (2005), who provided MIP to a quadratic program with box constraints.

It is well known that an MIP can be solved with provable global optimality by solution schemes such as the branch-and-bound algorithm (B&B, Martí and Reinelt, 2011). Essentially, the B&B algorithm keeps track of both a global lower bound and a global upper bound on the objective value of the global minimum. These bounds are updated by B&B by systematically partitioning the feasible region into multiple convex subsets and evaluating the feasible and relaxed solutions within each of the partitions. B&B then refines partitions repetitively over iterations. Theoretically, the global optimal solution is achieved, once the gap between the two bounds is zero. In practice, the B&B is terminated until the two bounds are close enough. The state-of-the-art MIP solvers incorporate B&B with additional features such as local optimization and heuristics to facilitate computation.

3.2.1. MIPGO for Nonconvex Learning with the SCAD Penalty

Let us introduce a notation. For two d-dimensional vectors Φ = (φ_i) ∈ ℝ^d and Δ = (δ_i) ∈ ℝ^d, a complementarity constraint 0 ≤ Φ ⊥ Δ ≥ 0 means that φ_i ≥ 0, δ_i ≥ 0, and φ_iδ_i = 0 for all i : 1 ≤ i ≤ d. A natural representation of this complementarity constraint is a set of logical constraints involving binary variables z = (z_i) ∈ {0, 1}^d:

$$\mathrm{\Phi }\ge 0;\mathrm{\Delta }\ge 0;\mathrm{\Phi }\le \mathcal{M}\mathbf{z};\mathrm{\Delta }\le \mathcal{M}(1-\mathbf{z});\mathbf{z}\in {\{0,1\}}^d.$$ (3.6)

The following theorem gives the key reformulation that will lead to the MIP reformulation.

Theorem 3.2

Program (2.4) is equivalent to a linear program with (linear) complementarity constraints (LPCC) of the following form:

$$min\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g-\frac{1}{2}\lambda {\gamma }_4^{\top }\mathbf{1};s.t.$$ (3.7)

$$\{\begin{array}{l}Q\beta +q+{\gamma }_1-{\gamma }_2+\mathcal{A}\rho =0;ng-{\gamma }_1-{\gamma }_2=0\hfill \\ n(a-1)g+nh-na\lambda \mathbf{1}-{\gamma }_3+{\gamma }_4=0\hfill \\ 0\le {\gamma }_1\top h-\beta \ge 0;0\le {\gamma }_2\top h+\beta \ge 0\hfill \\ 0\le {\gamma }_3\top g\ge 0;0\le {\gamma }_4\top \lambda -g\ge 0\hfill \\ 0\le \rho \top \mathbf{b}-{\mathcal{A}}^{\top }\beta \ge 0\hfill \\ \beta ,g,h,{\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4\in {ℝ}^d;\rho \in {ℝ}^m.\hfill \end{array}$$ (3.8)

The above LPCC can be immediately rewritten into an MIP. Rewriting the complementarity constraints in (3.8) into the system of logical constraints following (3.6), problem (2.4) now becomes

$$min\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g-\frac{1}{2}\lambda {\gamma }_4^{\top }\mathbf{1};s.t.$$ (3.9)

$$\{\begin{array}{l}Q\beta +q+{\gamma }_1-{\gamma }_2+\mathcal{A}\rho =0;ng-{\gamma }_1-{\gamma }_2=0\hfill \\ n(a-1)g+nh-na\lambda \mathbf{1}-{\gamma }_3+{\gamma }_4=0\hfill \\ {\gamma }_1\le \mathcal{M}{\mathbf{z}}_1;h_i-{\beta }_i\le \mathcal{M}(1-{\mathbf{z}}_1)\hfill \\ {\gamma }_2\le \mathcal{M}{\mathbf{z}}_2;h+\beta \le \mathcal{M}(1-{\mathbf{z}}_2)\hfill \\ {\gamma }_3\le \mathcal{M}{\mathbf{z}}_3;g_i\le \mathcal{M}(1-{\mathbf{z}}_3)\hfill \\ {\gamma }_4\le \mathcal{M}{\mathbf{z}}_4;\lambda -g\le \mathcal{M}(1-{\mathbf{z}}_4)\hfill \\ \rho \le \mathcal{M}{\mathbf{z}}_5;\mathbf{b}-{\mathcal{A}}^{\top }\beta \le \mathcal{M}(1-{\mathbf{z}}_5)\hfill \\ -\beta \le h;{\gamma }_2\ge 0;\beta \le h;{\gamma }_1\ge 0\hfill \\ g\ge 0;{\gamma }_3\ge 0;g\le \lambda ;{\gamma }_4\ge 0\hfill \\ \rho \ge 0;\mathbf{b}-{\mathcal{A}}^{\top }\beta \ge 0\hfill \\ {\mathbf{z}}_1,{\mathbf{z}}_2,{\mathbf{z}}_3,{\mathbf{z}}_4\in {\{0,1\}}^d;{\mathbf{z}}_5\in {\{0,1\}}^m\hfill \\ \beta ,g,h,{\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4\in {ℝ}^d;\rho \in {ℝ}^m,\hfill \end{array}$$ (3.10)

where we recall that 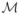is a properly large constant.

The above program is in the form of an MIP, which admits finite algorithms that ascertain global optimality.

Theorem 3.3

Program (3.9)–(3.10) admits algorithms that attain a global optimum in finite iterations.

Proof

The problem can be solved globally in finite iterations by B&B (Lawler and Wood, 1966) method.

The proof in fact provides a class of numerical schemes that solve (3.9)–(3.10) globally and finitely. Some of these schemes have become highly developed and even commercialized. We elect to solve the above problem using one of the state-of-the-art MIP solvers, Gurobi, which is a B&B-based solution tool. (Detailed information about Gurobi can be found at http://www.gurobi.com/.)

3.2.2. MIPGO for Nonconvex Learning with the MCP

Following almost the same argument for the SCAD penalized nonconvex learning, we can derive the reformulation of the MCP penalized nonconvex learning problem into an LPCC per the following theorem.

Theorem 3.4

Program (2.6) is equivalent to the following LPCC:

$$min\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}a\lambda {\mathbf{1}}^{\top }{\eta }_4-\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h;s.t.$$ (3.11)

$$\{\begin{array}{l}Q\beta +q+{\eta }_1-{\eta }_2+\mathcal{A}\rho =0\hfill \\ \frac{n}{a}g-\frac{n}{a}h-{\eta }_3+{\eta }_4=0;-n(\frac{1}{a}g+\lambda \mathbf{1})-{\eta }_1-{\eta }_2=0\hfill \\ 0\le {\eta }_1\top h-\beta \ge 0;0\le {\eta }_2\top h+\beta \ge 0\hfill \\ 0\le {\eta }_3\top g\ge 0;0\le {\eta }_4\top a\lambda \mathbf{1}-g\ge 0\hfill \\ 0\le \rho \top \mathbf{b}-{\mathcal{A}}^{\top }\beta \ge 0\hfill \\ \beta ,g,h,{\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4\in {ℝ}^d;\rho \in {ℝ}^m\hfill \end{array}$$ (3.12)

To further facilitate the computation, Program (3.11)–(3.12) can be represented as

$$min\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}a\lambda {\mathbf{1}}^{\top }{\eta }_4-\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h;s.t.$$ (3.13)

$$\{\begin{array}{l}q+Q\beta +{\eta }_1-{\eta }_2+\mathcal{A}\rho =0;\frac{n}{a}g-\frac{n}{a}h-{\eta }_3+{\eta }_4=0\hfill \\ -n(\frac{1}{a}g+\lambda \mathbf{1})-{\eta }_1-{\eta }_2=0\hfill \\ 0\le {\eta }_1\le \mathcal{M}{\mathbf{z}}_1;0\le h-\beta \le \mathcal{M}(1-{\mathbf{z}}_1)\hfill \\ 0\le {\eta }_2\le \mathcal{M}{\mathbf{z}}_2;0\le h+\beta \le \mathcal{M}(1-{\mathbf{z}}_2)\hfill \\ 0\le {\eta }_3\le M{\mathbf{z}}_3;0\le g\le \mathcal{M}(1-{\mathbf{z}}_3)\hfill \\ 0\le {\eta }_4\le \mathcal{M}{\mathbf{z}}_4;0\le a\lambda \mathbf{1}-g\le \mathcal{M}(1-{\mathbf{z}}_4)\hfill \\ 0\le \rho \le \mathcal{M}{\mathbf{z}}_5;\mathbf{b}-{\mathcal{A}}^{\top }\beta \le \mathcal{M}(1-{\mathbf{z}}_5);\mathbf{b}-{\mathcal{A}}^{\top }\beta \ge 0\hfill \\ {\mathbf{z}}_1,{\mathbf{z}}_2,{\mathbf{z}}_3,{\mathbf{z}}_4\in {\{0,1\}}^d;{\mathbf{z}}_5\in {\{0,1\}}^m\hfill \\ {\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4\in {ℝ}^d;\rho \in {ℝ}^m\hfill \end{array}$$ (3.14)

The computability of a global optimal solution to the above MIP is guaranteed by the following theorem.

Theorem 3.5

Program (3.13)–(3.14) admits algorithms that attain a global optimum in finite iterations.

Proof

The problem can be solved globally in finite iterations by B&B (Lawler and Wood, 1966) method.

Combining the reformulations in Section 3.2, we want to remark that the MIP reformulation connects the SCAD or MCP penalized nonconvex learning with the state-of-the-art numerical solvers for MIP. This reformulation guarantees global minimum theoretically and yields reasonable computational expense in solving (1.1). To acquire such a guarantee, we do not impose very restrictive conditions. To our knowledge, there is no existing global optimization technique for the nonconvex learning with the SCAD penalty or the MCP penalty in literature under the same or less restrictive assumptions. More specifically, for MIPGO, the only requirement on the statistical loss function is that it should be a lower-bounded quadratic function on the feasible region Λ with the Hessian matrix Q being symmetric. As we have mentioned in Section 2, an important class of sparse learning problems naturally satisfy our assumption. In contrast, LLA, per its equivalence to a majorization minimization algorithm, converges asymptotically to a stationary point that does not differentiate among local maxima, local minima, or saddle points. Hence, the resulting solution quality is not generally guaranteed. Fan, Xue and Zou (2014) proposed the state-of-the-art LLA variant. It requires restricted eigenvalue conditions to ensure convergence to an oracle solution in two iterations with a lower-bounded probability. The convergence of the local optimization algorithms by Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) both require the satisfaction of (conditions that imply) RSC. To our knowledge, MIPGO stipulates weaker conditions in contrast to the above solution schemes.

3.2.3. Numerical Stability of MIPGO

The representations of SCAD or MCP penalized nonconvex learning problems as MIPs introduce dummy variables to the original problem. These dummy variables are in fact Lagrangian multipliers in the KKT conditions of (2.4) or (2.6). In cases when no finite Lagrangian multipliers exist, the proposed MIPGO can result in numerical instability. To address this issue, we study an abstract form of SCAD or MCP penalized the nonconvex learning problems given as following.

$$min\left\{\mathcal{F}(\beta ,h,g):(\beta ,h)\in \stackrel{\sim }{\mathrm{\Lambda }},g\in {[0,M]}^d\right\},$$ (3.15)

where M > 0, Λ̃ := {(β, h) : β ∈ Λ, h ∈ ℝ^d, h ≥ β, h ≥ −β}, and 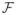: Λ̃ × [0, M]^d → ℝ is assumed continuously differentiable in (β, h, g) with the gradient ∇ 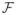being Lipschitz continuous. It may easily be verified that (2.4) and (2.6) are both special cases of (3.15). Now, we can write out the KKT conditions of this abstract problem as:

$${\nabla }_{\beta }\mathcal{F}(\beta ,h,g)+v_1-v_2+\mathcal{A}\rho =0$$ (3.16)

$${\nabla }_h\mathcal{F}(\beta ,h,g)-v_1-v_2=0$$ (3.17)

$${\nabla }_g\mathcal{F}(\beta ,g)-{\zeta }_1+{\zeta }_2=0$$ (3.18)

$$\begin{array}{ll}{\zeta }_{1,i}·g_i=0;\hfill & {\zeta }_{2,i}·(g_i-M)=0\hfill \\ {\zeta }_{1,i},{\zeta }_{2,i}\ge 0\hfill & \hfill \end{array}\}\forall i=1,\dots ,d$$ (3.19)

$$\begin{array}{ll}{v}_{1,i}·({\beta }_i-h_i)=0;\hfill & v_{2,i}·(-{\beta }_i-h_i)=0\hfill \\ v_{1,i}\ge 0;v_{2,i}\ge 0\hfill & \hfill \end{array}\}\forall i=1,\dots ,d$$ (3.20)

$$\rho \ge 0;{\rho }^{\top }({\mathcal{A}}^{\top }\beta -\mathbf{b})=0,$$ (3.21)

where ∇_β 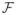(β, h, g) := ∂ 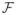(β, h, g)/∂β, ∇_g 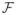(β, h, g) := ∂ 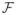(β, h, g)/∂g, and ∇_h 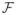(β, h, g) := ∂ 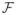(β, h, g)/∂h, and where ζ₁, ζ₂, υ₁, υ₂ ∈ ℝ^d and ρ ∈ ℝ^m are the Lagrangian multipliers that we are concerned with. For convenience, the i-th dimension (i = {1, …, d}) of these multipliers are denoted as ζ₁,_i, ζ₂,_i, υ_1,i, υ_2,i, and ρ_i, respectively. Notice that, since 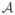is full-rank, then ρ is bounded if || 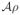|| is bounded, where we let ||·|| be an ℓ_p norm with arbitrary 1 ≤ p ≤ ∞. 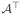(To see this, observe that ${\Vert \mathcal{A}\rho \Vert }_2=\sqrt{{\rho }^{\top }{\mathcal{A}}^{\top }\mathcal{A}\rho }$ and 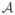is positive definite.)

Theorem 3.6

Denote a global optimal solution to problem (3.15) as (β^*, h^*, g^*). Assume that there exists a positive constant C₁ such that

$$max\{\Vert {\nabla }_{\beta }\mathcal{F}({\beta }^{\ast },h^{\ast },g^{\ast })\Vert ,\Vert {\nabla }_h\mathcal{F}({\beta }^{\ast },h^{\ast },g^{\ast })\Vert ,\Vert {\nabla }_g\mathcal{F}({\beta }^{\ast },h^{\ast },g^{\ast })\Vert \}\le C_1.$$

Then the Lagrangian multipliers corresponding to this global optimum, υ₁, υ₂, ζ₁, ζ₂, and ρ satisfy that

$$max\{\Vert v_1\Vert ,\Vert v_2\Vert ,\Vert {\zeta }_1\Vert ,\Vert {\zeta }_2\Vert \}\le C_1;\mathit{and}\Vert \mathcal{A}\rho \Vert \le 3C_1.$$ (3.22)

Proof

Recall that Λ is non-empty. Since 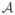is full rank and all other constraints are linear and non-degenerate, we have the linear independence constraint qualification satisfied at a global solution, which then satisfies the KKT condition. (i) In order to show that υ₁ and υ₂ are bounded, with (3.17), we have ||υ₁ + υ₂|| = ||∇_h 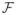(β^*, h^*, g^*)|| ≤ C₁. Noticing the non-negativity of υ₁ and υ₂, we obtain max{||υ₁||, ||υ₂||} ≤ ||υ₁ + υ₂|| = ||∇_h 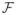(β^*, h^*, g^*)|| ≤ C₁. (ii) To show 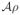is bounded, considering (3.16), || 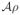|| = ||∇_β 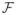(β, h, g)+ υ₁ − υ₂|| ≤ ||∇_h 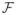(β^*, h^*, g^*)|| + ||υ₁|| + ||υ₂|| ≤ 3C₁. (iii) To show that ζ₁ and ζ₂ are bounded, we notice that, immediately from (3.19), ζ_1,i ≥ 0; ζ_2,i ≥ 0; and ζ_1,i · ζ_2,i = 0, for all i = 1, …, d. Thus, according to (3.18), C₁ ≥ ||∇_g 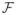(β^*, h^*, g^*)|| ≥ ||(max{ζ_1,i, ζ_2,i}, i = 1, …, d)||. Therefore, ||ζ₁|| ≤ C₁ and ||ζ₂|| ≤ C₁.

With Theorem 3.6, we claim that the Lagrangian multipliers corresponding to a global optimal solution cannot be arbitrarily large under proper assumptions. Hence, we conclude that the proposed method can be numerically stable. In practice, because ∇F is assumed Lipschitz continuous, we can simply impose an additional constraint ||β||_∞ ≤ C in the MIP reformulation for some positive constant C to ensure the satisfaction of (3.22). Conceivably, this additional constraint does not result in a significant modification to the original problem.

4. Comparison with the Gradient Methods

This section will compare MIPGO with Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) when 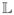:= 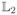. Thus the complete formulation is given as:

$$\underset{\beta \in {ℝ}^d}{min}\mathcal{L}(\beta )=\frac{1}{2}{\Vert y-X\beta \Vert }_2^2+n\sum _{i=1}^d{P}_{\lambda }(\mid {\beta }_i\mid ).$$ (4.1)

where X and y are defined as in Section 2.1. We will refer to this problem as SCAD (or MCP) penalized linear regression (LR-SCAD (or -MCP)). To solve this problem, Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) independently developed two types of computing procedures based on the gradient method proposed by Nesterov (2007). For the sake of simplicity, we will refer to both approaches as the gradient methods hereafter, although they both present substantial differentiation from the original gradient algorithm proposed by Nesterov (2007). To ensure high computational and statistical performance, both Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) considered conditions called “restricted strong convexity” (RSC). We will illustrate in this section that RSC can be a fairly strong condition in LR-SCAD or -MCP problems and that MIPGO may potentially outperform the gradient methods regardless of whether the RSC is satisfied.

In Loh and Wainwright (2015) and Wang, Liu and Zhang (2014), RSC is defined differently. These two versions of definitions are discussed as below: Let β_true = (β_true,i) ∈ ℝ^d be the true parameter vector and k = ||β_true||₀. Denote that $L(\beta ):=\frac{1}{2n}{\Vert y-X\beta \Vert }_2^2$. Then according to Loh and Wainwright (2015), L(β) is said to satisfy RSC if the following inequality holds:

$$L({\beta }^{\prime })-L({\beta }^{″})-\langle {\nabla }_{\beta }L({\beta }^{″}),{\beta }^{\prime }-{\beta }^{″}\rangle \ge \{\begin{array}{ll}{\alpha }_1{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2^2-{\tau }_1\frac{logd}{n}{\mid {\beta }^{\prime }-{\beta }^{″}\mid }^2\hfill & \text{for}\text{all}{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2\le 3\hfill \\ {\alpha }_2{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2-{\tau }_2\frac{logd}{n}\mid {\beta }^{\prime }-{\beta }^{″}\mid \hfill & \text{for}\text{all}{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2\ge 3\hfill \end{array}$$ (4.2)

for some α₁, α₂ > 0 and τ₁, τ₂ ≥ 0. Furthermore, Loh and Wainwright (2015) assumed (in Lemma 3 of their paper) that $\frac{64k\tau logd}{n}+\mu \le \alpha$ with α = min{α₁, α₂} and τ = max{τ₁, τ₂}, for some μ ≥ 0 such that $\mu {\Vert \beta \Vert }_2^2+{\sum }_{i=1}^p{P}_{\lambda }(\mid {\beta }_i\mid )$ is convex.

Wang, Liu and Zhang (2014) discussed a different version of RSC. They reformulated (4.1) into $\frac{\mathcal{L}(\beta )}{n}=\stackrel{\sim }{L}(\beta )+\lambda \mid \beta \mid$, where $\stackrel{\sim }{L}(\beta ):=L(\beta )+{\sum }_{i=1}^d{P}_{\lambda }({\beta }_i)-\lambda \mid \beta \mid$. According to the same paper, one can quickly check that L̃(β) is continuously differentiable. Then, their version of RSC, as in Lemma 5.1 of their paper, is given as:

$$\stackrel{\sim }{L}({\beta }^{\prime })-\stackrel{\sim }{L}({\beta }^{″})\ge \langle \nabla \stackrel{\sim }{L}({\beta }^{″}),{\beta }^{\prime }-{\beta }^{″}\rangle +{\alpha }_3{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2^2$$ (4.3)

for all $({\beta }^{\prime },{\beta }^{″})\in \{({\beta }^{\prime },{\beta }^{″}):{\sum }_{i:{\beta }_{\mathit{true},i}=0}\mathbb{I}({\beta }_i^{\prime }-{\beta }_i^{″}\ne 0)\le s\}$ for some α₃ > 0 and s ≥ k. Evidently, this implies that (4.3) also holds for all ||β′−β″||₀ ≤ s.

To differentiate the two RSCs, we will refer to (4.2) as RSC₁, and to (4.3) as RSC₂. A closer observation reveals that both RSCs imply that the objective function of the nonconvex learning problem is strongly convex in some sparse subspace involving k number of dimensions.

Lemma 4.1

Assume that L(β) satisfies RSC₁ in (4.2). If k ≥ 1, $\frac{64k\tau logd}{n}+\mu \le \alpha$, and $\mu {\Vert \beta \Vert }_2^2+{\sum }_{i=1}^p{P}_{\lambda }(\mid {\beta }_i\mid )$ is convex, then

$$\frac{1}{n}\mathcal{L}({\beta }^{\prime })-\frac{1}{n}\mathcal{L}({\beta }^{″})\ge \langle \frac{1}{n}\nabla \mathcal{L}({\beta }^{″}),{\beta }^{\prime }-{\beta }^{″}\rangle +{\alpha }_3{\Vert {\beta }^{\prime }-{\beta }^{″}\Vert }_2^2,\forall {\Vert {\beta }^{″}-{\beta }^{″}\Vert }_0\le s,$$ (4.4)

for some α₃ > 0, where s = 64k − 1, ∇ 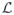(β″) ∈ [n∇L̃(β) + nλ∂|β|]_β=β″, and ∂|β| denotes the subdifferential of |β|.

The proof is given in the online supplement S3. From this lemma, we know that RSC₁, together with other assumptions made by Loh and Wainwright (2015), implies (4.4) for some s ≥ ||β_true||₀ = k for all k ≥ 1. Similarly for RSC₂, if the function L̃ satisfy (4.3), in view of the the convexity of λ|β|, we have that $\frac{\mathcal{L}(\beta )}{n}=\stackrel{\sim }{L}(\beta )+\lambda \mid \beta \mid$ satisfies (4.4) for some s ≥ ||β_true||₀. In summary, (4.4) is a necessary condition to both RSC₁ and RSC₂.

Nonetheless, (4.4) can be restrictive in some scenarios. To illustrate this, we conduct a series of simulations as following: We simulated a sequence of samples {(x_t, y_t) : 1 ≤ t ≤ n} randomly from the following sparse linear regression model: $y_t=x_t^{\top }{\beta }_{\mathit{true}}+{\epsilon }_t$, for all t = 1, …, n, in which d is set to 100, and β_true = [1; 1; 0_d−2]. Furthermore, ε_t ~ N (0, 0.09) and x_t ~ 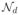(0, Σ) for all t = 1, …, n with covariance matrix Σ = (σ_ij) ∈ ℝ^d×d defined as σ_ij = ρ^|i−j|. This numerical test considers only SCAD for an example. We set the parameters for the SCAD penalty as a = 3.7 and λ = 0.2.

We conduct a “random RSC test” to see if the randomly generated sample instances can satisfy the RSC condition. Notice that both versions of RSC dictate that the strong convexity be satisfied in a sparse subspace that has only k number of significant parameters. In this example, we have k = 2. Therefore, to numerically check if RSC is satisfied, we conduct the following procedures: (i) we randomly select two dimensions i₁, i₂ : 1 ≤ i₁ < i₂ ≤ d; (ii) we randomly sample two points β¹, β² ∈ {β ∈ ℝ^d : β_i = 0, ∀i ∉ {i₁, i₂}}; and (iii) we check if a necessary condition for (4.4) holds. That is, we check if the following inequality holds, when β¹ ≠ β²:

$$\frac{\mathcal{L}({\beta }^1)+\mathcal{L}({\beta }^2)}{2}>\mathcal{L}\left(\frac{{\beta }^1+{\beta }^2}{2}\right).$$ (4.5)

We consider different sample sizes n ∈ {20, 25, 30, 35} and the covariance matrix parameters ρ ∈ {0.1, 0.3, 0.5} and constructed twelve sets of sample instances. Each set includes 100 random sample instances generated as mentioned above. For each sample instance, we conduct 10,000 repetitions of the “random RSC test”. If (4.5) is satisfied for all these 10,000 repetitions, we say that the sample instance has passed the “random RSC test”. Table 1 reports the test results.

Table 1.

Percentage for successfully passing the random RSC test out of 100 randomly generated instances.

ρ	n = 35	n = 30	n = 25	n = 20
0.1	93%	81%	53%	4%
0.3	94%	76%	39%	9%
0.5	55%	50%	21%	1%

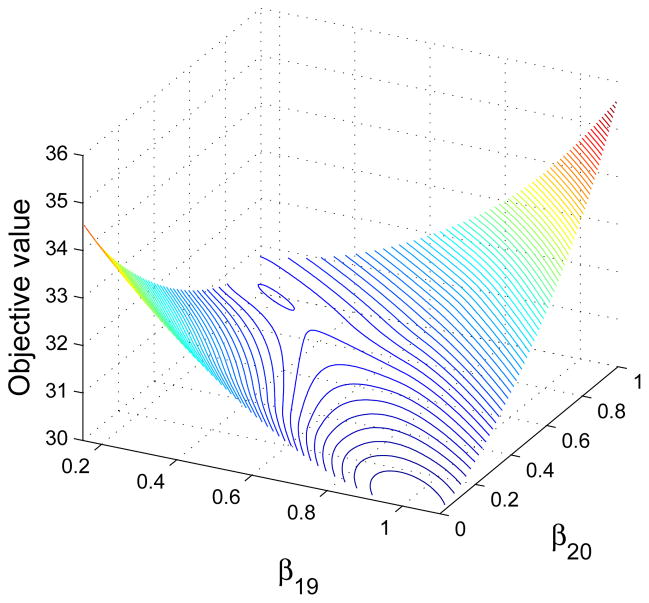
We observe from Table 1 that in some cases the percentage for passing the random RSC test is noticeably low. However, with the increase of sample size, that percentage grows quickly. Moreover, we can also observe that when ρ is larger, it tends to be more difficult for RSC to hold. Figure 1 presents a typical instance that does not satisfy RSC when n = 20 and ρ = 0.5. This figure shows the 3-D contour plot of objective function when the decision variable is within the subspace {β : β_i = 0, ∀i ∉ {19, 20}}. We can see that the contour plot apparently indicates nonconvexity of the function in the subspace, which violates (4.5).

Fig. 1.

A sample instance that fails in the random RSC test.

We then compare MIPGO with both gradient methods in two sets of the sample instances from the table: (i) the one that seems to provide the most advantageous problem properties (ρ = 0.1, and n = 35) to the gradient methods; and (ii) the one with probably the most adversarial parameters (ρ = 0.5, and n = 20) to the gradient methods. Notice that the two gradient methods are implemented on MatLab following the descriptions by Wang, Liu and Zhang (2014) and Loh and Wainwright (2015), respectively, including their initialization procedures. MIPGO is also implemented on MatLab calling Gurobi (http://www.gurobi.com/). We use CVX, “a package for specifying and solving convex programs” (Grant and Boyd, 2013, 2008), as the interface between MatLab and Gurobi. Table 2 presents our comparison results in terms of computational, statistical and optimization measures. More specifically, we use the following criteria for our comparison:

Table 2.

Comparison between MIPGO and the gradient methods. The numbers in parenthesis are the standard errors. GM₁ and GM₂ stand for the gradient methods proposed by Loh and Wainwright (2015) and Wang, Liu and Zhang (2014), respectively.

Method	ρ = 0.5, n = 20
	AD	FP	FN	Gap	Time
MIPGO	0.188 (0.016)	0.230 (0.042)	0 (0)	0 (0)	29.046 (5.216)
GM1	2.000 (0.000)	0 (0)	2 (0)	25.828 (0.989)	0.002 (0.001)
GM2	0.847 (0.055)	5.970 (0.436)	0 (0)	1.542 (0.119)	0.504 (0.042)
	ρ = 0.1, n = 35
MIPGO	0.085 (0.005)	0.020 (0.141)	0 (0)	0 (0)	27.029 (4.673)
GM1	2.000 (0.000)	0 (0)	2 (0)	31.288 (1.011)	0.002 (0.000)
GM2	0.936 (0.044)	6.000 (0.348)	0 (0)	4.179 (0.170)	0.524 (0.020)

• Absolute deviation (AD), defined as the distance between the computed solution and the true parameter vector. Such a distance is measured by ℓ₁ norm.

• False positive (FP), defined as the number of entries in the computed solution that are wrongly selected as nonzero dimensions.

• False negative (FN), defined as the number of entries in the computed solution that are wrongly selected as zero dimensions.

• objective gap (“Gap”), defined as the difference between the objective value of the computed solution and the objective value of the MIPGO solution. A positive value indicates a worse relative performance compared to MIPGO.

• Computational time (“Time”), which measures the total computational time to generate the solution.

AD, FP, and FN are commonly used statistical criteria, and “Gap” is a natural measure of optimization performance. In Table 2, we report the average values for all the above criteria out of 100 randomly generated instances aforementioned. From this table, we observe an outperformance of MIPGO over the other solution schemes on solution quality for both statistical and optimization criteria. However, MIPGO generates a higher computational overhead than the gradient methods.

5. Numerical Comparison on Optimization Performance with Local Linear Approximation

In this section, we numerically compare MIPGO with local linear approximation (LLA). We implement LLA on MatLab. In the implementation, we invoke the procedures of LLA iteratively until the algorithm fully converges. This shares the same spirit as the multistage procedure advocated by Huang and Zhang (2012). At each iteration, the LASSO subproblem is solved with Gurobi 6.0 using CVX (Grant and Boyd, 2013, 2008) as the interface. We report in the following a series of comparison results in terms of the optimization accuracy.

5.1. Numerical Tests on A Two-Dimensional Problem

In the following we conduct a numerical test on a two-dimensional LR-SCAD and a two-dimensional LR-MCP problem. We generate one instance for both of LR-SCAD and LR-MCP problems through the following procedures: We randomly generate β_true ∈ ℝ² with a uniformly distributed random vector on [−1, 5]² and then generate 2 observations x_t ~ 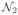(0, Σ), t ∈ {1, 2}, with covariance matrix Σ = (σ_ij) and σ_ij = 0.5^|i−j|. 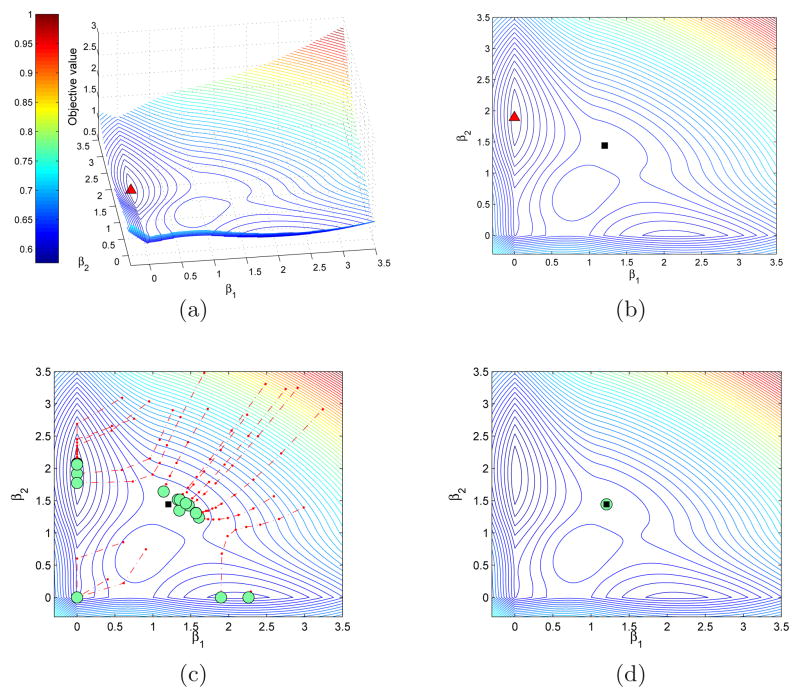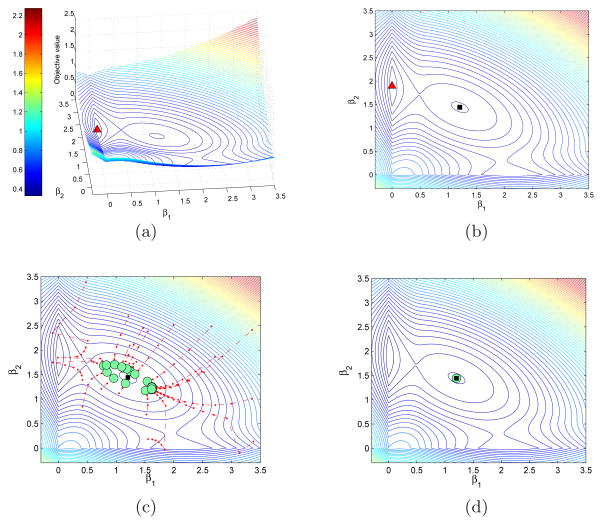Finally, we compute y_t as $y_t=x_t^{\top }\beta +{\epsilon }_t$ with ε_t ~ 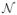(0, 1) for all t ∈ {1, 2}. Both the LR-SCAD problem and the LR-MCP problem use the same set of samples {(x_t, y_t) : t = 1, 2} in their statistical loss functions. The only difference between the two is the different choices of penalty functions. The parameters for the penalties are prescribed as λ = 1 and a = 3.7 for the SCAD and λ = 0.5 and a = 2 for the MCP. Despite their small dimensionality, these problems are noncon-vex with multiple local solutions. Their nonconvexity can be visualized via the 2-D and 3-D contour plots provided in Figure 2(a)–(b) (LR-SCAD) and Figure 3(a)–(b) (LR-MCP).

Fig. 2.

(a) 3-D contour plots of the 2-dimension LR-SCAD problem and the solution generated by MIPGO in 20 runs with random initial solutions. The triangle is the MIPGO solution in both subplots. (b) 2-D representation of subplot (a). (c) Trajectories of 20 runs of LLA with random initial solutions. (d) Trajectories of 20 runs of LLA with the least squares solution as the initial solutions.

Fig. 3.

(a). 3-D contour plots of the 2-dimension LR-MCP problem and the solution generated by MIPGO in 20 runs with random initial solutions. The triangle is the MIPGO solution in both subplots. (b). 2-D representation of subplot (a). (c). Trajectories of 20 runs of LLA with random initial solutions. (d). Trajectories of 20 runs of LLA with the least squares solution as the initial solutions.

We realize that the solution generated by LLA may depend on its starting point. Therefore, to make a fair numerical comparison, we consider two possible initialization procedures: (i) LLA with random initial solutions generated with a uniform distribution on the set [0, 3.5]² (denoted LLA_r), and (ii) LLA with initial solution set to be the least squares solution (denoted by LLA_LSS). (We will also consider LLA initialized with LASSO in later sections.)

To fully study the impact of initialization to the solution quality, we repeat each solution scheme 20 times. The best (Min.), average (Ave.), and worst (Max.) objective values as well as the relative objective difference (gap_(%)) obtained in the 20 runs are reported in Table 3. Here gap_(%) is defined

Table 3.

Test result on a toy problem. “gap_(%)” stands for the relative difference in contrast to MIPGO.

Penalty	Measure	LLAr	gap(%)	LLALSS	gap(%)	MIPGO
SCAD	Min	0.539	0.00	0.900	40.12	0.539
	Ave	0.911	40.85	0.900	40.12	0.539
	Max	2.150	74.93	0.900	40.12	0.539
MCP	Min	0.304	2.63	0.360	17.78	0.296
	Ave	0.435	31.95	0.360	17.78	0.296
	Max	1.293	77.11	0.360	17.78	0.296

$$\frac{\{\text{Objective}\text{of}\text{computed}\text{solution}\}-\{\text{Objective}\text{of}\text{MIPGO}\text{solution}\}}{\{\text{Objective}\text{of}\text{computed}\text{solution}\}}\times 100\%.$$

From the table we have the following observations:

1. LLA_r’s performance varies in different runs. In the best scenario, LLA attains the global optimum, while the average performance is not guaranteed.

2. LLA_LSS fails to attain the global optimal solution.

3. LLA with either initialization procedure yields a local optimal solution.

4. MIPGO performs robustly and attains the global solution at each repetition.

Figure 2(c) and Figure 3(c) present the search trajectories (dot dash lines) and convergent points (circles) of LLA_r for LR-SCAD and LR-MCP, respectively. In both figures, we observe a high dependency of LLA’s performance on the initial solutions. Note that the least squares solutions for the two problems are denoted by the black squares. Figure 2(d) and Figure 3(d) present the convergent points of LLA_LSS for LR-SCAD and for LR-MCP, respectively. LLA_LSS utilizes the least squares solution (denoted as the black square in the figure) as its starting point. This least squares solution happens to be in the neighborhood of a local solution in solving both problems. Therefore, the convergent points out of the 20 repetitions of LLA_LSS all coincide with the least squares solution. Even though we have n = d = 2 in this special case, we can see that choosing the least squares solution as the initial solution may lead the LLA to a non-global stationary point. The solutions obtained by MIPGO is visualized in Figure 2(b) and 3(b) as triangles. MIPGO generates the same solution over the 20 repetitions even with random initial points.

5.2. Numerical Tests on Larger Problems

In the following, we conduct similar but larger-scale simulations to compare MIPGO and LLA in terms of optimization performance. For these simulations, we randomly generate problem instances as follows: We first randomly generate a matrix T ∈ ℝ^d×d with the entry on i-th row and j-th column uniformly distributed on [0, 0.5^|i−j|] and set Σ = T^⊤T as the covariance matrix. Let the true parameter vector β_true = [3 2 10 0 1 1 2 3 1.6 6 0_1×(d−10)]. We then randomly generate a sequence of observations {(x_t, y_t) : t = 1, …, n} following a linear model $y_t=x_t^{\top }{\beta }_{\mathit{true}}+{\epsilon }_t$, where x_t ~ 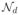(0, Σ), and ε_t ~ 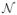(0, 1.44) for all t = 1, …, n. Finally, the penalty parameters are λ = 1 and a = 3.7 for SCAD and λ = 0.5 and a = 2 for MCP.

Following the aforementioned descriptions, we generate problem instances with different problem sizes d and sample sizes n (with 3 problem instances generated for each combination of d and n) and repeat each solution scheme 20 times. For these 20 runs, we randomly generate initial solutions for MIPGO with each entry following a uniform distribution on [−10, 10]. Similar to the 2-dimensional problems, we also involve in the comparison LLA with different initialization procedures: (i) LLA with randomly generated initialization solution whose each entry follows a uniform distribution on [−10, 10] (denoted LLA_r). (ii) LLA with zero vector as the initial solution (denoted LLA₀). (iii) LLA with the initial solution prescribed as the solution to the LASSO problem (denoted LLA₁). More specifically, the LASSO problem used in the initialization of LLA₁ is formulated as

$$\underset{\beta \in {ℝ}^n}{min}\frac{1}{2}{\Vert y-X\beta \Vert }_2^2+\omega \sum _{i=1}^d\mid {\beta }_i\mid$$ (5.1)

where X := (x₁, …, x_n)^⊤, y := (y₁, …, y_n)^⊤, and $\omega :=\frac{1}{10}n\lambda ·(K-1)$ at K-th run with 1 ≤ K ≤ 20. This is designed to examine how sensitive the performance the LLA₁ depends on the initial estimate. We would also like to remark that, when K = 1, the initial solution for LLA will be exactly the least squares solution. We would also like to remark that the LLA initialized with LASSO is the solution scheme proposed by Fan, Xue and Zou (2014).

The best (Min.), the average (Ave.), and the worst (Max.) objective values and the relative objective differences (gap_(%)) of the 20 runs for each instance are reported in the upper and lower panels of Table 4 for LR-SCAD and LR-MCP, respectively. Notice that for each problem scale, we generate three test instances randomly, but Table 4 only reports one of the three instances for each problem size due to the limit of space. Tables S1 and S2 in Appendix S4 will complement the rest of the results. According to the numerical results, in all instances with different dimensions, MIPGO yields the lowest objective value, and in many cases, gap_(%) value is nontrivially large. This indicates the outperformance of our proposed MIPGO over all counterpart algorithms.

Table 4.

Numerical comparison of LLA and the proposed MIPGO on LR-SCAD and LR-MCP problems with different problem scales. “TS” stands for “Typical Sample”.

		MIPGO	LLAr	gap(%)	LLA0	gap(%)	LLA1	gap(%)
LR-SCAD
TS 3	Min.	89.87	89.87	0.00	104.96	14.37	104.96	14.37
d = 10	Ave.	89.87	109.19	17.69	104.96	14.37	104.96	14.37
n = 10	Max.	89.87	162.93	44.84	104.96	14.37	104.96	14.37
TS 6	Min.	86.04	88.219	2.46	115.17	25.30	108.37	20.60
d = 20	Ave.	86.04	105.13	18.15	115.17	25.30	108.37	20.60
n = 10	Max.	86.04	143.51	40.05	115.17	25.30	108.37	20.60
TS 9	Min.	120.35	120.35	0.00	150.15	19.85	120.35	0.00
d = 40	Ave.	120.35	167.21	28.02	150.15	19.85	120.35	0.00
n = 15	Max.	120.35	203.18	40.76	150.15	19.85	120.35	0.00
TS 12	Min.	519.14	519.14	0.00	560.28	7.34	538.47	3.59
d = 200	Ave.	519.14	733.06	29.18	560.28	7.34	538.47	3.59
n = 60	Max.	519.14	959.00	45.87	560.28	7.34	538.47	3.59
TS 15	Min.	841.72	841.90	0.02	1003.69	16.14	873.44	3.63
d = 500	Ave.	841.72	981.73	14.26	1003.69	16.14	873.44	3.63
n = 80	Max.	841.72	1173.06	28.25	1003.69	16.14	873.44	3.63
TS 18	Min.	1045.22	1105.70	5.47	1119.84	6.66	1119.84	6.66
d = 1000	Ave.	1045.22	1135.84	7.98	1119.84	6.66	1119.84	6.66
n = 100	Max.	1045.22	1309.70	20.19	1119.84	6.66	1119.84	6.66
LR-MCP
TS 3	Min.	13.65	15.77	13.43	21.51	36.54	25.00	45.39
d = 10	Ave.	13.65	20.60	39.59	21.51	36.54	25.00	45.39
n = 10	Max.	13.65	32.83	58.41	21.51	36.54	25.00	45.39
TS 6	Min.	14.71	17.60	16.41	14.71	0.00	20.06	26.67
d = 20	Ave.	14.71	17.60	22.54	14.71	0.00	20.06	26.67
n = 10	Max.	14.71	17.60	65.38	14.71	0.00	20.06	26.67
TS 9	Min.	23.64	27.17	13.02	26.57	11.05	49.08	51.84
d = 40	Ave.	23.64	27.17	35.40	26.57	11.05	49.08	51.84
n = 15	Max.	23.64	27.17	57.98	26.57	11.05	49.08	51.84
TS 12	Min.	93.55	105.62	11.42	112.13	16.57	120.63	22.45
d = 200	Ave.	93.55	165.25	43.39	112.13	16.57	120.63	22.45
n = 60	Max.	93.55	596.52	84.32	112.13	16.57	120.63	22.45
TS 15	Min.	163.98	175.44	6.53	221.84	26.08	179.53	8.66
d = 500	Ave.	163.98	211.62	22.51	221.84	26.08	179.53	8.66
n = 80	Max.	163.98	237.56	30.97	221.84	26.08	179.53	8.66
TS 18	Min.	249.89	267.83	6.70	267.83	6.70	272.39	8.27
d = 1000	Ave.	249.89	322.24	22.25	267.83	6.70	272.39	8.27
n = 100	Max.	249.89	530.60	52.60	267.83	6.70	272.39	8.27

6. Numerical Comparison on Statistical Performance with Local Algorithms

We next examine MIPGO on the statistical performance in comparison with several existing local algorithms, including coordinate descent, LLA, and gradient methods. We simulate the random samples {(x_t, y_t), t = 1, …, n} from the following linear model: $y_t=x_t^{\top }({\beta }_{\mathit{true},i}:1\le i\le d-1)+{\beta }_{\mathit{true},d}+{\epsilon }_t$, where we let d = 1001, n = 100, and β_true,d is the intercept. β_true is constructed by first setting β_true,d = 0, then randomly choosing 5 elements among dimensions {1, …, d − 1} to be 1.5, and setting the other d − 6 elements as zeros. Furthermore, for all t = 1, …, n, we let ε_t ~ N(0, 1.44) and x_t ~ 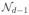(0, Σ) with Σ = (σ_ij) defined as σ_ij = 0.5^|i−j|. For both LR-SCAD and LR-MCP, we set the parameter a = 2, and tune λ the same way as presented by Fan, Xue and Zou (2014). We generate 100 instances using the above procedures, and solve each of these instances using MIPGO and other solutions schemes, including: (i) coordinate descent; (ii) gradient methods; (iii) SCAD-based and MCP-based LLA; and (iv) the LASSO method. The relative details of these techniques are summarized as follows:

• LASSO: The LASSO penalized linear regression, coded in MatLab that invokes Gurobi 6.0 using CVX as the interface.

• GM₁-SCAD/MCP: The SCAD/MCP penalized linear regression computed by the local solution method by Loh and Wainwright (2015) on Mat-Lab.

• GM₂-SCAD/MCP: The SCAD/MCP penalized linear regression computed by the approximate path following algorithm by Wang, Liu and Zhang (2014) on MatLab.

• SparseNet: The R-package sparsenet for SCAD/MCP penalized linear regression computed by coordinate descent (Mazumder et al., 2011).

• Ncvreg-SCAD/-MCP: The R-package ncvreg for MCP penalized linear regression computed by coordinate descent (Breheny and Huang, 2011).

• SCAD-LLA₁/MCP-LLA₁: The SCAD/MCP penalized linear regression computed by (fully convergent) LLA with the tuned LASSO estimator as its initial solution, following Fan, Xue and Zou (2014).

Notice that we no longer involve LLA_r and LLA₀ in this test, because a similar numerical experiment presented by Fan, Xue and Zou (2014) has shown that LLA₁ is more preferable than most other LLA variants in statistical performance.

Numerical results are presented in Table 5. According to the table, the proposed MIPGO approach estimates the (in)significant coefficients correctly in both SCAD and MCP penalties, and provides an improvement on the average AD over all the other alternative schemes.

Table 5.

Comparison of statistical performance. “Time” stands for the computational time in second. The numbers in parenthesis are the standard errors.

Method	n = 100, d = 1000
	AD	FP	FN	Time
LASSO	2.558 (0.047)	5.700 (0.255)	0 (0)	2.332 (0.108)
GM1-SCAD	0.526 (0.017)	0.600 (0.084)	0 (0)	4.167 (0.254)
GM1-MCP	0.543 (0.018)	0.540 (0.073)	0 (0)	4.42 (0.874)
GM2-SCAD	3.816 (0.104)	18.360 (0.655)	0 (0)	3.968 (0.049)
GM2-MCP	0.548 (0.019)	0.610 (0.083)	0 (0)	3.916 (0.143)
SparseNet	1.012 (0.086)	5.850 (1.187)	0 (0)	2.154 (0.017)
Ncvreg-SCAD	1.068 (0.061)	9.220 (0.979)	0 (0)	0.733 (0.007)
Ncvreg-MCP	0.830 (0.045)	3.200 (0.375)	0 (0)	0.877 (0.009)
SCAD-LLA1	0.526 (0.017)	0.600 (0.084)	0 (0)	31.801 (1.533)
MCP-LLA1	0.543 (0.018)	0.540 (0.073)	0 (0)	28.695 (1.473)
MIPGO-SCAD	0.509 (0.017)	0 (0)	0 (0)	472.673 (97.982)
MIPGO-MCP	0.509 (0.017)	0 (0)	0 (0)	361.460 (70.683)
Oracle	0.509 (0.017)

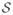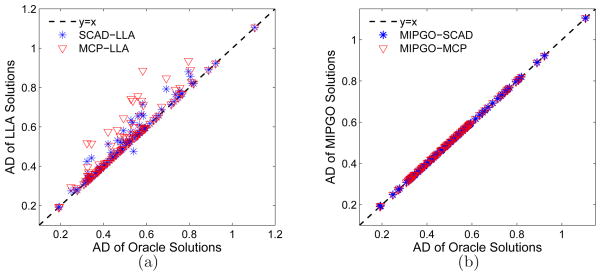
To further measure the performance of different schemes, we use the oracle estimator as a benchmark. The oracle estimator is computed as following: Denote by x_t,i as the i-th dimension of the t-th sample x_t, and by the true support set, i.e., $\mathcal{S}:=\{i:{\beta }_i^{\mathit{true}}\ne 0\}$. We conduct a linear regression using X̂ := (x_t,i : t = 1, …, n, i ∈ 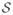) and y := (y_t). As has been shown in Table 5, MIPGO yields a very close average AD and standard error to the oracle estimator. This observation is further confirmed in Figure 4. Specifically, Figures 4.(a) and 4.(b) illustrate relative the performance of LLA₁ and of MIPGO, respectively, in contrast to the oracle estimators. We see that MIPGO well approximates the oracle solution. Comparing MIPGO and LLA₁ from the figures, we can tell a noticeably improved recovery quality by MIPGO in contrast to LLA₁.

Fig. 4.

Comparison between generated solutions and the oracle solutions in AD when (a) solutions are generated by LLA₁, and (b) solutions are generated by MIPGO. The horizontal axis is the AD value of the oracle solution for each simulation, while the vertical axis is the AD of generated solutions for the same simulation. The closer a point is to the linear function “y = x”, the smaller is the difference between the AD of a generated solution and the AD of the corresponding oracle solution.

Nonetheless, we would like to remark that, although MIPGO yields a better solution quality over all the other local algorithms in every cases of the experiment as presented, the local algorithms are all noticeably faster than MIPGO. Therefore, we think that MIPGO is less advantageous in terms of computational time.

6.1. A Real Data Example

In this section, we conduct our last numerical test comparing MIPGO, LLA, and the gradient methods on a real data set collected in a marketing study (Wang, 2009; Lan et al., 2013), which has a total of n = 463 daily records. For each record, the response variable is the number of customers and the originally 6397 predictors are sales volumes of products. To facilitate computation, we employ the feature screening scheme in Li et al. (2012) to reduce the dimension to 1500. The numerical results are summarized in Table 6. In this table, GM₁ and GM₂ refer to the local solution methods proposed by Loh and Wainwright (2015) and by Wang, Liu and Zhang (2014), respectively. LLA₀ denote the LLA initialized as zero. LLA₁ denote the LLA initialized as the solution generated by LASSO. To tune the LASSO, we implement LLA₁ choosing the coefficients ω in the LASSO problem (5.1) from the set {0.1×nKλ : K = {0, 1, …, 20}} and we select the ω that enables LLA₁ to yield the best objective value. Here the value of λ is the same as the tuning parameter of SCAD or MCP. As reported in Table 6, λ = 0.02 for SCAD, and λ = 0.03 for MCP, respectively. Observations from Table 6 can be summarized as following: (i) for the case with the SCAD penalty, the proposed MIPGO yields a significantly better solution than all other alternative schemes in terms of both Akaike’s information criterion (AIC), Bayesian information criterion (BIC), and the objective value. Furthermore, MIPGO also outputs a model with the smallest number of parameters. (ii) for the MCP case, both MIPGO and LLA₁ outperforms other schemes. Yet these two approaches have similar values for AIC and BIC. Nonetheless, MIPGO provides a better model as the number of nonzero parameters is smaller than the solution generated by LLA₁.

Table 6.

Results of the Real Data Example. “NZ”, #_0.05, and #_0.10 stand for the numbers of parameters that are nonzero, that has a p-value greater or equal to 0.05, and that has a p-value greater or equal to 0.1. “R²” denotes the R-squared value. “AIC”, “BIC” and “Obj.” stand for Akaike’s information criterion, Bayesian information criterion and objective function value.

Method	SCAD: λ = 0.02; a = 3.7
	NZ	#0.05	#0.10	R2	AIC	BIC	Obj.
GM1	1500	—	—	0.997	357.101	6563.691	212.279
GM2	401	401	401	0.698	246.886	1906.114	103.626
LLA0	185	119	115	0.864	−554.093	211.387	76.031
LLA1	181	83	80	0.912	−763.718	14.789	71.673
MIPGO	129	35	34	0.898	−796.581	−262.814	68.474
	MCP: λ = 0.03; a = 2
GM1	818	—	—	0.332	1448.966	5129.436	169.091
GM2	134	110	104	0.735	−296.624	−346.474	93.870
LLA0	96	5	6	0.856	704.654	−307.432	72.645
LLA1	113	2	2	0.902	−849.842	−382.279	69.292
MIPGO	109	3	3	0.899	−841.280	−390.267	68.591

7. Conclusion

The lack of solution schemes that ascertain solution quality to nonconvex learning with folded concave penalty has been an open problem in sparse recovery. In this paper, we seek to address this issue in a direct manner by proposing a global optimization technique for a class of nonconvex learning problems without imposing very restrictive conditions.

In this paper, we provide a reformulation of the nonconvex learning problem into a general quadratic program. This reformulation then enables us to have the following findings:

1. To formally state the complexity of finding the global optimal solution to the nonconvex learning with the SCAD and the MCP penalties.

2. To derive a MIP-based global optimization approach, MIPGO, to solve the SCAD and MCP penalized nonconvex learning problems with theoretical guarantee. Numerical results indicate that the proposed MIPGO outperforms the gradient method by Loh and Wainwright (2015) and Wang, Liu and Zhang (2014) and LLA approach with different initialization schemes in solution quality and statistical performance.

To the best of our knowledge, the complexity bound of solving the nonconvex learning with the MCP and SCAD penalties globally has not been reported in literature and MIPGO is the first optimization scheme with provable guarantee on global optimality for solving a folded concave penalized learning problem.

We would like to alert the readers that the proposed MIPGO scheme, though being effective in globally solving the nonconvex learning with the MCP and SCAD penalty problem, yields a comparatively larger computational overhead than the local solution method in larger scale problems. (See comparison of computing times in Table 5.) In the practice of highly time-sensitive statistical learning with hugh problem sizes, LLA and other local solution schemes can work more efficiently. However, there are important application scenarios where a further refinement on the solution quality or even the exact global optimum is required. MIPGO is particularly effective in those applications, as it is the only method that is capable of providing the refinement with theoretical guarantee.

Finally, we would like to remark that the quadratic programming reformulation of penalized least squares with the MCP and SCAD penalty can be further exploited to develop convex approximation, complexity analyses, and solution schemes for finding a local solution. Those will be the future extensions of the presented work herein.

8. Proofs of Theorems 3.2 and 3.4

In this section, we give proofs of Theorems 3.2 and 3.4.

Proof of Theorem 3.2

Recall that 1 denotes an all-ones vector of a proper dimension. The program has a Lagrangian 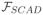given as:

$${\mathbb{F}}_{\mathit{SCAD}}(\beta ,g,h,{\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,\rho ):=\frac{1}{2}[{\beta }^{\top }Q\beta +n(a-1)g^{\top }g+2n{g}^{\top }h]+q^{\top }\beta -na\lambda {\mathbf{1}}^{\top }g+{\gamma }_1^{\top }(\beta -h)-{\gamma }_2^{\top }(\beta +h)+{\gamma }_3^{\top }(-g)+{\gamma }_4^{\top }(g-\lambda \mathbf{1})+{\rho }^{\top }({\mathcal{A}}^{\top }\beta -\mathbf{b}),$$

where ${\gamma }_1:=({\gamma }_{1,i})\in {ℝ}_{+}^d,{\gamma }_2:=({\gamma }_{2,i})\in {ℝ}_{+}^d,{\gamma }_3:=({\gamma }_{3,i})\in {ℝ}_{+}^d,{\gamma }_4:=({\gamma }_{4,i})\in {ℝ}_{+}^d$, and $\rho \in {ℝ}_{+}^m$ are Lagrangian multipliers. The KKT condition yields

$$\{\begin{array}{l}\frac{\partial {\mathbb{F}}_{\mathit{SCAD}}}{\partial \beta }:=Q\beta +q+{\gamma }_1-{\gamma }_2+\mathcal{A}\rho =0\hfill \\ \frac{\partial {\mathbb{F}}_{\mathit{SCAD}}}{\partial h}:=ng-{\gamma }_1-{\gamma }_2=0\hfill \\ \frac{\partial {\mathbb{F}}_{\mathit{SCAD}}}{\partial g}:=n(a-1)g+nh-na\lambda \mathbf{1}-{\gamma }_3+{\gamma }_4=0\hfill \end{array}$$ (8.1)

$$\left\{\begin{array}{l}{\gamma }_{1,i}\ge 0;{\gamma }_{1,i}·({\beta }_i-h_i)=0\hfill \\ {\gamma }_{2,i}\ge 0;{\gamma }_{2,i}·(-{\beta }_i-h_i)=0\hfill \\ {\gamma }_{3,i}\ge 0;{\gamma }_{3,i}·g_i=0\hfill \\ {\gamma }_{4,i}\ge 0;{\gamma }_{4,i}·(g_i-\lambda )=0\hfill \\ \rho \ge 0;{\rho }^{\top }({\mathcal{A}}^{\top }\beta -\mathbf{b})=0,\hfill \end{array}\right\}\forall i=1,\dots ,d$$ (8.2)

Since Λ is non-empty and 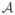is full rank, it is easy to check that the linear independence constraint qualification is satisfied. Therefore, the global solution satisfies the KKT condition. This leads us to an equivalent representation of (2.4) in the form:

$$min\frac{1}{2}[{\beta }^{\top }Q\beta +n(a-1)g^{\top }g+2n{g}^{\top }h]+q^{\top }\beta -na\lambda {\mathbf{1}}^{\top }g,s.t.$$ (8.3)

$$\{\begin{array}{l}\beta \in \mathrm{\Lambda };h\ge \beta ;h\ge -\beta ;0\le g\le \lambda \hfill \\ \text{Constraints}(8.1)-(8.2)\hfill \\ \beta ,g,h,{\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4\in {ℝ}_{+}^d;\rho \in {ℝ}_{+}^m.\hfill \end{array}$$ (8.4)

Then, it suffices to show that (8.3)–(8.4) is equivalent to (3.7)–(3.8).

Notice that the objective function (8.3) is immediately

$$\frac{1}{2}{\beta }^{\top }(Q\beta +q)+\frac{1}{2}{q}^{\top }\beta +\frac{1}{2}{g}^{\top }(n(a-1)g-n\alpha \lambda \mathbf{1}+2nh)-\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g=:I_1$$

Due to equalities (8.1),

$$I_1=\frac{1}{2}{\beta }^{\top }({\gamma }_2-{\gamma }_1)-\frac{1}{2}{\beta }^{\top }\mathcal{A}\rho +\frac{1}{2}{q}^{\top }\beta +\frac{1}{2}{h}^{\top }({\gamma }_1+{\gamma }_2)+\frac{1}{2}{g}^{\top }({\gamma }_3-{\gamma }_4)-\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g$$ (8.5)

Invoking the complementarity conditions in (8.2), we may have

$$I_1=\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g-\frac{1}{2}\lambda {\gamma }_4^{\top }\mathbf{1}.$$ (8.6)

Therefore, Program (8.3)–(8.4) is equivalent to

$$min{I}_1=\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}na\lambda {\mathbf{1}}^{\top }g-\frac{1}{2}\lambda {\gamma }_4^{\top }\mathbf{1}s.t.(8.4),$$ (8.7)

which is immediately the desired result.

Proof of Theorem 3.4

The proof follows a closely similar argument as that for Theorem 3.4. The Lagrangian 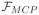of Program (2.6) yields:

$${\mathbb{F}}_{\mathit{MCP}}(\beta ,g,h,{\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,\rho ):=\frac{1}{2}{\beta }^{\top }Q\beta +q^{\top }\beta +n\frac{1}{2a}{g}^{\top }g-n{\left(\frac{1}{a}g-\lambda \mathbf{1}\right)}^{\top }h+{\eta }_1^{\top }(\beta -h)+{\eta }_2^{\top }(-\beta -h)-{\eta }_3^{\top }g+{\eta }_4^{\top }(g-a\lambda \mathbf{1})+{\rho }^{\top }({\mathcal{A}}^{\top }\beta -\mathbf{b})$$ (8.8)

where 1 denotes an all-ones vector of a proper dimension, and where ${\eta }_4\in {ℝ}_{+}^d$ and $\rho \in {ℝ}_{+}^m$ are Lagrangian multipliers. The KKT condition yields

$$\{\begin{array}{l}\frac{\partial {\mathbb{F}}_{\mathit{MCP}}}{\partial \beta }:=q+Q\beta +{\eta }_1-{\eta }_2+\mathcal{A}\rho =0\hfill \\ \frac{\partial {\mathbb{F}}_{\mathit{MCP}}}{\partial g}:=\frac{n}{a}g-\frac{n}{a}h-{\eta }_3+{\eta }_4=0\hfill \\ \frac{\partial {\mathbb{F}}_{\mathit{MCP}}}{\partial h}:=-n(\frac{1}{a}g-\lambda \mathbf{1})-{\eta }_1-{\eta }_2=0\hfill \end{array}$$ (8.9)

$$\{\begin{array}{l}{\eta }_1^{\top }(\beta -h)=0;{\eta }_2^{\top }(-\beta -h)=0\hfill \\ {\eta }_3^{\top }g=0;{\eta }_4^{\top }(g-a\lambda \mathbf{1})=0;{\rho }^{\top }({\mathcal{A}}^{\top }\beta -\mathbf{b})=0\hfill \\ {\eta }_1\ge 0;{\eta }_2\ge 0;{\eta }_3\ge 0;{\eta }_4\ge 0;\rho \ge 0.\hfill \end{array}$$ (8.10)

Since Λ is non-empty and 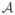is full rank, it is easily verifiable that the linear independence constraint qualification is satisfied. This means the KKT system holds at the global solution. Therefore, Imposing additional constraints (8.9)–(8.10) in program (2.6) will not result in inequivalence. Notice that the object function in (2.6) equals

$$I_2:=\frac{1}{2}{q}^{\top }\beta +(\frac{1}{2}{q}^{\top }+\frac{1}{2}{\beta }^{\top }Q)\beta +\frac{n}{2a}{g}^{\top }(g-h)-\frac{1}{2}n\left(\frac{1}{a}{g}^{\top }-\lambda {\mathbf{1}}^{\top }\right)h+\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h$$ (8.11)

Per (8.9), we obtain

$$I_2=\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{({\eta }_1-{\eta }_2+\mathcal{A}\rho )}^{\top }\beta +\frac{1}{2}{g}^{\top }({\eta }_3-{\eta }_4)+\frac{1}{2}{({\eta }_1+{\eta }_2)}^{\top }h+\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h$$ (8.12)

Further noticing (8.10) we obtain

$$\begin{array}{l}{I}_2=\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho +\frac{1}{2}{g}^{\top }({\eta }_3-{\eta }_4)+\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h\\ =\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}{g}^{\top }{\eta }_4+\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h\\ =\frac{1}{2}{q}^{\top }\beta -\frac{1}{2}{\mathbf{b}}^{\top }\rho -\frac{1}{2}a\lambda {\mathbf{1}}^{\top }{\eta }_4+\frac{1}{2}\lambda n{\mathbf{1}}^{\top }h\end{array}$$

which immediately leads to the desired result.