The evolution of the competition–dispersal trade-off affects α- and β-diversity in a heterogeneous metacommunity

Abstract

Difference in dispersal ability is a key driver of species coexistence in metacommunities. However, the available frameworks for interpreting species diversity patterns in natura often overlook trade-offs and evolutionary constraints associated with dispersal. Here, we build a metacommunity model accounting for dispersal evolution and a competition–dispersal trade-off. Depending on the distribution of carrying capacities among communities, species dispersal values are distributed either around a single strategy (evolutionarily stable strategy, ESS), or around distinct strategies (evolutionary branching, EB). We show that limited dispersal generates spatial aggregation of dispersal traits in ESS and EB scenarios, and that the competition–dispersal trade-off strengthens the pattern in the EB scenario. Importantly, individuals in larger (respectively (resp.) smaller) communities tend to harbour lower (resp. higher) dispersal, especially under the EB scenario. We explore how dispersal evolution affects species diversity patterns by comparing those from our model to the predictions of a neutral metacommunity model. The most marked difference is detected under EB, with distinctive values of both α- and β-diversity (e.g. the dissimilarity in species composition between small and large communities was significantly larger than neutral predictions). We conclude that, from an empirical perspective, jointly assessing community carrying capacity with species dispersal strategies should improve our understanding of diversity patterns in metacommunities.

1. Introduction

Ecological differentiation is considered as a driver of stable coexistence among competing species since the origin of community ecology [1–3]. In this context, resource partitioning plays an important role, but numerous theoretical [4–6] and experimental [7,8] studies have emphasized that trade-offs between local competitive ability and dispersal of species in patchy environments (so-called competition–colonization or competition–dispersal trade-offs) also favour coexistence. Both empirical studies and field surveys suggest that these trade-offs are a distinctive characteristic of communities from many natural systems [9,10], and are sometimes associated with wide variation in dispersal among species belonging to the same community (e.g. [11] for the tree community of Barro Colorado Island). However, whether (and how) they affect patterns of species diversity in natural communities remains debatable [12,13]. One reason is that studies trying to explain such patterns using empirical data on dispersal variation and potential trade-offs with competitiveness remain scarce and focused on simple communities including a few species at best [12,13]. Gathering such data is, indeed, a highly demanding endeavour in complex natural communities.

A less demanding, though more indirect, approach to the role of trade-offs on species diversity patterns is the ‘pattern-to-process’ approach in which these patterns are used to infer the underlying processes, and therefore to distinguish among coexistence theories. However, the theory of species coexistence based on the competition–dispersal trade-off has mostly been developed in terms of ‘patch dynamics' [5,14,15], considering monospecific communities and focusing on species diversity at the ‘metacommunity’ scale only. Such assumptions are far from realistic for most natural systems and prevent studying diversity patterns within sites. The metacommunity framework provides more general models, giving more or less weight to basic processes such as dispersal, demographic stochasticity, or competition (see [15] for a review). In particular, neutral models [16–18] constitute an interesting entry into metacommunity dynamics: they assume ecological equivalence of species [6] and attribute a major role to the balance between demographic stochasticity and dispersal. Importantly, these models yield accurate quantitative descriptions of community structure [19]. An outstanding example is the fit of a neutral model to the rank–abundance diagram of tropical trees in Barro Colorado Island [20]. We suggest here that neutral models could be used for building predictions about the effects of interspecific competition–dispersal trade-offs on diversity patterns, providing a more sophisticated basis than patch-dynamics models for pattern-to-process approaches.

We know of only two studies that assessed the impact of interspecific heterogeneity of dispersal on species diversity patterns by comparing these patterns to neutral predictions. Liu et al. [21] introduced several dispersal levels in an otherwise neutral model. They showed that the rank–abundance diagram of a community could not be used to detect heterogeneous dispersal because this pattern is already very well predicted by a purely neutral model. Janzen et al. [22] showed that using seed-dispersal traits when analysing rank–abundance patterns of tree species in Barro Colorado Island could lead to the rejection of a purely neutral model in favour of an alternative hypothesis involving interspecific dispersal. Both [21] and [22] considered the effect of interspecific heterogeneity of dispersal on community structure through variation in propagule pressure: species with higher dispersal exert a stronger propagule pressure and are therefore better represented locally. However, in such models, dispersal does not trade-off with local competitive ability (assumed to be identical among species): species with higher dispersal always thrive in all communities. The conditions for regional coexistence are unfortunately not considered in these studies which focus on species diversity within communities. Introducing a metacommunity structure in which species can coexist within local communities and a competition–dispersal trade-off in models such as those of [21,22] should allow the study of conditions for the regional coexistence of dispersal strategies as a result of a trade-off with local competition; which is the focus of our study.

Dispersal has a genetic basis in many species [23–25] and can evolve quickly under selection [26,27], suggesting that interspecific variation along a competition–dispersal trade-off should not only be ecologically stable, but also evolutionarily stable, at the metacommunity scale. The evolution of dispersal has been considered in several theoretical studies [28,29], though mostly in single-species metapopulations, especially to explore whether dispersal is stabilized by selection around an evolutionarily stable strategy (ESS), or whether it can diversify towards several strategies (evolutionary branching, EB). We are particularly interested in the latter scenario in which the coexistence among strategies verifies both ecological and evolutionary stability. Several processes can generate EB on dispersal (e.g. spatial and temporal fluctuations of environmental conditions [30–32]). In particular, Massol et al. [33] showed that variation in the strength of kin selection owing to variation in carrying capacity among populations is sufficient to generate disruptive selection on dispersal and EB, without calling for fluctuations. Their model includes both an explicit metapopulation structure and a competition–dispersal trade-off. We upscaled it to metacommunity level which allowed us to explore whether dispersal polymorphism has an effect on diversity within communities and dissimilarity among communities compared with a neutral model without dispersal polymorphism. This extends the current framework for interpreting species distribution to the competition–dispersal coexistence theory.

2. Methods

(a). Model with dispersal evolution (model M₁)

Model M₁ simultaneously describes the evolutionary dynamics of dispersal and the temporal change in species diversity in a metacommunity. Individuals share several attributes: a species label, a dispersal parameter d, the cost of dispersal c, the probability (μ) and magnitude (σ) of mutations on dispersal, and the speciation probability ν. These attributes are real numbers between 0 and 1, except σ which lies between 0 and 0.1. Individuals belong to communities which are described by their carrying capacity K (i.e. the number of individuals they can harbour). The metacommunity is made of N communities which can have different carrying capacities.

Mortality occurs continuously, and dead individuals are immediately replaced through a lottery process. Each death–replacement cycle starts with a ‘death’ event: a randomly chosen individual is removed from the metacommunity. Each individual constantly produces a very large number of propagules normalized to 1 for the lottery. A fraction 1−d of propagules remains in the community and a proportion d is dispersed in the metacommunity, which induces a trade-off between local competition and dispersal. A proportion c of dispersed propagules are lost (dispersal cost). Dispersed propagules have equal chance of reaching all communities, meaning that an individual exports d(1 − c)/N propagules to each community. The model is therefore spatially implicit. A dead individual is replaced by either a local or an imported propagule in proportion to their occurrence (lottery). The new individual has the same dispersal probability as its parent (d) with probability 1 − μ. When mutation occurs (probability μ), the dispersal probability differs from that of the parent by ±σ min (10d, 10(1−d), 1), σ being the maximum amplitude of a mutation. This function was chosen to ensure both (i) a non-biased change in dispersal whatever the value of d and (ii) a mutant dispersal probability within the (0, 1) interval (σ = 0.01 in our simulations). In addition, with probability ν, the new individual belongs to a new species that never occurred before in the metacommunity (i.e. point speciation; see [18]). Speciation has no effect on dispersal and does not interact with the mutation dynamics. A new cycle then starts. Calling 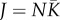the total number of individuals in the metacommunity, the expected lifetime of an individual is J cycles, such that a ‘generation’ can be defined as J cycles.

Following [33] (equations 4 and 5), the mean 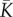, squared coefficient of variation 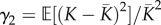, and standardized skewness 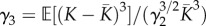of carrying capacity distribution among communities determine whether EB or ESS of dispersal should occur. Here, we studied metacommunities in which communities can harbour only two carrying capacities K₁ and K₂ (K₁ < K₂). We note π₁ the proportion of communities with carrying capacity K₁. We selected two examples of metacommunities (‘symmetric’ and ‘asymmetric’) corresponding to the ESS and EB scenarios on dispersal (table 1 and electronic supplementary material, appendix S1). The symmetric metacommunity is comprised of an equal number of small and large communities (π₁ = 0.5), whereas the asymmetric metacommunity is essentially made of small communities (π₁ = 36/37 ≈ 0.97). These metacommunities display the same 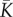and γ₂ values, as well as the same number of communities (N). Keeping 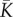and N constant yields the same overall number of individuals in the metacommunity, which implies the same rate of occurrence of new species and the same singular value of dispersal 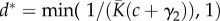in the two metacommunities (i.e. the value at which branching or evolutionary stability may occur, see [33]). We set the mean carrying capacity of communities to 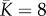and the number of communities in the metacommunity to N = 1 110 (see electronic supplementary material, appendix S1), so that both metacommunities contained J = 8 880 individuals.

Table 1.

Parameters of symmetric and asymmetric metacommunities, corresponding to the evolutionary predictions and summary statistics of simulations. The two metacommunities verify: 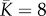and γ₂ = 9/16 ≈ 0.56, N = 1 110 patches. π₁ represents the proportion of patches with carrying capacity K₁. In both cases, other parameters are set to: μ = 0.01, σ = 0.01, ν = 10⁻⁴, c = 0.1. ESS, evolutionary stable strategy; EB, evolutionary branching.

metacommunity		symmetric	asymmetric
distribution of carrying capacities	K1	2	7
	K2	14	44
	π1	0.5	36/37≈0.97
prediction on dispersal evolution		ESS	EB

At the beginning of the first cycle, all individuals harboured the same dispersal value set to the singular value d*. Species identities were attributed using the urn sampling scheme developed for the neutral model of species diversity with multiple communities [34]. In both cases, mutation and speciation parameters were set to: μ = 0.01, σ = 0.01, ν = 10⁻⁴. These parameters were chosen so as to (i) remain close to the assumption of adaptive dynamics (limiting the rate and size of mutations of dispersal), (ii) ensure evolutionary dynamics that are fast enough to exhibit the outcomes of interest with simulations of tractable length and size, and (iii) keep a separation of timescales between speciation and mutation processes. We explored three values of dispersal cost (c = 0, 0.1, and 0.5). As the results were qualitatively similar, we only reported results for c = 0.1 in the main text (full results are in the electronic supplementary material, appendix).

For both symmetric and asymmetric metacommunities, 100 independent simulations were run over 20 000 generations (ca 1.77 × 10⁸ death–replacement cycles), a value large enough to reach a stationary dispersal distribution. Simulations were run using the Java programming language (source code doi:10.6084/m9.figshare.3145831).

(b). Neutral model (model M₀)

Model M₀ is a particular case of model M₁ in which all individuals from the metacommunity display the same dispersal value and dispersal does not evolve (i.e. μ = 0). M₀ is thus a neutral model in which individual dispersal is explicitly described. Expected patterns of species diversity can be derived analytically in this model using a coalescent approach (inspired by [35]; electronic supplementary material, appendix S4).

(c). Trait and species diversity patterns

We explored the spatial structure of the dispersal parameter in the final state of simulations produced by model M₁ using T-statistics [36], a tool to decompose the metacommunity-wide variance of dispersal into the relative contributions of several levels of organization: individual (I), community (C), and metacommunity (R, for regional). We focused on T_IC/IR, the proportion of dispersal variance at metacommunity level explained by the variation of individual dispersal within communities. Low T_IC/IR means that individuals from a community tend to be similar, which we call dispersal clumpiness. We tested whether T_IC/IR is lower than expected for two null models using a randomization procedure. First, we preserved the species label and dispersal value of individuals, but permuted their community identity among communities (keeping community size constant). Under the second model, we permuted dispersal values among species but preserved the occurrence and relative abundances of species in communities. In this second test, we overlooked intraspecific variation by first attributing to individuals the average metacommunity trait value of their species. Randomization proceeded such that individuals from species A were attributed the trait from species B, etc. The mean observed T_IC/IR values in the 100 replicated simulations was compared with the mean of the null distribution, obtained by applying the randomization procedure to each simulation output and re-computing T_IC/IR.

When comparing predictions from models M₀ and M₁ in terms of species diversity patterns, we focused on measures of (i) diversity within communities (α-diversity), (ii) differentiation among communities (β-diversity), and (iii) diversity at metacommunity scale (γ-diversity). We defined D_α(K_i) as the probability that two individuals sampled in the same community with carrying capacity K_i belong to different species. D_α(K_i) is a standard index of diversity usually called the Simpson index [37]. To evaluate the differentiation between community pairs, we used D_β(K_i, K_j) defined as the probability that two individuals drawn from distinct communities with carrying capacities K_i and K_j belong to different species. D_γ, defined as the probability that two individuals randomly sampled in the metacommunity belong to different species, was used at the metacommunity scale.

3. Results

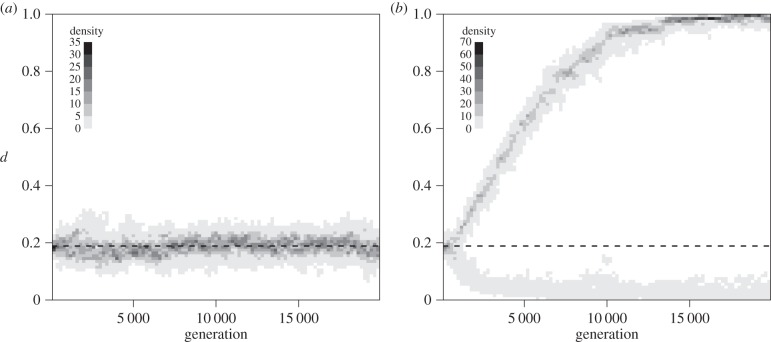
When allowing dispersal to evolve (model M₁), our simulations corroborated the theoretical predictions of adaptive dynamics (figure 1). In the symmetric metacommunity (metacommunity 1), variation in dispersal remained concentrated around d*, in agreement with the ESS prediction. In the asymmetric metacommunity (metacommunity 2), two distinct values emerged owing to the evolutionary dynamics, in agreement with the EB prediction. The difference between these dispersal values decreased with the dispersal cost c (electronic supplementary material, appendix S2 and figure A2.1) and increased with the square coefficient of the variation in carrying capacity (γ₂; electronic supplementary material, appendix S2 and figure A2.2). Following species composition of the asymmetric metacommunity over time during and after dispersal branching (figure 2) further showed that (i) species that appeared before branching could persist in both branches long after branching, but ultimately went extinct because of speciation and demographic stochasticity and (ii) species that appeared after branching stayed in their original branch. No species was present in both evolutionary branches at the end of 95 of our 100 replicates; it is therefore possible to characterize ‘dweller’ and ‘drifter’ species, harbouring low and high dispersal values, respectively. The situation is very different under the ESS scenario in which, by definition, all species had similar dispersal values at all time.

Figure 1.

Examples of dispersal distributions through time in model M₁ for symmetric (a) and asymmetric metacommunity (b) respectively (see table 1 for metacommunity features). One simulation run is represented in each panel. The grey shades refer to individuals' density when all species are pooled together (null in the white areas). Time is given in generation numbers. Parameters describing dispersal evolution are μ = 0.01 and σ = 0.01, and the cost of dispersal is c = 0.1.

Figure 2.

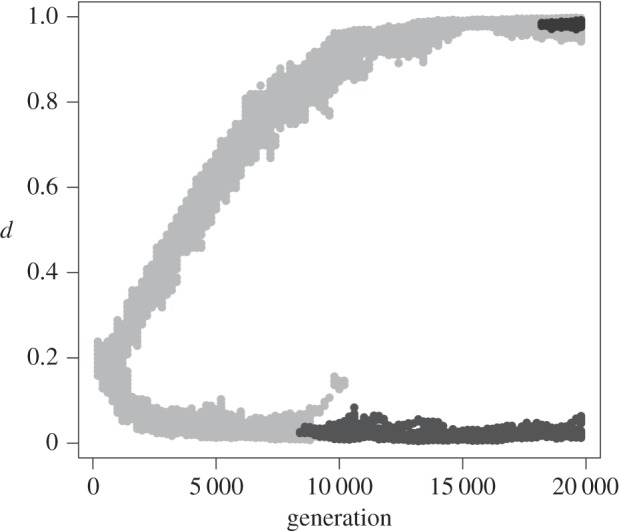
Monitoring of dispersal in three species from the asymmetric metacommunity during the simulation presented in figure 1b (out of 506 species observed over the whole simulation). Each species is represented by a shade of grey. A grey dot is drawn at (d, t) if an individual of the considered species with trait d occurs in the community at generation t. The species in light grey is initially present before branching and persists after branching, but goes extinct in the lower branch. The other two species appear after branching through speciation, in a single branch.

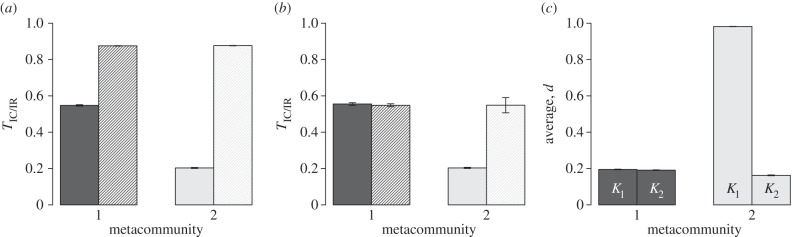
The proportion of variance of dispersal among individuals within communities was significantly lower than expected under a random permutation of individual position (i.e. T_IC/IR was significantly lower than random expectation using the first randomization procedure; figure 3a), especially in the asymmetric metacommunity. When permuting species traits while preserving their abundance in each community (figure 3b), T_IC/IR under the ESS scenario was not significantly different from the randomized value while a significantly lower value was observed under the EB scenario. We further observed that the average dispersal was significantly larger in communities with small carrying capacity than in those with large carrying capacity in the two metacommunities (figure 3c), a pattern that we call the ‘carrying capacity–dispersal relationship’ below. Electronic supplementary material, appendix S3 provides an analytical argument to explain the emergence of this pattern. The carrying capacity–dispersal relationship was much less pronounced in the symmetric metacommunity (ESS) than in the asymmetric one (EB). All these results are robust to variation in the dispersal cost (electronic supplementary material, appendix S3 and figures A3.1 and A3.2).

Figure 3.

Analysis of dispersal pattern in symmetric (1) and asymmetric (2) metacommunities. (a) Testing T_IC/IR using full permutation of individual positions. Bars represent observed (plain bars) and randomized values (striped bars) of T_IC/IR at generation 20 000 averaged over 100 independent simulations. Results for both metacommunity 1 (dark grey bar) and 2 (light grey bar) are shown. For each bar, a 95% CI based on central limit theorem is provided. (b) Similar to panel (a), but overlooking intraspecific variability and permuting only species dispersal values. (c) Average dispersal value in small (bars labelled ‘K₁’) and large (bars labelled ‘K₂’) communities for metacommunity 1 (dark grey) and 2 (light grey). 95% CI of these average value based on central limit theorem approximation are reported for each bar. Testing whether mean dispersal was higher in small communities yielded that the observed difference is statistically significant in both metacommunitites (test based on the central-limit theorem normal approximation; p = 0.0001 in metacommunity 1, p < 10⁻¹² in metacommunity 2).

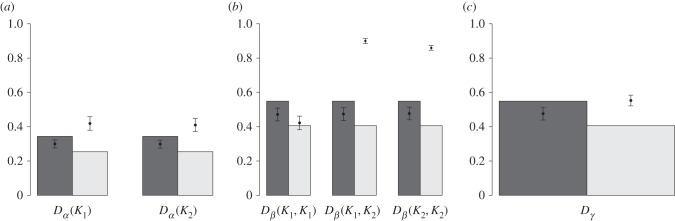
Under the ESS scenario, all species harboured similar dispersal strategies, and the carrying capacity–dispersal relationship was weak (but still significant). We therefore expected species diversity patterns (D_α, D_β, and D_γ) to closely match the predictions of our neutral model M₀. Under the EB scenario, dweller and drifter species emerged, as well as a strong carrying capacity–dispersal relationship. We therefore expected species diversity patterns to strongly deviate from model M₀ predictions. In particular, we expected a higher D_β(K₁, K₂) than in model M₀, because small communities are occupied by drifter species, whereas large communities are occupied by dweller species. We derived analytical expressions of D_α(K_i), D_β(K_i, K_j), and D_γ in model M₀ (electronic supplementary material, appendix S4) which were validated using simulations (electronic supplementary material, figure A4.2). D_α(K_i) and D_β(K_i, K_j) depend on the dispersal rate (d*), the dispersal cost (c), the speciation rate (ν) and the mean, variance and asymmetry of the distribution of the carrying capacities across the metacommunity, but not on the carrying capacities K_i and K_j. Higher asymmetry of the distribution always had a negative impact on D_α, D_β, and D_γ (electronic supplementary material, figure A4.3). In the examples considered here, in which the coefficient of variation was kept constant but asymmetry varied, the neutral diversity at community (D_α) and metacommunity levels (D_γ) as well as the dissimilarity among communities (D_β) in the symmetric metacommunity were thus predicted to be higher than in the asymmetric metacommunity (figure 4).

Figure 4.

Estimates and 95% CI of D_α (a), D_β (b), and D_γ (c) in the symmetric and asymmetric metacommunities obtained from model M₁ simulations compared with neutral predictions. Grey bars provide the analytical predictions of the neutral model M₀ with d = d* (computed from the left column of electronic supplementary material, table A4.3) for symmetric (dark grey) and asymmetric (light grey) metacommunities. Simulation parameters are given in table 1. A point is associated with each grey bar, which represents the average estimate value obtained from 100 independent simulations of model M₁. A 95% CI of the expected diversity/dissimilarity value under model M₁ is reported around each point.

We computed the unbiased 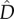estimates (defined in electronic supplementary material, appendix S5) of D_α(K₁), D_α(K₂), D_β(K₁, K₁), D_β(K₁, K₂), D_β(K₂, K₂), and D_γ from our simulations of model M₁ and compared them with the analytical predictions of M₀ (figure 4). In the symmetric metacommunity (dispersal ESS), 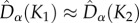, and 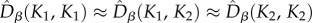, in line with neutral predictions. However, all 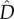estimates were lower than the neutral predictions. In the asymmetric metacommunity (EB; figure 4), the 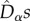were also similar between small and large communities, in line with the predictions of model M₀, but this time larger than the neutral expectations. 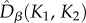and 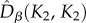were, as expected, higher than the neutral expectations. These deviations from the neutral predictions of both 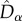and 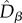resulted in a larger 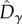than predicted by the neutral model (figure 4). Note also that 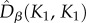and 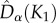were very similar in the asymmetric metacommunity (figure 4), indicating that, when sampling two individuals in small communities, the probability of getting two different species did not depend on whether individuals were drawn from the same or from different communities. These results were robust to changing the dispersal cost (electronic supplementary material, appendix S5, figures A5.1 and A5.2).

4. Discussion

(a). Dispersal in metacommunities

We built a metacommunity model including dispersal evolution which reproduces the central result obtained by Massol et al. [33] at the metapopulation scale: increasing asymmetry in the distribution of carrying capacities generates variance in the strength of kin competition among communities, which triggers evolutionary branching and the emergence of distinct dispersal strategies in the metacommunity. We could therefore compare an ESS scenario in which individual dispersal shows little variation around a single value (symmetric metacommunity) and an EB scenario in which dispersal is distributed around two distinct levels (asymmetric metacommunity).

Our analysis of dispersal distribution within and among communities showed that under both scenarios, a negative carrying capacity–dispersal relationship emerges. This pattern stems from the three following effects. First, all communities have similar immigrant pool compositions, because dispersal is not limited by distance in our model. Second, in small communities, the temporal dynamics of average species abundances in these small communities are mostly driven by immigration, and are similar to those of the immigrant pool. Third, the deterministic local competition effect dominates in large communities, which induces a shift of relative abundances towards the dominance of low dispersers and the extinction of high dispersers (i.e. competitive exclusion).

The carrying capacity–dispersal relationship echoes several observations on within-species dispersal polymorphism in natural metapopulations. For example, a majority of migrants originates from small ephemeral patches, rather than from large patches, in a rock pool metapopulation of the cladoceran Daphnia magna [38]. However, a competition–dispersal trade-off may not be the only driver of such patterns in natural metapopulations as variation in both age (when extinctions occur) and connectivity of populations play an important role in the distribution of dispersal phenotypes among populations [39]. Whether the carrying capacity–dispersal relationship occurs at the interspecific level in natural metacommunities is less documented to date. Our work predicts that species occurring preferentially in communities with large (resp. small) carrying capacities should be dwellers (resp. drifters). A comparison of traits assumed to be good proxies of dispersal, such as dispersal attributes of seeds in plant communities (see [40] for an example in grassland communities) might be a first approach to test this prediction. More refined statistical approaches based on dispersal kernel estimation [11,41] is a further possibility. A combination of genetic and demographic data collected in several species might also return relevant information on dispersal, as already done in metapopulations of single species [42].

A strong carrying capacity–dispersal relationship (like in the EB scenario) has potential to generate dispersal clumpiness, as small (resp. large) communities tend to harbour more drifters (resp. dwellers) than expected under random permutations of individuals in space. However, dispersal clumpiness can emerge even in the absence of strong carrying capacity–dispersal relationship as exemplified in the ESS scenario. This stems from the fact that when dispersal is limited, individuals which are in the same community tend to be more closely related than individuals randomly sampled at the metacommunity scale. This generates clumpiness of both species [43] and values of heritable traits, which in turn yields a lower T_IC/IR than expected when permuting individuals across the metacommunity. Interestingly, this should caution against interpreting all significantly low T_IC/IR as signals of some kind of ‘environmental filtering’ associated with the considered trait (as suggested by Violle et al. [36]) when using a null model randomizing individual position in space. By contrast, our second randomizing procedure (permuting average species trait only) exhibits two properties addressing the above-described limits: it preserves the variation of species abundance among communities and it removes the effects of increased relatedness within populations by considering average species traits. Under the ESS scenario, the variance within communities was not significantly lower than the one expected under the null model, which corroborates the idea that the significantly low T_IC/IR observed when randomizing individual positions is mostly due to the effect of limited dispersal and not to dispersal polymorphism (which is limited in this case). Under the EB scenario, the dispersal strategies were still significantly more similar within communities than predicted by the null model. Permuting average species traits can therefore be used to disentangle the effects of limited dispersal on spatial patterns of dispersal (null model not rejected) from those of dispersal polymorphism (null model rejected), and should be preferred to permuting individual positions whenever limited dispersal is thought to play a role in diversity patterns.

(b). Neutral predictions on species diversity patterns

Our neutral model makes two important predictions about species diversity patterns. First, α- and β-diversity should not vary (in expectation) among communities with different carrying capacities. In several neutral metacommunity models, Simpson diversity (used here) can vary among patches [44,45]. However, this variation is mostly explained by differences in connectivity (i.e. the number of immigrants per generation) among patches induced by specific network structures. As we were primarily interested in the relationship between the evolutionary dynamics of dispersal and diversity patterns, we focused on a simple spatial structure in which connectivity is similar between all patches, irrespective of their carrying capacity, a situation for which we could derive evolutionary predictions. Our model might be extended to more complex community networks in which the neutral expectations have already been derived and that better describe the spatial structure of some real metacommunities, such as dendritic networks for rivers [46,47]. The limiting step here would be to derive eco-evolutionary predictions about dispersal polymorphism in complex networks with variable connectivity among patches, a point that has been little explored up to now [48].

Second, our neutral model predicts that species γ-diversity should decrease with the asymmetry of the carrying capacity distribution in the metacommunity. This can be intuitively explained by the fact that, in more asymmetric metacommunities, drift is stronger, because more individuals belong to small communities. Here, we focused on the prediction about asymmetry as it is the feature of carrying capacity distribution that discriminates dispersal evolution scenarios [33]. Yet, the analytical results derived from our neutral model may allow a more comprehensive exploration of the effects of carrying capacity distribution on species γ-diversity (electronic supplementary material, figure A4.3) and thus contribute to current research in conservation biology, in particular with respect to reserve design [49]. However, this is beyond the scope of this work.

In the two examples of metacommunities considered in our study, we derived neutral predictions about diversity patterns with a priori knowledge of the relevant parameters (carrying capacities and dispersal cost). However, it may not be straightforward to obtain these parameters in natural systems. One alternative would be to fit the neutral model to observed diversity patterns in order to estimate their most likely values. The sampling formulae that have been derived for classic neutral models considering spatially implicit metacommunities allow computing maximum-likelihood estimates [34,50,51]. Such a formula is not available for our model, but the carrying capacities of communities and the dispersal cost could be estimated by looking for values that yield predictions about expected diversity and dissimilarity that best fit the observed diversity and dissimilarity estimates (e.g. using a least-squares approach).

(c). Effects of dispersal polymorphism on species diversity

Our neutral predictions (model M₀) incorporate the influence of speciation, drift, and limited dispersal. Comparing the neutral predictions of species diversity patterns with model M₁, in which dispersal can evolve, reveals the additional effects (i) of mutational variance around the selective optima in the ESS scenario and (ii) of disruptive selection of dispersal in the EB scenario. To the best our knowledge, our study is the first to suggest studying the effects of a competition–dispersal trade-off as an evolutionarily driven deviation from the neutral theory of metacommunity assembly.

In the ESS scenario (symmetric metacommunity), both the diversity within communities and the dissimilarity among communities do not depend on carrying capacity, which is consistent with the neutral predictions. This was rather expected as species are distributed around the same dispersal value, with some variation owing to mutation, leading to metacommunity dynamics close to neutrality. However, lower diversity and lower dissimilarity than expected under a neutral model suggest that the mutational variance of dispersal generates fitness differences among individuals, which scale up to a slight fitness heterogeneity among species. Slightly maladapted species are more quickly eliminated than expected under the neutral model which yields a lower diversity at the metacommunity scale and consequently decreases both the diversity within communities and the dissimilarity among communities. More generally, our results suggest that when there is a unique selective optimum on a given trait (i.e. stabilizing selection), neutral models which overlook intra- and interspecific variance in this trait may overestimate species diversity.

Under EB, the following general picture of the metacommunity emerged: (i) each large community harbours a mostly endemic community of species that are good local competitors but nearly never disperse (dwellers) and (ii) drifter species freely disperse across the metacommunity, dominating small communities and maintaining themselves at low frequency through mass effect in large communities although they are locally outcompeted by dwellers. From point (i) derives the higher dissimilarity among large communities than expected under the neutral model. Point (ii) explains why the diversity of small communities equals the dissimilarity among small communities. The mass effect of drifters in large communities explains why diversity/dissimilarity in small communities (D_α(K₁)) matches the diversity observed in a single large community (D_α(K₂)) although the former includes many more individuals. We also emphasize that, when EB occurs, both α- and β-diversities are higher than predicted by the neutral model. Dispersal polymorphism increases the species coexistence potential at the metacommunity scale.

Our work suggests that the study of diversity patterns in metacommunities would greatly benefit from documenting dispersal traits of species, so as to identify dwellers and drifters. This point was previously made by Janzen et al. [22] in their study of the Barro Colorado tropical tree community: they concluded from combining local abundances of species with seed dispersal traits that immigration was stronger for biotically dispersed tree species (which would therefore be drifters) than for abiotically dispersed ones (which would therefore be dwellers). Importantly enough, biotically dispersed species are dominant in Barro Colorado Island. This point cannot be discussed in the Janzen et al. framework, as dispersal does not trade-off with any other features (it is a structural property of their model that drifters dominate in any community). By contrast, our model suggests a biological interpretation of drifters' dominance: the carrying capacity of Barro Colorado Island may be too small to let dwellers reach large enough population sizes to durably settle and counterbalance the immigration of drifters.

Beyond analysing a single community, testing whether small communities (i) have more similar species composition than they have with large communities and (ii) harbour species with higher dispersal abilities than large communities may reveal that a competition–dispersal trade-off affects species coexistence at the metacommunity scale. In addition, the EB scenario of our model illustrates how considering dispersal may contribute to avoid misinterpreting species diversity patterns. First, dweller species are abundant in one or a few large communities and absent elsewhere, but this is not due to local environmental filtering or adaptation. Dwellers should here show the same fitness in all communities, irrespective of size. Second, large communities simultaneously harbour dwellers and drifters the relative abundances of which fluctuate around stable values in time (results not shown), and this is not due to some local coexistence mechanisms but rather to mass effect from the metacommunity.

5. Conclusion

To the best of our knowledge, our study proposes the first theoretical model integrating dispersal evolution in a multi-species context and deriving predictions about species diversity patterns. Interestingly, it includes three of the four paradigms of metacommunity assembly identified by Leibold et al. [15]: it simultaneously borrows from (i) the ‘patch-dynamics' view by considering a competition–dispersal trade-off as a coexistence mechanism, (ii) the ‘mass-effect’ view as drifter species can persist in patches owing to immigration, although they are less fit locally, and (iii) the neutral view as species diversity in the metacommunity ultimately stems from an equilibrium between speciation and stochastic extinction. Our approach should now be extended to other traits contributing to the local adaptation of species in patches with heterogeneous environmental conditions (see [52]) but keeping the focus on the evolutionary and ecological significance of the considered polymorphisms, as we did here with dispersal. This would integrate the fourth metacommunity paradigm, species sorting [15], and might pave the way to a unified framework for pattern-based approaches of metacommunity assembly processes.

Authors' contributions

F.L., P.J., and F.M. built the project. F.M. performed the analysis of dispersal evolution. T.P. ran the simulations. F.L. derived the neutral predictions and analysed the simulations. F.L., P.J., and F.M. wrote the paper.

Competing interests

The authors declare no competing interest.

Funding

F.L. was supported by fellowships from AgroParistech, the Agropolis foundation and the Swedish University of Agricultural Science, and by money from IRSTEA. T.P. was supported by a fellowship from the Université de Montpellier. This work was supported by money from CNRS to P.J. and F.M., and from the French ANR (AFFAIRS project in the BIOADAPT programme–P.I.: Dr P. David—grant no. 12-ADAP-005; ARSENIC project—P.I.: Dr F. Massol—grant no. 14-CE02-0012).