Combining tumor genome simulation with crowdsourcing to benchmark somatic single-nucleotide-variant detection

Abstract

The detection of somatic mutations from cancer genome sequences is key to understanding the genetic basis of disease progression, patient survival and response to therapy. Benchmarking is needed for tool assessment and improvement but is complicated by a lack of gold standards, by extensive resource requirements and by difficulties in sharing personal genomic information. To resolve these issues, we launched the ICGC-TCGA DREAM Somatic Mutation Calling Challenge, a crowdsourced benchmark of somatic mutation detection algorithms. Here we report the BAMSurgeon tool for simulating cancer genomes and the results of 248 analyses of three in silico tumors created with it. Different algorithms exhibit characteristic error profiles, and, intriguingly, false positives show a trinucleotide profile very similar to one found in human tumors. Although the three simulated tumors differ in sequence contamination (deviation from normal cell sequence) and in subclonality, an ensemble of pipelines outperforms the best individual pipeline in all cases. BAMSurgeon is available at https://github.com/adamewing/bamsurgeon/.

Declining costs of high-throughput sequencing are transforming our understanding of cancer^1–3 and facilitating delivery of targeted treatment regimens^4–6. Although new methods for detecting cancer variants are rapidly emerging, their outputs are highly divergent. For example, four major genome centers predicted single-nucleotide variants (SNVs) for The Cancer Genome Atlas (TCGA) lung cancer samples, but only 31.0% (1,667/5,380) of SNVs were identified by all four⁷. Calling somatic variants is a harder problem than calling germline variants⁸ because of variability in the number of somatic mutations, extent of tumor subclonality and effects of copy-number aberrations.

Benchmarking somatic variant detection algorithms has been challenging for several reasons. First, benchmarking is resource intensive; it can take weeks to install and hundreds of CPU-hours to execute an algorithm. Second, evolving technologies and software make it difficult to keep a benchmark up to date. For example, the widely used Genome Analysis Toolkit was updated five times in 2013. Third, establishing gold standards is challenging. Validation data may be obtained on independent technology or from higher-depth sequencing, but routines used to estimate ‘ground truth’ may exhibit sources of error similar to those of the algorithms being assessed (for example, alignment artifacts). Privacy controls associated with personal health information hinder data sharing. Further, most research has focused on coding aberrations, restricting validation to <2% of the genome. Fourth, sequencing error profiles can vary between and within sequencing centers⁹. Finally, most variant-calling algorithms are highly parameterized. Benchmarkers may not have equal and high proficiency in optimizing each tool.

To identify the most accurate methods for calling somatic mutations in cancer genomes, we launched the International Cancer Genome Consortium (ICGC)-TCGA Dialogue for Reverse Engineering Assessments and Methods (DREAM) Somatic Mutation Calling Challenge (“the SMC-DNA Challenge”)¹⁰. The challenge structure allowed us to perform an unbiased evaluation of different approaches and distribute the process of running and tuning algorithms by crowdsourcing. To create tight feedback loops between prediction and evaluation, we generated three subchallenges, each based on a different simulated tumor-normal pair with a completely known mutation profile and termed IS1, IS2 and IS3 (Supplementary Note 1 and Supplementary Fig. 1). To produce these large-scale benchmarks, we first developed BAMSurgeon, a tool for accurate tumor genome simulation^11–14.

Our analyses of error profiles revealed characteristics associated with accuracy that could be exploited in algorithm development. Strikingly, many algorithms, including top performers, exhibit a characteristic false positive pattern, possibly owing to introduction of deamination artifacts during library preparation. We also found that an ensemble of several methods outperforms any single tool, suggesting a strategy for future method development.

RESULTS

Generating synthetic tumors with BAMSurgeon

Defining a gold standard for somatic mutation detection is fraught with challenges: no tumor genome has been completely characterized (i.e., with all real somatic mutations known); thus, estimates of precision and recall are subject to the biases of site-by-site validation. False negatives are particularly difficult to study without a ground truth of known mutations. Typically, validation involves targeted capture followed by sequencing, sometimes on the same platform. To address the lack of fully characterized tumor genomes, simulation approaches are often used. Existing approaches to create synthetically mutated genomes simulate reads and their error profiles either de novo on the basis of a reference genome¹⁵ (https://github.com/lh3/wgsim/) or through admixture of polymorphic (for example, dbSNP) sites between existing BAM sequence alignment files¹⁶. In the first approach, simulated reads can only approximate sequencing error profiles, which vary between and within sequencing centers, and it is challenging to add mutations at multiple user-specified variant allele frequencies (VAFs) to simulate subclones. In the second, platform-specific error profiles are accurate, but the repertoire of spiked-in mutations is limited to examples detected previously, and thus already known to be discoverable. An overview of these approaches is in Supplementary Note 2.

BAMSurgeon represents a third approach: directly adding synthetic mutations to existing reads (Fig. 1a). BAMSurgeon can add mutations to any alignment stored in BAM format, including RNA-seq and exome data. It can generate mutations at any allelic fraction, allowing simulation of multiple subclones or sample contamination; can avoid making mutations incongruent with existing haplotypes; and supports copy-number variation–aware addition of mutations if copy-number information is available. In addition, BAMSurgeon supports an increasing number of alignment methods, allowing testing of aligner-caller combinations on the same mutations.

Figure 1.

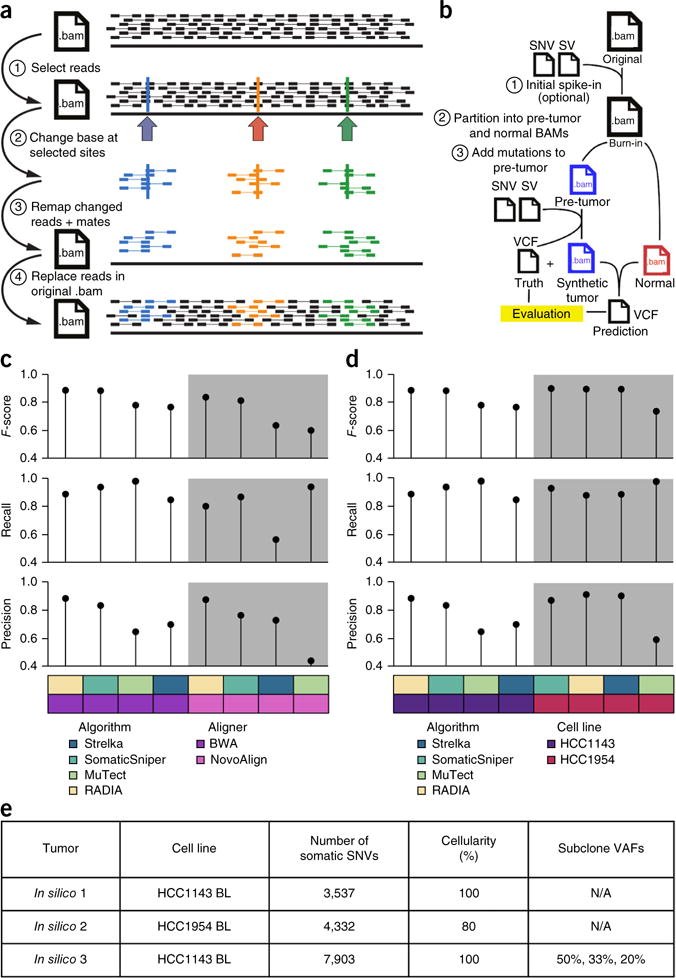
BAMSurgeon simulates tumor genome sequences. (a) Overview of SNV spike-in. (1) A list of positions is selected in a BAM alignment. (2) The desired base change is made at a user-specified variant allele fraction (VAF) in reads overlapping the chosen positions. (3) Altered reads are remapped to the reference genome. (4) Realigned reads replace corresponding unmodified reads in the original BAM. (b) Overview of workflow for creating synthetic tumor-normal pairs. Starting with a high-depth mate-pair BAM alignment, SNVs and structural variants (SVs) are spiked in to yield a ‘burn-in’ BAM. Paired reads from this BAM are randomly partitioned into a normal BAM and a pre-tumor BAM that receives spike-ins via BAMSurgeon to yield the synthetic tumor and a ‘truth’ VCF file containing spiked-in positions. Mutation predictions are evaluated against this ground truth. (c,d) To test the robustness of BAMSurgeon with respect to changes in aligner (c) and cell line (d), we compared the rank of RADIA, MuTect, SomaticSniper and Strelka on two new tumor-normal data sets: one with an alternative aligner, NovoAlign, and the other on an alternative cell line, HCC1954. RADIA and SomaticSniper retained the top two positions, whereas MuTect and Strelka remained third and fourth, independently of aligner and cell line. (e) Summary of the three in silico tumors described here.

Briefly, the software works by selecting sites using coverage information from the target BAM file. Mutations are spiked in by modifying reads covering the selected sites, realigning a requisite number to achieve the desired alternate allele fraction, and merging the reads back into the original BAM by replacement. Realistic tumors are created (Fig. 1b) by partitioning a high-depth BAM, optionally with ‘burn-in’ mutations to differentiate it from the original BAM, into two disjoint subset BAMs. One receives the spike-in mutations to become the simulated tumor; the other is left intact and is the matched normal. The result is a synthetic tumor-normal pair and a VCF file of true positives (TPs). BAMSurgeon is open source and highly parameterized, thereby allowing fine-tuning of characteristics such as tumor purity, subclone number and coverage thresholds.

To demonstrate BAMSurgeon’s utility, we performed a series of quality-control studies. First, we took the sequence of the HCC1143 BL cell line and created two separate synthetic tumor-normal pairs, each using the same set of spiked-in mutations but with different random read splitting. We executed four widely used, publicly available mutation callers on each pair: MuTect¹⁶, RADIA (RNA and DNA integrated analysis)¹⁷, Strelka¹⁸ and SomaticSniper¹⁹. We assessed performance on the basis of recall (fraction of spiked-in mutations detected), precision (fraction of predicted SNVs that are true) and F-score (harmonic mean of precision and recall). Ordering and error profiles were largely independent of read splits: RADIA and SomaticSniper retained first and second place, whereas MuTect and Strelka were third and fourth (Supplementary Fig. 2). Second, we generated alignments of HCC1143 using the Burrows-Wheeler Aligner (BWA) and NovoAlign with and without insertion or deletion (indel) realignment. Caller ordering was largely independent of aligner used (Fig. 1c). Finally, we tested whether BAMSurgeon results are influenced by genomic background by taking the same set of mutations and spiking them into both HCC1143 and HCC1954 BWA-aligned BAMs. Caller ordering was largely independent of cell line (Fig. 1d).

The ICGC-TCGA DREAM Somatic Mutation Calling Challenge

To maximize participation, we began with three synthetic genomes each generated by applying BAMSurgeon to an already-sequenced tumor cell line, thereby avoiding data access issues associated with patient-derived genomes. The tumors varied in complexity, with IS1 being the simplest and IS3 being the most complex. IS1 had a moderate mutation rate (3,537 somatic SNVs), 100% tumor cellularity and no subclonality. In contrast, IS3 had a higher mutation rate (7,903 somatic SNVs) and three subpopulations present at different VAFs. Tumor and normal samples had ~450 million 2-by-101-bp paired-end reads produced by an Illumina HiSeq 2000 sequencer, resulting in ~30× average coverage (Fig. 1e and Supplementary Table 1). Sequences were distributed via the GeneTorrent client from Annai Systems. As a supplement to local computing resources, participants were provided cost-free access to the Google Cloud Platform, where Google Cloud Storage hosted the data and the Google Compute Engine enabled scalable computing. Contestants registered for the SMC-DNA Challenge and submitted predicted mutations in VCF format through the Synapse platform²⁰ (https://www.synapse.org/#!Synapse:syn312572/). Multiple entries were allowed per team, and all scores were displayed on public, real-time leaderboards (Supplementary Table 1). To assess overfitting, we excluded a fraction of each genome from leaderboard scores during the challenge.

Over 157 d, we received 248 submissions from 21 teams, as well as 21 submissions by the SMC-DNA Challenge administration team to prepopulate leaderboards. A list of all submissions, along with a description of the pipeline used in each, is in Supplementary Table 2 and the Supplementary Data 1. The set of all submissions shows clear precision-recall trade-offs (Fig. 2a and Supplementary Fig. 3) and distinctions amongst top-performing teams. Performance metrics varied substantially across submissions: for the simplest tumor, IS1, recall ranged from 0.559 to 0.994, precision from 0.101 to 0.997 and F-score from 0.046 to 0.975.

Figure 2.

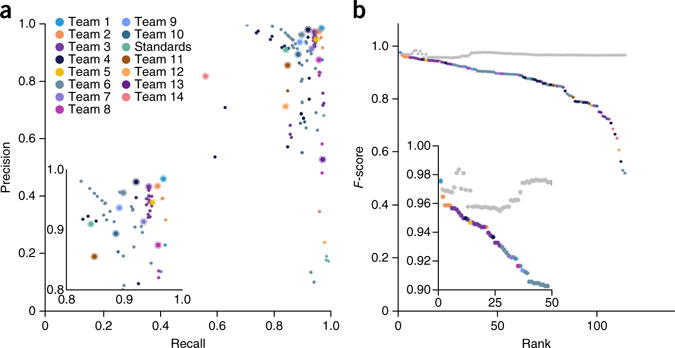
Overview of the SMC-DNA Challenge data set. (a) Precision-recall plot for all IS1 entries. Colors represent individual teams, and the best submission (top F-score) from each team is circled. The inset highlights top-ranking submissions. (b) Performance of an ensemble somatic SNV predictor. The ensemble was generated by taking the majority vote of calls made by a subset of the top-performing IS1 submissions. At each rank k, the gray dot indicates performance of the ensemble algorithms ranking 1 to k, and the colored dot indicates the performance of the algorithm at that rank.

We then used the “wisdom of the crowds”^12,13 by aggregating predictions into an ensemble classifier. We calculated consensus SNV predictions by majority vote (TP or false positive, FP) at each position across the top k submissions. For IS1, consensus predictions were comparable to those of the best-performing teams (F-score = 0.955–0.984; Fig. 2b). The consensus achieved high precision (range: 0.968–0.999; Supplementary Fig. 4a) while maintaining recall (range: 0.939–0.971; Supplementary Fig. 4b). To assess robustness we evaluated the majority vote predictions of randomly selected sets of submissions. The consensus classifier improved and stabilized as submissions were added (Supplementary Fig. 5). Consensus classifiers for IS2 and IS3 outperformed the best method and showed stable performance (Supplementary Figs. 3 and 4).

Effects of parameterization

The within-team variability caused by version and parameter changes was often comparable to that across different teams: 25.6% of variance in IS1 occurred within teams. Critically, this does not reflect overfitting: a team’s best submission yielded nearly identical performance on the leaderboard and held-out data (for IS1 the median difference was −1.87 × 10⁻³, ranging from −0.091 to 0.032; Supplementary Fig. 6). F-scores were tightly correlated between training and testing data sets (Spearman’s rank correlation coefficient (ρ) = 0.98 for all three tumors; Fig. 3a), as were precision and recall (Supplementary Fig. 7). The large variability in accuracy of submissions within a single team highlights the very strong impact of tuning parameters during the challenge. Initial submissions by a team (Fig. 3b) tended to achieve a favorable recall with an unsatisfactory precision. The median team improved its F-score from 0.64 to 0.91 (range of improvement: 0.18–0.98) by exploiting leader-board feedback. Similar results were observed for IS2 and IS3 (Supplementary Figs. 6 and 7).

Figure 3.

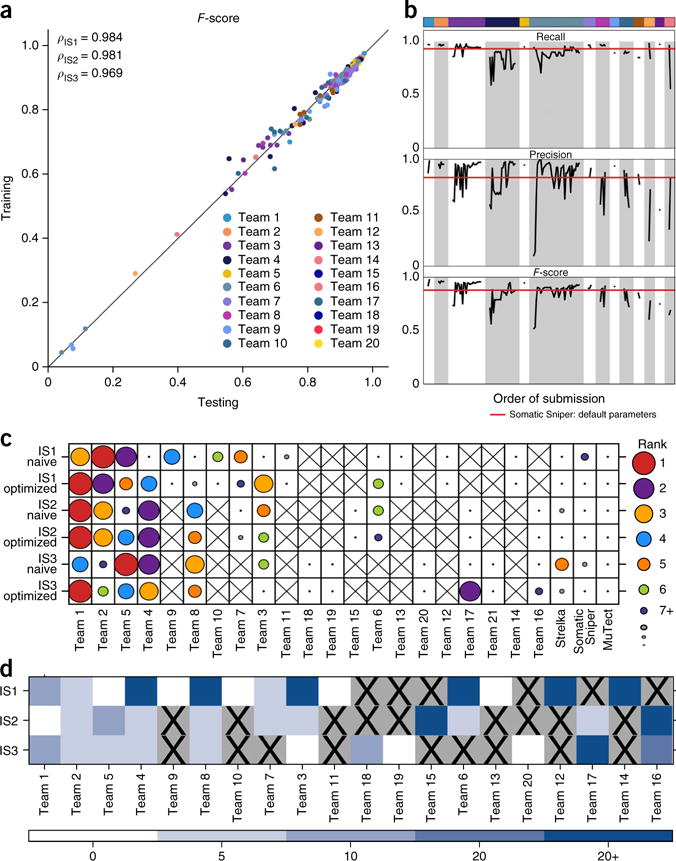
Effects of algorithm tuning. (a) The performance of groups on the training data set and on the held-out portion of the genome (~10%) are tightly correlated (Spearman’s ρ = 0.98) and fall near the plotted y = x line for all three tumors. (b) F-score, precision and recall of all submissions made by each team on IS1 are plotted in the order they were submitted. Teams were ranked by the F-score of their best submissions. Color coding as in a. The horizontal red lines give the F-score, precision and recall of the best-scoring algorithm submitted by the Challenge administrators, SomaticSniper. A clear improvement in recall, precision and F-score can be seen as participants adjusted parameters over the course of the challenge. Bar width corresponds to the number of submissions made by each team. (c) For each tumor, each team’s initial (“naive”) and final (“optimized”) submissions are shown, with dot size and color indicating overall ranking within these two groups. An “X” indicates that a team did not submit to a specific tumor (or changed the team name). Algorithm rankings were moderately changed by parameterization. (d) For each tumor, we assessed how much each team was able to improve its performance. The color scale represents bins of F-score improvement.

We considered the ranking of each team within each tumor based on initial (“naive”) and best (“optimized”) submissions. In general, rankings were moderately changed by parameterization: when a team’s naive submission ranked in the top 3, its optimized submission remained among the top 3 66% of the time (Fig. 3c). Nevertheless, teams routinely improved their overall performance, with 39% able to improve their F-score by at least 0.05 through parameter tuning and 25% improving it by more than 0.20 (Fig. 3d). These improvements did not lead to overfitting (Fig. 3a,b), a result emphasizing the importance of verification data for algorithm tuning.

Effects of genomic localization

In subsequent analyses, we focused on the single highest F-score submission from each team, supplemented by submissions generated by executing widely used algorithms with default parameters (for example, MuTect, Strelka, SomaticSniper and VarScan). We first examined the effect of genomic location on prediction accuracy. For IS1, F-scores differed significantly between intergenic, intronic, untranslated and coding regions (P = 6.61 × 10⁻⁷; Friedman rank-sum test; Fig. 4a). Predictions were more accurate for coding SNVs (median F-score = 0.95 ± 0.13; ±s.d. unless otherwise noted) than for those in UTRs (median = 0.93 ± 0.14; P = 3.3 × 10⁻³; paired Wilcoxon rank-sum test), introns (median = 0.91 ± 0.17; P = 2.3 × 10⁻⁵) or intergenic regions (median = 0.90 ± 0.19; P = 7.6 × 10⁻⁶). This may reflect algorithm tuning on exome sequences or differences in either sequence characteristics or completeness of databases used for germline filtering across these different genomic regions. These trends were replicated in IS2 and IS3 (Supplementary Fig. 8a,b).

Figure 4.

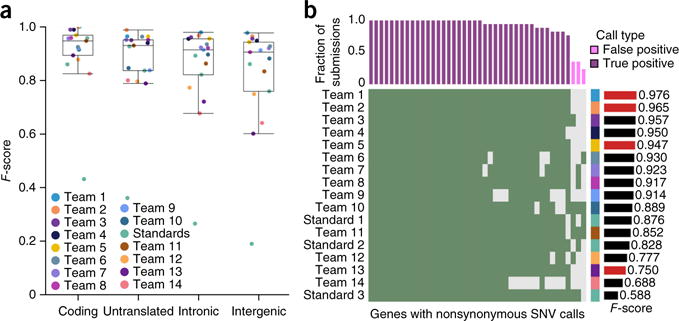
Effects of genomic localization. (a) Box plots show the median (line), interquartile range (IQR; box) and ±1.5× IQR (whiskers). For IS1, F-scores were highest in coding and untranslated regions and lowest in introns and intergenic (P = 6.61 × 10⁻⁷; Friedman rank-sum test). (b) Rows show individual submissions to IS1; columns show genes with nonsynonymous SNV calls. Green shading means a call was made. The upper bar plot indicates the fraction of submissions agreeing on these calls, and the color indicates whether these are FPs or TPs. The bar plot on the right gives the F-score of the submission over the whole genome. The right-hand side covariate shows the submitting team. All TPs are shown, along with a subset of FPs.

Next, we evaluated error rates on nonsynonymous mutations, which are the most likely to be functionally relevant (Fig. 4b and Supplementary Fig. 8c,d). Teamwise ranks were generally preserved across different genomic regions (Supplementary Fig. 9), and performance metrics were well correlated (Supplementary Fig. 10) across genomic regions. Nevertheless, few teams achieved 100% accuracy on nonsynonymous mutations. On IS1, 4/18 teams (ranked 1st, 2nd, 5th and 15th on the entire genome) achieved 100% accuracy on nonsynonymous mutations. The remaining submissions contained false negatives (FNs; 3/13), FPs (4/13) or both (6/13). Most nonsynonymous SNVs in IS1 were correctly detected by all submissions (22/39), but 7/39 were missed (i.e., FNs) by at least two teams. These results hold when all individual submissions were considered (Supplementary Fig. 11). In more complex tumors, more errors were seen. No team achieved 100% accuracy on nonsynonymous mutations in IS2: the top two teams made one and four errors, respectively. For IS3, two teams (ranked second and third overall) had 100% SNV accuracy, and error profiles differed notably between subclonal populations (Supplementary Fig. 12). Thus, even in the most accurately analyzed regions of the genome, there are significant inter-algorithm differences in prediction accuracy.

Next we asked whether error rates differed across chromosomes as well as between functional regions. For IS1, we observed a surprisingly large F-score range across chromosomes from 0.76 (chromosome 21, chr21) to 0.93 (chr11) compared to with resampled null chromosomes of equal size (chr21, 0.90 ± 0.074; chr11, 0.90 ± 0.076). The poor prediction accuracy for chr21 was an outlier: the next worst-performing chromosome was chr1 (F-score = 0.87). Chr21 showed lower F-scores than that expected by chance (false discovery rate (FDR) = 3.6 × 10⁻²⁵; two-way ANOVA), whereas chr11 showed higher F-scores (FDR = 2.8 × 10⁻³, two-way ANOVA; Supplementary Table 3). The reduced prediction accuracy on chr21 was observed in both FPs (Supplementary Fig. 13a) and FNs (Supplementary Fig. 13b). We compared a series of 12 variables thought to influence prediction accuracy (Supplementary Table 4). FPs on chr21 showed higher reference-allele counts (mean of 33 versus 23 for the rest of the genome; P < 0.01, one-way ANOVA) and base qualities (sum of 1,268 versus 786; P < 0.01, one-way ANOVA) than FPs on other chromosomes (Supplementary Table 5). These chromosome-specific trends influenced all algorithms in similar ways: permutation analysis showed no chromosome or submission with more variability than that expected by chance (Supplementary Fig. 14a). Interestingly, there was no evidence of chromosome-specific error on IS2 and IS3, making its origins and generality unclear (Supplementary Figs. 14b,c, 15 and 16). We premasked chromosomes to exclude regions containing structural variations, and there was no evidence of kataegis (small genomic regions with a localized concentration of mutations) in any tumor²¹ (Supplementary Fig. 17). These results highlight the variability of mutational error profiles across tumors.

Characteristics of prediction errors

We next exploited the large number of independent analyses to identify characteristics associated with FPs and FNs. We selected the best submission from each team and focused on 12 variables (Supplementary Table 4). In IS1, 9/12 variables were weakly associated with the proportion of submissions that made an error at each position (0 ≤ ρ ≤ 0.1; Supplementary Figs. 18–29). To evaluate whether these factors contribute simultaneously to somatic SNV prediction error, we created a Random Forest²² for each submission to assess variable importance (Supplementary Table 6). Key variables associated with FP rates (Fig. 5a) included allele counts and base and mapping qualities. Intriguingly, each of these was associated with increased error for some algorithms and reduced error for others. Key determinants of FN rates included mapping quality and normal coverage (Fig. 5b). The characteristics of FNs and FPs differed for most algorithms for IS1 (median ρ = 0.40; range: −0.19 to 0.71; Supplementary Fig. 30), IS2 (Fig. 5c,d) and IS3 (data not shown).

Figure 5.

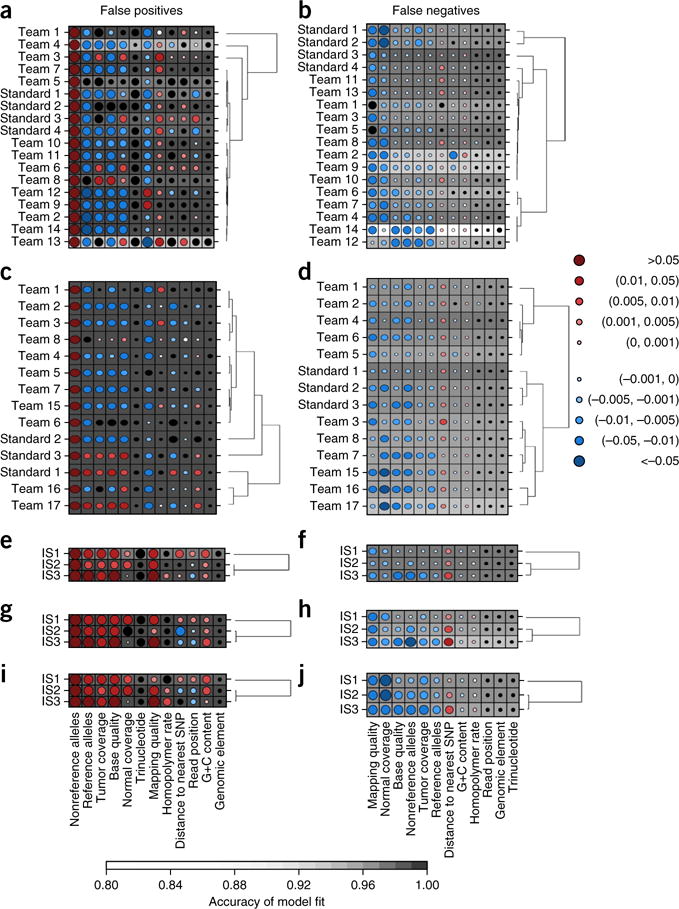
Characteristics of prediction errors. (a–j) Random Forests assess the importance of 12 genomic variables on SNV prediction accuracy (Online Methods). Random Forest analysis of FPs (a,c,e,g,i) and FNs (b,d,f,h,j) for IS1 (a,b) and IS2 (c,d) as well as for all three tumors using default settings with widely used algorithms MuTect (e,f), SomaticSniper (g,h) and Strelka (i,j). Dot size reflects mean change in accuracy caused by removing this variable from the model. Color reflects the directional effect of each variable (red for increasing metric values associated with increased error; blue for decreasing values associated with increased error; black for factors). Background shading indicates the accuracy of the model fit (see bar at bottom for scale). Each row represents a single set of predictions for a given in silico tumor, and each column shows a genomic variable. SNP, single-nucleotide polymorphism.

To further compare error profiles across tumors, we executed three widely used somatic SNV prediction algorithms with default settings: MuTect (Fig. 5e,f), SomaticSniper (Fig. 5g,h) and Strelka (Fig. 5i,j). Error profiles showed universal, algorithm-specific and tumor-specific components. For example, elevated nonreference allele counts were associated with FPs in all tumors for all three methods. FNs were much more sensitive to coverage in the normal sample for Strelka than for other algorithms (Fig. 5j). The largest notable tumor-specific difference was strong association of normal sample coverage with FPs in IS1 and IS2, but not IS3, for all algorithms (Fig. 5e,g,i).

Given the importance of context-specific errors in sequencing^23–25, we evaluated trinucleotide bias. BAMSurgeon spike-ins (TPs) had no trinucleotide bias relative to the genome (Supplementary Fig. 31), but FPs showed two significant biases in all three tumors (P < 2.2 × 10⁻¹⁶, χ² test; Fig. 6). First, NCG-to-NTG errors accounted for the four most enriched trinucleotides. This profile, along with elevated NCN-to-NAN and NTN-to-NCN mutations, closely matches the age signature (Signature 1A) detected in human cancers²⁶. Second, mutations of a C to create a homopolymeric trinucleotide (i.e., ACA-to-AAA, GCG-to-GGG, TCT-to-TTT) accounted for the 6th–8th most enriched profiles. Because both these signatures were detected in positions with no spike-ins, they are entirely artifactual. The Signature 1A profile was detected in the FPs of some, but not all, submissions (Supplementary Fig. 32) and was not associated with specific sequencing characteristics (Supplementary Fig. 33 and Supplementary Table 7).

Figure 6.

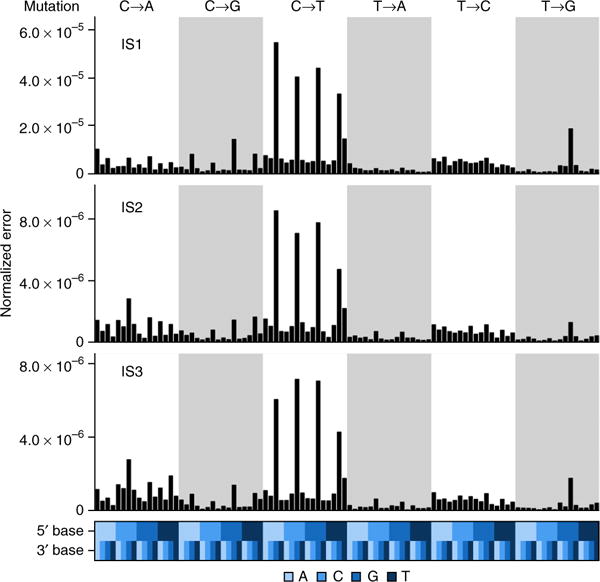
Trinucleotide error profiles. Proportions of FP SNVs are normalized to the number observed in the entire genome (top) binned by trinucleotide context (bottom) for IS1–IS3.

DISCUSSION

The crowdsourced nature of the SMC-DNA Challenge created a large data set for learning general error profiles of somatic mutation detection algorithms and gives specific guidance. We see diverse types of bias across the three tumors, along with a trinucleotide profile of FPs closely resembling the mutational Signature 1A found in primary tumors, likely reflecting spontaneous deamination of 5-methylcytosine at NCG trinucleotides²⁶. Algorithms may be detecting low levels present in all cells, artifacts may arise in sequencing (for example, library preparation artifacts) or current algorithms may have higher error rates at NCG trinucleotides. Rigorous mutation verification appears critical before mutational signature generation. As seen with previous challenges^12,13, ensembles were comparable to the best individual submission, even when including many poorly performing submissions. This suggests that mutation calls should be made by aggregating multiple algorithms, although this strategy would need tuning to account for its significant computational demands.

The real-time leaderboard highlighted the critical role of parameterization: teams were able to rapidly improve, particularly in precision, once they had an initial performance estimate. Robust ensemble learners may eventually eliminate the problem of parameter optimization, but meanwhile, many studies may benefit from a multistep procedure. An initial analysis would be followed with a round of experimental validation and then a final parameter optimization. The lack of overfitting suggests a modest amount of validation data may suffice, although studies on larger numbers of tumors are needed to optimize this strategy. Indeed, participants were often able to improve performance over time, which suggests that, as with previous crowdsourced challenges, real-time feedback can yield improved methods without overfitting^12,13.

Perhaps the most notable impact of this Challenge has been the creation of ‘living benchmarks’. Since the ground truth was revealed, 204 new submissions have been made by 22 teams who are using the Challenge data for pipeline evaluation and development. We will keep leaderboards open indefinitely to allow rapid comparison of methods, and we hope journals will expect benchmarking on these data sets in reports of new somatic SNV detection algorithms.

METHODS

Methods and any associated references are available in the online version of the paper.

ONLINE METHODS

Synthetic tumor generation

An overview of the process for generating synthetic tumor-normal pairs using BAMSurgeon is shown in Figure 1. BAMSurgeon supports SNV, Indel and SV spikein, each accomplished by a separate script (addsnv.py, addindel.py and addsv.py). As the results presented in this paper only cover single-nucleotide mutations, the SNV portion of the software will be discussed. Sites for single-nucleotide mutations are represented by a single base in the reference genome; three examples are shown in Figure 1a indicated by the blue, orange and green arrows; let S be one of these sites. A column of n bases b_0…n ∈ {A,T,C,G} from n reads is aligned over reference position S. Let the reference base R ∈ {A,T,C,G}. The variant allele fraction (VAF) at S refers to the fraction of bases in b at S, where b ≠ R. In BAMSurgeon, the VAF is specified for each site independently and implemented so that for each site S, n × VAF reads are selected and the bases b in those reads aligned to position S are changed to some base m ∈ {A,T,C,G}, where m ≠ b ≠ R (Fig. 1a, step 2). Optionally, a minimum alternate allele fraction (let this be a) can be specified such that the specified mutation at S will not be made if any other position sharing a read with position S has VAF ≥ a. For the synthetic tumors analyzed in this paper, this value was set to a = 0.1. This effectively prevents mutation spike-in ‘on top’ of existing alternate alleles and avoids making mutations that would be inconsistent with existing haplotypes. For each site, modified reads are output to a temporary BAM file, and reads are realigned using one of the supported methods, which currently includes bwa backtrack²⁷, bwa mem²⁸, Bowtie2 (ref. 29), GSNAP³⁰ and NovoAlign (http://www.novocraft.com/) (Fig. 1a, step 3). For each site, a number of parameters govern whether a mutation will be made successfully. These include minimum read depth, i.e., |b|, which defaults to 5; minimum read depth for the mutation, i.e., |m|, which defaults to 2; and a minimum differential coverage |b_after|/|b_before|, which must be ≥0.9 by default. For these last three parameters, the synthetic tumor analyzed in this paper was generated using these default values. If any of these criteria are not met, the mutation at the failing site is skipped and will not appear in the ‘truth’ output. All remapped mutations are merged together and then merged with the original BAM at the end of the process (Fig. 1a, step 4). This scheme also allows for parallelization, which is implemented in each of the BAMSurgeon tools.

The procedure for generating synthetic tumor-normal pairs using BAMSurgeon is outlined in Figure 1b. This process requires a high-coverage BAM file; for IS1, HCC1143 BL was used, obtained from https://cghub.ucsc.edu/datasets/benchmark_download.html. To differentiate this from the original BAM file (step 1 of Fig. 1b), we selected 10,000 single-nucleotide sites at random using the script included in etc/randomsites.py in the BAMSurgeon distribution, requiring that the selected bases be present in the GRCh37 reference (i.e., positions not represented by the ‘N’ gap character) and covered by at least ten reads in the original high-coverage BAM file. Of these, 9,658 were added to the original BAM using addsnv.py (Supplementary Data 2) as well as structural mutations not discussed here. This ‘burned-in’ BAM was then sorted by read name using SAMtools sort-n, and the read pairs were distributed randomly into two BAMs, with each read pair having 50% chance to end up in one or the other of the output BAMs (step 2, Fig. 1b). A script to accomplish this is included in the BAMSurgeon distribution in etc/bamsplit.py. Because the original BAM contained 60× genome coverage worth of reads, each of the split BAMs contained ~30× worth of reads. One of the two BAMs was arbitrarily designated ‘synthetic normal’ and the other ‘pre-tumor’. We again selected 4,000 single-nucleotide sites at random and used addsnv.py to add these to the ‘pre-tumor’ BAM (step 3, Fig. 1b). Of these, 3,537 were added to the BAM file (Supplementary Data 2). The relevant settings for addsnv.py were as follows: -s 0.1 -m 0.5 -d 0.9 –mindepth 5 –minmutreads 2. Following addition of structural mutations, the resulting ‘synthetic tumor’ was post-processed to ensure adherence to the SAM format specification using the script etc/postprocess.py, included in the BAMSurgeon distribution. The resulting tumor-normal pair was validated via ValidateSamFile. jar (part of the Picard tool set: http://broadinstitute.github.io/picard/) and distributed to participants. Given the mutations spiked into the synthetic tumor, a ‘truth’ VCF was generated and used as the ground truth against which participant mutation calls returned in VCF format were judged using the evaluation script available at https://github.com/Sage-Bionetworks/ICGC-TCGA-DREAM-Mutation-Calling-challenge-tools.

BAMSurgeon robustness

To test the robustness of BAMSurgeon, we compared the output of four commonly used algorithms— MuTect¹⁶, RADIA¹⁷, SomaticSniper¹⁹ and Strelka¹⁸—on the original data set against the output when an alternate aligner (NovoAlign), cell line (HCC1954) or read split was used. The same spike-in set of mutations was used in each control case. The following algorithm procedures were used for each control case.

First, MuTect (v.1.14) was run with default parameters and the per-chromosome VCF output was concatenated using Picard MergeVcfs (v.1.107). Only calls flagged with “PASS” were retained.

Second, RADIA (github-July-11-2014) was run with default parameters, and the output VCF files were filtered using the radia filter script with default parameters. After the filtered VCF files were indexed using igvtools (v2.3.12)³¹, the VCFs were merged together using VCFtools (v0.1.11)³². Finally, high-confidence somatic SNVs were extracted to generate the final VCF file.

Third, somatic SNV candidates were detected using bam-somaticsniper (v.1.0.2) with the default parameters except-q option (mapping quality threshold). The -q was set to 1 instead of 0 as recommended by the developer. To filter the candidate SNVs, we generated a pileup indel file for both normal BAM and tumor BAM files using SAMtools (v0.1.6). The SomaticSniper package provides a series of Perl scripts to filter out possible FPs (http://gmt.genome.wustl.edu/packages/somatic-sniper/documentation.html). First, standard and LOH filtering were performed using the pileup indel files, and then the bam-readcount filter (bam-readcount downloaded on 10 January 2014) was applied with a mapping quality filter -q 1 (otherwise default settings). In addition, we ran the FP filter. Finally, the high-confidence filter was used with the default parameters. The final VCF file that contains high-confidence somatic SNVs was used.

Last, the configuration script was used to set up the Strelka (v1.0.7) analysis pipeline. The default configuration file for BWA was used with the default parameters with the exception of SkipDepthFilters - depth filter was turned off. Following the configuration step, somatic SNVs were called using eight cores. This step automatically generates a VCF file containing confident somatic SNVs, and the VCF file was used.

The resulting predictions were compared using recall (equation (1)), precision (equation (2)) and F-score (equation (3)).

$$\text{recall}=\#\text{of true positives}/(\#\text{of true positives}+\#\text{of false negative)}$$ (1)

$$\text{precision}=1-\left(\#\text{of}\text{false}\text{positive}/\left(\#\text{of}\text{true}\text{positives}+\#\text{of}\text{false}\text{positives}\right)\right)$$ (2)

$$F-\text{score}=2\times \left(\text{precision}\times \text{recall}\right)/\left(\text{precision}+\text{recall}\right)$$ (3)

Univariate analysis

A subset of all submissions was used for downstream analysis; this subset consisted of the best submission from each team along with four default submissions submitted by SMC-DNA Challenge admins: MuTect, SomaticSniper, Strelka and VarScan³³ using default parameters. A list of all positions called by at least one of these submissions was generated (including all true SNV positions). For each of these positions, 12 genomic factors were calculated: depth of coverage in tumor and normal data set, median mapping quality, read position, number of reference alleles, number of nonreference alleles, sum of base qualities, homopolymer rate, G+C content, region type, distance to nearest germline single-nucleotide polymorphism (SNP) and trinucleotide sequence spanning position. Coverage was calculated using BEDTools³⁴ coverage (v2.18.2), which calculated the number of reads at each position in both the tumor and normal BAM files. Mapping quality was extracted from the tumor BAM file by converting the BAM file to a BED file using BEDTools bamtobed (v2.18.2) and calculating the median quality score at each position using BEDTools groupby (v2.18.2). The median read position of each genomic position was extracted using Bio-SamTools Pileup (v1.39). Number of reference alleles, number of alternate alleles and sum of base qualities were determined using SAMtools³⁵ mpileup (v0.1.18). Both homopolymer rate and G+C content were measured over a 201-bp window (±100 bp from position) determined using BEDTools getfasta (v2.18.2). Homopolymer rate was measured using the following equation, where n represents the number of bases in each homopolymer and N represents the number of homopolymers:

$$\text{homopolymer}\text{rate}=\left({\displaystyle {\sum }_{i=1}^N\cdot n_i^2}\right)/N$$ (4)

G+C content was measured using the equation

$$\mathrm{G}+\text{Ccontent}=\left(\#\mathrm{G}+\mathrm{C}\right)/\text{window}\text{length}$$ (5)

Annovar region-based annotation (v.2012-10-23) was used to annotate the genomic elements at each position—classifying as intergenic, intronic, untranslated and exonic. SNPs were called using the Genome Analysis ToolKit (GATK)³⁶ UnifiedGenotyper, VariantRecalibrator and ApplyRecalibration (v2.4.9). The distance to the closest SNP was calculated using BEDTools closest (v2.18.2).

Finally, a recent study showed that cancer types show unique somatic SNV signatures defined by the SNV base change and the trinucleotide context surrounding the variation²⁶. To explore the effect of both on SNV prediction, we added base changes (as defined by submitted VCF files) and trinucleotide context (extracted using BEDTools getfasta) to our model.

To determine the relationship between each variable and prediction success, we plotted each genomic variable against the proportion of submissions that made an error at each position. The Spearman correlation coefficient and corresponding P value were calculated for continuous variables, and a one-way ANOVA was run on categorical variables (base change, trinucleotide context and coding region).

Multivariate analysis

A Random Forest was used to model the effect of all 12 genomic variables on SNV prediction. Prior to modeling, the correlation between variables was tested. Variables were loosely correlated, with the exception of tumor and normal coverage and reference and alternate allele counts. Because of this correlation, the cforest implementation of Random Forest from the R package Party (v1.0-13) was used to reduce correlation bias^22,37–39. Average decrease in accuracy, as output by the function varimp from the same package, was used to quantify the importance of each variable: the larger the decrease in accuracy, the more important the variable in explaining prediction accuracy. Each tree predicts whether a submission called an SNV at that position. Ten thousand trees were created, and at each branch three variables were randomly selected for node estimation. This model was run on each submission, analyzing true and false SNV positions separately (number of observations can be found in Supplementary Table 7). One submission, 2319000, failed to converge when the model was run with 10,000 trees, so the model was run with 1,000 trees on this submission (only). The directional effect of each variable was determined by calculating the median difference between a sample from each response category using the Wilcoxon rank test. Variable importance was compared across submissions and visualized with a dot map—generated using lattice (v0.20-29) and latticeExtra (v0.6-26)—where dot size and color reflect the mean decrease in accuracy and directional effect of the variable for that submission, respectively, and background shading shows the accuracy of the model fit (for example, Fig. 4a). Finally, submissions were clustered by variable importance using the Diana algorithm.

Trinucleotide analysis

The trinucleotide context (±1 bp) at each SNV called was found using BEDTools getfasta (v.2.18.2). Trinucleotide counts were calculated, ensuring that forward and reverse strands were binned together (for example, ATG was binned with CAT). These bins were further stratified by the base change of the central base as documented in the submitted FCF files. For three FP positions, out of approximately 200,000, the base change specified did not align with the reference, i.e., the base change specified was from T to C, whereas the trinucleotide at that position was AGT. These positions were considered to be alignment errors, and the positions were removed from the analysis. The distribution of trinucleotides in each base change was plotted and normalized using the trinucleotide distribution of the genome.

$$\text{normalized}\text{error}=\left(\#\text{observed}\text{in}\text{subset}\right)/\left(\#\text{observed}\text{in}\text{genome}\right)$$ (6)

Genomic trinucleotide counts were found by pattern matching each trinucleotide in the FASTA reference file. Again these trinucleotides found in either the forward or reverse strand were binned together. TP and FP positions were plotted separately to compare distributions. Both trinucleotide distributions were tested against the genomic distribution using a χ² test for given probabilities in the R statistical environment (v.3.0.3).

Coding versus noncoding

To determine whether position functionality affected SNV prediction, we annotated all positions using Annovar region-based annotation (v.2012-10-23) to determine the genomic element of each SNV. Positions called by at least one submission (including all true SNVs) were binned into intergenic (n = 24,226), intronic (n = 10,893), untranslated (n = 252) and coding (n = 211) regions. The F-score of positions in these regions was calculated and visualized in a strip plot generated using lattice (v0.20-29) and latticeExtra (v0.6-26). The difference in F-score over the four regions was tested using Friedman rank-sum test to account for the effect of each submission. The difference in F-score of each pair of regions was compared using the paired Wilcoxon rank-sum test.

Accuracy in exonic regions

The F-score was calculated in a subset of SNVs located in exonic regions corresponding to known genes (as determined by Annovar gene-based annotation (v.2012-10-23)). It was hypothesized that algorithms would have increased prediction success in these regions owing to the negative clinical impact that prediction errors would have. Out of the 126 called positions in functional genes, a further subset of 42 positions was extracted and classified on the basis of mutation functionality; only nonsynonymous SNVs were present in this subset (as determined by Annovar). Selection criteria ensured that these positions were called by four or more of the submissions. Lattice (v0.20-29) and latticeExtra (v0.6-26) were used to compare the difference in prediction success of submissions in this subset.

Chromosomal bias of predicted SNVs

The F-score of each submission on each chromosome was calculated individually. A box plot, generated using lattice (v0.20-29) and latticeExtra (v0.6-26), suggested differences in F-scores over chromosomes. To quantify the chromosome variation seen, we implemented a two-way ANOVA incorporating chromosomes and submissions.

Resulting P values were adjusted for multiple-hypothesis testing using FDR⁴⁰. To account for the variation seen in chromosome 21, we compared the distributions of ten genomic variables (Supplementary Table 5) in both FNs and FPs on chromosome 21 against the remaining genome using the Wilcoxon rank-sum test. P values were adjusted for multiple testing using the false discovery rate method.

To further analyze chromosomal bias, we compared the rank of each submission on individual chromosomes to the overall rank of the submission. The significance of the observed variation was tested by generating a null distribution similar to that previously described. The F-score of null ‘chromosomes’ (randomly sampled positions over 10,000 iterations) was calculated and used to rank submissions. The deviation of each submission on each chromosome from its overall rank was weighed by the difference in overall F-score accuracy between the chromosome rank and overall rank. We then determined the number of times, over the 10,000 iterations, that the deviation seen in the null ranks was greater than the deviation in the chromosomal ranks. This count was divided by 10,000 to produce the probability of observing the chromosomal variation by chance alone (or the P value) for each submission on each chromosome. The variation and corresponding P value were visualized using a dot map generated using lattice (v0.20-29) and latticeExtra (v0.6-26).