Partial Unfolding and Refolding for Structure Refinement: A Unified Approach of Geometric Simulations and Molecular Dynamics

Abstract

The most successful protein structure prediction methods to date have been template-based modeling (TBM) or homology modeling, which predicts protein structure based on experimental structures. These high accuracy predictions sometimes retain structural errors due to incorrect templates or a lack of accurate templates in the case of low sequence similarity, making these structures inadequate in drug-design studies or molecular dynamics simulations. We have developed a new physics based approach to the protein refinement problem by mimicking the mechanism of chaperons that rehabilitate misfolded proteins. The template structure is unfolded by selectively (targeted) pulling on different portions of the protein using the geometric based technique FRODA, and then refolded using hierarchically restrained replica exchange molecular dynamics simulations (hr-REMD). FRODA unfolding is used to create a diverse set of topologies for surveying near native-like structures from a template and to provide a set of persistent contacts to be employed during re-folding. We have tested our approach on 13 previous CASP targets and observed that this method of folding an ensemble of partially unfolded structures, through the hierarchical addition of contact restraints (i.e., first local and then nonlocal interactions), leads to a refolding of the structure along with refinement in most cases (12/13). Although this approach yields refined models through advancement in sampling, the task of blind selection of the best refined models still needs to be solved. Overall, the method can be useful for improved sampling for low resolution models where certain of the portions of the structure are incorrectly modeled.

Introduction

Currently, template based modeling (TBM) is the most successful protein structure prediction method, leveraging the volume and variety of structures in the Protein Data Bank.^1,2 These methods often reliably capture the correct topologies for small proteins, and can achieve high accuracy predictions in high-homology cases. Much of this progress has come from improvements in template libraries and in methods for identifying templates,³ yet it remains a major challenge to refine predicted structures beyond the best template available.⁴ The so-called refinement problem has drawn much attention through the biannual CASP (Critical Assessment of Techniques for Protein Structure Prediction) competition.² CASP results show than when target success is compared against target difficulty recent improvements have, in fact, been slow.⁵ In the case of membrane proteins, homology predictions become even more challenging due to the low number of experimentally determined membrane structures (approximately 2500 membrane structures within the Protein Data Bank) as compared to globular proteins, leading to poor templates or no homology hits.

Physical models, now, offer a natural marriage with bioinformatics based techniques; the latter can drastically narrow the conformational landscape while physics-based methods add template-free refinement that, in principle, offers high transferability to novel folds, new sequences, and even artificial proteins. Molecular dynamics (MD) studies have found that structural stabilities and approximate conformational free energies (force fields + implicit solvation models) can correctly discriminate native structures from decoy structures.^6–10 MD simulations have also successfully refined bioinformatics models provided they were long enough (100ns or more) to permit adequate sampling.^8,11–13 Advancements in computational power and forcefield accuracy make it possible to observe reversible folding and unfolding in more than 400 events across MD simulations of 12 proteins.¹⁴ It is now possible to reproduce both the structures and folding thermodynamics of a variety of small proteins and peptides using physics-based approaches.^15–29 Moreover, refinement protocols have also seen improvement using enhanced sampling methods such as multicanonical techniques³ or replica exchange molecular dynamics (REMD),^30–33 where multiple copies of a system are simulated in tandem across a spectrum of temperatures. The addition of energetic restraints to lock into place high-confidence substructures that further narrow the conformational search space has also significantly increased refinement efficiency and accuracy.^{3,15,18–23,30,33–38} It is very exciting to see that such approaches utilizing physics-based forcefields and restrained all-atom explicit water MD are better than other heuristic approaches in increasing the accuracy of server predicted template models. In the last two CASP refinement competitions (CASP11 and CASP10), the physics methods were shown to produce the best results.^{36, 39, 40}

Recent CASP results have been promising, however there still exists a significant challenge when the structures targeted for refinement differ dramatically (are poorly predicted) from the native state, particularly when secondary structures are misfolded.^{8,11,13,41,42} In these cases, the major barrier lies in sampling a protein's highly rugged energy landscapes. The predominant question is “how does one adequately sample this furrowed conformational space while avoiding local energetic minima to reach the native structure?” Here we develop a new synergistic method, which addresses the problem of sampling rugged conformational landscapes to find the native state, uniting state-of-the-art techniques from geometric simulation and advanced REMD algorithms. Our refinement method mimics the mechanism of a chaperone that rehabilitates misfolded proteins by causing them to unfold partially and subsequently re-fold into the native structure.

Thus, inspired by the nature of protein chaperones, we produce locally unfolded regions of the target protein (i.e., partially unfolded protein conformations) by pulling the two terminal ends of the protein in different directions using a geometric based simulation called FRODA.^43,44 This unfolding step has two important functions. First, it enables the determination of actual native contacts by analyzing the persistent contacts throughout the unfolding trajectory. Second, it decreases the degrees of freedom sampled, thereby increasing the speed of refining misfolded parts when the correct native contacts are used as restraints. Partially unfolded conformations are then simultaneously refolded and refined using a physics-based refinement protocol called hierarchically restrained replica exchange molecular dynamics (hr-REMD).^23,43,45 We have tested this method on 13 structures from the CASP9 and CASP10 refinement target sets. Among these cases, our approach refined 12 of the 13 targets with an average decrease in RMSD 0.51Å (ranging from a decrease of −1.42Å to a decrease of −0.16Å) and an average increase of 2.14 in GDT-TS.

Methods

Unfolding by FRODA

Proteins targeted for refinement are first unfolded using the Framework Rigidity Optimized Dynamics Algorithm (FRODA), used to create a topologically diverse ensemble of partially unfolded structures. Here, the template structure is first coarse-grained using a graph-theoretical algorithm known as the pebble game, implemented within the FIRST program,⁴⁶ which uses covalent bond information to decompose the protein into rigid units, keeping covalent bond lengths and non-torsional covalent angles fixed. These rigid units are comprised of a minimum of three atoms which can be shared amongst adjacent units and include constraints from higher-order covalent bonds, such as peptide bonds or double bonds. As such, a single amino acid can be decomposed into multiple rigid units.

The strain within the protein is evaluated using an energetic function made up of harmonic constraints,

$$E_{\mathit{\text{protein}}}=E_{\mathit{\text{sh}}}+E_{\mathit{\text{gt}}}+E_{\mathit{\text{lt}}}$$ (1)

where E_sh is the energy of shared constraints, E_lt is the energy of half-harmonic “less than” constraints and E_gt is the energy of half-harmonic “greater than” constraints.

$$E_{\mathit{\text{sh}}}=\frac{1}{2}{k}_{\mathit{\text{st}}}\mathrm{\Delta }{x}^2$$ (2)

$$E_{\mathit{\text{gt}}}=\{\begin{array}{cc}\hfill \frac{1}{2}{k}_i{(x-x_0)}^2,\hfill & \hfill x<x_0\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}$$ (3)

$$E_{\mathit{\text{lt}}}=\{\begin{array}{cc}\hfill \frac{1}{2}{k}_j{(x-x_0)}^2,\hfill & \hfill x>x_0\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}$$ (4)

Shared constraints are used to prevent any separation of rigid units with shared atoms, and Δx is the separation between the rigid units. The spring constant k_st is calibrated such that distances between rigid units that share atoms are never greater than 0.02Å.

Greater than constraints model steric interactions and are used to enforce a minimum distance between atoms, x − x₀. Here, the k_i′s are the Ramachandran spring constant (k_rm) and the torsional angle (k_tr) spring constant. The associated Ramachandran harmonic potential is chosen to reproduce the barrier height associated with O_i−1 – C_β barrier clash in the Ramachandran plot of alanine dipeptide⁴⁴ while the torsional angle harmonic potential is calibrated to match the anti/gauche barrier of n-butane.⁴⁷

Less than constraints model hydrogen bonds, salt bridges and hydrophobic interactions and can be broken during the unfolding process. Hydrogen bonds and salt bridges are defined to be those bonds that have an energy < −1.0 kcal/mol according to a modified Mayo potential.⁴⁵ The k_j spring constants (k_h and k_sb) are calibrated to model transition molecular dynamics pathways.⁴⁸ Each of these less than constraints has a maximum load they can bear, beyond which they are removed, where the default extension being is set as 0.15Å to prevent distortion of the protein structures. The values for all spring constants used here can be found in prior work from de Graff et. al.⁴³

Before unfolding a structure, the backbone atoms of both the C and N-terminal residues must be assigned a new set of atomic coordinates which correspond to an extension of their original spatial separation; that is, increasing the protein’s end-to-end Euclidean distance. While an optimal unfolding distance will vary from protein to protein, some generalizations can be made. A fully unfolded protein N amino acids long would have a total end-to-end distance of roughly 3.8 · N Å; structures unfolded to this extent provide no useful information regarding contact analysis and would require complete refolding in any molecular dynamics simulation before refinement would even be possible, akin to having performed a structural prediction. However, we have found that even when using projected end-to-end separation distances of 1 · N Å, a large portion of the conformations generated by FRODA are unfolded to an extent such that they retain less than 50% of the original structure’s contacts, making much of the unfolding ensemble of little use for subsequent refinement. For this work, r_final, the distances used to generate unfolded state were automated, evaluated empirically using the expression

$$r_{\mathit{\text{final}}}=r_{\mathit{\text{initial}}}+(N_{\mathit{\text{non}}}·1\AA )$$ (5)

where r_initial is the original Euclidean separation between C-terminal and N-terminal backbone atoms and N_non is the number of amino acids not part of any secondary structure. While β-sheet or α-helix residues are not counted when calculating r_final, they are able to unfold just as any other region of the protein, subject to the harmonic constraints mentioned previously.

Using r_final, the backbone atoms of the terminal residues are assigned a new projected set of Cartesian coordinates. Unfolding then proceeds as follows: a random move of 0.05Å is proposed and is subsequently accepted if the RMSD between the current atomic coordinates and final projected atomic coordinates decreases. The structure is then relaxed, resulting in an equilibrium strain distribution. If any of the constraints exceed the maximum extension, they are removed. The extension is set to 0.15Å to prevent distortion of the protein structures. During each step new hydrogen bonds and hydrophobic interactions can form, allowing for non-native intermediate interactions. Newly formed hydrogen bonds are identified as bonds between two atoms (hydrogen and a hydrogen acceptor) of an energy less than −1.0kcal/mol according to a modified Mayo potential. Likewise, the new hydrophobic interactions are added between two nonpolar carbon or sulfur atoms of hydrophobic residues that are separated by no more than 3.9Å. Unfolding proceeds until the backbone atoms of the initially targeted residues reach their assigned, final Cartesian coordinates.

The unfolding trajectory is then clustered using k-means clustering and the high confidence contacts (i.e., contacts that are in 90% or more of all the snapshots in the unfolding trajectory) are identified. A contact between two residues is defined when the Euclidean distance between their centroids is within 8Å. Clustered structures containing less than 50% of the original target’s contacts are discarded. Using unfolding distances calculated from equation 5, we find that there are generally few structures close to or below this threshold (See Figure S1).

Hierarchically Restrained Replica Exchange Molecular Dynamics with Reservoir

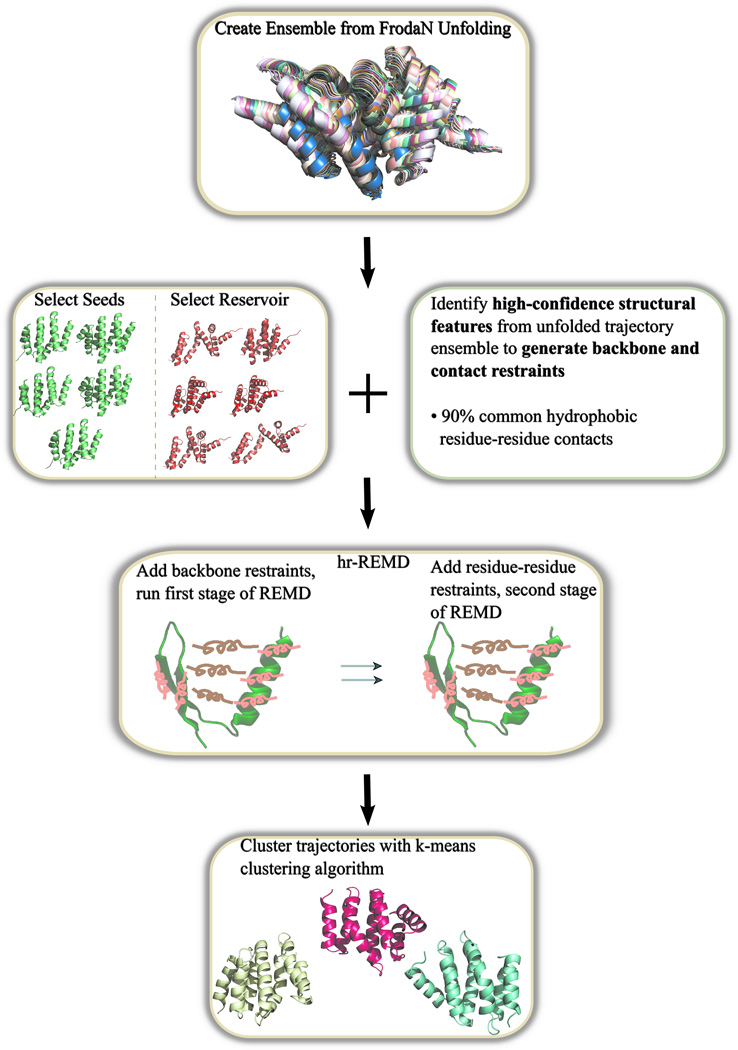
The partially unfolded structures are then relaxed and make up the initial seed structures and reservoir structures for the hierarchically restrained replica exchange molecular dynamics simulation (hr-REMD). All reservoir structures are coupled to an infinite temperature replica where a structure from the reservoir can be swapped into the highest replica during the REMD run. The infinite temperature is simply a means to ensure an adequate acceptance rate of exchange between the reservoir and the highest temperature replica during REMD. Although this leads to non-Boltzmann statistics, the periodic exchanges between the randomly chosen conformations from the reservoir and the highest temperature replica, in a manner of J-walking, can increase the conformational sampling and r-REMD converges more rapidly than REMD.⁴⁹ The simulation includes replicas that range in temperature from 270K to 450K, using the AMBER forcefield⁵⁰ (ff99SB) with the General Born Surface Area (GB5)⁵¹ implicit solvent model and a surface tension of 0.5kcal/mol•Å². For the target structures used in this work, the total number of replicas per simulation ranged between 20 to 35, depending on sequence length. A swap between replicas is attempted every picosecond and a molecular dynamics time step of 2fs is used. The number of replicas is set in order to optimize the likelihood of two replicas contiguous in temperature swapping structures to approximately 50%. The exact number or replicas is determined depending on the chain length using an empirical formula. The temperature of the replicas is exponentially distributed between the minimum and maximum temperature of 270K and 450K, respectively. We apply the restraints hierarchically where local contacts, contacts 5 or fewer residues apart within the sequence, are added as harmonic NMR distance restraints (0.5kcal/mol• Ų) and the structures are simulated for 2ns. This allows for the formation of correct secondary structures. For the last 3ns, non-local contacts, contacts greater than 5 residues apart within the sequence, are added into the simulation. Once the 5ns REMD simulation is completed, the final nanosecond of the lowest eight replicas are clustered and scored by RMSD from the target structure and DFIRE⁵² score. Structures with a low RMSD and high DFIRE score are selected as refined structures, a scoring method originally used by the Feig group.^{20, 21} Figure 1 illustrates the workflow.

Figure 1.

Flowchart of refinement protocol. Refinement begins with geometric unfolding, followed by seed structures and contact list generation, hr-REMD and finishing with the clustering of the simulation trajectories.

Results

Refinement simulations were carried out for a selection of CASP9 and CASP10 refinement targets provided from bioinformatics-based methods. Each target was unfolded using FRODA followed by 5ns REMD in which the first 2ns included only local restraints (restraints that have 5 or less residue sequential separation) followed by 3ns using both local and non-local contacts. The conformations sampled for each target were then clustered and scored to find a refined structure. All discussions of particular targets presented in this section refer to the best refined model produced from our protocol.

We used several metrics commonly employed in some of the recent CASP competition to assess the quality of the refined structures from our approach; the root-mean square deviation (RMSD), global distance test (GDT-TS),^53,54 MolProbity⁵⁵ and DSSP.⁵⁶ While RMSD is a metric that captures the deviations of the entire structure's backbone, GDT-TS characterizes to what extent the fraction of high quality parts have improved or worsened while not capturing the low quality parts. For example, if a small region of a chain had a very high RMSD with respect to the experimental structure, a significant refinement over this region would have a greater impact on RMSD improvement than GDT-TS improvement. However, RMSD is a metric that typically increases with chain length while GDT-TS is given as a percentage. As a result, GDT-TS is widely used when comparing refinement or prediction methods across different proteins in CASP evaluations. The other two criteria used for evaluation are MolProbity, which measures the steriochemical quality of a structure, and DSSP, which captures the secondary structure composition. DSSP can be particularly important to include in evaluations, as large changes to secondary structure can go unnoticed when referring only to metrics related to backbone accuracy. To generate our listed DSSP scores, we identify amino acids as being part of an alpha helix, a beta sheet, or neither through DSSP tools. With these three classifications we compare the secondary structure designations of our models to that of the native conformation on a residue-to-residue basis. The overlap between the two is represented as a percentage.

In reporting our results, we first identified the structure with the lowest RMSD from the target structure among clustered structures, taken as the most refined conformation, and then further evaluated in terms of GDT-TS, MolProbity and DSSP. In total, we have 12/13 structures refined based on RMSD, 8 of which also showed GDT-TS improvement. We also report 10/13 of our best structures improved MolProbity score and 8/13 increased in DSSP.

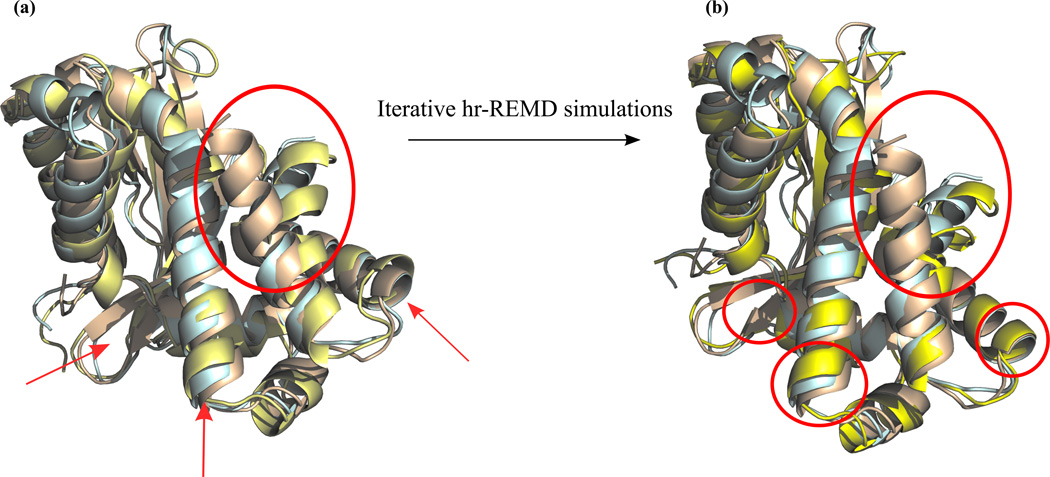
Although the improvement in RMSD generally coincides with improvement in GDT-TS as well, we also observe some cases where RMSD values improve while GDT-TS worsens. This is likely due to the nature of our protocol. The unfolding process allows for large structural changes to take place. Subsequently, during refolding by REMD there can be a negative impact on the spatial alignment of certain secondary structural motifs as compared to the experimental structure, especially in cases where an insufficient amount of long-range contacts have been captured. One demonstrative example of this effect is in the structure of TR661. Here we find marginal improvement in RMSD (−0.16 Å from target) and a significant decrease in GDT-TS (−11.74). Upon further analysis, we find that our structure has refined by correcting a significantly misaligned portion of the large α-helix of residues 167–182 at the C-terminus (Figure 2-a). The improvement towards the native structure of this helix results in a large conformational change over a small region, which inevitably has significant effects on the re-arrangement of surrounding regions, causing small deviations to backbone alignment. For the case of TR661, we performed iterative REMD runs where the clustered structures of the previous 5ns simulation were used as initial structures for subsequent REMD runs, along with the new restraints obtained from the consensus contacts,. As shown in Figure 2-b, GDT-TS further improved from 66 to 70 and RMSD also improved to 2.5Å from original RMSD of 2.78Å. The re-refinement procedure is a method to address the increase in RMSD and decrease in GDT; theoretically this iterative implementation of our protocol could be generalized to any target. However, it is possible that non-native contacts can be extracted and added to the simulation using this iterative technique. More testing over multiple targets will be necessary to see if multiple iterations eventually cause a decrease in overall structural refinement. Additionally, within the bounds of a CASP competition refinement deadline, this would require a significant increase in computational resources and may not be feasible, particularly with larger targets.

Figure 2.

Overlay of native structure (PDB code: 4FCZ), CASP model structure TR661 and refined structure in wheat, blue and yellow aligned using PyMol⁵⁸. Left side shows large improvement in terminal helix from the model structure along with misalignments of other regions. Right side shows improvements of misaligned regions with iterative hr-REMD simulations.

The partial unfolding and refolding in our approach allows us to make significant refinement in the secondary structure, including the formation or extension of β−sheets and the formation of α−helices. In the case of TR557 we were able to form a α-helical turn that was completely absent from the target structure by correctly unfolding a misformed hairpin. The refinement of this target highlights the importance of using multiple criteria to evaluate a structure. We have only a small improvement in the overall backbone alignment of this protein, shown with a GDT-TS improvement of 1.40. However, as mentioned previously, refinement of one particularly poorly predicted region of a protein will have a much more significant impact on RMSD and here we find an RMSD improvement of 1.42Å from an original RMSD of 4.06Å. Quantitatively, we are able to distinguish this as an accurate secondary structure formation from a general backbone misalignment correction by including the DSSP score, which shows that our refined target has a 16.8% higher secondary structure accuracy when compared to the experimental structure. Unfortunately, just as the geometric unfolding of structures presents the opportunity to make significant improvements to the secondary structures of a protein, it can also allow for the opposite to take place as seen in the case of TR624. This structure was another one of the three in which RMSD improved but GDT-TS did not and, in this particular case, coincided with a large decrease in DSSP. Here we unfolded a large portion of an antiparallel beta sheet in which the connecting loop and nearby regions of the sheets near the loop were largely misaligned relative to the experimental conformation. The unfolding process gave us the opportunity to re-align this region of the protein during REMD, largely responsible for the overall RMSD improvement, but did not accurately reform the correct regions of the original beta sheet.

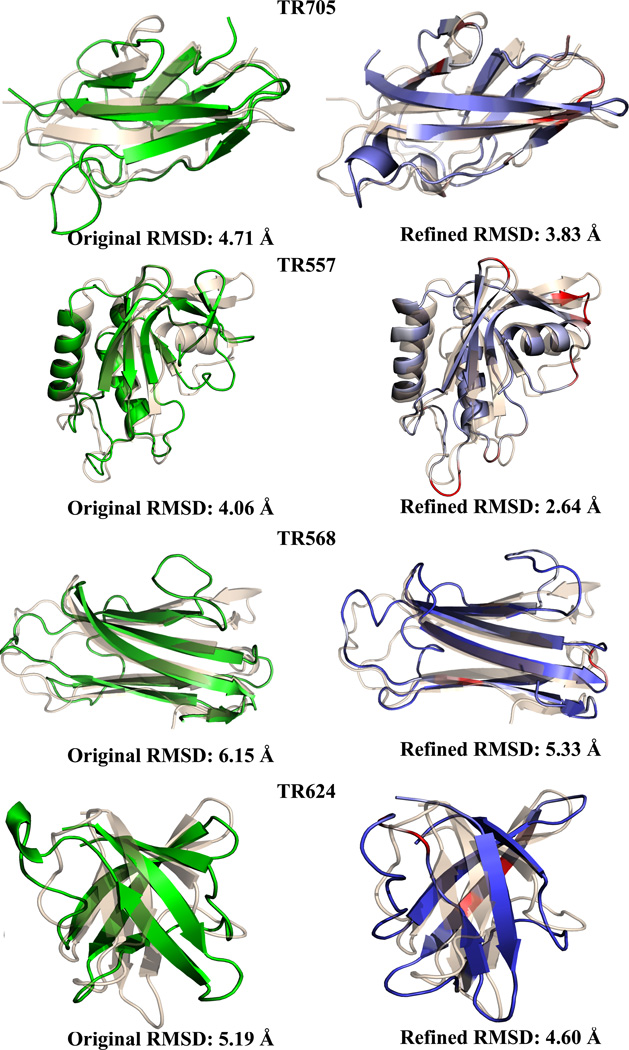
Finally, we have been able to refine poor resolution structures with a high RMSD from the experimental structure, which are, in general, much more challenging for refinement due to the lack of information. Among the four cases (TR557, TR568, TR624 and TR705) where the RMSD is larger than 4Å (Figure 3), our method successfully refined all four in terms of RMSD and three out of the four in GDT-TS. For instance, TR568 had a starting RMSD of 6.15Å which was decreased to 5.33Å and showed a GDT-TS increase of 2.84 and a DSSP score improvement of 5% and TR705, starting with a 4.71Å RMSD was refined to 3.83 with a GDT-TS increase of 5.73 and a 2.3% DSSP score improvement.

Figure 3.

Improvements for starting models with an RMSD of 4 Å or greater. Left side shows starting model in green, right side shows refined structure colored by root mean square fluctuations. All structures superimposed onto the native (wheat) using PyMOL⁵⁸. PDB codes of native structure, top to bottom: 4FTD, 2KYY, 3N6Y, 3NRL.

Failed cases are often a result of incorrect restraints or sampling issues related to the chain size or solvation model. The drifting of structures further from the native state during simulation is likely a result of force field inaccuracies. The addition of residue-residue contacts is an attempt to circumvent these inherent inaccuracies. The number of replicas needed for a simulation over a given temperature range increase as the square root of the number of degrees of freedom. In addition, larger proteins have more accessible conformations. These two factors likely contribute towards increasing the simulation time needed to adequately refold and sample conformations of larger proteins. This is was found to be true for example in the case of TR661, a structure with a complex topologies and a longer folding time than many of the other targets. An insufficient number of restraints will allow the structure to drift and cause an increase in the sampling time necessary for refinement. Non-native contacts (i.e. contacts not found in the experimental structure) are more problematic as they can lock regions of the protein into incorrect conformations that prevent the sampling of more native-like conformations.

Non-native contacts were a prominent issue regarding the refinement of TR569, in which the most poorly predicted portion of the protein was a loop region (residues 50–60). The inclusion of non-native contacts was further compounded by issues in using implicit solvation when attempting to refine loops, previously reported by Chen and Brooks⁵⁷ making refinement of this loop of the protein particularly difficult. In an effort to evaluate the magnitude of these additive effects we performed a 2ns REMD simulation using the clusters from our initial 5ns simulation of TR569 as seeds and included native contacts between residues 50–63 as restraints in addition to our original contacts. Here we were able to reduce the RMSD to 2.52Å and increase GDT-TS by 5.06, compared to an RMSD of 2.70Å and a change in GDT-TS of −0.63 from our best cluster of our original REMD simulation. Capturing a high number of native contacts while minimizing non-native contacts becomes increasingly more important in the refinement of targets that are already very close to the native conformation (RMSD < 2Å).

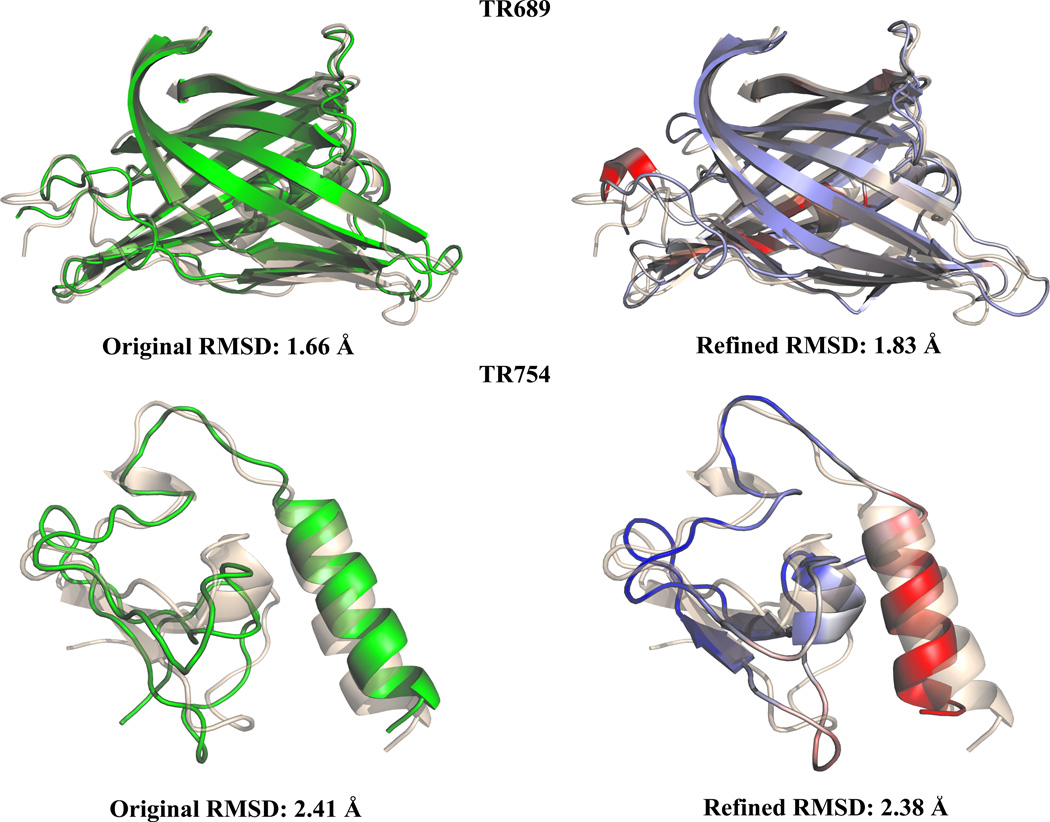
One of the structures we were unable to refine, TR689 (Figure 4), had multiple challenges in that it was a large structure (234 residues) with a very low RMSD (1.8Å). In this case, we were unable to accurately sample the conformational space to allow for refinement within the limit of a 5ns simulation largely due to the size of the protein. Additionally, the inclusion of contacts not found in the experimental structure will have an even greater impact for such highly resolved targets. This proved to be a particularly challenging structure, as only four groups competing in CASP10 were able to refine the target, with a maximum GDT-TS increase of 1.4. Other specifics can lead to failed cases, such as dimer-dimer interactions which our refinement process does not inherently capture. TR754 contains a zinc ion which effects the conformation of the experimental structure and as a result greatly increased the difficulty of refinement (Figure 4). During CASP10 only two groups were able to successfully refine this structure, with a maximum GDT-TS improvement of 0.73. Overall, based on our results, we observe that our current refinement approach can be useful for small to medium sized proteins (i.e., those with 100–200 residues) with misaligned parts.

Figure 4.

Two of our failed cases for refinement with starting models in green, refined structures colored by R.M.S, fluctuations and native structures in wheat aligned using PyMol.⁵⁸ TR689 (Native PDB code: 4FVS) had an extremely low starting RMSD making further refinement challenging. TR754 (Native PDB code: 2LV9) contains zinc ions, an interaction that our methodology is unable to capture. TR754 was a particular challenge for all CASP 9 participants.

Discussion

Does Reservoir REMD with hierarchical restraints enable the partially unfolded regions of the protein to refold correctly?

REMD allows for enhanced conformational sampling and accelerated convergence to the native structure, a method first used for protein structure refinement by Chen and Brooks, where they restrained parts of the protein likely thought to be native.¹⁵ In REMD, multiple structures (or replicas) are simultaneously and independently simulated at different temperatures and, at set intervals during the simulation, allowed to exchange structures with their nearest temperature neighbor. The advantage over traditional molecular dynamic simulations is twofold. Performing multiple simulations of a structure over varying temperatures enables a significant amount of parallelization thereby greatly increasing the computational efficiency in thoroughly sampling the conformational space. Additionally, the temperature exchange between replicas (generally governed by a Monte Carlo-type algorithm) constitutes a random walk in temperature space, reducing the probability of the simulated structures becoming trapped in local energy minima. The structures with the lowest free energy will generally be found in the lower temperature replicas and, given sufficient sampling, be represented by a large percentage clusters of the conformations explored at these lower temperatures.

Restraining native regions of the protein is critical in refinement using physics-based forcefields during REMD. The Shaw Group¹⁴ and Feig Group²¹ have both extensively tried refinement without any harmonic restraints and found that structures drift considerably with little to no improvement. The addition of residue-residue contacts^{35, 36} has the potential advantage of locking the structure close to the native state, preventing the structure from drifting away from the native, and reducing the degrees of freedom that are needed to be sampled. This lowers the computational time necessary, but can also limit the extent to which a protein can be refined when n-native contacts are introduced.

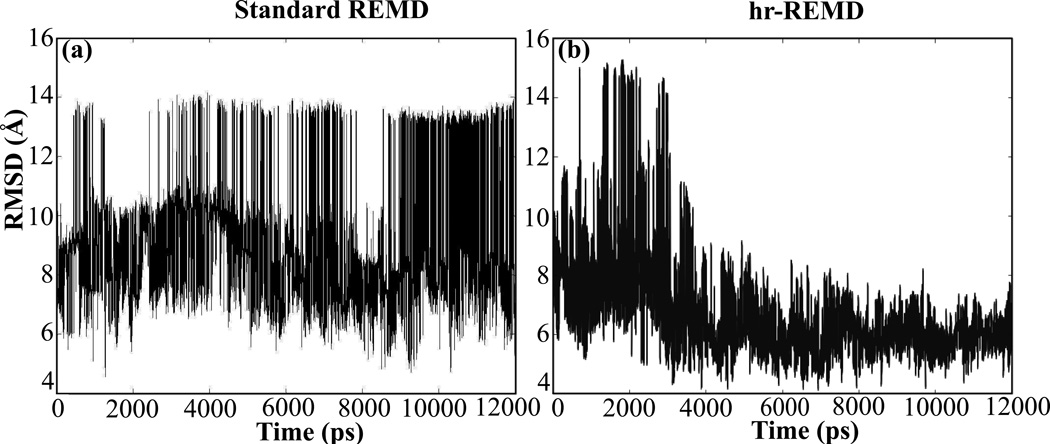
We use a similar approach of adding restraints to REMD simulations for structural refinement with two additional features, the first of which being the hierarchical application of residue-residue restraints. The list of contacts to be used as restraints for a particular target is generated by clustering the unfolding trajectory and identifying high confidence contacts, those found in at least 90% of the unfolding trajectory. We assume that these contacts are largely those found in the experimental structure, which was shown to be true for most targets with an average of 70% of these restraints being native with an upper range of 85% and a lower range of 60%. Initially, only local contacts are used as restraints during the first part of the simulation with non-local contacts being added later. The hierarchal application of contacts used in our methodology gradually decreases the degrees of freedom of the system as the simulation progresses, allowing for more efficient sampling and a more computationally manageable search for the native state. Figure 5 shows that T0311 converges faster towards the correct experimental structure when restraints are added hierarchically compared to conventional refinement in which all restraints are added simultaneously for a given REMD simulation. Additionally, restraining the local interactions first allows for local refinement (secondary structure) to occur before global refinement (tertiary structure).

Figure 5.

Comparison of RMSD as a function of simulation time between standard REMD (a) and hr-REMD (b) for CASP model structure T0311 (best predicted structure). hr-REMD shows a faster convergence to a lower RMSD over traditional REMD

Our second feature is the use of a reservoir of structures coupled to the highest temperature replica, which has been shown to enhance sampling.^30,49 The structures in the reservoir are comprised of structures clustered from the full unfolding trajectory. Incorporating a large amount of partially unfolded structures allows our simulation to explore a topologically diverse set of conformations which, in turn, allows for more efficient sampling, particularly if different conformations exist in the reservoir that are near the native state.

We partially unfold the target structure by pulling the two terminal ends of the protein in opposite directions, a process with several advantages. First, it enables us to unfold regions of the protein that were previously misfolded due to incorrect homology alignment. Second, beginning a REMD simulation with areas of the protein already unfolded accelerates the convergence of the simulation to more native-like folds by reducing the number of conformational changes the structure must sample to correctly refold these misfolded regions. Finally, through the consensus contacts that exist in all partially unfolded structures from our unfolding trajectory, we are able to obtain high confidence native contacts. For example, the model TR557 has the C-terminal end as a β-strand, a region, which actually exists as a α−helix in the experimental structure. When we unfold the target structure with the incorrect C-terminal hairpin using FRODA, the C-terminal beta strand part unfolds first. When we refold using the consensus contacts of the unfolded ensemble we observe it turns into the correct helical structure leading to a major improvement (−1.42Å). While FRODA is not currently accurate enough to consistently unfold only the misfolded regions of a protein, interesting applications arise when the portion of the structure in need of refinement can be reliably identified. When this information is available, unfolding and, subsequently, refinement can be made significantly more accurate. In these cases one can lock additional degrees of freedom in place for the rest of the structure and only sample degrees of freedom from the misfolded portions of the protein, greatly increasing the sampling efficiency of a simulation and potential for refinement.

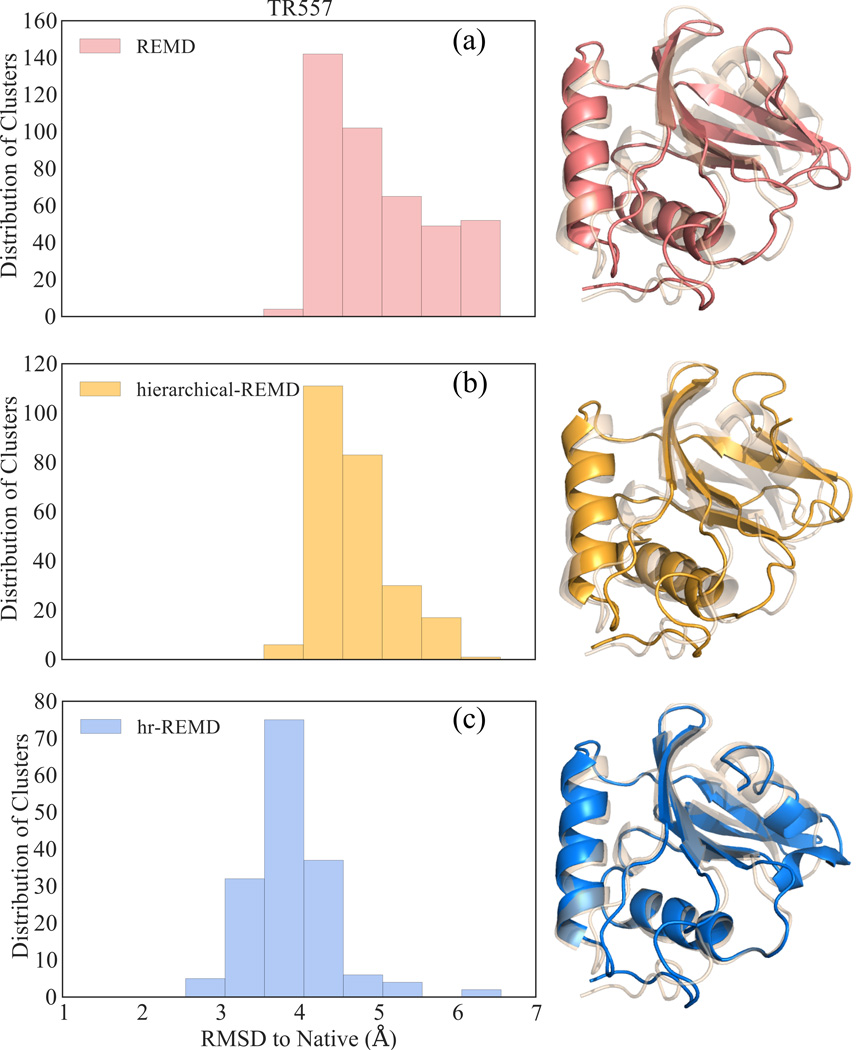
In order to compare how much each feature of our methodology helps us during the refining process, we performed several tests. First, as a control set, we use only the target TR557 as the initial structure and the contacts of the target are used as restraints, applied all at once, as in conventional REMD. In Figure 6-a, where all RMSD values below 4.06Å represent structural improvements, we see that with this protocol less than 1% of the structures are refined, and the refinement is minimal for the improved structures. This is likely caused by two factors. First, having all the contacts of the target locks the structure into the original target's conformation. The simulations cannot widely sample configuration closer to the native state. Thus, the simulation is not able to rapidly unfold and refold the C-terminal end of the chain. Additionally, the sampling will not be as extensive with only multiple copies of the target structure used as replicas for each simulation temperature. By partially unfolding the chain and gathering the unfolding consensus contacts we do not restrain the n-native β-strand configuration of the C-terminal end. The simulations with the initial structures whose C-terminal end completely unfolded enables fast and effective exploration of the conformational space of this region. We then explicitly tested the effect of including partially unfolded structures as replica structures, as opposed to multiple copies of the original target. Here we again used TR557 as a seed structure, this time adding restraints extracted from the unfolding trajectory hierarchically. Consistent with the observation in Figure 6-b this leads to a much faster convergence, not allowing the structure to drift further away from the native conformation. However, only 2% of the clustered structures produced at the end of the 5ns simulation are refined, indicating that the sampling is not as robust as compared to our method shown in Figure 6-c, where we use the structures with partially unfolded C-terminal end as initial seeds along with the contact restraints, leading to 70% of all clustered structures showing an RMSD improvement.

Figure 6.

Distribution of clustered structures after three different approaches using REMD for starting model TR557. All structures under 4.06 Å RMSD (i.e. original RMSD of the target) are improved. Traditional REMD is in pink (a), REMD with restraints added hierarchically in yellow (b) and hr-REMD in blue (c). Best models of each method superimposed on native structure (PDB code: 2KYY) in wheat.

Are empirical energy scores useful in blind selection?

In our earlier approach for the blind selection of refined targets, we chose the top 5 most populated structures in the lowest temperature replica as refined candidates. The nature of REMD, in which temperature switching of structures obeying a Boltzmann distribution, eventually leads to the structure with the lowest free energy residing in the lowest temperature replica assuming the force field is sufficiently accurate. The largest populated cluster of the lowest replica is expected to be the lowest free energy structure, and therefore, closest to the native state. However, we have found 5ns REMD simulations, as presented here, are not long enough to reach this type of convergence. When we extended the runs of TR557 up to 25ns with 30 replicas giving a total of 750ns, we did indeed find the highest percentage populated cluster to be a refined structure with a RMSD of 2.8Å compared to original target of 4.06Å.

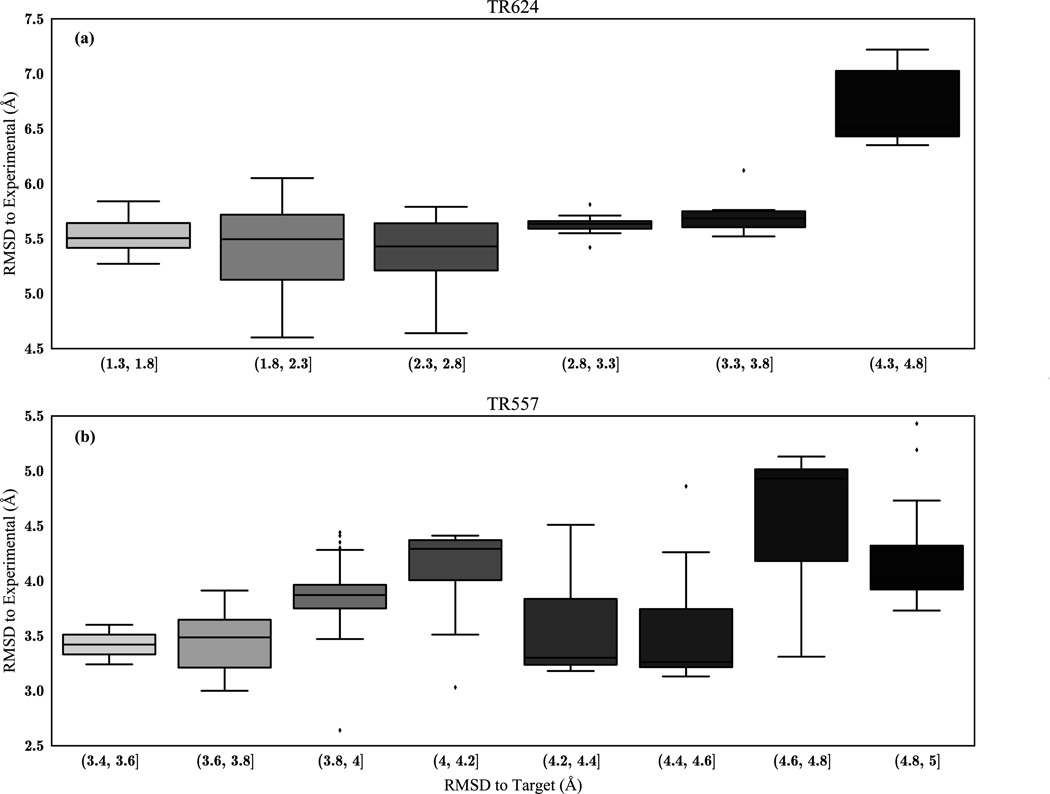
Achieving this level of convergence of REMD runs requires a significant amount of computational power and time. To circumvent this barrier, we turn to the common strategy of heuristic energy functions in conjunction with the RMSD from the initial target (iRMSD) to blindly select the best refined models among hundreds of clustered structures. First, the lowest eight temperature replicas are clustered and their iRMSDs and corresponding DFIRE energies are computed. We sort these structures based on their iRMSD and discard those with a very high deviation, based on the assumption that the structures with large deviations in iRMSD from the target have also drifted significantly from the native structure. While we find this to typically be true, it is not always a direct relationship; occasionally we pass over more highly refined models that exist at higher iRMSD values (Figure 7).

Figure 7.

Boxplot of RMSD to starting model vs. RMSD to native conformation of refined structures. Generally, structures that have not changed significantly from the starting model will be lower in RMSD to the experimental structure, but only to an approximation.

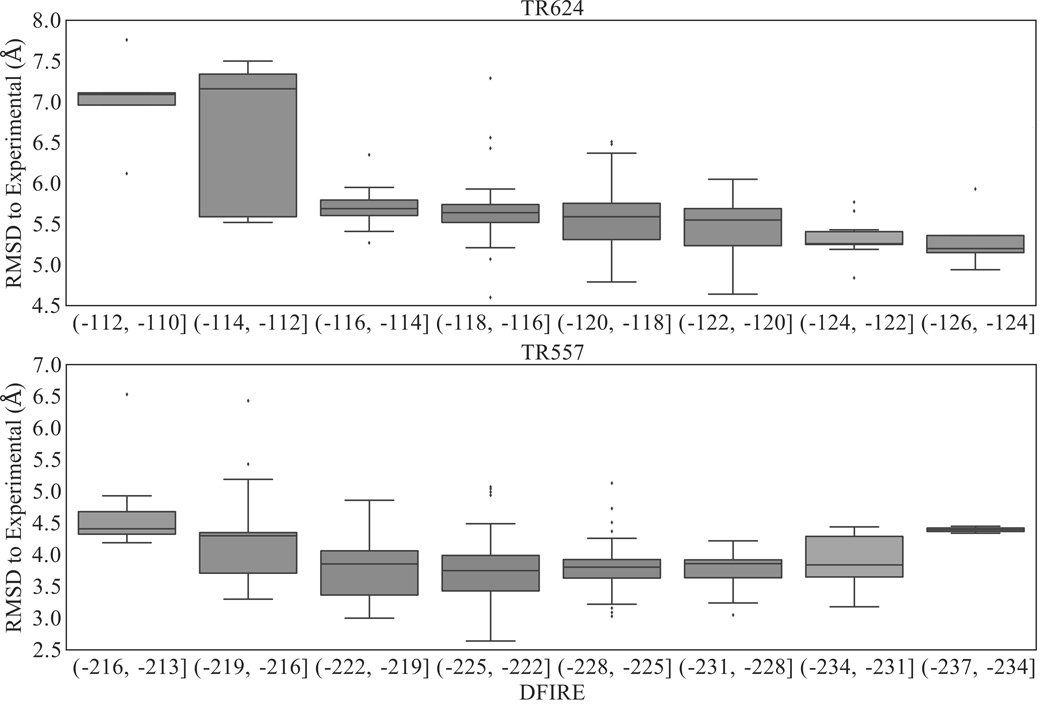
Within this subset of structures (i.e., low iRMSD), we then select the top five (as this is the number of structures that can be submitted to CASP per target in the refinement category) with the lowest DFIRE scores as potentially refined models. Our performance as related to our top five selected structures can be found in Tables 1 and 2. This selection criterion works the majority of the time, where we find RMSD improvements in 12/13 structures, 7 of which also show GDT-TS improvement. However, this procedure does not select the most refined model (see Table 1). The blind scoring and selection of putative structures remains one of the largest challenges in protein structural refinement; when evaluating only our “model 1” (the model with the lowest iRMSD amongst the top five selected structures with lowest DFIRE scores) we find RMSD and GDT improvements in 8/13 and 5/13 of these structures, respectively. While it is generally safe to select a structure with a low DFIRE score, there often exists more accurate models with higher DFIRE that this protocol will overlook (Figure 8-a). This may be related to the fact that DFIRE is parameterized for residue-residue interactions and, as a result, does not necessarily differentiate the best improvements in backbone alignment. In the case of TR624 the trend is more pronounced, where the lower DFIRE score is directly correlated to a lower native RMSD (Figure 8-b), but for TR557 DFIRE would be a poor standalone evaluation metric for distinguishing native from non-native conformations, which indicates that there are some inherent limitations towards this type of heuristic approach. The combination of backbone deviations from the target structure with energetic scoring as a selection method is used by several other groups.^20,21

Table I.

Refinement Scoring RMSD / GDT

Target	Residue Length	Original RMSD (Å)	Best Δ RMSD (Å)	Model 1 Δ RMSD (Å)	Best of five RMSD Δ (Å)	Best Δ GDT	Model 1 Δ GDT	Best of five Δ GDT
TR557	125	4.06	−1.42	−0.26	−0.28	1.40	−5.6	−2.76
TR568	97	6.15	−0.82	0.1	−0.26	2.58	−1.55	2.58
TR569	79	3.01	−0.31	0.23	0.23	−0.63	−0.56	−0.56
TR624	69	5.19	−0.59	−0.25	−0.25	−3.62	−2.17	−2.17
TR661	185	2.74	−0.16	0.45	−0.01	−11.74	−17.8	−12.20
TR662	75	2.03	−0.38	−0.19	−0.28	7.00	5.33	6.67
TR674	132	3.44	−0.56	−0.25	−0.25	0.00	−5.87	−5.87
TR681	224	2.27	−0.53	−0.11	−0.41	7.61	4.69	2.79
TR689	234	1.66	0.17	0.48	0.43	−5.60	−13.70	−12.70
TR704	235	2.78	−0.83	−0.39	−0.54	16.07	7.45	2.70
TR705	96	4.71	−0.88	−0.56	−0.67	5.73	4.69	7.03
TR723	132	2.23	−0.32	−0.13	−0.13	7.58	3.44	3.44
TR754	68	2.41	−0.03	0.80	0.80	1.43	−8.82	−8.82

Performance of methodology based upon RMSD and GDT change from initial target structure. “Best” indicates the most improved structure overall evaluated by RMSD improvement. “Best of 5” are structures selected blindly using a combination of iRMSD and DFIRE. Model 1 represents the structure with the lowest iRMSD amongst the five blindly selected structures.

Table II.

Refinement Scoring MolProbity / DSSP

Target	Best MolProb	Best Δ MolProb	Model 1 MolProb	Model 1 Δ MolProb	Best DSSP (%)	Best Δ DSSP (%)	Model 1 DSSP (%)	Model 1 Δ DSSP (%)
TR557	1.43	0.12	1.19	−0.12	88.8	16.8	79.2	7.2
TR568	1.30	−0.11	1.80	0.39	78.4	5.2	62.3	−10.9
TR569	1.42	0.25	1.31	0.14	74.7	0.0	70.9	−3.8
TR624	1.66	−0.22	1.82	−0.06	68.1	−21.7	82.6	−7.2
TR661	1.47	0.87	1.45	0.85	90.2	−4.3	85.9	−8.6
TR662	1.25	−0.91	1.52	−0.64	90.7	−1.3	86.7	−5.3
TR674	1.49	−1.39	1.53	−1.35	87.9	2.3	79.5	−6.1
TR681	1.29	−1.58	1.46	−1.41	76.8	5.4	87.6	16.2
TR689	1.24	−1.79	1.63	−1.40	81.3	−5.6	79.8	−7.1
TR704	2.13	−0.58	1.34	−1.37	93.2	6.0	90.6	3.4
TR705	1.43	−2.07	1.51	−1.99	69.8	2.1	61.5	−6.2
TR723	1.49	−0.67	1.21	−0.95	90.1	6.8	87.9	4.6
TR754	1.63	−0.31	0.97	−0.97	85.3	4.7	83.8	3.2

Performance of methodology based upon MolProbity and DSSP. “Best” indicates the most improved structure overall evaluated by RMSD improvement. Model 1 represents the structure with the lowest iRMSD to the target amongst five models selected blindly, using a combination of DFIRE and iRMSD.

Figure 8.

Boxplot of DFIRE values vs. RMSD to native conformation of refined structures. Lower DFIRE generally indicates a more stable model, likely closer to the native conformation, but this trend is not constant amongst all proteins.

Conclusion

We have presented a method for refinement using fast geometric-based FRODA simulations for unfolding proteins to form a set of initial partially putative structures that forms a reservoir for a hierarchically restrained replica exchange molecular dynamics (hr-REMD) simulation.

The use of a reservoir and addition of hierarchical contacts leads to refolding of the structure along with a refinement in most cases (12/13) and this method is currently suitable for small to medium size proteins; particularly for low resolution models where certain parts are considered to be modeled incorrectly. Current methods can make small but consistent improvements on template structures for shorter chain lengths. The future of refinement methods lay in creating more global improvements to structure.