Helicobacter pylori strains vary cell shape and flagellum number to maintain robust motility in viscous environments

Summary

The helical shape of the human stomach pathogen Helicobacter pylori has been suggested to provide mechanical advantage for penetrating the viscous stomach mucus layer. Using single-cell tracking and quantitative morphology analysis we document marked variation in cell body helical parameters and flagellum number among H. pylori strains leading to distinct and broad speed distributions in broth and viscous gastric mucin media. These distributions reflect both temporal variation in swimming speed and morphologic variation within the population. Isogenic mutants with straight-rod morphology showed 7–21% reduction in speed and a lower fraction of motile bacteria. Mutational perturbation of flagellum number revealed a 19% increase in speed with 4 vs. 3 median flagellum number. Resistive force theory modeling incorporating variation of both cell shape and flagellum number predicts qualitative speed differences of 10–30% among strains. However, quantitative comparisons suggest RFT underestimates the influence of cell body shape on speed for helical shaped bacteria.

Introduction

Cell shape diversification is suggested to be one mechanism that helps bacteria cope and adapt to different environments (Young, 2007). For the Gram-negative bacterium Helicobacter pylori, which colonizes the stomach of approximately half of the world’s population, helical shape is thought to enhance motility through the highly viscous mucus overlying the gastric epithelium to which it adheres. Persistent colonization with H. pylori increases risk for gastroduodenal diseases including gastric and duodenal ulcers, gastric adenocarcinoma, and gastric B-cell lymphoma of mucosa-associated lymphoid tissue (MALT) (Peek and Crabtree, 2006; Wroblewski and Peek, 2013). As a neutrophile, H. pylori can survive only minutes in the stomach lumen (Schreiber et al., 2004) and overcomes this acidic environment using urease, an enzyme that hydrolyzes urea to produce NH₃, locally elevating the pH to near neutral. Flagella-mediated motility is essential for infection in several species of pathogenic bacteria (Duan et al., 2013). Successful colonization of the stomach by H. pylori requires both urease (Eaton et al., 1991; Tsuda et al., 1994a; Tsuda et al., 1994b; Nakamura et al., 1998), and flagella-mediated, chemosensory-directed motility (Eaton et al., 1996; Terry et al., 2005; Howitt et al., 2011; Rolig et al., 2012). Furthermore, urease activity may be directly relevant to motility.

Our earlier study showed that H. pylori is immobile in a purified porcine gastric mucin (PGM) gel at low pH, although flagella could be seen rotating (Celli et al., 2009). Upon addition of urea, the bacteria became mobile (Celli et al., 2009) because the hydrolysis of urea elevates the pH triggering a transition of PGM from a soft viscoelastic gel to a viscous solution (Celli et al., 2005; Celli et al., 2007). These experiments suggest that the helical shape of H. pylori does not help it bore its way like a corkscrew through the gel-like mucus layer of the stomach, as had been previously proposed (Yoshiyama and Nakazawa, 2000; Montecucco and Rappuoli, 2001). However, could the helical shape enhance the swimming of H. pylori in viscous solutions of PGM?. To the best of our knowledge, this question has not been examined by systematically comparing the motility of helical and rod-shaped mutants of the same species of bacteria.

From a hydrodynamics viewpoint, the shape of a swimmer is known to alter translational and rotational drag on the cell body, which can affect swimming speed and the bacterium’s ability to sense chemotactic gradients in different environments (Dusenbery, 1998). Berg and Turner suggested that a helical cell shape would result in additional corkscrew-like propulsion for bacteria moving in viscous environments (Berg and Turner, 1979). Ferrero and Lee observed that in highly viscous methylcellulose (MC) solutions of varying viscosity (>100 cP), different clinical strains of helical-shaped Campylobacter jejuni were more motile than rod-shaped bacteria from several different species, Vibrio cholerae, Salmonella enteritidis, and Escherichia coli (Ferrero and Lee, 1988). Karim et al. showed that H. pylori and C. jejuni swim faster in liquid broth as compared to E. coli, presumably due to their helical cell body shape (Karim et al., 1998). However, both these studies compare different species of bacteria, which have differences in flagellum morphology, number and arrangement, and possibly motor output, making conclusions on the influence of cell body shape difficult to interpret.

We and others approached the role of H. pylori’s cell shape in stomach colonization using genetic screens to identify cell shape-determining (csd) genes required for H. pylori’s characteristic helical cell morphology (Sycuro et al., 2010; Bonis et al., 2010; Sycuro et al., 2012; Sycuro et al., 2013). H. pylori cell shape mutants show impaired stomach colonization in a mouse infection model, suggesting helical cell shape is important for initial colonization and/or persistence in the stomach (Sycuro et al., 2010; Bonis et al., 2010; Sycuro et al., 2012). Several csd genes encode peptidases that modify the bacterial cell wall, composed of peptidoglycan (PG), which is responsible for rigidity and cell shape in most bacteria (Cabeen and Jacobs-Wagner, 2005). Elimination of the PG peptidases Csd4 or Csd6 yielded bacteria with straight rod morphology, but the mutants show normal flagellation and cell growth properties (Sycuro et al., 2012; Sycuro et al., 2013). While we had previously shown a semi-solid agar motility defect for csd4 straight rod mutants (Sycuro et al., 2012), another group suggested that csd6 mutants (H. pylori strain G27) show enhanced motility in semi-solid agar as compared to wild-type (Asakura et al., 2010), but the morphology of the csd6 mutant was not assessed. In Campylobacter jejuni, deletion of pgp2, a homolog to H. pylori csd6, results in straight rod morphology and mutants show motility defects in semi-solid agar, defects in biofilm formation, and reduced fitness in a chick colonization model (Frirdich et al., 2014).

Here, we present a detailed study relating morphology and motility using optical and electron microscopy to measure cell shape and flagellum parameters, and live-cell imaging to track individual bacteria to examine swimming behavior in several polymer solutions including the physiologically relevant porcine gastric mucin (PGM). PGM is homologous to the human glycoprotein MUC5AC, the major secreted mucin expressed in the stomach mucosa by surface epithelial cells (Sellers et al., 1987; Bansil et al., 2013). PGM has been shown to exhibit similar rheological properties to human mucus scraped from the surface of the gastric mucosa, making it an ideal comparison to H. pylori’s niche environment (Schrager and Oates, 1974; Pearson et al., 1980; Bell et al. 1984; Bell et al., 1985). Gastric mucus is believed to have two layers differing in mucin concentration, a thin firmly adherent, high concentration layer (around 30 mg mL⁻¹), and an overlying loosely adherent layer of mucus on the luminal surface (15 mg mL⁻¹) (Taylor et al., 2004). We provide further insight into the effects of cell body shape morphology and flagellum number on H. pylori swimming speed using a resistive force theory model (Gray and Hancock, 1955). Combined experimental and theoretical findings indicate that H. pylori’s natural variation in cell body shape and flagellum number independently contribute to robust motility in viscous environments, including gastric mucin.

Results

Gastric mucin shows physiologically relevant solution and gel-like properties

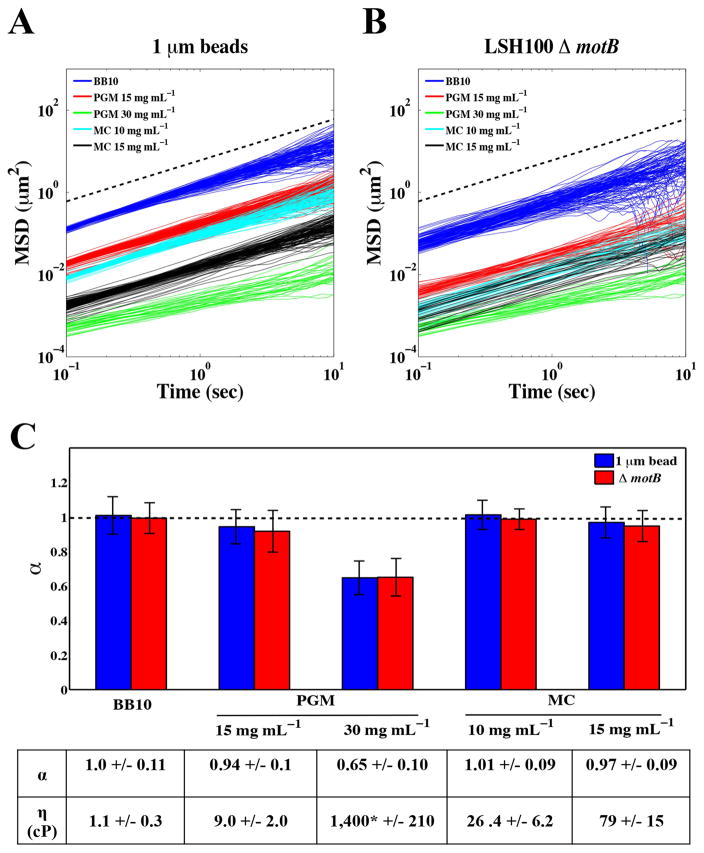
To examine the micro-rheological properties of the environment in which H. pylori motility is to be measured we used microscopic single particle tracking. This technique probes the Brownian motion of particles (for a review see Cicuta and Donald, 2007) and has been previously applied to investigate the microrheology of PGM (Lieleg et al., 2010; Bansil et al., 2013; Georgiades et al., 2014). To model the viscous environment of the human gastric mucosa where H. pylori resides, we used physiologically relevant concentrations of PGM of 15 and 30 mg mL⁻¹. For comparison to previous work on H. pylori motility in viscous solutions (Hazell et al., 1986; Worku et al., 1999), we also examined methylcellulose solutions at concentrations of 10 and 15 mg mL⁻¹. Fig. 1A shows the averaged mean squared displacement (MSD = 〉r(t)²〈, μm²) of 1μm diameter fluorescent polystyrene particles calculated from the measured position (r(t)) as a function of time (t). To confirm that bacteria experience a similar environment, we also tracked ΔmotB mutants, which retain wild-type flagellum structure but have non-functional flagellum motors (Ottemann and Lowenthal, 2002) (Fig. 1B). We found that the MSD values of non-motile bacteria were smaller relative to those acquired for diffusing particles (Fig. 1B). This reflects the increased drag due to the larger size and anisotropic shape of bacteria compared to spherical particles. The time dependence of the MSD is usually described using the relation 〉r(t)²〈 = At^α. In a viscous fluid, particles exhibit normal Brownian diffusion with the exponent α = 1 and A = 4D, where A is the constant of proportionality and D is the diffusion constant of the particle (Cicuta and Donald, 2007). In complex fluids, such as viscoelastic gels, particles exhibit sub-diffusive behavior with an exponent of α < 1.

Figure 1. Physiologic concentrations of gastric mucin exhibit solution and gel-like properties.

Mean square displacement (MSD, μm²) values as a function of time (sec) for 1 μm fluorescent particles (A) and LSH100 ΔmotB bacteria (B) in broth (BB10), PGM (15 mg mL⁻¹ and 30 mg mL⁻¹) and MC (10 mg mL⁻¹ and 15 mg mL⁻¹) along with (C) Average power of law exponents (α). Average viscosity values (η, cP) and their standard deviations are summarized in the table above (see text for calculation details). All error bars represent standard error and dashed lines represent linear scaling of MSD over time (α=1). *This value is significantly larger compared to the others due to the gel-like nature of PGM at 30 mg mL⁻¹.

By fitting the ensemble averaged MSD, we obtained the exponent α and A. For each solution, the values of α were the same for both polystyrene particles and ΔmotB bacteria (Fig. 1C). Brownian diffusion (α = 1) was observed in broth, PGM at 15 mg mL⁻¹, and MC solutions of 10 and 15 mg mL⁻¹, implying these solutions behave as viscous liquids (Fig. 1C). The viscosities (η) (cP) of each solution were calculated from the measured bead diffusion constants via the Stokes Einstein relation (η=kT/6πRD), where T and R represent temperature and bead radius, respectively (Fig. 1C). Sub-diffusive behavior was observed for PGM at 30 mg mL⁻¹ (α =0.65 +/− 0.10), implying that at this higher concentration, PGM is a gel-like viscoelastic polymer (see Bansil et al., 2013 for a brief review of viscoelasticity). Our results are in agreement with the observations of Georgiades et al., where a transition to viscoelastic behavior was observed in PGM at 25 mg mL⁻¹ (Georgiades et al., 2014). Our results suggest that PGM at 30 mg mL⁻¹ displays gel-like properties that resemble the rheological gel-like environment of mucus near the gastric epithelium, and PGM at 15 mg mL⁻¹ displays solution-like properties that resemble the rheological environment that H. pylori encounters as it swims through the gastric mucus found near the acidic lumen of the stomach (Taylor et al., 2004). We used these PGM concentrations in our in vitro experiments to model the solution and gel-like environments of stomach mucus and to examine H. pylori motility.

Wild-type H. pylori strains display diverse and distinct cell body and flagellum morphologies

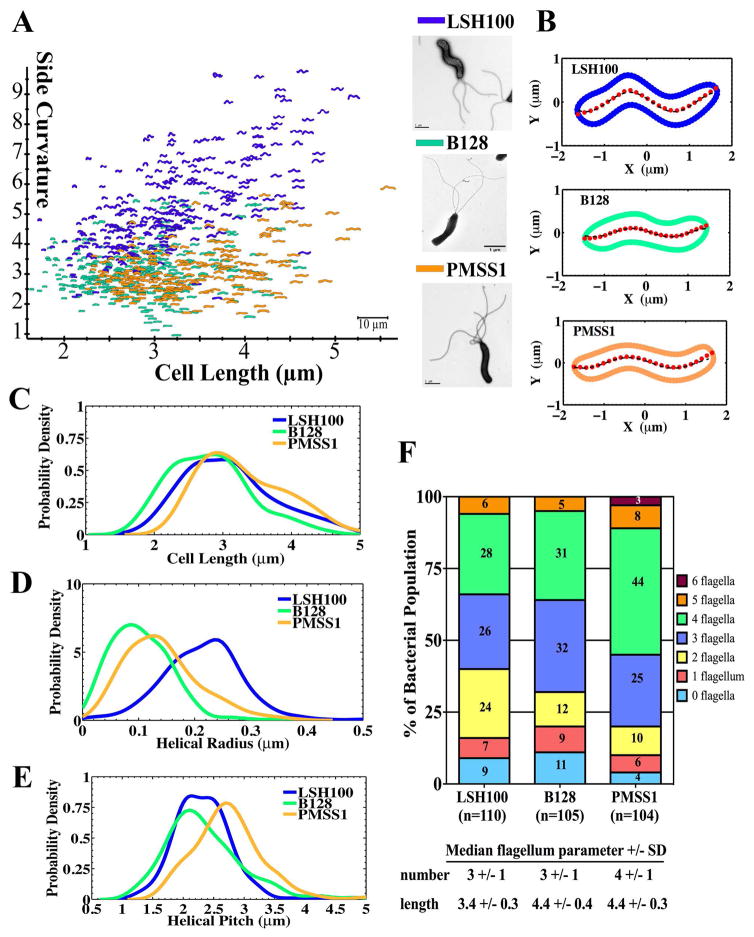
To address the impact of cell morphology on motility, we began by analyzing the morphology of three unrelated wild-type strains: LSH100, B128, and PMSS1 (Table S1). Helicobacter pylori clinical strains show a high degree of genetic and phenotypic variability and there is no consensus lab strain used by the H. pylori research community. These commonly used strains were all isolated from symptomatic human patients on three different continents (PMSS1-Australia, LSH100-Europe, B128-North America) and robustly colonize mice (LSH100, PMSS1, B128) or mongolian gerbils (B128), the major small animal models of H. pylori stomach infection. Cell morphology was characterized by analyzing phase contrast images using the CellTool software (Pincus and Theriot, 2007; Lacayo et al., 2007; Sycuro et al., 2010), which has been previously used to segregate H. pylori cells based on different shape parameters, including cell length, diameter, and side curvature (Sycuro et al., 2010; Sycuro et al., 2012; Sycuro et al. 2013). Side curvature is the measure of the total curvature of a bacterial cell excluding its poles and the curvature itself is defined as the reciprocal of the radius of a circle that is tangent to a curve made at any point (Sycuro et al., 2010). Wild-type H. pylori strains display heterogeneous morphologies ranging from straight to predominantly helical, and bacterial cells of different cell lengths were observed within each population (Fig. 2A). As summarized in Table 1, all three strains have similar values of cell diameter but distinct cell length and side curvature profiles.

Figure 2. Wild-type H. pylori strains display diverse cell shape and flagellum morphologies.

(A) Side curvature vs. cell length (μm) for individual bacterial cells imaged using phase contrast microscopy of LSH100 (blue, n=282), B128 (green, n=274), and PMSS1 (orange, n=222) bacteria. Inset panel: TEM images of each. Scale bar = 1 μm. Data combined from two independent cultures for each strain. (B) Representative bacterial centerlines (red dots) for each wild-type strain fitted with a generalized sine function, $y=Rsin(\frac{2\pi }{P}x+\delta )$ (black dashed line); R, helical radius; P, helical pitch; δ, phase shift term (δ ≈ π for the bacteria shown). (C–E) Smooth histograms of probability density for cell length (μm) (C), helical radius (μm) (D), and helical pitch (μm) (E) of LSH100 (n=262), B128 (n=272), and PMSS1 (n=215) bacteria. (F) Flagellum number counts measured from SEM or TEM images reported as percent of the total bacterial population examined (n=104–110 bacteria).

Table 1.

Average cell body and helical parameters of wild-type H. pylori strains.

Strain	Average cell body parameters from CellToola				Average helical parametersb
	n	Cell length (μm)	Side Curvature	Cell diameter (μm)	n	Helical radius (μm)	Helical pitch (μm)
LSH100	282	3.17	5.26	0.55	262	0.22	2.3
B128	274	2.82	3.08	0.58	272	0.10	2.4
PMSS1	222	3.33	3.10	0.57	215	0.14	2.8

^aCell body parameters acquired from CellTool.

^bHelical parameter measurements acquired from fitting centerlines to a sinusoid.

To further characterize helical morphology, we obtained the helical radius (R) and pitch (P) (length of one complete helical turn) using centerline measurements provided by CellTool. For each bacterial cell, centerlines were fitted using a sine function $y=\mathit{Rsin}(\frac{2\pi }{P}x+\delta )$ (Fig. 2B). Figures 2C–E show the distribution of each strains’ cell length, helical radius, and helical pitch, and their average values are summarized in Table 1. All strains showed overlap in cell length distributions, but the B128 population shows a higher probability of shorter cells (Fig. 2C). PMSS1 showed an increased helical pitch as compared to both LSH100 and B128 (Fig. 2E), while LSH100 showed significantly increased helical radius as compared to both B128 and PMSS1 (Fig. 2D and Table 1). These observations correlated well with LSH100 having increased side curvature (Fig. 2A and Table 1), while B128 and PMSS1 showed smaller values consistent with a smaller radius.

We also examined flagellum morphologic parameters using transmission electron microscopy (TEM) and scanning electron microscopy (SEM) (see Experimental Procedures). The three wild-type strains showed a mixed population of cells with 0 to 6 uni-polar flagella (Fig. 2F). LSH100 and B128 shared a median flagellum number of 3 +/− 1 (+/− standard deviation), while PMSS1 had a median flagellum number of 4 +/− 1 and a higher proportion of bacteria with 4 to 6 flagella (55%) relative to LSH100 (34%) and B128 (36%) (Fig. 2F). LSH100 had a median flagellum length of 3.4 +/− 0.3 μm, which was shorter than both PMSS1 (4.4 +/− 0.3 μm) and B128 (4.4 +/− 0.4 μm) (Fig. 2F).

In summary, the three wild-type H. pylori strains examined varied in multiple cell morphologic parameters expected to influence motility, including cell length (B128 shortest), helical radius (LSH100 highest), flagellum number (PMSS1 highest), and flagellum length (LSH100 shortest).

Wild-type H. pylori strains display a broad distribution of swimming speeds

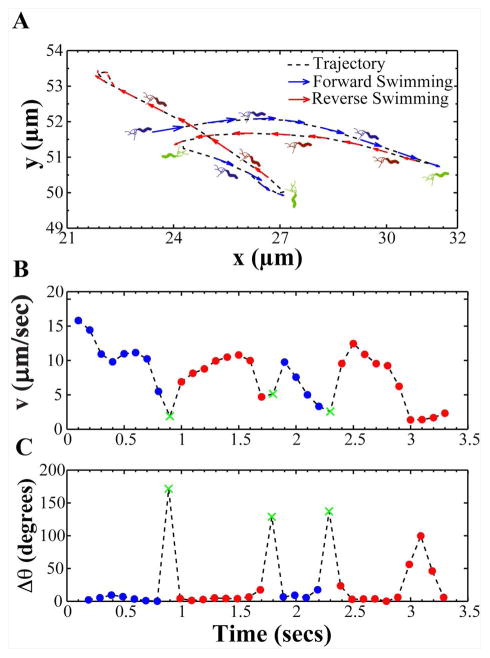
To examine H. pylori motility, we used live-cell imaging and particle-tracking methods to automatically track hundreds of individual bacterial cells in broth and in viscous PGM or MC media. We collected videos of bacteria swimming at the mid-level plane between the coverslip and the glass slide. We tracked bacteria from ten second videos, which allowed us to capture bacteria swimming in the field of view and it provided sufficient time to acquire a broad sampling of each bacterium’s instantaneous swimming speeds (Fig. S1). The recorded videos show that H. pylori exhibits a complex motion consisting of periods of straight swimming (runs), interrupted by short periods of directional reorientation and/or reversal in swimming direction (see Video 1). Figure 3A shows a representative bacterial trajectory and Fig. 3B shows its corresponding instantaneous speed as a function of time. The speed is observed to vary between high values (~ 10 – 15 μm/s) and low values of ~ 1 μm/s. The low speeds show a one to one correspondence with reorientation events represented by a large change in swimming direction (Δθ) as shown in Fig. 3C. Using a similar method to Son et al. (Son et al., 2013) we classified reorientations as any event where abrupt decreases in bacterial swimming speed (v_{local min}< (v_avg/2)) happened or Δθ was significantly larger than angle changes resulting from rotational diffusion (Δθ > 25 degrees was used exclusively in this study). Reversals were classified as any reorientation event for which the directional angle change Δθ > 110 degrees (Fig. 3A). In our analysis, the direction of swimming observed at the start of the video was considered “forward” solely as an annotation relevant to the video frame and not relative to bacterial polarity. Polarity could not be determined because bacterial flagella were not observable at the magnification and optical resolution of our experiments. After a reversal occurred, bacteria were assumed to swim in the reversed direction until another reversal event took place. Using these criteria, all trajectories were segmented into forward and reverse swimming directions and reorientation events. From the segmented trajectories, we calculated several motility parameters: instantaneous swimming speeds (the speed between two points of a track); reversal frequency (reversals per second) and speed measurements of both forward and reverse directions; and percent track linearity (%TL, the ratio of average straight line velocity (μm/s) to average swimming speed (μm/s) x 100%). Measurements acquired during reorientation events were excluded from our speed calculations.

Figure 3. A representative bacterial trajectory depicting the swimming motion of H. pylori.

(A) A representative bacterial trajectory of H. pylori is shown segmented into forward (blue) and reverse swimming directions (red). In our analysis, the direction of swimming observed at the start of the video was considered forward. A reversal in swimming direction (green) was identified when bacteria exhibited a large angle change (Δθ) > 110 degrees. Upon a reversal, bacteria were assumed to continue swimming in the reversed direction (red) until another reversal took place. (B) Instantaneous forward and reversal swimming speeds and (C) change in swimming angle (Δθ) of the bacterium in panel A over the course of time it was tracked (X (green) denotes reversals in swimming direction).

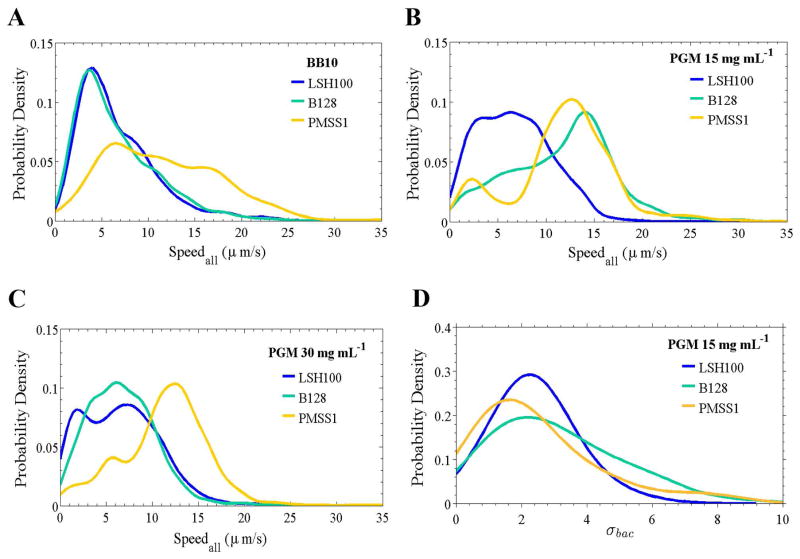
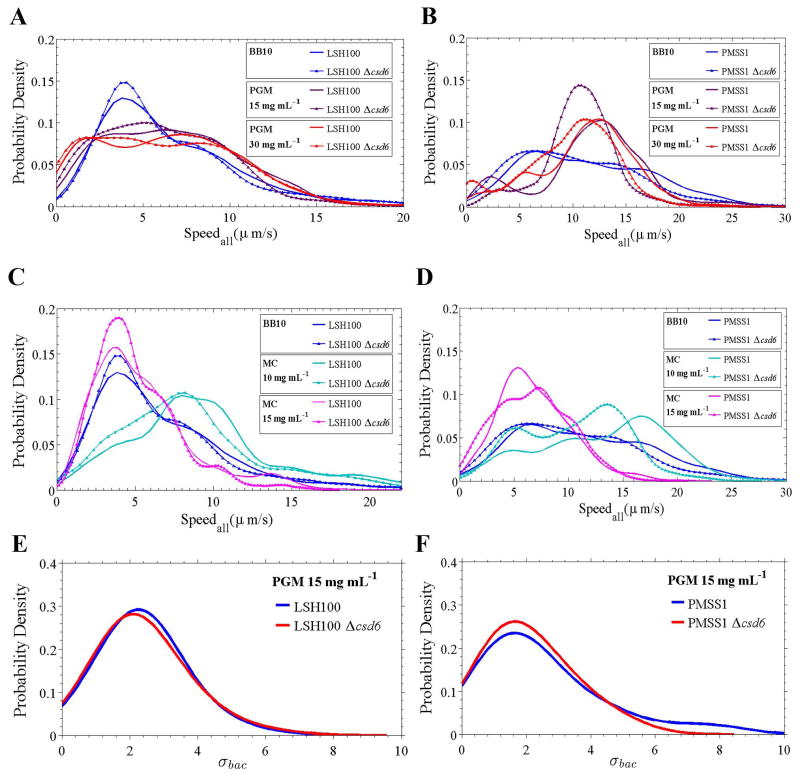
As shown in Fig. 4A–C, the three wild-type H. pylori strains exhibited broad overlapping distributions of instantaneous swimming speeds in broth and PGM. These distributions are concatenations of instantaneous swimming speeds from all bacterial cells analyzed for each strain and in each solution tested. The shapes of these broad speed distributions depend on both strain and medium in a complex way, presumably reflecting the differences in cell shape, number of flagella, and flagellum length. To characterize such broad distributions it is not enough to use a single average. We therefore computed the average speed (v_avg), median speed (v_m), maximum speed (v_max), and standard deviation (σ) of the distribution of speeds (Table 2). The maximum swimming speed gives a measure of the fastest swimming speed, likely arising when all flagella motor are firing in synchrony.

Figure 4. Wild-type H. pylori strains display diverse speed profiles and temporal variation in swimming speed.

Smooth histograms summarizing speed distributions for all bacteria analyzed (Speed_all) for LSH100, B128, and PMSS1 bacteria swimming in broth (BB10) (A), in viscous solutions of PGM (15 mg mL⁻¹) (B), and in gel-like PGM solutions (30 mg mL⁻¹) (C). (n=100 bacteria analyzed in each case) (C). Representative data is from one of two or three independent experiments for each strain and the median swimming speeds of each wild-type strain are summarized in Table 2. K-S p = 0.1100 for LSH100 vs. B128 in BB10; p < 0.0001 for LSH100 vs. PMSS1, and B128 vs. PMSS1 in BB10; and p < 0.0001 for LSH100 vs. B128, LSH100 vs. PMSS1, and B128 vs. PMSS1 in viscous PGM media. (D) Smooth histograms summarizing the standard deviation distributions acquired for each individual bacterium’s speed trajectory, σ_bac, of each wild-type strain in a viscous solution of PGM at 15 mg mL⁻¹. K-S p = 0.0050 for LSH100 vs. B128; p = 0.0314 for LSH100 vs. PMSS1, and p = 0.0082 for B128 vs. PMSS1. K-S p <0.05 was considered significant.

Table 2.

Speeds for wild-type bacteria and straight rod mutants swimming in broth and viscous media.

Solution	Strain		n	Inst. values	vavg (μm/s)	vm (μm/s)	vmax (μm/s)	σ	K-S p-valuec	% reduction to vm relative to WT
BB10		B128	99	2105	6.6	5.5	28.0	4.3
	LSH100	WT	100	2538	6.8	5.7	48.0	4.7	0.0955	7%
		Δcsd6	100	2058	6.5	5.3	30.1	4.1
	PMSS1	WT	100	1975	11.6	10.8	49.2	6.3	<0.0001	11%
		Δcsd6	100	1930	10.5	9.6	38.8	6.0
PGMa 15 mg mL−1		B128	100	2112	11.7	12.5	36.6	5.5
	LSH100	WT	100	3325	6.7	6.5	29.1	3.8	<0.0001	11%
		Δcsd6	100	3886	6.2	5.8	22.8	3.6
	PMSS1	WT	100	2073	11.8	12.2	39.3	5.3	<0.0001	11%
		Δcsd6	100	2550	10.7	10.8	28.4	3.6
PGM 30 mg mL−1		B128	100	2752	6.7	6.5	41.9	3.7
	LSH100	WT	100	2790	6.6	6.4	30.1	4.2	0.0005	8%
		Δcsd6	100	2951	6.3	5.9	33.3	4.2
	PMSS1	WT	100	2224	11.3	11.8	34.8	4.7	<0.0001	13%
		Δcsd6	100	2276	9.7	10.3	24.8	4.4
MCb 10 mg mL−1	LSH100	WT	100	2076	9.5	8.8	46.1	5.2	<0.0001	10%
		Δcsd6	100	2151	8.6	7.9	39.4	5.0
	PMSS1	WT	100	1874	13.2	14.2	32.2	5.8	<0.0001	21%
		Δcsd6	100	2251	10.6	11.2	24.2	4.6
MC 15 mg mL−1	LSH100	WT	100	3194	5.5	4.8	26.1	3.3	<0.0001	6%
		Δcsd6	100	3544	5.1	4.5	16.6	2.6
	PMSS1	WT	48	965	6.9	6.4	20.6	3.3	0.0104	NRd
		Δcsd6	48	1201	6.8	6.8	17.9	3.4

^aPGM: Purified gastric mucin at pH 6.0.

^bMC: Methylcellulose.

^cFor K-S tests used to compare WT to mutant cumulative distributions of swimming speeds, p-values < 0.05 are considered significant.

^dNR: No reduction.

First considering LSH100 and PMSS1, Fig. 4A–C shows that LSH100 speed distributions are different from those of PMSS1, having lower speeds than PMSS1 in all three solutions. For example, in all three solutions v_avg and v_m are almost twice as large for PMSS1 compared to LSH100 and the standard deviation is approximately 30–40% larger (Table 2). Although v_avg of LSH100 and PMSS1 does not vary much between broth and PGM, these strains show increased proportion of higher swimming speeds in PGM compared to broth. This observation is also confirmed by the change in v_m. For LSH100 we find v_m = 5.7 μm/s in broth, which increases to 6.5 μm/s in PGM at 15 mg mL⁻¹, and exhibits a similar median swimming speed of 6.4 μm/s in PGM at 30 mg mL⁻¹ (Table 2).

B128 shows similar speed distributions to LSH100 in broth and PGM at 30 mg mL⁻¹ (Fig. 4A,C), while its speed distribution shifts to higher speeds in PGM at 15 mg mL⁻¹, becoming more similar to PMSS1 (Fig. 4B). This may be attributed to that fact that the shape of B128 is similar to PMSS1 but its flagellum parameters are closer to those of LSH100 (Fig. 2F). B128 also exhibits the non-monotonic trend in PGM observed for LSH100 and PMSS1 (Table 2).

In addition to monitoring the speed of swimming bacteria, we also recorded the number of bacteria that appeared non-motile for LSH100 and PMSS1 in broth and PGM. Bacteria that exhibited displacements < 0.3 μm were classified as non-motile (immobile). The percentage of immobilized bacteria in all solutions (10–50%) exceeded the percentage of bacteria with zero flagella (4–9%), and increased with increasing viscosity of the media (Table 3). PMSS1 had the fewest percent-immobilized bacteria and the highest v_m in all solutions. Thus, the tendency to not be immobilized in the viscoelastic PGM gel correlates with swimming speed.

Table 3.

Fraction of immobile bacteria in broth and viscous PGM media.

Strain		BB10		PGMa 15mg mL−1		PGM 30 mg mL−1
		n	% immobileb	n	% immobile	n	% immobile
LSH100	WT	977	20	536	24	820	50
	Δcsd6	494	21	546	30	456	52
Increase in % immobile bacteria relative to WT		5%		25%		4%
PMSS1	WT	558	10	330	15	456	38
	Δcsd6	371	13	328	21	504	51
Increase in % immobile bacteria relative to WT		30%		40%		34%

^aPGM: Purified gastric mucin at pH 6.0.

^bBacteria exhibit displacements < 0.3 μm (MSD < 0.1 μm²).

Speed distributions also reflect temporal variation of individual bacteria

The speed distributions shown in Fig. 4 arise from two unrelated factors: (i) variation in bacterial cell shape and size in the population, and (ii) variation in the swimming speed of individual bacteria over time. As seen in Fig. 3B, individual bacteria alter their swimming speed by an order of magnitude over the time of tracking (typically 1–10 seconds). This temporal variation cannot result from variation in cell morphology, which should remain constant during the track time (H. pylori doubling time is 2.5 – 4 hours, depending on the strain, under these growth conditions). In order to separately assess the temporal variation we processed the trajectories of each bacterium and obtained the standard deviation of each bacterium’s speed, σ_bac. Figure 4D shows the distribution of speed standard deviations, σ_bac, for the three different H. pylori strains in PGM at 15 mg mL⁻¹. The breadth of the σ_bac distributions (4D) indicate that population level speed variation (4B) is largely due to speed variation within individual bacterial trajectories (as illustrated for an example bacterium in Fig. 3B). LSH100, B128, and PMSS1 showed slightly different distributions (K-S statistics, p < 0.05 for all comparisons) suggesting they may have different swimming dynamics in PGM (Fig. 4D). We obtained similar results when comparing LSH100 to B128 and PMSS1 to B128 in PGM in 30 mg mL⁻¹ (Fig. S2), although these differences were not observed when comparing LSH100 to PMSS1 in PGM 30 mg mL⁻¹ (K-S, p =0.89). Interestingly, all wild-type strains showed similar distributions in broth (K-S, p >0.05) (Fig. S2). These results indicate that the temporal variation in swimming speeds of H. pylori depends on both the strain and swimming environment, and the breadth of the speed distribution is largely due to individual bacteria varying their swimming speed in time.

Helical cell shape promotes increased motility in broth and viscous media

To directly address whether the helical cell shape of H. pylori impacts its motility, we compared the motility of helical wild-type bacteria to isogenic straight rod mutants (Δcsd6) of LSH100 (see Videos 1–2). We first confirmed that the cell shape mutant did not show altered flagellum number or length (Table 4 and Fig. S3), as previously described (Sycuro et al., 2012). We found that while the overall speed distribution of the LSH100 Δcsd6 mutant was similar to wild-type LSH100 in broth (Fig. 5A), v_m decreased by 7% (Table 2). In addition, straight rods displayed an 11% reduction in v_m in PGM at 15 mg mL⁻¹, and an 8% reduction in v_m in PGM at 30 mg mL⁻¹ (Table 2). While the reduction in speed between the Δcsd6 mutant and wild-type is statistically significant in the PGM solutions (K-S, p <0.0001), it is not so in the broth solution (K-S, p =0.0955) (Table 2).

Table 4.

Median flagellum parameters of wild-type H. pylori and isogenic straight rod mutants.

Strains	Median flagellum parametera +/− SDb
	n	Flagellumnumber	n	Flagellum length (μm)
LSH100	110	3 +/− 1	15	3.4 +/− 0.3
LSH100 Δcsd6	109	3 +/− 1	15	3.3 +/− 0.4
PMSS1	104	4 +/− 1	15	4.4 +/− 0.3
PMSS1 Δcsd6	105	4 +/− 1	15	4.2 +/− 0.2

^aFlagellum number counts were acquired from SEM images and flagellum length measurements were acquired from TEM images.

^bStandard Deviation (SD).

Figure 5. Straight rod mutants show decreased swimming speeds in broth and viscous media.

Speed distributions for all bacteria analyzed (Speed_all) for wild-type and Δcsd6 isogenic straight rod mutants in broth (BB10) and viscous PGM media (15 and 30 mg mL⁻¹) (A, B), and in broth (BB10) and viscous MC media (10 and 15 mg mL⁻¹) (C, D). One of two or three independent experiments are shown. (E, F) Smooth histograms summarizing the standard deviation distributions acquired for each individual bacterium’s speed trajectory, σ_bac, of wild-type LSH100 (E) and PMSS1 bacteria (F) as compared to their respective isogenic straight rod mutants in viscous solutions of PGM at 15 mg mL⁻¹. The distributions show similar temporal speed variation profiles between wild-type and straight rod mutants, where K-S p = 0.44 for LSH100 vs. LSH100 Δcsd6, and p = 0.57 for PMSS1 vs. PMSS1 Δcsd6.

To further test the generality of this phenomenon, we generated a csd6 deletion mutant in the PMSS1 strain background. We first analyzed the cell shape of this strain and found that deletion of csd6 resulted in straight rod morphology, measured as loss of cell curvature (Fig. S4), as previously shown in LSH100 (Sycuro et al., 2013). The PMSS1 Δcsd6 straight rod mutant also had normal flagellum number and length compared to wild-type (Table 4 and Fig. S3). In this case, we found significant differences between Δcsd6 mutant and wild-type speed distributions in broth and in viscous PGM solutions (Fig. 5B), with a slightly larger reduction in median swimming speed compared to LSH100 (Table 2). For example, straight rods displayed an 11% reduction in v_m in broth and in PGM at 15 mg mL⁻¹, and a 13% reduction in a gel-like PGM environment at 30 mg mL⁻¹ (Table 2).

To investigate whether straight rods exhibited reduced swimming speeds in a different viscous polymer solution, we analyzed their swimming speeds in viscous MC media (see Videos 3–4). In agreement with our results in PGM, we found significant differences in swimming speed distributions (Fig. 5C,D) and reduced median swimming speeds between straight rods and their respective wild-type strains (Table 2). Both straight rods mutants also showed a higher fraction of immobilized bacteria relative to their respective wild-type strains. This effect was most pronounced in PGM at 15 mg mL⁻¹ where a 25 and 40% increase was observed for LSH100 and PMSS1, respectively (Table 3 and Fig. S5). Our results with straight rod mutants indicate that helical morphology enhances the fraction of motile H. pylori and their swimming speed. Motility enhancement was seen in all solutions but did not show an obvious dependence on viscosity.

Loss of helical morphology does not alter temporal speed variation, cell reversals, or track linearity

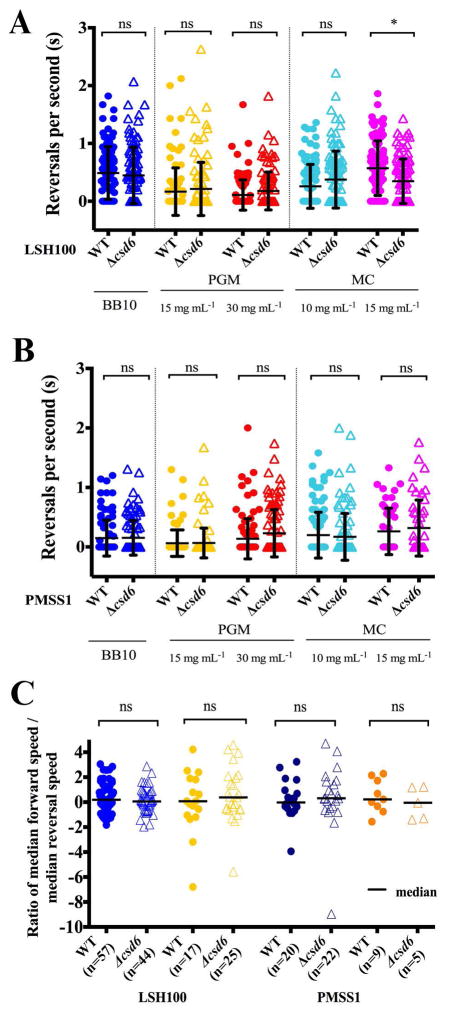
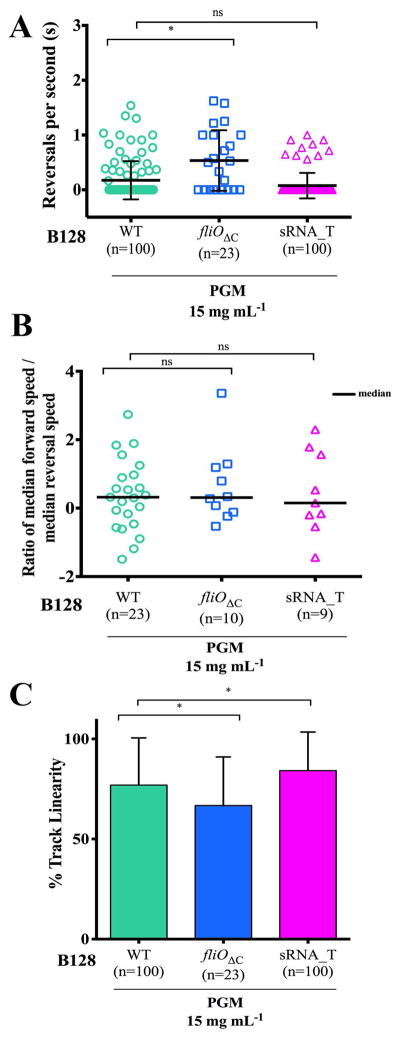
We utilized the cell trajectory data of the two wild-type and isogenic Δcsd6 straight rod mutant strains to investigate whether other motility parameters were affected by perturbation of helical cell morphology. Analysis of the individual bacterium’s speed standard deviations, σ_bac, indicated that the variation in swimming speed with time was similar for the Δcsd6 mutants when compared to wild-type bacteria in PGM at 15 mg mL⁻¹ (Fig. 5E,F) and in broth or PGM at 30 mg mL⁻¹ (Fig. S6). We did not observe differences in reversal frequency between wild-type strains and their respective isogenic straight rod mutants in broth or viscous PGM or MC media (Fig. 6A,B). We also calculated the ratios of median forward swimming speed to median reversal swimming speed for individual bacterial cells that reversed and maintained at least 3 instantaneous forward or reversal speed values while swimming. We did not observe any significant differences in the ratios acquired for wild-type strains and their respective isogenic straight rod mutants in any of the solutions tested (Fig. 6C and data not shown). All strains exhibited relatively similar median ratios, close to 1 (Fig. 6C).

Figure 6. Reversal frequency and ratio of forward to reverse speed are similar across wild-type strains and shape mutants.

(A, B) Dot plots summarizing the number of reversals per second of wild-type H. pylori strains and isogenic Δcsd6 straight rod mutants in LSH100 (A) and PMSS1 (B) strains in broth (BB10) and in viscous PGM or MC media. Mean values of reversals per second are shown as bolded black lines and error bars indicate one standard deviation from the mean. Data shown is from one of two or three representative experiments for each strain. (C) Dot plots summarizing individual ratios of median forward swimming speed to median reversal swimming speed acquired for each bacterial cell that reversed and maintained at least 3 instantaneous forward or reversal speed values while swimming in broth or viscous PGM solutions (15 mg mL⁻¹). Ratios are plotted on a log₂ scale and median values are shown as bolded black lines. All data shown is from the same experiment in Fig. 5. *K-S p <0.05 was considered significant and ns = no significant difference.

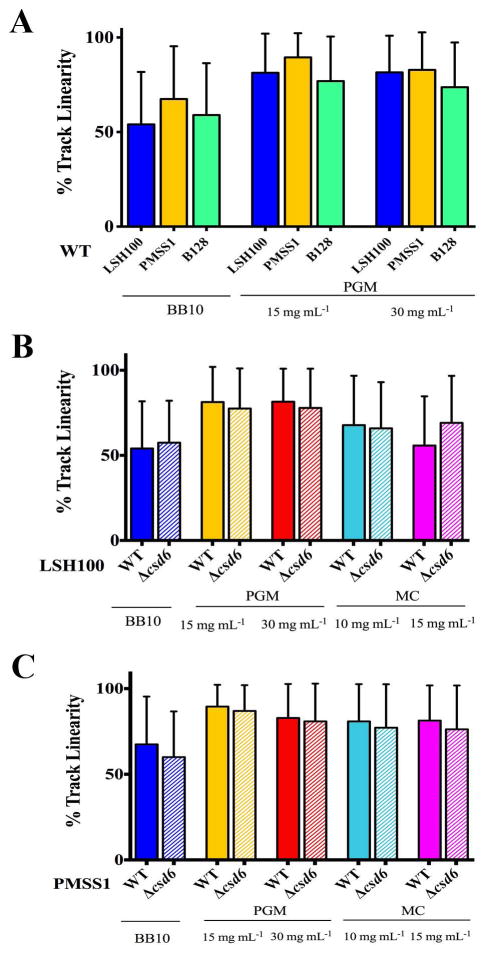
Finally, we examined percent track linearity (%TL) as a measure of cell path trajectory. Wild-type H. pylori strains showed more continuous straight runs in viscous solutions of PGM compared to broth (Fig. 7A), as previously described (Celli et al., 2009). We did not observe any differences in %TL between wild-type strains and their respective isogenic straight rod mutants in broth and in viscous PGM or MC media (Fig. 7B,C, and Table S3). Thus, while wild-type H. pylori strains show increased %TL in their swimming trajectories in viscous solutions of PGM, this increase in % TL does not require helical cell shape. Our results indicate that while loss of helical cell shape reduces the swimming speed of H. pylori, helicity does not influence any other measured aspect of motility.

Figure 7. H. pylori show increased % track linearity in their swimming trajectories in viscous PGM media, irrespective of cell shape.

Bar histograms show cell path trajectory as percent track linearity (%TL) between wild-type H. pylori strains (solid bars, A–C) and isogenic Δcsd6 straight rod mutants (hashed bars, B–C) in LSH100 and PMSS1 strains, as calculated from the ratio of straight-line velocity to curvilinear velocity in broth (BB10) and in viscous PGM or MC media. Error bars represent SD and mean %TL values are summarized in Table 2. Data are from the same experiments shown in Figs 4 and 5.

H. pylori swimming speed correlates with flagellum number

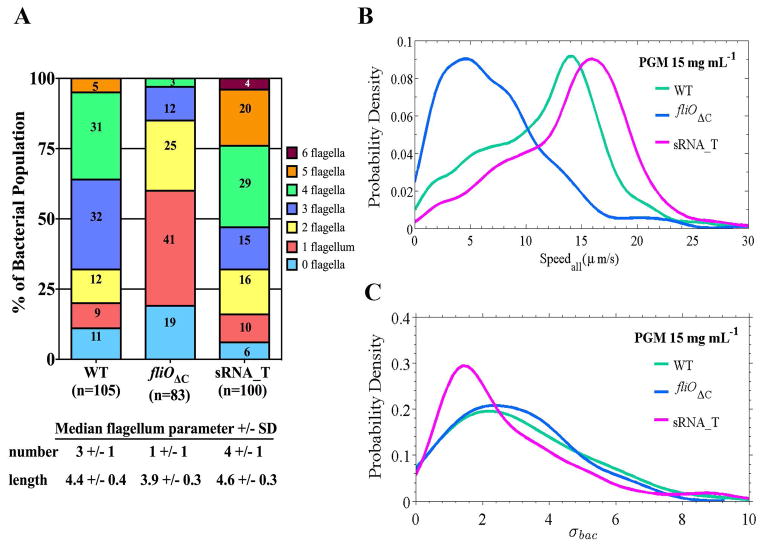
Our studies suggest that multiple aspects of the cell body morphology of helical bacteria may influence H. pylori swimming speed. In addition, flagellation may contribute to the swimming speed differences observed between wild-type H. pylori strains, as suggested by the increased swimming speed profiles in all media for PMSS1 which has a median flagellum number of 4 compared to 3 for B128 and LSH100 (Fig. 2F). To test the effect of flagellum number on H. pylori swimming speed, we utilized mutations that lead to altered flagellation in strain B128. For an isogenic strain with a reduced number of flagella, we used a fliO_ΔC mutant which bears a C-terminal truncation in the flagella export apparatus protein FliO (Tsang & Hoover, 2014) and has a median flagellum number of 1 +/− 1 (Fig. 8A). For an isogenic stain with an increased number of flagella, we used a putative small non-coding RNA mutant (designated sRNA_T; locus tag HPnc7700 in H. pylori 26695), which has a median flagellum number of 4 +/− 1 (Fig. 8A). sRNA_T was identified from a transcriptome analysis of H. pylori 26695 and is predicted to be transcribed from a FliA-dependent promoter (Sharma et al., 2010). HPnc7700 is located downstream of the 16s rRNA gene and downstream of HP1439, which encodes a hypothetical protein of unknown function. HP1439 and HPnc7700 are in the same orientation and in the opposite orientation of the 16s rRNA gene. The HP1439 homolog in strain B128 (HPB128_16g92) is predicted to be longer than HP1439 (155 versus 81 amino acid residues) and overlaps the sequence coding the putative sRNA_T, and so the sRNA_T mutant is potentially deficient for both sRNA_T and the product of HPB128_16g92.

Figure 8. Swimming speed correlates with flagellum number.

(A) Individual bacteria were analyzed for the number of flagella from TEM images and are reported as percent of the total bacterial population examined (n=83–105). (B) Speed distributions for all bacteria analyzed (Speed_all) and (C) distributions summarizing the standard deviation of each individual bacterium’s speed trajectory, σ_bac, acquired for wild-type B128 and its isogenic flagellar mutants, fliO_ΔC and sRNA_T, in viscous solutions of PGM (15 mg mL⁻¹). Representative data is from one of two independent experiments for each strain. The mutant speed distributions are significantly different from wild-type B128, where K-S p <0.05 in each case (see Table 5). No significant difference in temporal speed variation was observed between wild-type B128 and sRNA_T (p=0.10); B128 vs. fliO_ΔC (p=0.98); or sRNA_T vs. fliO_ΔC (p=0.29).

The B128 sRNA_T mutant has a flagellation profile more similar to PMSS1 (Figs 2F and 8A). In addition to perturbing flagellum number, we found that both these mutations altered other cell morphology parameters. Both the fliO_ΔC and sRNA_T mutants displayed increased cell lengths (though similar to PMSS1), and increased cell curvature profiles (but still smaller than LSH100) relative to wild-type B128 (Table S4 and Fig. S7). These results suggest that perturbation of flagella assembly may influence helical cell morphology and cell length in H. pylori.

We analyzed the swimming speeds of the different flagellar mutants in viscous PGM solutions (15 mg mL⁻¹) (see Videos 5–6). We were only able to analyze speeds from a small bacterial population (n=23) for the fliO_ΔC mutant because of difficulties finding fields of individual motile bacteria and because cells tended to clump (31%) as compared to wild-type (0.43%) (Table 5). A positive correlation between flagellum number and swimming speed was observed with significantly reduced swimming speeds (50% reduction in v_m) for fliO_ΔC bacteria and increased swimming speeds (19% increase in v_m) for the sRNA_T mutant (Fig. 8B and Table 5). The B128 sRNA_T mutant also showed a higher v_m that was 18% faster than PMSS1 in this solution (14.9 μm/s vs. 12.2 μm/s) (Tables 2 and 5). The standard deviation of swimming speeds, σ_bac, (Fig. 8C) suggest that sRNA_T displays similar swimming dynamics to wild-type B128 (K-S, p=0.29), fliO_ΔC displays similar swimming dynamics to wild-type B128 (K-S, p=0.98), and fliO_ΔC displays similar swimming dynamics to sRNA_T (K-S, p=0.57). Thus, altering flagellation does not impact temporal behavior in the swimming speed of individual bacteria. We observed a higher fraction of immobilized bacteria (82%) for fliO_ΔC, but saw a smaller fraction for the sRNA_T mutant as compared to wild-type B128 (14% vs. 36%, respectively) (Table 5).

Table 5.

Speeds, percent track linearity, and the fraction of immobile wild-type bacteria and flagellar mutants in viscous PGM solutions (15 mg mL⁻¹).

	PGMa 15 mg mL−1
	WT B128	B128 fliOΔC	B128 sRNA_T
n	100	23	100
Inst. values	2112	553	1673
vavg (μm/s)	11.7	7.2	14.2
vm (μm/s)	12.5	6.3	14.9
vmax (μm/s)	36.6	29.8	40.5
σ	5.5	4.8	5.6
K-S p-valueb	<0.0001		<0.0001
% reduction to vm relative to WT	50%		19% increase
Average %TL	77%	67%	84%
K-S p-valueb for % TL	0.041		0.037

n	461	270	440
%Immobilec	36%	82%	14%
%clumpsd	0.43%	31%	0.68%

^aPGM: Purified gastric mucin at pH 6.0.

^bFor K-S tests used to compare WT to mutant cumulative distributions of swimming speeds and percent track linearity (%TL), p-values < 0.05 are considered significant.

^cFraction of immobile bacteria in viscous PGM solutions. Bacteria exhibit displacements < 0.3 μm (MSD < 0.1 μm²).

^dFraction of clumped bacteria in viscous PGM solutions.

To explore whether variation in flagellum number influences other aspects of swimming, we analyzed reversals, ratio of forward and reversal swimming speeds, and cell path trajectory for wild-type bacteria and the flagellar mutants. We observed minimal effects of changing flagellum number on reversal frequency and the ratio of forward to reverse swimming speeds (Fig. 9A,B). However, we observed differences in track linearity between wild-type and the flagellar mutants (Fig. 9C). Reduced speeds and track linearity for the fliO_ΔC mutant may result from a combination of increased cell length, increased cell curvature, and decreased flagellum number. The sRNA_T showed increased track linearity, suggesting that like PMSS1, sRNA_T may have increased directional persistence while swimming due to a higher proportion of bacteria with 4 or more flagella (Fig. 9C).

Figure 9. Increased flagellation minimally affects reversal frequency, but increases % track linearity in H. pylori.

(A) Dot plots summarizing the number of reversals per second acquired for wild-type B128 and isogenic flagellar mutants in viscous PGM solutions (15 mg mL⁻¹). Mean values of reversals per second are shown as bolded black lines and error bars indicate one standard deviation from the mean. The fliO_ΔC shows a significant difference to wild-type B128 (K-S, p = 0.0114). (B) Dot plots summarizing individual ratios of median forward swimming speed to median reversal swimming speed acquired for each bacterial cell swimming in PGM (15 mg mL⁻¹). Ratios are plotted on a log₂ scale and median values are shown as bolded black lines. (C) Bar histograms showing % track linearity (%TL) for wild-type B128 and isogenic flagellar mutants in PGM (15 mg mL⁻¹). Error bars show one standard deviation from the mean and mean %TL values are summarized in Table 5. *K-S p <0.05 was considered significant and ns = no significant difference.

Resistive force theory modeling requires variation in both cell shape and flagellum number to explain speed differences observed between H. pylori strains

In order to gain further insight into our experimental results and the dependence of H. pylori’s swimming speed on cell shape, we used Resistive force theory (RFT) (Gray and Hancock, 1955). RFT has previously been used to model swimming of Caulobacter crescentus (Li and Tang, 2006) and Vibrio alginolyticus (Magariyama et al., 1995) by approximating their bacterial cell body as an ellipsoid and the flagellum as a rotating rigid helix. The bacteria were then assumed to swim in a Newtonian fluid and long-range hydrodynamic interactions were neglected. These simplifications make it possible to derive an analytical expression for the bacterium’s swimming speed in terms of the motor torque on the flagellum, and the translational and rotational drag on the cell body and helical flagella bundle.

We used a similar approach for H. pylori but instead modeled its cell body as a thick helical rod, a geometry representative of its helical cell shape. The flagella bundle was modeled as a single thin helix attached at one end of the helical cell body. With this geometry, the equations of motion for the cell body and flagellum can be written and solved analytically (for details on this derivation see Experimental Procedures). The final result is that swimming speed is proportional to the flagella bundle motor torque, T_m, via a shape factor S_h, ν_h = S_hT_m. The motor torque, T_m, represents the influence of the flagella motors on swimming while the shape factor, S_h, represents the effects of the translational and rotational drag of the cell body and flagella bundle. The shape factor relies on cell body and flagella geometry, and although the motor torque for H. pylori has yet to be measured, analysis of the shape factor provides insight into how different cell geometries affect swimming speed, with some geometries more efficiently converting motor torque to speed.

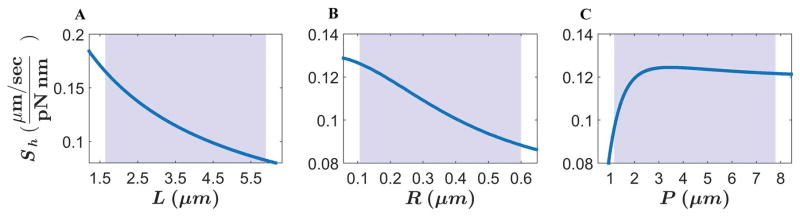
To examine how the shape factor depends on cell body helical parameters, we calculated S_h for a typical H. pylori bacterium with a cell length L = 3.1 μm, helical pitch P = 2.5 μm, helical radius R = 0.15 μm, and cell diameter D = 0.56 μm. These cell body parameters are the mean cell body measurements acquired for the three wild-type H. pylori strains: LSH100, B128, and PMSS1 (Table 1). For the flagella bundle, we used a bundle thickness of d = 0.07 μm; a flagellum pitch of p = 1.58 μm; and a helical radius of r = 0.14 μm (see Experimental Procedures); and a flagellum length of l = 4.1 μm (the mean flagellum length of all the wild-type strains). Figure 10 shows the dependence of S_h on one cell shape parameter at a time (L, P, or R) keeping the other two parameters constant. In the parameter ranges observed for H. pylori (shaded blue region), S_h decreases monotonically with increasing L or R (Fig. 10A,B), while it exhibits a non-monotonic dependence on P (Fig. 10C), exhibiting a shallow maximum at P ≈ 3.4 μm with a very slight decrease thereafter. This maximum corresponds to a speed maximum for bacteria with a pitch angle of approximately 15º. Our model predicts that in order to have a large S_h value, and hence a faster speed for the same motor torque, a helical cell must have a short cell length, small helical radius, and a helical pitch of approximately 3.4 μm.

Figure 10. Resistive force theory model predicts that variation in helical body length (L), helical radius (R), and helical pitch (P) alter H. pylori’s shape factor, S_h.

Calculated shape factor (S_h) for a bacterium with helical cell body shape. In each plot, the dependence of S_h is shown for a single cell body parameter L (A), R (B), or P (C) while keeping the other two parameters constant. The parameters that were not varied were maintained at a cell length L = 3.1 μm; helical pitch P = 2.5 μm; helical radius R = 0.15 μm; cell diameter D = 0.56 μm; flagellum length l = 4.1 μm; flagella pitch p = 1.58 μm; flagella helical radius r = 0.14 μm; and flagella bundle thickness d = 0.07 μm. These are the average helical cell body or flagella parameters from the wild-type H. pylori strains LSH100, B128, and PMSS1. The blue shaded regions represent the range (min to max) of the cell shape parameters observed experimentally for LSH100, B128, PMSS1, and the B128 sRNA_T mutant (Fig. 2 and Fig. S7).

To compare how the variation in cell shape for the different strains alters their shape factor, we calculated S_h for LSH100, B128, PMSS1, and the B128 sRNA_T flagellar mutant (Table 6). For each strain, S_h was calculated using their average cell body parameters (Table 1 and Table S3) and the same flagella bundle parameters described above. Table 6 shows that S_h for LSH100, PMSS1, and B128 sRNA_T all have similar values, while B128 has the largest S_h value (10% larger than all other strains). This is a result of the small average cell length and helical radius of B128 as compared to the other strains (Table 1). These shape factor differences would produce about a 10% change in swimming speed if all strains produced a similar motor torque on the flagella bundle. However, the differences in swimming speed in PGM at 15 mg mL⁻¹ were observed to be much larger (~ 0 – 90%). By comparing the ratios of shape factors to the ratios of swimming speeds (Table 6), we conclude that differences in shape factor alone do not fully explain the differences observed between wild-type strains in their experimental swimming speeds.

Table 6.

Comparison of experimental median speeds in PGM 15 mg mL⁻¹ and predictions of Resistive Force Theory model implementations.

Strain	Median speed in PGMa 15 mg mL−1(μm/s)	Shb +/− SEc	ShNfd +/− SEb
LSH100	6.5	115 +/− 10	345
PMSS1	12.2	120 +/− 7	480
B128	12.5	132 +/− 8	396
B128 sRNA_T	14.9	116 +/− 8	464

Strains compared	Ratio of median speed in PGMa 15 mg mL−1	Ratio of Sh +/− SEb	Ratio of ShNf +/− SEb
sRNA_T/B128	1.2	1.9 +/− 0.1	1.2 +/− 0.1
sRNA_T/PMSS1	1.2	1.0 +/− 0.1	1.0 +/− 0.1
B128/PMSS1	1.0	1.1 +/− 0.1	0.8 +/− 0.1
LSH100/PMSS1	0.5	1.0 +/− 0.1	0.7 +/− 0.2

^aPGM: Purified gastric mucin at pH 6.0.

^bSE: Standard error.

^cS_h: Shape factor.

^dS_hN_f: the product of shape factor and median flagellum number.

Our experimental results show that H. pylori strains vary flagellum number (Fig. 2F) and flagellum number correlates with swimming speed (Fig. 8). Based on this, we make the simplest hypothesis that the flagella bundle motor torque, T_m, increases proportionally with the number of flagella (N_f ) in the flagella bundle, where T_m = N_f T_f and T_f is the torque produced by a single flagellum. With this modification the swimming speed can be written as a function of both the shape factor and flagellum number, ν_h = (S_h N_f)T_f. Table 6 shows the product of S_h N_f as calculated for each wild-type strain and the sRNA_T mutant using their respective median flagellum numbers. The product of the shape factor and flagellum number predicts larger differences, ~20–30% among the different strains as compared to the shape factors alone. The ratio of S_h N_f agrees very well with the experimental ratio of swimming speeds observed for B128 and its flagellar mutant sRNA_T, thus, reflecting primarily the change in flagellum number, albeit with a small variation in cell length. The predicted ratio of S_h N_f for B128 and sRNA_T, relative to PMSS1, were within 10% of their measured speed ratios (Table 6). However, for LSH100 compared to PMSS1, the predicted ratio of S_h N_f does not agree well with the experimentally measured ratio of speeds, suggesting that the RFT model has some limitations in modeling the effects of helical shape.

Discussion

While variation in cell morphologic parameters among strains and between species have long been noted, our studies provide an in-depth, quantitative analysis of H. pylori’s natural variation in helical cell and flagellum morphology, and how these parameters impact H. pylori’s motility in viscous environments. Most of the previous studies of H. pylori motility provide numbers for only the average or maximum speed. Given the wide distribution of speeds, we suggest that conclusions based only on the variation of a single speed parameter with varying external conditions could be misleading as the shape of these broad, asymmetric distributions is not fully described by a single parameter such as the average, thus higher moments of the distribution are required to describe the shape of an asymmetric distribution. Our motility studies of three unrelated wild-type H. pylori strains in broth and viscous solutions of PGM reveal the swimming speed distributions reflect both temporal variation in the speed of individual bacteria (Fig. 4) and morphological variation within the population (Fig. 2).

The observed broad distribution of swimming speeds was largely due to temporal variation in swimming speed, which we characterized using the distribution of individual bacterium’s standard deviation in speed, σ_bac (Fig. 4). Wild-type H. pylori strains exhibited temporal variation that was dependent on their swimming environment, however loss of helical cell shape or perturbed flagellation did not affect how individual bacteria vary their swimming speed with time. Our data suggest that temporal speed variation is not influenced by morphology, but can be influenced by bacteria-medium interactions, and may reflect fluctuations due to flagella bundling-unbundling events and/or the stochastic behavior in motor activity.

The speed distributions also vary depending on which polymer solution (and at what concentration) the bacteria swims in. Of particular interest is the observation that compared to broth H. pylori’s swimming speeds are slightly higher in PGM at both physiologically relevant concentrations; the higher mucin concentration corresponding to that in the mucus close to the epithelial surface, and the lower mucin concentration similar to that in the luminal layer. We observed a non-monotonic variation in H. pylori swimming speed, and increased proportions of immobile bacteria as the viscosity of PGM increased (Table 3 and Fig. S5). Caldara et al. observed a similar behavior in Pseudomonas aeruginosa, where bacteria displayed increased swimming speeds in PGM (although at lower PGM concentrations) (Caldara et al., 2012). Yeung et al. found that addition of mucin at physiological concentrations promoted the ability of P. aeruginosa to exhibit rapid motility across the surface of agar (Yeung et al., 2012). The physical mechanism responsible for the increase in motility of H. pylori in viscous PGM solutions is unclear. Possible factors may relate to molecular interactions of bacteria with mucin and the viscoelastic nature of mucin solutions. Recent studies suggest H. pylori may directly bind mucins and glycolipids in gastric mucus (Naughton et al., 2013), and there is a growing body of theoretical work exploring how polymer viscoelasticity alters bacterial swimming (Lauga and Powers, 2009).

In methylcellulose, we observed an increase in swimming speed, at a viscosity of 26 cP, followed by a decrease at a higher viscosity of 76 cP (Table 2). This non-monotonic behavior agrees with previous H. pylori motility studies in methylcellulose (Worku et al., 1999), along with other studies of bacteria in viscous polymer solutions (Shoesmith, 1960; Schneider and Doetsch, 1974; Greenberg and Canale-Parola, 1977a; Ferrero and Lee, 1988). Recent work by Martinez et al. suggests that this non-monotonic behavior may be caused by non-Newtonian shear thinning causing the flagellum to experience a lower effective viscosity than the cell body (Martinez et al., 2014). We did not probe the length and time scales at which flagella interact with the polymer environment in this study and leave quantifying the shear thinning effects of gastric mucin and methylcellulose on bacterial motility for future work.

To directly address the impact of H. pylori’s helical cell body shape on motility, we examined the swimming speeds of isogenic straight rod mutants that had similar flagellum length and number to wild-type bacteria. In PGM solutions, which best mimic the different rheological environments H. pylori experiences in the stomach, we observed an 8–13% increase in speed of the helical bacteria compared to straight rods (Table 2). We also observed that helical cell shape increased the fraction of motile bacteria (Fig. S5 and Table 3). This effect was most pronounced in PGM concentrations that resemble the mucin concentrations found in the outer mucus layer, which H. pylori must quickly penetrate to escape from the acidic lumen.

The effect of helical shape on motility has been explored in Spirochete bacteria that have periplasmic flagella and utilize a running wave mode of translational motility distinct from that used by bacteria with external flagella (Dombrowski et al., 2009; Charon et al., 2012). Spontaneous mutants of Spirochaeta halophila that retain flagella but have lost helical cell morphology show decreases in maximal swimming velocity and a lower minimum immobilizing viscosity (MIV) (Greenberg and Canale-Parola, 1977b). Interestingly, this study also explored the behavior of related strains and species that varied in their helical parameters, characterized as having “tight” or “loose” coils. While they did not observe a correlation between helical pitch and maximum velocity or the viscosity at which maximum velocity occurred, they observed marked variation in the MIV (300–1,000 cP) among strains with “tight” coils having the highest MIV. While helical parameters were not precisely quantified, their results appear consistent with our observations that helical shape provided a similar increase in swimming speed regardless of viscosity of the medium or helical pitch angle of the parent strain, as well as a more pronounced effect of helical morphology on the percent of immobile bacteria.

Recently Liu et al. observed that Caulobacter crescentus, a bacteria with crescent cell shape and external flagella, enhances its motility by precessing its crescent cell body in a helical trajectory (Liu et al., 2014). Although these bacteria have a different cell geometry compared to H. pylori, their findings are consistent with our observations that the shape of the cell body can enhance flagella-mediated motility. Overall, our findings on the effect of H. pylori’s helical cell shape on its motility add to a growing consensus that the bacterial cell bodies may play a larger role in motility than previously thought.

In addition to cell shape, we also measured a significant contribution of flagellum number to H. pylori swimming speed. Increased flagellation (+1) of B128 through deletion of the sRNA_T gene resulted in an increase in median swimming speed (19%), track linearity, and a smaller fraction of bacteria immobilized in PGM (Figs 8 and 9, and Table 5). The sRNA_T mutant bacteria were also longer than the parent strain B128 (Table S3), suggesting that an increase in flagellum number may enhance flagellar propulsion and overcome the propulsive drag provided by helical bacteria with increased cell length. Work by Mears et al. found an analogous finding for E. coli, as cells with increased flagellum number were observed to have increased cell length and a slight increase in swimming speed (Mears, 2014). In another E.coli study, Darnton et al. suggested that torque on a single flagellum and the flagella bundle are similar and an increase in flagellum number does not result in an increase in swimming speed (Darnton et al., 2007). They postulated that torque is dissipated when the peritrichous flagella of E. coli have to bend around the cell body to form the flagella bundle (Darnton et al., 2007). Perhaps consistent with this finding, induction of secondary lateral flagella in the single polar flagellated bacterium Shewanella putrefaciens resulted in higher directional persistence and spreading in soft agar, but lower swimming speeds (Bubendorfer et al., 2014). The lophotrichous flagella of H. pylori may lessen this effect, but as of now its flagella bundling behavior has not been explored. Future experiments imaging the flagella of swimming bacteria should shine light on the flagella bundling behavior and the effect altering flagellum number has on bundling.

To further understand the role of cell morphology on swimming speed, we compared the influence of helical cell shape and number of flagella on swimming speed using a resistive force theory model. Assuming a constant motor torque, the swimming speed of a helical bacteria is predicted to decrease with increasing cell length and helical radius, suggesting the fastest swimming speeds are obtained by bacteria with small cell lengths and small radii. However, altering helical cell shape led to a relatively small change in the RFT predicted swimming speeds, ~ 10%, in contrast to the large changes in swimming speeds observed experimentally (as much as a 90%) for wild-type strains with different shape morphologies. Varying the motor torque using a simple linear dependence of motor torque on flagellum number produced a larger change in swimming speed, 20–30%, than that produced by only altering cell shape. Combining both the effect of cell shape and flagellum number, we were able to explain the observed differences in swimming speed for B128 and its flagellar mutant, which reflect mostly the change in flagellum number. Comparing the other strains, which differ in both flagellum number and shape, produced mixed results. A comparison of the ratios of RFT predictions for PMSS1 to those of B128 and sRNA_T showed better agreement with experimental results than predictions comparing PMSS1 to LSH100. Our results indicate that while both cell shape and flagellum number independently affect swimming speed, flagellum number contributes to a larger alteration in speed as compared to changing cell shape. Recent modeling studies of bacteria with different numbers of peritrichous flagella predict that swimming speed increases logarithmically with increased flagellation (Kanehl and Ishikawa, 2014). While we assumed a linear model based on our experimental observations, a logarithmic dependence gives comparable results, predicting an increase of ~ 26% when comparing bacteria with four vs. three flagella, and supports our observations that swimming speed correlates with flagellum number.

While the RFT model provided insight into the relative effect of cell shape and flagellum number on swimming speed it has inherent limitations. In particular, the model predictions are based on cell shape parameters of an average or “typical” bacterium. However, the average or median speed measured from the speed distribution does not correspond to the speed of the average bacterium. Hence, the present state of modeling is capable of qualitative predictions, and one has to be careful in drawing detailed quantitative comparisons. The model’s underestimation of the speed difference between LSH100 and PMSS1 also suggests it may underestimate the shape factor due to the more curved shape of LSH100. Recent work by Rodenborn et al. showed that RFT can lead to inaccurate predictions for a helical flagellum with helical parameters in the range of L>3P or P<6R (Rodenborn et al., 2013). These inaccuracies are due to RFT neglecting long-range interactions of the fluid flow from different parts of the helix. While our calculations for the cell body are outside the cited ranges, L/P ≈ 1.2 and P/R≈10, Rodenborn et al. modeled a very thin helix (helical thickness to helical radius D/R ≈ 0.06), which was meant to mimic the flagellum. For the H. pylori cell body, the helical radius is comparable to the cell thickness D/R ≈ 2, meaning long-range hydrodynamic interactions may play a larger role. In light of this, we are currently exploring the use of a numerical solution of the hydrodynamic equations based on a regularized Stokeslet method (Cortez et al., 2005) to further probe the swimming of helical cells.

Another aspect absent in our model is medium specific interactions. Our experimental results show medium specific changes in H. pylori swimming speed and temporal swimming behavior, which the RFT model cannot explain. Recently, Spagnolie et al. modeled a rotating helix in a viscoelastic fluid and showed that the swimming speed of the helix can increase or decrease depending on the combination of its helical parameters and the viscoelastic parameters of the medium (Spagnolie et al., 2013). These effects could explain the increase in swimming speeds we observed for helical bacteria swimming in PGM solutions, however making any direct link between swimming speed and swimming medium properties requires further study.

While efficient motility is essential for persistent colonization of the gastric mucus layer by this pathogen to get to its extracellular niche and during turnover of mucus and gastric epithelial cells, our study raises the question as to whether there may be selective pressures in addition to swimming speed that dictate H. pylori cell shape and flagellum number. Although both helicity and flagellum number alter swimming speed, it is noteworthy that their alteration resulted in a smaller change in speed (~1 μm/s) than the observed changes in an individual bacterium’s speed with time (~1–5 μm/s). In addition, growth of a subpopulation of straight rod and curved cells along with bacteria with zero to two flagella persist in all strains analyzed (this work and Sycuro et al., 2010). Having cells within the population with less flagella or a straight rod shape may play an unknown benefit to H. pylori unrelated to motility. Extending our cell-based morphologic studies to infected stomach tissues may begin to reveal whether different morphologies favor different niches within the stomach that include the surface mucus, gastric glands, and epithelial cell surface.

Experimental Procedures

Bacterial strains and culture conditions

Strains used in this study are described in Table S1. We used three unrelated wild-type H. pylori strains: LSH100, a derivative of the sequenced human clinical isolate G27 (Baltrus et al., 2009; Lowenthal et al., 2009); PMSS1, also called 10700 (Lee et al., 1997; Arnold et al., 2011); and B128 (McClain et al., 2009) and mutant derivatives of these strains. Bacteria were cultured on horse blood plates or in liquid media containing 90% (v/v) Brucella broth (BD Biosciences) and 10% fetal bovine serum (GIBCO) (BB10) in the absence of antimicrobials as previously described (Sycuro et al., 2010). Cells were maintained at 37ºC under microaerobic conditions in a tri-gas incubator equilibrated to 10% CO₂ and 10% O₂. Plates were incubated 24–72 hours and liquid cultures were incubated for 12–16 hours under constant agitation at 200 rpm. For resistance marker selection, horse blood plates were supplemented with chloramphenicol (15 μg mL⁻¹).

Morphology analysis

Wild-type H. pylori LSH100 and PMSS1, and wild-type B128 and its respective flagellar mutants (fliO_ΔC and sRNA_T) were grown in liquid culture to an optical density at 600 nm (O.D. ₍₆₀₀₎) of 0.3–0.7. Bacteria were fixed (4% Paraformaldehyde, 1X PBS, and 25% Glycerol) and added to 0.1% poly-L-lysine (Sigma Aldrich) coated coverslips that were placed on a pre-cleaned microscope slide, and were then sealed with VaLP (1:1:1 Vaseline: Lanolin: Paraffin). Single focal plane images were collected using a 100 X ELWD Plan APO (NA 1.40 oil) objective mounted on a Nikon TE 200 microscope, equipped with a Nikon CoolSNAP HQ CCD camera controlled by MetaMorph software (MDS Analytical Technologies). Quantitative morphology analysis of manually thresholded phase-contrast images was performed as described in Sycuro et al. using the CellTool software program (Lacayo et al., 2007; Pincus & Theriot, 2007; Sycuro et al., 2010). Centerline data for each strain was obtained from CellTool, imported to MATLAB, and fitted to a generalized sine curve, $y=Rsin(\frac{2\pi }{P}x+\delta )$, where R and P represent the helical radius and helical pitch, respectively, and δ is a phase term added to allow for an arbitrary origin of the sine function. Cells with non-helical morphologies resulted in poor fitting, characterized by a large sum of squared error (SSE > 0.2), and were removed from our data sets. The number of cells used to generate cell shape models were LSH100, n=262; PMSS1, n=215; B128; n=272; B128 fliO_ΔC, n=296; and B128 sRNA_T, n=305.

Transmission Electron Microscopy (TEM) and Scanning Electron Microscopy (SEM) of H. pylori cells

TEM of H. pylori was performed as described in Lowenthal et al., 2009, and cells were visualized with a JEOL JEM 1400 transmission electron microscope. SEM of H. pylori was performed as described in Sycuro et al., 2013. Digital images were manipulated using Image J and Adobe Photoshop.

H. pylori flagellum length measurements and flagellum number counts

Flagellum number counts were acquired from SEM (LSH100 and PMSS1 and their respective straight rod mutants) or TEM images (B128 and the flagellar mutants). The number of flagella was counted from 83 – 110 different bacteria per strain. Flagellum length measurements were acquired from TEM images collected from the same preparation for all strains. TEM images were uploaded to Image J and calibrated using the scale bar (1 μm) of images acquired at 2500 – 3000 X. Using the segmented line selection tool, flagellum length was measured for one flagellum per cell, four times each, from 15 different bacteria per strain to provide average lengths and standard deviations from the means.

Generation of knockout isogenic mutants

An isogenic mutant of csd6 (HPG27_477) in the PMSS1 strain background was generated by transfer of the mutation constructed in the LSH100 strain background (Sycuro et al., 2013) using natural transformation (Wang et al., 1993). Transformants were confirmed by PCR using primers homologous to upstream and downstream flanking regions for each gene using the primers indicated in Table S2. The mutation was then backcrossed into PMSS1 once by isolating genomic DNA from the resulting strain for natural transformation of PMSS1. The resulting backcrossed clones were evaluated by PCR to confirm replacement of the wild-type allele with the null allele (csd6). Clones were checked for urease activity and motility, and single clones were used for quantitative morphology analyses and the motility studies.

An isogenic mutant of motB (HPG27_772) was constructed in the LSH100 strain background as described above. Genomic DNA of motB bearing a transposon insertion was acquired from the mutant library generated in H. pylori G27 (Salama et al., 2004) and was used for natural transformation of LSH100.

Deletion of sRNA_T was generated in H. pylori B128 by the following procedure. Overlapping PCR was used to generate an amplicon that contained a kanamycin resistance cassette (aphA3) gene flanked by ~500 bp regions located upstream and downstream of the target sRNA. Primers used for PCR are listed in Table S2. The region upstream of sRNA_T was amplified using the upstream forward and the upstream reverse primers. The 5′-end of the upstream reverse primer contained sequence corresponding to one end of the aphA3 cassette. The region downstream of sRNA_T was amplified using the downstream forward and the downstream reverse primers. The 5′-end of the downstream forward primer contained sequence corresponding to the other end of the aphA3 cassette. The aphA3 cassette was amplified using the kan forward and kan reverse primers. Overlapping PCR via the complementary regions of the amplified aphA3 cassette and the amplicons of the regions flanking the target gene generated a PCR product with the aphA3 cassette between the flanking regions. The resulting amplicon was introduced into H. pylori B128 by natural transformation. Replacement of sRNA_T with the aphA3 cassette was confirmed by PCR using genomic DNA from kanamycin resistant transformants as a template, and was further verified by sequencing the resulting amplicons.

Preparation of purified PGM

PGM was isolated from mucosal scrapings of pig stomach epithelium and purified by Sepharose CL-2B column chromatography followed by density gradient ultracentrifugation as described in (Celli et al., 2009). Lyophilized PGM powder was allowed to reach room temperature before opening tubes to avoid condensation. The powder was weighed and 7.5 mg was dissolved in 400 μL of sterile H₂O to prepare a 15 mg mL⁻¹ solution with bacteria, and 15 mg was dissolved in 800 μL of sterile H₂O to prepare a 30 mg mL⁻¹ solution with bacteria. PGM was allowed to hydrate and equilibrate for 48 hours at 4ºC before use.

Preparation of methylcellulose

Stock solutions of methylcellulose (MC) from Sigma Aldrich (M0261) were prepared by making 20 mg mL⁻¹ (wt/vol) solutions in sterile H₂O, where the mixture was slowly agitated overnight at room temperature using a tube rotator. The approximate viscosity of a 20 mg mL⁻¹ MC solution was 400 cP (approximate molecular weight, 41,000, Sigma Aldrich, M 0262).

Measuring the viscosity of broth and viscous media by particle-tracking microrheology

Fluorescent polystyrene latex beads (1.001 +/− 0.01 μm diameter) (Polysciences Inc.) were added to broth or viscous PGM or MC sample to provide a final bead concentration of 0.05% beads by volume in a final volume of 1 mL. Flagellated but nonmotile bacteria (LSH100 ΔmotB) were grown in liquid broth (BB10) at an O.D. ₍₆₀₀₎ of 0.3 – 0.7. Bacteria was added to each solution to produce a 10% bacteria mixture by volume, and bacteria were examined after 45 min of incubation in each solution at 37ºC under microaerobic conditions. A 10 μL volume of bead or bacteria solution was then pipetted onto a glass slide with a secure spacer (Secure-Seal, Sigma-Aldrich) and covered with a coverslip. Samples were imaged using an Olympus IX 70 microscope (40 X Plan N, 0.45 NA) with QCAM CCD camera (Qimaging) at 20 fps and 0.2312 μm pixel size. Fluorescent beads were excited using an Olympus BH2 Mercury arc source while bacteria were imaged using phase contrast with light from a halogen bulb. Focus was set to the center and middle Z-positions of the sample in order to minimize edge effects. Videos were captured at 30 s intervals using Micro-Manager open source acquisition software (Edelstein et al., 2010) and were analyzed in MATLAB v7.12.0 using a particle-tracking routine that finds the center of intensity of each bead or bacterium using a polynomial Gaussian fit (Rogers et al., 2007). Beads or bacterium that drifted were dedrifted using a custom MATLAB routine and superfluous tracked objects were removed.

Motility assay in purified PGM and methylcellulose solutions

Bacteria were grown in liquid culture broth to an O.D. ₍₆₀₀₎ of 0.5 – 0.7 and kept warm at 37°C under microaerobic conditions until use. 10 μL of culture was added to 80 μL of PGM solution and 10 μL of pH 6 buffer (0.1 M phosphate-succinate) to produce a 10% bacteria mixture by volume and the final PGM concentrations used were 15 mg mL⁻¹ and 30 mg mL⁻¹. For methylcellulose solutions, 10 μL of culture was added to a solution that consisted of 50 μL of MC stock solution (20 mg mL⁻¹) and 40 μL of pH 6 buffer (0.1 M phosphate-succinate), to produce a 10% bacteria mixture by volume and a final concentration of MC at 10 mg mL⁻¹. To produce a 10% bacteria mixture by volume and a final concentration of MC at 15 mg mL⁻¹, 10 μL of culture was added to 75 μL of MC solution (20 mg mL⁻¹) and 15 μL of pH 6 buffer (0.1 M phosphate-succinate). Bacteria were incubated for 45 min in their respective PGM or MC solutions at 37ºC under microaerobic conditions prior to imaging. After the incubation period, each cell suspension was mixed by gentle pipetting and 10 μL was applied to standard glass microscope slides with secure imaging spacers (9 mm in diameter × 0.12 mm depth, Secure-Seal, Sigma-Aldrich). A coverslip was placed over the sample and was securely sealed. Samples were immediately imaged at room temperature using a Nikon TE 200 inverted microscope (60 X ELWD Plan Fluor, 0.7 NA Phase lens, depth field of ~5 μm) and ten second videos were captured for bacteria swimming in the mid-level plane between the coverslip and glass slide, which is ~60 μm in depth, using a Nikon CoolSNAP HQ CCD camera (100 millisecond intervals over a 10 s period (10 fps), 0.109 μm/pixel) and MetaMorph software (MDS Analytical Technologies). Bacteria were tracked using the Volocity software (v6.1) (Elmer, 2011).

Tracking of swimming bacteria using Volocity (v6.1)

Videos were processed and converted to 8-bit files using ImageJ (Rasband, 1997–2014) and uploaded to the particle-tracking program in Volocity v6.1 to generate tracks based on the centroid position of each object identified (area, 0.05 – 8.0 μm²). Individual trajectories were obtained for at least 10 frames of the video (1 s) (see Fig. S1). Bacteria showing a displacement less than 0.3 μm or a mean squared displacement (MSD) less than 0.1 μm² were considered to be immobile and were removed. Individual trajectories of 100 bacteria were acquired, examined visually to ensure accuracy, and imported into MATLAB v7.12.0 for smoothing using a five point Savitsky-Golay filter to remove noise effects caused by wiggling trajectories (Hyon et al., 2012) and finite tracking resolution (Son et al., 2013). Stops, reorientations, swimming speeds, and reversal events were segmented and were used to describe H. pylori motion.

Analysis of the fraction of immobile bacteria in broth and viscous PGM media

Videos gathered for tracking individual bacterial cells for velocity analysis were used to determine the fraction of motile and nonmotile (immobilized) bacteria in broth and PGM media. We classified all bacteria with displacements less than 0.3 μm as immobile and bacteria with displacements greater than 0.3 μm as motile. The percentage of immobilized bacteria was calculated by dividing the total number of nonmotile cells by the total number of bacterial cells. The total bacterial population included nonmotile bacteria and motile bacteria (bacteria with displacements between 0.3 – 1.5 μm, and bacteria with displacements > 1.5 μm that were processed through MATLAB and segmented to acquire swimming speeds after tracking by Volocity). The number of clumped bacteria (clusters of aggregated bacteria) was analyzed for B128 and the flagellar mutants in viscous PGM solutions (15 mg mL ⁻¹). The percentage of clumped bacteria was calculated by dividing the total number of clumps by the total bacterial population. The total bacterial population consisted of the number of clumped bacteria, nonmotile cells (individual cells with displacements < 0.3 μm), and motile cells (as described above).

Resistive force theory mathematical modeling

At low Reynolds number the forces, F_c and F_f, and torques, T_c and T_f, on a bacterium must balance.

$$\begin{array}{l}{F}_c+F_f=0\\ T_c-T_f=0\\ T_m-T_f=0\end{array}$$

Here c, f, and m denote the cell body, flagellum, and motor, respectively. Resistive force theory states that the forces and torques on an object are proportional to the local speed and angular rotation rate of that object, with the constant of proportionality determined by the object’s geometry and viscosity of the liquid (Gray and Hancock, 1955).

We modeled the cell body of wild-type H. pylori as a rigid helix while the bacterium’s helical flagellum was assumed to bundle and form a single helix. The total force on a translating and rotating helix is a sum of the translational drag, F_drag = -α_hv_h, and rotational propulsion, F_propulsion = γ_hω_h, while total torque is a sum of the rotation drag, T_drag = β_hω_h, and translation drag, T_propulsion = -γ_hv_h. Here α_h, β_h, and γ_h represent the translational, rotational, and propulsion drag coefficients of a helical cell body, respectively. In an analogous way, the flagellum has translational, rotational, and propulsion drag coefficients which we designate as α_f, β_f, and γ_f.

Using the force and torque equations above, along with force torque balance between the cell body and flagellum, we solved for the swimming speed of a helical cell body, v_h, in terms of the motor torque, T_m. The swimming speed can be written as the product of T_m, and a shape factor, S_h, that depends on the cell body and flagellum drag coefficients.

$$\begin{array}{c}{v}_h=S_h{T}_m\\ S_h=\frac{\frac{{\gamma }_h}{{\beta }_h}+\frac{{\gamma }_f}{{\beta }_f}}{{\alpha }_h+{\alpha }_f-\frac{{\gamma }_h}{{\beta }_h}{\gamma }_h-\frac{{\gamma }_f}{{\beta }_f}{\gamma }_f}\end{array}$$

To calculate S_h we used previously derived expressions for α_h, β_h, and γ_h in terms of the cell body parameters: cell length (L), helical pitch (P), helical radius (R), and pitch angle (Φ) (Rodenborn et al., 2013) with local normal (C_n) and tangential (C_t) force expressions derived by Gray and Hancock (Gray and Hancock, 1955). Using the same formula, the flagellum coefficients α_f, β_f, and γ_f, can be written in terms of the flagellum helical length (l), pitch (p), radius (r), pitch angle (ϕ), and local normal (c_n) and tangential (c_t) forces.

$$\begin{array}{c}{\alpha }_h=(C_n{\text{sin}}^2(\mathrm{\Phi })+C_t{\text{cos}}^2(\mathrm{\Phi }))L\\ {\beta }_h=(C_n{\text{cos}}^2(\mathrm{\Phi })+C_t{\text{sin}}^2(\mathrm{\Phi }))R^{2}L\\ {\gamma }_h=(C_n-C_t)\text{sin}(\mathrm{\Phi })\text{cos}(\mathrm{\Phi })RL\\ {\alpha }_f=(c_n{\text{sin}}^2(\mathrm{\varphi })+c_t{\text{cos}}^2(\mathrm{\varphi }))l\\ {\beta }_f=(c_n{\text{cos}}^2(\mathrm{\varphi })+c_t{\text{sin}}^2(\mathrm{\varphi }))r^{2}l\\ {\gamma }_f=(c_n-c_t)\text{sin}(\mathrm{\varphi })\text{cos}(\mathrm{\varphi })rl\end{array}$$

Using these expressions, the drag coefficients and shape factor were calculated using average cell shape measurements acquired from CellTool (Fig. 2). For wild-type H. pylori strains, we used the average helical parameters acquired from fitting the centerlines of each bacterial cell within each wild-type population (Fig. 2B and Table 1). We acquired a uniform flagellum diameter (d, ~0.07 μm), and used the average flagellum length (l) acquired from measurements done on TEM and SEM images (Fig. 2 and Table 4, and Fig. S3). Because the flagellum helical pitch (p) and helical radius (r) for H. pylori have not been measured, we assumed a helical flagellum form similar to that of Vibrio alginolyticus, where p = 1.58 μm and r = 0.14 μm (Magariyama et al., 1995) for all bacteria examined in this study. All numerical calculations and manipulations were done using MATLAB v7.12.

Statistical analysis

We used the Kolmogorov-Smirnov (K-S) statistics tool in CellTool to assay differences in cell shape morphology, including cell length and side curvature distributions, as described in detail in Sycuro et al., 2010 and 2012. To make statistical comparisons between wild-type helical radius, helical pitch, and pitch angle distributions, and comparisons between wild-type vs. mutant temporal variation in swimming speed, unpaired nonparametric Kolmogorov-Smirnov (K-S) tests were performed using MATLAB v7.12.0. To make statistical comparisons between wild-type vs. mutant instantaneous speed distributions; cell path trajectories; frequency of reversals; and the ratios of forward and reversal swimming speeds; unpaired nonparametric Kolmogorov-Smirnov (K-S) tests were performed using GraphPad Prism version 6.00 for Windows (GraphPad Software, La Jolla, CA USA). Statistics for the temporal analysis of wild-type vs. mutant was done using unpaired nonparametric Kolmogorov-Smirnov (K-S) tests in MATLAB v7.12.0. For each comparison, a K-S p-value < 0.05 was considered significant.