Evaluation of CM5 Charges for Nonaqueous Condensed-Phase Modeling

Abstract

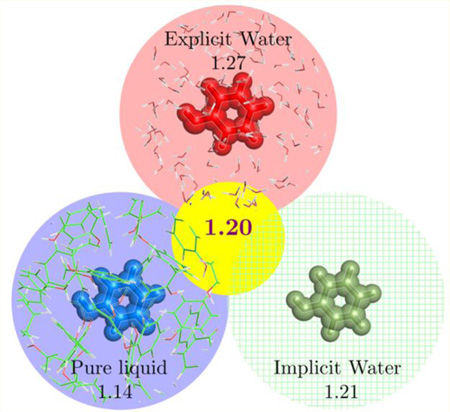
Partial atomic charges for neutral molecules from quantum mechanical calculations are typically scaled for use in molecular modeling of liquid-phase systems. Optimal scale factors of 1.14 for CM1A and 1.27 for CM5 charges were previously determined for minimizing errors in free energies of hydration. The adequacy of the 1.14*CM1A and 1.27*CM5 models are evaluated here in pure liquid simulations in combination with the OPLS-AA force field. For 22 organic liquids, the 1.14*CM1A and 1.27*CM5 models yield mean unsigned errors (MUEs) of ca. 1.40 kcal/mol for heats of vaporization. Not surprisingly, this reflects overpolarization with the scale factors derived for aqueous media. Prediction of pure liquid properties using CM5 charges is optimized using a scale factor of 1.14, which reduces the MUE for heats of vaporization to 0.89 kcal/mol. However, due to the impracticality of using different scale factors in different explicit-solvent condensed-phase simulations, a universal scale factor of 1.20 emerged for CM5 charges. This provides a balance between errors in computed pure liquid properties and free energies of hydration. Computation of free energies of hydration by the GB/SA method further found that 1.20 is equally suited for use in explicit or implicit treatments of aqueous solvation. With 1.20*CM5 charges, a variety of condensed-phase simulations can be pursued while maintaining average errors of 1.0 kcal/mol in key thermodynamic properties.

Graphical abstract

INTRODUCTION

Despite the development of force fields including polarization and multipole moments, such as AMOEBA,¹ a monopole approximation of atomic charge continues to offer viable and affordable representations of electrostatic interactions in simulations of organic and biomolecular systems.^2–6 Historically, several strategies have been followed to determine appropriate partial atomic charges. Charges have been obtained by partitioning a quantum mechanical (QM) electron charge density into atomic populations,⁷ by fitting to reproduce the QM-derived electrostatic potential (ESP) surrounding a molecule,^8,9 or by optimization to minimize errors in other physical observables.^10–15 For example, nonbonded Coulombic and Lennard-Jones parameters in OPLS force fields have been parametrized to reproduce experimental heats of formation and densities of neat organic liquids since their inception 30 years ago.¹⁶

The strategy of determining atomic charges to fit observable properties is also followed for the CMx charge models from Cramer, Truhlar, and co-workers.^10–15 In this instance, charges from Mulliken,¹⁷ Löwdin,¹⁸ redistributed Löwdin,¹⁹ or Hirshfeld²⁰ population analyses are empirically corrected to better reproduce gas-phase molecular dipole moments. Charge model 5 (CM5), the latest installment of the CMx series, is unique in that atomic charges are now derived from Hirshfeld charges.¹⁵ This change allows CM5 charges to remain consistent over a wide range of electronic structure methods and basis sets while using only a single set of model parameters. More reasonable charges are obtained for buried atoms, and less dependence on molecular conformation has been observed.¹⁵ Furthermore, CM5 parametrization has been extended to every atom in the periodic table. These CM5 attributes offer an appealing new approach for determination of partial atomic charges for a variety of theoretical applications.

The generation of large numbers of novel molecules in combinatorial and medicinal chemistry dictates a clear need for molecular mechanics methods. For molecules where force field parameters are lacking, intramolecular and van der Waals parameters usually can be estimated by analogy to existing parameters. However, determination of partial charge assignments is not straightforward.²¹ One solution is to use QM, notwithstanding the myriad choices for partial charge determination.^7–15 Free energies of hydration have traditionally been computed to evaluate the performance of different charge models.^{2–5,22–27} In this manner, CM5 charges have recently been tested for use in explicit solvent simulations by computing free energies of hydration for 62 molecules in conjunction with the OPLS-AA force field.²² Free energies of hydration were calculated by combined Monte Carlo and free energy perturbation simulations (MC/FEP), and CMx charges were scaled to account for solute polarization upon solvation.²⁴ An optimal scale factor of 1.27 was determined to minimize errors with experiment. 1.27*CM5 mean unsigned errors (MUE) in computed free energies of hydration were between 1.1 and 1.3 kcal/mol, an improvement upon the 1.14*CM1A charge model, which produced MUEs of 1.2–1.5 kcal/mol. CM5 results were also in general accord with OPLS_2005²⁶ and AM1-BCC/GAFF²⁷ results. Finally, 1.27*CM5 computed free energies of hydration were confirmed to be consistent when charges were derived from five different density function methods and four different basis sets. Thus, CM5 charges were recommended for general use in condensed-phase simulations.

Given its good performance for aqueous solutions, it is desirable to consider CM5 charges for broader modeling. With the increasing application of computational chemistry in medicinal and biophysical chemistry, one instinctively turns to consider protein–ligand complexes. In many protein targets, however, the binding site may be buried and reflect a dielectric constant smaller than that for pure water.^28,29 The concern exists that ligands in a protein binding site may be over polarized if CMx charges are used with scale factors determined from water alone. This article seeks to address this concern by evaluating the performance of CM5 charges in nonaqueous condensed-phase simulations. The adequacy of scaled 1.14*CM1A and 1.27*CM5 charges, in conjunction with the OPLS-AA force field, is assessd by computing heats of vaporization (ΔH_vap) and pure liquid densities (ρ) for 22 pure organic liquids (Figure 1). These results are compared to those from the OPLS-AA force field, which was parametrized to reproduce these properties. The goal of this study is not to surpass OPLS-AA but to examine the performance of CM5 charges in a broadly applicable force field, OPLS/CM5, and to gauge whether it is an improvement over OPLS/CM1A.²¹ CMx charges are used in conjunction with unmodified OPLS-AA Lennard-Jones and bonded parameters in these methods. Although refinement of Lennard-Jones parameters to better couple with CMx charges is possible in isolated cases, we seek procedures readily applicable to a broad range of molecules that necessitate only OPLS-AA atom-type assignments and a single QM calculations to provide the partial atomic charges. Thus, modification of Lennard-Jones parameters is not considered here. Instead, this article focuses on tuning the scaling factor for the CM5 charges, as the choice of 1.27 does overpolarize charges, leading to substantial errors in ΔH_vap and ρ. A more universal CM5 scale factor is determined by seeking a balance in errors for computed ΔG_hyd, ΔH_vap, and ρ.

Figure 1.

Molecular structures for the 22 organic liquids investigated in this work.

COMPUTATIONAL DETAILS

Pure Liquid Simulations

Metropolis Monte Carlo³⁰ (MC) pure liquid simulations were performed with the BOSS software package³¹ in the isothermal isobaric ensemble at 25 °C and 1 atm pressure. N-Methylacetamide (NMA) was run at 100 °C.³² Detailed descriptions of the computational procedure are reported elsewhere.^32–39 Briefly, all intramolecular interactions and Lennard-Jones parameters were represented with the OPLS-AA force field. Solvent charges employed standard OPLS-AA, CM1A, and CM5 partial atomic charges. CM1A and CM5 charges were generated from single-point calculations of optimized OPLS-AA geometries. CM1A charges were computed in conjunction with AM1 calculations in BOSS.⁴⁰ CM5 charges are not available in BOSS and were generated from a BOSS–Gaussian interface.⁴¹ Hirshfeld charges were first obtained from a M06-2X/6–311+(2df,2p) calculation^42,43 in Gaussian 09, revision A.02.⁴⁴ CM5PAC⁴⁵ was next used to generate CM5 charges from Hirshfeld charges. The BOSS-Gaussian interface loaded unmodified CM5 charges into BOSS, which averaged charges for symmetric atoms and applied the appropriate scale factor. As described below, investigated CM5 scale factors ranged between 1.00 and 1.27. MC simulations were executed for cubes of 267 molecules using periodic boundary conditions. Nonbonded interactions were truncated at cutoff distances (r_cutoff) of 11–15 Å. In general, molecules with three heavy atoms or less employed 11 Å cutoffs; aromatic, amide, hexane, and cyclohexane molecules employed 15 Å cutoffs; and all other molecules used 13 Å cutoffs. Intermolecular interactions were quadratically smoothed over the last 0.5 Å, and a Lennard-Jones energy correction was included for interactions neglected beyond the cutoff.¹⁶ All solvent intra- and intermolecular degrees of freedom were sampled. Ranges for translation and rotation were adjusted to give MC acceptance ratios of 25–40%.

To compute pure liquid heats of vaporization and densities, both gas- and liquid-phase MC simulations were performed for a set of 22 molecules (Figure 1). Heats of vaporization were calculated according to eq 1;³² densities were calculated from average liquid volumes. For gas-phase simulations, 4 million (M) configurations were used for equilibration, and averaging was done for an additional 4M configurations (4M/4M). For condensed-phase simulations, 20M/20M configurations were performed to ensure that all properties were properly converged. For all simulations, the batch means method was used to compute statistical uncertainties (±σ). Batch sizes of 1M configurations were used, and computed uncertainties were less than 0.05 kcal/mol for heats of vaporization and 0.002 g/cm³ for densities.

$$\mathrm{\Delta }{H}_{\text{vap}}=E_{\text{intra}}(g)-(E_{\text{intra}}(l)+E_{\text{inter}}(l))+RT$$ (1)

Free Energies of Self-solvation

After identifying a universal CM5 scale factor, free energies of self-solvation (AG_self) were investigated for 12 molecules with MC/FEP molecular annihilations. Solvent boxes and simulation parameters mirrored those used in the pure liquid simulation, except that one solute molecule is progressively annihilated. Molecular annihilations followed procedures previously outlined using 40–60M/80M configurations of MC sampling in the liquid phase.^22,46 Free energy changes were computed via the Zwanzig equation⁴⁷ over 21 λ-windows of combined simple overlap (SOS) and double wide sampling (DWS).⁴⁸ Molecules were annihilated by perturbing all charges and Lennard-Jones nonbonded parameters to zero in two steps with molecule shrinking in the last step. Computed uncertainties were below 0.20 kcal/mol, in general accord with prior studies.²²

GB/SA Free Energies of Hydration

For completeness, 1.14*CM1A and 1.20*CM5 free energies of hydration using the generalized Born/surface area (GB/SA) implicit solvent model, introduced by Still et al.,⁴⁹ were investigated for 424 molecules. En route, optimal scale factors of CM1A and CM5 charges were calculated for GB/SA calculations. Prior to calculation, a conformational search was performed for each molecule to identify the minimum energy structure. CMx charges were then obtained in the same manner as above for the minimum energy structure. CMx charges were first scaled by 1.00, 1.09, 1.18, 1.27, and 1.36, and free energies of hydration were calculated at each scale factor. Interpolated quadratic fits were employed to locate the scale factor with the minimum error. Performing calculations at scale factors near interpolated minima confirmed the optimal scale factors for the CM1A and CM5 methods.

RESULTS

Pure Liquid Simulations

Pure liquid heats of vaporization and densities were computed in combination with the OPLS-AA force field. Standard OPLS-AA, 1.14*CM1A, and 1.27*CM5 charges were employed as a means to evaluate the performance of CMx charges in nonaqueous explicit solvent condensed-phase environments. These tests serve as a model for eventual representation of protein–ligand interactions that take place in environments less polar than water itself. Computed heats of vaporization and densities are listed in Tables 1 and 2, respectively; differences with experiment are graphically illustrated in Figure 2. Table S1 also compares the presently recomputed OPLS-AA results with previously published values.

Table 1.

Computed Heats of Vaporization (kcal/mol) for 22 Organic Liquids with OPLS-AA and the 1.14*CM1A and 1.27*CM5 Charge Models at 25 °C

molecule name	OPLS-AA	1.14*CM1A	1.27*CM5	exp.a
acetic acid	12.26	13.52	14.46	12.49
acetone	7.23	7.74	8.92	7.48
acetonitrile	7.57	7.63	9.76	8.01
aniline	11.88	16.41	14.61	12.60
benzonitrile	12.52	14.45	15.49	12.54
cyclohexane	7.56	7.64	7.61	7.86
diethylamine	7.68	7.54	7.46	7.48
diethyl ether	6.90	7.01	7.22	6.56
N,N-dimethylacetamide	13.44	14.34	15.57	11.75
ethanethiol	6.67	6.48	6.68	6.58
ethanol	10.29	9.06	10.19	10.11
furan	6.91	8.01	7.17	6.56
hexane	7.54	7.48	7.34	7.54
methanol	9.00	7.60	8.84	8.95
methyl acetate	7.99	10.00	10.12	7.72
nitroethane	9.78	14.16	11.72	9.94
N-methylacetamideb	13.87	16.12	19.06	13.30
phenol	14.58	14.63	14.30	13.82
propylamine	7.90	8.93	7.23	7.47
pyridine	9.76	11.16	11.16	9.61
pyrrole	10.32	13.81	12.37	10.80
tetrahydrofuran	7.52	7.66	8.08	7.61
MUE	0.35	1.41	1.37

^aRefs 32–40.

^bAt 100 °C.

Table 2.

Computed Densities (g/cm³) for 22 Organic Liquids with OPLS-AA and the 1.14*CM1A and 1.27*CM5 Charge Models at 25 °C

molecule name	OPLS-AA	1.14*CM1A	1.27*CM5	exp.a
acetic acid	1.066	1.102	1.093	1.044
acetone	0.797	0.811	0.840	0.784
acetonitrile	0.759	0.755	0.805	0.776
aniline	1.013	1.041	1.025	1.017
benzonitrile	0.994	1.011	1.020	1.001
cyclohexane	0.752	0.750	0.751	0.774
diethylamine	0.706	0.697	0.693	0.699
diethyl ether	0.707	0.705	0.712	0.708
N,N-dimethylacetamide	0.963	0.990	0.986	0.936
ethanethiol	0.859	0.854	0.860	0.833
ethanol	0.798	0.776	0.789	0.785
furan	0.935	0.956	0.944	0.931
hexane	0.640	0.640	0.636	0.661
methanol	0.779	0.736	0.763	0.786
methyl acetate	0.943	0.997	0.997	0.928
nitroethane	1.024	1.114	1.070	1.040
N-methylacetamideb	0.917	0.967	0.977	0.894
phenol	1.052	1.063	1.055	1.058
propylamine	0.719	0.740	0.701	0.711
pyridine	0.968	0.986	0.985	0.978
pyrrole	0.971	1.013	0.996	0.966
tetrahydrofuran	0.853	0.852	0.858	0.884
MUE	0.014	0.031	0.027

^aRefs 32–40.

^bAt 100 °C.

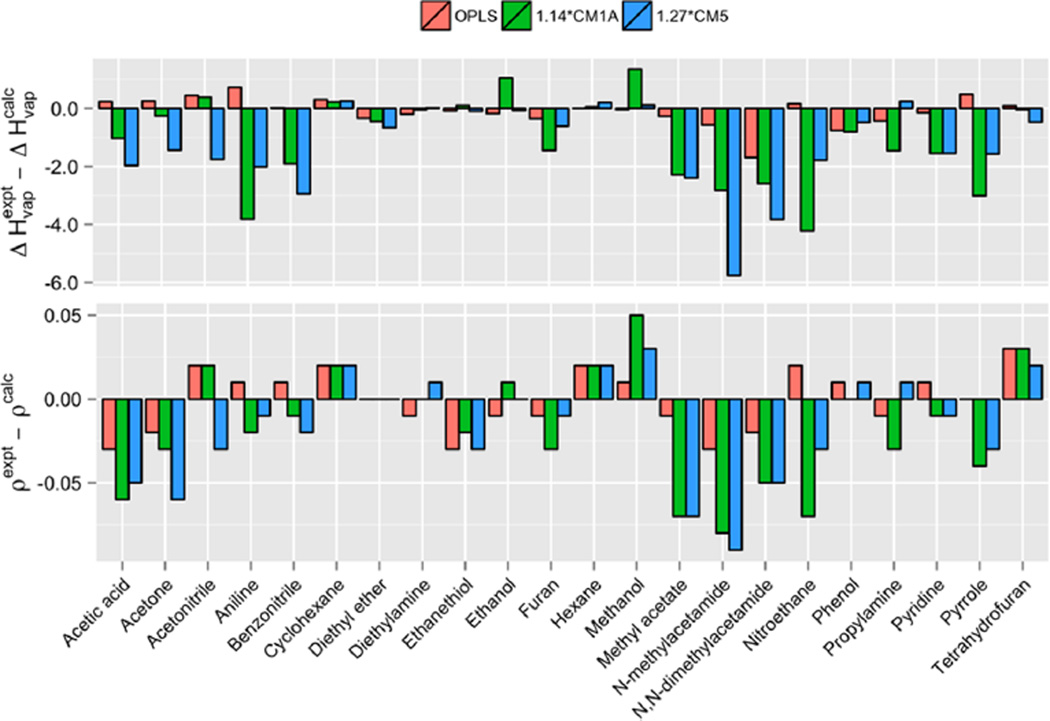
Figure 2.

Signed errors in computed heats of vaporization (ΔH_vap) and densities (ρ) of 22 organic liquids from OPLS-AA (orange), OPLS/1.14*CM1A (green), and OPLS/1.27*CM5 (blue) force fields.

As expected, the OPLS-AA force field performed well. This is unsurprising since it was parametrized to reproduce ΔH_vap and ρ.^21,32–40 The present results are in good agreement with literature values (Table S1). Differences can be attributed mostly to improved convergence resulting from the use of increased MC sampling in the present work. The largest discrepancy is 1.45 kcal/mol for N,N-dimethylacetamide. In this case, force field parameters were updated in 2004 to improve computed free energies of hydration for tertiary amides.²³ However, this appears to adversely affect the pure liquid properties by a small degree. All other OPLS-AA results are close to experiment; a MUE of 0.35 kcal/mol is obtained for ΔH_vap, and a MUE of 0.01 g/cm³ is found for ρ.

It is clear from Tables 1 and 2 that 1.14*CM1A and 1.27*CM5 perform less well than OPLS-AA. Both approaches yield mean unsigned errors of ca. 1.40 kcal/mol for ΔH_vap and 0.03 g/cm³ for densities. The percent errors are ca. 13.0% for ΔH_vap and ca. 3.0% for densities. Since densities are more sensitive to LJ parameters, and all simulations use the same OPLS-AA LJ parameters, the agreement between CMx densities and experiment is not surprising. Errors are not independent, however, as clear correlations can be seen for ΔH_vap and ρ. Overly strong intermolecular interactions causing too positive ΔH_vap also contract the solvent box, increasing ρ. Heats of vaporization are generally more sensitive to the partial atomic charges and greater errors result. Errors above 1.50 kcal/mol for computed heats of vaporization were obtained for nitrogen-containing molecules including aniline, benzonitrile, N,N-dimethylacetamide, N-methylacetamide, nitroethane, pyridine, and pyrrole. One source of error could be the lack of explicit nitrogen lone pair sites;⁵⁰ however, the OPLS-AA results display considerable accuracy for these molecules with no additional charged sites.³⁷ In the present investigation, the enhanced errors likely stem from overpolarized CMx charges. For both the 1.14*CM1A and 1.27*CM5 models, errors less than 0.50 kcal/mol are found for cyclohexane, diethylamine, ethanethiol, hexane, and tetrahydrofuran. 1.27*CM5 gave similarly low errors for ethanol, methanol, phenol, and proplyamine.

Deviations in liquid properties can be attributed to problems with salient features such as hydrogen-bonding interactions, solvent dipole moments, and liquid structure. If the degree of hydrogen bonding in a liquid is overestimated, then overly large heats of vaporization should result. Similar trends are expected for strengthened dipole–dipole interactions, although with reduced impact owing to weaker interactions. Table 3 reports the computed average number of hydrogen bonds per molecule in the protic polar solvents and average molecular dipole moments for polar solvents. The average numbers of hydrogen-bond contacts per molecule were determined by integrating X···H radial distribution functions (RDF), where X = N or O up to the first minima. The contact numbers were then multiplied by the number of donating or accepting sites per molecule to determine the average number of hydrogen bonds per molecule (Table 3). Average dipole moments were calculated by BOSS over the course of the simulation. Focusing on the CMx results, most instances of overestimated heats of vaporization correlate with too many hydrogen bonds or too large dipole moments compared to OPLS-AA. The amines provide interesting examples. For diethylamine, hydrogen bonds and dipole moment showed good correlation with OPLS-AA, and both 1.14*CM1A and 1.27*CM5 models reproduced ΔH_vap with errors less than 0.1 kcal/mol. In contrast, for aniline, too many hydrogen bonds were obtained with CM1A, and an overestimated dipole moment was found for CM5. The result is that the scaled CMx models overestimate the heat of vaporization by more than 2.0 kcal/mol. For proplyamine, 1.27*CM5 yielded fewer hydrogen bonds than OPLS-AA and 1.14*CM1A yielded more; heats of vaporization were proportionally under and overestimated. Similar patterns can be deduced for the other molecules containing alcohol, amide, nitrile, nitro, and carbonyl functional groups in Table 3. Overall, these trends suggest that CM5 charges are overpolarized when scaled by 1.27 in nonaqueous environments.

Table 3.

Average Number of Hydrogen Bonds and Average Molecular Dipole Moments for Polar Solvents with OPLS-AA, 1.14*CM1A, and 1.27*CM5 charges

solvent	OPLS-AA	1.14*CM1A	1.27*CM5
Number of Hydrogen Bonds
acetic acid	1.94	1.93	1.97
aniline	0.96	1.47	1.00
diethylamine	0.70	0.65	0.78
ethanol	1.92	1.90	1.96
methanol	1.94	1.92	1.98
N-methylacetamide	1.98	1.71	2.02
phenol	1.74	1.24	1.46
propylamine	1.23	1.50	1.05
pyrrole	1.60	1.85	1.80
Average Dipole Moments (D)
acetic acid	1.63	2.14	2.24
aniline	1.23	1.95	2.44
benzonitrile	3.23	4.90	5.82
acetonitrile	4.14	4.31	4.94
diethylamine	1.70	1.71	1.56
N,N-dimethylacetamide	4.71	4.27	5.22
diethyl ether	1.49	1.45	1.75
methyl acetate	1.95	2.25	2.45
ethanol	2.39	1.98	2.09
ethanethiol	2.03	1.97	2.07
furan	0.76	0.64	0.86
acetone	3.12	3.28	3.73
methanol	2.32	2.07	2.23
nitroethane	3.78	5.32	4.83
N-methylacetamide	4.11	3.84	4.92
phenol	2.02	1.89	1.92
propylamine	1.84	2.13	1.78
pyridine	2.34	1.79	2.57
pyrrole	1.90	1.65	1.99
tetrahydrofuran	2.01	1.85	2.18

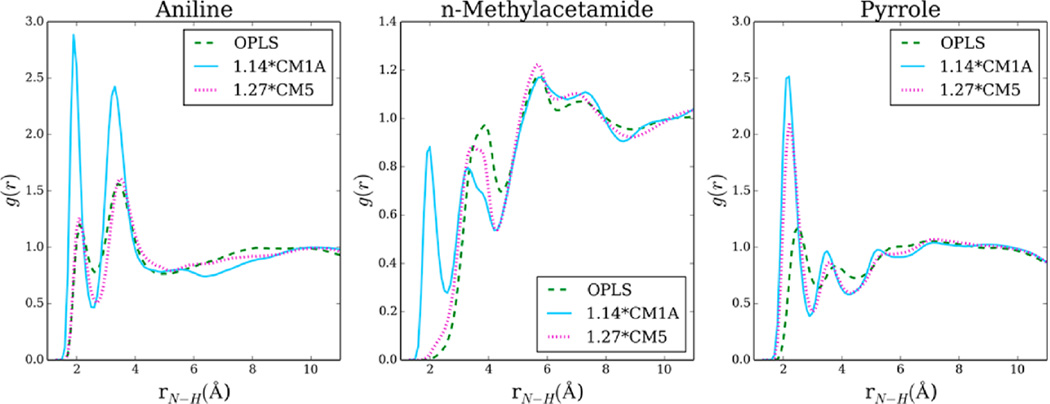
Changes in hydrogen bonding and dipole–dipole interactions also affect the structures of liquids. To demonstrate this, N···H radial distribution functions (RDFs) for aniline, N-methylacetamide, and pyrrole are shown in Figure 3. For these three molecules, excessive hydrogen bonding is reflected in the 1.14*CM1A and 1.27*CM5 radial distribution functions, as shown by the enhanced and shifted first and second peaks. For N-methylacetamide, 1.14*CM1A charges produce a new peak in the RDF corresponding to NMA dimers interacting via π-type hydrogen bonds (Figure S1). This artifact of 1.14*CM1A is not observed in 1.27*CM5 or OPLS-AA simulations and makes the CM1A alternative less appealing. For CMx liquids with comparable hydrogen bonds per molecule or solvent dipole moments, compared to OPLS-AA, liquid RDFs agree well, suggesting that liquid structures are consistent between the different charge models (Figure S2).

Figure 3.

N···H radial distribution functions from OPLS-AA, OPLS/1.14*CM1A, and OPLS/1.27*CM5 pure liquid simulations.

Overall, OPLS-AA is the best of these models for representing pure liquids. The 1.27*CM5 model performed equivalently to 1.14*CM1A, although for amides the errors in heats of vaporization are significantly larger with 1.27*CM5. Detailed analyses of radial distribution functions, hydrogen bonding, and molecular dipole moments suggest that 1.27*CM5 charges are too polar for use in pure liquid simulations. Thus, a smaller scale factor for CM5 charges is needed.

Identifying a Universal CM5 Scale Factor

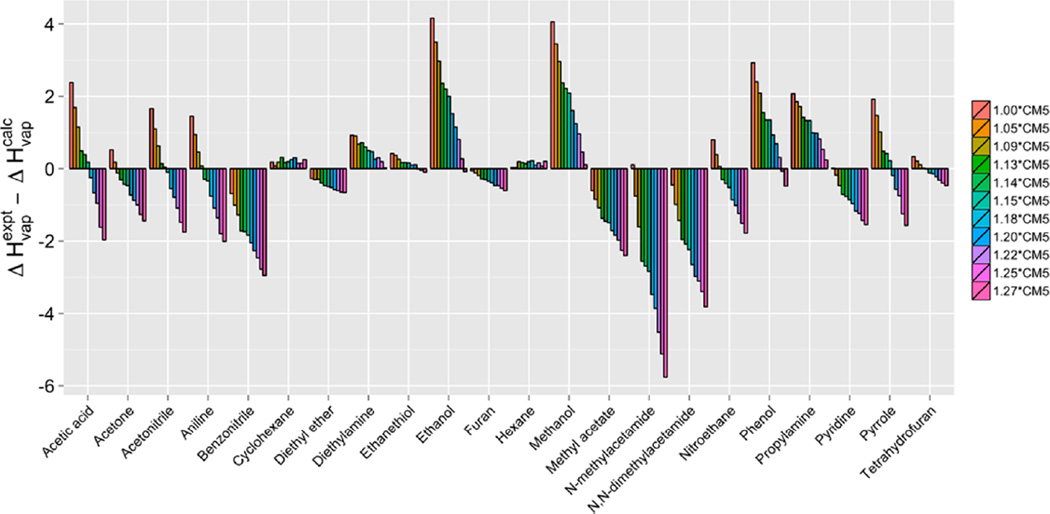
A new scale factor for CM5 charges was subsequently optimized for the pure liquids. A series of simulations using CM5 charges was performed, initially using scale factors of 1.00, 1.09, 1.18, and 1.21. Quadratic interpolation of the ΔH_vap results from 1.00–1.27 implied that the optimal scale factor was near 1.14 (Figure S3). Pure liquid simulations performed with CM5 scale factors of 1.13, 1.14, and 1.15 confirmed that the optimal scale factor is 1.14. Deviations in ΔH_vap as a function of CM5 scale factors are presented in Figure 4. Not surprisingly, polar molecules showed the largest dependence on the scale factor. Mean unsigned errors in ΔH_vap and ρ for 22 liquids at each scale factor are tabulated in Table 4. Densities remained almost constant across the spectrum of scale factors. CM5 charges scaled by 1.14 yielded the lowest MUE of 0.89 kcal/mol for ΔH_vap and a MUE of 0.023 g/cm³ for densities. A comparison between the liquid properties calculated from 1.14*CM5 and 1.27*CM5 charges is shown in Figure S4. The scale factor of 1.14 greatly improved the calculation of liquid properties compared to 1.27 for most molecules except alcohols. With 1.14*CM5 charges, only methanol, ethanol, benzonitrile, N-methylacetamide, and N,N-dimethylacetamide showed errors above 1.5 kcal/mol. With the reduced scale factor, 12 molecules show errors less than 0.5 kcal/mol (Table S4).

Figure 4.

Signed errors in computed heats of vaporization (ΔH_vap) as a function of CM5 scale factors. Scale factors range from 1.00 (orange) to 1.27 (pink).

Table 4.

MUEs in Heats of Vaporization (kcal/mol) and Densities (g/cm³) for Pure Liquid Simulations Using CM5 Charges Scaled by Different Factors

scale factor	ΔHvap	ρ
1.00	1.18	0.031
1.05	1.03	0.028
1.09	0.95	0.026
1.13	0.90	0.025
1.14	0.89	0.023
1.15	0.90	0.023
1.18	0.97	0.022
1.20	1.06	0.024
1.22	1.12	0.024
1.25	1.24	0.025
1.27	1.37	0.027

By minimizing the MUEs in ΔH_vap, independent scale factors, in principle, can be determined for each molecule (Table S2). Although not useful as a general methodology, this does provide an accurate means of using CM5 charges for isolated pure liquid simulations. For all 22 molecules, independently optimized scale factors yielded mean unsigned errors of 0.14 kcal/mol and 0.02 g/cm³ for ΔH_vap and ρ, respectively (Table S2). Methanol, ethanol, phenol, diethyl-amine, and proplyamine preferred scale factors above 1.25. In contrast, some molecules prefer unscaled charges, including N-methylacetamide, N,N-dimethylacetamide, furan, and pyridine. Finally, cyclohexane and hexane showed no dependence on scale factor since they are dominated by Lennard-Jones interactions. It is clear that any general scale factor recommended for use with CM5 charges represents a compromise.

It would be impractical to recommend two optimal scale factors for employing CM5 charges in different explicit solvent simulations, 1.14 for nonaqueous and 1.27 for aqueous environments. This is especially true when studying protein– ligand interactions since binding site electrostatics are expected to vary for different protein targets. Instead, a universal CM5 scale factor can be decided upon by balancing errors between heats of vaporization from pure liquid simulations and free energies of hydration from aqueous simulations (Table 5). Data from aqueous simulations utilizes recent results from the evaluation of CM5 charges for reproducing free energies of hydration.²² In that work, solute–solvent long-range Lennard-Jones corrections (LRC)⁵¹ were not included in computed free energies of hydration, but we have since found them to be beneficial. The previous ΔG_hyd (1.27*CM5) results with LRCs added are reported in Table 5. LRCs have been automatically accounted for by BOSS for nonaqueous pure liquid simulations for many years,¹⁶ but they have not been tested for computed free energies of hydration. For the test set of 42 molecules originally investigated, CM5 MUEs reduce to 0.89 kcal/mol with a scale factor of 1.23 when long-range corrections are included. The results are improved most for larger molecules, which have larger LRCs. A compromise for the scale factor is now apparent (Table 5). A combined MUE of ca. 1.0 kcal/mol may be achieved with scale factors between 1.18 and 1.23. For simplicity, 1.20 is recommended as the universal CM5 scale factor. If one is not modeling aqueous media, then a scale factor of 1.14 is preferable.

Table 5.

MUEs in ΔH_vap and ΔG_hyd Using CM5 Charges with Different Scale Factors (kcal/mol)

		ΔGhyd
scale factor	ΔHvap	without LRCa	with LRCb
1.05	1.03	2.66	2.08
1.09	0.95	2.31	1.73
1.14	0.89	1.86	1.32
1.18	0.97	1.52	1.04
1.20	1.06	1.37	0.94
1.23	1.15	1.21	0.87
1.27	1.37	1.10	0.98

^aRef 22.

^bCorrected for long-range Lennard-Jones interactions (LRC) (ref 51).

Free Energies of Self-solvation

A further study was performed to evaluate the performance of universal 1.20*CM5 charges by calculating free energies of self-solvation (ΔG_self). These tests were performed using 12 molecules for which experimental data are available.⁵² The MC/FEP annihilation results are reported in Table 6; signed errors are shown in Figure S5. All charge models performed well. OPLS-AA performed the best, with a MUE of 0.26 kcal/mol. 1.14*CM1A and 1.20*CM5 charges perform equivalently, with errors near 0.6 kcal/mol. Overall, the agreement with experiment is encouraging since all models yield errors less than 1.0 kcal/mol, a typical limit in free energies of hydration.⁵³ Principal outliers for 1.20*CM5 are acetic acid, methanol, ethanol, and methyl acetate. ΔG_self for methanol and ethanol are underestimated due to the insufficient hydrogen bonding with 1.20*CM5 charges. ΔG_self for methyl acetate and acetic acid are too favorable owing to enhanced dipole moments. Overall, a scale factor of 1.20 provides an appealing balance between 1.14 and 1.27 for CM5 charges for a variety of applications.

Table 6.

Computed ΔG_self (kcal/mol) Using OPLS-AA, 1.14*CM1A, and 1.20*CM5 Charge Models

molecule	OPLS-AA	1.14*CM1A	1.20*CM5	exp.a
acetic acid	−6.56	−7.77	−7.62	−5.89
acetonitrile	−4.16	−4.26	−4.84	−4.89
cyclohexane	−4.41	−4.13	−4.04	−4.42
diethylamine	−3.77	−3.85	−3.76	−3.93
diethyl ether	−3.44	−3.74	−3.88	−3.44
methyl acetate	−4.04	−5.25	−5.31	−4.14
ethanol	−4.90	−4.00	−4.08	−5.08
hexane	−3.84	−4.04	−3.88	−4.05
acetone	−3.95	−4.16	−4.52	−4.20
methanol	−4.52	−3.69	−3.74	−4.86
propylamine	−3.53	−4.25	−3.31	−3.89
tetrahydrofuran	−3.94	−4.21	−4.38	−4.23
MUE	0.27	0.58	0.61

^aRef 52.

Further Validation

An additional set of 15 molecules was considered to validate the performance of 1.20*CM5 charges for condensed-phase modeling. Heats of vaporization, pure liquid densities, and solvation free energies were again studied using the same methodologies as before. Molecules were selected from published benchmark studies where experimental data was available for all properties.^{52–54,56–60} The results are summarized in Tables 7 and 8; signed errors are graphically displayed in Figure S8.

Table 7.

Heats of Vaporization (kcal/mol) and Liquid Densities (g/cm³) of 15 Additional Molecules Using OPLS-AA and 1.20*CM5 Charge Models at 25 °C

	ΔHvap			density
molecule	1.20*CM5	OPLS-AA	exp.a	1.20*CM5	OPLS-AA	exp.a
2,2-dimethylbutane	6.60	6.45	6.62	0.651	0.649	0.644
o-xylene	10.65	10.88	10.38	0.870	0.875	0.876
benzyl alcohol	13.44	14.55	15.68b	1.018	1.028	1.042b
butanoic acid	14.78	14.61	13.92	0.983	0.975	0.953
cyclohexanone	12.06	12.00	10.79	0.945	0.938	0.942
1,2-dichloroethane	7.63	8.27	8.40	1.211	1.236	1.246
1,4-dioxane	10.31	9.35	9.23	1.014	1.000	1.034c
1,2-dimethyoxyethane	10.41	9.55	8.70	0.883	0.857	0.864
N,N-dimethylformamide	13.29	11.42	11.37	0.973	0.957	0.943
propionitrile	9.08	8.23	8.61	0.748	0.744	0.776
2-propanol	9.95	11.42	10.88	0.785	0.807	0.781
nitromethane	10.59	9.39	9.23	1.121	1.111	1.130
N-methylformamide	17.38	14.46	13.44	1.042	1.022	1.000
1-chloropropane	6.57	6.62	6.78	0.871	0.870	0.890c
triethylamine	8.26	8.61	8.33	0.731	0.728	0.723
MUE	1.14	0.49		0.019	0.016

^aRefs 52–54 and 56–60.

^bAt 24 °C.

^cAt 20 °C.

Table 8.

Free Energies of Hydration and Self-solvation (kcal/mol) of 15 Additional Molecules Using OPLS-AA and 1.20*CM5 Charge Models at 25 °C^a

	ΔGhyd			ΔGself
molecule	1.20*CM5	OPLS-AA	exp.b	1.20*CM5	OPLS-AA	exp.b
2,2-dimethylbutane	3.24	3.38	2.51	−3.27	−3.15	−3.60
o-xylene	−0.74	−1.60	−0.90	−4.76	−5.62	−5.96
benzyl alcohol	−4.16	−5.69	−6.63	−5.76	−7.52	−8.61
butanoic acid	−5.59	−4.95	−6.36	−7.97	−7.37	−7.37
cyclohexanone	−4.07	−3.04	−4.91	−7.28	−6.41	−6.26
1,2-dichloroethane	−0.15	−0.94	−1.79	−4.16	−4.57	−4.70
1,4-dioxane	−4.52	−2.32	−5.06	−6.45	−4.78	−5.09
1,2-dimethyoxyethane	−6.57	−3.49	−4.84	−5.26	−4.74	−4.60
N,N-dimethylformamide	−7.63	−6.71	−7.80	−8.76	−6.48	−6.47
propionitrile	−3.90	−3.94	−3.85	−5.00	−4.39	−5.12
2-propanol	−3.08	−4.39	−4.75	−4.55	−5.42	−5.09
nitromethane	−4.05	−3.41	−4.02	−6.31	−5.04	−5.38
N-methylformamide	−10.09	−6.88	−10.00	−12.28	−10.27	−8.27
1-chloropropane	1.30	1.28	−0.33	−3.50	−3.46	−3.80
triethylamine	−0.96	−1.59	−3.22	−4.12	−4.38	−4.50
MUE	0.99	1.28		1.14	0.43

^aLennard-Jones LRCs included.

^bRefs 52–54 and 56–59.

For pure liquid properties, OPLS-AA charges again perform the best. MUEs for OPLS-AA were 0.49 kcal/mol for ΔH_vap and 0.016 g/cm³ for ρ, compared to 1.20*CM5 MUEs of 1.14 kcal/mol and 0.019 g/cm³. ΔH_vap errors greater than 1.5 kcal/mol for 1.20*CM5 charges were observed for N-methylformamide, N,N-dimethylformamide, 1,2-dimethoxyethane, and benzyl alcohol. As discussed earlier, amides prefer a CM5 scaling factor less than 1.20, whereas alcohols prefer a scale factor greater than 1.20 (Table S2). Similarly, errors less than 0.50 kcal/mol were observed for 2,2-dimethylbutane, o-xylene, propionitrile, 1-chloropropane, and triethylamine. In general, these results are consistent with trends discussed earlier.

Table 8 summarizes the performance of OPLS-AA and 1.20*CM5 charges for calculating free energies of hydration and free energies of self-solvation. 1.20*CM5 performs very well with MUEs of 0.99 kcal/mol for free energies of hydration and 1.14 kcal/mol for free energies of self-solvation. Molecules with errors less than 0.50 kcal/mol include o-xylene, N,N-dimethylformamide, propionitrile, nitromethane, and N-methylformamide for ΔG_hyd and 2,2-dimethylbutane, propionitrile, 1-chloropropane, and triethylamine for ΔG_self. The ΔG_self errors reflect similar errors in ΔH_vap. The larger ΔG_self error for 1.20*CM5 compared to OPLS-AA again stems from N-methylformamide, N,N-dimethylformamide, and benzyl alcohol, all of which yielded errors greater than 2.0 kcal/mol despite performing well for ΔG_hyd. Collectively, this validation confirms that average errors of ca. 1.0 kcal/mol can be achieved from a variety of simulations by using the balanced CM5 scale factor of 1.20 in conjunction with the OPLS-AA force field.

CMx GB/SA Free Energies of Hydration

All results up to this point have focused on explicit solvent-based MM simulations. Free energies of hydration for small molecules can be accurately calculated using explicit solvent simulations, but as the system size increases, the cost of computation also increases. Implicit solvent models such as the generalized Born/surface area method offer the ability to predict free energies of hydration at reduced computational costs with comparable accuracy.⁴⁹ This method is also amenable to use of CMx charges in conjunction with the OPLS-AA force field.⁵⁵ In this section, the performance of CM1A and CM5 charges for predicting ΔG_hyd via GB/SA was evaluated for 424 diverse molecules.⁵⁴ In a prior study with CM1A, the 1.14 scale factor was found to be nonoptimal for use with GB/SA; instead, a scale factor of 1.07 was recommended.⁵⁵ In anticipation that the 1.20 scale factor for CM5 also may be nonideal, best scale factors were again determined for CM1A and CM5 charge models for use with GB/SA implicit solvent calculations.

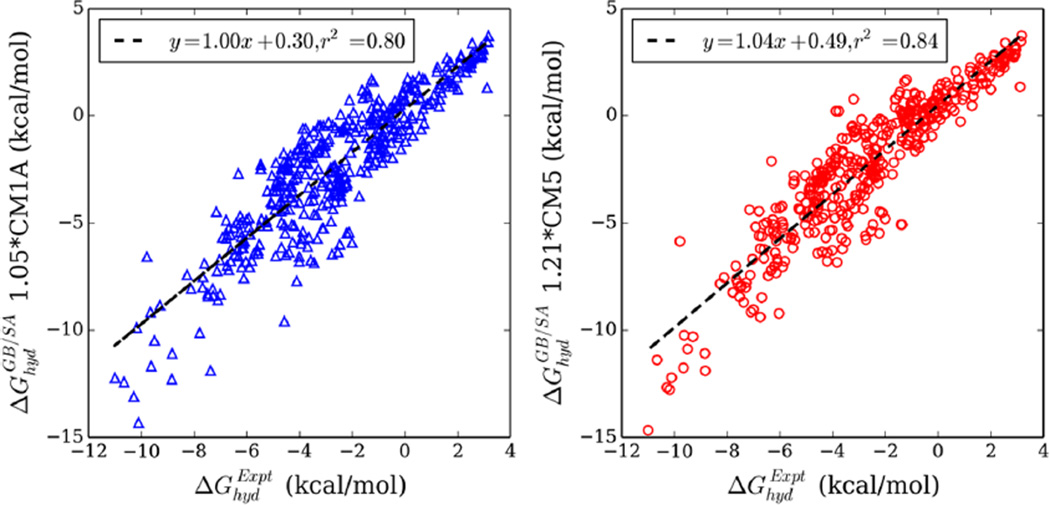
GB/SA free energies of hydration were calculated with CM1A and CM5 charges at scale factors between 1.00 and 1.36. Quadratic fits suggested, and independent calculations confirmed, the best scale factors to be 1.05 and 1.21 for CM1A and CM5 charges (Figure S6 and Table S4). The CM1A scale factor of 1.05 is close to the previously identified scale factor of 1.07. With the best scale factors of 1.05 and 1.21 for CM1A and CM5, the MUEs are 1.14 and 1.06 kcal/mol. Figure 5 provides a comparison between experimental and GB/SA free energies of hydration using 1.05*CM1A and 1.21*CM5 charges. Both plots yield decent fits, with best fit slopes of 1.0 and intercepts below 0.5. The slightly larger correlation coefficient for 1.21*CM5 suggests less scatter for the data set, compared to 1.05*CM1A. Carbonyl, halide, hydrocarbon, and N-heterocyclic-containing compounds are well-modeled by both charge models with MUEs less than 1.0 kcal/mol (Figure S7). Nitriles appeared to be poorly represented with CM5, whereas CM1A struggled with nitro-containing compounds. For alcohols, amines, and sulfur-containing molecules, both CMx models yield mean unsigned errors between 1.0 and 2.0 kcal/mol. Given the agreement between scale factors for use of CM5 charges in explicit or implicit solvation models, 1.20 and 1.21, the universal scale factor of 1.20 is appropriate for use with GB/SA and CM5 with no loss of accuracy (Table S4)

Figure 5.

GB/SA free energies of hydration calculated with 1.05*CM1A (blue triangles) and 1.21*CM5 charges (red circles) compared to experiment. Dashed lines represent best fit lines of the data.

CONCLUSIONS

In this study, the performance 1.27*CM5 and 1.14*CM1A charges in conjunction with the OPLS-AA force field has been evaluated in pure liquid simulations. It was expected that the optimal scale factor of 1.27 for CM5 charges obtained from computation of free energies of hydration would be too large for less polar media than water. For the 22 organic liquids, the OPLS-AA force field provided the best agreement with experiment. 1.27*CM5 and 1.14*CM1A charge models performed comparably well, but they yielded high errors in computed heats of vaporization. Inflated hydrogen bonding and dipole–dipole interactions in the CMx liquids were identified as problematic. Extensive simulation results led to determination of an optimal CM5 scale factor of 1.14 for pure organic liquids and, ultimately, to a universal scale factor of 1.20 for mixed systems. The universal scale factor provides a balance in errors for computed pure liquid properties and free energies of hydration. Investigation of implicit solvation via GB/SA also confirmed 1.20 as an appropriate scale factor for CM5 charges with either explicit or implicit treatments of the solvent; an average error of ca. 1.1 kcal/mol was obtained free energies of hydration of 424 molecules. Overall, 1.20*CM5 charges are recommended for use in modeling aqueous solutions with a significant organic component, including biomolecular systems.