Shape of the BMI-Mortality Association by Cause of Death, Using Generalized Additive Models: NHIS 1986–2006

Abstract

Objectives

Numerous studies have examined the association between body mass index (BMI) and mortality. The precise shape of their association, however, has not been established. We use nonparametric methods to determine the relationship between BMI and mortality.

Method

Data from the National Health Interview Survey-Linked Mortality Files 1986-2006 for adults aged 50 to 80 are analyzed using a Poisson approach to survival modeling within the generalized additive model (GAM) framework.

Results

The BMI-mortality association is more V shaped than U shaped, with the odds of dying rising steeply from the lowest risk point at BMIs of 23 to 26. The association varies considerably by time since interview and cause of death. For instance, the association has an inverted J shape for respiratory causes but is monotonically increasing for diabetes deaths.

Discussion

Our findings have implications for interpreting results from BMI-mortality studies and suggest caution in translating the findings into public health messages.

Introduction

The sharp increase in the prevalence of overweight and obesity among U.S. adults in recent decades is a pressing public health issue. More than a third of American adults are overweight and another third are obese (Flegal, Carroll, Ogden, & Curtin, 2010; Hedley, Ogden, Johnson, Carroll, Curtin, & Flegal, 2004; NHLBI, Obesity Initiative Expert Panel, 1998). ¹ Given that this distribution implies over 150 million American adults with excess body weight, understanding how overweight and obesity are associated with increased health risks and mortality is critical to public health policies and interventions. At the national level, the costs attributable to overweight and obesity are estimated at around US$100 billion annually (Finkelstein, Fiebelkorn, & Wang, 2003). Most of this cost is due to obesity-related negative health outcomes, which range from elevated levels of biological risk indicators such as C-reactive protein to the manifestation of chronic conditions such as diabetes, heart disease, and osteoarthritis, as well as physical limitations, low self-assessed health, and poor health-related quality of life (Alley et al., 2010; Diehr et al., 2008; Marinou, Tousoulis, Antonopoulos, Stefanadi, & Stefanadis, 2010; McDade, Rutherford, Adair, & Kuzawa, 2009; Stommel & Schoenborn, 2010; Wee et al., 2008; Zajacova & Burgard, 2010).

Among the various measures used to assess the health implications of overweight and obesity, mortality has received perhaps the most attention. The literature clearly shows that relative to having moderate body weight, both very low and very high BMIs are associated with increased mortality (Allison, Zhu, Plankey, Faith, & Heo, 2002; Bender, Jockel, Trautner, Spraul, & Berger, 1999; Flegal, Graubard, Williamson, & Gail, 2007; Flegal et al., 2005; Greenberg, 2001; Lee, Manson, & Hennekens, 1993; Zhu, Heo, Plankey, Faith, & Allison 2003). We lack consensus, however, about the shape of the BMI-mortality relationship for the majority of the adult population, which falls between normal and low obese body weight. Across numerous studies, which have examined samples of varied age, race/ethnicity, and sex compositions, the lowest risk BMI for mortality ranged from values below 22 to above 30 (for instance, see Flegal et al., 2005; Greenberg, 2006; Greenberg, Fontaine, & Allison, 2007; McGee, 2005; Mokdad, Marks, Stroup, & Gerberding, 2004).

One problem that complicates determination of the shape of the association between BMI and mortality is inherent in the modeling approach used in the previous studies. Standard survival analyses force one of two shapes on the association: researchers specify the BMI-mortality association as a quadratic function or they categorize BMI, with cutpoints typically at the threshold values specified by the NHLBI guidelines. In the quadratic model specification, the shape of the association is strongly influenced by the tails of the BMI distribution whereas the bulk of the observations necessarily follow a parabolic shape, which may or may not correspond to the true association (Durrleman & Simon, 1989; Mehta & Chang, 2009). The categorical model specification forces a step function that assumes no variation in mortality within each BMI category. With this type of specification, additionally, the conclusions depend on the choice of the reference BMI category. Theoretically, model fit could be used to compare how well the models fit the data, but in practice authors do not assess model fit in their articles. In part, this is because it is challenging to assess the model fit of survival models with data collected using a complex sampling design.

To our knowledge, only two studies have attempted to model the shape of the BMI-mortality association more flexibly, using a nonparametric approach (Gronniger, 2006; Mehta & Chang, 2009). Both found mortality risk to be relatively unchanging across a wide range of BMI values, increasing only among those with very low and very high body weights. These studies, however, were not survival analyses, but instead treated death as a dichotomous variable (alive or dead) at the end of the follow-up period. Such an approach is problematic because the results are strongly driven by the length of the follow-up period. In the extreme, if the follow-up period is long enough, all respondents will simply be recorded as dead, with no differentiation by length of survival taken into account.

Ignoring the length of the follow-up period could strongly shape results, because deaths occurring in the early years of follow-up tend to be associated with low BMIs. This relationship may be spurious, a result of an underlying disease process that causes both weight loss and death. Previous studies have dealt with this problem by excluding deaths that occurred in early years of the follow-up period (Greenberg, 2006; Greenberg et al., 2007; Manson et al., 1995). Such a correction, however, has meant deleting a large and nonrandom portion of the study sample, a problem for any analysis aiming to obtain unbiased and generalizable findings. Additionally, some authors have found that dropping deaths occurring in the early follow-up period is ineffective for dealing with confounding due to preexisting disease (Allison, Faith, Heo, Townsend-Butterworth, & Williamson 1999; Allison, Heo, Flanders, Faith, & Williamson, 1997). Ours is the first study that documents precisely how the BMI-mortality relationship changes across single years of the follow-up period.

The ultimate goal of BMI-mortality research is to understand the causal mechanisms that link excess body weight to disease processes. Some chronic conditions are strongly linked to excess body weight, including major causes of death such as cardiovascular disease (Gregg et al., 2005; McTigue & Kuller, 2008; Van Gaal, Mertens, & De Block, 2006) and diabetes (Ford, 1999; Kahn, Hull, & Utzschneider, 2006; Mokdad et al., 2003). Cancers represent another major group of causes of death, but have a weaker relationship to body weight (Calle, 2007; Calle & Kaaks, 2004; Flegal et al., 2007; Reeves et al., 2007), and for causes of death such as accidents and firearm deaths, there is likely little direct causal effect of BMI. Correspondingly, an analysis of the relationship between BMI and mortality that stratifies by different causes of death is crucial for understanding the causal effects of excess body weight on health among older adults.

The aim of this article is to determine the shape of the BMI-mortality association among older adults. We conduct a nonparametric survival analysis of all-cause mortality. We also address two issues crucial for making progress toward understanding causal associations: (a) we examine how the lag time between BMI measurement and death affects their association, and (b) we explore variation in the association across major causes of death. We employ generalized additive models (GAMs), a type of semiparametric regression model (Hastie & Tibshirani, 1990; Wood, 2006), to analyze a large, nationally representative data set with a long follow-up period. This approach allows the data to fully determine the functional shape of the BMI-mortality relationship in a survival framework. Finally, we assess variation in the association between BMI and mortality across different major causes of death, because the degree of variation may impact conclusions drawn from all-cause mortality analyses.

Data and Method

Data

The analyses use the National Health Interview Survey (NHIS) data for the years 1986-2004, linked to multiple cause-of-death (MCD) files from the National Death Index that include deaths through 2006. The NHIS is a large annual cross-sectional health survey conducted via face-to-face household interviews by the National Center for Health Statistics (NCHS) to obtain a sample representative of the civilian noninstitutionalized U.S. population. Every year, around 100,000 households are selected for interviews. The total household response rate was about 90% in the early 2000's; the rates were more than 95% in the earlier years (Massey, Moore, Parsons, & Tadros, 1989) and declined to 89% in 2000 (Centers for Disease Control and Prevention, 2002). Additional information about the sampling design is available in Massey et al. (1989) for the 1985-1994 period and in Botman, Moore, Moriarity, and Parsons (2000) for the 1995-2004 period.² Vital status for adults who participated in 1986-2000 NHIS was determined by a probabilistic match to the National Death Index (Lochner, Hummer, & Cox, 2007); the combined data set is referred to as the NHIS-MCD.

Sample

The analyses are based on non-Hispanic White men and women who were 50 to 80 years old at the time of the interview and whose BMI was between 15 and 45 points. We restricted the sample to non-Hispanic White adults because both BMI distribution and survival differ substantially across race and ethnic groups (Flegal et al., 2010; Hummer, Rogers, Nam, & LeClere, 1999).³ The race/ethnic-stratified models that would be needed to appropriately deal with this variation were not feasible here due to the space limitations. The upper age boundary was set to 80 because of indications that the matching of death information was less successful among older respondents (Masters, Brown and Hayward, unpublished analyses). The lower age boundary defined a sample with an appreciable mortality hazard by excluding young adults. The BMI range was chosen to exclude the small percentage of individuals (0.4%) with extreme values of body mass index. The high mortality rate for very under and overweight adults has been described extensively and data sparseness at the boundaries of the distribution may present estimation problems. Auxiliary analyses that included this group (available on request) were substantively equivalent to the results shown here.

Variables

Body mass index (BMI) was calculated from self-reported height and weight using the standard formula BMI = 703*(weight in pounds/squared height in inches). About 3.2% of respondents were missing BMI information and were excluded from analyses. The missingness occurred if they did not provide their height or weight, or if their height or weight were top coded or bottom coded and thus their BMI was not calculated.

The NHIS-MCD linked mortality data file included the underlying cause of death and select contributing causes coded using the ICD-10 classification. We categorized causes of death into four groups, which represent the leading causes of death in the United States (Jemal et al., 2008): cardiovascular disease, respiratory including lung cancer, cancer excluding lung cancer, diabetes, and other causes. Lung cancer was included among lower respiratory diseases such as COPD or emphysema because all these diseases are strongly affected by smoking. As sensitivity analyses, we also estimated models where lung cancer was included with cancers rather than respiratory conditions. The reclassification did not substantively affect the findings (available on request). The “other causes” category is very heterogeneous and the findings do not have a meaningful interpretation. Hence, it was omitted from the cause-specific analysis. Duration of follow-up to censoring or death was measured in years and ranged from 0 to 20. All models controlled for age in single years and marital status (dichotomized, with married as reference). Analyses were stratified by sex because of differences between men and women in how their BMI was related to mortality (Calle, Thun, Petrelli, Rodriquez, & Heath, 1999). There were no missing values on these three variables. Additional variables were used in auxiliary sensitivity analyses. We adjusted for region of residence and education; these predictors did not substantively change the findings. We have also estimated models where baseline health and disabilities were controlled for, using self-rated health and “bed disability days,” the two variables that were available across all study years in the data set. As might be expected, when controlling for these health factors, the BMI-mortality association attenuated substantially. The general shape of the curve, however, including the position of the nadir, remained substantively the same. Results of all sensitivity analyses are available on request.

Analysis

To lay the groundwork for the main analyses, we compared three models of mortality hazard as a function of parametrically specified BMI: Cox proportional hazard models, Poisson models with the log of duration as offset, and Poisson models estimated on a person-year data structure (Carstensen, 2005). This initial analytic step had two motivations. First, we showed that the results from these three different approaches to survival models (Cox proportional hazard and the two Poisson specifications) produced similar findings. This comparison was necessary because generalized additive models (GAMs) cannot be estimated within the proportional hazard survival structure, necessitating the Poisson models. We required two Poisson model specifications, one using person-level data with log duration since interview as an offset and the second using person-year data, because the former was more parsimonious but the latter allowed us to model the time to death as an independent predictor. Detailed mathematical and empirical comparison of Cox and Poisson models can be found elsewhere (Barros & Hirakata, 2003; Callas, Pastides, & Hosmer, 1998; Frome, 1983). Second, we showed that our findings matched those from the existing literature, which typically has used Cox proportional hazard models.

The GAM used in the main analyses is an extension of the generalized linear model in that one or more predictors are specified using a smooth function f(x) (Hastie & Tibshirani, 1986). The general structure of the GAM is η= β₀ + f₁(x₁) + … + f_k(x_k), where a smooth monotonic link function g(μ) transforms the expected value of y, μ to η. The y can follow any distribution from the exponential family; in our analyses, the outcome is Poisson-distributed with the link function g (μ) = log (μ)

The key advantage of GAMs over parametric GLMs is their flexibility in determining the f(x) functions from the data, which avoids the need for a priori assumptions about the shape of a predictor's effects (Beck & Jackman, 1998; Hastie & Tibshirani, 1990; Stone, 1985), such as the stepwise linear or quadratic functional forms typically used to specify the association between BMI and mortality risk. The f(x) functions can be constructed using various spline smoothing functions; the thin plate regression spline smoother is used here (Wood, 2003). This smoother is efficient to compute and the position of the knots is estimated directly from the data. The smoothness of f(x) is calculated with the aim of optimal balance between the fit to the data versus a penalty for excessive “wiggliness” of the functions.

The GAMs are estimated using penalized maximum likelihood, typically iteratively reweighted least squares (Andersen, 2009; Wood, 2006). After the basis for the function f(x) is chosen, the GAM reduces to a GLM, which makes it possible to conduct standard model building and diagnostic procedures. Model fit is estimated using either generalized cross-validation (GCV) based on the prediction mean square error, unbiased risk estimator (UBRE), or Akaike's information criterion (AIC). Confidence intervals for parameter estimates are calculated using the posterior distribution of the model coefficients. Different models can be compared using an approximation to the likelihood ratio test for nested models.

Finally, GAMs can accommodate the “interaction” of two or more predictors, in a way that is conceptually comparable to interactions in GLMs. The joint smooth function of the predictors was specified using tensor product smooths, optimal for variables measured on different scales—here, years since interview and BMI. We used this “interaction” to determine the BMI-mortality association across different values of time since interview. We have also conducted a sensitivity analysis with a BMI by age interaction. The results corroborated the literature in finding that the optimal BMI for longevity becomes higher with age of respondents (results not shown due to space constraints but are available on request).

Cause-specific mortality and BMI associations were estimated within a framework of competing risks. Death from a specific cause of death was treated as an event, whereas deaths from all other causes were treated as censoring because they removed the individual from the risk of dying from the specific cause. Results are presented graphically as line graphs with 95% confidence intervals, showing the estimated functional form for the effect of BMI on mortality. Findings from the interaction models that estimate the joint effect of BMI and time to death are shown in three-dimensional plots. The mgcv library (Wood, 2006) in R version 2.9.2 was used to estimate the models.

Results

Table 1 presents characteristics of the analysis sample. The mean age at interview was 62.7 years for men and 63.8 years for women. At the time of interview, men's mean BMI was 26.6 and women's BMI was 25.7—in the low overweight range for both groups. Considering the conventional categories of BMI, women and men were similarly likely to be obese (about 18% of each group), but more men were overweight (47.8% vs. 31.5% among women) and more women were in the normal-weight range (47.5% vs. 33.4% among men). On average, the respondents contributed about 10 years of follow-up. During the follow-up time, 34% of the male respondents died, at average age of 75 years, as did 27% of the female respondents, at an average age of 78 years. The modal cause of death was cardiovascular disease for both sexes.

Table 1. Characteristics of the Analysis Sample at Interview and Follow-Up, By Sex.

	Men			Women			Sex difference
	N	%	Mean (SE)	N	%	Mean (SE)
Total	122,248	100		144,054	100
Age at interview			62.7 (0.4)			63.8 (0.4)	p < .001
BMI			26.6 (0.2)			25.7 (0.2)	p < .001
BMI, categorized							p < .001
Underweight	1,025	0.8		4,279	2.8
Normal weight	41,799	33.4		69,195	47.5
Overweight	58,344	47.8		45,074	31.5
Obese	21,080	18.0		25,506	18.2
Education			13.0 (0.3)			12.8 (0.2)	p <.001
Proportion married	98,228	78.9		85,343	58.2		p < .001
Follow-up information
Years of follow-up			9.9 (0.4)			10.4 (0.4)	p < .001
Proportion died	45,410	34.3		43,363	27.4		p < .001
Age at death			75.1 (0.6)			77.6 (0.6)	p < .001
Cause of death (as proportion of total deaths)							p < .001
Cardiovascular	15,117	33.2		13,338	30.6
Respiratorya	8,855	19.6		7,235	17.0
Cancera	8,615	19.2		8,009	18.7
Diabetes	1,121	2.5		1,299	3.0
Other	11,524	25.4		13,305	30.7

Note: The analysis sample is restricted to non-Hispanic White men and women, age 50-80 at interview, with BMI between 15 and 45. Descriptive figures and tests of sex differences are adjusted for sampling design; Ns capture the actual count of observations in the data set.

^aLung cancer is excluded from the cancer category and included in the respiratory category.

Table 2 shows results from a parametric Cox proportional hazard and two Poisson models of all-cause mortality for men and women, using a quadratic specification for BMI. The first Poisson model was estimated on a person-level data set with log duration as offset. The second Poisson model was estimated on a person-year data set. As discussed above, these models were estimated to provide a baseline for comparison with the existing published literature, and to demonstrate empirically that these three modeling approaches yield very comparable findings. The comparability is important because almost all existing literature has used Cox models, whereas we needed to switch to the Poisson approach for the nonparametric modeling. In all models and for both sexes, BMI was a significant predictor of the hazard of mortality, even net of important sociodemographic predictors like age, education, and marital status. A simple calculation shows that the lowest point of the BMI-mortality curve occurred at BMI of 28.1 for men and 27.2 for women.⁴ These values correspond to published findings, with lowest mortality risk for older men and women in the overweight range.

Table 2. Comparison of Cox and Poisson Models of All-Cause Mortality.

	Men			Women
	Cox	Poisson 1	Poisson 2	Cox	Poisson 1	Poisson 2
Age	1.10*** [1.09,1.10]	1.08*** [1.08,1.09]	1.09*** [1.09,1.09]	1.10*** [1.10,1.10]	1.09*** [1.09,1.09]	1.10*** [1.10,1.10]
BMI	0.97*** [0.96,0.97]	0.97*** [0.96,0.97]	0.97*** [0.96,0.97]	0.98*** [0.98,0.99]	0.98*** [0.98,0.99]	0.99*** [0.98,0.99]
BMI2	1.01*** [1.01,1.01]	1.01*** [1.01,1.01]	1.01*** [1.01,1.01]	1.00*** [1.00,1.00]	1.00*** [1.00,1.00]	1.00*** [1.00,1.00]
Education	0.99*** [0.99,0.99]	0.99*** [0.99,0.99]	0.99*** [0.99,0.99]	0.99*** [0.99,0.99]	0.99*** [0.99,0.99]	0.99*** [0.99,0.99]
Married	0.76*** [0.74,0.77]	0.80*** [0.78,0.81]	0.75*** [0.74,0.77]	0.80*** [0.78,0.82]	0.83*** [0.81,0.84]	0.81*** [0.80,0.83]

Note: Poisson I model is estimated on a person-level data with log duration as offset. Poisson 2 is estimated on a person-year data set. Exponentiated coefficients; 95% CI in brackets

^*p < .05.

^**p <.01.

^***p < .001.

Figure 1 offers a visual comparison of the parametric Poisson model results shown in Table 2 against results from comparable GAM models. The GAM results share similarities with the results obtained from parametric models with a quadratic specification in that the risk of mortality increases steadily toward both the lower and higher BMI levels. There are two important differences, though. In the parametric (quadratic) models, the lowest mortality occurs among adults in the mid-overweight range. The GAM results show the nadirs of the mortality curve at lower BMIs. The difference is particularly pronounced for women, among whom the nadir of the mortality risk curve occurs at BMI of about 27 in the parametric models but below 25 in the GAM models. The second difference is that the mortality increases more sharply among adults with BMIs below and above the optimal weight. In this respect, the functional form for BMI is closer to a V shape than a U shape, especially among men.

Figure 1.

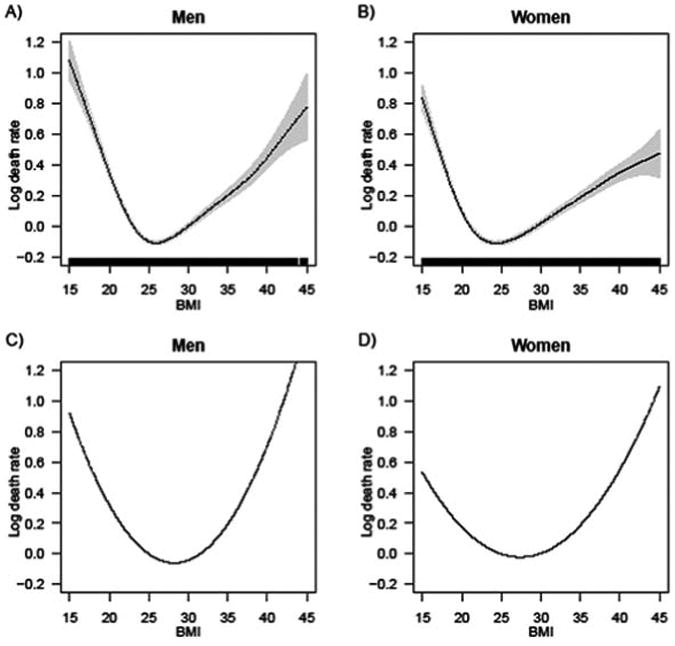
Comparison of results from GAM and GLM Poisson models of all-cause mortality as a function of BMI. In the first row (Panel A for men and Panel B for women), the shape of the BMI mortality association is freely estimated from the data. In the second row (Panel C for men and Panel D for women), the functional form for BMI is specified to be quadratic, in accordance with previous literature

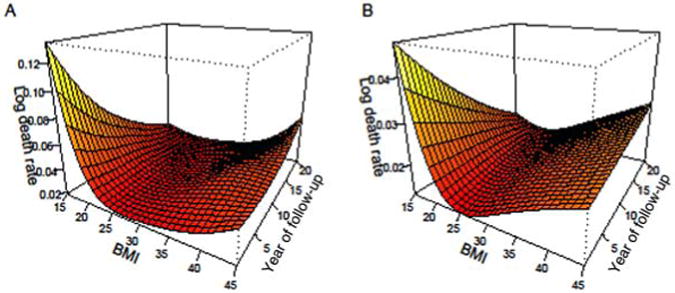
Duration of follow-up time has been shown as an important mediating factor in the BMI-mortality relationship in past research. Figure 2 displays results from “interaction” models that demonstrate how the association between BMI and all-cause mortality varies by time since interview for men (Panel A) and women (Panel B). The results are similar for men and women: shortly after the interview, low BMI is associated with a particularly high risk of dying. Over time, this association changes: low BMIs are gradually less strongly associated with mortality, whereas individuals who reported high BMIs at the interview have increasingly higher chances of dying. These patterns are likely due to reverse causality processes, whereby serious disease like cancer causes weight loss—hence, individuals who report low BMIs at interviews may be those who have low weight because they are seriously ill and are therefore likely to die shortly after the interview.

Figure 2. The association between BMI and all-cause mortality across the duration of follow-up time, for men (Panel A) and women (Panel B).

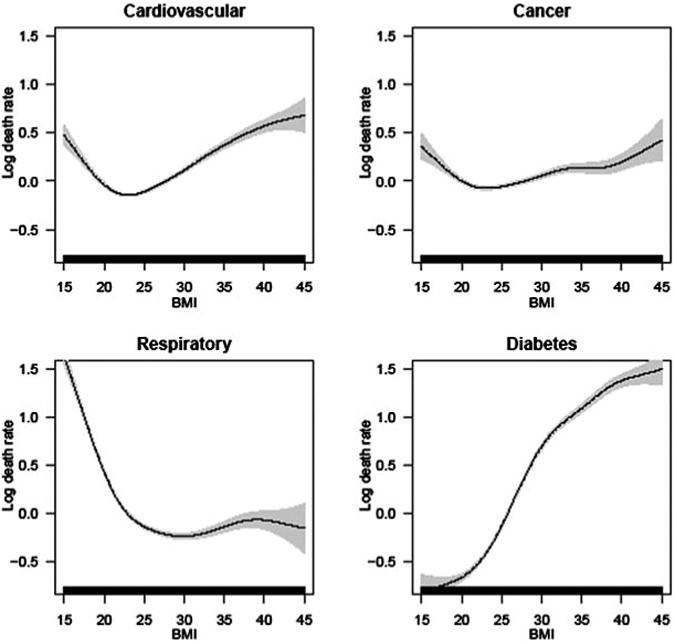
Finally, Figure 3A for men and Figure 3B for women show the association of BMI with cause-specific mortality, focusing on cardiovascular, respiratory, cancer, and diabetes deaths. These results demonstrate substantial variation among the four groups in the functional form of the BMI-mortality association. For cardiovascular deaths, the association is U or V shaped for men and women, with the risk of dying increasing steadily from high-normal BMI to even higher BMIs. The nadir of the mortality curve is around 25 for men and 22-23 for women, considerably less than for all-cause mortality. The relationship between BMI and cancer is flatter compared to the association with other causes. For respiratory deaths, mortality is particularly high at underweight and normal BMIs and relatively low throughout the overweight and low-obese range. This pattern is likely due to smoking, whereby smokers tend to have lower body weights (Flegal, Troiano, Pamuk, Kuczmarski, & Campbell, 1995) and suffer increased mortality from respiratory illnesses such as lung cancer or emphysema. Finally, diabetes mortality shows a clear, strong, monotonically increasing risk from very low to high BMIs for both men and women. The similarity between men and women in how each cause is affected by BMI points to biological underpinnings of the relationship.

Figure 3A. The association between BMI and cause-specific mortality for selected causes of death, for men.

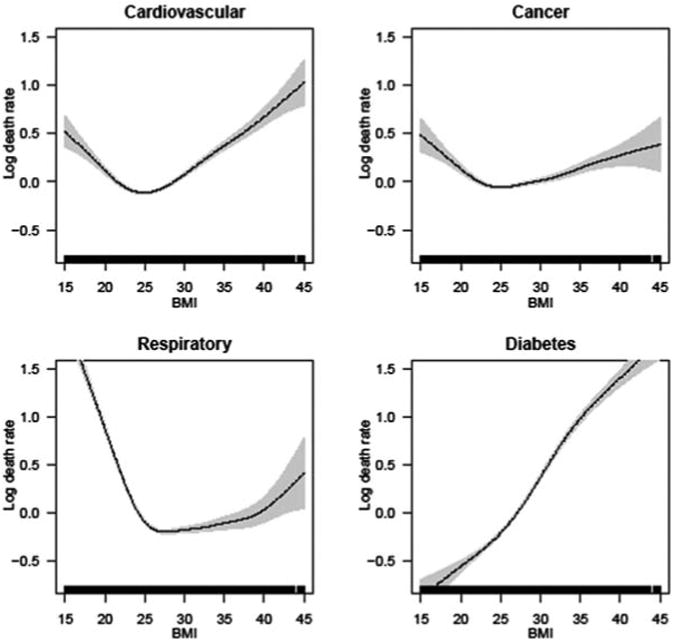
Figure 3B. The association between BMI and cause-specific mortality for selected causes of death, for women.

Discussion

Despite the wealth of research addressing the effects of body weight on mortality, the shape of the association has not been established beyond the general curvilinear pattern, in which high and low BMIs are associated with an increased mortality risk. We suggest that parametric models used in almost all previous studies impose an priori form for the BMI-mortality relationship, potentially biasing results. Nonparametric models, by contrast, are better suited to exploring the association because they have the flexibility to allow the data to reveal the actual shape of the association. In this article, we used nonparametric generalized additive models to examine the shape of the BMI-mortality association for all-cause and cause-specific mortality in non-Hispanic White male and female older adults. In a broad sense, our study corroborates the extensive literature, in that we also found higher mortality risk among adults with both high and low BMIs. However, our investigation revealed several new findings.

First, the association between BMI and all-cause mortality appears to be more of a V shape, rather than the U shape widely reported in the literature. The U shape demonstrated repeatedly in prior studies is a necessary result of the quadratic specification for BMI typically used. To the degree these new results are supported in other studies, our findings imply that the BMI-mortality association may more effectively studied using splines than a quadratic form. The placement of the knot for the spline function could be determined using a nonparametric exploratory analysis like those presented here. Our findings suggest that the lowest mortality is associated with BMIs just above 25 for men and slightly below 25 for women.

Our findings counter those of the previous two studies that used nonparametric models to estimate the BMI-mortality association (Durrleman & Simon, 1989; Mehta & Chang, 2009). These studies found that mortality risk was similar across a wide range of body weights. The difference between their findings and ours may arise because these two previous articles did not conduct a survival analyses, but treated death as a binary outcome.

Second, we showed how the duration of follow-up before death affects the observed BMI-mortality association. For deaths that occur after only a short follow-up period, low BMI represents higher risk than high BMI. A reversal occurs as follow-up time extends, whereby high BMI becomes more strongly associated with mortality than low BMI. The finding itself is not new (Allison et al., 1999; Greenberg, 2001) but this is the first study to provide a clear picture of the process over the course of 20 years of follow-up.

Finally, the study highlighted the substantial differences in the BMI-mortality association for different causes of death. Cardiovascular death risk shows a V-shaped association with BMI, and there is a similar but weaker pattern for cancer deaths. However, the risk for respiratory deaths is clearly highest at low BMI, whereas the risk for a diabetes-related death moves in the opposite direction, increasing steadily with body weight. These cause-specific results are important for various reasons. First, they suggest that period changes in the composition of causes of death may shift the observed relationship between BMI and overall mortality. For instance, diabetes has a strong positive association with BMI. As a greater proportion of deaths occurs due to diabetes because of an increased prevalence of the disease in the population, then the relationship between BMI and all-cause mortality may become more like that for diabetes and the nadir of the BMI-mortality curve may shift to lower body weights. Second, the findings imply that recommendations about optimal body weight for health and longevity should accommodate substantial variability in the association of body weight with different health and mortality outcomes. And third, they elucidate the potential connections between the mortality literature and clinical and biomedical studies that focus on the mechanisms through which excess adiposity affects the physiology of the human organism and causes disease. By disaggregating all-cause mortality into specific causes of death, we can isolate the BMI effects for specific diseases of groups of diseases, which can then be connected to the literature on the prevalence of those diseases by BMI.

The goal of this study was to more carefully analyze the shape of the BMI-mortality association. There are limitations in our data and analyses that make these finding only a first step toward optimal modeling of their association. For instance, smoking information would be helpful in understanding the pattern observed for respiratory deaths, but it is not available in the core NHIS data. The measurement of BMI used here is limited by its self-reported nature and because it is only measured a single time at the NHIS interview. Ideally, we would want to observe how BMI changes over time for individuals to better understand the effect of changes in body weight on subsequent mortality.

The results of our study have several important implications, despite these limitations. First, it may be erroneous to draw implications about “optimal” body weights from standard parametric survival models. In particular, researchers should explore the shape of the association between body weight and various outcomes before imposing an inflexible analytic form on the relationship, because doing so may lead to biased findings. And second, given the variability in the BMI-mortality relationship for different causes of death, public health researchers should use caution when using the mortality results to make recommendations about optimal BMI for general health.