A noisy linear map underlies oscillations in cell size and gene expression in bacteria

Abstract

During bacterial growth, a cell approximately doubles in size prior to division, upon which it splits into two daughter cells. This process is subjected to the inherent perturbations of cellular noise^1,2 and thus requires regulation for cell-size homeostasis. The mechanisms underlying cell-size control and their dynamics consequences remain poorly understood due to the difficulty in sizing individual bacteria over long periods of time in a high-throughput manner. Here, we measured and analyzed long-term, single-cell growth and division across different Escherichia coli strains and growth conditions³. We found that a subset of cells in a population exhibited transient oscillations in cell size with periods that stretch across multiple (>10) generations. Our analysis revealed that a simple law governing cell size control – a noisy linear map – explains the origins of these cell-size oscillations across all strains. This noisy linear map implements a negative feedback on cell-size control: a cell with a larger initial size tends to divide earlier, whereas one with a smaller initial size tends to divide later. Combining simulations of cell growth and division with experimental data, we demonstrate that this noisy linear map generates transient oscillations, not just in cell size, but also in constitutive gene expression. Our work provides new insights into the dynamics of bacterial cell-size regulation with implications for the physiological processes involved.

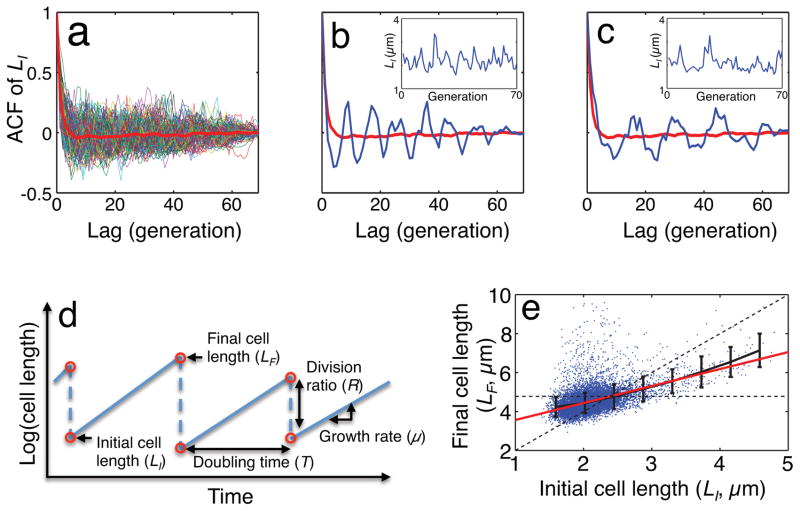
We used a “mother machine” microfluidic device³ and time-lapse microscopy to monitor long-term cell-size dynamics in E. coli at the single-cell level. The device enables the measurement of cell size and gene expression for hundreds of E. coli mother lineages over thousands of minutes³ and also allows continuous medium infusion to maintain balanced growth. We first analyzed temporal dynamics of the initial cell size (cell size at birth, or L_I) by computing its autocorrelation function (ACF). To our initial surprise, some lineages of mother cells (30–40%) exhibited long-term oscillations in cell size whose period could be longer than 10 generations. These oscillations were masked when averaged across the ensemble of all mother lineages (Fig. 1). The periods of these oscillations were variable across lineages. For example, the period was about eight generations in one lineage (Fig. 1b) but about 16 generations in another (Fig. 1c).

Figure 1. Transient oscillations in cell size.

a, ACF of all lineages (n = 160) and their average (thick red line).

b, An example of L_I oscillation with a period of ~8 generations.

c, Another example of L_I oscillation with a period of ~16 generations.

d, Definition of growth parameters.

e, A noisy linear map in cell size control: final cell size (L_F) is plotted against initial cell size (L_I) (n = 11168). Black and red lines show binned average and linear regression line, respectively. The slope of the regression line (a) is 0.871 with 95% confidence interval of 0.842–0.901. The two dotted lines show y = 2x and y = b. The error bars indicate standard deviation of each bin.

How might these long-term oscillations emerge, why do they have variable periods, and why do they only occur in a subset of cell lineages? At a fundamental level, oscillations require negative feedback. If so, what might constitute this negative feedback in our system? We reasoned that negative feedback emerged from cell-size control: to maintain an average cell size over generations, a cell may sense its size and adjust either its growth rate (in biomass accumulation) during a cycle, the length of the cell cycle, or both. Such a control mechanism could provide the required negative feedback.

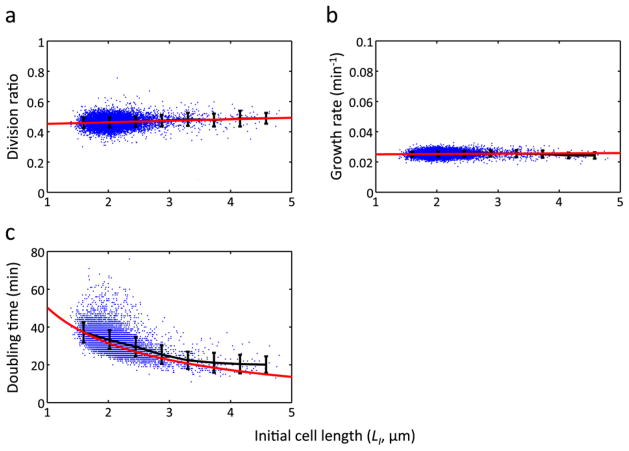
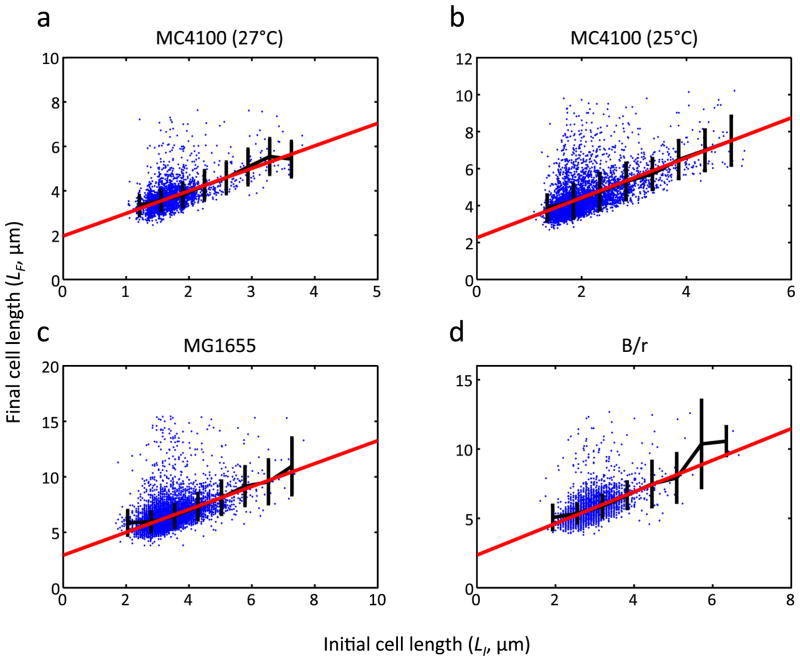
To test this notion, we measured various growth-related parameters (Fig. 1d) as a function of the initial cell size (Fig. 1e and Extended Data Fig. 1). We found that the final cell size (cell size before division, or L_F) could be described, on average, by a linear function of the initial cell size, L_F = aL_I + b (Fig. 1e). The slope of this linear function (a = 0.871) was < 2, which reflects negative-feedback control of cell size. We verified that this linear function also holds for different growth conditions (27°C and 25°C) and two other E. coli strains (MG1655 and B/r; data sets from a previous study³) (Extended Data Fig. 2). Our data showed that both the division ratio (R) and growth rate (μ) were relatively independent of initial size (Extended Data Fig. 1a, b). However, the doubling time (T) was negatively correlated with the initial size (Extended Data Fig. 1c), providing the basis for the negative-feedback control. That is, a mother cell with smaller initial size tended to grow for a longer duration than the average; a mother cell with a larger initial size tended to grow for a shorter duration than the average. Recent studies^4–6 examining cell-size homeostasis in bacteria also reported this observation of modulation of division time.

Based on our observation of a linear relationship between L_I and L_F, we examined the extent to which a simple autoregressive model with noise might explain our experimentally observed data:

$$L_I(n+1)=(a{L}_I(n)+b+\eta )/2.$$ Eq. 1

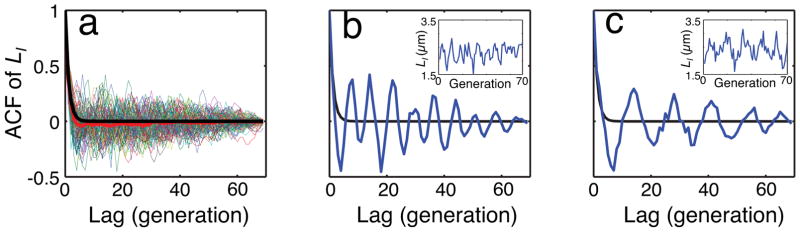
Here, L_I (n) is the initial size at generation n, and η is Gaussian white noise, representing the scatter around the linear regression line in Fig. 1e. Using this “noisy linear map” between the initial and final cell sizes, we numerically simulated the dynamics of L_I in 100 lineages, each for 70 generations (i.e., typical duration in our experiment). The ensemble average ACF of the simulated L_I dynamics followed a simple exponential decay, consistent with the experimental observation and theory⁷, R(τ) = (a / 2)^|τ| (Fig. 2a). However, some of the individual realizations showed distinct oscillations with variable periods (Fig. 2b, c). A time-frequency analysis of the simulated L_I dynamics over longer duration (Methods) showed that the dominant frequency in a single lineage changed over time (Extended Data Fig. 3a). This indicates that the observed oscillations were transient and could arise and disappear in single lineages.

Figure 2. Simulated transient cell-size oscillations using the noisy linear map (Eq. 1).

a, ACF of L_I for 100 simulations (thin lines). The thick red line shows the average ACF; the thick black line shows the theoretical calculation. a = 0.871, b = 2.70 μm, and σ₁ (standard deviation of η) = 0.548 μm were used for these simulations. These values are based on the characterization in Fig. 1e and the root-mean-square error of the regression was used for σ₁.

b and c, ACF of two typical oscillatory time courses (insets).

How does cell-size control affect the frequency and amplitude of these apparent oscillations? As indicated by a rescaled equation (Methods, Eq. 2), the noisy linear map has a single free parameter, a, that dictates the overall temporal dynamics. Biologically, a represents the strength of cell-size control; its value can be experimentally measured and it is likely determined by the molecular mechanisms underlying cell-size control^8–11 (Supplemental Information) and growth conditions. For a = 0, the cell size in one generation is not influenced by that in the previous generation (i.e., very strong regulation); thus the cell-size dynamics are determined by the noise term. For 0 < a < 2, the cell size in one generation retains a ‘memory’ of the previous generation (i.e., weaker regulation). a cannot exceed 2 because otherwise cell size will grow or shrink without bound. To investigate the effect of a on the transient oscillations, we simulated the cell-size dynamics for 70 generations using the rescaled linear map (Eq. 2) with different a values, and compared the probability of transient oscillations and frequency of individual cells (Methods).

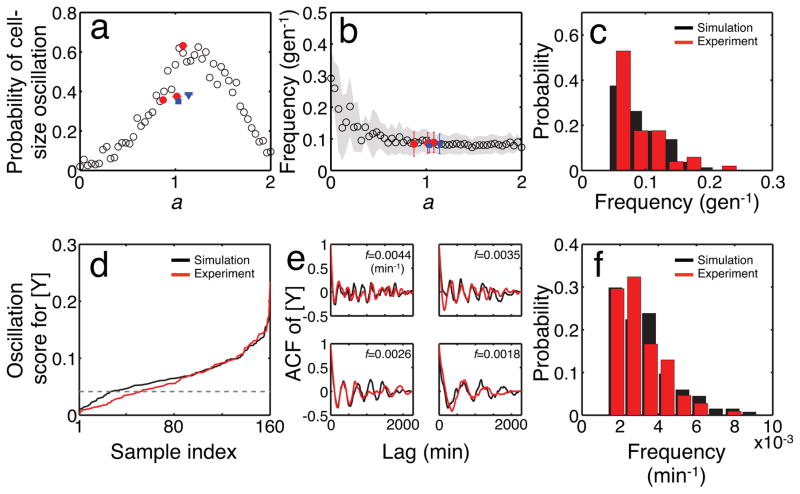
The simulation showed that the probability of transient oscillations was negligible when a was close to 0; the dynamics were dictated by the noise term (Fig. 3a). As a increased, the probability of transient oscillation also increased and peaked at around a = 1.3, above which it started to decline. The linear map acts as a low-pass filter to η (Methods, Eq. 3)⁷. When a = 0, there is no filtering and the system contains all frequencies, on average, at the same power. As a increases, the system suppresses high-frequency components and concentrates the power to the low-frequency domain, and thus slowing down the dynamics (Extended Data Fig. 3b). This filtering can generate transient low-frequency oscillations in some cells. The subsequent decline can be explained by considering how a affects the time scale of the dynamics. Our finite observation window (70 generations) limits the lowest observable oscillation frequencies, and so an extreme slow-down of the dynamics reduces the probability of oscillation for large a. The effect of this slowing down is also seen in the oscillation frequency, where the oscillation frequency decreases with a and levels off due to the limited observation time window (Fig. 3b and Extended Data Fig. 3c).

Figure 3. Dependence of cell size oscillation on a, and oscillations in gene expression.

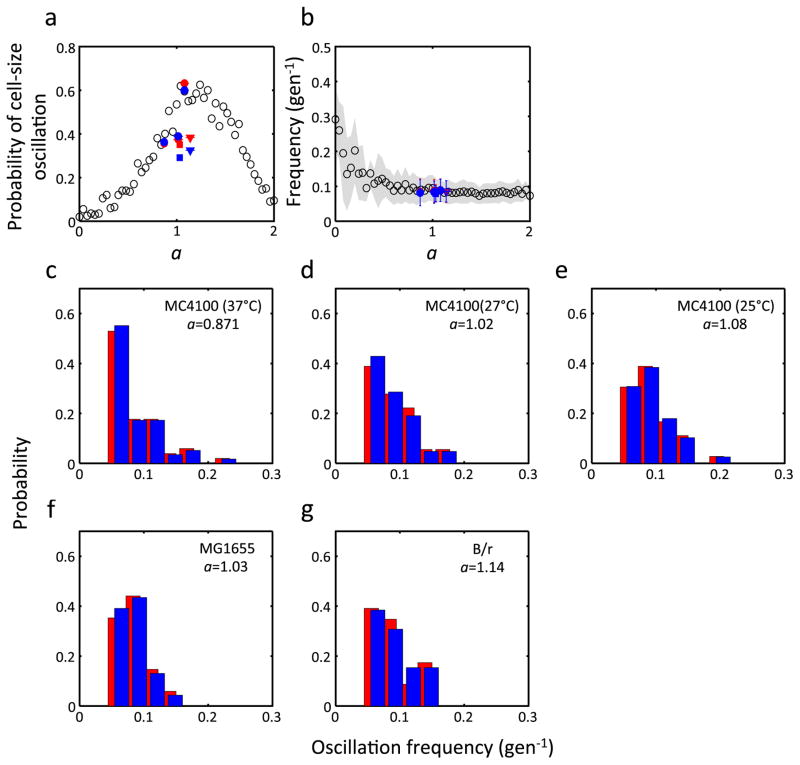
a, Dependence of the probability of oscillation on a. For each value of a, 200 simulations were run using the rescaled linear map (Eq. 2). Closed symbols indicate analysis of our own experimental data (MC4100 grown at 37°C, 27°C and 25°C, red circles from left to right (n = 143, 48, and 57, respectively)) and previously published data (MG1655, blue square (n = 97); B/r strain, blue triangle (n = 60)). Only lineages without aberrant cell cycles are shown (Methods). The horizontal error bars indicate the 95% confidence interval.

b, Dependence of the average oscillation frequency on a using the same data set presented in a. Only lineages that were considered oscillatory were used for the calculation (n = 51 (37°C), 18 (27°C), and 36 (25°C) for MC4100, 34 for MG1655, and 23 for B/r strain). The shaded region represents standard deviation. As in a, closed symbols indicate analysis of experimental data; the vertical error bars indicate standard deviation.

c, Distributions of oscillation frequencies from experimental (MC4100, 37°C; n = 51) and simulated (n = 80) cell-size dynamics. Simulations were done with a = 0.88 using Eq. 2.

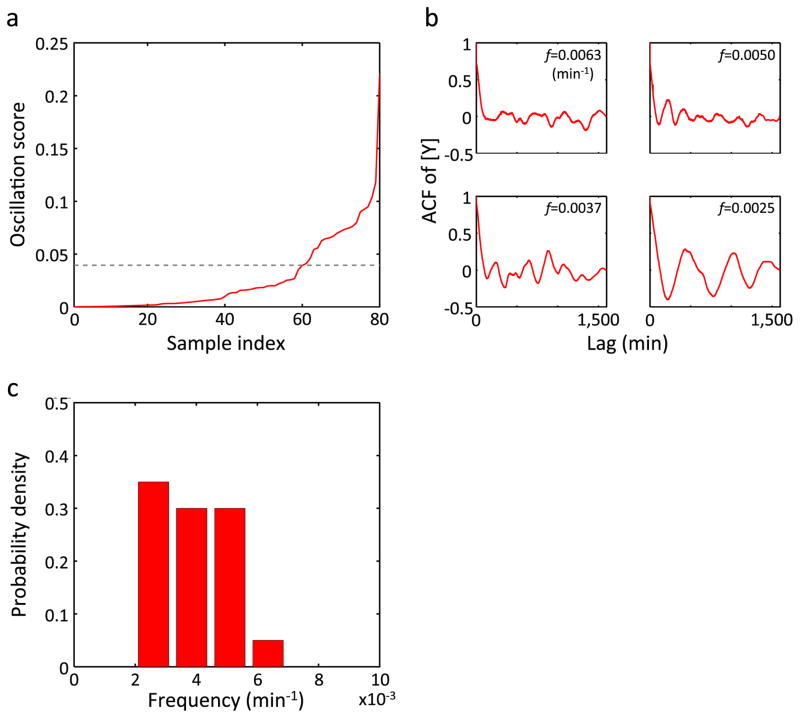
d, Oscillation scores of simulated (black, Methods) and experimental (MC4100 at 37°C, red) YFP concentrations ([Y]). The data were sorted according to the oscillation score and shown in an ascending order. The dashed line indicates a threshold for the oscillation score (Methods).

e, ACFs of [Y] for four different frequencies. For each frequency (indicated in each panel), the sample with the highest score (above the threshold) is shown for simulation (black) and experiment (red).

f, Distributions of oscillation frequencies in [Y] for simulation (black, n = 134) and experiment (red, n = 108).

The noisy linear map provides a simple explanation for the experimentally observed oscillations: both the probability of oscillation and the range of oscillation frequencies analyzed from our experiments show excellent agreement with the simulation (Fig. 3a, b, red symbols). We observed similar oscillations in previously published data sets in different strains³, and they are also consistent with our simulation though to a lesser degree (Fig. 3a, b, blue symbols). The agreement between simulation and experiment was improved when aberrant cell growth such as spontaneous cell filamentation was excluded from the data set (Extended Data Fig. 4). Finally, a close look at the distribution of oscillation frequencies reveals the dominance of low frequencies for both simulations and experimental data (Fig. 3c). Taken together, our analyses support the notion that the noisy linear map can explain the spontaneous transient oscillations in cell size.

The same principle of noisy linear map is also applicable to molecules in the cell. Consider constitutive production of a protein with negligible degradation. At steady-state growth, the quantity of the protein on average doubles during a cell cycle and halves upon cell division, generating dynamics similar to cell size. Dilution of molecules by cell division inherently acts to maintain a steady-state level of the molecule. In our experiment, the yellow fluorescent protein (YFP) was constitutively expressed in cells. Indeed, analysis of the experimental data revealed a noisy linear map similar to that for cell size (i.e., 0 < a = 1.05 < 2; Extended Data Fig. 5). As such, tracking the amount of the total per-cell protein at the beginning of each cell cycle should also reveal transient oscillations, just as observed in L_I. However, it is not evident whether the protein concentration ([Y]) would also oscillate. To examine this aspect, we simulated the stochastic gene expression in each cell coupled with long-term cell-size dynamics using a noisy linear map (Methods). Our simulations indeed predicted transient oscillations in the protein concentration (Fig. 3d, e, black lines).

Consistent with the model prediction, analysis of experimental data revealed transient oscillations in [Y] (Fig. 3d, e, red lines). The periods of these oscillations spanned many cell cycles and could be close to 20 cell cycles (Fig. 3e, f; period of ~600 min where average doubling time is ~33 min). We confirmed this observation in other growth conditions (Extended Data Figs 6 and 7) and previously published data sets³ that used other E. coli strains under different experimental conditions (Extended Data Figs 8 and 9). Despite the different experimental settings, our analysis consistently revealed oscillations in cell size and gene expression in each data set. This consistency indicates the generality of our conclusions.

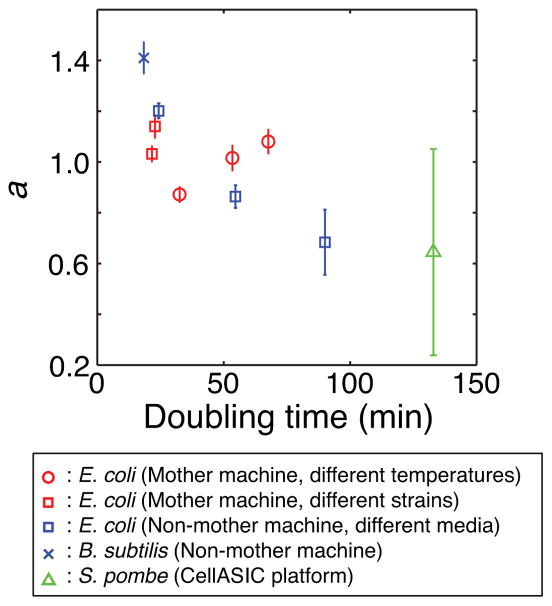
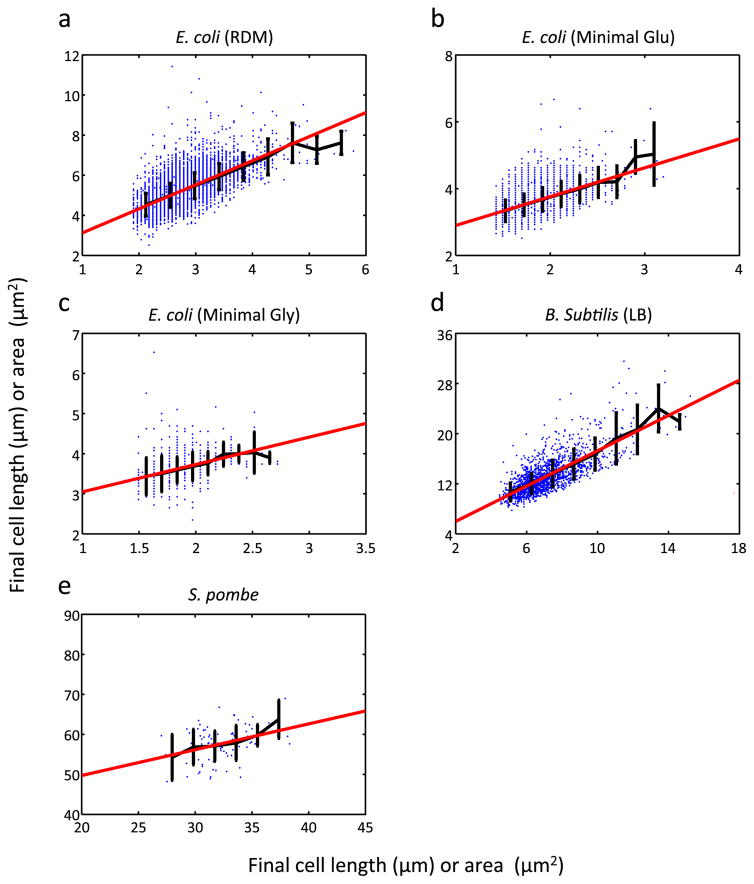
We further probed the generality of the noisy linear map in other data sets that examined (1) E. coli growth in another type of microfluidic device under three different growth media¹², (2) growth of another rod-shaped bacterium, Bacillus subtilis¹², and (3) growth of rod-shaped fission yeast. All these data sets revealed the existence of a noisy linear map (Fig. 4 and Extended Data Fig. 10). A recent study also showed a consistent result for the fission yeast¹³. We note that the cell-size control strength, a, is generally not equal to 1; instead, it varies depending on growth conditions, strains, and species (Fig. 4). This conclusion differs from the “adder” model^5,6,14, which states that cells add a constant volume (or mass) between divisions. The adder model requires a = 1. Our analysis suggests that the adder model^5,6 may represent a special case of cell-size control and might not be generally applicable to different bacterial strains, species, or growth conditions.

Figure 4. a in different data sets.

The slope (a) of the linear map was derived from 10 different data sets and plotted as a function of cell doubling time. ‘Mother machine’ refers to our own data sets (‘different temperatures’) and the data sets from Wang et al³ (‘different strains’). ‘Non-mother machine’ refers to the data set from Moffitt et al¹². ‘CellASIC platform’ refers to the S. pombe experiment performed using the CellASIC system (a commercially available microfluidic device). The error bars indicate the 95% confidence interval.

Our work reveals a simple model of cell-size control and its physiological consequence in gene expression. The strength of cell-size control may vary according to underlying molecular mechanisms and growth conditions (Fig. 4, Supplementary Information). This change would lead to varying degree of spontaneously generated pulsatile gene expression, which has been implicated in stress response, signaling, and development^15–17. As cell-size control is a fundamental aspect of biology, it may represent a primitive means to generate spontaneous pulsatile gene expression for these functions. Also, recent studies^18–20 found that the bacterial proteome is partitioned into distinct sectors, which can be adjusted to optimize resource allocation under different growth conditions. Our observation of spontaneous, long-term oscillations in gene expression suggests that such balance may be adjusted dynamically even under a fixed growth condition. As the bacterial ‘growth law’ revealed by the previous work was based on population-level measurements^18–20, it would be interesting to investigate this empirical law at the single-cell level. Efforts have already been put to elucidate how fluctuation in catabolic gene expression affects cell growth and vice versa²¹. Finally, the noisy linear map could be exploited in interfacing with synthetic gene circuits. Studies have shown that interactions between host physiology and exogenous gene circuits can lead to novel behaviors^22–24. Given the ability of the noisy linear map to generate transient oscillations in gene expression, it would be interesting to examine its effects on synthetic oscillators^25–27.

Methods

Fabrication of microfluidic device

We followed the previously published procedure to fabricate the “mother machine”³ except that our mold was reverse-fabricated from the original mother machine device. This was done by pouring epoxy onto the original mother machine device (kind gift from Dr. Jun). Replicas of the mother machine were then created by pouring PDMS onto this mold and solidifying the polymer at 80°C for 30 minutes. The resulting PDMS device was then bonded to a glass cover slip by plasma treatment.

Cell strain, growth condition, microscopy, and microfluidics

An E. coli strain MC4100 that constitutively expresses YFP (galK::P_lac-yfp amp^R; kind gift from Dr. Kishony²⁸) was used in our experiments. For long-term imaging of these cells in the microfluidic device, a similar procedure as described in³ was followed. Briefly, cultures were grown overnight in LB at 37°C. The overnight culture was diluted 100 fold in 5ml fresh LB and grown at 37°C. At sufficiently high density, this culture was concentrated about 20 fold by centrifugation for loading into the mother machine using a syringe. The device was then spun for three minutes using a mini centrifuge to help trap cells in the side channels of the device. Prior to loading, the device was cleaned using 70% ethanol, washed twice with distilled water, and all liquid was then expunged with air. Fresh LB was then introduced to remove cells not trapped and a continuous flow (100 μl/h) was maintained. Throughout the experiment, carbenicillin (50 μg/ml) was added in growth medium. Images were acquired at one-minute intervals using DeltaVision Elite microscope (Applied Precision) with a motorized stage and an Evolve EM-CCD camera (Photometrics) with either 100x DIC objective or 60x phase objective. When 60x phase objective was used, additional x2 auxiliary magnification was also used. Prior to the experiment, the microscope and its growth chamber were equilibrated at an appropriate temperature (25, 27, or 37°C), and the temperature was maintained throughout the experiment.

For the experiment with S. pombe, JM1645 strain that constitutively expresses GFP (pAct1-GFP::leu1-32 h-; kind gift from Dr. Moseley at Dartmouth University) was grown overnight in 3ml YE4S medium at 30°C. The overnight culture was diluted 100 fold into fresh 3ml YE4S and grown at 30°C for 4.5 hours. Cells were then sonicated for 30 seconds to separate at medium intensity (Diagenode Bioruptor UCD-200). Cells were loaded into a CellASIC Y04C plate (EMD Millipore). A medium flow rate was kept at 3psi, and the middle chamber (4μm in height) was used for imaging. Images were acquired every three minutes using DeltaVision Elite microscope with a motorized stage and a CoolSNAP CCD camera (Photometrics) with 60x phase objective. The temperature was kept at 30°C throughout the experiment.

Image analysis

For mother machine experiments, we developed a custom program using C++ and FIJI for image segmentation. The segmentation of cells was performed based on fluorescent images by finding minima of fluorescent intensity along the channel direction of the mother machine. The segmented images were checked manually and corrected. CellStat (Fraunhofer-Chalmers Centre, Gothenburg, Sweden)²⁹ was used for image segmentation of the experiment with S. pombe.

Data processing (mother machine data)

For both our own data sets and previously published data sets, cell divisions were detected based on the change in cell length– a division event is identifiable in the data sets as a clear and large drop in the size of the mother cell. We selected cell lineages that contained measurements of full 70 generations. This resulted in 160 (37°C), 54 (27°C) and 65 (25°C) lineages for MC4100, 158 lineages for MG1655, and 80 lineages for B/r strain. To minimize the effect of erroneous segmentation, we ignored spontaneous “spikes” in cell length, which were occasionally observed in the previously published data³. Cells occasionally undergo aberrant cell growth such as filamentation. For the analysis performed in Fig. 1e and Extended Data Figs 1, 2, and 5, we excluded these instances, by discarding data points in which (1) initial cell length was larger than L̄ + 2σ_L (L̄ and σ_L are the average and standard deviation of the cell size distribution, respectively) or (2) final cell length was larger than 2(L̄ + 2σ_L). We also excluded cell cycles whose initial cell length was smaller than L̄ − 2σ_L. This latter condition was to mainly exclude data points that appear to result from erroneous segmentation in the previously published data sets. Our own data sets (i.e., MC4100) contained only one such instance. To eliminate incorrect segmentations, we assumed cell divisions to be at least 10 minutes apart and excluded cell cycles in which L_F < L_I (only found in the published data sets). These procedures filtered out ~0.6% of total cell cycles. For the analysis performed in Fig 3a–c and Extended Data Fig 4, unless otherwise noted, cell lineages that contained aberrant cell cycles described above were excluded from the analysis.

We note that the published data sets were available and accessed in the form of processed data sets rather than the actual movies of cell growth themselves. As such, we were unable to manually correct for possible segmentation errors other than using the criteria described above. This inability could account for lower probability of oscillation as compared with the model prediction (Fig. 3a)–the cell size dynamics is more susceptible to these errors than the linear map. Indeed, when the above criteria were used to process the data, it led to a clear improvement in agreement with the simulations (Extended Data Fig. 4). Our own data sets were subject to manual segmentation checks based on the movies and were largely devoid of these errors.

Data processing (Data from the Cluzel lab¹²)

For each condition (E. coli with three growth media and B. subtilis), we chose to analyze an experiment performed with 4% agarose. All complete cell cycles were subject to the above processing, and the same exclusion criteria as the mother machine data were uniformly applied for filtering. As a result, ~0.6% of total cell cycles were filtered out.

Data processing (S. pombe experiment)

For the S. pombe experiment, microscope images were analyzed using CellStat (Fraunhofer-Chalmers Centre, Gothenburg, Sweden)²⁹. Cell area, instead of cell length, was used to derive the linear map. Since this experiment was performed in the CellASIC platform and the throughput was much lower than the mother machine (87 cell cycles), apparent filamentous events were manually inspected and two cell cycles were excluded. These two events were visually obvious and well separated from the other cell cycles in the distribution. The total of 85 cell cycles were used for the linear map analysis (Extended Data Fig. 10e).

Analysis of noisy linear map

The noisy linear map (Eq. 1 in the main text)

$$L_I(n+1)=(a{L}_I(n)+b+\eta )/2$$

can be rescaled by

$$\begin{array}{l}{x}_n=\frac{L_I(n)-L_I^{ss}}{{\sigma }_1}\\ \text{and}{L}_I^{SS}=\frac{b}{2-a}.\end{array}$$

Here, σ₁ is the standard deviation of the noise term η, and $L_I^{ss}$ is the steady state of L_I(n). This gives

$$x(n+1)=(ax(n)+n^{\prime })/2,$$ Eq. 2

where η′ = η/σ₁. We assume a Gaussian white noise for η, and then η′ is also a Gaussian white noise with η′ ~ N(0,1). This rescaling shows that the dynamics of noisy linear map is solely dependent on a. For the analysis performed in Fig. 3a–c, we used this rescaled model to examine the effect of a on oscillation characteristics.

As discussed in the main text, the autocorrelation function of the system is given by R(τ) = (a/2)^|τ| and then the power spectrum of, X(f), for 0 ≤ a < 2 is given by³⁰

$$X(f)={\mid H(f)\mid }^2{S}_{\eta }(f)=\frac{1}{1-acos2\pi f+{\left(\frac{a}{2}\right)}^2},$$ Eq. 3

where H(f) is a transfer function of the system (at frequency f), and S_η(f) = 1 is the power spectrum of η′. With a = 2, the dynamics becomes Brownian noise, and X(f) = 1/(2πf)². As a increases, the system suppresses high frequency components and concentrates the power to the low frequency domain (Extended Data Fig. 3b).

Time-frequency analysis of L_I dynamics

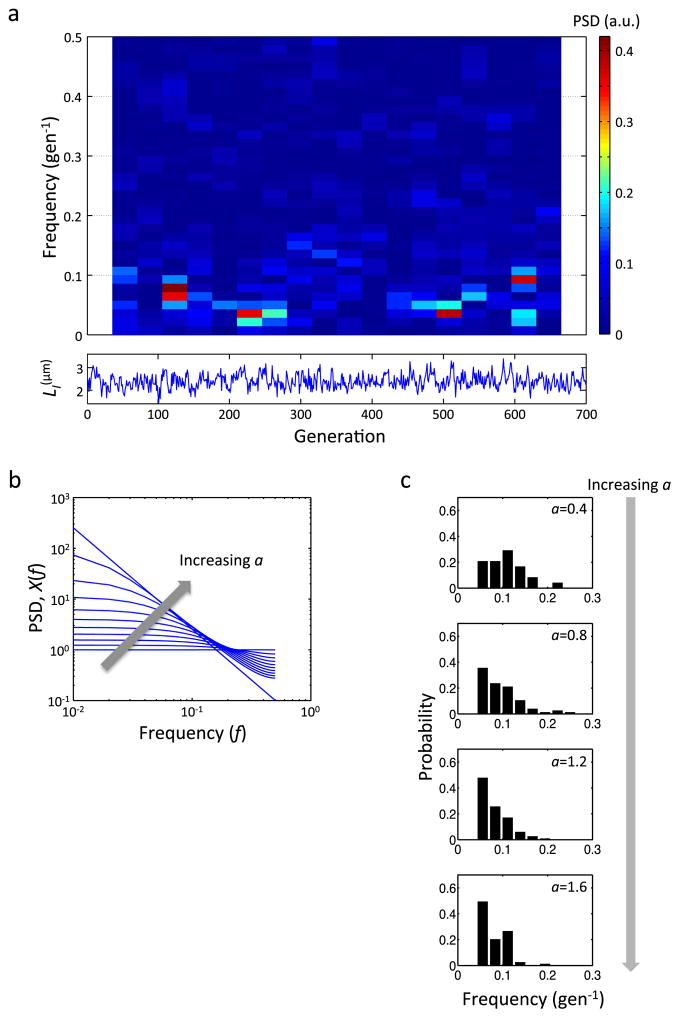
To gain further insights into L_I dynamic, we performed a time-frequency analysis. Specifically, we simulated the process for a much longer duration (700 generations as opposed to the 70 generations that we could observe experimentally) using Eq. 1 in the main text, and then calculated power spectrum density (PSD) for each period of 70 generations with 50% overlap. That is, PSDs were calculated for data from 1^st to 70^th generation, 36^th to 105^th generations, 71^st to 140^th generations, and so on. A single frequency occasionally dominated the system and then disappeared, creating a patchy appearance of the plot (Extended Data Fig. 3a). Consistent with our experimental observations (Fig. 1b, c) across an ensemble of single cells, the dominant frequency in a single cell changed across time. In some time windows, no dominant frequency was observed, which indicates that the observed oscillations are transient and can arise and disappear in single cells or across an ensemble of cells (Extended Data Fig. 3a).

Simulation of gene expression under cell size regulation

To examine gene expression dynamics in the presence of cell size regulation by simulation, we combined the noisy linear map and stochastic gene expression model. For each simulation, we first generated cell size dynamics based on the noisy linear map as follows:

1. Compute L_F(n) using L_F(n) = aL_I(n) + b + η but ensure L_F(n) > L_I(n).

2. Assuming a constant growth rate, μ, construct cell size profile using L(t) = L_I(n)e^μt, 0 ≤ t ≤ T where L_I(n)e^μT = L_F(n).

3. Compute L_I(n + 1) using L_I(n + 1) = L_F(n)R where R ~ N(0.5, σ₂), but ensure 0 < R < 1.

4. Iterate Step 1–3.

Two bounds were applied to the noisy linear map model to accommodate biological constraints. First, in Step 1 we ensured that the final cell size L_F(n) is larger than the initial cell size L_I(n), and that T ≥ 10 min. Second, in Step 3 the division was made stochastic within the boundary 0 < R < 1. In Figure 3d–f, the parameter values for a, b, σ₁ (standard deviation of η), and σ₂ were derived from the experimental observations of the MC4100 strain grown at 37°C (a = 0.871, b = 2.70, σ₁ = 0.548, and σ₂ = 0.0344).

After generating a cell size profile, the dynamics of constitutive gene expression was simulated using the Gillespie algorithm with following reactions:

$$\begin{array}{c}\ast \stackrel{k_m}{\to }\text{mRNA},\\ \text{mRNA}\stackrel{d_m}{\to }\ast ,\\ \text{mRNA}\stackrel{k_p}{\to }\text{mRNA}+\text{protein},\\ \text{protein}\stackrel{d_p}{\to }\ast .\end{array}$$

In these simulations, we assumed: k_m = 2 molecules/min, d_m = 0.2 min⁻¹, k_p = 0.1 min⁻¹, and d_p = 0.001 min⁻¹. Upon cell division, mRNA and protein molecules were binomially distributed to the progeny based on the division ratio (R), and the simulation continued to the next cell cycle. To make the analysis of simulation results comparable to that of experimental data, the simulation results were sampled at the same time resolution as the experimental data.

Power spectrum analysis and scoring of oscillation

To quantify the goodness of oscillation and extract a main frequency of the oscillation, we develop a scoring system based on power spectrum analysis. First, a PSD estimate (S(f_i)) of temporal data of length l was computed for individual courses using Welch’s method (pwelch function in Matlab). The number of segments and overlap used were 3 and 50–53%, respectively (for the analysis of L_I(l = 70), the overlap of 19/36 ~= 53% was used to have 3 complete segments, but for the analysis of [Y] the overlap was 50%). A maximum peak (S(f_c)) is then found and the score (z) is calculated as follows:

$$\begin{array}{c}z=\frac{S(f_c)}{{\sum }_i^{N}S(f_i)}\left(1-\frac{H(S)}{H_{\mathit{max}}}\right),\\ \text{with}H(S)=-{\sum }_{i\text{for}S(f_i)\le S(f_c)}^{N}P(f_i){log}_{2}P(f_i)\\ \text{and}{H}_{\mathit{max}}=-{log}_2\frac{1}{M},\end{array}$$

where N is the number of bins resulting from the discrete Fourier transform, M ≤ N is the number of bins where S(f_i) ≤ S(f_c) and i > 1 (i.e., non-DC (non-constant) component), and H(S) is the information entropy. The first and second terms of z represent the dominance and peakiness of the maximum peak, respectively, and f_c corresponds to the oscillation frequency. We note that the first non-DC component was not considered as a peak, and thus the slowest oscillation frequency f_min detected by this method is the second non-DC component in the PSD (i.e., 2/N). Likewise, the fastest oscillation frequency f_max corresponds to the second to last component in the PSD (i.e., 1/2 − 1/N).

In order to separate oscillatory dynamics from non-oscillatory ones, we needed to set a threshold for the oscillation score. To this end, we determined this threshold, z_c, based on the scores of noisy sine waves with various frequencies:

$$x_t=sin\left(2\pi {\phi }_{j}t\right)+\epsilon \left(t=1,2,\dots l\text{and}\epsilon ~N(0,1)\right),$$

where, f_min ≤ φ_j ≤ f_max = max(f_i) (i = 1, 2, …, N). We sampled the total of 101 different frequencies (i.e., j = 1, 2, …, 101 and φ_j+1 − φ_j = (f_max − f_min)/100. In principle, these noisy sine waves represent true oscillatory dynamics. We ran 100 simulations for each φ_j, and calculated the average (μ_z(φ_j)) and standard deviation (σ_z(φ_j)) of the scores. Then, the threshold z_c was defined as

$$z_c=\frac{1}{101}{\sum }_j^{101}\left({\mu }_z\left({\phi }_j\right)-{\sigma }_z\left({\phi }_j\right)\right).$$

z_c varies depending on the data set (e.g., different l). For L_I dynamics, z_c = 0.0166 whereas for [Y] dynamics of MC4100 (37°C), MC4100 (27°C), MC4100 (25°C), MG1655, and B/r, z_c = 0.0414, 0.0439, 0.0450, 0.0390, and 0.0394, respectively.

Dependence of cell doubling time on initial cell size

At the fundamental level, the cell size control can be achieved by modulating either growth rate (μ) or doubling time (T). Our analysis shows that growth rate is relatively independent of the initial cell size (Extended Data Fig. 1a, b), but doubling time has a decreasing trend with initial cell size (Extended Data Fig. 1c). This indicates that the cell size regulation is mainly achieved via modulation of doubling time rather than growth rate. This is consistent with a recent analysis of long-term E. coli growth data ⁴. Given the linear relationship between the initial and final cell sizes (L_F = aL_I + b), and assuming a constant growth rate and exponential cell growth (L_F = L_Ie^μT) during cell cycle³¹, we can derive an expression for the doubling time,

$$T=ln(a+b/L_I)/\mu .$$ Eq. 4

This equation shows good agreement with our experimental observation (Extended Data Fig. 1c, red line).

Extended Data

Extended Data Figure 1. Analysis of cell growth parameters.

Division ratio (a), growth rate (b), and doubling time (c) are plotted against initial cell length (n = 11168). Black and red lines show binned average and trend line, respectively. In a and b, the trend lines are the linear regression line whereas Eq. S3 was used in c. The error bars indicate standard deviation of each bin.

Extended Data Figure 2. A noisy linear map in E. coli cell size control across different growth temperatures and strains.

The same analysis as in Fig. 1e (L_I vs. L_F) was performed for MC4100 grown at 27°C (a, n = 3772), MC4100 grown at 25°C (b, n = 4539), MG1655 grown at 37°C (c, n = 10964), and B/r strain grown at 37°C (d, n = 5541). The data sets for MG1655 and B/r strain were from a previous study³. Black and red lines show binned average and linear regression line, respectively. From a to d, a = 1.02, 1.08, 1.03, and 1.14, respectively. The error bars indicate standard deviation of each bin.

Extended Data Figure 3. Frequency analysis of noisy linear map.

a, Time-frequency analysis of the noisy linear map model for L_I. The upper panel shows a spectrogram of 700-generation simulation constructed using 70-generation segments with 50% overlap. The lower panel shows the temporal dynamics of L_I. The same parameters as in Fig. 2a were used. b, The power spectrum of noisy linear map (X(f)). Eq. 3 is plotted for different a (0 ≤ a ≤ 1.8 with 0.2 interval). X(f) = 1 / (2πf)² for a = 2 is the straight line in this log-log plot. Note that the maximum value of f is 0.5 as the time resolution is 1 generation. c, Dependence of oscillation frequencies on a simulated using the rescaled linear map (Eq. 2). The noisy linear map model was simulated (Fig. 3a–c) and the distributions of oscillation frequencies are shown for four different values of a (from top to bottom, n = 24, 76, 117, and 79, respectively).

Extended Data Figure 4. Comparison of L_I oscillation characteristics between all lineages (blue) and lineages without aberrant cell cycles (red).

Probability of oscillation (a), average oscillation frequency (b), and distributions of oscillation frequencies (c–g) are shown. In a and b, filled symbols represent experimental data (data shown in red are the same as Fig. 3a, b): circles are MC4100 grown at three different temperatures; squares and triangles are MG1655 and B/r strain, respectively. The unfilled circles were generated from simulations using the rescaled linear map (Eq. 2, the same plot as Fig. 3a, b). In a, the data shown in blue include 160 (37°C), 54 (27°C), and 65 (25°C) lineages for MC4100, 158 lineages for MG1655, and 80 lineages for B/r strain. The data shown in red include 143 (37°C), 48 (27°C), and 57 (25°C) lineages for MC4100, 97 lineages for MG1655, and 60 lineages for B/r strain. In b–g, only lineages that were considered oscillatory were used. For the data set in blue, n = 58 (37°C), 21 (27°C), and 39 (25°C) for MC4100, 46 for MG1655, and 26 for B/r strain. For the data set in red, n = 51 (37°C), 18 (27°C), and 36 (25°C) for MC4100, 34 for MG1655, and 23 for B/r strain.

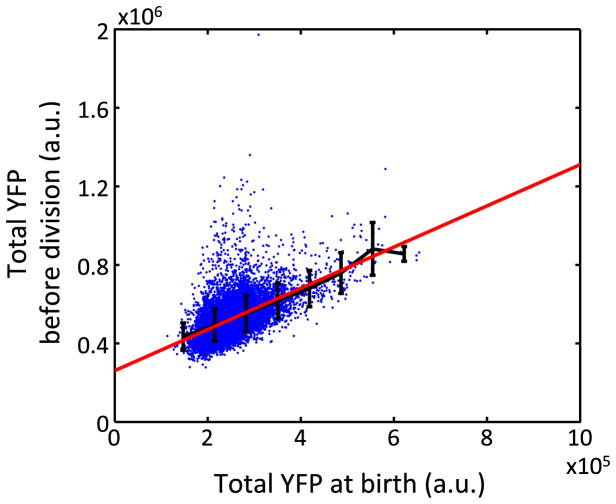
Extended Data Figure 5. A noisy linear map in total per-cell YFP.

Total YFP before division is plotted against total YFP at birth (n = 11168), revealing a linear map with a = 1.05. Black and red lines show binned average and the linear regression line, respectively. The error bars indicate standard deviation of each bin.

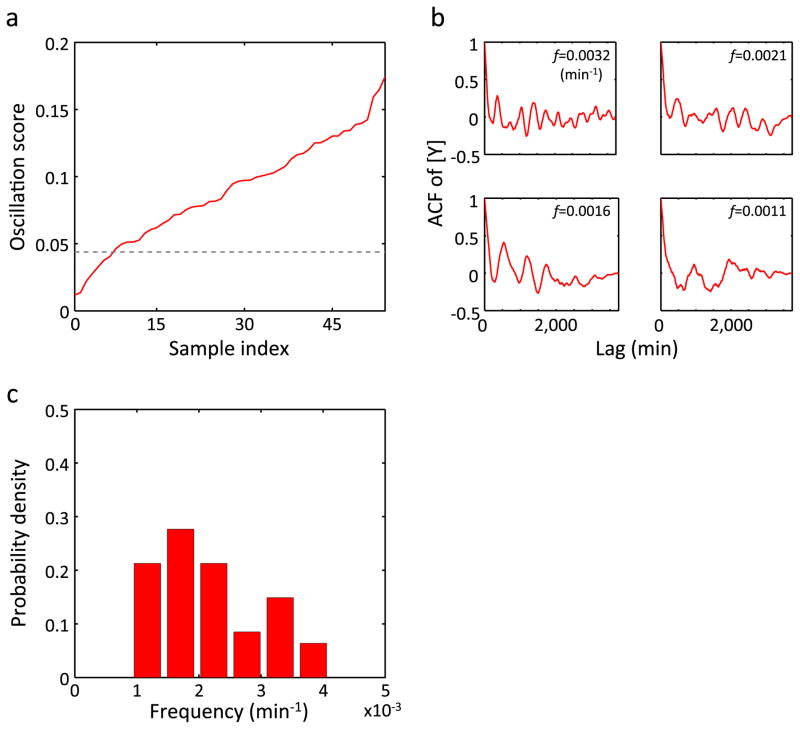
Extended Data Figure 6. Oscillation in [Y] observed in MC4100 at 27°C.

a, Oscillation scores of YFP concentration are shown in an ascending order. The dashed line indicates a threshold for oscillation. b, For four different oscillation frequencies, ACFs with the highest oscillation scores are shown. c, The distribution of oscillation frequencies (n = 47).

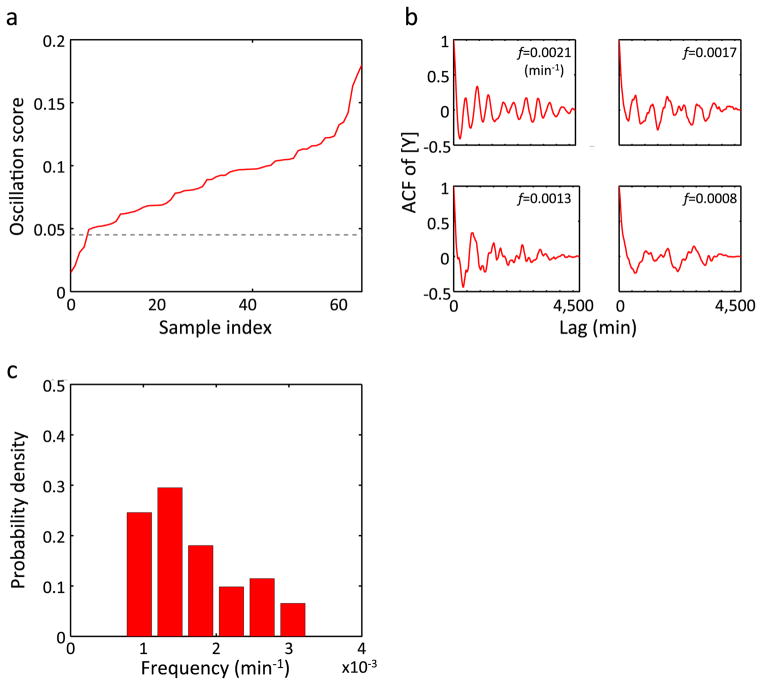
Extended Data Figure 7. Oscillation in [Y] observed in MC4100 at 25°C.

The same plots as in Extended Data Fig. 6 but for MC4100 grown at 25°C. n = 61 in c.

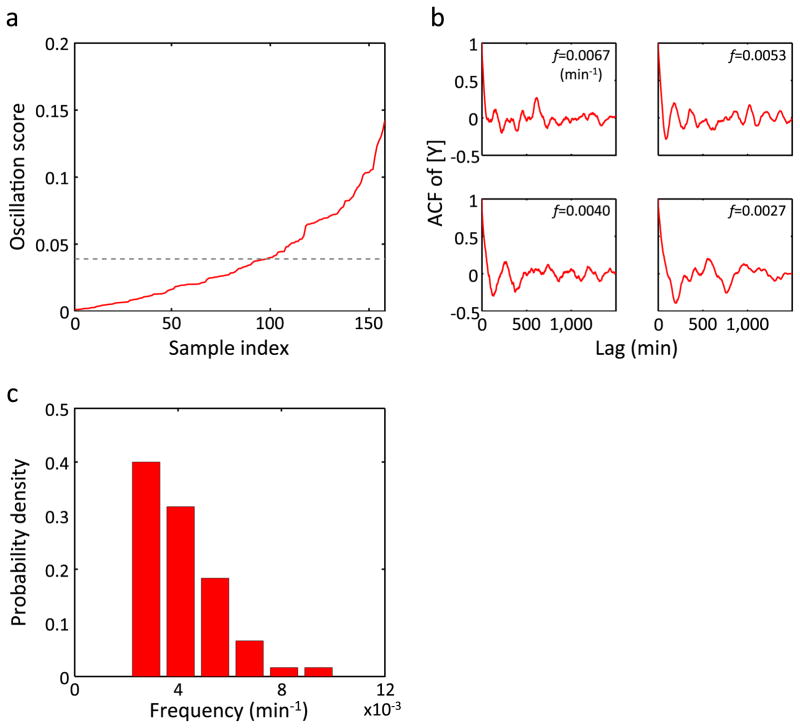
Extended Data Figure 8. Oscillation in [Y] observed in MG1655.

The same plots as in Extended Data Fig. 6 but for MG1655³. n = 60 in c.

Extended Data Figure 9. Oscillation in [Y] observed in B/r strain.

The same plot as in Extended Data Fig. 6 but for B/r strain³. n = 20 in c.

Extended Data Figure 10. A noisy linear map in cell size control in the data sets from Moffitt et al¹² and our experimental data of S. pombe.

The same analysis as in Fig. 1e (L_I vs. L_F) was performed. These data sets were obtained using a microfluidic device different from the mother machine. a–c show E. coli growth under three different media as indicated (n = 8795, 4637, and 684, respectively), d shows growth of B. subtilis (n = 1592), and e shows growth of S. pombe (n = 85). Black and red lines show binned average and the linear regression line, respectively. From a to e, a = 1.20, 0.864 0.684, 1.41, and 0.645, respectively. a–d show cell length (μm) and e shows cell area (μm²). The error bars indicate standard deviation of each bin.