DNA Sequence-Dependent Ionic Currents in Ultra-Small Solid-State Nanopores

Abstract

Measurements of ionic currents through nanopores partially blocked by DNA have emerged as a powerful method for characterization of the DNA nucleotide sequence. Although the effect of the nucleotide sequence on the nanopore blockade current has been experimentally demonstrated, prediction and interpretation of such measurements remain a formidable challenge. Using atomic resolution computational approaches, here we show how the sequence, molecular conformation, and pore geometry affect the blockade ionic current in model solid-state nanopores. We demonstrate that the blockade current from a DNA molecule is determined by the chemical identities and conformations of at least three consecutive nucleotides. We find the blockade currents produced by the nucleotide triplets to vary considerably with their nucleotide sequence despite having nearly identical molecular conformations. Encouragingly, we find blockade current differences as large as 25% for single-base substitutions in ultra small (1.6 nm × 1.1 nm cross section; 2 nm length) solid-state nanopores. Despite the complex dependence of the blockade current on the sequence and conformation of the DNA triplets, we find that, under many conditions, the number of thymine bases is positively correlated with the current, whereas the number of purine bases and the presence of both purine and pyrimidines in the triplet are negatively correlated with the current. Based on these observations, we construct a simple theoretical model that relates the ion current to the base content of a solid-state nanopore. Furthermore, we show that compact conformations of DNA in narrow pores provide the greatest signal-to-noise ratio for single base detection, whereas reduction of the nanopore length increases the ionic current noise. Thus, the sequence dependence of nanopore blockade current can be theoretically rationalized, although the predictions will likely need to be customized for each nanopore type.

Introduction

When an electric field is applied transverse to a membrane containing a small pore filled with electrolyte solution, the pore acts as a bottleneck to ion transport and, therefore, the ion current through the system is determined by minuscule details of pore and any object that happens to be within the pore^1,2. Nucleic acid molecules, being negatively charged, can also be driven through the pore, albeit at a much slower rate than monatomic ions³. For narrow pores similar in diameter to nucleic acids, ions contributing to the total current must travel very near the nucleic acid; therefore, the ion current can be sensitive to atomic-level details of the nucleic acid^3–5. However, identification of nucleic acid bases from measured such ionic current blockade has proven to be not all that straightforward⁶.

A number of difficulties in distinguishing sequences from ion current measurements have been overcome, or at least partially addressed^7–9. Rational engineering of biological nanopore^10,11 and coupling to biological enzymes^12,13 have made sequencing of natural DNA polymers possible^14,15. The recognition capability of biological nanopores has been extended to enable detection of epigenetic modifications^16–18, DNA damage^19,20 and RNA sequences²¹. Improvements in nanopore fabrication technology^22–24, reduction of noise^25–29, and the use of two-dimensional materials^30–34 have made DNA sequencing with solid-state nanopores feasible, and considerably expanded the repertoire of physical measurements that could be used for DNA sequence recognition^35–42.

Despite such progress, there have been no substantial improvements in understanding the physical mechanisms that give rise to the nucleotide sequence dependence of ion current traces from nucleic acids⁴³. For example, in α-hemolysin, DNA homopolymers of purine bases have been observed to give larger reductions in the ionic current than pyrimidine bases^5,44, while, in MspA, this relation is reversed⁴⁵. The current blockades from a DNA fragment in MspA were found to be modulated by at least four nucleotides^12,14, with the current modulation amplitudes in no obvious relation to the current amplitudes produced by DNA of uniform sequences⁴⁵. Similarly, several different rankings of blockade currents from DNA homopolymers have been reported for solid-state nanopores^29,46–48 These differences may arise from the distinct conformations that DNA adopts within the constriction of different nanopores as well as the differences in ion distributions due the charge and shape of the nanopore walls. Most importantly, the sensitivity of ionic current blockades to the nucleotide sequence of DNA in solid-state nanopores remains to be determined, as well as the conditions that would be optimal for sequence determination.

In this study, we use molecular dynamics (MD)⁴⁹ and Brownian dynamics (BD)⁵⁰ simulations to elucidate the effect of the nucleotide sequence of a DNA strand on the blockade currents the strand produces in model solid-state nanopores. Using the all-atom MD approach, we first characterize the interactions of individual ions with DNA nucleotides by computing three-dimensional potentials of mean force (3D PMF). Obtained thereby atomically-precise maps of ion–DNA interactions are then used in BD simulations to determine the intrinsic resolution of sequence-specific ionic current blockade, the blockade currents produced by all possible combination of nucleotide triples, the effect of DNA conformation and pore geometry on discrimination of single-base substitutions. We demonstrate that, despite a complex dependence of the blockade current on the nucleotide sequence of DNA, this dependence can be rationalized using a simple theoretical model.

Results

Rather than focusing on a particular experimental system, we chose to use for our study so-called phantom representations of nanopore systems⁵¹, which are mathematically defined objects that mimic, in MD or BD simulations, cylindrical nanopores with smooth corners. The featureless, atomically smooth surfaces of phantom nanopores minimize the effect surface interactions, allowing us to elucidate the general features of blockade current dependence on the nucleotide sequence. Although we have previously shown that the nucleotide content of double-stranded DNA can affect the nanopore ionic current^33,52, here we focus our investigation on ionic current blockades produced by single-stranded DNA, which is the most common experimental target. The majority of our simulations are carried out at 0.1 M concentration of KCl electrolyte, which is considerably smaller than the concentration typically employed in a nanopore experiment⁵³. Our choice of ion concentration was motivated by the anticipated use of biological enzymes to control the speed of DNA translocation through solid-state nanopores⁵⁴, which requires ionic conditions close to physiological. Furthermore, our computational method is both most accurate and computationally efficient at physiological ion concentrations³³.

This study specifically focuses on ionic current blockades in ultra-small solid-state nanopores, such as nanopores in 2D materials^30–32,55 or thinned silicon nitride membranes^46,56. The setup of our simulations corresponds to an experimental situation where DNA translocation is arrested for the duration of the ionic current measurement. Experimentally, such a situation is realized when the DNA translocation process has a stepwise character, whereby prolonged arrests of DNA motion alternate with rapid displacements of the molecule. Such step-wise translocation can be realized with the help of a biological enzyme^12,13, electrostatic^57,58 or optical⁴² fields or can occur spontaneously, for example, in graphene nanopore systems⁵⁹.

Ion–DNA nucleotide interactions

Conceptually, motion of an ion through a nanopore blocked by DNA is best described by a drift-diffusion model, where the diffusive component of the motion is governed by a 3D map of ion diffusivity, while the deterministic component is prescribed both by this map and a 3D potential of mean force (PMF) map that specifies the interaction free energy of the ion with the nanopore and DNA³³. Within such a model, the solvent effects are incorporated implicitly in both the 3D PMF and diffusivity maps and, in the case of a multi-ion system, through the effective ion–ion interactions.

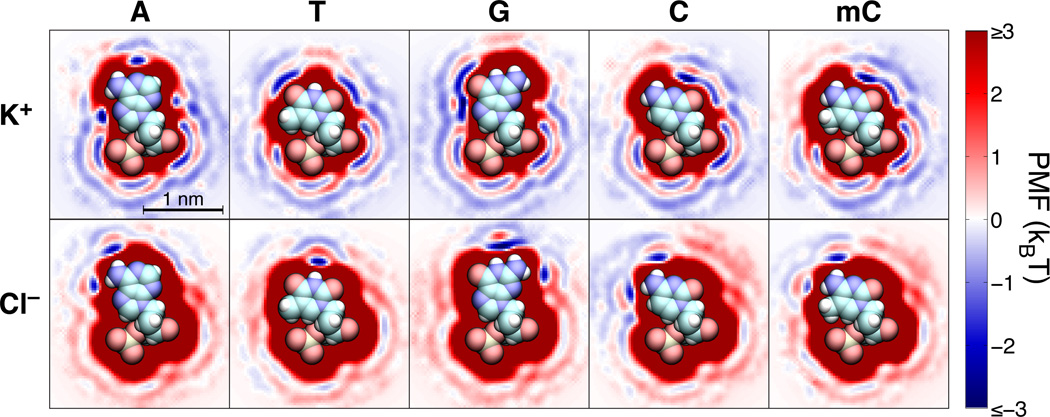
We have previously shown that all-atom MD simulations can be used to obtain the 3D PMF maps of nanopores blocked by DNA nucleotides, the effective ion–ion PMFs and the local diffusivity maps³³. The key components of the nanopore system’s 3D PMF map are the 3D PMF maps of individual DNA nucleotides, which prescribe the ion–nucleotide interaction free energy. Figure 1 illustrates the 3D PMF maps of isolated adenine (A), thymine (T), guanine (G), cytosine (C), and 5-methylcytosine (mC) nucleotides in water. In general, due to the negative charge of DNA, K⁺ ions have a higher affinity for the nucleotides and are more likely to approach them than Cl⁻ ions. This greater affinity is reflected in the dominant contribution of the K⁺ ions to the blockade current in both solid-state state⁶⁰ and biological^61,62 nanopore systems. Furthermore, as K⁺ ions are more likely to come in close contact with DNA than Cl⁻ ions, the sequence dependence of the blockade current is more likely to originate from the modulation in the K⁺ component of the current. However, as each nucleotide in a DNA strand carries the same overall charge (−e, where e is the charge of a proton), the overall electrical charge of the DNA nucleotides cannot by itself produce the sequence dependence of the ionic current.

Fig. 1.

The interaction free energy of K⁺ and Cl⁻ ions with individual DNA nucleotides. Each image shows a cross section of the corresponding three-dimensional free energy map within the plane of the nucleotide’s base. The three-dimensional free-energy maps were obtained by the umbrella sampling method from explicit solvent all-atom MD simulations³³. The energies are shown in units of k_BT at a temperature of 295 K. Atomic renderings of the nucleic acid structures are faithfully overlaid on the free-energy cross sections. Hydrogen, carbon, nitrogen, oxygen, and phosphorus atoms are shown, respectively, as white, cyan, blue, red, and beige spheres.

Steric exclusion is the most obvious physical effect that can produce the sequence dependence of the ionic current. Deep red regions in the 3D PMF maps shown in Figure 1 represents the high energy volumes inaccessible to both K⁺ and Cl⁻ ions because of steric interactions between the ions and the atoms of the nucleotides. The bulky purines (A and G) have larger sterically excluded regions than the smaller pyrimidines (T, C, and mC); the methyl groups at the 5′-position in thymine and in 5′-methylcytosine slightly increase the steric footprint of those nucleotides with respect to cytosine. For similar placement of nucleotides in a nanopore, one can naïvely expect the purines to block the flow of ions more effectively than pyrimidines. As we show below, such a simplistic interpretation of the steric effect fails to completely describe the sequence dependence of the ionic current blockades.

Beyond steric effects, Figure 1 shows that each base creates a unique free energy landscape that must be traversed by ions passing nearby. As K⁺ is the major contributor to the ion current and on average approaches the nucleic acid more closely, we will focus our discussion on interactions between the bases and K⁺ ions, although similar rules govern interactions with Cl⁻, albeit with the effect of atomic partial charges on the bases reversed. We first note that the high affinity regions (low PMF values) near the oxygens of the phosphate group and the O4′ oxygen atom of the deoxyribose ring (at the bottom of the molecules in Figure 1) are not expected to substantially contribute to the sequence dependence of the blockade current as all five DNA nucleotides have similar affinity to K⁺ in these regions. Other local free energy minima appear where the ions come in close contact with nucleotide atoms that carry substantial opposing partial charges, which for K⁺ are the negatively charged ketone oxygens and heterocycle C=N–C nitrogens. Adenine has three small attractive patches near its C=N–C nitrogens, while the two ketone oxygens of thymine, which are less sterically blocked, produce broader regions of low free-energy. Guanine and cytosine possess a ketone oxygen atom just adjacent to a C=N–C nitrogen, producing a single, broad low free-energy region. On the other hand, primary amines, carrying protruding positively charged hydrogens, effectively increase the steric footprint of A, G, and C bases for K⁺ ions. For example, the free-energy minimum near the N3 nitrogen of adenine (on the right side of the molecule in Figure 1) is suppressed in guanine due to the influence of the latter’s adjacent primary amine.

The PMF maps in Figure 1 also reveal the prominent effect of hydration: many portions of each base are ringed by two or more layers of relatively low free energy, separated by barriers of 1 k_BT or more. The regions of strong attraction to particular atoms, discussed in the previous paragraph, lie in the first hydration shell, and are often encircled by broader regions of low free energy in the second hydration shell. These latter regions correspond to ions separated from the oppositely charged atom by a monolayer of water molecules. Intermediate positions of the ion, for which it is not in direct contact with the atom, but for which there is not enough space for a water molecule to squeeze between, appear as free-energy barriers. Hydration was recently shown to enable the dependence of the blockade current on the DNA sequence in the MspA nanopore⁶³.

Recent all-atom MD simulations have shown that reduction of ion mobility near DNA has a considerable effect on the blockade current^64,65. Previously, we found ion mobility µ_elec (related to ion diffusivity D as D = k_BT µ_elec/q, where q is the ion’s charge and k_B is the Boltzmann constant) to exponentially increase with the distance between the ion and DNA surface, reaching a bulk value approximately 1 nm away from the nearest DNA atom³³. Our calculation, however, revealed no substantial dependence of the ion mobility on the type of DNA basepairs. Thus, we estimate the diffusivity considering only the distance from the ion to the molecular surface of the DNA, neglecting any explicit sequence dependence of the diffusivity owing to the different physicochemical properties of the bases.

Blockade currents produced by isolated nucleotides

We have previously used the 3D PMF maps of isolated nucleotides, Figure 1, to predict the ionic current blockades produced by the nucleotides when placed in a graphene nanopore⁵⁹. Although the all-atom MD method is capable of predicting the sequence specificity of the ionic current blockades^33,62,63,66, it comes with a great computational cost. The atomic-resolution Brownian dynamics (ARBD) method^33,67 can provide the same information as the all-atom MD method at a fraction of the computational cost when certain assumption about the system are met. First, to be able to resolve the subtle differences in the atomic configurations of the DNA nucleotides, the ARBD method requires atomically precise 3D PMF maps such as the ones shown in Figure 1. Second, matching the ARBD and MD ionic currents requires, as input parameters for the ARBD simulation, the ion diffusivity values and their dependence on the distance from DNA and the nanopore surface. Finally, the applications of the ARBD method is presently limited to static conformations of DNA, although it is theoretically possible to use ARBD to compute ionic current values for a set of DNA conformations and predict the average ionic current knowing the statistical weight of each conformation.

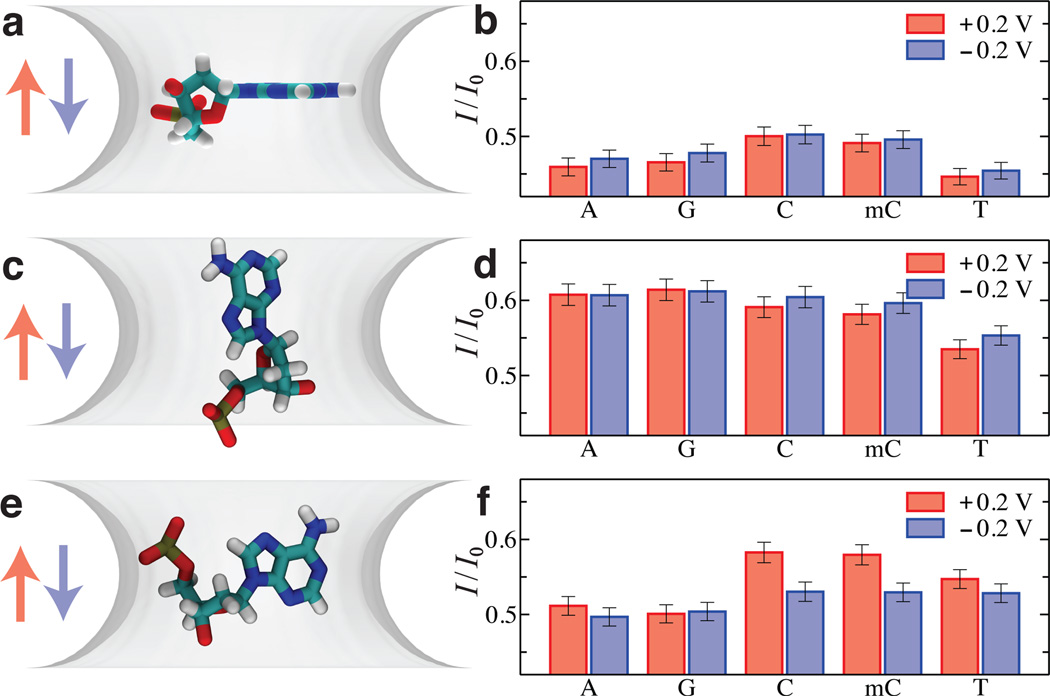
Using the ARBD method, we have determined the dependence of the blockade current on the type and conformation of isolated DNA nucleotides placed in a model nanopore⁵⁹. Figure 2 shows the examples of the DNA conformations considered along with the corresponding values of the ionic current blockades. When placed with their bases orthogonal to the direction of the ionic current, Figure 2a, the currents for C and mC nucleotides are higher than those of A and G nucleotides; the lowest current is recorded for the T-nucleotide system, Figure 2b. Such an orientation also makes the current blockade insensitive to the direction of the applied bias within the statistical accuracy of our ionic current determination. Orienting the DNA bases along the nanopore axis, Figure 2c, considerably increases the blockade current for all single nucleotide systems, Figure 2d. Most importantly, the blockade currents of the C, mC, A, and G systems become equal within the statistical error of the current determination, whereas the current in the T-nucleotide system remains considerably lower than that in the other four systems. Finally, orienting the DNA bases to normal to the plane of the graphene membrane and placing the nucleotide normal to the direction of the transmembrane bias, Figure 2e, produces yet another pattern of ionic current blockades, with A and G nucleotides producing the lowest current blockades, followed by T nucleotides, followed by C and mC nucleotides, with the current of the latter two systems being considerably affected by the direction of the transmembrane bias, Figure 2f.

Fig. 2.

Blockade current from isolated nucleotides. (a) Placement of isolated nucleotides in a phantom nanopore system. The phantom pore is represented by a 3D PMF map built to reproduce the dimensions of a circular nanopore (2.4 nm in diameter) in a three-layer graphene membrane. The pore is shown as a semitransparent isosurface of its PMF map at 0.5 k_BT; the map’s values are zero in bulk solution and change near the membrane surface according to the 1D PMF of ion-graphene interaction determined by all-atom MD⁵⁹. In addition to the 3D PMF map of the nanopore, each system contains a 3D PMF map of an isolated nucleotide (not shown) geometrically transformed to match the target nucleotide conformation (shown in all-atom representation). For this target conformation, five systems were built containing the 3D PMF map of either an A, G, C, mC, or T nucleotide. In all five systems, the phosphate and sugar groups of the nucleotides have the same coordinates; the plane of each nucleotide’s base is aligned with the midplane of the membrane. For clarity, only one system (containing an A nucleotide) is shown. The final simulation system also contains K⁺ and Cl⁻ ions (not shown); solvent is modeled implicitly. (b) ARBD simulation of ionic current blockades produced by isolated nucleotides in a phantom nanopore. The relative ionic current blockade (I/I₀) for the A, G, C, mC, and T nucleotide systems were obtained from the ARBD simulations of the systems illustrated in panel a. The simulations were carried out at 0.1 M bulk concentration of KCl and at ±200 mV transmembrane biases. The color of the arrows in panel a indicates the direction of the transmembrane bias. Multiple ~80 ns-long ARBD simulations were performed for each system, for an aggregate simulation time of 9 µs per system. Error bars show 95% confidence intervals, which are about 1% of the corresponding mean current values. (c–f). Same as in panel a (c, e) and panel b (d, f) but for two other target conformations of the DNA bases. Adapted from Ref. 59.

The ionic current blockades produced by isolated DNA nucleotides in a graphene nanopore reveals no systematic dependence of the blockade current on the excluded volume of the nucleotides. The blockade current is seen to be as sensitive to the orientation of the nucleotide as to their chemical structure. This result suggests that, for ionic current blockades to report of the type of individual DNA nucleotides, their conformational degrees of freedom must be reduced, in the nanopore, to several well-defined states. Practical means for reducing the conformational heterogeneity may include steric confinement with the help of a molecular adaptor⁶⁸, binding to the nanopore surface⁵⁹ or perhaps yet another undiscovered mechanism⁴⁷.

Intrinsic resolution of sequence-specific blockade current

The promise of 2D materials such as graphene and MoS₂ to nanopore sequencing of DNA is in amplification of single nucleotide contributions to the nanopore blockade current. Indeed, the thickness of such materials can be smaller than the typical spacing of nucleotides in a strand of DNA (about 0.7 nm), focusing the effect of ionic current reduction to the few nucleotides confined within the nanopore. Nevertheless, all-atom MD simulations have shown that hydrophobic adhesion of ssDNA to pristine single layer graphene makes the nanopore ionic current blockades less sensitive to the nucleotide sequence than the blockades recorded from nanopores in two- or three-layer graphene membranes⁵⁹. Coating a graphene membrane with a molecular repellent⁶⁹ or using a less hydrophobic yet atomically thin MoS₂ membranes^34,55 seems to alleviate the DNA adhesion problem, making the intrinsic resolution of the nanopore system a geometrical property of the membrane, the atomic structure of DNA and the size of the charge carrier used to probe the nucleotide sequence.

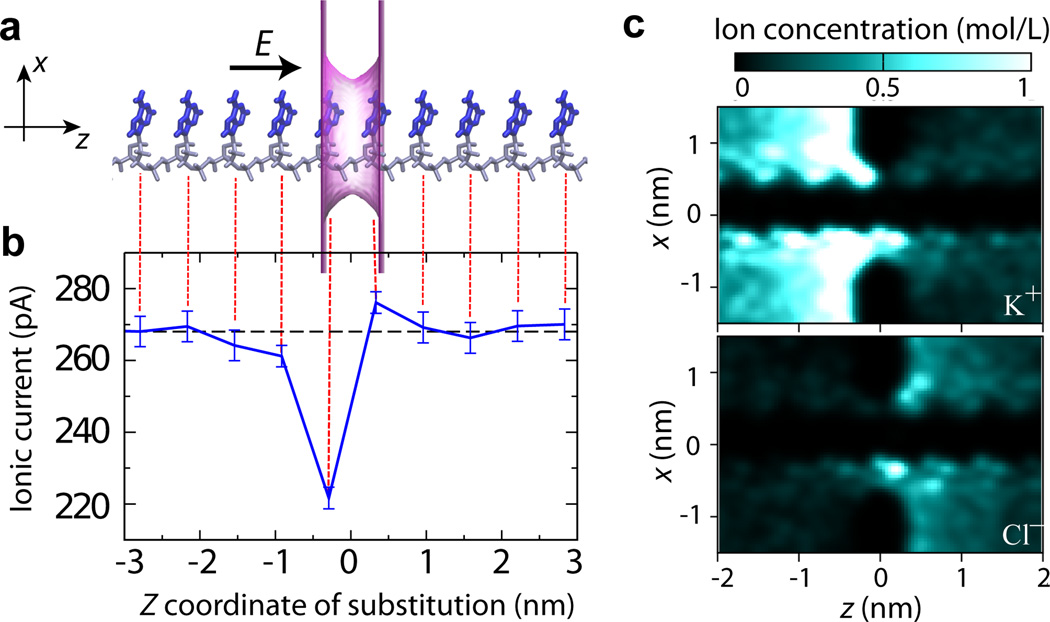
To evaluate the intrinsic resolution of an ultra-small solid-state nanopore, we consider a system comprising a poly(dA)₁₈ strand threaded through the smallest possible phantom nanopore that can accommodate the DNA strand without steric clashes, Figure 3a. The estimated physical dimensions of an all-atom equivalent of such a phantom pore are a 1.6 nm × 1.1 nm cross section and a 0.7 nm length. To eliminate any possible effect of DNA conformation, the DNA homopolymer was assumed to have a stretched conformation, which in practice was obtained by translating the conformation of a single nucleotide along the nanopore axis. Upon converting the all-atom representation into a 3D PMF map, the blockade current was simulated using the ARBD method at a +175 mV transmembrane bias and 0.1 M bulk KCl concentration. The dashed black line in Figure 3b shows the blockade current recorded from the poly(dA)₁₈ homopolymer.

Fig. 3.

The effect of the location of a single nucleotide substitution on the ionic current blockade. (a) Schematics of a simulation system. A poly(dA)₁₈ homopolymer in an idealized (repeat) conformation it threaded through a phantom nanopore. The phantom nanopore has an elliptical cross section of 1.6 nm × 1.1 nm and an effective thickness of 0.7 nm. The phantom pore is shown as a translucent magenta surface; the bases and backbone of DNA are drawn in blue and gray, respectively; only ten nucleotides nearest to the pore are shown. The arrow indicates the direction of the applied electric field that produces a transmembrane bias of 175 mV. The system contains K⁺ and Cl⁻ ions (not shown) corresponding to bulk ion concentration is 0.1 M. (b) Ionic current (blue) as a function of the location of a single G base substitution in a poly(dA) homopolymer. The center of the phantom pore is located at z = 0. Each data point was obtained by averaging multiple ARBD trajectories for an aggregate simulation time of 10 µs; the error bars indicate the standard error of the mean. The dashed black line indicates the ionic current for the poly(dA) homopolymer (without any base substitutions). The image of the simulation system (panel a) is aligned with the z-coordinate axis of the plot to visually indicate the locations of the G base substitutions. (c) The local concentration of K⁺ (top) and Cl⁻ (bottom) ions near the nanopore. The density maps illustrate the average ion distribution within the x – z cross section of the simulation system along the nanopore axis (the z axis).

Next, we used the PMF subtraction protocol described and validated in our previous study³³ to evaluate the blockade currents produced upon replacement of individual A bases with G bases. Note that the base replacement process neither alters the conformation of the DNA backbone nor the orientation of the base’s plane. As expected, changes in the DNA sequence away from the nanopore (|z| > 2 nm) had no significant effect on the blockade current, which remained indistinguishable from the value obtained for the poly(dA)₁₈ strand, Figure 3b. The largest effect of single nucleotide substitution was observed for the base located 0.3 nm upstream from the nanopore midplane (z = −0.3 nm): the blockade current was reduced by 50 pA, ≈ 19% of the poly(dA)₁₈ value. In contrast, the same substitution introduced 0.3 nm downstream from the nanopore midplane (at z = 0.3 nm) produced small yet statistically significant increase of the blockade current relative to the poly(dA)₁₈ baseline. The lack of symmetry in current changes with regard to the placement of the substitutions may seem surprising; however, it is likely a product of the large asymmetry in the ion concentration in the nanpore system. According to Figure 3c, the concentration of K⁺ is considerably enhanced (in comparison to the bulk value) at the z < 0 (upstream) side of the membrane, whereas a smaller yet statistically significant enhancement of Cl⁻ concentration is seen for z > 0. Taking into account the identical conformations of the G base substitution at both placements (at z = ± 0.3 nm) of the substitution within the poly(dA)₁₈ strand, it becomes apparent that the effect of a single nucleotide substitutions depends not only on the nucleotide type or the microscopic conformation of the substitution but also on its position within the nanopore.

Notably, bases located outside the physical limits of the nanopore were found to significantly affect the blockade current, for example, the G substitution at z = −0.92 nm, Figure 3b. The electric field lines followed by the ions converge on a scale similar to the radius of the pore opening⁷⁰. Thus, the region in which the electric field is focused extends beyond the pore openings into two hemispheres having radii approximately equal to that of the nanopore. In addition to the bases confined to the nanopore, bases located within these two hemispheres are likely to significantly modulate the ionic current. Thus, the length of the DNA fragment probed by the ionic current measurement is approximately 2a + L, where a is the radius of the pore and L is its length. The minimum diameter of a nanopore that can accommodate a DNA strand without affecting the DNA conformation is about 1.6 nm, which becomes 1.3 nm if the bases are forced against the backbone. Therefore, even for a membrane consisting of a single atomic layer, the minimum length of a DNA molecule that modulates the ion current is about 2 nm, or 3–4 DNA nucleotides, which is consistent with the results of our ARBD calculations presented in Figure 3. Stochastic displacement of a DNA strand through the nanopore constriction can further increase the number of DNA nucleotides affecting the blockade current⁶³.

Blockade current of three-nucleotide ssDNA fragments

As we have shown above, even for an ultra-small nanopore, the blockade current is determined by at least three consecutive DNA nucleotides. To systematically investigate the dependence of the blockade current on the nucleotide sequence, we next computed the blockade currents for all possible sequence substitutions in three-nucleotide DNA fragments. To produce the 64 triplet variants, we used the base replacement method³³ that neither alters the conformation of the DNA backbone nor the orientation of the base’s plane.

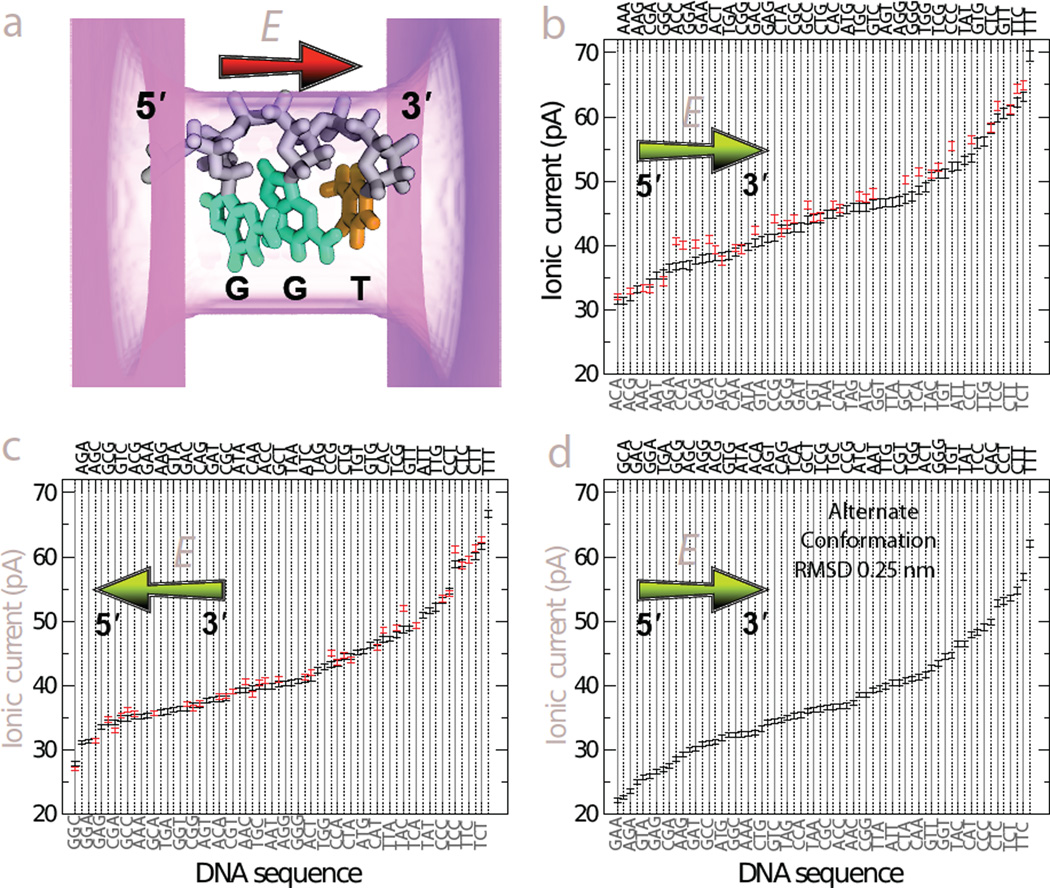
Figure 4a illustrates a typical conformation of a DNA triplet used for our ARBD calculations of the blockade current. Hereafter, we follow the 5′-to-3′ notation for DNA sequences, omitting the DNA termini for brevity. Because the blockade current depends on the direction of the electric field with respect to the 5′-to-3′ direction and DNA backbone⁶¹, we used the same set of 64 DNA triplet configurations to obtain two sets of the blockade current data corresponding to parallel, Figure 4b, and anti-parallel, Figure 4c, orientations of the applied electric field with respect to the 5′-to-3′ direction of the DNA backbone. An entirely different set of 64 triplet systems was generated using a different microscopic conformation of the same DNA strand; the root-mean-square deviation (RMSD) between the atomic coordinates of the two conformations was 0.25 nm. The second set of DNA triplets was used for the ARBD calculations under an electric field directed along the 5′-to-3′ direction of the backbone, Figure 4d. Supporting Information Tables S1, S2 and S3 provide the values of the blockade currents.

Fig. 4.

Blockade currents from DNA triplets. (a) Schematic representation of a typical simulation system. A three-nucleotide fragment of ssDNA is placed in a phantom nanopore. The pore is shown as a translucent magenta surface; the pore’s length and cross section are 2.0 nm and 1.6 nm × 1.1 nm, respectively. The backbone of DNA is shown in gray; the G and T bases are shown in cyan and orange, respectively. The red arrow indicates the direction of the applied electric field with respect to the 5′-to-3′ direction of the DNA backbone. The actual ARBD systems contain a 3D–PMF of the nucleotide triplet merged with the 3D–PMF map of the phantom pore and K⁺ and Cl⁻ ions corresponding to 0.1 M bulk concentration. (b) Blockade currents from 64 canonical DNA triplets (black) arranged in an ascending order. Red marks indicate the blockade current from DNA triplets where cytosine was replaced by 5′-methylcytosine. The chartreuse arrow indicates the direction of the applied electric field with respect to the 5′-to-3′ direction of the DNA backbone. The error bars represent the standard error of the mean. The triplet sequence labels alternate between the bottom and top of the plot, with the labels on the bottom being associated with solid gray lines and those on the top associated with dotted black lines. Each data point represents the average of an ensemble of independent ARBD simulations at a 175 mV transmembrane bias; the aggregate duration of the ARBD simulations for each data point is ~15 µs. (c) Same as in panel b, except that the applied electric field is anti-parallel to the 5′-to-3′ direction of the DNA backbone. The aggregate duration of the ARBD simulations for each data point is 30 µs. (d) Same as in panel b, except for a different microscopic configuration of a DNA triplet; the RMSD between the two atomic structures is 0.25 nm. The aggregate duration of the ARBD simulations for each data point is 30 µs. Numerical values of the blockade currents from panels b,c and d are listed in Supporting Tables S1, S2 and S3, respectively.

Despite variations in the exact current values under different conditions, there are several aspects of Figure 4b,c,d that appear to be general. First, we note that the largest current, by a substantial margin, is calculated for the sequence TTT in all three cases. Likely owing to the small size of the T and C, the highest 4–8 current values contain only these two bases. On the other hand, the effect of C bases in concert with A and G bases is somewhat enigmatic, as the lowest currents in Figure 4b,c and the second lowest current in Figure 4d are for sequences containing one C base and two larger purine bases.

Given the statistical uncertainty in the current values, which is represented in the plots by standard error of the mean and varies from 0.3 to 0.5 pA, some of the triplets are not statistically distinct. However, because DNA translocating through a pore is read sequentially, it may, in practice, be possible to identify the sequence with high confidence despite ambiguity at a single stage of the translocation⁵². Even considering individual blockade states, many subsets of sequences are mutually distinguishable. Notably, the canonical homopolymers yield unique currents for all systems considered here, and have the consistent ascending order of AAA, GGG, CCC, TTT.

Overall, the range of blockade currents obtained from simulations of DNA triplets in ultra-thin solid-state nanopores appears to be quite similar to that experimentally measured for the MspA nanopore¹⁴. The ordering of the ionic current blockades, however, differ substantially between the two systems, suggesting that different mechanisms producing the sequence-dependent blockades are at play. In the case of MspA, bulkier purine homopolymers were found to block the current less than pyrimidines⁴⁵, which, according to all-atom MD simulations⁶³, can be attributed to packing of DNA nucleotides in the MspA constriction: purines are less likely to fit in the MspA constriction while preserving the base stacking pattern of ssDNA then pyrimidines. In contrast, all triplets considered for our ARBD simulations maintained the same base stacking pattern, Figure 4a. In comparison to the limited number of experimental studies that reported ionic current blockades from DNA homopolymers in solid-state nanopores, our calculations are in partial agreement with the data from Drndic, Radenovic and Chen labs ^46–48 but disagree with the blockade ranking reported by Kim and co-workers²⁹. The lack of consensus about the qualitative ranking of experimental current blockades may in fact indicate their high sensitivity to the nanopore size and membrane material.

To test the effect of cytosine methylation on the blockade current, we constructed 37 additional DNA triplet systems were all C bases were replaced with their methylated variants and repeated our ARBD simulations. In biology, the 5′-methylcytosine modifications occur at different sequence contexts in bacteria, plants, and vertebrates. Here, we do not consider such realistic contexts and plot in Figure 4b,c the blockade current for all mC-containing triplets alongside with the values of unmethylated triplets, which facilitates direct comparison of the two. Only in a few cases are the triplets containing mC bases readily distinguishable from the corresponding canonical triplets, notably, for the biologically important CpG steps, for example, CCG sequence in Figure 4b and CGA and CCG sequences in Figure 4c. Interestingly, the sequence with the most modifications, mCmCmC, has a current that is not statistically distinct from CCC, with a difference of 0.3 ± 0.7 pA, while the other four homopolymers differ by more than 4 pA from one another. Overall, substitution of a C base with an mC base was observed to increase the blockade current, although the effect varied considerably from triplet to triplet. Experimentally, single methylated cytosines were found to block the nanopore ionic current considerably more (by ~20% of the cytosine level) than their canonical variants upon binding to a cyclodextrin adapter of an alphahemolysin pore⁶⁸. In a CpG step, methylation of cytosine was observed to substantially reduce the blockade current in alphahemolysin¹⁶ but moderately increase it in MspA ^17,18, with the current modulation values being dependent on the flanking sequence. In solid-state nanopores, methylation of cytosine was found to have no measurable effect on the blockade current⁷¹, although similar measurements performed for other epigenetic markers revealed detectable changes^71,72.

Simple scoring functions for prediction of blockade currents of DNA triplets

Given an arbitrary DNA sequence, can one predict the nanopore blockade current? A brute-force MD simulation is, in principle, capable of making such a prediction; however, the timescale associated with the exploration of DNA’s conformational space⁶³ and uncertainties associated with experimental characterization of solid-state nanopore surfaces make such prediction challenging. A much more feasible alternative is development of a theoretical model that can describe, albeit with a lower precision, the dependence of the blockade current on the DNA sequence. Using our DNA triplets data, we show below that, indeed, a simple theoretical model can account for the sequence dependence of the simulated blockade currents.

To evaluate the performance of a theoretical model, we determine a correlation coefficient between the blockade currents observed in our ARBD simulations and computed using the theoretical model, Table 1. A correlation coefficient close to 1 (or −1) indicates a strong correlation (or anti-correlation) between the model and the data, whereas a correlation coefficient of 0 indicates the lack of such correlation.

Table 1.

Correlation coefficients between the simulated current blockades reported in the indicated figures and various theoretical models.

Quantity	Figure 4b	Figure 4c	Figure 4d
NA	−0.40	−0.63	−0.43
NT	0.71	0.77	0.60
NG	−0.51	−0.16	−0.46
NC	0.20	0.02	0.28
NA+NG	−0.79	−0.69	−0.76
NA+NT	0.27	0.12	0.15
NA+NC	−0.17	−0.52	−0.12
NT − NA − NG	0.84	0.82	0.77
Best linear fit	0.84	0.83	0.77
NT − NA − NG − d	0.90	0.87	0.82
Best nonlinear fit	0.92	0.89	0.89

Here, N_X refers to the number of X bases in the three-nucleotide sequence; the variable d = 1 when the sequence contains a mixture of purines (A, G) and pyrimidines (T, C); d = 0 otherwise. “Best linear fit” refers to the least-squares linear fit to the simulated ionic current data using the number of A, T and G bases as independent variables. “Best nonlinear fit” refers to the best possible model depending only on N_A, N_T, N_G, and N_C.

First, we consider the number of each type of base in the sequence, N_A, N_T, N_G, and N_C, each of which range from 0 to 3. For triplets of canonical bases, there are only 20 possible combinations of base counts. Hence, a model based only on counts of bases can produce no more than 20 unique current values and cannot generate all the complexity seen in Figure 4 or account for the position of a single substitution with respect to the direction of the applied bias, Figure 3. Nonetheless, such a model can capture many of the general trends in the simulated blockade currents.

As we inferred from Figure 4, the number of T bases, N_T is positively correlated with the blockade current magnitude. Likewise, the number of A bases and the number G bases show negative correlations, although somewhat weaker. The correlation is especially weak for the number of G bases in the simulations where applied electric field is anti-parallel to the 5′-to-3′ direction of the DNA backbone. C bases are observed in sequences associated with some of the highest and lowest currents and, hence, the number of C bases in a sequence is not a good predictor of the blockade current. Beyond the counts of individual bases, we consider other groupings in Table 1. Notably, the number of purines, N_A + N_G, shows a stronger negative correlation with the current than either of the individual numbers alone. Because the number of pyrimidines, N_T + N_C, represents the same grouping, it yields identical correlation coefficients (with the sign reversed) and need not be considered. No other two-base grouping yields substantial, robust correlations. Furthermore, three-base groupings are equilvalent to the individual-base results already shown. Given the high currents seen for sequences containing only T and C bases and the other correlations already discussed, we construct the quantity N_T – N_A – N_G, which ranges from −3 to 3. This quantity yields a greater correlation with the current than either the number of T bases or the number of purine bases. It gives a correlation coefficient very similar to the linear least-squares fit to the data, constructed as

$$L(N_{\mathrm{A}},N_{\mathrm{T}},N_{\mathrm{G}})=a_{\mathrm{A}}{N}_{\mathrm{A}}+a_{\mathrm{T}}{N}_{\mathrm{T}}+a_{\mathrm{G}}{N}_{\mathrm{G}}+b.$$ (1)

In the above expression, we consider only the numbers of A, T and G bases as independent variables because the number of C bases can be expressed as the combination of the other three: N_C = 3 – N_A – N_T – N_G. Using all data from Figure 4b,c,d, the least-squares fit yields a_A = −5.59, a_T = + 4.44, a_G = −4.69, and b = 46.09; the correlation coefficients are provided in Table 1.

With nonlinear relationships, it is possible to obtain even better correlation. The linear combination N_T –N_A – N_G fails to capture a subtle trend in the data of Figure 4. N_T – N_A – N_G attains its lowest value (−3) for sequences consisting of only of A or G bases; however, many of the lowest currents contain two purines and a pyrimidine, often C. Therefore, we define d, the “diversity”, as 0 if the sequence contains only purines or only pyrimidines and +1 if it contains a mixture of the two. The quantity N_T – N_A – N_G – d captures several trends in the data and shows a higher correlation than the best-fit linear model. In fact, the correlation of this simple model with the data is very close to that of the best nonlinear fit constructed using N_A, N_T, N_G, and N_C as independent parameters.

We would like to stress that our simple theoretical model is not expected to describe the ranking of ionic current blockades in any solid-state nanopore. To the contrary, differences in the nanopore shape and surface chemistry are expected to influence the ensemble of conformations realized by ssDNA and hence the distribution of the blockade currents. We nevertheless expect a simple theoretical model to describe the blockade current distribution within a given class of solid-state nanopores, as long as the current distributions from individual nanopores within the class are statistically similar.

Effect of molecular conformation

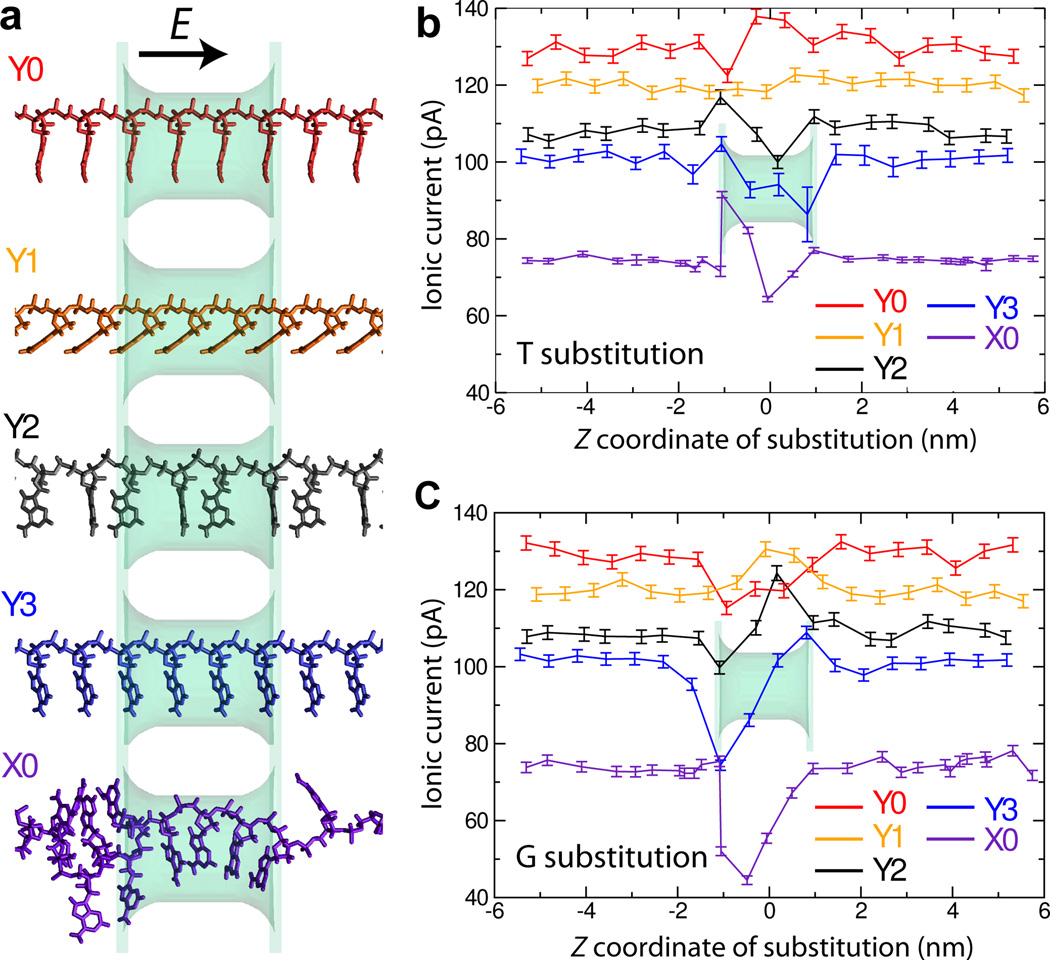
Above, we computed the blockade currents produced by all possible permutations of a three-nucleotide DNA fragment for two similar conformations of the fragments, Figure 4b,d. Let us now consider in greater detail the influence of the conformation on base discrimination. Figure 5a shows the five conformations considered in this work. Owing to the reduced computational expense in calculating the free-energy maps and relative ease of interpretation, the conformations labeled Y0, Y1, and Y3 have a one-nucleotide periodicity, while conformation Y2 repeats every two nucleotides. Conformation X0, which is considerably more disordered, was replicated only once to span the entire simulation cell (11.5 nm) along the z axis in a periodic manner. As in our study of the intrinsic resolution of the blockade current, Figure 3, we characterize here the effect of the DNA conformation on the resolving capability of the blockade current by computing the blockade currents produced by a single nucleotide substitution (T in Figure 5b and G in Figure 5c) in a poly(dA) homopolymer.

Fig. 5.

Influence of DNA conformation on the change of the blockade current upon single base substitution. (a) Molecular rendering of the DNA conformations considered. The DNA is shown using molecular bonds; the color of the rendering matches the color of data plots in panels b and c. The phantom pore (shown as a semi-transparent molecular surface) is 1.6 nm × 1.1 nm in cross section and 2.0 nm in length. In all systems, the applied electric field is directed parallel to the 5′-to-3′ direction of the DNA backbone; the transmembrane bias is 175 mV, the bulk concentration of KCl is 0.1 M. The root-mean-square deviation (RMSD) between the coordinates of the four nucleotides nearest to the nanopore in any two conformations vary from 1.2 Å(between Y0 and Y3) to 8.7 Å(between Y2 and X0); Supporting Table S4 lists the RMSD values for all pairs of conformations. (b) Simulated blockade current produced by a poly(dA) DNA strand containing a single T-base substitution versus the location of the substitution. The color of the lines indicate the microscopic conformation of the DNA strand, panel a. (c) Same as in panel b but for a single G-base substitution.

The DNA conformation is seen to considerably affect the blockade current, which ranged from 77 to 130 pA for the poly(dA) homopolymer, Figure 5b,c. As in the case of an ultra-thin nanopore, Figure 3, single substitutions are seen to considerably affect the blockade current when they are made near or within the 2 nm-long pore. The T base substitution near the entrance of the pore for K⁺ ions traveling in the direction of the electric field (z < 0) yields an increase in current for conformations Y2, Y3, and X0, whereas the same substitution at the other end of the nanopore leads to a reduction of the current for these same conformations, Figure 5b. This trend seems to be inverted for conformation Y0, while little if any significant change can be seen for conformation Y1. The G-base substitution near the entrance of the pore (z < 0), produces a significant drop in the ion current for all conformations except Y1, Figure 5c. The same substitution at the other end of the nanopore increases the current over the poly(dA) value for conformations Y2 and Y3, whereas the current gradually approaches the poly(dA) value for conformation X0.

Although the current blockades from single-base substitutions appear to strongly depend on the conformation of DNA, the character of the current change upon single base substitution appears to show some robust trends. The conformation X0, which may be regarded as the most realistic, shows the most dramatic modulations compared to the other conformations. The placement of either T or G substitutions within that conformations alters the current in a similar manner as in conformations Y2 and Y3, which is also similar to the changes reported in Figure 3. The response of the blockade current to T and G substitutions in the other two conformations (Y0 and Y1) is different but also of lower amplitude. Specifically, conformations Y0 and Y1 show the least sequence dependence in terms of the relative change of blockade currents (I_X -I_A)/I_A, where X is the type of a substitution, after taking into account the higher baseline currents of the poly(dA) homopolymer, I_A. Notwithstanding some obvious trends, it is, however, clear that robust differentiation of DNA sequences requires elimination of the conformational degrees of freedom by either placement of the DNA nucleotides in similar conformations every time they enter a nanopore, which is ideal for fast sequencing, or averaging out over conformational degrees of freedom within each measurement of the sequence-specific current.

Effect of pore geometry

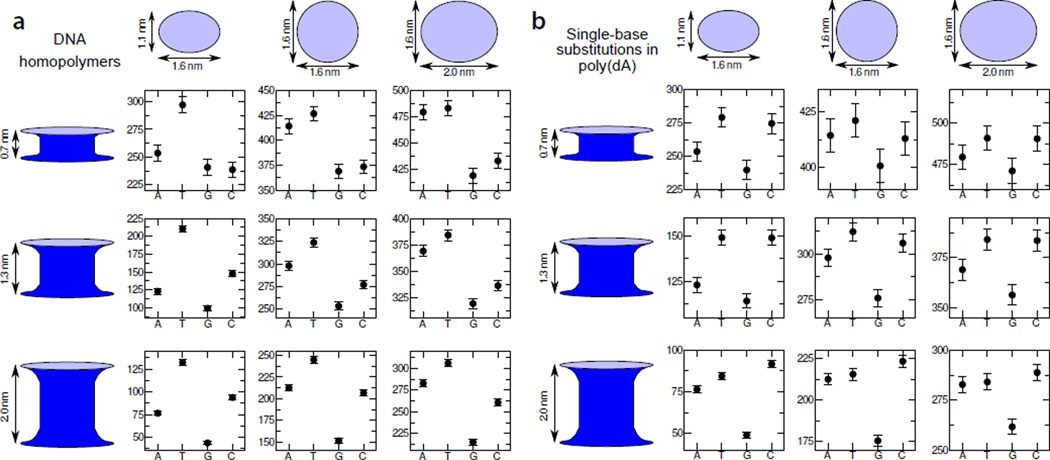
So far, we’ve discussed the effects of the DNA sequence and conformation on the blockade current. Obviously, the properties of the nanopore, in particular, its physical dimensions can influence the blockade currents as well. To systematically study the effect of pore cross section and length on differentiation of DNA blockade currents, we simulated the blockade currents from the four DNA homopolymers and from a poly(dA) homopolymer containing a single T, G or C substitution for nine model nanopore geometries, Figure 6.

Fig. 6.

Effect of pore geometry on DNA sequence differentiation. (a) Blockade currents of four DNA homopolymers in nine nanopores. The four data points in each plot specify the blockade currents of A, C, G and T homopolymers obtained using the ARBD method at a 175 mV bias and 0.1 M bulk concentration of KCl. The aggregate simulation time for each data point is 2 µs. The plots in each column are associated with different pore cross sections, which are detailed at the top of the figure. Each row is associated with a different pore length (or, equivalently, membrane thickness). All ARBD models featured the same conformations of the DNA strand, denoted as X0 in Figure 5. The electric field was applied parallel to the 5′-to-3′ direction of the DNA backbone. (b) Blockade current of a poly(dA) homopolymer with the base nearest the center of the nanopore remaining A, or substituted with a T, G, or C base. The layout of the figure is similar to that of panel a. The data set for the 1.6 nm × 1.1 nm cross section / 2.0 nm length nanopore partially duplicate the data shown in Figure 5.

As can be expected from physical considerations, increasing the cross section of the pore or decreasing its length consistently leads to an increase in the current. However, irrespective of the pore geometry, the homopolymer currents span roughly 60 pA, Figure 6a, while those for single-base substitutions in poly(dA) span about 25–50 pA, Figure 6b. The lack of a strong dependence on the pore cross section can be easily understood: a larger pore cross section permits more ions to pass through the pore, but, since the increased accessible cross-sectional area is not in the immediate vicinity of the DNA bases, the additional current shows little sequence dependence. Although the total sampling time was 2 µs for all data points reported in Figure 6a,b, the blockade currents through pores of larger cross sections are characterized by larger error bars. As shot noise is the dominant source of noise in our simulations, the error of ionic current determination is proportional to $\sqrt{I}$ for a total current I. Thus, the increased current is associated with increased shot noise, which is not compensated by enhanced sequence dependence. A similar situation can be expected in the presence of other noise sources^25–27, including the 1/f noise, as the magnitude of the current fluctuation is generally proportional to the value of the current. The effect of the pore length is not quite as easy to intuit as that of the cross section; however, as for the larger cross sections, the shorter pores lead to higher currents and less favorable signal-to-noise ratios.

The pore geometry does not appear to substantially alter the general trends of the blockade current dependence on the DNA sequence. First, for both global (Figure 6a) or local (Figure 6b) substitutions in any given pore geometry, the highest and lowest current values are dominated by T and G substitutions, respectively. For each pore, the G homopolymer or G substitution yields the lowest current or a current value statistically indistinguishable from the lowest current. Sequences containing T bases are consistently associated with the highest currents, except for the single-base substitution in the pore having a 1.1 nm × 1.6 nm cross section and a 2.0 nm length, where the greater C current is statistically significant. The ranking of A and C bases is less consistent, with the A homopolymer yielding currents less than those of the C homopolymer when the cross section remains small, but reversing when the cross section is increased.

In summary, we find the most favorable signal-to-noise ratios for the greatest pore length (2.0 nm) and the smallest pore cross section (1.1 nm × 1.6 nm) studied. The latter cross section is near the minimum size that can accommodate single-stranded DNA without introducing considerable distortions to its structure. While increasing the pore length from 0.7 to 2.0 nm yields more favorable signal-to-noise ratios, increasing it further would likely increase the number bases modulating the current and possibly making disambiguation of different sequences more difficult. Please note that all nanopores considered here could accommodate the same DNA strand without steric clashes. Reducing the pore cross section below 1.6 nm × 1.1 nm can alter the DNA conformations and thereby substantially change the patten of blockade currents.

Conclusion

In the present work, we used microscopic simulations to determine the origins of sequence-dependent ion current in nanopores containing DNA. We expect that this work will be useful in the design of future nanopore sequencing experiments. We have determined that the ion current is a convolution of contributions from at least 3–4 nucleotides, with a strong dependence on the configuration of the nucleotides within the pore. We have identified a scoring function for three-nucleotide subsequences that serves as a rough predictor of the ion current through our model pores for different DNA sequences but similar molecular conformations. It remains to be seen how transferable this scoring function may be since, in heterogeneous pores, such as proteins, the bases may interact differently with the pore walls and, hence, adopt distinct conformations depending on the sequence. The model pores used here may better represent more homogeneous pores such as those in graphene. A pore with a 1.1 nm by 1.6 nm cross section and a 2 nm length possessed the best ratio between the sequence-dependent component of the ion current and the shot noise compared with pores of larger cross sections and shorter lengths.

The methods presented here might be extended to more realistic pore models, representing, for instance, the electrostatic environment within a protein pore. The present work has shown the importance of the DNA conformation in determining the sequence-dependent current. While we have considered only fixed DNA conformations, the conformation of real DNA likely fluctuates substantially during the passage of ions, and this may need to be taken into account. It will be important to analyze the conformations of DNA in realistic pores and identify any sequence-dependence in the propensity for different conformations.

Methods

Molecular dynamics protocols

All simulations were performed with the program NAMD 2.7⁷³. Atomic interactions were computed as defined by the CHARMM27 force field for nucleic acids⁷⁴, including the TIP3P model and the Beglov and Roux parameters for K⁺ and Cl⁻ ions⁷⁵. The equations of motion were integrated with 1,2, and 4 fs timesteps for bonded, short-range nonbonded, and long-range electrostatic interactions using a multiple timestepping algorithm⁷⁶. Electrostatic interactions were calculated via the particle-mesh Ewald method⁷⁷, while van der Waals interactions were truncated with a smooth 0.7–0.8 nm cutoff. All covalent bonds, including those with hydrogen atoms, were modeled by a harmonic potential energy function.

Periodic boundary conditions were active in all three directions. Explicit water molecules and 100 mmol/L KCl were added to the models of single-stranded DNA using VMD⁷⁸, assuring a water layer of at least 3 nm between images in the lateral directions. The systems’ dimensions were 4.8 × 4.8 nm² normal to and ~11.5 nm along the z axis. A Langevin thermostat with a damping constant of 0.2 ps⁻¹ was used to maintain the temperature at 295 K. Each system underwent 1 ns of equilibration at a pressure of 101 kPa maintained by the Langevin piston method⁷⁹. Afterward, the system volume was chosen to be the average over the last 0.5 ns of the equilibration. All production simulations, including free-energy calculations, were performed with this fixed volume. The program VMD⁷⁸ was used for analysis and visualization, including the generation of the molecular renderings used in the present work.

DNA conformations

The DNA conformations were extracted from all-atom molecular dynamics simulations of poly(dA) molecules. Conformations X0 and X1 were extracted from a simulation of a 14-nucleotide single-stranded DNA molecule. To approximate a much longer molecule and permit tiling of the free-energy map, the two ends of the molecule were bonded to each other across the periodic boundary to yield a continuous molecule. Conformations Y0, Y1, and, Y3 were extracted from a simulation of a similarly periodic molecule consisting of a single nucleotide, while conformation Y2 was taken from a simulation of a two-nucleotide periodic molecule. The conformations indicated here are illustrated in Figure 5.

Free-energy calculations

Calculation of the 3D PMF maps was performed as described in our previous work³³. The periodic nature of the DNA conformations allowed them to be replicated in a consistent manner along the axis of the DNA. To reduce the effect of periodic boundary conditions, the single nucleotide conformations (Y0, Y1, Y3) were repeated four times along the axis of the DNA and conformations Y2 and X0 were repeated twice. Umbrella sampling windows⁸⁰ were centered on the nodes of a 3D close-packed lattice with a distance of 0.25 nm between nodes. Nodes that were farther than 0.68 nm from any atom of the target portion of the DNA were discarded as well as those that were closer than 0.22 nm from any DNA atom. For window w, a single K⁺ or Cl⁻ ion was restrained by the bias energy U_w = K|r – r_w|², where K = 0.0938 kcal/(mol Å ²) and r_w is the position of the lattice node. During the umbrella sampling simulations, each atom of the DNA was restrained to its initial position with a spring constant of 2.0 kcal/(mol Å ²). Conformations Y0, Y1, and Y3 required 262 windows for each of the K⁺ and Cl⁻ ions to sample one unique nucleotide, while conformation Y2 used 395 windows for a two-nucleotide segment. Generating the free-energy maps for conformations X0 and X1 was the most costly, requiring 1477 windows to obtain a map of a unique 14-nucleotide segment. Each umbrella sampling simulation lasted 7–12 ns. The weighted histogram analysis method⁸⁰ was used to construct the complete three-dimensional free-energy maps.

Ion current calculations

The ion currents were calculated by the atomic-resolution Brownian dynamics method that we described in our previous work³³. This method has the resolution and accuracy to yield estimates of sequence-dependent current while being efficient enough to accrue milliseconds of simulated time in a few days on commodity computers. A membrane occupying the xy plane and the phantom pore along the z axis were modeled by a smoothly varying force representing a repulsive interaction between the ions and the membrane material³³. The pores were of elliptical cross sections that widened near the opening. The DNA molecules were modeled by transforming and duplicating the free-energy maps described above. To produce varied sequences (the original conformations consisted only of A bases), base substitutions were performed by adding and subtracting 3D PMF maps of single nucleotides as in Ref.³³. The ion–ion interactions, steric exclusion by the DNA and long-range electrostatic interactions between the ions and DNA were handled as described in the same reference. The Brownian dynamics simulations were performed with a 10 fs timestep. An electric field was applied along the z axis to obtain the target transmembrane potential difference⁸¹.