PyClone: Statistical inference of clonal population structure in cancer

Abstract

We introduce a novel statistical method, PyClone, for inference of clonal population structures in cancers. PyClone is a Bayesian clustering method for grouping sets of deeply sequenced somatic mutations into putative clonal clusters while estimating their cellular prevalences and accounting for allelic imbalances introduced by segmental copy number changes and normal cell contamination. Single cell sequencing validation demonstrates that PyClone infers accurate clustering of mutations that co-occur in individual cells.

Human cancer progresses under Darwinian evolution where (epi)genetic variation alters molecular phenotypes in individual cells¹. Consequently, tumours at diagnosis often consist of multiple, genotypically distinct cell populations (Supplementary Fig. 1)². These populations, referred to as clones, are related through a phylogeny and act as substrates for selection in tumour micro-environments or with therapeutic intervention^{2, 3}. The prevalence of a particular clone measured over time or in anatomic space is a reflection of its growth and proliferative fitness. Thus, ascertaining the dynamic prevalence of clones can identify precise genetic determinants of phenotypes such as acquisition of metastatic potential or chemotherapeutic resistance.

In this contribution, we provide a statistical model for analysis of deeply sequenced (coverage >1000x) mutations to identify and quantify clonal populations in tumours, which extends to modelling mutations measured in multiple samples from the same patient. Our approach uses the measurement of allelic prevalence to estimate the proportion of tumour cells harbouring a mutation (referred to herein as the ’cellular prevalence’). Due to the cell lysis involved in the preparation of bulk samples for sequencing, we cannot determine the complete set of genomic aberrations defining a clonal population. However, assuming clonal populations follow a perfect (no site can mutate more than once in the tree) and persistent (mutations do not disappear or revert) phylogeny we can identify and quantify the prevalence of clonal populations. These assumptions imply that clusters of mutations occurring at the same point in the clonal phylogeny are present at shared cellular prevalences. Thus, clusters of mutations can be used as markers of clonal populations. (Limitations for when these assumptions do not hold are presented in the Supplementary Discussion).

Despite progress in measuring allele prevalence with deep sequencing^4–8, statistical approaches to cluster deep digital sequencing of mutations into biologically relevant groupings remain under-developed, with poorly understood analytical assumptions. The allelic prevalence of a mutation is a compound measure of several factors: the proportion of contaminating normal cells, the proportion of tumour cells harbouring the mutation and the number of allelic copies of the mutation in each cell, plus uncharacterized sources of technical noise. Consequently, allelic prevalence does not straightforwardly relate to cellular prevalence. This is particularly exacerbated when only single sample allelic prevalence estimates are taken. Multiple sample measurements (taken in time^{5, 9} or space¹⁰) have two distinct advantages: reduction of noise due to repeated measures and the potential to identify sets of mutations whose cellular prevalences shift together. The latter is a route to precisely identifying clones whose prevalences are changing under selective pressures.

To systematically address these deficiencies, we developed PyClone: a novel, hierarchical Bayes statistical model (Supplementary Figs. 2 and 3). The inputs to the model are a set of deeply sequenced mutations from one or more samples derived from the same cancer, and a measure of allele-specific copy number at each mutation locus in each sample (Supplementary Fig. 4). PyClone outputs posterior densities for model parameters including the cellular prevalence for each mutation in the input (Supplementary Fig. 5) and the clustering structure over the mutations (Supplementary Figs. 6 – 11). The posterior densities of these quantities are then post-processed to give interpretable point estimates of the cellular prevalences and mutational clustering.

The PyClone framework (full mathematical and implementation details in the Supplementary Note) overcomes the challenges outlined earlier through four novel modelling advances. First, it uses Beta-Binomial emission densities which more effectively models datasets with more variance in allelic prevalence measurements relative to a Binomial model. Second, flexible priors over mutational genotypes are used, reflecting how allelic prevalence measurements are deterministically linked to zygosity and coincident copy number variation events. Third, Bayesian non-parametric clustering is used to simultaneously discover groupings of mutations and the number of groups. This obviates fixing the number of groups a priori, and allows for cellular prevalence estimates to reflect uncertainty in this parameter. Fourth, multiple samples from the same cancer may be analysed jointly to leverage the scenario where clonal populations are shared across samples. Simulated data sets systematically illustrate improvements in performance of each of the novel modelling components (Supplementary Figs. 12 and 13).

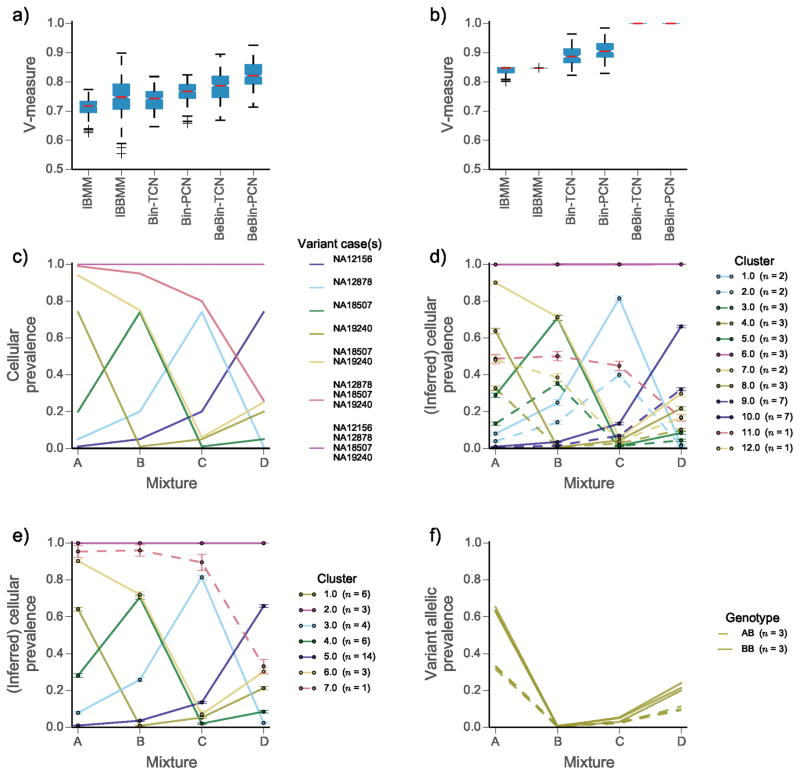
We first evaluated our approach on idealized datasets (Fig. 1), produced by physical mixtures of DNA extracted from four 1000 genomes project samples^{11, 12} (Online Methods). Each mixture contained DNA in approximate proportions of 0.01, 0.05, 0.20, 0.74. Specific single nucleotide variants were amplified using PCR, and then sequenced deeply on the Illumina MiSeq platform. This dataset simulates a hierarchically related population with ground truth for quantitative benchmarking (Fig. 1c). We selected positions with variants present in exactly one case, shared by specific subsets of cases, and shared by all cases (Online Methods). We compared PyClone using combinations of emission densities and genotype priors to two genotype naive methods: an infinite Binomial mixture model (IBMM) and an infinite Beta-Binomial mixture model (IBBMM) (Online Methods). Empirical comparisons to ground truth showed that PyClone with Beta-Binomial emission densities (BeBin-PCN and BeBin-TCN) outperformed all other methods based on clustering accuracy by V-measure¹³ (Online Methods). Performance gains were consistent when analyzing each dataset separately (Fig. 1a) or all four samples jointly (Fig. 1b). Accounting for mutational genotype and joint inference each conferred independent performance gains with best results obtained when using PyClone BeBin-PCN. To illustrate the effect of accounting for mutational genotype, we randomly selected one of the ten joint analysis runs contrasting PyClone BeBin-PCN with IBBMM, a baseline analogous to clustering the raw allelic data without considering mutational genotype. IBBMM output 12 clusters, consistently assigning heterozygous and homozygous SNPs from each ground truth cluster to separate clusters (Fig. 1d). By contrast, PyClone identifies the 7 correct clusters (Fig. 1e), placing heterozygous and homozygous SNPs from the same clusters together (Fig. 1f).

Figure 1.

Comparison of clustering performance for the mixture of normal tissues dataset | We compare the infinite Binomial mixture model (IBMM); infinite Beta-Binomial mixture model (IBBMM); PyClone using binomial emission densities and total copy number (Bin-TCN) or parental copy number (Bin-PCN) prior; PyClone using Beta-Binomial emissions and the parental (BeBin-PCN) or total (BeBin-TCN) copy number prior. (a) Comparison of methods when analysing each mixture experiment separately and (b) analysing all four mixtures jointly. (c) Expected cellular prevalence of each cluster across the four mixture experiments. (d) Inferred cellular prevalences and clustering using the IBBMM model and (e) PyClone BeBin-PCN model to jointly analyse all four mixtures. Solid lines (d, e) indicate clusters for which SNVs are predominatly homozygous (BB) and dashed lines indicate clusters for which SNVs are predominatly heterozygous (AB), in the event an equal number of both types of SNVs is present the cluster is drawn as a solid line. (f) Variant allelic prevalence for mutations assigned to cluster 1 by PyClone BeBin-PCN model. Dashed lines represent heterozygous SNVs and solid lines represent homozygous SNVs. (a, b) Whiskers indicate 1.5 the interquartile range, red bars indicate the median, and boxes represent the interquartile range. (d, e) Error bars indicate the mean standard deviation of MCMC cellular prevalences estimates for mutations in a cluster. (d, e, f) The number of mutations n in each cluster is shown in the legend in parentheses.

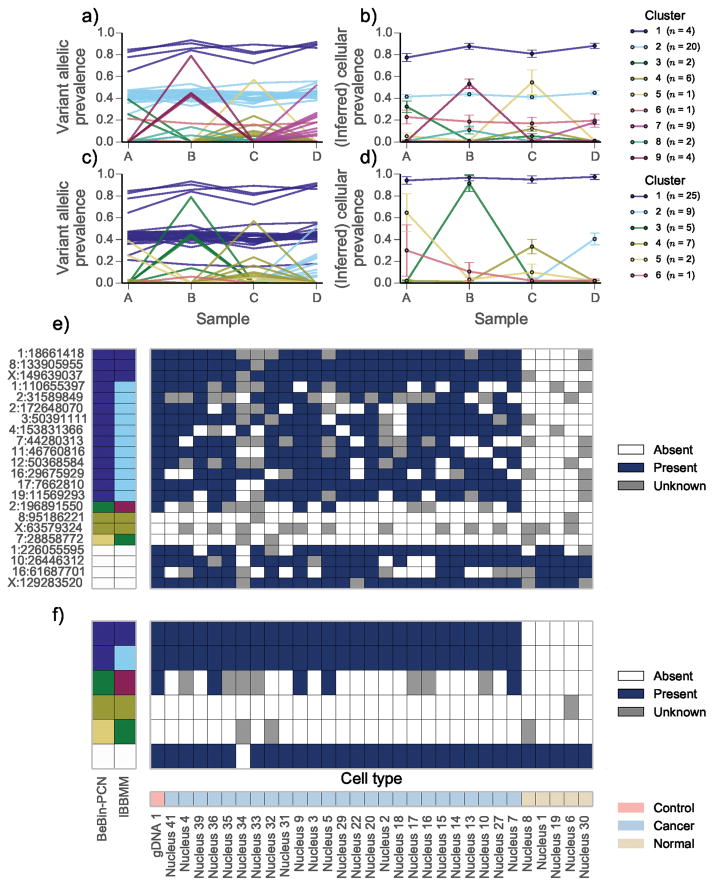
We next compared results from multi-sample BeBin-PCN and IBBMM in the cancer setting, using recently published mutational profiles of multiple samples from a high grade serous ovarian cancer (HGSOC)¹⁴. Four spatially separated samples were taken from a primary, untreated ovarian tumour (study case 2). Mutations called in exomes were deeply sequenced (~5000x), yielding 49 validated mutations. Copy number priors were obtained from high-density genotyping arrays (Online Methods).

IBBMM inferred 9 clusters, whereas PyClone identified 6 clusters. Clusters 1, 2 and 6 identified by IBBMM showed a similar pattern of variation across the four samples. PyClone placed these 25 mutations together in cluster 1 (Fig. 2a). We propose these mutations strictly co-occurred, with the observed variation in allelic prevalence due to differing mutational genotypes. Supporting this hypothesis, 75% (3/4) mutations placed in cluster 1 by IBBMM were predicted to be in regions of loss of heterozygosity, whereas 90% (18/20) mutations placed in cluster 2 by IBBMM were in regions predicted to be diploid heterozygous. The single mutation placed in cluster 6 by IBBMM fell in a region predicted to have major copy 3 and minor copy 1 (Supplementary Table 1). Major and minor copy refer to the number of copies of the most or least prevalent allele in the genotype respectively.

Figure 2.

Joint analysis of multiple samples from high grade serous ovarian cancer (HGSOC) 2 | The variant allelic prevalence for each mutation color coded by predicted cluster using the (a) IBBMM and (c) PyClone with BeBin-PCN model to jointly analyse the four samples. The inferred cellular prevalence for each cluster using the (b) IBBMM and (d) BeBin-PCN methods. As in Fig. 1 the cellular prevalence of the cluster is the mean value of the cellular prevalence of mutations in the cluster. (e) Presence or absence of variant allele at target loci in single cells from sample B. Loci with less than 40 reads covering them are coloured gray. Predicted clusters for each method are show on the left, with white cells indicating non-somatic control positions. (f) Presence or absence of IBBMM clusters in single cells from sample B. Clusters were deemed present if any mutation in the cluster was present. (b, d) Error bars indicate the mean standard deviation of MCMC cellular prevalences estimates for mutations in a cluster. The number of mutations n in each cluster is shown in the legend in parentheses.

The sum of allelic prevalences for IBBMM clusters 1 and 2 exceeded 1.0 implying cells exist with mutations from both clusters, with another group of cells containing only mutations from cluster 1. PyClone predicted mutations from IBBMM cluster 1 and cluster 2 strictly co-occurred. To test these competing hypotheses we performed single cell sequencing of tissue from sample B, obtaining reliable measurements for 25 nuclei. When interpreting the data we advise the reader that failure to detect a mutation in single cell data can occur even if the mutation is present due to biased PCR amplification of alleles. To clarify the competing hypothesis generated by IBBMM and PyClone, we collapsed the raw data to presence or absence of clusters predicted by IBBMM, where a cluster was determined to be present in a cell if any mutation from the cluster was present (Fig. 2f). IBBMM cluster 1 mutations were always detected with mutations from IBBMM cluster 2 (Fig. 2e,f). This is parsimonious with IBBMM clusters 1 and 2 comprising a single cluster, as predicted by PyClone. Results from a second HGSOC case from the same study led to similar conclusions (Supplementary Results, Supplementary Fig. 14, Supplementary Table 2).

In summary, we have introduced a novel statistical approach for inference of clonal population structures in human cancers from deep digital sequencing of mutations, with supporting validation from single-cell sequencing experiments. Discussion on the limitations, future directions and generalizability of the approach are included in the SI. The advances we present have practical implications for inference of clonal populations, and show measurable reductions in spurious inference relative to current approaches. As the practice of measuring allelic prevalences during the treatment cycle^{15, 16} or through retrospective analysis of multiple samplings increases^{10, 14, 17}, we suggest PyClone will contribute a robust statistical inference approach for studying selection patterns underpinning disease progression in cancer.

Online Methods

1 PyClone model and implementation

The full description of the PyClone model, its derivatives used in the benchmarking experiments, methods used for synthetic data generation, methods for copy number prior elicitation and implementation details are provided in the Supplementary Note.

2 Running PyClone and MCMC analysis

For the synthetic model comparison and normal mixing experiments all analyses involving the PyClone genotype aware models, IGMM, IBMM and IBBMM models were run for 10,000 MCMC iterations discarding the first 1,000 samples as burnin and no thinning was done. For the synthetic investigation varying the number of mutations and HGSOC analyses we used 100,000 iterations of the sampler discarding the first 50,000 as burnin. To generate cellular frequency plots we fit Gaussian kernel density estimators to the post-burnin MCMC trace using the scipy 0.12.0 Python library. To assess convergence for high grade serous ovarian cancers we ran three MCMC chains from random starting positions. The posterior densities of the cellular prevalence estimates were then inspected to ensure they were visually similar (Supplementary Figs. 8 and 11). For the synthetic dataset and normal mixing experiment this was not done due to the large number of runs. In general we have found that 10,000 – 100,000 iterations is sufficient for convergence in datasets with 100s of mutations.

To cluster the data we formed the pairwise posterior similarity matrix (the matrix indicating how frequently any two mutations appeared in the same cluster in the post-burnin trace). We then hierarchically clustered the data using average linkage, and the resulting dendrogram was used as a guide to find a clustering which optimised the MPEAR criterion described in Fritsch et al.¹⁸ (the code for doing this is built into PyClone). We note there are other approaches such as using the sample with the highest posterior probability to infer flat clusters using a DP, but Fritsch et al.¹⁸ have shown these tend to perform poorly in comparison to the method we use. Because this step requires the formation of the posterior pairwise similarity matrix the computational complexity scales as O(N²).

3 Evaluation and benchmarks

To assess the clustering performance of the methods we computed the V-measure ¹³, calculated using the scikits-learn Python package 0.14.1. V-measure is a measure of clustering accuracy between 0 and 1 where a V-measure score of 1 represents perfect clustering. Cellular prevalence estimates were evaluated using the mean error over MCMC samples, where a mean error of 0 represents perfect cellular prevalence estimates. Explicitly, for each mutation the mean of the post-burnin trace of the cellular prevalence parameter was used as a point estimate. The absolute difference between this value and the true value for each mutations in each dataset was computed. For each of the datasets the mean value of the absolute error across mutations was taken and used to generate the boxplots. Statistical analysis was performed with the aov and TukeyHSD functions in the R statistical computing package using RStudio v.0.96.331.

4 Alternative Methods

To compare genotype aware clustering to other clustering methods that ignore genotype, we implemented three standard clustering models in the PyClone software package: the infinte Gaussian mixture model (IGMM), the infinite Binomial mixture model (IBMM), and the infinite Beta Binomial mixture model (IBBMM). We interpreted the probability of success for the IBMM, and the mean parameter m for the IBBMM as the cellular prevalence of mutations. For the IGMM analysis we first computed the variant allelic prevalence for each mutation and then clustered these values, interpreting the mean of the clusters as the cellular prevalence. All MCMC analysis, clustering and cellular frequency inference was done as described earlier and in the Supplementary Note. All methods implemented in the PyClone software package, including the IGMM, IBMM and IBBMM use the PyDP package to perform inference. Thus any variation in performance should be due to differing distributional assumptions, not inference methods or implementation.

5 Normal tissue mixture experiments

For the idealized mixture data presented in Fig. 1, data from mixture experiments A (SRR385938), B (SRR385939), C (SRR385940) and D (SRR385941) from Harismendy et al.¹² were downloaded from the NCBI short read archive. Each dataset was generated by physically mixing DNA from four tissue samples from the 1000 genomes project in different proportions. Thus mixtures were generated from the source DNA material and not in-silico. The resulting mixtures were then subjected to targeted amplification using the UDT-Seq protocol and sequenced on the Illumina MiSeq platform.

FASTQ files were extracted from the downloaded .sra files using the fastq-dump–split-files–clip command from the NCBI SRA-SDK version 2.3.33. Sequences were aligned to the targeted genome using mem command from the bwa 0.7.5a package. Count data was extracted from the BAM files using a custom Python script which filtered out positions with base or mapping qualities below 10. Because the primers used in the UDT-Seq protocol were designed to target mutational hotspots in cancer and not the SNP positions we were analysing, some candidate positions lay near the start or end of the primers. These positions tended to show significant strand bias which could translate to biased allelic abundance estimates. To address this, the count data was post-processed to remove positions showing significant strand bias (P < 0.05) as determined using a Fisher exact test. No multiple test correction was done.

Primer start and stop positions for the UDT-Seq protocol were obtained from Supplemental Table 2 of Harismendy et al.¹². We downloaded hg19 from UCSC website and used primer positions to build a targeted reference alignment file which contained only the regions spanned by the primers.

Variants positions in the four cases used were previously identified in Ng et al.¹⁹. We compiled a list of positions with variants in: i) exactly one of the four cases used in the mixture; ii) shared by NA18507 and NA19240; iii) shared by NA18507, NA19240 and NA12878; iv) shared by all four cases. For SNPs present in multiple cases we only considered positions that had the same genotype in all the variant cases. We manually removed positions which appeared to have variant allelic prevalence deviating significantly from the expected values. These outliers were either due to incorrect annotation of the genotype in one of the four cases, or because sequencing appeared to work poorly at the target location. The position coordinates were converted from hg18 to hg19 coordinates using the UCSC liftover program.

The position selected simulated an idealized cancer consisting of seven clonal cell populations which evolved according to a bifurcating tree. SNPs in all four cases represent the root of the tree. SNPs present in 2 or 3 cases represent interior nodes of the tree. SNPs unique to each sample represent leaf nodes in the tree.

Because the dataset was highly imbalanced for variants with the BB genotype we randomly down sampled the BB positions to obtain 10 smaller datasets of 37 mutations with a 50:50 representation of positions with AB and BB genotypes for the nodes with SNVs in exactly one of the samples. There were not enough mutations in the interior nodes to do this, so we used all mutations for these nodes.

The predicted genotypes from Ng et al.¹⁹ were used to determine the homologous copy number for the PCN prior as follows: for the positions predicted to have the AB genotype in the variant sample we set the major and minor copy numbers to 1; for positions with the BB genotype in the variant sample we set the major copy number to 2 and the minor copy number to 0.

Benchmarking in this experiment was measured by the ability to correctly group mutations based on the known, but held-out reference clustering (Fig. 1c). Reference clustering was defined by the case(s) harbouring the variant genotype. To be explicit, we expected seven clusters to be identified: one for SNPs present in all cases; one for SNPs present in NA18507, NA19240 and NA12878; one for SNPS present in NA18507 and NA19240; and four clusters for SNPs unique to each case. Since we knew which SNPs were present in each case we could compute a ground truth clustering based on the above expectation. The challenge for the methods we considered was to correctly predict the co-occurrence of SNPs from the same ground truth clusters with different genotypes. We would expect methods which ignore genotype to fail at this task.

We did not attempt to benchmark cellular prevalence estimates for this dataset since the cellular prevalence values were only approximately correct due to experimental variability in the mixing of the tissues.

6 Copy number analysis

In the following section array refers to Affymetrix SNP6.0 arrays. No other array platform was used for copy number analysis.

Normalisation and feature extraction

ASCAT and OncoSNP both require that the input data be suitably normalised and that the B allele fraction (BAF) and log R ratio (LRR) be extracted from the raw CEL files. To do this we used a modified version of the workflow described on the PennCNV-Affy website (www.openbioinformatics.org/penncnv/penncnv_tutorial_affy_gw6.html). To extract features in the hg19 coordinate system we mapped the supplied Pen-nCNV .pfb and .gcmodel files using the annotations in the GenomeWideSNP_6,Full,na31,hg19,HB20110328.ugp file downloaded from the AROMA project (aroma-project.org). We used only steps 1.2 and 1.4 of the PennCNV workflow to perform normalisation and BAF/LRR extraction. The output of step 1.4 was passed to OncoSNP. For ASCAT we applied the PennCNV GC correction to the output of step 1.4 since ASCAT has no built in GC normalisation strategy.

ASCAT

We used ASCAT²⁰ version 2.1 for all analyses. We used the paired analysis mode to analyse the tumour and matched normal arrays jointly. The standard ASCAT workflow and default parameters described in the software manual were used for all analyses.

PICNIC

The latest version of PICNIC²¹ as of 06/10/13 was used for all analyses. For all analyses PICNIC was run using only the tumour array. The parameter files supplied with PICNIC were mapped to hg19 coordinates using the GenomeWideSNP_6,Full,na31,hg19,HB20110328.ugp file downloaded from the AROMA project (aroma-project.org). Quantitative pathology estimates were used to inform the prior for normal contamination in the PICNIC inference procedure. The standard PICNIC workflow as described in the software manual with default parameters was performed for all analyses. Since PICNIC performs normalisation and feature extraction as part of its analysis, raw CEL files were passed as inputs.

OncoSNP

We used OncoSNP²² version 1.3 for all analyses. We used the paired analysis mode to analyse the matched normal and tumour arrays jointly. We used the stromal contamination and intra tumour heterogeneity modes. We also included the X chromosome in the analysis. With these modifications, the OncoSNP workflow and default parameters described in the software manual were used for all analyses.

7 High grade serous ovarian cancer

Multiple PyClone analyses were performed, one analysis per copy number prediction method (Supplementary Results). We specified the priors for cellularity estimation in PICNIC based on quantitative pathology estimates. Allelic count data was obtained from Bashashati et al. ¹⁴. We obtained count data from additional mutations not validated as somatic from the authors. For each copy number method we used the homologous copy number information to elicit priors for PyClone using the PCN strategy, and set the tumour content for the PyClone analysis to the value predicted by the copy number method. MCMC analysis and post-processing of the trace was done as discussed in the Supplementary Note.

8 Single-cell genotyping of frozen high grade serous ovarian cancers

Nuclei preparation and sorting

Single cell nuclei were prepared using a sodium citrate lysis buffer containing Triton X-100 detergent. Solid tissue samples were first subjected to mechanical homogenization using a laboratory paddle-blender. The resulting cell lysates were passed twice through a 70-micron filter to remove larger cell debris. Aliquots of freshly prepared nuclei were visually inspected and enumerated using a dual counting chamber hemocytometer (Improved Neubauer, Hausser Scientific, PA) with Trypan blue stain. Single nuclei were flow sorted into individual wells of microtitre plates using propidium iodide staining and a FACSAria II sorter (BD Biosciences, San Jose, CA).

Multiplex and singleplex PCRs

Somatic coding SNVs catalogued and validated in bulk tissue genome sequencing experiments were picked for mutation-spanning PCR primers design using Primer3 ²³. Common sequences were appended to the 5′ ends of the gene-specific primers to enable downstream barcoded adaptor attachment using a PCR approach. Multiplex (24) PCRs were performed using an ABI7900HT machine and SYBR GreenER qPCR Supermix reagent (Life Technologies, Burlington, ON). The 24-plex reaction products from each nucleus were used as input template to perform 48 singleplex PCRs using 48.48 Access Array IFCs according to the manufacturer’s protocol (Fluidigm Corporation, San Francisco, CA). Flow sorting plate wells without nuclei and 10 ng gDNA aliquots were used for negative and positive control reactions, respectively.

Nuclei-specific amplicon barcoding and nucleotide sequencing

Pooled singleplex PCR products from each nucleus were assigned unique molecular barcodes and adapted for MiSeq flow-cell NGS sequencing chemistry using a PCR step. Barcoded amplicon libraries were pooled and purified by conventional preparative agarose gel electrophoresis. Library quality and quantitation was performed using a 2100 Bioanalyzer with DNA 1000 chips (Agilent Technologies, Santa Clara, CA) and a Qubit 2.0 Fluorometer (Life Technologies, Burlington, ON). Next-generation DNA sequencing was conducted using a MiSeq sequencer according to the maufacturer’s protocols (Il-lumina Inc., San Diego, CA).

Bioinformatic analysis

Paired end FASTQ files from the MiSeq sequencer were aligned to human genome build 37 downloaded from the NCBI using the mem command from the bwa²⁴ 0.7.5a package. Allelic count data was extracted from the BAM files using a custom Python script which filtered out positions with base or mapping qualities below 10. Any loci with fewer than 40 reads of coverage was deemed unusable and assigned an unknown status in plots. We removed any cell in which more than 80% of the loci were unusable. We also removed any loci which were unusable in more than 80% of cells.

Stochastic biased amplification of alleles due to limiting quantities of DNA in single cells made it difficult to detect presence or absence of the variant allele using allelic prevalence. To address this we applied a statistical test to determine the presence or absence of the variant allele. The null hypothesis for the test was that the variant allele was absent, thus we only observe reads with the variant allele due to sequencing error. We computed the proportion of reads with a variant allele at all positions on the amplicon targeting a loci, excluding the target loci. For these positions we defined the variant allele as the non reference allele with the most reads supporting it. We used the mean of these values as the estimated sequencing error rate. This value was used to perform a one tailed Binomial exact test. For each cell we multiple test corrected the p-values for all loci with coverage using the Benjamini-Hochberg procedure. We used a false discovery rate of 0.001 to determine if a variant allele was present. These methods have been applied in previous work and additional details are reported therein^{4, 9}.