Engineering Near-Field SEIRA Enhancements in Plasmonic Resonators

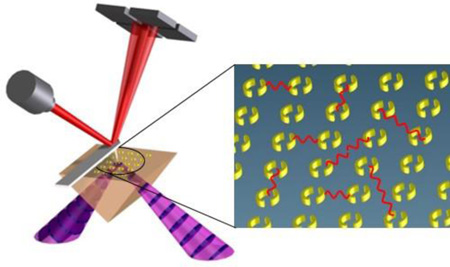
Abstract

Engineering of the optical resonances in plasmonic resonators arrays is achieved by virtue of the intrinsic properties to the constituent structures such as composition, size and shape and by controlling the inter-resonator interactions by of virtue the array geometrical arrangement. The nanoscale confinement of the plasmonic field enhances light-matter interactions enabling, for instance, the surface enhanced infrared absorption (SEIRA) effect. However, the subwavelength confinement also poses an experimental challenge for discriminating the response stemming from the individual resonators and from the collective response in densely packed arrays. In this work, the photothermal induced resonance (PTIR) technique is leveraged to obtain nanoscale images and spectra of near-field SEIRA hot spots observed in isolated plasmonic resonators of different shapes and in selected resonators within closely packed plasmonic arrays informing on whether the interactions with neighboring resonators are beneficial or otherwise. Results are correlated with far-field spectra and theoretical calculations.

Graphical abstract

Metamaterials are artificially engineered materials that derive their properties from a combination of composition and structure, rather than from composition alone.^1–6 Metamaterials attract great interest because they exhibit electromagnetic properties that differ from those of naturally occurring materials. For example, the interplay between composition and structure allows bending electromagnetic waves at arbitrary angles and engineering the permittivity (ε) and the permeability (μ) of those constructs.^1–5 Such unique properties enable a plethora of applications hitherto unavailable such as perfect lenses,³ electromagnetic cloaks,⁴ miniaturized antennas⁶ etc. Among metamaterials, split ring resonators (SRRs) consist of a metallic loop with one or more gaps (see Figure 1a) and are among the most studied nanostructures. It is well known that SRR and other plasmonic materials display wavelength-tunable resonances as a function of size and shape.^5–9 Plasmonic resonances have the merit of confining light to nanoscale volumes of matter (hot-spots) resulting in locally enhanced light-matter interactions. In the mid-IR, this property can be leveraged for chemical identification by increasing the sensitivity of IR spectroscopy, an effect known as surface enhanced infrared absorption (SEIRA).^10–19

Figure 1.

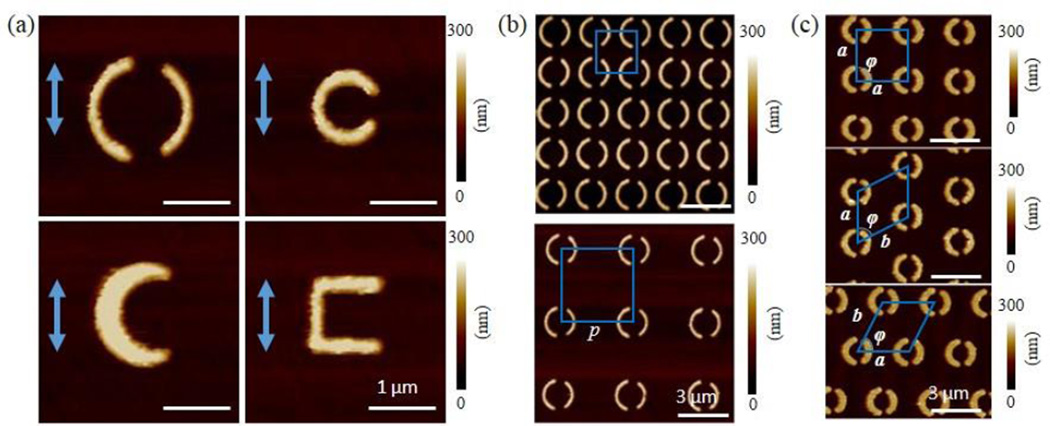
(a) AFM images for isolated (p = 10 µm) plasmonic resonators of different shapes; A-SRR (top-left), Cr-SRR (bottom-left), C-SRR (top-right) and U-SRR (bottom-right). Arrows shows the electric field polarization of incident IR laser. (b) AFM images for A-SRR arrays with different pitches: 2.0 µm (top) and 3.6 µm (bottom) (c) AFM images of A-SRR arrays with different unit cell arrangements: square (top), vertically shifted centered rectangular (middle) and horizontally shifted centered rectangular (bottom). The blue shapes represent the unit cell of each array.

Typically SRRs are arranged in periodic arrays and their constituent structures have characteristic dimensions that are smaller than their plasmon resonant wavelength (λ) in free space. The plasmonic excitation and SEIRA enhancement in these arrays can be engineered by controlling the intrinsic properties of the resonator (i.e. composition, size, shape, etc.) and by controlling the inter-resonator interactions (i.e. pitch and arrangement). Strategies to enhance the intrinsic properties of the resonators includes the fabrication of structures supporting Fano resonances¹² or leveraging metal-dielectric-metal architectures.²⁰ Strategies to increase the response of the resonators via inter-resonator interactions include the fabrication of tightly spaced structures,²¹ that exploits near-field interactions to provide enhanced fields between neighboring structures, or the fabrication of arrays with spacing close to the resonators’ effective plasmon resonant wavelength to enable the coherent and collective excitation of plasmonic structures.^{14, 22} For a given nanostructure characterized by plasmon resonant wavelength (λ) and arranged in a 2D array, four different interaction regimes are possible as a function of the pitch. i) If p >> λ/n_eff, where n_eff is the effective refractive index, the long-range inter-resonator interactions are weak and the resonators can be considered as isolated. ii) If p ≈ λ/n_eff, diffractive far-field interactions between the nanostructures in the array may create constructive interference, leading to collective modes characterized by sharp plasmonic resonances and typically high sensitivity.^{14, 22} iii) If p < λ/n_eff but with the structures still well separated that the near-field interactions are negligible, the long-range inter-resonator interactions typically reduce the resonator cross-section due to destructive interference. iv) if p < λ/(10·n_eff) the near-field interactions become important and can also give rise to high sensitivity.²¹

Theoretical modelling plays a primary role in the engineering of these materials because the sub diffraction confinement of plasmons, in typically closed packed arrays, challenge diffraction-limited techniques to discriminate the properties stemming from the individual resonators and from the collective response of the array. In the mid-IR the role of inter-resonator interactions have been highlighted in a few studies.^{14, 23, 24} For example, SRR arrays with different pitches have been measured in the far-field^25–27 and their response was explained by the magneto-electric point scattering theory.^{28, 29} This fully analytical model accounts for the inter-resonator interactions via the electric and magnetic dipole moments, induced by light excitation.

In this regard, the extinction cross section (σ_ext) of isolated SRRs has been measured in the near-IR by the spatial modulation technique^{27, 30} or in the visible by Fourier microscopy³¹ but we are not aware of similar studies in the mid-IR.In the mid-IR, high resolution images of the near-field of plasmonic nanomaterials have been obtained by scanning scattering near-field optical microscopy (s-SNOM)^32–35 and by photothermal induced resonance (PTIR)^{10, 36, 37} techniques. Recent reviews discussing the state of the art of these techniques can be found elsewhere.^{38, 39} PTIR^40–42 combines the resolution of atomic force microscopy (AFM) with the specificity of absorption spectroscopy in both the mid-IR and visible ranges.⁴³ PTIR has recently attracted attention because, in addition to images of the near-field, the nanoscale PTIR spectra provide a quantitative measure of the local SEIRA enhancement.^{10, 37} PTIR is also finding increasingly wider application in materials science^44–49 and biology.^{50, 51} The main goal of this paper is to exploit the PTIR method to single out and measure the SEIRA response deriving from specific plasmonic resonators in closely packed arrays and to evaluate whether their response is positively or negatively affected by the interactions with neighboring resonators.²¹ Here, the near-field SEIRA hot-spot intensities are measured for SRRs of different shapes: asymmetric (A-SRR), crescent-shaped (Cr-SRR), “C”-shaped (C-SRR), “U”-shaped (U-SRR), that are either isolated or organized in periodic arrays with different pitches and arrangements. The results are compared with far-field ensemble measurements and with magneto-electric point scattering calculations. The range of pitches studied in this work include the case of the isolated resonators and p < λ/n_eff, approaching the limit where the near-field interaction become important but do not include the case of the coherent excitation of plasmonic arrays (p ≈ λ/n_eff),^{14, 22} see discussion. Results show that for the isolated resonators the A-SRR geometry provides the strongest SEIRA hot spots. For U-SRRs arranged square lattice arrays with different pitches, the near-field SEIRA enhancement of each resonator increases as a function of the pitch, in agreement with theoretical calculations of the resonator’s extinction cross section (σ_ext), which also increases with the pitch. Although the inter-resonators interactions reduce the resonators’ intrinsic σ_ext, the higher resonator density of closely packed arrays overcompensates the reduction of σ_ext and provides the stronger response in the far-field. In contrast, the locally measured SEIRA enhancement in A-SRR arrays is a non-monotonic function of the pitch because of the constructive hotspot overlap in the most closely-packed array (i.e. the near-field interactions overcompensate the smaller σ_ext, typical of arrays with the smaller pitches). Finally, by analyzing arrays composed of resonators of the same size, shape and density but with different unit cell arrangements, the PTIR data show that the perturbation introduced by the second order inter-resonator interactions on the near-field SEIRA enhancement is small.

Sample Preparation

To enable PTIR measurements, the resonators were fabricated on zinc selenide right angle prisms by electron-beam lithography and lift-off using custom adaptors,⁴¹ see experimental for details. To discriminate the contributions to near-field SEIRA enhancement stemming from the constituent resonators (i.e. size and shape) from the ones stemming from the inter-resonator interactions (i.e. spacing and arrangement) in periodic SRR arrays, three sets of samples were fabricated (see Figure 1). The effect of the resonator shape on the near-field SEIRA enhancement was evaluated with a set of samples consisting of resonators of different shapes separated by a large pitch (10 µm) so that the inter-resonators interactions can be considered negligible. Hereafter we will refer to these samples as “isolated resonators”. Because the resonant wavelengths of plasmonic structures are a function of the nanostructure size and shape, resonators with different shapes of a given characteristic size typically display different resonant wavelengths. Consequently, to compare the near-field enhancements of resonators with different shapes displaying resonances in approximately in the same spectral region, we choose resonators of different sizes (Figure 1a). The dimensions of the resonators as measured by AFM are summarized in table 1. The thickness for all the gold resonators was 180 nm ± 10 nm, as measured by AFM. To study the inter-resonators dipolar interactions, a second set of samples consisting of 7 square arrays composed of resonators with the same sizes and shapes as the isolated resonators but with different pitches (p) were fabricated (28 samples total). As a representative example, Figure 1b shows the AFM images of two A-SRR arrays with p = 2.0 µm and p = 3.6 µm respectively. Finally, to evaluate the effect of the higher order interactions on the SEIRA enhancement, a third set of samples consisting of A-SRR of the same size and shape as the isolated A-SRR organized in different arrangements: square (unit cell a = b, φ = 90°) and two centered rectangular (unit cell a ≠ b, φ ≈ 53°) were fabricated (see Figure 1c). For these latter samples, the lattice constants were chosen to be approximately twice the size of the resonators (≈ 3 µm), Figure 1c. In particular, the two centered rectangular arrays can be thought of as constructed from a square array by shifting every other column of the array vertically by a half unit cell, or by shifting every other row of the array horizontally by a half unit cell, respectively. Because the resonators’ density of square and centered rectangular lattices is the same, these arrays were used to evaluate the effect of higher order inter-resonators interactions on the near-field SEIRA enhancement, which should be a weak function of the near-neighbor configurations and resonators’ shapes.

Table 1.

Characteristic dimensions of the isolated resonators as measured by AFM: A-SRR (outer diameter), Cr-SRR (outer diameter), C-SRR (outer diameter) and U-SRR (lateral dimension), respectively. Plasmon resonant wavelength as measured by FTIR corresponding to square array composed of resonators of the same size and with pitches of approximately twice the characteristic dimensions. The isolated resonators (p = 10 µm) were too sparse to yield a measurable far-field FTIR spectrum for a direct comparison. The uncertainties in the resonators dimensions represent a single standard deviation in the measurements on nominally identical resonators. The uncertainty in the plasmon resonant wavelengths and Q factors represent a single standard deviation from Lorentian fitting of FTIR resonance peak.

Shape	Characteristic dimension (µm)	Resonance Wavelength (µm)	Q-factor
A-SRR	1.75 ± 0.05	8.85 ± 0.05	13.9 ± 0.5
Cr-SRR	1.65 ± 0.05	9.05 ± 0.05	5.1 ± 0.3
C-SRR	1.20 ± 0.05	9.00 ± 0.05	5.7 ± 0.3
U-SRR	1.15 ± 0.05	9.70 ± 0.05	3.6 ± 0.3

Results and Discussion

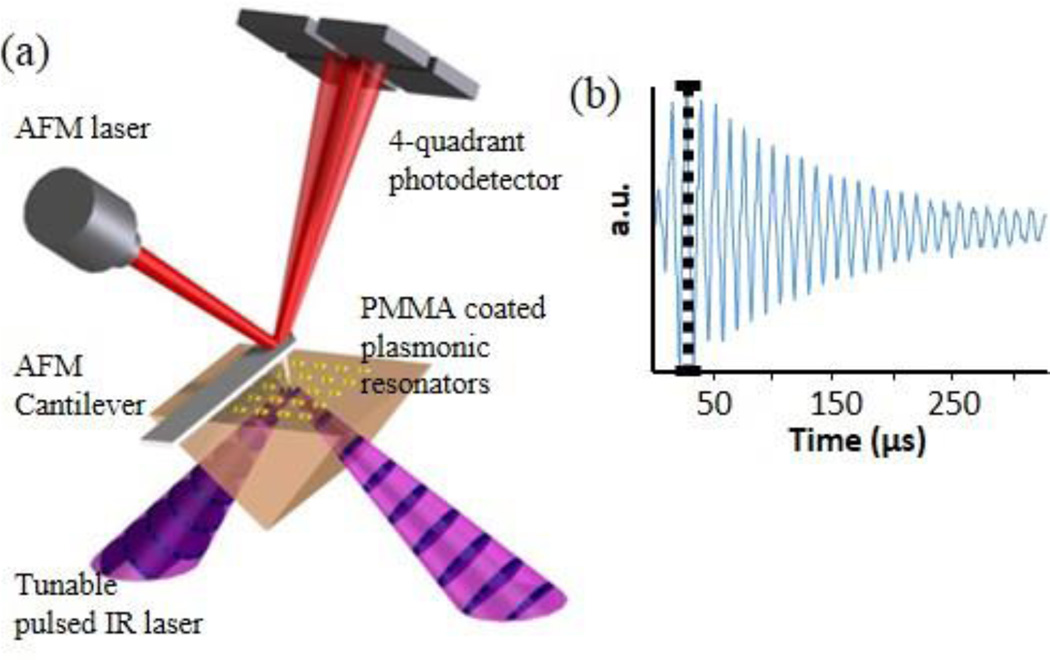
After fabrication, far-field Fourier transformed infrared (FTIR) spectra were recorded with an IR microscope and nanoscale topography images of the bare resonators were obtained by an AFM microscope. Prior to the PTIR experiments, a 200 nm thick poly-methyl methacrylate (PMMA) film was spin-coated on each sample. In the PTIR experiments, the samples were illuminated at 45° by total internal reflection from the prism side as shown in Figure 2a. In all PTIR measurements, the light polarization was in the sample plane along the direction (vertical) indicated by the arrows in Figure 1a. The absorption of a laser pulse by the sample induces heating, sample expansion, and mechanical excitation of the AFM cantilever in contact with the sample. The resulting cantilever oscillations have an amplitude that is proportional to the absorbed energy (Figure 2b) and are monitored by a four quadrant detector. PTIR maps are obtained by illuminating the sample at a constant wavelength while scanning the AFM tip and plotting the amplitude of the tip deflection as a function of the tip location. Local infrared spectra were obtained by positioning the AFM tip in a desired location and by plotting the maximum amplitude of the tip deflection as a function of the excitation wavelength.

Figure 2.

(a) Schematic of the PTIR measurement setup. (b) The PTIR signal intensity is determined by the maximum amplitude of the cantilever ring down signal (black dotted line) which is proportional to the energy absorbed by the sample.

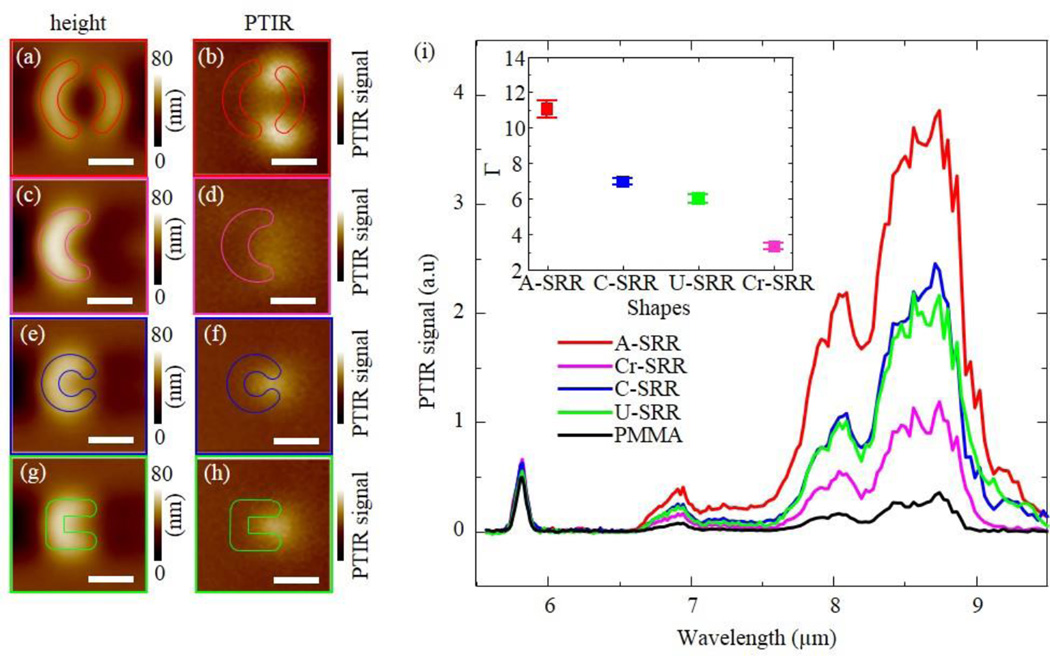
Figure 3a–h show pairs of topography and PTIR maps for the isolated resonators obtained illuminating the sample at 1142 cm⁻¹ (corresponding to the PMMA C-O stretching absorption). Because the PTIR signal is proportional to the absorbed energy, to the sample thermal expansion and it is inversely proportional to the thermal conductivity,^{41, 42, 47, 52} the contribution of absorption in the resonators due to ohmic dissipation to the intensity of the PTIR images in Figure 3 is negligible.¹⁰ Consequently, the PTIR images represent a direct image of the SEIRA enhancement in the near-field displaying hot-spots in regions where the SEIRA enhancement is most prominent. Such enhancement arises from the local electromagnetic field confinement which occurs near the gaps or terminations of the plasmonic structures. Figure 3i compare the PTIR spectra of PMMA obtained from the hot-spot locations with the spectrum of the PMMA film obtained ≈ 100 µm away from the resonators (see Experimental for details). For the resonators’ geometrical parameters used in this work, the PTIR spectra and maps show that the A-SRR structure provides the strongest SEIRA enhancement, followed by C-SRR and U-SRR structures and then by Cr-SRR, which displays the weakest hotspots. We define the SEIRA enhancement factor (Γ) at a given wavelength as the ratio of the PTIR intensity in the hot-spot with respect to the PTIR intensity in the PMMA film obtained 100 µm away from the resonators. The values of Γ obtained in the experiments are a function of the electromagnetic field confinement which is related to the resonator’s quality factor (Q-factor),⁵³ convoluted with the lateral resolution of the PTIR experiments (≈ 100 nm). The range of Γ measured in this work (from ≈ 3 to ≈ 11, see inset of figure 3i) may appear much lower than record values (10⁴ – 10⁵), estimated for monolayer samples coating plasmonic antennas.¹⁴ However, for monolayer samples, Γ represent the average SEIRA enhancement within the volume of the monolayer in the hotspot location (typically 1 nm³ to 10 nm³). In the PTIR experiments, Γ is average over the whole volume probed under the tip (i.e. 1.6 × 10⁶ nm³, assuming 100 nm resolution), suggesting a considerably high enhancement in proximity of the plasmonic resonator surface. The Q factors of the resonators were evaluated from the far-field reflection spectra (see Table 1). According to the spectra, the A-SRR geometry displays the highest Q-factor (13.9 ± 0.5) followed by C-SRR, Cr-SRR and U-SRR in decreasing order. The large Q factor of the A-SRR geometry stems from the characteristic Fano resonance¹² which provides a better confinement of the SEIRA hotspots in the near-field. Because the lateral resolution of our experiments enables resolving two hot-spots for A-SRR and Cr-SRR but only one for C-SRR and U-SRR; despite the larger Q-factor of Cr-SRR, the tighter near-field confinement in U-SRR provides a stronger local enhancement in the PTIR measurements.

Figure 3.

Isolated (p = 10 µm) plasmonic resonators. (a)–(h) pairs of simultaneously obtained AFM height (left) and PTIR (right) images for each resonator shape: ; A-SRR (a, b), Cr-SRR (c, d), C-SRR (e, f) and U-SRR (g, h). PTIR images were obtained by illuminating the sample at 8.75 µm (1142 cm⁻¹), corresponding to the C-O stretching of PMMA. The resonators’ outlines were drawn based on AFM topography images obtained before coating the samples with a PMMA film. All PTIR images are displayed with a common intensity scale and all scale bars are 1 µm. (i) the PTIR spectra from the hot-spots locations of panels b, d, f, h are compared with the spectrum of the PMMA film obtained away from the resonators (black). The inset displays the enhancement factors (Γ) for the near-field hotspots at 8.75 µm (1142 cm⁻¹). The uncertainty in enhancement factor represent a single standard deviation in the measurement of the PTIR spectral intensity ratio with respect to the PMMA reference.

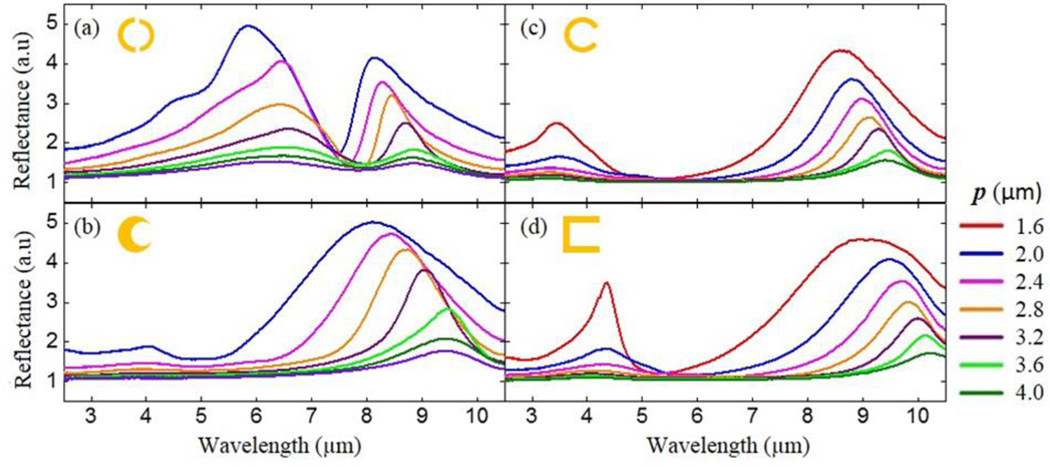
For each resonator shape, the far-field reflection spectra of the uncoated arrays are displayed in Figure 4 as a function of p. The plasmon resonant peaks shift to longer wavelengths (red-shift) as the inter-resonator spacing increases for all sets of samples. In the simple dipole model,^{26, 27} as p is increased, the electric and magnetic dipole-dipole interactions between neighboring resonators induce a red-shift or blue-shift in the plasmonic resonance, respectively.²⁶ Consequently, for resonators studied here, the electric dipole-dipole interactions are dominant. Additionally, a broadening of the plasmonic peak is observed for decreasing p starting from p ≈ 3.2 µm for all resonators’ shapes, which can be explained by the super-radiant decay of the electric dipoles.^{5, 25, 26} Those results are consistent with previous transmission experiments in visible range.²⁶

Figure 4.

FTIR spectra of A-SRR (a), Cr-SRR (b), C-SRR (c) and U-SRR square arrays with different pitches (p).

To elucidate the effects of the resonator interactions in the far- and near-field, we calculated the optical response of square U-SRR arrays of different pitches based on magneto-electric point scattering theory,^{28, 29} which gives a full analytical model for anisotropic magneto-electric scatterers including SRRs. In this model, SRRs are approximated by local electric and magnetic dipole moments with a dynamic polarizability in response to the incident fields. This generalized model accounts for the coupling and cross coupling between electric and magnetic dipoles to the incident electric and magnetic fields. Commonly, dipole-quadrupole and other higher-order multipolar interactions are neglected in this analysis. According to this model the optical properties of a single SRR can be described by a vector whose component are the resonator’s electric (p) and magnetic (m) dipole moments that are related to the incident electric (E) and magnetic (H) fields, by 6 × 6 polarizability tensor $\overleftrightarrow{\alpha }$ as

$$\left(\begin{array}{c}\hfill p\hfill \\ \hfill m\hfill \end{array}\right)=\overleftrightarrow{\alpha }\left(\begin{array}{c}\hfill E\hfill \\ \hfill H\hfill \end{array}\right),$$ (1)

where $\overleftrightarrow{\alpha }$ should includes radiation damping to satisfy the optical theorem (i.e. energy conservation).²⁸ The magneto-electric point scattering theory can be extended to scatterers arranged into a two-dimensions lattice by summing all dipole-dipole interactions between SRRs in the lattice using the dyadic Green function.²⁹ In a periodic array, the SRRs position in the lattice is defined by the lattice vectors R_mn = ma₁ + na₂ (where m and n are integers and a_1,2 are the basis vectors of the array). The electric (p₀₀) and magnetic (m₀₀) dipole moments of SRR at origin position can be expressed extending equation (1) as:

$$\left(\begin{array}{c}\hfill p_{00}\hfill \\ \hfill m_{00}\hfill \end{array}\right)={[{\overleftrightarrow{\alpha }}^{-1}-{\mathrm{\Sigma }}_{m\ne 0,n\ne 0}{\overleftrightarrow{G}}^0(R_{mn})e^{i{k}_{\Vert }·R_{mn}}]}^{-1}\left(\begin{array}{c}\hfill E\hfill \\ \hfill H\hfill \end{array}\right)$$ (2)

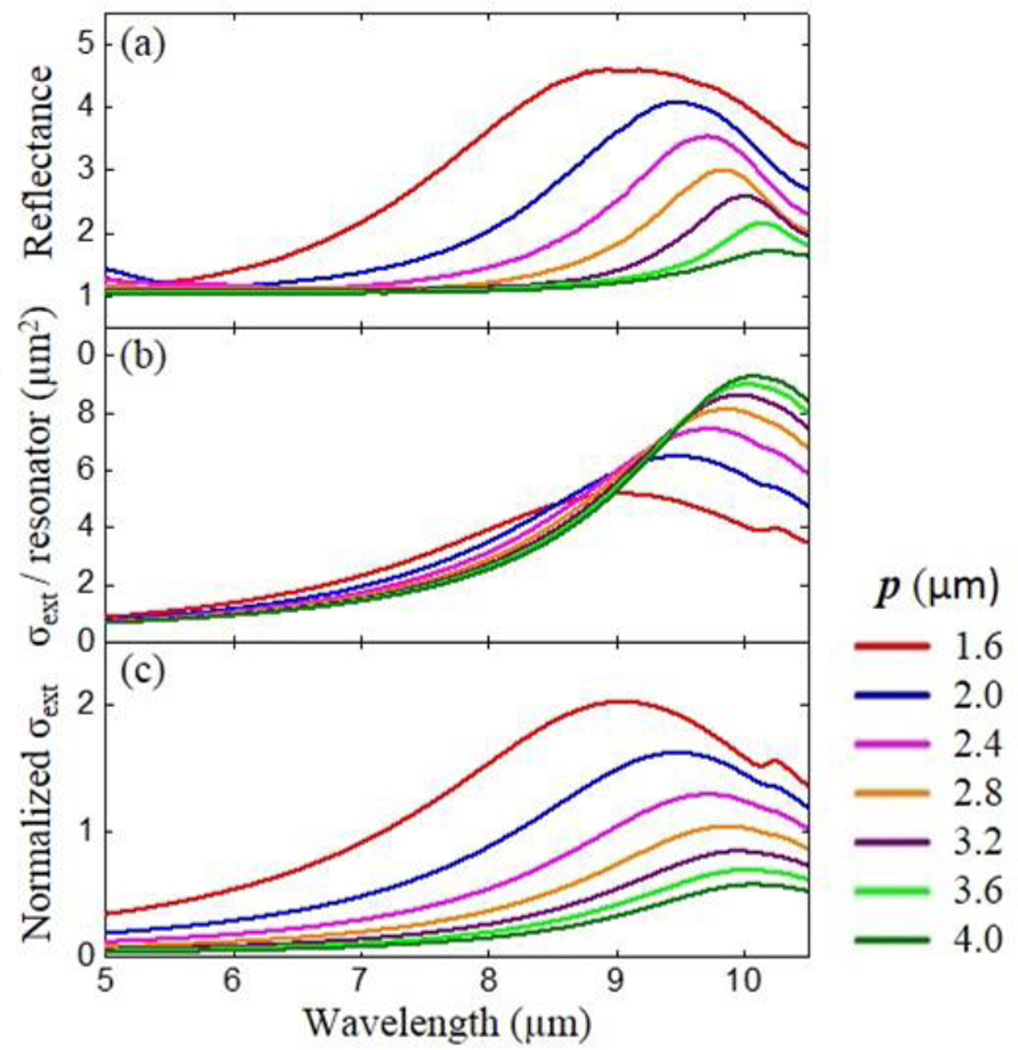
where ${\overleftrightarrow{G}}^0$ is the dyadic Green function and k is wave vector. For the calculations a set of parameters appropriate for our U-SRR was used: resonance wavelength of λ = 10.2 µm, volume V = 1.35 × 1.35 × 0.15 µm³ and dimensionless polarizability coefficients (η_E, η_H, η_C) = (0.63, 0.12 0.28) as in P. Lunnemann et. al.²⁹ We choose the resonance wavelength of 10.2 µm for isolated SRR by extrapolating the resonant wavelength obtained from the far-field FTIR spectra in Figure 4d. Figure 5a shows the FTIR reflection spectra for U-SRR arrays with different pitches and the calculated σ_ext per resonator (Figure 5b) obtained from the imaginary part of all the 11 component of effective polarizability tensor. The extinction cross section (σ_ext) of isolated SRRs has been measured in the near-IR by the spatial modulation technique^{27, 30} or in the visible by Fourier microscopy³¹ but we are not aware of similar studies in the mid-IR. The calculated σ_ext is consistent with the experimental results which show red shifting and narrowing of the plasmonic peak for larger p. However, the maximum of the calculated σ_ext increases in intensity as p increases. In contrast, the maximum of the reflection spectra decreases in intensity as the pitch increases because of the lower resonator density per unit area. After normalizing σ_ext by the unit cell area of each arrays (Figure 5c), we obtain a good agreement with the FTIR measurements. We can summarize these results as follows: in the near-field, the stronger response is obtained for isolated resonators, but in the far-field the higher density of resonators in closely packed arrays overcompensates the reduction in the resonator’s cross section and yields the stronger response. Using a different formalism, the reduction in the resonator cross-section can be alternatively described by the destructive interference due to the excitation of resonators that are out of phase with the light scattered by neighboring resonators.¹⁴ It is important to note that for cases where p ≈ λ/n_eff (not studied here), special conditions will occur as a function of the light incident angle, analyte refractive index and wavelength, along particular in plane directions where the resonators are all excited in phase, giving raise to larger SEIRA enhancements.¹⁴ The collective excitation of plasmonic structure is typically characterized by very sharp plasmonic resonances that provide greater sensitivity across a narrower spectral range.^{14, 22} Because one of the benefits of IR spectroscopy, and the main driver of our work, is the identification of chemical composition of unknown samples, determining the particular combinations of structure, pitch, wavelength, incidence angle and sample refractive index leading to the maximum constructive interference is not our main goal. We also note that the FTIR setup used here that illuminates the sample with a wide range of incident angles simultaneously (see experimental) and the nature of the samples (continuous PMMA films) which display rapid variation of the refractive index as a function of wavelength⁵⁴ (in correspondence of absorption peaks) are not ideal for that purpose.

Figure 5.

(a) FTIR spectra in U-SRR arrays (the same data in Figure 4d with different scale). (b) Theoretical calculation of the extinction cross section per resonator (c) theoretical calculation of the extinction cross section normalized by unit cell area of the U-SRR array.

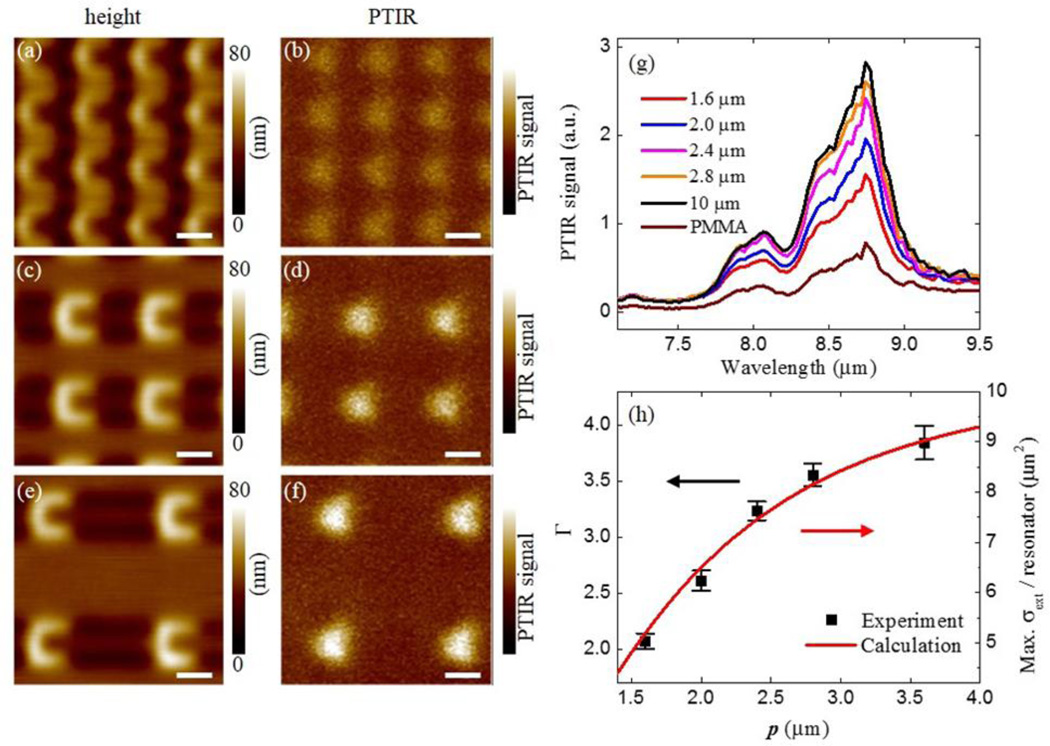
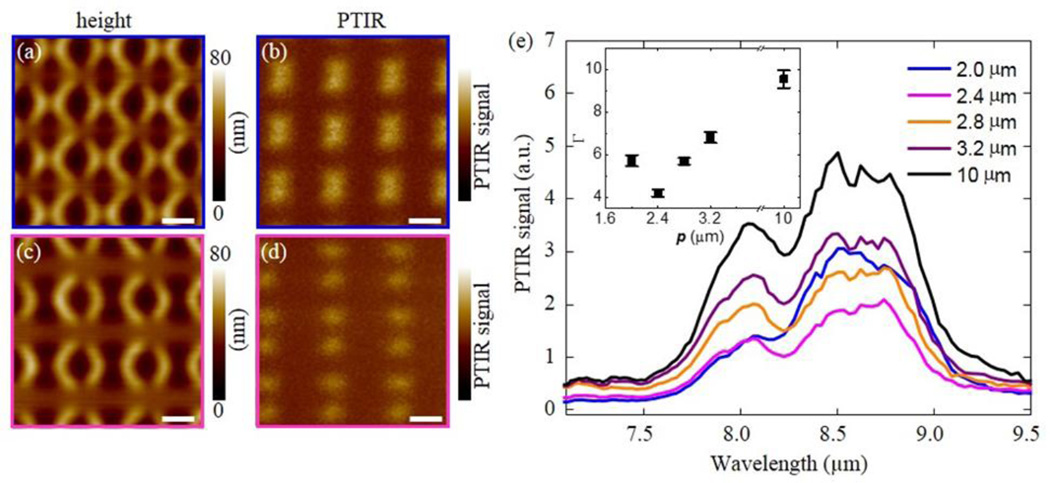
After coating these U-SRR samples with PMMA, the PTIR images and spectra clearly show that the hot-spot intensity becomes stronger as the pitch is increased and saturates at the value for the isolated resonator (Figure 6). We define the local SEIRA enhancement factor (Γ) as the ratio of the PTIR signal intensity in the hot-spot with respect to the PTIR signal intensity in PMMA film away from the resonators. Figure 6h compares the experimentally determined values of Γ at 8.75 µm (corresponding to PMMA vibrational absorption) with the calculated maximum value for σ_ext as a function of p. The good agreement between the two quantities suggests that the near-field response is directly proportional to σ_ext. In contrast, the near-field SEIRA enhancement in A-SRR arrays was found to be a non-monotonic function of p (Figure 7) because for the most closely packed array (Figure 7a, b) the hot-spots intensity of neighboring resonators overlaps. The increased PTIR signal in closely packed array is also clearly observed in PTIR spectra (Figure 7e). Because the dimensionless polarizability coefficients required by the magneto-electric point scattering theory for resonators of arbitrary shape are not available in the literature, this results highlight the utility of the PTIR analysis for characterizing the near-field response of plasmonic resonators.

Figure 6.

(a)–(f) Height (left column) and PTIR (right column) images in U-SRR arrays with pitches of 1.6 µm (a, b), 2.4 µm (c, d) and 3.6 µm (e, f). PTIR images were obtained at 8.75 µm (1142 cm⁻¹). PTIR images are displayed with same intensity scale and all scale bars are 1 µm. (g) PTIR spectra in U-SRR arrays with different pitches measured at hot-spot location and in the bare PMMA film away from the resonators. (h) Comparison between PTIR enhancement factors (Γ) for the near-field hotspots at 8.75 µm and theoretical calculation of extinction cross section per resonator from Figure 5b. The uncertainty in enhancement factor represent a single standard deviation in the measurement of the PTIR spectral intensity ratio with respect to the PMMA reference.

Figure 7.

(a) Height (left column) and PTIR (right column) images in A-SRR arrays with pitches of 2.0 µm (a, b) and 2.4 µm (c, d). PTIR images are obtained at 8.75 µm (1142 cm⁻¹). The PTIR images are displayed with the same intensity scale and all scale bars are 1 µm. (e) PTIR spectra in A-SRR arrays with different pitches measured at the hot-spot locations. The inset displays the enhancement factors (Γ) for the near-field hotspots at 8.75 µm. The uncertainty in enhancement factor represent a single standard deviation in the measurement of the PTIR spectral intensity ratio with respect to the PMMA reference.

PTIR data obtained on plasmonic arrays composed of resonators of the same size and shape and density but with different arrangements are compared in figure S1-Sn of the supporting information. The PTIR spectra recorded in correspondence of the SEIRA hot-spot locations show a weak influence of the resonator arrangement on the near-field SEIRA enhancement, suggesting that the effect of the higher order interactions between the resonators should be small and that the magnetic scattering theory provides a good approximation to describe the optical response of these resonators.

Conclusion

SRRs arrays with different shapes, pitches and arrangements displaying plasmonic resonances in the mid-IR were fabricated and measured in the near- and far-field. The PTIR technique was used to measure SEIRA enhancement maps and spectra in the near-field. Results for isolated resonators show that that the near-field enhancement is strongly dependent on the shape of the SRR. In the conditions of the PTIR experiments (45° incident light from the dielectric side) A-SRRs show the strongest near-field SEIRA enhancement. Calculations for U-shaped resonators arranged in a square lattice show that the inter-resonator dipole-dipole interactions in closed packed arrays reduces the extinction cross section per resonator. Consistently, PTIR spectra and maps show that the near-field SEIRA enhancement increases as a function of the pitch saturating to the case of the isolated resonator. Far-field FTIR ensemble spectra show that the higher density of resonators in arrays with a smaller pitch overcompensates the reduction in the resonator cross section and provides the strongest response. For A-SRR square arrays, the near-field SEIRA enhancement is non-monotonic function of pitch thanks to the overlap of hot-spots belonging to neighboring resonators for arrays with a small pitch. These results highlight the merits of the PTIR measurements for evaluating the contributions of individual resonators and inter-resonator interactions to the SEIRA enhancement in the near-field.

Experimental

Nanostructures Fabrication

All chemicals were used as received without further purification. Resonators arrays were fabricated directly on ZnSe right angle prisms, which were cleaned in an ultrasonic bath with acetone (1 min) and isopropyl alcohol (1 min) followed by oxygen plasma cleaning (15 min). A PMMA bilayer (250 nm and 300 nm) positive electron beam resist was spun (25 Hz) using a custom adaptor⁴¹ and cured (140 °C for 15 min and 30 min respectively) before depositing an aluminum charge dissipation layer (30 nm ± 5 nm) with an electron-beam evaporator. The resonator arrays were written with electron beam lithography (100 kV accelerating voltage, 1000 µC/cm² electron beam dose) using another custom adaptor.⁴¹ The aluminum layer was then removed using an aqueous tetramethylammonium hydroxide (2.4 % volume fraction) solution and the pattern was developed in a mixture of methyl iso-butylketone and isopropyl alcohol. A thin chromium adhesion layer (≈ 5 nm) and a gold layer (180 nm ± 10 nm) were deposited by electron-beam deposition. Finally, the ASRRs arrays were obtained after lift of inin N-methyl-2-pyrrolidone PMMA remover. All arrays have dimensions of 300 µm by 300 µm. After preliminary characterization, a 200 nm PMMA film was spun coated on the resonators arrays.

FTIR characterization

Far-field Fourier transform infrared (FTIR) reflectance spectra were recorded with an IR microscope equipped with a 36× reverse Cassegrain objective (NA = 0.52) which illuminates the sample from all directions at angles between 15° and 30° from the sample normal. Light polarization was controlled with wire grid polarizer to have the electric field linearly polarized in the direction (vertical) indicated by the arrows in Fig. 1 (a) for all samples. The spectra were collected through a fixed aperture of 200 µm × 200 µm. Consequently the number of resonators sampled depends on the density of the resonators in the array. 128 spectra (4 cm⁻¹ resolution) were acquired and averaged for each sample.

PTIR characterization

PTIR experiments were carried out using a commercial PTIR setup that consists of an AFM microscope operating in contact mode and a wavelength tunable (from 2.5 µm to 9.76 µm) pulsed laser source (maximum energy per pulse used was 0.4 µJ) The laser consist of an optical parametric oscillator based on a non-critically phase-matched ZnGeP₂ crystal. A set of three motorized mirrors was used in to control the light polarization at the sample. Although the laser spot size at the sample is large (≈ 30 µm), the AFM cantilever provides nanoscale spatial resolution by transducing locally the small sample expansion in large cantilever oscillations. The low repetition rate of the laser (1 kHz) assures that a new pulse excites the sample and cantilever after they have returned to equilibrium. The acquisition of the sample topography and PTIR maps was synchronized so that to each AFM pixel correspond a PTIR pixel obtained by averaging 32 consecutive laser pulses. The pixel size was 50 nm × 50 nm in all PTIR images. PTIR spectra were obtained by averaging the cantilever deflection amplitude of 256 individual laser pulses at each wavelength to increase the signal to noise ratio. The spectra were obtained by tuning the laser at intervals of 4 cm⁻¹. PTIR spectra of 4 to 8 individual hot-spots were measured and averaged to compare the near-field SEIRA enhancements of different SRR arrays. Because the two A-SRRs centered rectangular arrays were fabricated separately on different substrates, as opposed to the other samples groups which were obtained together in one fabrication process, a normalization procedure of the hot-spot intensity was necessary to account for sample to sample thickness variation. First, to account for sample-to-sample PMMA thickness variations, the PMMA spectrum obtained 100 µm away from the resonators from one sample was used as a reference and the equivalent PMMA spectrum from the other sample was normalized in its respect to yield a spectral scaling factor. To compensate the sample to sample variations for the gold thickness and shape, the spectra were further normalized with respect to the hot-spot intensity of nominally identical square arrays on each samples. Commercially available 450 µm long silicon contact-mode AFM probes with a nominal spring constant between 0.07 N/m and 0.4 N/m were used for this study.