Molecular dynamics of protein A and a WW domain with a united-residue model including hydrodynamic interaction

Abstract

The folding of the N-terminal part of the B-domain of staphylococcal protein A (PDB ID: 1BDD, a 46-residue three-α-helix bundle) and the formin-binding protein 28 WW domain (PDB ID: 1E0L, a 37-residue three-stranded anti-parallel β protein) was studied by means of Langevin dynamics with the coarse-grained UNRES force field to assess the influence of hydrodynamic interactions on protein-folding pathways and kinetics. The unfolded, intermediate, and native-like structures were identified by cluster analysis, and multi-exponential functions were fitted to the time dependence of the fractions of native and intermediate structures, respectively, to determine bulk kinetics. It was found that introducing hydrodynamic interactions slows down both the formation of an intermediate state and the transition from the collapsed structures to the final native-like structures by creating multiple kinetic traps. Therefore, introducing hydrodynamic interactions considerably slows the folding, as opposed to the results obtained from earlier studies with the use of Gō-like models.

I. INTRODUCTION

The development of physics-based methods to study protein folding and to predict protein structures continues to be an important field of computational biology.^1–9 Coarse-grained models are of great interest in the field because they enable us to extend the time- and size-scale of simulations by orders of magnitude.^10–13 However, coarse-grained representation usually makes use of implicit solvent. The potential energy contribution from interactions of the protein molecules with the solvent is usually included in the effective coarse-grained potentials but, apart from this, the solvent influences folding dynamics through the friction and stochastic forces. These are usually accounted for by a Langevin-dynamics treatment, in which each site experiences the non-conservative forces from the solvent individually. However, these forces also lead to a solvent-mediated apparent drag of two objects moving through a liquid, which is known as hydrodynamic interactions (HIs).^14–16 These interactions can be accounted for by introducing a non-diagonal matrix of friction coefficients, referred to as, e.g., the Rotne-Prager (RP) tensor¹⁷ and its modification, the Rotne-Prager-Yamakawa (RPY) tensor,^17,18 whose off-diagonal elements depend on the distances between the objects involved.

The influence of HIs on polymer collapse^19–21 was studied by modeling a polymer chain as beads connected by a finitely extendable nonlinear elastic potential, with an effective interaction potential represented by the Lennard-Jones function. This model showed that the introduction of HIs sped up polymer collapse.^20,21 This effect was also observed by Chang and Yethiraj¹⁹ who found that, without HIs, the compact polymer globule could not be formed, and the system got trapped in a non-ergodic metastable state.

The role of HIs in protein folding has been discussed by Tanaka,¹⁴ who suggested that HIs could have a major effect on protein-folding pathways, as well as on the final state. HIs in proteins, modeled by using the RPY tensor, were investigated with Gō-like models and Brownian Dynamics (BD) with the use of the Ermak-McCammon algorithm.²² In that work, HIs were found to speed up folding by a factor of 2 to 3 for proteins composed of 56 to 149 residues. On the other hand, the decrease of the folding rate of the individual secondary-structure elements, the α-helix and the β-hairpin (16-residues-long), was observed.¹⁶ Similar results were obtained by Cieplak and Niewieczerzał.¹⁵ They suggested that the acceleration is due to faster initial collapse. However, those investigations concerned Gō-like protein models, in which the interaction pattern is highly simplified; the interaction potentials have minima for native long-range interactions and are repulsive-only for non-native interactions while, in reality, the character of long-range residue-residue interactions depends only on the kinds of residues involved.

HIs were also conceptualized as interactions that occur between molecules. With the use of BD simulations and the RPY tensor, Ando and Skolnick found²³ that, in the crowded cell interior, the decrease of the diffusion coefficients for macromolecules, compared to infinitely dilute water solution, is most likely caused by HIs and excluded-volume effects. The influence of intermolecular HIs on other biological phenomena such as formation of lipid membranes,²⁴ protein-protein association,²⁵ the sliding motion of protein along DNA,²⁶ and the diffusion processes within an idealized biological cell²⁷ was also studied.

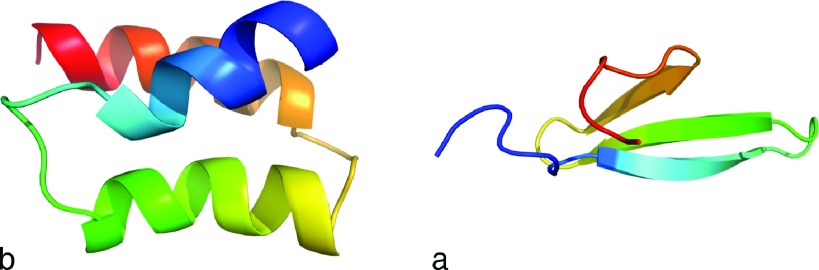
For many years, we have been developing a physics-based coarse-grained force field for the simulation of protein structure and dynamics.^28–34 We implemented Langevin dynamics in UNRES^35,36 to study protein folding. Despite the medium resolution of the force field resulting from the coarse-grained nature of the UNRES model, it proved successful in protein-structure prediction,^37–40 in simulations of the pathways, kinetics, and free-energy landscapes of protein folding,^41–44 effect of mutation on protein folding and stability,^45,46 as well as in studying biologically important processes.^7,47–50 In the study reported here, as an attempt to find a realistic mean-field description of the dynamic effect of the solvent, we introduced HIs in UNRES Langevin dynamics and assessed the effect of these interactions on the pathways and kinetics of folding of two small proteins, the N-terminal domain of staphylococcal protein A, which has the structure of a three-α-helix bundle (PDB ID: 1BDD; 46 residues)⁵¹ and a formin-binding protein WW domain, which is a three-stranded anti-parallel β-sheet (PDB ID: 1E0L; 37 residues).⁵² The experimental structures of these two proteins are shown in Figure 1. These proteins will hereafter be referred to by their PDB IDs.

FIG. 1.

Cartoon representation of model 1 of NMR experimental structures of the (a) 1BDD and (b) 1E0L.

II. METHODS

A. The UNRES force field

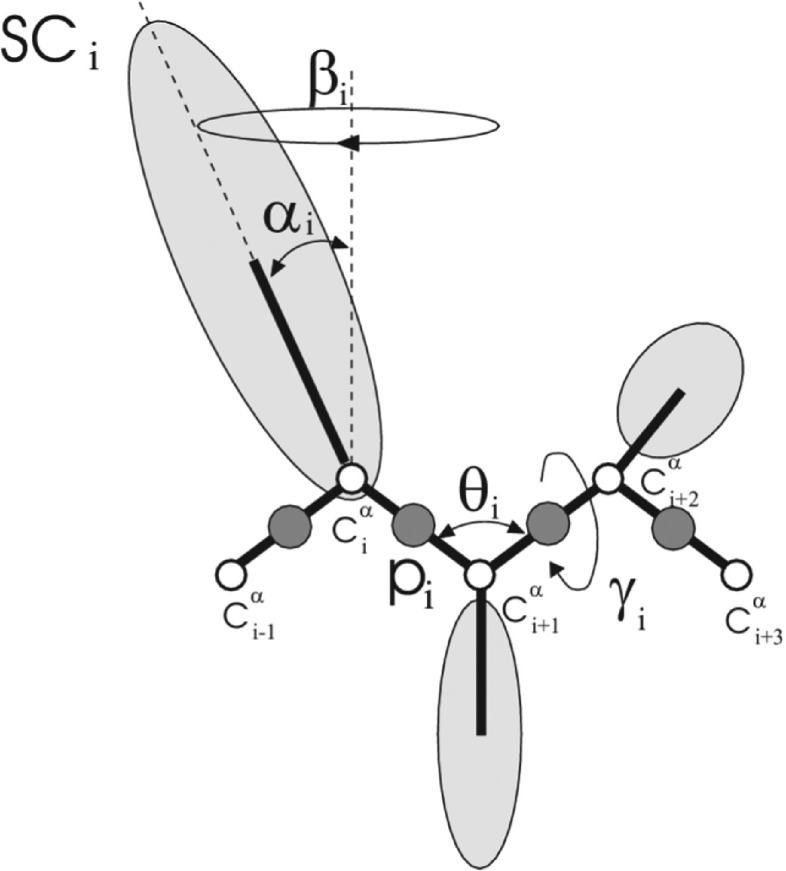
In the UNRES model,^28–34 Figure 2, a polypeptide backbone is represented as a sequence of α-carbon (C^α) atoms linked by virtual bonds. A peptide group (p) is placed in the middle of each backbone virtual bond and a side chain (SC) is attached to the respective C^α atom. Only the peptide groups and the side chains are interaction sites and the C^αs serve to define the geometry.

FIG. 2.

The UNRES model of the polypeptide chain. Dark circles represent united peptide groups (p), white circles represent the C^α atoms, which serve as geometric points, and ellipsoids represent side chains (SCs). The p’s are located half-way between two consecutive C^α atoms. The virtual-bond angles θ, the virtual-bond dihedral angles γ, and the angles α_SC and β_SC that define the location of a side chain with respect to the backbone are also indicated.

The UNRES energy function is expressed by

$${\displaystyle U=w_{\mathit{SC}}\sum _{i<j}{U}_{{\mathit{SC}}_{i}S{C}_j}+w_{\mathit{SC}p}\sum _{i\ne j}{U}_{{\mathit{SC}}_i{p}_j}+w_{pp}^{VDW}\sum _{i<j-1}{U}_{p_i{p}_j}^{VDW}+w_{pp}^{el}{f}_2\left(T\right)\sum _{i<j-1}{U}_{p_i{p}_j}^{el}+w_{\mathit{tor}}{f}_2\left(T\right)\sum _i{U}_{\mathit{tor}}\left({\gamma }_i\right)+w_{\mathit{tor}d}{f}_3\left(T\right)\sum _i{U}_{\mathit{tor}d}({\gamma }_i,{\gamma }_{i+1})+w_b\sum _i{U}_b\left({\theta }_i\right)+w_{\mathit{rot}}\sum _i{U}_{\mathit{rot}}({\alpha }_{{\mathit{SC}}_i},{\beta }_{{\mathit{SC}}_i})+w_{\mathit{bond}}\sum _i{U}_{\mathit{bond}}\left(d_i\right)+w_{\mathit{corr}}^{\left(3\right)}{f}_3\left(T\right)U_{\mathit{corr}}^{\left(3\right)}+w_{\mathit{corr}}^{\left(4\right)}{f}_4\left(T\right)U_{\mathit{corr}}^{\left(4\right)}+w_{\mathit{turn}}^{\left(3\right)}{f}_3\left(T\right)U_{\mathit{turn}}^{\left(3\right)}+w_{\mathit{turn}}^{\left(4\right)}{f}_4\left(T\right)U_{\mathit{turn}}^{\left(4\right)},}$$ (1)

where θ_i is the ith backbone virtual-bond angle, γ_i is the ith backbone virtual-bond-dihedral angle, α_i and β_i are the polar angles defining the location of the united side-chain center of residue i, and d_i is the length of the ith virtual bond, which is either a C^α⋯C^α virtual bond or a C^α⋯SC virtual bond, Figure 2. Each energy term, U, is multiplied by an appropriate weight, w_x, and the terms corresponding to factors of order higher than 1 are additionally multiplied by the respective temperature factors, f_n(T),^30,53 defined by

$${\displaystyle f_n\left(T\right)=\frac{ln\left[exp\left(1\right)+exp(-1)\right]}{ln\left\{exp\left[{\left(T/T_{\circ }\right)}^{n-1}\right]+exp\left[-{\left(T/T_{\circ }\right)}^{n-1}\right]\right\}},}$$ (2)

where T_∘ = 300 K.

In this study, two versions of the UNRES force field that differ in terms of parameterization were used; one was calibrated with the albumin-binding GA module (PDB ID: 1GAB⁵⁴),³⁰ and the second one was calibrated with the engrailed homeodomain (PDB ID: 1ENH⁵⁵) and the Fbp28 WW domain (PDB ID: 1E0L⁵²)³³ for simulations of 1BDD and 1E0L protein, respectively. Although recently⁵⁶ we parameterized a version of UNRES with better transferability, these two versions were already used with success in protein-folding studies.^42–46

B. Langevin dynamics

The implementation of Langevin dynamics to the UNRES model has been described in earlier work.³⁶ The Langevin equations of motion in virtual bond coordinates are given by Eq. (3). Briefly, the variables are the C^α⋯C^α and C^α⋯SC virtual-bond vectors, denoted by dC_∘, dC₁, dC₂,…, dC_n−1 (where ${\mathbf{dC}}_{\mathbf{i}}\mathbf{=}{\mathbf{r}}_{{\mathbf{C}}_{\mathbf{i}\mathbf{+1}}^{\mathbf{\alpha }}}\mathbf{-}{\mathbf{r}}_{{\mathbf{C}}_{\mathbf{i}}^{\mathbf{\alpha }}}\mathbf{,}$ ${\mathbf{r}}_{{\mathbf{C}}_{\mathbf{i}}^{\mathbf{\alpha }}}$ denotes the Cartesian coordinates of the ith C^α atom and $\mathbf{d}{C}_{\circ }=r_{C_1^{\alpha }}$ places the first C^α atom in the coordinate system) and dX₂, dX₂, … , dX_n−1 (where ${\mathbf{dX}}_{\mathbf{i}}\mathbf{=}{\mathbf{r}}_{{\mathbf{SC}}_{\mathbf{i}}}\mathbf{-}{\mathbf{r}}_{{\mathbf{C}}_{\mathbf{i}}^{\mathbf{\alpha }}}$). These vectors are combined into the vectors of generalized coordinates, $\mathbf{q}={\left[{\mathbf{dC}}_{\mathbf{\circ }}\mathbf{,}\hspace{0.17em}{\mathbf{dC}}_{\mathbf{1}}\mathbf{,}\hspace{0.17em}{\mathbf{dC}}_{\mathbf{2}}\mathbf{,}\mathbf{\dots }\mathbf{,}\hspace{0.17em}{\mathbf{dC}}_{\mathbf{n}\mathbf{-1}}\mathbf{,}\hspace{0.17em}{\mathbf{dX}}_{\mathbf{2}}\mathbf{,}\hspace{0.17em}{\mathbf{dX}}_{\mathbf{2}}\mathbf{,}\mathbf{\dots }\mathbf{,}\hspace{0.17em}{\mathbf{dX}}_{\mathbf{n}\mathbf{-1}}\right]}^{\mathbf{T}}$

$${\displaystyle \mathbf{G}\ddot{\mathbf{q}}=-\nabla U\left(\mathbf{q}\right)+{\mathbf{f}}^{\mathbf{fric}}+{\mathbf{f}}^{\mathbf{rand}},}$$ (3)

where the inertia-matrix G is defined by

$${\displaystyle \mathbf{G}={\mathbf{A}}^{\mathbf{T}}\mathbf{MA}+\mathbf{H},}$$ (4)

where M is a diagonal matrix of the masses of all the interacting sites, and H is a diagonal matrix (part of the inertia matrix corresponding to the internal stretching motions of the virtual bonds). A is the matrix that transforms the virtual-bond coordinates to Cartesian coordinates. The frictional force in virtual bond coordinates is given by

$${\displaystyle {\mathbf{f}}^{\mathbf{fric}}=-{\mathbf{A}}^{\mathbf{T}}\mathbf{\Gamma }\mathbf{A}\dot{\mathbf{q}},}$$ (5)

where, in the absence of HIs, the friction super-matrix is given by

$${\displaystyle \mathbf{\Gamma }=\left[\begin{array}{cccc}\hfill {\gamma }_1\mathbf{I}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\gamma }_2\mathbf{I}\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill {\gamma }_N\mathbf{I}\hfill \end{array}\right],}$$ (6)

where I is a 3 × 3 identity matrix and the friction coefficient for the ith site and γ_i is calculated from the Stokes equation as follows:

$${\displaystyle {\gamma }_i=6\pi (R_i+R_w){\eta }_w,}$$ (7)

where R_i and R_w are the radii of the site and water, respectively, and η_w is the water viscosity. Thus, for the purpose of the calculation of the friction and stochastic forces, each site is modeled as a sphere.³⁶

In Langevin stochastic dynamics, the temperature is kept constant (on average) by applying frictional (damping) forces along with the compensating stochastic forces to the force centers. The average stochastic forces are related to the frictional forces by the fluctuation-dissipation theorem.⁵⁷ This model closely mirrors the physical dynamics of the system, i.e., the stochastic forces model the solvent molecules impinging against the protein, and the frictional forces model the Stokes drag (also due to the solvent) on each interaction site. Therefore, to obtain the information about protein dynamical motions, kinetics, and pathways, this model is an appropriate one to choose.

C. Introduction of hydrodynamic interactions into the UNRES force field

The HIs between unequal virtual-spheres representing the SCs and ps are modeled by the use of the RP tensor, and empirical averages are used for the radii of the spheres.^58,59 To compute the hydrodynamic drag, both the SCs and ps will be considered as virtual spheres that experience a Stokes drag from the solvent. This approximation had been used in previous investigations of the effect of HIs on protein folding.¹⁶

As each spherical site (SC or p) moves through the solvent, it creates a wake in the solvent that will perturb all surrounding force centers. This perturbing force is referred to as the HI force. It does not alter the form of the UNRES potential since the UNRES potential contains all the conservative forces acting on the coarse-grained model of the protein while the HIs modify the non-conservative damping term in the Langevin equation. A molecular dynamics (MD) study of the motion of a sphere in a viscous Lennard-Jones fluid has shown that the results of continuum hydrodynamics work even if the sphere is comparable in size to that of the fluid molecules.⁶⁰ This justifies the use of continuum fluid equations to calculate the HIs.

The effective radii for virtual spheres representing the amino-acid side chains have been taken from Levitt.⁶¹ The effective radius for the peptide group (p) was set to 5 Å, based on the van der Waals radius of the peptide group. This radius was estimated from calculations of potential of mean force surfaces for interacting peptide groups.⁶²

The force ${\mathbf{f}}_{\mathbf{i}}^{\mathbf{h}}$ that the solvent exerts on the ith particle is determined, in general, by the instantaneous momentum p_i and position r_i of all the N particles in the solvent,

$${\displaystyle {\mathbf{f}}_{\mathbf{i}}^{\mathbf{h}}=f_i^h({\mathbf{p}}_{\mathbf{i}}\left(t\right),\dots ,{\mathbf{p}}_{\mathbf{N}}\left(t\right),{\mathbf{r}}_{\mathbf{i}}\left(t\right),\dots ,{\mathbf{r}}_{\mathbf{N}}\left(t\right)).}$$ (8)

The superscript h indicates a hydrodynamic force. In our system, the N particles are virtual spheres representing ps and the SCs. For the fluid dynamics of the protein-solvent HIs, the Navier-Stokes equation, for typical diameters and velocities of the virtual spheres, and typical solvent viscosity, can be linearized allowing one to write the hydrodynamic forces as linear functions of the velocities,⁶³

$${\displaystyle {\mathbf{f}}_{\mathbf{i}}^{\mathbf{h}}=-\sum _{j=1}^N{\mathbf{\Gamma }}_{\mathbf{ij}}({\mathbf{r}}_{\mathbf{1}},{\mathbf{r}}_{\mathbf{2}},\dots ,{\mathbf{r}}_{\mathbf{N}}){\mathbf{v}}_{\mathbf{j}},}$$ (9)

where Γ is the 3 × 3 microscopic friction tensor. In a very dilute solution, there is approximately no HI between any of the virtual spheres. Therefore, Eq. (5) reduces to

$${\displaystyle {\mathbf{f}}_{\mathbf{i}}^{\mathbf{h}}=-\gamma {\mathbf{v}}_{\mathbf{i}},}$$ (10)

where γ is the friction coefficient for isolated (i.e., hydrodynamically uncoupled) virtual spheres. This is the form for the friction in the unmodified UNRES-MD algorithm.³⁶

To first order HIs, for large separations between the force centers, it can be taken into account by modification of the off diagonal elements as follows:

$${\displaystyle \left[\begin{array}{c}\hfill {\mathbf{v}}_{\mathbf{1}}\hfill \\ \hfill {\mathbf{v}}_{\mathbf{2}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{v}}_{\mathbf{N}}\hfill \end{array}\right]=-\beta \left[\begin{array}{cccc}\hfill {\mathbf{D}}_{\mathbf{11}}\hfill & \hfill {\mathbf{D}}_{\mathbf{12}}\hfill & \hfill \dots \hfill & \hfill {\mathbf{D}}_{\mathbf{1N}}\hfill \\ \hfill {\mathbf{D}}_{\mathbf{21}}\hfill & \hfill {\mathbf{D}}_{\mathbf{22}}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill {\mathbf{D}}_{\mathbf{N1}}\hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathbf{D}}_{\mathbf{NN}}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{f}}_{\mathbf{1}}^{\mathbf{h}}\hfill \\ \hfill {\mathbf{f}}_{\mathbf{2}}^{\mathbf{h}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{f}}_{\mathbf{N}}^{\mathbf{h}}\hfill \end{array}\right],}$$ (11)

where the D_ijs are the 3 × 3 diffusion tensors, put into a 3N × 3N diffusion super-matrix to relate velocity, v_i, of each force center (i.e., virtual sphere), to the hydrodynamic force, ${\mathbf{f}}_{\mathbf{i}}^{\mathbf{h}}$, on each virtual sphere, and β = 1/k_BT, with Boltzmann constant k_B and temperature T.

The friction super-matrix is related to the diffusion super-matrix by a generalization of the Stokes-Einstein relation

$${\displaystyle {\mathbf{\Gamma }}^{-\mathbf{1}}=\beta \mathbf{D}.}$$ (12)

From these equations the friction super-matrix is determined.

The random forces are computed by taking the square root of the friction super-matrix³⁶ according to the fluctuation-dissipation theorem⁵⁷

$${\displaystyle {\mathbf{f}}^{\mathbf{rand}}=\sqrt{\frac{2RT}{\delta t}}{\mathbf{A}}^{\mathbf{T}}{\mathrm{\Gamma }}^{1/2}\mathbf{N}(0,1),}$$ (13)

where δt is the size of the time step, and N(0, 1) is a multi-dimensional normal distribution with zero mean and unit variance.

Two specific forms for the interaction tensor will be considered. The first form assumes that the perturbing force at point j can be considered to be a point force. This assumption, along with the two approximations (Stokes’ equation and incompressibility), enables us to solve for the HI tensor analytically. The result is the Oseen-Burgers tensor^64,65

$${\displaystyle \mathbf{D}=\frac{kT}{8\pi \mu r}(\delta +{\delta }_{\mathbf{r}}\otimes {\delta }_{\mathbf{r}}),}$$ (14)

where δ is a unit tensor of dimension 3 × 3, δ_r is a unit vector pointing from the point where a force makes a disturbance in the solvent to the field point where the resulting disturbance is determined, δ_r ⊗ δ_r is a dyad of δ_r; r is the distance between these two points, and μ is the solvent viscosity. Mathematically, since the perturbing force can be represented as a Dirac-delta function, the Oseen-Burgers tensor is the Green function for the Stokes equation for incompressible flow and fluid dynamics similar to that found in protein dynamics.⁶⁶

A second form of the interaction tensor extends Eq. (14) to consider the perturbing sphere to have a finite radius, in which case the interaction tensor is the generalized RPY tensor.¹⁷ The interaction tensor for spheres of unequal radii a_i, a_j that are non-overlapping^17,18,58 is

$${\displaystyle \mathbf{D}=\frac{1}{8\pi \mu r}[(\mathbf{I}+\frac{{\delta }_{\mathbf{r}}\otimes {\delta }_{\mathbf{r}}}{r^2})+\left(\frac{a_i^2+a_j^2}{r^2}\right)(\frac{1}{3}\mathbf{I}-\frac{{\delta }_{\mathbf{r}}\otimes {\delta }_{\mathbf{r}}}{r^2})]\mathit{if}r\ge a_i+a_j.}$$ (15)

In the case of overlapping unequal virtual spheres, one modifies the RP tensor⁶⁶ to

$${\displaystyle \mathbf{D}=\frac{1}{6\pi \mu a_{ij}}[(1-\frac{9}{32}\frac{r}{a_{ij}})\mathbf{I}+\frac{3}{32}\frac{{\delta }_{\mathbf{r}}\otimes {\delta }_{\mathbf{r}}}{r{a}_{ij}}]\mathit{if}r<a_i+a_j}$$ (16)

with an average radius a_ij proposed on an empirical basis.⁶⁷ In this paper, a cubic average radius, $a_{ij}={\left(\frac{{a_i}^3+a_j^3}{2}\right)}^{1/3}$, is used when the virtual-spheres overlap.

The purpose of using the RP tensor instead of the simpler Oseen-Burgers tensor is to ensure that the friction matrix remains positive-definite. This is important so that we can take the square root of this matrix to find the stochastic forces according to the fluctuation-dissipation theorem as indicated by Eq. (13). It can be proven that the RP tensor is positive-definite.⁶⁶

The diagonal term of the friction super-matrix (or diffusion super-matrix) is also altered by the inclusion of HIs since the perturbing fluid disturbance propagates away from each virtual-sphere and is reflected off all the other virtual-spheres and propagates back to the original virtual-sphere that caused the disturbance. In effect, there is a self-interaction term. On the other hand, the HIs (solvent interaction) propagate infinitely fast only for incompressible fluids.⁶⁸ In a real fluid, the HIs will propagate at the speed of sound. For typical distances between the virtual spheres in a folding protein, the HI disturbance will have insufficient time to reflect off of the adjacent virtual spheres and cause a self-interaction; therefore, the diagonal terms in Equation (4) or (9) were left unaltered.

D. Simulation and analysis procedure

To assess the effect of HIs on the folding of 1BDD and 1E0L, multi-trajectory canonical MD simulations with UNRES were carried out for each of them in the classical Langevin mode and with HIs included, at temperatures 300 K for 1BDD and 335 K for 1E0L, respectively, which are below the simulated transition mid-point temperatures equal to 320 K⁶⁹ and 339 K,⁴⁵ respectively. In summary, four series of simulations were carried out: 1BDD without HIs, 1BDD with HIs, 1E0L without HIs, and 1E0L with HIs, respectively. Each series of simulation consisted of 200 trajectories run with the 4.89 fs time step. Each trajectory was run for 1 μs UNRES time for 1BDD (both with and without HIs), 1.2 μs UNRES time for 1E0L without HIs, and 5.0 μs UNRES time for 1E0L with HIs, which corresponds to about 1, 1.2, and 5.0 ms of real time, respectively, because of averaging out secondary degrees of freedom in UNRES.^35,36 All trajectories were started from an extended structure. To speed up the simulations, the viscosity of water was scaled down by a factor of 100, as in our earlier work.^35,36

For each of the four series of simulations, hierarchical cluster analysis using Ward’s minimum variance method^70,71 was performed for every 10th trajectory in order to find possible intermediate structures or kinetic traps that might have occurred during simulation. Then the obtained families were classified based on the C^α-RMSD of the mean structure of the cluster from the experimental structure as native (C^α-RMSD below 6 Å), intermediate (C^α-RMSD between 6 and 10 Å) or unfolded (C^α-RMSD higher than 10 Å). For each cluster, the representative conformation was defined as the conformation of the cluster which had the lowest C^α-RMSD from the mean conformation of the cluster. For each of the two proteins, the representatives of the clusters of the intermediate structures corresponding to simulations without (5 clusters for 1E0L and 2 clusters for 1BDD, respectively) and with HIs (8 clusters for 1E0L and 5 clusters for 1BDD, respectively) were then compared to find possible differences between the intermediates obtained with each of the two Langevin-dynamics regimes considered. The cross-cluster C^α-RMSD values are collected in Tables I and II of the supplementary material for 1E0L and 1BDD, respectively, and the structures are superposed in Figure SM9 of the supplementary material. As can be seen from Tables I and II of the supplementary material,⁷² the RMSD values between the clusters corresponding to one (without HI or with HI) Langevin-dynamics regime do not differ from those corresponding to two different regimes; according to Student’s test,⁷³ the differences between the same- and different-regime RMSDs are insignificant. The structures of the intermediates are also similar (Figure SM9 of the supplementary material).⁷² It can, therefore, be concluded that the structure of the intermediate does not change remarkably after including HIs. Consequently, for each protein, the representative conformation of the intermediate structure was selected as the conformation closest to the mean conformation over all clusters of intermediate structures; this was the conformation with the lowest sum of cross-cluster C^α-RMSDs (shown in the bottom rows of Tables I and II of the supplementary material).⁷²

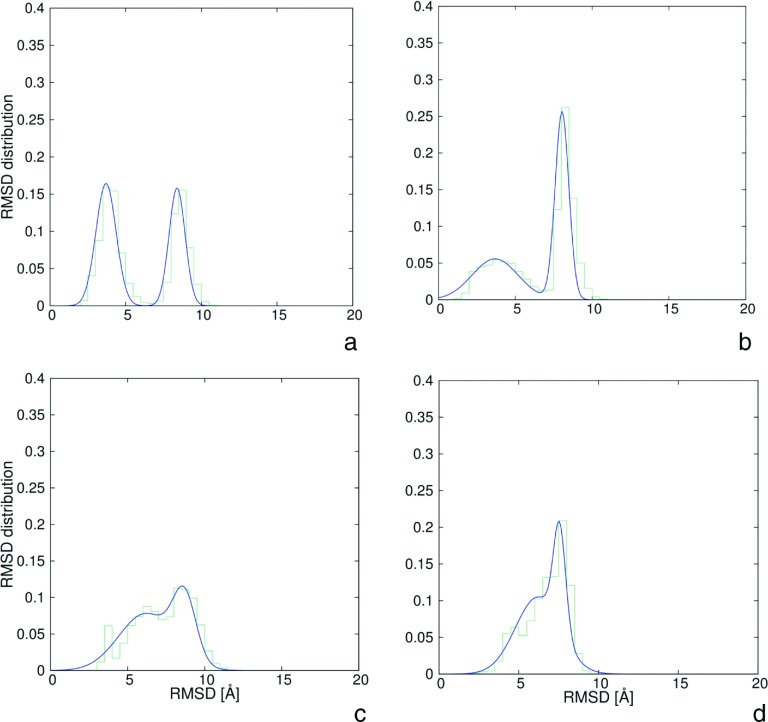
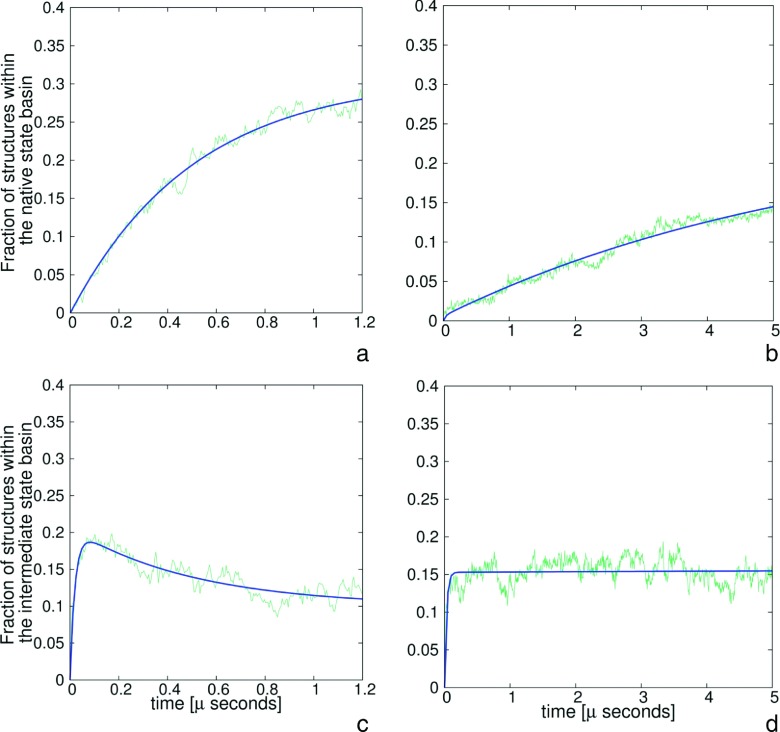
To determine the C^α-RMSD thresholds for the native and intermediate structures, the probability distributions of C^α-RMSD from the respective experimental or intermediate structures were calculated for each quarter of the simulation. For 1BDD (both with and without HIs), the time windows from 0.00 to 0.25 μs, from 0.25 to 0.50 μs, from 0.50 to 0.75 μs, and from 0.75 to 1.00 μs were set. For 1E0L without including the HIs, time windows were set from 0.0 to 0.3 μs, from 0.3 to 0.6 μs, from 0.6 to 0.9 μs, and from 0.9 to 1.2 μs, respectively, while for 1E0L with inclusion of HIs the windows were set from 0.00 to 1.25 μs, from 1.25 to 2.50 μs, from 2.50 to 3.75 μs, and from 3.75 to 5.00 μs, respectively. The C^α-RMSD bin size was set to 0.5 Å. The C^α-RMSD range of values was from 1 Å (the native or intermediate structure) to 42 Å (the extended structure). For 1BDD, the plots of the C^α-RMSD distributions from the native and from the intermediate structure, respectively, corresponding to the last time windows of simulations with inclusion of HIs (for which the intermediates last longer) are shown in Figures 3(a) and 3(b), respectively. For 1E0L, the plots are shown in Figures 3(c) and 3(d), respectively. Detailed plots of the time evolutions of the C^α-RMSD distributions are shown in the supplementary material.⁷² It can clearly be seen that two peaks are present. The first peak occurs at lower C^α-RMSD and corresponds to structures that are similar to the reference structure (native or intermediate), while the second peak corresponds to structures not similar to the respective reference structure. To facilitate the determination of the cutoffs of the reference-like structures, the distributions were fitted to a sum of two Gaussians (Eq. (17)), with the use of the nonlinear least-squares (NLLS) Marquardt-Levenberg⁷⁴ algorithm implemented in the GNUPLOT program (http://www.gnuplot.info)

$${\displaystyle f_g\left(x\right)=\sum _{i=1}^N\frac{C_i}{{\left(2\pi \right)}^{\frac{1}{2}}{\sigma }_i}exp[-\frac{{(x-{\mu }_i)}^2}{2{\sigma }_i^2}]}$$ (17)

where f_g is the fitted distribution at each time window obtained with the optimal parameters, x is the C^α-RMSD, N = 2 is the number of Gaussian terms, C_i is the multiplier for each Gaussian and represents a measure of the population of each Gaussian, and μ_i and σ_i are the mean and the standard deviation of each Gaussian, respectively.

FIG. 3.

Plots of probability distribution of C^α-RMSD values from the native and intermediate structures (green rugged lines) corresponding to the last time windows of simulations with inclusion of HIs and double-Gaussians fits to these plots (blue smooth lines) (Eq. (17)): (a) for the native structure of 1BDD, (b) for intermediate structure of 1BDD, (c) for the native structure of 1E0L, (d) for intermediate structure of 1E0L.

Based on the C^α-RMSD distributions, the cutoffs on the C^α-RMSDs from the respective experimental structures to assign a conformation to the native-structure family were set at 5.5 Å for 1BDD and 4.5 Å for 1E0L, respectively, and the cutoffs from the respective intermediate structures to assign a conformation to an intermediate-structure family were set at 5.5 Å and 5.0 Å for 1BDD and 1E0L, respectively. The cutoffs used ensured that no structure belongs to both native-like and intermediate-structure families simultaneously.

The fractions of native (f_N) or intermediate (f_I) structures as a functions of time were calculated for each of the proteins with and without HIs as averages over all 200 trajectories, as given by the following equations, respectively:

$${\displaystyle f_N\left(t\right)=\frac{n_N\left(t\right)}{n_{\mathit{traj}}},}$$ (18)

$${\displaystyle f_I\left(t\right)=\frac{n_I\left(t\right)}{n_{\mathit{traj}}},}$$ (19)

where n_N(t) is the number of trajectories for which the native conformation appears at time t, n_I(t) is the number of trajectories for which the intermediate conformation appears at time t and n_traj = 200 is the total number of trajectories.

Subsequently, biexponential functions (Eqs. (20) and (21)) were fitted, with the use of the nonlinear least-squares (NLLS) Marquardt-Levenberg⁷⁴ algorithm implemented in the GNUPLOT program (http://www.gnuplot.info), to the simulated f_N(t) and f_I(t) curves,

$${\displaystyle f_N\left(t\right)=C_1\left[1-m_{1}exp\left(-\frac{t}{{\tau }_1}\right)-(1-m_1)exp\left(-\frac{t}{{\tau }_2}\right)\right],}$$ (20)

$${\displaystyle f_I\left(t\right)=C_2\left[1-m_{2}exp\left(-\frac{t}{{\tau }_1}\right)-(1-m_2)exp\left(-\frac{t}{{\tau }_2}\right)\right],}$$ (21)

where C₁ and C₂ can be considered as the equilibrium fractions of the native and intermediate states, respectively, and τ₁ and τ₂ are the respective decay times.

III. RESULTS AND DISCUSSION

A. Effect of HIs on simulated folding

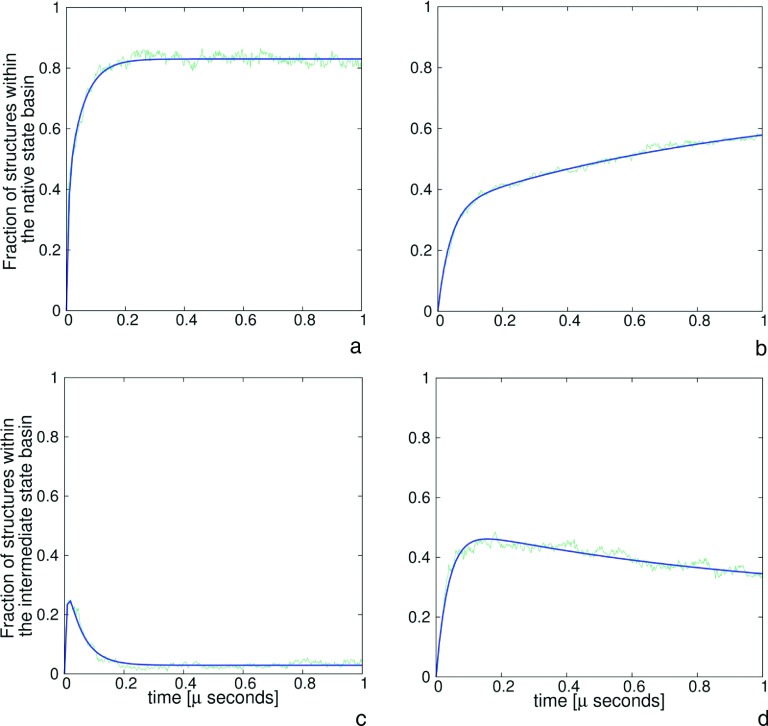
The percentages of trajectories that resulted in folded structures for all four series of simulations are collected in Table I. As can be seen, introducing HIs depletes the fraction of folded trajectories considerably. Thus, introducing HIs slows down the folding. The decrease of folding rate upon introducing HIs is apparent from Figures 4(a), 4(b), 5(a), and 5(b) in which the time evolution of the fraction of the native structure is displayed. Different results were obtained in an earlier study by Frembgen-Kesner and Elcock¹⁶ with the use of Gō-like models, in which 11 proteins with sizes comparable to those of 1BDD and 1E0L were investigated, and HIs were accounted for by using the RPY tensor. These researchers found that the overall folding rate increased 2 to 3 times. On the other hand, they also found that the rate of the formation of secondary-structure elements (α-helices and β-hairpins) decreased.

TABLE I.

The percentage of trajectories that folded to the native structure.

Protein	Percentage of folded trajectories (%)
1BDD without HIs	85
1BDD with HIs	59
1E0L without HIs	31
1E0L with HIs	15

FIG. 4.

Plots of the fractions of native ((a) and (b)) and intermediate ((c) and (d)) structures as a function of time for 1BDD protein without HIs ((a) and (c)) and with HIs ((b) and (d)). Green rugged lines present the simulated data and blue lines correspond to the fits of multi-exponential functions (Eqs. (20) and (21)).

FIG. 5.

Plots of the fractions of native ((a) and (b)) and intermediate ((c) and (d)) structures as a function of time for 1E0L without HIs ((a) and (c)) and with HIs ((b) and (d)). Green rugged lines present the simulated data and blue lines correspond to the fits of multi-exponential functions (Eqs. (20) and (21)).

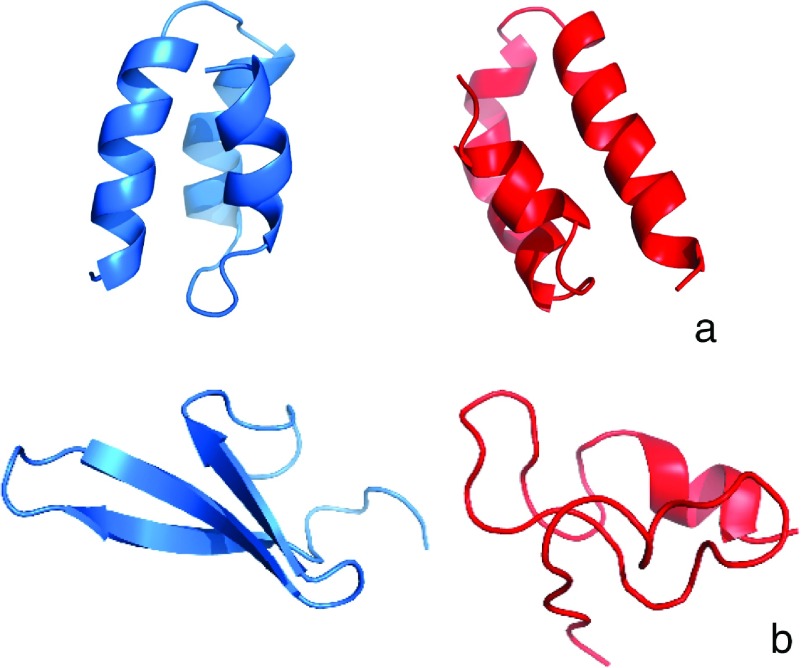
The reason for the slowing-down of the folding when HIs are included is the appearance of intermediates. These structures are shown in Figures 6(a) and 6(b) for 1BDD and 1E0L, respectively. The intermediate in the simulated folding of 1BDD is the mirror image of the native structure (Figure 6(a)); this intermediate was observed in our earlier studies of the folding of protein A with the UNRES force field^41–43 and in an all-atom study of this protein with the ECEPP/3 force field.⁷⁵ For 1E0L, the intermediate is a compact β-sheet-like structure but without regular peptide-group contacts and not well formed secondary structure except for a small α-helical section. This result is consistent with those of the NMR studies of the C-terminal β-hairpin of the IGG protein^76–78 and the N-terminal β-hairpin of the formin-binding WW domain⁷⁹ in which only hairpin-like structures without hydrogen bonds or even short α-helical sections were observed depending on temperature. Also, the C-terminus is bent in the opposite direction compared to the native structure (Figure 6(b)). Such structures were observed in our earlier studies of the free-energy landscapes of the folding of 1E0L and its mutants.^44–46

FIG. 6.

Comparisons of the native (blue) and intermediate (red) structures of (a) 1BDD and (b) 1E0L proteins.

Figures 4(c) and 4(d) show the time evolution of the fractions of the intermediate for 1BDD in the plain-Langevin and Langevin-with-HI simulations, while Figures 5(c) and 5(d) show the fractions of the intermediate for 1E0L. It can be seen that, for 1BDD simulations without HIs (Figure 4(c)), the fraction of the intermediate increases sharply during the first 200 ps of simulations and then decreases quickly. Conversely, inclusion of HIs results in very slow decay of the intermediate (Figure 4(d)). For 1E0L, the intermediate decays very slowly even in plain-Langevin simulations (Figure 5(c)) and effectively reaches a steady state when the HIs are included (Figure 5(d)). This result conforms well with the predictions by Tanaka¹⁴ that HIs could have a major effect on the selection of the kinetic pathway of protein folding.

The fast formation and slow decay of intermediates after including HIs occur because of the hydrodynamic drag and create kinetic traps. This finding enables us to reconcile our results with the results obtained by Frembgen-Kesner and Elcock¹⁶ with the use of Gō-like models. With Gō-like models, attractive interactions occur only between residues that are in contact with the native structure. Therefore, hydrodynamic drag helps to form only the native contacts; non-native interactions are always repulsive and, therefore, the respective contacts will never form. Conversely, in UNRES, the interactions depend only on the kind of residues involved and, therefore, intermediates with non-native interactions are formed quite frequently.

B. Kinetics of the simulated folding

To compare the simulated folding of the two proteins studied without and with the presence of the HIs, first-order kinetic equations (Eqs. (20) and (21)) were fitted to the fractions of native and intermediate structures. All obtained coefficients are summarized in Table II. The faster growing exponential term, characterized by the smaller value of τ, can be identified with the fast, two-state folding pathway while the slow growing exponential term, characterized by the greater value of τ, with the slow, three-state folding pathway, that includes an intermediate state. Thus, the coefficient C₁ identifies the fraction of the trajectories that represent the fast rate, while the coefficient C₂ identifies the fraction of the slow rate.

TABLE II.

Fitted coefficients in Eqs. (20) and (21) for 1BDD and 1E0L without and with HIs.

Protein	τ1 (μs)	τ2 (μs)	C1	m1	C2	m2
1BDD without HIs	6.33 × 10−3	5.32 × 10−2	0.830	0.460	0.029	12.694
1BDD with HIs	3.85 × 10−2	9.53 × 10−1	0.760	0.485	0.257	1.975
1E0L without HIs	2.08 × 10−2	5.08 × 10−1	0.309	0.039	0.100	2.075
1E0L with HIs	2.89 × 10−2	5.81 × 100	0.246	0.024	0.156	0.980

As can be seen from Table II, including HIs results in the increase of the decay times τ corresponding to both the fast and slow rates for both proteins; however the increase of τ₂ (corresponding to the slow rates that involve intermediates) is more pronounced than that of τ₁. This observation strongly suggests that HIs slow down the simulated folding, especially when intermediates are involved. This conclusion is also consistent with the facts that the C₂ coefficients of Eq. (21), which can be regarded as the “equilibrium fractions” of intermediates, are increased upon inclusion of HIs, indicating that the intermediates become persistent when HIs are included (Table II).

IV. CONCLUSIONS

In this work, HIs were implemented in the Langevin-dynamics simulation procedure with the UNRES force field. The influence of HIs on protein folding was investigated with the examples of a small α-helical (1BDD) and a small β-sheet (1E0L) protein. The introduction of HIs was found to slow down the folding compared to plain-Langevin simulations. We found that the decrease of the folding rate resulted from fast formation of persistent intermediates that contain non-native residue-residue contacts, when the HIs were turned on, because of the hydrodynamic drag of interacting sites toward each other. This result seems to contradict the results of an earlier study by Frembgen-Kesner and Elcock¹⁶ carried out with the use of Gō-like models, in which it was found that HIs sped up the folding. However, in Gō-like models, the interactions between only the residues that form contacts in the native state are assigned potentials with a minimum, while all other interactions are all-repulsive. Therefore, although HIs facilitate the approach of any objects towards each other, only the native contacts will survive after they are formed. Conversely, in UNRES, the character of interactions depends on the kinds of residues involved and not on the native- or non-native character of the contact between them and, therefore, non-native contacts can survive for a longer time, creating kinetic traps. In reality, the formation of residue-residue contacts is governed by their physicochemical properties and not by the position in the sequence and, therefore, the results obtained in our study seem to be more realistic than those obtained with the use of structure-biased Gō-like models.

On the other hand, HIs are a feature of a macroscopic description of motion through a solvent, which assumes a continuous solvent governed by the Navier-Stokes equation, even though the UNRES sites (peptide groups and side chains) are not much larger in size than a water molecule. For this reason, HIs modeled in a mean-field fashion can result in too fast of an uncorrelated approach of residues, thus generating kinetic traps. The HIs can be more adequate for studies of the behavior of larger systems such as the interior of cells or lipid membrane formation investigated by Ando and Skolnick.^23,24