Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2015 Sep 9;24(6):924–930. doi: 10.1038/ejhg.2015.197

Phenotypic extremes in rare variant study designs

Gina M Peloso 1,2,3, Daniel J Rader 4, Stacey Gabriel 2, Sekar Kathiresan 1,2,3,5, Mark J Daly 1,2,6,7, Benjamin M Neale 1,2,6,7,*
PMCID: PMC4867440  PMID: 26350511

Abstract

Currently, next-generation sequencing studies aim to identify rare and low-frequency variation that may contribute to disease. For a given effect size, as the allele frequency decreases, the power to detect genes or variants of interest also decreases. Although many methods have been proposed for the analysis of such data, study design and analytic issues still persist in data interpretation. In this study we present sequencing data for ABCA1 that has known rare variants associated with high-density lipoprotein cholesterol (HDL-C). We contrast empirical findings from two study designs: a phenotypic extreme sample and a population-based random sample. We found differing strengths of association with HDL-C across the two study designs (P=0.0006 with n=701 phenotypic extremes vs P=0.03 with n=1600 randomly sampled individuals). To explore this apparent difference in evidence for association, we performed a simulation study focused on the impact of phenotypic selection on power. We demonstrate that the power gain for an extreme phenotypic selection study design is much greater in rare variant studies than for studies of common variants. Our study confirms that studying phenotypic extremes is critical in rare variant studies because it boosts power in two ways: the typical increases from extreme sampling and increasing the proportion of relevant functional variants ascertained and thereby tested for association. Furthermore, we show that when combining statistical evidence through meta-analysis from an extreme-selected sample and a second separate population-based random sample, power is lower when a traditional sample size weighting is used compared with weighting by the noncentrality parameter.

Introduction

Common variant association studies (CVASs), such as those testing alleles with >5% minor allele frequency (MAF), have used genotyping arrays to analyze single-nucleotide polymorphisms (SNPs) across the genome. The search for rare variants that influence phenotypic variation has been made possible through the development of next-generation sequencing technologies.1, 2 Rare variant association studies (RVASs) are a more complex process compared with CVASs, as they include both discovery of variation contributing to disease and subsequent testing of the discovered variation.3, 4 Statistical analysis of rare variation is further complicated by the limited number of alleles of a given variant in the sample that necessitates the aggregation of variants across a gene or region. The basic approach is to take a collapsed count of the number of minor alleles at a given threshold for the putatively functional variants (CMC).5 Others have extended the CMC method to weight variants in the test statistic by the MAF6 to optimize the allele frequency threshold used (VT)7 or propose a different statistical approach that is robust to variants of opposite effect (C-α and SKAT).8, 9 The power to detect association with the various proposed gene-based methods is dependent on the underlying genetic architecture of the gene.10, 11, 12

The relative power of different study designs for CVASs has been well established.13 For all genetic studies, selecting the extremes of the phenotype distribution improves power; a concept in genetics that can be traced back to seminal work by Lander and Botstein.14 More recently, it has been established that extreme sampling performs better than random population-based sampling for single rare variants, with the apparent effect size increasing with more and more stringent selection thresholds,15 but limited studies have explored the effect when variants are aggregated within a gene. Studies have shown that extreme sampling can enrich for the presence of causal variants16, 17 and, furthermore, that extreme phenotypic sampling and/or a two-stage analysis can lead to gains in power.17, 18, 19 Lee et al20 compare available gene-based tests and discuss design strategies for RVASs. Meta-analysis frameworks have been proposed to combine individual variant score statistics across studies and reconstruct gene-based tests,21 but this may lead to biases when selection, sequencing, and quality control differ between studies. Another framework for meta-analysis is combining gene-based association statistics, but the effect on power of meta-analyzing gene-based association results from two rare variant studies with different study designs remains a question.

In this study we performed targeted sequencing of a set of genes and extracted rare variant data from ABCA1, as it is known to have an effect on high-density lipoprotein cholesterol (HDL-C). We then examined association in two contrasting samples: an extreme-selected sample and a population-based random sample. HDL-C is a well-studied heritable quantitative trait22 and there are reports of rare coding variation contributing to abnormal lipid profiles. Genes related to low HDL-C – ABCA1, APOA1, and LCAT – have been found by studying families with extreme HDL-C phenotypes. Furthermore, extreme sampling strategies in the population cohorts have also shown association between rare variation in these genes and low HDL-C.23

Here, we demonstrate empirically different strength of association between rare variants in ABCA1 with HDL-C using a random population-based sample in contrast to a phenotypic extreme-selected sample. Based on this observation we performed a simulation study to attempt to reconcile the causes of the differences in association and answer the following questions: (1) What is the impact of phenotypic selection on rare variant study designs in contrast to common variant association?; and (2) What impact does this have when meta-analyzing rare variant results?

Subjects and methods

Extreme samples

Individuals of European ancestry who have had an abnormally high or low HDL-C level (<35 mg/dl for women and <28 mg/dl for men or >100 mg/dl for women and >80 mg/dl men) within the past 5 years were recruited to participate in a study from a lipid specialty clinic at the University of Pennsylvania. Individuals with no history of liver disease or HIV and who are not currently pregnant, nursing, or taking hormone replacement therapy or niacin had ~40 ml of blood drawn. Plasma lipid levels were measured and individuals with HDL-C levels greater than the 95th percentile were selected for targeted sequencing (n=389, mean HDL-C=102 mg/dl). Healthy age- and sex-matched controls with plasma HDL-C levels <25th percentile were also sequenced (n=387, mean HDL=32 mg/dl). The exons of ~900 genes including ABCA1 were sequenced in the 776 individuals of self-reported European descent. After extensive quality control measures, 731 individuals remained. Of this group, 701 individuals had HDL-C values distinctly either above the 95th percentile or below the 25th percentile for their age and sex and genotypes within ABCA1. The final targeted sequencing association analysis was performed on 351 individuals with low HDL-C levels (mean HDL-C=32 mg/dl) and 350 individuals with very high HDL-C levels (mean HDL-C=102 mg/dl) (Table 1).

Table 1. Descriptive statistics of the samples.

  High HDL Low HDL Random sample
N 350 351 1600
HDL (mg/dl) 102±19 32±5 51±15
Female 49% 50% 50%
Age (SD) 60±12 62±14 36±9.6
Open in a new tab

The 350 high HDL subjects were in the top 5% tail, and the 351 low HDL subjects were in the bottom 25% tail. The random sample was from the Framingham Heart Study Offspring Cohort and was not selected based on phenotype. Values reported were mean±SD or percentages.

Population samples

To select individuals from the general population, we drew from the well-described Offspring cohort of the Framingham Heart Study (FHS). The FHS is a three-generation, prospective, community-based, family study begun in 1948 and designed to identify the factors that contribute to cardiovascular disease. The original FHS cohort24 includes 5209 men and women who in 1948 were between the ages of 30 and 62 years, residing in the town of Framingham, Massachusetts, and who had not yet developed cardiovascular disease. The FHS Offspring cohort25 consists of 5124 of the adult children and spouses (enrolled in 1971) of the original individuals. A total of 1623 randomly selected, unrelated FHS Offspring cohort participants were included in this study. FHS Offspring participants were studied longitudinally over the course of 8 clinical exams (NIH dbGaP accession number: phs000007.v18.p7). The exons of ~200 genes including ABCA1 were sequenced in 1623 individuals of self-reported European descent from FHS. The data can be downloaded from dbGaP Study Accession: phs000307.v10.p9. After extensive quality control measures 1600 individuals remained for analysis (Table 1).

DNA sequencing methods and quality control

A custom hybrid capture array was used to sequence ABCA126 as part of two different targeted sequencing studies (one of ~900 genes for the extreme sample and ~200 genes for the random sample). DNA libraries were barcoded using the Illumina index read strategy and sequenced with an Illumina HiSeq2000 (San Diego, CA, USA). Reads were mapped to the human genome hg19 with the BWA algorithm,27 variants called with the Genome Analysis Toolkit (GATK) Unified Genotyper Module,28 and annotated using SnpEFF.29, 30 Samples that failed in any step of the solution hybrid selection component of the targeted sequencing process were excluded. Population clustering was assessed through multidimensional scaling using pruned common variants (>5% MAF) with high call rates and that were not in linkage disequilibrium. Outliers on a plot of the first two principal components generated from multidimensional scaling were excluded. Samples with heterozygosity rates (number of heterozygote sites/number of variants per sample) and singleton counts three interquartile ranges above the median were also excluded. Variants with low mean depth (<8) and low call rate (<95%) were excluded. Observed variation in ABCA1 was submitted to the LOVD database (www.lovd.nl/ABCA1; patient IDs 00046624–00046771).

Statistical analysis

We created a collapsed count of the number of minor alleles for nonsynonymous variants with <5% frequency for ABCA1 in each study. We tested the association between the ABCA1 count and outcome adjusting for age and sex. We used linear regression with continuous HDL-C for the population samples and logistic regression for the extreme-selected samples. All analyses were implemented in the R statistical package (version 3.0, Vienna, Austria).

Simulation study

We simulated a model where the percent variance explained by a gene is either (1) driven by rare variants or (2) driven by a single common variant. We used ABCA1 as a representative gene, and used the variants identified in the EVS (http://evs.gs.washington.edu/EVS/). There were 120 missense variants observed in the EVS, 38 predicted to be probably damaging, 17 possibility damaging, and 65 benign by PolyPhen2 (PPH2).31 For each replicate, we tested for association between a collapsed count of variant carriers and the simulated phenotype. We did not set out to compare the various methods for gene-based testing but rather to study the effect of extreme sampling on power. All simulations were performed in the R software package (version 3.0).

Simulation mimicking real data

We simulated 1000 replicates of ABCA1 for 7000 individuals from a population based on the observed frequencies (p) in EVAS using (1−p)2 for the homozygous major allele, 2p(1−p) for heterozygous, and p2 for homozygous minor allele probabilities for each variant. Based on PPH2 predictions, we assigned each variant to be neutral or have a 1-SD (or 1/2-SD) effect (σ) with the following probabilities: 30% for probably damaging, 5% for possibly damaging, and 1% for benign. Effects were simulated to be in the same direction. We modeled an additive effect of the variants and simulated a phenotype based on the genotypes. A 1-SD unit effect was chosen to obtain results with adequate power. We also simulated a common variant with a MAF of 0.25 and a common variant phenotype with 0.06-SD effect (given the known common variant in ABCA1).32 We then random sampled 3000 individuals, and 350 cases with the highest simulated phenotype, and 350 controls with the lowest simulated phenotype. These sample sizes gave us similar empirical power for the common variant analysis using the Genetic Power Calculator (http://pngu.mgh.harvard.edu/~purcell/gpc/) and through simulation (Supplementary Table S2). In each set of selected individuals, we tested for association between a collapsed count of the number of variants observed and the simulated phenotype. We summarized the results over all the replicates to obtain estimates of power for each selection strategy.

Simulation with fixed sample size for rare and common analysis and maximum power simulation

We simulated 1000 replicates of variation in ABCA1 for 10 000 individuals from a population based on the observed EVS variant frequencies and assigned each variant to be neutral or have a 1-SD effect (σ)based on PPH2 predictions, as before. To determine the robustness of the results, we also simulated 0.5-SD and 1.5-SD effects for the rare variants. We simulated a common variant as described in the previous section. For the fixed sample size simulation, we then selected a proportion of subjects (between 0.01 and 0.5) with the highest simulated phenotype as cases, the same proportion of subjects with the lowest simulated phenotype as controls, and contrasted that with a random sample of the same sample size (cases+controls). In each set of selected individuals, we tested for association between a collapsed count of the number of variants observed and the simulated phenotype. We summarized the results over all the replicates to obtain estimates of power for each selection strategy. For the maximum power simulation, we used the genetic power calculator33 to determine the number of individuals needed for the random sample so that the extreme sample and the random sample had the same power for the common variant.

Simulation comparing sampling strategies

We simulated 1000 replicates of ABCA1 for 1 000 000 individuals as a population based on the observed EVS variant frequencies in order to simulate the selection of extremes from a population. First, we simulated all variants to be neutral to examine type I error. Then, as described above, we assigned variants to have neutral or 1-SD effects based on PPH2 predictions given the following probabilities: 30% for probably damaging, 5% for possibly damaging, and 1% for benign (model 1), and simulated a phenotype based on the genotypes. We then varied the amount of variation that we set to be functional by assigning each variant to be neutral or have an effect given the following probabilities for the PPH2 prediction classes: 50% for probably damaging, 20% for possibly damaging, and 5% for benign (model 2; more functional variation), and 10% for probably damaging, 1% for possibly damaging, and 0.1% for benign (model 3; more neutral variation). We took random samples of 1100, 2100, 5100, and 10 100 individuals and compared that with selecting 100 cases and 100 controls from the 5, 1, 0.1, and 0.01% tails, and selected 100 cases from the 5, 1, 0.1, and 0.01% tail and 1000 random samples. In each set of selected individuals, we tested for association between a collapsed count of the number of variants observed and the simulated phenotype. We summarized the results over all the replicates to obtain estimates of power for each selection strategy.

Meta-analysis simulation

We simulated two populations as described above, assigning each variant to be neutral or have a 1-SD effect based on PPH2 predictions. We selected the 2% tails for the extreme-selected sample (200 cases and 200 controls) and 1000 individuals for the random sample. For each of 1000 replicates, we tested for association between a collapsed count of the number of variants observed and the simulated phenotype in each sample (the extreme-selected sample and the population-based random sample). We then combined the results from the two simulated studies through a Z-score-based meta-analysis with the following weights: (1) sample size, (2) common variant power, and (3) rare variant power. We also used weights of γ for the random sample and 1−γ for the extreme-selected sample, where γ ranged from 0 to 1. When γ=0, the meta-analysis is based only on the extreme-selected sample, and when γ=1, the meta-analysis is based only on the population-based random sample.

Results

Empirical association results in extremes and population samples

The mean HDL-C in high HDL-C group was 102 mg/dl compared with 32 mg/dl in the low HDL-C group (Table 1), whereas the mean HDL-C in the random sample was 51 mg/dl. The two groups of the HDL extreme-selected samples had similar distributions of age and similar proportions of each sex. The random sample had a similar sex ratio but was younger (mean: 36 years old) compared with the two extreme-selected samples.

Using missense variants with MAF <5%, we found an association of HDL-C with ABCA1 in the extreme sample (P=0.0006). This was based on 31 variants that were polymorphic in extremes (Supplementary Table S1). In contrast, using the population-based sample, the P-value was 0.03, based on 35 variants observed. Of note, the rate of variation is different between the population-based sample and extreme sample. With the extreme sampling, approximately half of the sample size was necessary to obtain the same number of variants as with the population-based sample.

Of the 31 variants that were observed in the extremes, 10 of them were seen in the population-based sample. When these 10 variants were tested in the population-based sample, no evidence for association was found (P=0.53), but we did find that the individuals who carried one of the 10 variants also found in the extreme sample (n=58) had, on average, higher mean HDL (52 mg/dl, Zmean=0.95) compared with individuals who carried one of the 25 variants (n=38) that were not also observed in the extreme samples (46 mg/dl, Zmean=0.70). Furthermore, the fraction of individuals who are in the 5% tails for the 10 variants also found in the extremes was 19% compared with only 5% of individuals with one of the 25 variants also not observed in the extremes. This suggests that the extreme sampling approach enriches for functional variation.

When collapsing variants in a gene-based test, a frequency filtered is often applied. When performing analysis of extreme samples, the frequency of variants in the population can be used instead of the frequency in the sample because the frequency of associated alleles will be distorted with the selection. We analyzed our extremes filtering on the MAF observed in the European Americans from the EVS and found that the association evidence improved (P=0.0003) compared with the filtering based on the frequency observed in the studied sample (P=0.0006).

Simulation mimicking real data

In an attempt to reconcile the difference observed in results between the extreme-selection and the population-based random selection samples, we simulated data for these two study designs with the respective sample sizes fixed based on equal power to detect a common variant association. Under this design we find that for the rare variant test, using extremes is more powerful, even with a reduced sample size (Supplementary Table S2). The difference in power is diminished when causal variants are simulated to have smaller effects. Power is still greater in the extreme samples when variant effects were simulated to not all be the same size (Supplementary Table S2). We found that extreme cases have a higher proportion of functional variants compared with a random sample (Supplementary Figure S1) and that the sample size needed to capture all potentially functional rare variation is considerably larger when randomly sampling the population in contrast to extreme phenotypic selection. Furthermore, the mean effect size across the 1000 replicates is 67% higher when only variants simulated to be functional are aggregated (mean effect size=−0.49) compared with aggregating all putatively functional variants (mean effect size=−0.16) in the extreme phenotypic selection sample. The extreme selection is affecting both the discovery of variants and the phenotypic distribution.

Simulation with fixed sample size for rare and common analysis and maximum power simulation

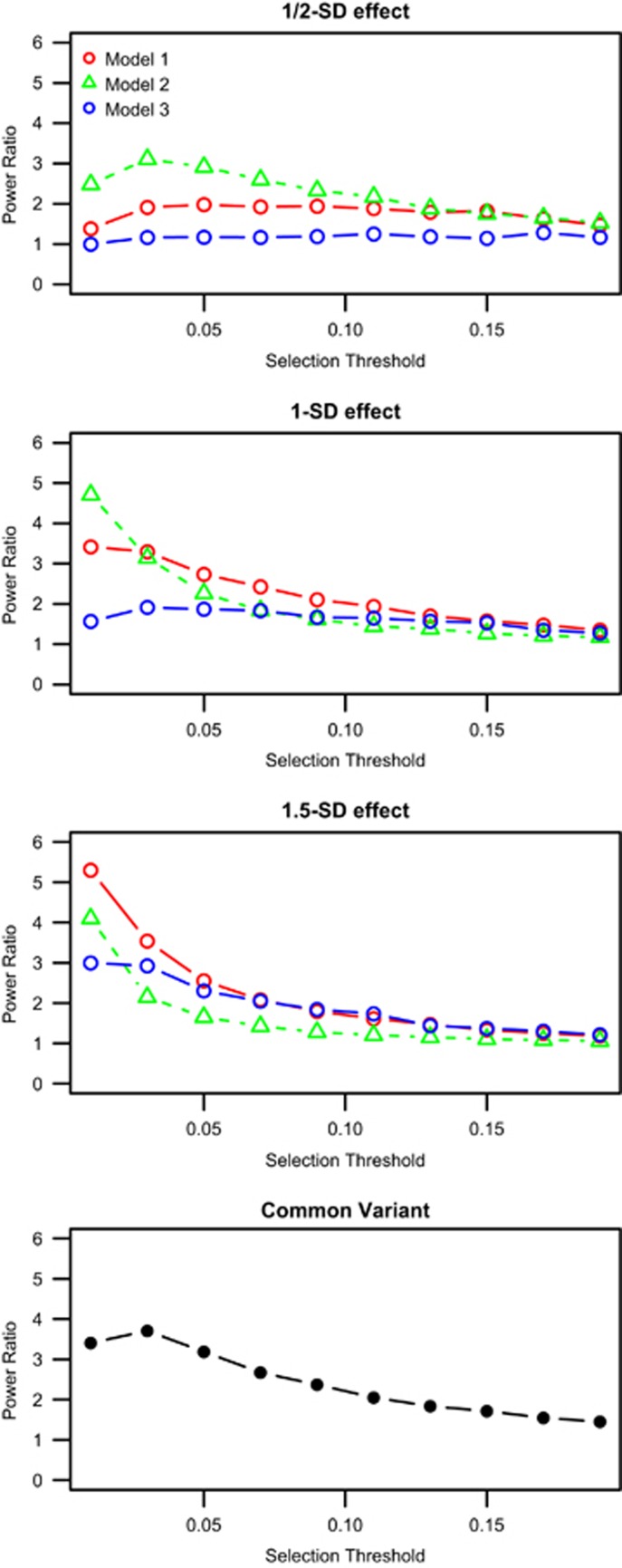
To study the effect of the phenotypic selection threshold, we simulated 10 000 individuals and then selected individuals at different thresholds (1–20% in 2% increments). We found that for a fixed sample size and selection thresholds <20%, both the CV and RV tests have higher power for a case–control design than using a population-based random sample (Figure 1 and Supplementary Figure S2). We also observed that for a fixed sample size and a rare variant test, a smaller individual variant effect gives a smaller difference in power between a population-based random sample and an extreme case–control sample selection. For example, at a 5% selection threshold for the extremes and equal sample size for the population-based random sample and a 1/2-SD effect for each variant, the power is 0.07 compared with 0.15, respectively, but for a 1.5-SD effect, the power is 0.65 compared with 0.25. Increasing the fraction of functional variants in a gene yields power increases overall, as would be expected, but also increases the gap in power between population-based random samples and phenotypic extreme case–control samples. Conversely, as the amount of variation that is functional decreases, the apparent power difference also diminishes. When we used the genetic power calculator to fix the power between case–control and random sample analysis for the common variant, we found that the case–control sample was always more powerful than the random sample for the RV test (Table 2).

Figure 1.

Figure 1

Open in a new tab

Ratios of power from the fixed sample size simulation. Samples were simulated with equal numbers for the population-based random sample (RS) and the extreme case–control (CC) sample. The x axis is Threshold, the threshold for selecting the extreme samples. The y axis is the Power Ratio, the ratio of the CC power over the RS power. The first three plots are for the rare variant tests with three different models. The last panel is the power difference for the common variant. The probability that specific class of mutations are function was simulated as follows: Model 1 – prob=0.3, poss=0.05, benign=0.1; model 2 – prob=0.5, poss=0.2, benign=0.05 (increases the amount of variation that is functional); model 3 – prob=0.1, poss=0.01, benign=0.001 (decreases the amount of variation that is functional).

Table 2. Power estimates from simulation with power fixed for the case–control and random sample common analysis.

    Power
Threshold n.rs RV.RS RV.CC CV.CC CV.RS.
0.01 1410 0.179 0.296 0.291 0.311
0.02 2330 0.257 0.363 0.416 0.451
0.05 4250 0.387 0.440 0.673 0.678
0.1 6140 0.447 0.458 0.801 0.829
0.2 7830 0.517 0.477 0.903 0.903
0.3 8050 0.492 0.432 0.912 0.906
0.4 7450 0.507 0.408 0.893 0.888
0.5 6360 0.451 0.366 0.827 0.820
Open in a new tab

Abbreviations: Threshold, the threshold for selecting the extreme samples; RV, rare variant test; CV, common variant test; n.rs, sample size for the random sample for equal power to the extreme case–control design for a common variant (MAF=0.25 and a 0.06-SD effect).

The power between the extreme case–control (CC) and population-based random sample (RS) for the common variant was fixed using the genetic power calculator. A 1-SD effect was simulated for each functional variant.

Simulation comparing sampling strategies

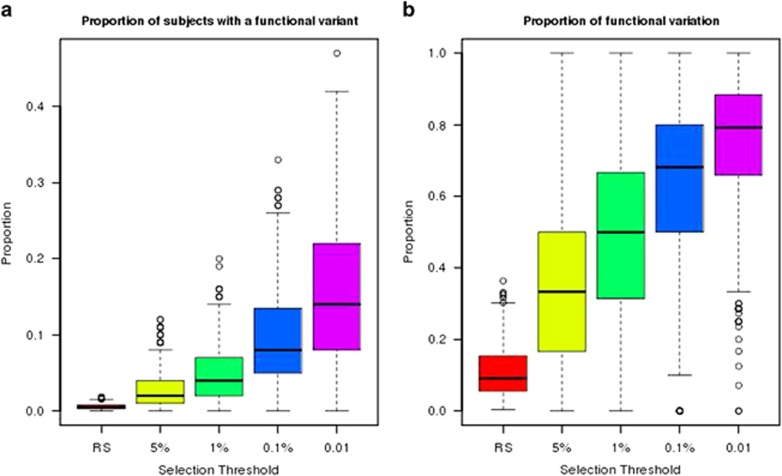
We simulated 1 million samples for the ABCA1 gene, and sampled sets of random individuals of various study sizes as well as 100 cases from the tail. Type I error was well controlled (Supplementary Table S3). From this simulation, we found selecting 100 cases from the 1% tail and 1000 random sample is more powerful than a random sample of 1100 individuals (41 vs 17%) (Table 3). Furthermore, increasing the phenotypic selection threshold yields greater gains in power. For example, selecting 100 cases in the 1% tail and 1000 random samples gives similar power to a random sample of 5100 individuals. We also find there is greater gain in power from more extreme sampling of 100 cases and 100 controls than sequencing 1000 more subjects. This is because of a larger proportion of subjects with a functional variant in the extremes and a higher proportion of functional variation, with increasing proportions as the tail becomes more extreme (Figure 2). Here, a key consideration is the magnitude of the effect size for the functional alleles. In the presence of alleles with a strong phenotypic impact, extreme sampling pays greater dividends in terms of power. As the effect size weakens, so too does the impact of very extreme selection on power.

Table 3. Power estimates from simulation comparing sampling strategies.

Sampling Common variant test Power Rare variant test Power
Random sample of 1100 0.227 0.166
Random sample of 2100 0.4 0.251
Random sample 5100 0.728 0.433
Random sample of 10 100 0.946 0.563
c/c 100/100 from 5% tails 0.187 0.123
c/c 100/100 from 1% tails 0.289 0.270
c/c 100/100 from 0.1% tails 0.424 0.527
c/c 100/100 from 0.01% tails 0.532 0.758
c/c 100 from 5% tail and 1000 random samples 0.090 0.197
c/c 100 from 1% tail and 1000 random samples 0.137 0.413
c/c 100 from 0.1% tail and 1000 random samples 0.183 0.695
c/c 100 from 0.01% tail and 1000 random samples 0.251 0.879
Open in a new tab

A million samples were generated for variants in ABCA1 and a phenotype with a 1-SD effect for each rare functional variant and 0.06-SD for the common variant (MAF=0.25). Various selection methods were used to select subjects from the generated samples and power was computed for the rare variant test and the common variant test. c/c, case/control.

Figure 2.

Figure 2

Open in a new tab

Amount of variation in extremes compared with random sample. (a) Proportion of subjects with a functional variant. (b) Proportion of functional variants. Results are based on 1000 replicates and 1-SD effect for each rare functional variant. RS, random sample of 10 000 individuals.

Meta-analysis simulation

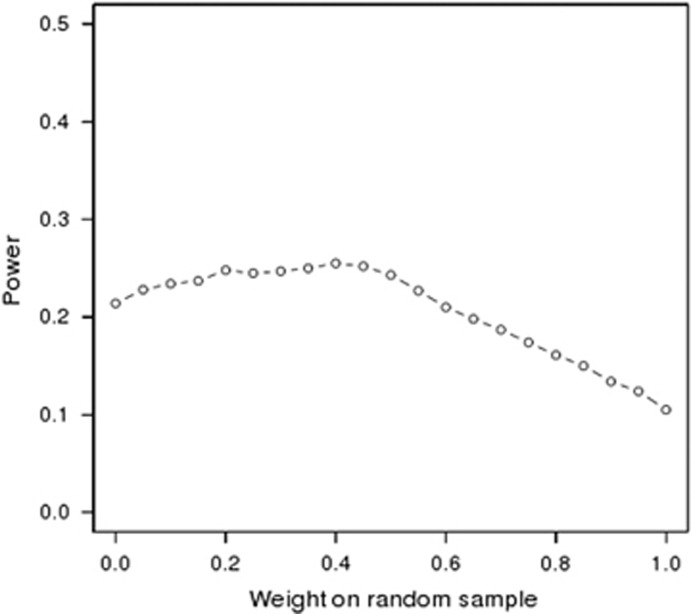
We simulated two studies: a random sample of 1000 individuals (study 1) and a 2% extreme-selected sample of 200 cases and 200 controls (study 2). We then performed a Z-based meta-analysis of these two simulated studies with different weighting schemes. We found that when we weighted by sample size, a traditional approach to combining statistical evidence, we had lower power than when we weighted by the noncentrality parameter (NCP) from the studies (0.209 vs 0.252). Power was nearly identical when weighting by the common variant test NCP and the rare variant test NCP (0.248 vs 0.252). Weighting by sample size increases the contribution of the random sample to the meta-analysis in comparison with weighting by the NCP. Using a range of values for the weighting, we found that the optimal weighting when combining an extreme-selected sample with a population-based random sample will up-weight the extreme-selected sample (Figure 3) beyond what would be considered by the relative sample size. In our scenario, the optimal weighting occurred when the random sample had a 40% weight and the extreme-selected sample had a 60% weight.

Figure 3.

Figure 3

Open in a new tab

Power from meta-analysis of a population-based random sample and an extreme-selected sample. Power is based on 1000 replicates and 1-SD effect for each rare functional variant. The extreme-selected sample has a sample size of 400 (200 cases and 200 controls) and the population-based random sample has a sample size of 1000. Power is optimal when the population-based random sample has 40% of the weight and the extreme-selected sample has 60% of the weight. This is in contrast to a sample size weighted meta-analysis that would up-weight the random sample.

Taking our original results of the association between HDL-C and ABCA1 in both the population-based random sample and the extreme-selected sample, we found the meta-analyzed P-value using the sample sizes is 7.7 × 10−4, but when we use the optimal weighting found above, the P-value became almost an order of magnitude more significant (P=4.9 × 10−5).

Discussion

From real data, we observed substantive differences in the results from rare variant analysis from two different study designs for HDL-C and the ABCA1 gene. We then confirm through a simulation study that the search for rare genetic effects differs fundamentally with an extreme sampling design in contrast to using a population-based random sample. We find that although cross-sectional and extreme samples lead to similar results for common variants, this is not the same for a burden of rare variants and we strongly advocate for extremes in sequencing studies, where possible. As is the case in other analytic settings, the use of phenotypic extremes tends to lead to an overestimate of the effect of the variant and tends to overestimate the proportion of functionally active variants in a region, both of which support the value of population-based samples.34 However, much larger sample sizes will be needed in order to have the power to detect associations in these instances.

We showed that as the selection threshold is made more stringent, extreme selection continues to gain further power. This selection strategy is not only boosting the typical power gains from selection but also concentrating the functional variants in the sample. As previously reported,16 this is the critical step to the design of a rare variant association study. If individuals are not selected for the functional variants, there will be no power to detect the association. Also, we found that the power boost in extreme-phenotype selection compared with a population-based random sample is larger as the effect sizes of the variants increase.

We concentrated on the effect of extreme sampling when designing (RVASs), whereas Zuk et al3 addressed key questions on testing missense alleles, frequency thresholds for inclusion into the test, the use of isolated populations, and the value of gene-set analysis. Our work is complementary to this and highlights that studying extreme samples is critical not only because of the greater association power per individual, but because of the higher rate of relevant functional variants ascertained by sequencing and thereby tested for association.

There are many statistical tests available for testing rare variants with complex traits5, 6, 7, 8, 9 and simulation studies show that these tests behave similarly in many situations but depend on many factors such as the proportion of causal variants, the variants effect sizes and frequencies, and consistency of direction of effects.1, 35 We do not address which rare variant test should be used, but provide an intuitive explanation of why extreme sampling is beneficial for sequencing studies.

Finally, the results from this study will not only affect single cohort analyses but also, perhaps most importantly, have serious ramifications for combining results from multiple independent studies, a point that has not been previously addressed. As a natural extension, meta-analysis of multiple RVASs will be more powerful when the individual studies contributing are extreme-selected samples for the trait of interest and will be less powerful with population-based random samples. Furthermore, traditional approaches for combining evidence across studies such as weighting by sample size is inefficient. As the effect size is expected to be larger for the extreme-sampling designs compared with a random sample design, a weighting scheme that is more balanced to this effect will have better performance. As an alternative to weighting by sample size, we suggest that studies should be weighted by the expected NCP, conditional on the genetic model. Unfortunately, the genetic model is largely unknown, but previously established positive control genes with known effects on phenotype can be used to calibrate the expected NCP of studies in a meta-analysis.

In conclusion, we have provided practical evidence on the benefits of using extreme samples for rare variant studies and highlighted an issue with the traditional weighting scheme used when evidence from multiple studies with different study designs are combined.

Acknowledgments

GMP is supported by the National Heart, Lung, and Blood Institute of the National Institutes of Health under Award Number K01HL125751. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Information
Click here for additional data file. (210.4KB, pdf)

References

  1. Kiezun A, Garimella K, Do R et al: Exome sequencing and the genetic basis of complex traits. Nat Genet 2012; 44: 623–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Kryukov GV, Shpunt A, Stamatoyannopoulos JA, Sunyaev SR: Power of deep, all-exon resequencing for discovery of human trait genes. Proc Natl Acad Sci USA 2009; 106: 3871–3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Zuk O, Schaffner SF, Samocha K et al: Searching for missing heritability: designing rare variant association studies. Proc Natl Acad Sci USA 2014; 111: E455–E464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Do R, Kathiresan S, Abecasis GR: Exome sequencing and complex disease: practical aspects of rare variant association studies. Hum Mol Genet 2012; 21: R1–R9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Li B, Leal SM: Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet 2008; 83: 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Madsen BE, Browning SR: A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet 2009; 5: e1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Price AL, Kryukov GV, de Bakker PI et al: Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet 2010; 86: 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Neale BM, Rivas MA, Voight BF et al: Testing for an unusual distribution of rare variants. PLoS Genet 2011; 7: e1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X: Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet 2011; 89: 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Basu S, Pan W: Comparison of statistical tests for disease association with rare variants. Genet Epidemiol 2011; 35: 606–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lee S, Wu MC, Lin X: Optimal tests for rare variant effects in sequencing association studies. Biostatistics 2012; 13: 762–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lange LA, Hu Y, Zhang H et al: Whole-exome sequencing identifies rare and low-frequency coding variants associated with LDL cholesterol. Am J Hum Genet 2014; 94: 233–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Spencer CC, Su Z, Donnelly P, Marchini J: Designing genome-wide association studies: sample size, power, imputation, and the choice of genotyping chip. PLoS Genet 2009; 5: e1000477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lander ES, Botstein D: Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 1989; 121: 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Guey LT, Kravic J, Melander O et al: Power in the phenotypic extremes: a simulation study of power in discovery and replication of rare variants. Genet Epidemiol 2011; 35: 236–246. [DOI] [PubMed] [Google Scholar]
  16. Barnett IJ, Lee S, Lin X: Detecting rare variant effects using extreme phenotype sampling in sequencing association studies. Genet Epidemiol 2013; 37: 142–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li D, Lewinger JP, Gauderman WJ, Murcray CE, Conti D: Using extreme phenotype sampling to identify the rare causal variants of quantitative traits in association studies. Genet Epidemiol 2011; 35: 790–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kang G, Lin D, Hakonarson H, Chen J: Two-stage extreme phenotype sequencing design for discovering and testing common and rare genetic variants: efficiency and power. Hum Hered 2012; 73: 139–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lamina C: Digging into the extremes: a useful approach for the analysis of rare variants with continuous traits? BMC Proc 2011; 5 (Suppl 9): S105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee S, Abecasis GR, Boehnke M, Lin X: Rare-variant association analysis: study designs and statistical tests. Am J Hum Genet 2014; 95: 5–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Tang ZZ, Lin DY: Meta-analysis for discovering rare-variant associations: statistical methods and software programs. Am J Hum Genet 2015; 97: 35–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Strang AC, Hovingh GK, Stroes ES, Kastelein JJ: The genetics of high-density lipoprotein metabolism: clinical relevance for therapeutic approaches. Am J Cardiol 2009; 104: 22E–31E. [DOI] [PubMed] [Google Scholar]
  23. Cohen JC, Kiss RS, Pertsemlidis A, Marcel YL, McPherson R, Hobbs HH: Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science 2004; 305: 869–872. [DOI] [PubMed] [Google Scholar]
  24. Kannel WB, Dawber TR, Kagan A, Revotskie N, Stokes J: Factors of risk in the development of coronary heart disease—six year follow-up experience. The Framingham Study. Ann Intern Med 1961; 55: 33–50. [DOI] [PubMed] [Google Scholar]
  25. Kannel WB, Feinleib M, McNamara PM, Garrison RJ, Castelli WP: An investigation of coronary heart disease in families. The Framingham offspring study. Am J Epidemiol 1979; 110: 281–290. [DOI] [PubMed] [Google Scholar]
  26. Gnirke A, Melnikov A, Maguire J et al: Solution hybrid selection with ultra-long oligonucleotides for massively parallel targeted sequencing. Nat Biotechnol 2009; 27: 182–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Li H, Durbin R: Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 2009; 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. DePristo MA, Banks E, Poplin R et al: A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat Genet 2011; 43: 491–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bick AG, Flannick J, Ito K et al: Burden of rare sarcomere gene variants in the Framingham and Jackson Heart Study cohorts. Am J Hum Genet 2012; 91: 513–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Cingolani P, Platts A, Wang le L et al: A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly 2012; 6: 80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Adzhubei IA, Schmidt S, Peshkin L et al: A method and server for predicting damaging missense mutations. Nat Methods 2010; 7: 248–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Teslovich TM, Musunuru K, Smith AV et al: Biological, clinical and population relevance of 95 loci for blood lipids. Nature 2010; 466: 707–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Purcell S, Cherny SS, Sham PC: Genetic Power Calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 2003; 19: 149–150. [DOI] [PubMed] [Google Scholar]
  34. Flannick J, Thorleifsson G, Beer NL et al: Loss-of-function mutations in SLC30A8 protect against type 2 diabetes. Nat Genet 2014; 46: 357–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ladouceur M, Dastani Z, Aulchenko YS, Greenwood CM, Richards JB: The empirical power of rare variant association methods: results from sanger sequencing in 1,998 individuals. PLoS Genet 2012; 8: e1002496. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (210.4KB, pdf)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES