Abstract
The image information acquisition ability of a conventional camera is usually much lower than the Shannon Limit since it does not make use of the correlation between pixels of image data. Applying a random phase modulator to code the spectral images and combining with compressive sensing (CS) theory, a spectral camera based on true thermal light ghost imaging via sparsity constraints (GISC spectral camera) is proposed and demonstrated experimentally. GISC spectral camera can acquire the information at a rate significantly below the Nyquist rate, and the resolution of the cells in the three-dimensional (3D) spectral images data-cube can be achieved with a two-dimensional (2D) detector in a single exposure. For the first time, GISC spectral camera opens the way of approaching the Shannon Limit determined by Information Theory in optical imaging instruments.
Conventional Camera, as one of the most important appliances to get image information, records the image of an object based on the point-to-point correspondence between the object-space and the image-space. Because the correlation between pixels of image1 can’t be applied, the image information acquisition efficiency of such conventional point-to-point imaging mode is much lower than the Shannon Limit2,3 determined by Information Theory in optical imaging instruments4,5,6,7,8,9. Unlike the conventional direct point-to-point imaging mode, the resolution of the pixels of ghost imaging is determined by the correlation of light field fluctuations corresponding to the two pixels respectively, which can be measured on-line or pre-determined10,11. Combining with compressive sensing (CS) theory1,12,13,14,15,16, ghost imaging via sparsity constraints (GISC) has many potential applications including super-resolution imaging17,18,19, three-dimensional (3D) computational imaging with single-pixel detectors20, 3D remote sensing21,22, imaging through scattering media23,24, object tracking25, object authentication26,27 and X-ray Fourier transform diffraction imaging28,29,30.
For thermal light ghost imaging, according to the illumination source, it can be classified to two categories: ghost imaging with pseudo-thermal light and true thermal light. Ghost imaging with true thermal light and sunlight have been respectively demonstrated by detecting the temporal fluctuation of thermal light and applying the intensity correlation between the intensity distributions at the reference arm and the test arm31,32,33. Comparing with ghost imaging with pseudo-thermal light, this scheme of ghost imaging with true thermal light has to face the difficulty of detecting the temporal fluctuation of true thermal light which requires the response time of detector less than the coherence time of true thermal light 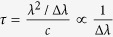 (λ is the wavelength, Δλ is the linewidth, c is the speed of light) which can be as short as femtosecond. In order to increase the coherence time of the illumining true thermal light, monochrome imaging is required which results in the vast majority of radiation energy from the target scene being filtered out, making the energy efficiency of ghost imaging applying the temporal fluctuation of true thermal light very low. Moreover, the fluctuating true thermal field needs to be split before the light field illuminating the object in the system and recorded in the reference path, which makes the scheme even more difficult to be applied in remote sensing.
(λ is the wavelength, Δλ is the linewidth, c is the speed of light) which can be as short as femtosecond. In order to increase the coherence time of the illumining true thermal light, monochrome imaging is required which results in the vast majority of radiation energy from the target scene being filtered out, making the energy efficiency of ghost imaging applying the temporal fluctuation of true thermal light very low. Moreover, the fluctuating true thermal field needs to be split before the light field illuminating the object in the system and recorded in the reference path, which makes the scheme even more difficult to be applied in remote sensing.
In this paper, for the first time, we propose a spectral camera based on true thermal light ghost imaging via sparsity constraints (GISC spectral camera) without a splitter. GISC spectral camera modulates the true thermal light into a spatially fluctuating pseudo-thermal light using a spatial random phase modulator34,35 which, at the same time, also acts as a random grating generating the uncorrelated speckles for different wavelengths, the 3D spectral images data-cube is then modulated into a two-dimensional (2D) data plane and GISC spectral camera can achieve the whole wavelength image in a single exposure, leading to a more convenient detection process and higher energy efficiency compared to ghost imaging applying the temporal fluctuation of true thermal light. Combining with CS, GISC spectral camera can acquire the information at a rate significantly below the Nyquist rate which opens the way of approaching the Shannon Limit determined by Information Theory in optical imaging instruments3,4,5,7.
Schematic and Resolution
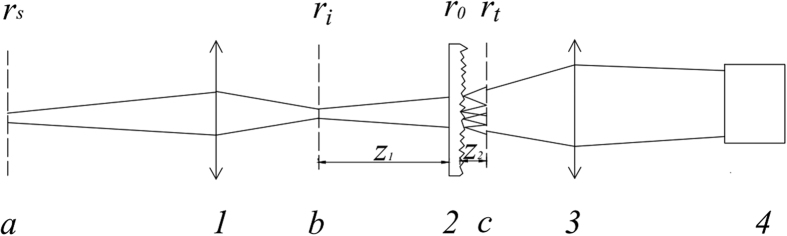
The schematic of GISC spectral camera is shown in Fig. 1. The system consists of (1) an imaging system, which projects the object image in the object plane ‘a’ onto the first image plane ‘b’, (2) a spatial random phase modulator, which disperses the image with different wavelengths as a random grating and modulates the image to generate the speckles in plane ‘c’34,35, (3) a microscope objective, which magnifies the speckles in plane ‘c’, and (4) a charge-coupled device (CCD) detector recording the magnified speckles.
Figure 1. Schematic of GISC spectral camera.
(a) The object plane; (b) the first image plane; (c) the speckles plane; (1) an imaging system; (2) a spatial random phase modulator; (3) a microscope objective; (4) CCD detector.
Denoting the spectral light intensity distribution in the first image plane ‘b’ by Ib(ri, λl) and the intensity distribution in plane ‘c’ by Ic(rt) respectively, we have36
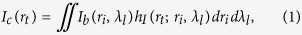 |
where hI(rt; ri, λl) is the incoherent intensity impulse response function, rt is the coordinate in plane ‘c’, ri and λl are respectively the coordinate and wavelength of the light intensity distribution in the first image plane ‘b’. To record the pre-determined reference spatial intensity fluctuation of the pseudo-thermal light without objects, a coherent monochrome point source at pixel 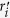 with wavelength
with wavelength 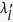 in the first image plane ‘b’, denoted as
in the first image plane ‘b’, denoted as 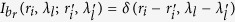 , is used to illuminate the spatial random phase modulator, and the recorded light intensity
, is used to illuminate the spatial random phase modulator, and the recorded light intensity 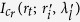 in the plane ‘c’ is given by
in the plane ‘c’ is given by
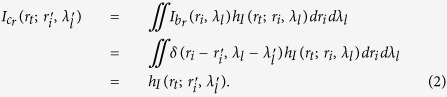 |
During the imaging process, the intensity distribution in the first image plane ‘b’ 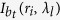 is simply the image, denoted as Ti(ri, λl), of the object Ts(rs, λl) in the object plane ‘a’,
is simply the image, denoted as Ti(ri, λl), of the object Ts(rs, λl) in the object plane ‘a’,
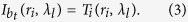 |
Combining Eqs (1,2) with (3), the intensity distribution 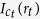 in the speckle plane ‘c’ is
in the speckle plane ‘c’ is
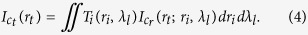 |
Eq. (4) shows that 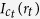 is the Ti(ri, λl) weighted integration of the pre-determined reference spatial intensity fluctuation of pseudo-thermal light
is the Ti(ri, λl) weighted integration of the pre-determined reference spatial intensity fluctuation of pseudo-thermal light 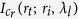 . Therefore, each pixel rt of CCD detector is equivalent to a measurement of the bucket detector in the test arm of ghost imaging scheme. The second-order correlation function between the spatial intensity fluctuation in the pre-determined reference arm and test arm is defined as
. Therefore, each pixel rt of CCD detector is equivalent to a measurement of the bucket detector in the test arm of ghost imaging scheme. The second-order correlation function between the spatial intensity fluctuation in the pre-determined reference arm and test arm is defined as
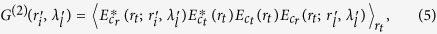 |
where 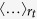 is the ensemble average about the coordinate of the light intensity distribution rt. Combining Eqs (2,4) with (5), the second-order correlation function
is the ensemble average about the coordinate of the light intensity distribution rt. Combining Eqs (2,4) with (5), the second-order correlation function 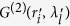 is given by
is given by
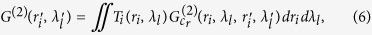 |
where 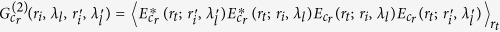 is the second-order correlation function of the light fields at different pixels and wavelengths in the first image plane ‘b’. In order to calculate
is the second-order correlation function of the light fields at different pixels and wavelengths in the first image plane ‘b’. In order to calculate 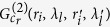 , the height autocorrelation function of the spatial random phase modulator is assumed as37
, the height autocorrelation function of the spatial random phase modulator is assumed as37
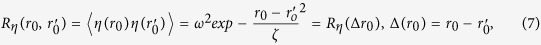 |
where 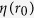 and
and 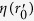 are respectively the height of the spatial random phase modulator at r0 and
are respectively the height of the spatial random phase modulator at r0 and 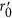 , ω and ζ are respectively the height standard deviation and transverse correlation length of the spatial random phase modulator. Assuming that the light field fluctuations in the speckles plane ‘c’ corresponding to pixel
, ω and ζ are respectively the height standard deviation and transverse correlation length of the spatial random phase modulator. Assuming that the light field fluctuations in the speckles plane ‘c’ corresponding to pixel 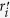 in the first image plane ‘b’ with wavelength
in the first image plane ‘b’ with wavelength 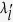 obeys the complex circular Gaussian distribution,
obeys the complex circular Gaussian distribution, 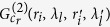 can be written as
can be written as
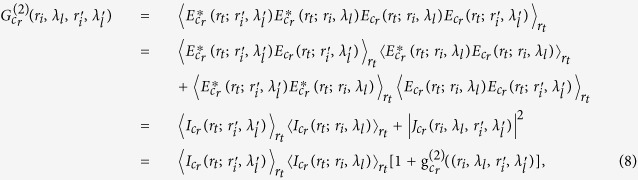 |
where
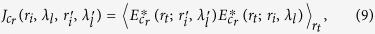 |
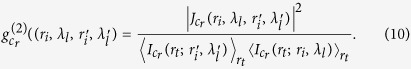 |
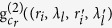 is defined as the normalized second-order correlation function of the light fields at different pixels and wavelengths in the first image plane ‘b’. According to the Fresnel diffraction theorem, the light field in the speckles plane ‘c’ propagated from pixel
is defined as the normalized second-order correlation function of the light fields at different pixels and wavelengths in the first image plane ‘b’. According to the Fresnel diffraction theorem, the light field in the speckles plane ‘c’ propagated from pixel 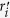 in the first image plane ‘b’ with wavelength
in the first image plane ‘b’ with wavelength 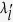 is
is
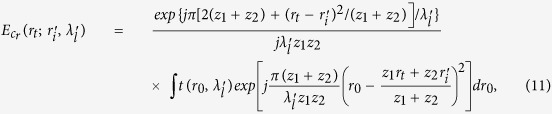 |
where 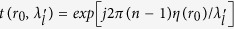 is the transmission function of the spatial random phase modulator.
is the transmission function of the spatial random phase modulator. 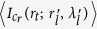 and
and 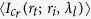 are respectively given by
are respectively given by
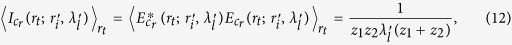 |
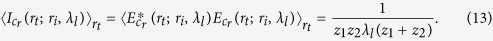 |
Substituting Eqs (7,9,11) into (10) yields
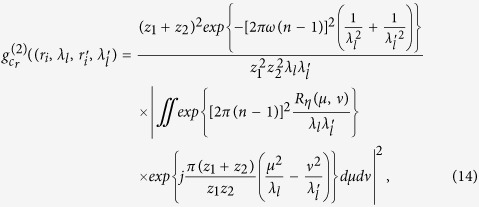 |
where
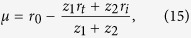 |
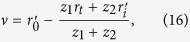 |
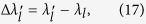 |
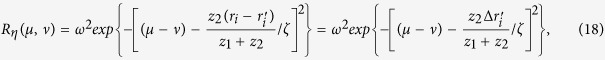 |
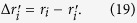 |
Assuming 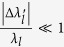 , we have
, we have
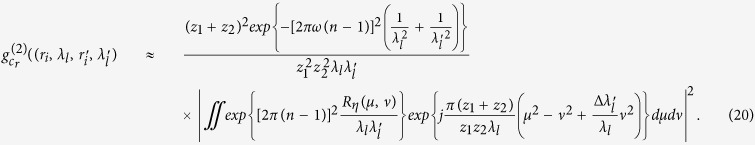 |
Assuming 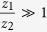 , and the diameter σ of the illuminated region in the spatial random phase modulator by each cells of 3D data-cube in calibration satisfies πσ2/λlz2 < 1,
, and the diameter σ of the illuminated region in the spatial random phase modulator by each cells of 3D data-cube in calibration satisfies πσ2/λlz2 < 1, 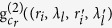 is given by
is given by
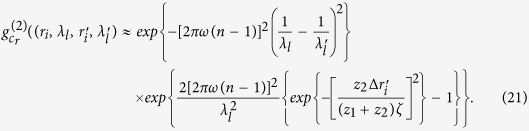 |
Taking Eqs (8,12,13,21) into (6), we get the correlation function of intensity fluctuations38
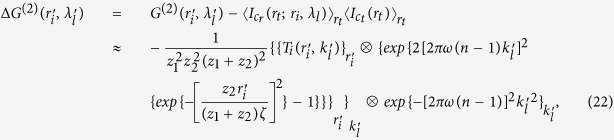 |
where 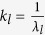 ,
, 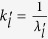 , ⊗ denotes the operation of convolution. Eq. (22) specifies that
, ⊗ denotes the operation of convolution. Eq. (22) specifies that 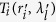 can be separated from the correlation function of intensity fluctuations
can be separated from the correlation function of intensity fluctuations 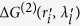 , and the resolution is determined by the normalized second-order correlation
, and the resolution is determined by the normalized second-order correlation 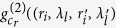 at different pixels and wavelengths in the first image plane ‘b’. When
at different pixels and wavelengths in the first image plane ‘b’. When 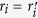 , according to Eq. (14), the normalized second-order correlation function of the light fields at pixel
, according to Eq. (14), the normalized second-order correlation function of the light fields at pixel 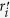 in the first image plane ‘b’ with two different wavelengths is given by
in the first image plane ‘b’ with two different wavelengths is given by
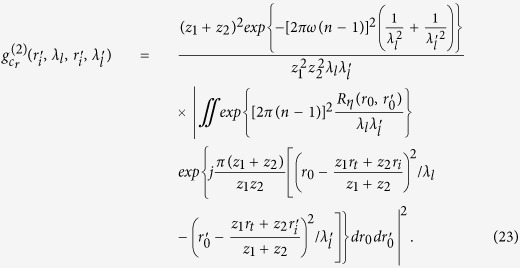 |
Similarly, when 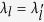 , according to Eq. (14), the normalized second-order correlation function of the light fields at two different pixels in the first image plane ‘b’ with wavelength
, according to Eq. (14), the normalized second-order correlation function of the light fields at two different pixels in the first image plane ‘b’ with wavelength 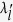 is given by
is given by
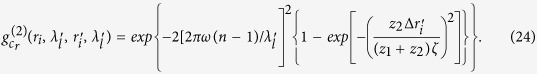 |
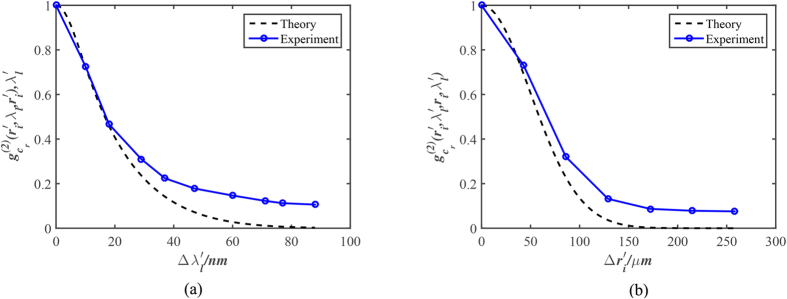
Figure 2(a,b) respectively show the comparison of 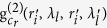 and
and 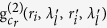 between experiment and theory, and the experiment diagram is given in Fig. 1 with z1 = 20 mm, z2 = 0.3 mm, ω = 2.1 μm, ζ = 16.75 μm, n = 1.516 and the central wavelength
between experiment and theory, and the experiment diagram is given in Fig. 1 with z1 = 20 mm, z2 = 0.3 mm, ω = 2.1 μm, ζ = 16.75 μm, n = 1.516 and the central wavelength 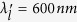 .
.
Figure 2.
(a) The normalized second-order correlation function of the light fields 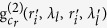 at pixel in the first image plane ‘b’ with two different wavelengths; (b) The normalized second-order correlation function of the light fields
at pixel in the first image plane ‘b’ with two different wavelengths; (b) The normalized second-order correlation function of the light fields 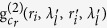 at two different pixels in the first image plane ‘b’ with wavelength
at two different pixels in the first image plane ‘b’ with wavelength 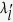 .
.
The Measurement Matrix & Reconstruction Algorithm
There are many methods to improve the imaging quality of ghost imaging39,40,41. However, ghost imaging reconstructions based on the ensemble statistics cannot provide the criterion of the necessary number of sampling for a perfect imaging, which makes it impossible to optimize the design of ghost imaging system. Combining with CS which provides the recovery condition of perfect reconstruction, the quantitative analysis for the necessary measurements data can be made. Under the framework of CS theory, the measurement matrix of GISC spectral camera is obtained as follows: each of the speckle intensity distributions generated by a point light source at pixel 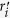 in the
in the  spectrum band in the first image plane ‘b’ is recorded by the randomly selected
spectrum band in the first image plane ‘b’ is recorded by the randomly selected 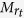 pixels of CCD detector and reshaped as a column vector of length M of the measurement matrix. Repeating the process for all the N image pixels in the first image plane ‘b’ and all the L spectral bands, one may have the pre-determined random measurement matrix AM×K, where K = L × N. If we denote the unknown spectral object image as a K-dimensional column vector XK×1, and reshape the modulated object intensity distribution recorded by the same M pixels of CCD detector in a similar way as a column vector YM×1, then we may have the discrete from Eq. (4),
pixels of CCD detector and reshaped as a column vector of length M of the measurement matrix. Repeating the process for all the N image pixels in the first image plane ‘b’ and all the L spectral bands, one may have the pre-determined random measurement matrix AM×K, where K = L × N. If we denote the unknown spectral object image as a K-dimensional column vector XK×1, and reshape the modulated object intensity distribution recorded by the same M pixels of CCD detector in a similar way as a column vector YM×1, then we may have the discrete from Eq. (4),
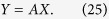 |
Spectral object image is usually both spatially and spectrally correlated, which has already been utilized in spectral image reconstructions42,43,44. The reconstruction of the spectral object image can generally be regarded as solving a minimization problem which penalizes both the l1 norm and the nuclear norm of the data matrix:
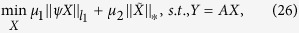 |
where 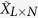 a matrix representation of the spectral object image whose columns represent different bands of the spectral object image, ψ the sparsifying transform, μ1 and μ2 the weight coefficients and μ1, μ2 > 0. In this work, we use a modified approach based on the method described by Eq. (26)45:
a matrix representation of the spectral object image whose columns represent different bands of the spectral object image, ψ the sparsifying transform, μ1 and μ2 the weight coefficients and μ1, μ2 > 0. In this work, we use a modified approach based on the method described by Eq. (26)45:
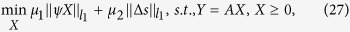 |
where 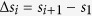 , is the subtraction of the largest singular value s1 and the other si. The solution of Eq. (27) tends to have a simultaneous low-effective-rank and sparse structure, which much improves the reconstruction quality with low sampling rate.
, is the subtraction of the largest singular value s1 and the other si. The solution of Eq. (27) tends to have a simultaneous low-effective-rank and sparse structure, which much improves the reconstruction quality with low sampling rate.
Experimental Results
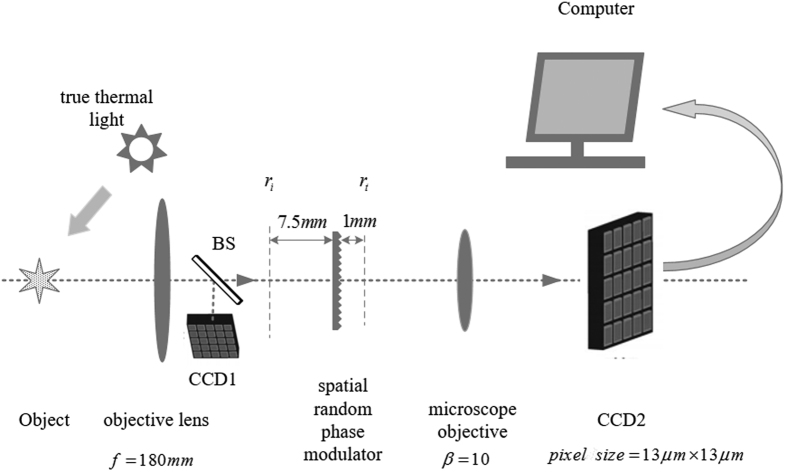
In the experimental setup of GISC spectral camera shown in Fig. 3, the imaging system (Tamron AF70-300 mm f/4-5.6) with focal length of f = 180 mm projects the object image onto the first image plane, a beam splitter (BS) with split ratio 50:50 splits the light field into two paths, CCD1 detector (AVT Sting F-504C with pixel size of 3.45 μm × 3.45 μm) is placed in one of the two paths at the position of the first image plane of the system to obtain the conventional image of the object for comparison, a spatial random phase modulator (SIGMA KOKI CO., LTD. DFSQ1-30C02-1000) disperses the images with different wavelengths acting as a random grating and modulates the image to generate the speckles, a microscope objective with magnification β = 10 and the numerical aperture N.A. = 0.25 magnifies the speckles which are then recorded by CCD2 detector (Andor iKon-M) with the pixel size 13 μm × 13 μm. The first image plane is divided into Nx × Ny = 140 × 140 pixels with the square of each pixel approximately equal to Δrs determined by the Eq. (24). The number of spectrum bands for single exposure is 7, and the images in two wavelength ranges of 520 ~ 580 nm and 620 ~ 680 nm are respectively obtained in two exposures, while the theoretical spectral resolution is 20 nm in the experimental setup according to Eq. (23).
Figure 3. Experimental setup of GISC spectral camera.
In order to compare the spectral & spatial resolution of GISC spectral camera with the theoretical resolution, as shown in Fig. 4, the spectral object ‘SIOM’ with different parts passing through different wavelengths has been selected, and the illuminating source is a xenon lamp. The original spectral images of ‘SIOM’ obtained by CCD1 detector placed in the first image plane ‘b’ with corresponding narrowband filter in front of it are shown in Fig. 4 (pixel size is equal to the theoretical resolution of reconstructed images by GISC spectral camera for comparing them). The corresponding modulated object intensity distribution Y is achieved by CCD2 detector of GISC spectral camera and the reconstructed spectral images of ‘SIOM’ with 30% sampling rate of 3D date-cube are shown in Fig. 5. The comparison between the original and reconstructed spectral images shows that the resolution of GISC spectral camera is in accordance with the theoretical calculation.
Figure 4. The original spectral images of ‘SIOM’ obtained by CCD1 detector placed on the first image plane ‘b’ with corresponding narrowband filter in front of it, showing all the channels from 620 ~ 680 nm.
Figure 5. The reconstructed spectral images of ‘SIOM’ with 30% sampling rate of 3D date-cube, showing all the channels from 620 ~ 680 nm.
The images of the outdoor scene consisting of Mario & Luigi with sunlight illumination are shown in Fig. 6. Figure 6(a) is obtained by a camera, while Fig. 6(b,c) respectively show the pictures taken by CCD1 detector with narrowband filters of 550 ± 10 nm and 650 ± 10 nm in front of it (pixel size is equal to the theoretical resolution of reconstructed images by GISC spectral camera for the sake of comparison). The reconstructed spectral images of Mario & Luigi with 30% sampling rate of 3D date-cube are shown in Fig. 7. The experimental results show that the spectral imaging ability of GISC spectral camera for complex scenes is also pretty good.
Figure 6.
Mario & Luigi taken by (a) a camera; (b) CCD1 detector passing through narrowband filters of 550 ± 10 nm; (c) CCD1 detector passing through narrowband filters of 650 ± 10 nm.
Figure 7. The reconstructed spectral images of Mario & Luigi with 30% sampling rate of 3D date-cube, showing all the channels from 520 ~ 580 nm and 620 ~ 680 nm.
Discussion and Conclusion
Based on Information Theory, the transmitted information of an imaging system can be described by the entropy2,3
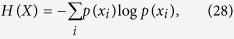 |
where p(xi) is the probability of xi occurrence. For the conventional direct point-of-object-space to point-of-image-space imaging mode, the conditional entropy H(X|Y) = 0, and thus the channel capacity of the conventional monochrome camera is
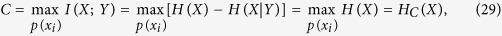 |
where I(X; Y) is the mutual information, 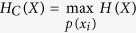 the maximum information entropy of source X for conventional imaging instrument, which is the Shannon Limit of the imaging system. According to the principle of maximum entropy1, the information content of an image is maximized when p(xi) is Gaussian distribution with average power constraints, which doesn’t contain any useful information. Therefore, the entropy of the image with structured information H(X) has
the maximum information entropy of source X for conventional imaging instrument, which is the Shannon Limit of the imaging system. According to the principle of maximum entropy1, the information content of an image is maximized when p(xi) is Gaussian distribution with average power constraints, which doesn’t contain any useful information. Therefore, the entropy of the image with structured information H(X) has
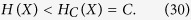 |
Eq. (30) shows that the image information acquisition efficiency of such conventional point-to-point imaging mode is lower than the Shannon Limit determined by Information Theory in optical imaging instruments. The channel capacity of an imaging system based on Information Theory for conventional optical imaging instruments is4,5,6,7
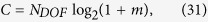 |
where m is signal to noise ratio (SNR), NDOF is degrees of freedom and has
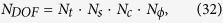 |
where Nt, Ns, Nc and Nϕ are respectively time, spatial, color and polarization degrees of freedom. Spatial degrees of freedom Ns has6
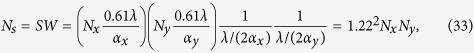 |
where S is the image area, W is the space bandwidth, αx, αy and Nx, Ny are respectively the image-space aperture angle and the resolved pixel number in the image-space of coordinate x and y. The color degrees of freedom Nc depend on the number of spectral channels, while polarization degrees of freedom Nϕ is determined by the independent polarization state. According to Eqs (28,31,33), the channel capacity of the con-ventional camera in our experiment (where 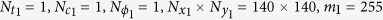 ) is
) is 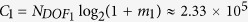 , and the corresponding transmitted information of Fig. 6(b) is
, and the corresponding transmitted information of Fig. 6(b) is 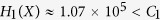 . In order to transmit the 520 ~ 580 nm wavelength ranges data, the required channel capacity of the conventional camera (where
. In order to transmit the 520 ~ 580 nm wavelength ranges data, the required channel capacity of the conventional camera (where 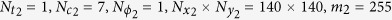 ) is C ≈ 1.63 × 106, while the required channel capacity in GISC spectral camera with 30% sampling rate in our experiment is C3 ≈ 4.90 × 105. C3 < C2 shows that GISC spectral camera has the higher information acquisition efficiency in a single exposure compared to the conventional camera. With the development of optical imaging technology, many new imaging technologies (such as CT image46) are not based on the point-to-point imaging mode. However, because the correlation between pixels of image data doesn’t be applied in the imaging reconstruction algorithm, the information acquisition efficiency of those new coding imaging technology also can’t approaching the Shannon Limit determined by Information Theory for conventional optical imaging instruments. However, GISC imaging solution applies a spatial random phase modulation to satisfy the restricted isometry property (RIP)17 required by applying CS that makes the improvement of information acquisition efficiency of the imaging system possible. Comparing with CS imaging technology (such as Single-Pixel Imaging via Compressive Sampling47, coded aperture snapshot spectral imagers48), which forces on the compressive sampling of electric signal after photoelectric conversion to improve the channel capacity utilization efficiency of the electric signal, GISC imaging solution improves the optical channel capacity utilization efficiency and achieves the compressive sampling of the image data during the imaging acquisition process, which opens the way of approaching the Shannon Limit determined by Information Theory in optical imaging instruments. As a new optical imaging technology, GISC spectral camera provides a unique solution for the spectral imaging of dynamic processes. This GISC imaging solution may also be expanded to other multi-dimensional information (such as polarization information) acquisition49, ultra-fast measurement50, and super-resolution imaging18,51,52.
) is C ≈ 1.63 × 106, while the required channel capacity in GISC spectral camera with 30% sampling rate in our experiment is C3 ≈ 4.90 × 105. C3 < C2 shows that GISC spectral camera has the higher information acquisition efficiency in a single exposure compared to the conventional camera. With the development of optical imaging technology, many new imaging technologies (such as CT image46) are not based on the point-to-point imaging mode. However, because the correlation between pixels of image data doesn’t be applied in the imaging reconstruction algorithm, the information acquisition efficiency of those new coding imaging technology also can’t approaching the Shannon Limit determined by Information Theory for conventional optical imaging instruments. However, GISC imaging solution applies a spatial random phase modulation to satisfy the restricted isometry property (RIP)17 required by applying CS that makes the improvement of information acquisition efficiency of the imaging system possible. Comparing with CS imaging technology (such as Single-Pixel Imaging via Compressive Sampling47, coded aperture snapshot spectral imagers48), which forces on the compressive sampling of electric signal after photoelectric conversion to improve the channel capacity utilization efficiency of the electric signal, GISC imaging solution improves the optical channel capacity utilization efficiency and achieves the compressive sampling of the image data during the imaging acquisition process, which opens the way of approaching the Shannon Limit determined by Information Theory in optical imaging instruments. As a new optical imaging technology, GISC spectral camera provides a unique solution for the spectral imaging of dynamic processes. This GISC imaging solution may also be expanded to other multi-dimensional information (such as polarization information) acquisition49, ultra-fast measurement50, and super-resolution imaging18,51,52.
Additional Information
How to cite this article: Liu, Z. et al. Spectral Camera based on Ghost Imaging via Sparsity Constraints. Sci. Rep. 6, 25718; doi: 10.1038/srep25718 (2016).
Footnotes
Author Contributions The scheme of GISC spectral camera was proposed by S.H., J.W. and Z.L. based on the preliminary work of [16]. The experiment and theoretical derivation were completed by Z.L., with help from J.W., E.L. and X.S. S.T. developed the reconstruction algorithm, with help from E.L. The suggestion of understanding the GISC scheme from the view point of information theory is proposed by S.H. The manuscript was written by Z.L., S.T. and S.H. All authors agreed on the final content of the manuscript.
References
- Jacobs E., Fisher Y. & Boss R. Image compression: A study of the iterated transform method. Signal Process. 29, 251–263 (1992). [Google Scholar]
- SHANNON C. A mathematical theory of communication. Bell Sys. Tech. Jour. 27, 397–423, 623–656 (1948). [Google Scholar]
- Cover T. M. & Thomas J. A. Elements of information theory 657–687 (John Wiley & Sons, 2012). [Google Scholar]
- Elias P. Optics and communication theory. JOSA 43, 229–232 (1953). [Google Scholar]
- Francia G. Resolving power and information. JOSA 45, 497–499 (1955). [Google Scholar]
- Di Francia G. T. Degrees of freedom of an image. JOSA 59, 799–804 (1969). [DOI] [PubMed] [Google Scholar]
- Tan W. Optical information theory-retrospect and prospect. Optics Precis. Eng. 3, 17–22 (1982). [Google Scholar]
- Huck F. O., Fales C. L., Alter-Gartenberg R., Park S. K. & Rahman Z.-u. Information-theoretic assessment of sampled imaging systems. Opt. Eng. 38, 742–762 (1999). [Google Scholar]
- Strange B. A., Duggins A., Penny W., Dolan R. J. & Friston K. J. Information theory, novelty and hippocampal responses: unpredicted or unpredictable? Neural Netw. 18, 225–230 (2005). [DOI] [PubMed] [Google Scholar]
- Kolobov M. I. Quantum imaging 79–110 (Springer Science & Business Media, 2007). [Google Scholar]
- Shapiro J. H. & Boyd R. W. The physics of ghost imaging. Quantum Inf. Process. 11, 949–993 (2012). [Google Scholar]
- Gonzalez R. C., Woods R. E. & Eddins S. L. Digital image processing using MATLAB (Pearson Education India, 2004). [Google Scholar]
- Donoho D. L. Compressed sensing. IEEE Trans. Inform. Theory 52, 1289–1306 (2006). [Google Scholar]
- Candès E. J., Romberg J. & Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory 52, 489–509 (2006). [Google Scholar]
- Eldar Y. C. & Kutyniok G. Compressed sensing: theory and applications (Cambridge University Press, 2012). [Google Scholar]
- Wu J. et al. Snapshot compressive imaging by phase modulation. Acta Phys. Sin-CH ED 34, 1011005 (2014). [Google Scholar]
- Gong W. & Han S. Experimental investigation of the quality of lensless super-resolution ghost imaging via sparsity constraints. Phys. Lett. A 376, 1519–1522 (2012). [Google Scholar]
- Wang H., Han S. & Kolobov M. I. Quantum limits of super-resolution of optical sparse objects via sparsity constraint. Opt. Express 20, 23235–23252 (2012). [DOI] [PubMed] [Google Scholar]
- Gong W. & Han S. High-resolution far-field ghost imaging via sparsity constraint. Sci. Rep. 5, 9280 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun B. et al. 3d computational imaging with single-pixel detectors. Science 340, 844–847 (2013). [DOI] [PubMed] [Google Scholar]
- Zhao C. et al. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 101, 141123 (2012). [Google Scholar]
- Gong W. et al. Three-dimensional ghost imaging ladar. arXiv preprint arXiv:1301.5767 (2013).
- Gong W. & Han S. Correlated imaging in scattering media. Opt. Lett. 36, 394–396 (2011). [DOI] [PubMed] [Google Scholar]
- Bina M. et al. Backscattering differential ghost imaging in turbid media. Phys. Rev. Lett. 110, 083901 (2013). [DOI] [PubMed] [Google Scholar]
- Magaña-Loaiza O. S., Howland G. A., Malik M., Howell J. C. & Boyd R. W. Compressive object tracking using entangled photons. Appl. Phys. Lett. 102, 231104 (2013). [Google Scholar]
- Chen W. & Chen X. Object authentication in computational ghost imaging with the realizations less than 5% of nyquist limit. Opt. Lett. 38, 546–548 (2013). [DOI] [PubMed] [Google Scholar]
- Xu X., Li E., Yu H., Gong W. & Han S. Morphology separation in ghost imaging via sparsity constraint. Opt. Express 22, 14375–14381 (2014). [DOI] [PubMed] [Google Scholar]
- Cheng J. & Han S. Incoherent coincidence imaging and its applicability in x-ray diffraction. Phys. Rev. Lett. 92, 093903 (2004). [DOI] [PubMed] [Google Scholar]
- Zhang M. et al. Lensless fourier-transform ghost imaging with classical incoherent light. Phys. Rev. A 75, 021803 (2007). [Google Scholar]
- Wang H. & Han S. Coherent ghost imaging based on sparsity constraint without phase-sensitive detection. Europhys. Lett. 98, 24003 (2012). [Google Scholar]
- Zhang D., Zhai Y.-H., Wu L.-A. & Chen X.-H. Correlated two-photon imaging with true thermal light. Opt. Lett. 30, 2354–2356 (2005). [DOI] [PubMed] [Google Scholar]
- D’Angelo M. & Shih Y. Quantum imaging. Laser Phys. Lett. 2, 567–596 (2005). [Google Scholar]
- Liu X.-F. et al. Lensless ghost imaging with sunlight. Opt. Lett. 39, 2314–2317 (2014). [DOI] [PubMed] [Google Scholar]
- Giglio M., Carpineti M. & Vailati A. Space intensity correlations in the near field of the scattered light: a direct measurement of the density correlation function g (r). Phys. Rev. Lett. 85, 1416 (2000). [DOI] [PubMed] [Google Scholar]
- Cerbino R. et al. X-ray-scattering information obtained from near-field speckle. Nat. Phys. 4, 238–243 (2008). [Google Scholar]
- Goodman J. W. Introduction to Fourier optics 154–160 (Roberts and Company Publishers, 2005). [Google Scholar]
- Cheng C.-F., Qi D.-P., Liu D.-L. & Teng S.-Y. The computational simulations of the gaussian correlation random surface and its light-scattering speckle field and the analysis of the intensity probability density. Acta Phys. Sin-CH ED 48, 1635–1643 (1999). [Google Scholar]
- Gatti A., Brambilla E., Bache M. & Lugiato L. A. Ghost imaging with thermal light: comparing entanglement and classicalcorrelation. Phys. Rev. Lett. 93, 093602 (2004). [DOI] [PubMed] [Google Scholar]
- Chan K. W. C., O’Sullivan M. N. & Boyd R. W. High-order thermal ghost imaging. Opt. Lett. 34, 3343–3345 (2009). [DOI] [PubMed] [Google Scholar]
- Gong W. & Han S. A method to improve the visibility of ghost images obtained by thermal light. Phys. Lett. A 374, 1005–1008 (2010). [Google Scholar]
- Ferri F., Magatti D., Lugiato L. & Gatti A. Differential ghost imaging. Phys. Rev. Lett. 104, 253603 (2010). [DOI] [PubMed] [Google Scholar]
- Oymak S., Jalali A., Fazel M., Eldar Y. C. & Hassibi B. Simultaneously structured models with application to sparse and low-rank matrices. IEEE Trans. Inform. Theory 61, 2886–2908 (2015). [Google Scholar]
- Golbabaee M. & Vandergheynst P. Compressed sensing of simultaneous low-rank and joint-sparse matrices. arXiv preprint arXiv:1211.5058 (2012).
- Golbabaee M. & Vandergheynst P. Joint trace/tv norm minimization: A new efficient approach for spectral compressive imaging. In Image Processing (ICIP), 2012 19th IEEE International Conference on, 933–936 (IEEE, 2012).
- Zhang H., He W., Zhang L., Shen H. & Yuan Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Ceosci. Remote Sens. 52, 4729–4743 (2014). [Google Scholar]
- Hsieh J. Computed tomography: principles, design, artifacts, and recent advances (SPIE: Bellingham, WA, , 2009). [Google Scholar]
- Duarte M. F. et al. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 25, 83 (2008). [Google Scholar]
- Kittle D., Choi K., Wagadarikar A. & Brady D. J. Multiframe image estimation for coded aperture snapshot spectral imagers. Appl. Optics 49, 6824–6833 (2010). [DOI] [PubMed] [Google Scholar]
- Morgan S. P. & Stockford I. Surface-reflection elimination in polarization imaging of superficial tissue. Opt. Lett. 28, 114–116 (2003). [DOI] [PubMed] [Google Scholar]
- Gao L., Liang J., Li C. & Wang L. V. Single-shot compressed ultrafast photography at one hundred billion frames per second. Nature 516, 74–77 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoho D. L. Superresolution via sparsity constraints. SIAM J. Math. Anal. 23, 1309–1331 (1992). [Google Scholar]
- Candès E. J. & Fernandez-Granda C. Towards a mathematical theory of super-resolution. Commun. Pur. Appl. Math. 67, 906–956 (2014). [Google Scholar]