Highlight
Combined gas exchange and carbon isotope discrimination measurement and modeling is used to detect and estimate the contribution of the C4 cycle in the C3-C4 intermediate species.
Key words: Carbon isotope discrimination, C3-C4, intermediate photosynthesis, Flaveria, F. brownii, F. floridana.
Abstract
The presence and activity of the C4 cycle in C3-C4 intermediate species have proven difficult to analyze, especially when such activity is low. This study proposes a strategy to detect C4 activity and estimate its contribution to overall photosynthesis in intermediate plants, by using tunable diode laser absorption spectroscopy (TDLAS) coupled to gas exchange systems to simultaneously measure the CO2 responses of CO2 assimilation (A) and carbon isotope discrimination (Δ) under low O2 partial pressure. Mathematical models of C3-C4 photosynthesis and Δ are then fitted concurrently to both responses using the same set of constants. This strategy was applied to the intermediate species Flaveria floridana and F. brownii, and to F. pringlei and F. bidentis as C3 and C4 controls, respectively. Our results support the presence of a functional C4 cycle in F. floridana, that can fix 12–21% of carbon. In F. brownii, 75–100% of carbon is fixed via the C4 cycle, and the contribution of mesophyll Rubisco to overall carbon assimilation increases with CO2 partial pressure in both intermediate plants. Combined gas exchange and Δ measurement and modeling is a powerful diagnostic tool for C4 photosynthesis.
Introduction
C4 photosynthesis is a highly efficient carbon fixation system characterized by the presence of a biochemical carbon pump with the capacity of increasing the CO2 partial pressure (pCO2) at the site of ribulose 1,5-bisphosphate carboxylase/oxygenase (Rubisco) to concentrations higher than ambient air (Hatch et al., 1967; Hatch, 1987; Ehleringer et al., 1991). This increases photosynthetic rates and reduces photorespiration, potentially improving nitrogen and water use efficiency (Hibberd et al., 2008; Langdale, 2011). Most C4 species show a common anatomical pattern, called Kranz anatomy, that leads to the separation of enzyme functions in two compartments, the mesophyll and the bundle sheath cell (Brown, 1975). CO2 is first hydrated into bicarbonate in the mesophyll cell cytoplasm in a reversible reaction catalyzed by carbonic anhydrase (CA) (Badger and Price, 1994). Carbon is then fixed by phosphoenol pyruvate carboxylase (PEPC), localized exclusively in the mesophyll, into four-carbon acids that diffuse to the internally adjacent bundle sheath cell, where they are decarboxylated and the released CO2 is refixed by Rubisco.
The most productive crops, such as maize, sorghum and sugar cane, are C4 plants, exemplifying the higher efficiency of this system over the C3 photosynthetic pathway present in most plant species, including major crops like wheat and rice. For this reason, there is currently a strong interest in implementing the advantages of C4 photosynthesis in to C3 crops with the aim of increasing yield, to keep pace with the food needs of a growing world population (von Caemmerer et al., 2012; Karki et al., 2013; Leegood, 2013). This kind of approach is boosting research on genetic, biochemical and physiological aspects of C4 photosynthesis. However, the initial phases of these initiatives are not expected to produce fully functional C4 plants, but plants showing incomplete C4 phenotypes like those observed in C3-C4 intermediate species, which have been considered remnants of the evolution from C3 ancestors to C4 plants (Rawsthorne, 1992; Sage et al., 2011). They show Kranz or Kranz-like leaf anatomy, but the activity of C4-related enzymes, such as PEPC, is lower compared to strict C4 plants, and enzyme compartmentation is incomplete, with Rubisco and PEPC present in both the mesophyll and the bundle sheath cells (Cheng et al., 1988; Brown and Hattersley, 1989; Byrd et al., 1992). These factors reduce the efficiency of the carbon concentrating mechanism. In intermediate plants, a photorespiratory CO2 pump, also known as the C2 cycle or glycine shuttle, transports glycine formed during mesophyll photorespiration to the bundle sheath where it is decarboxylated and the CO2 refixed, thus increasing overall CO2 assimilation rate and reducing the effect of photorespiration (Monson et al., 1984; Sage et al., 2012; Schulze et al., 2013; Keerberg et al., 2014). The genus Flaveria has been the focus of numerous studies in the past because it comprises C3, C4 and C3-C4 intermediate species, the later showing different degrees of C4 activity (Ku et al., 1983; McKown et al., 2005).
The C4 cycle contribution to growth has been difficult to quantify in intermediate species. In these plants, a steeper initial slope in the CO2 response of the CO2 assimilation rate compared to a strict C3 plantis expected. However, this trait is also affected by Rubisco content and its kinetic properties, so conclusions are not straightforward (von Caemmerer, 2000; von Caemmerer and Quick, 2000). Another important manifestation of C4 activity in intermediate species is a reduction of the O2 sensitivity of CO2 assimilation and the compensation point (Γ) due to a proportion of Rubisco being contained in the bundle sheath (BS) and thus not in direct contact with air (Byrd and Brown, 1989; Dai et al., 1996). With the photorespiratory pump causing a similar effect, separating and quantifying the contribution of each biochemical pathway through this approach is not possible. The C4 cycle activity relative to overall photosynthesis in intermediates has been estimated in the past by metabolite profiling, but recent reports indicate that metabolite accumulation is strongly dependent on the leaf zone sampled and its developmental stage (Monson et al., 1986; Leegood and von Caemmerer, 1994; Wang et al., 2014).
In order to develop a deeper understanding of the physiology of both natural and artificial C3-C4 intermediates, better tools are needed to evaluate the contribution of C4 photosynthesis to overall assimilation. One signature of the activity of PEPC as the initial CO2 fixation enzyme is a change in carbon isotopic discrimination (Δ) during photosynthesis. Whereas Rubisco has a strong preference for the lighter isotope, 12C, over the heavier isotope, 13C, PEPC is less discriminating, which causes an important difference in the biochemical fractionation between C3 and C4 plants (O’Leary, 1981; Farquhar, 1983). Incomplete C4 photosynthesis in C3-C4 intermediates is also reflected in Δ, with both PEPC and mesophyll Rubisco acting as the initial CO2 fixing enzymes and their relative activities determining the resulting Δ. Mathematical models describing CO2 assimilation and isotopic discrimination in these plants have been previously developed (von Caemmerer and Hubick, 1989; von Caemmerer, 1992). However, attempts to characterize Flaveria intermediate species by studying carbon-isotope ratios in dry matter resulted in C3-like profiles, and were interpreted as having little or no contribution of the C4 system to plant growth, which was in contradiction to results from metabolite analysis (Monson et al., 1988; Byrd et al., 1992).
Tunable diode laser (TDL) absorption spectroscopy allows relatively rapid measurements of Δ concurrently with gas exchange, and has been used to analyze and compare C3 and C4 species (Tazoe et al., 2011; von Caemmerer et al., 2014). The present work uses this technique, combined with mathematical modeling, as a tool to determine the presence and contribution of C4 photosynthesis in C3-C4 intermediate plants. An updated mathematical model of carbon isotope discrimination for C3-C4 intermediate species is proposed, which considers the effect of mesophyll conductance and allows the calculation of the biochemical fractionation. The strategy was applied to the study of Flaveria bidentis (C4), F. pringlei (C3), F. floridana (C3-C4) and F. brownii (C4-like). F. floridana has been described as a C2 plant with elevated PEPC activity, but it was unclear if a C4 cycle is actually contributing to total carbon assimilation in this species (Monson et al., 1986, 1988; Leegood and von Caemmerer, 1994; Dai et al., 1996). F. brownii, on the other hand, was initially considered a C4 species, but later experiments proved incomplete enzyme compartmentation, with a small proportion of Rubisco activity present in the mesophyll cells, and it was then reclassified as a C4-like intermediate species (Holaday et al., 1984; Monson et al., 1987; Moore et al., 1989). In the present study, concurrent Δ and gas exchange measurement and modeling allowed the detection and estimation of the C4 cycle in the intermediate species, proving itself as a powerful diagnostic tool for C4 photosynthesis.
Materials and methods
Plant material and growth conditions
Flaveria bidentis was propagated from seeds and F. pringlei, F. brownii and F. floridana were propagated from cuttings (Brown and Hattersley, 1989; Whitney et al., 2011). Plants were grown in 30 l pots in a garden soil mix fertilized with Osmocote (Scotts, Australia) in a glasshouse under natural light conditions, at 28/18°C day/night temperatures, respectively. Pots were watered daily.
Responses of CO2 assimilation rate and CO2 compensation point to O2 partial pressure
Two Li-Cor 6400XTs (Li-Cor, USA) were used to measure CO2 assimilation at a range of reference pCO2 (388, 0, 24, 48, 73, 97, 145, 194, 291, 388, 485, 582 and 776 μbar). N2 and O2 were mixed in different ratios by mass flow controllers (Omega Engineering Inc., USA) to generate a range of O2 partial pressures (pO2; 20, 50, 100, 200 and 300mbar) supplied to the LI-6400s. Response curves of CO2 assimilation rate (A) to intercellular pCO2 (Ci), A/C i curves, were repeated sequentially at each pO2. The measurements were made at 25°C, a flow rate of 500 μmol s−1 and 1500 μmol quanta m−2 s−1, inside a growth cabinet at 25°C. Four plants from each species were analyzed. The compensation point (Γ) was calculated from the A/C i curves at each pO2, as the intercellular CO2 concentration where net CO2 assimilation is zero.
To study the inhibitory effect of O2 on assimilation rate, we compared the CO2 assimilation rate at a reference pCO2 of 380 μbar at each pO2.
Concurrent gas exchange and Δ measurements and calculations of mesophyll conductance
Two Li-Cor 6400XTs (Li-Cor, USA) coupled to a tunable-diode laser absorption spectroscope (TDLAS, model TGA100A, Campbell Scientific, Inc., USA) as described in Tazoe et al. (2011) were used for concurrent measurements of gas exchange and carbon isotope discrimination (Bowling et al., 2003; Griffis et al., 2004; Pengelly et al., 2012; Evans and von Caemmerer, 2013). Plants were transferred from the glasshouse to a growth cabinet with fluorescence lights (TRIL1175, Thermoline Scientific Equipment, Australia) at 25°C and one young fully expanded leaf was placed in each of the 6cm2 leaf chambers. Measurements were made at a leaf temperature of 25°C, a flow rate of 200 μmol s−1, 1500 μmol quanta m−2 s−1 and 20mbar pO2. The desired pO2 was achieved as described above and supplied to the Li-Cors 6400. Reference pCO2 was changed stepwise to 392, 980, 686, 490, 294, 196, 98, 49 and 392 μbar and measurements were made every 4min for at least 30min at each pCO2. Dark respiration (R d) was measured at the end of an A/C i curve at 392 μbar pCO2 and 20mbar pO2 by switching off the Li-Cor lamp. Three or four plants from each species were analyzed. Δ was calculated as previously described (Evans et al., 1986; Evans and von Caemmerer, 2013).
Mesophyll conductance (g m) was calculated for F. pringlei from concurrent gas exchange and Δ measurements at the above range of reference pCO2 and 19mbar pO2, applying the equations previously described and including the ternary effects of transpiration rate (Farquhar and Cernusak, 2012; Evans and von Caemmerer, 2013). This method is only valid for C3 species. For intermediate and C4 species, we assumed the same CO2 response of g m found in F. pringlei, and scaled the absolute value at ambient pCO2 to obtain the best fit of the A and Δ models for the observed results (see Results section).
Mathematical models
The overall rate of net CO2 assimilation (A) for C3-C4 intermediate plants was previously described (von Caemmerer, 1992, 2013):
| (1) |
where A m is the assimilation in the mesophyll and A s is the assimilation in the bundle sheath, which are defined as:
| (2) |
| (3) |
so:
| (4) |
where V p is PEPC carboxylation and β is the fraction of the CO2 produced from photorespiration in the mesophyll (F m) that is released in the bundle sheath. For simplification, bundle sheath respiration and photorespiration are not taken into account in eq. 4. The term L is the leak rate of CO2 out of the bundle sheath, and can be expressed as:
| (5) |
and
| (6) |
where ϕ (leakiness) is the ratio of the leak rate of CO2 out of the bundle sheath and the supply rate of CO2 to the bundle sheath . When pO2 is low, F m can be considered 0.
V m and R m are Rubisco carboxylation and day respiration in the mesophyll, respectively. V p and V m are calculated as described in von Caemmerer (2000):
| (7) |
| (8) |
and
| (9) |
where C m and C i are mesophyll and intercellular pCO2, respectively. K c and K o are the Michaelis-Menten constants for CO2 and O2 respectively, expressed as a partial pressure. Although the pCO2 in the cytosol (site of PEPC carboxylation) and the chloroplast (site of Rubisco carboxylation) of the mesophyll cell are presumably different due to diffusional limitations, the same value (C m) was assumed in both compartments (von Caemmerer, 2000, 2013; Tholen and Zhu, 2011).
When the rate of PEP regeneration is limiting, V p=V pr, where V pr is a constant. V m,max is the maximum Rubisco carboxylation in the mesophyll, and V p,max is the maximum PEPC carboxylation (Table 1). When RuBP becomes limiting, V m in eq. 6 can be given by an electron transport limited rate (W j), as previously described (von Caemmerer, 2000, 2013).
Table 1.
Values assigned to variables for model fitting purposes
When fitting F. brownii as a strict C4 and F. floridana as a strict C3 species, values were assigned to obtain the best fitting without considering measured enzyme activities.
| Variable | Definition | F. pringlei | F. bidentis | F. brownii | F. brownii (strict C 4) | F. floridana | F. floridana (strict C 3) | Origin of the value |
|---|---|---|---|---|---|---|---|---|
| a | Fractionation during diffusion in air (‰) | 4.4 | 4.4 | 4.4 | 4.4 | 4.4 | 4.4 | Farquhar (1983) |
| ab | Fractionation during diffusion through the boundary layer (‰) | 2.9 | 2.9 | 2.9 | 2.9 | 2.9 | 2.9 | Griffiths et al. (2007) |
| abs | Leaf absorptance | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | von Caemmerer (2000) |
| al | Fractionation during diffusion in water (‰ | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | Griffiths et al. (2007) |
| β | Fraction of the photorespired CO2 released in the bundle sheath | 1 | 1 | 1 | 1 | 1 | 1 | Assigned |
| b3 | Fractionation during carboxylation by Rubisco (‰) | 29 | 29 | 29 | 29 | 29 | 29 | Roeske and O’Leary (1984) |
| b4 | Combined fractionation by the C4 cycle (‰) | na | −5.7 | −5.7 | −5.7 | −5.7 | na | O’Leary (1981) |
| bs | Fractionation during CO2 dissolution in water (‰ | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 | von Caemmerer (1992) |
| c | gm scaling constant | 0.666a | 0.8b | 0.666b | 0.666b | 0.78b | 0.78b | a, measured in this work; b, assigned from model fitting |
| e | fractionation during mitochondrial respiration | 2.91 | 3.54 | 3.51 | 3.51 | 3.72 | 3.72 | Calculated as e=δ13Ccylinder-δ13Catmosphere |
| F | Correction coefficient for spectral quality | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | von Caemmerer (2000) |
| Jt | Total electron transport rate (μmol electrons m−2 s−1) | 120 | 400 | 440 | 700 | 250 | 0 | Assigned [von Caemmerer (2000), eq. 5.17] |
| Jm | Electron transport rate allocated to mesophyll C3 cycle | 120 | 0 | 40 | 0 | 200 | 240 | Assigned [von Caemmerer (2000), eq. 5.17] |
| KC | Rubisco Michaelis–Menten constant for CO2 (μbar) | 359 | 605 | 383 | 383 | 395 | 395 | Kubien et al. (2008) |
| KO | Rubisco Michaelis–Menten constant for O2 (μbar) | 528 000 | 507 000 | 300 000 | 300 000 | 544 000 | 544 000 | Kubien et al. (2008) |
| KP | PEPC Michaelis–Menten constant for PEP (μbar) | n.a. | 80 | 80 | n.a. | 80 | n.a. | Bauwe (1986) |
| Rd | Mitochondrial respiration (μmol m−2 s−1) | 0.6 | 0.4 | 1.3 | 1.3 | 1.7 | 1.7 | Measured in the dark in this work |
| s | Fractionation during leakage (‰) | n.a. | 1.8 | 1.8 | 1.8 | 1.8 | n.a. | von Caemmerer (1992) |
| Vm, max | Maximum Rubisco carboxylation rate in the mesophyll (μmol m−2 s−1) | 60a | 0b | 15b | 0b | 90a | 130b | a, measured in this work; b, assigned |
| VP, max | Maximum PEP carboxylation rate (μmol m−2 s−1) | 0a | 90a | 80a | 80b | 15a | 0b | a, measured in this work; b, assigned |
| VPr | PEP regeneration rate (μmol m−2 s−1) | 0 | 36 | 32 | 50 | 8 | 0 | Assigned |
| φ | Leakiness | n.a. | 0.28 | 0.21 | 0.3 | 0.40 | n.a. | Assigned from model fitting |
| θ | Empirical curvature factor | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | Ubierna et al. (2011) |
n.a., not applicable.
Theory developed by Farquhar et al. (1982) and Farquhar (1983) showed that photosynthetic carbon isotope discrimination can be described by equations having diffusion and biochemistry dependent terms. The equation of Δ presented by (Griffiths et al., 2007), which takes into account the effect of g m, was modified to incorporate the ternary effects of transpiration rate as suggested by Farquhar and Cernusak (2012):
| (10) |
where a l is the fractionations during diffusion in water and b s is the fractionation as CO2 enters solution. The term , where E denotes the transpiration rate and the total conductance to CO2 diffusion including boundary layer and stomatal conductance. The symbol aʹ denotes the combined fractionation during diffusion in the boundary layer and in air, and is calculated as:
| (11) |
where a is the fractionation during diffusion in air, a b is the fractionation during diffusion in the boundary layer, and C a, C l, C i are the pCO2 in the air, leaf surface and intercellular space respectively. The biochemical fractionation, Δ bio, is the integrated net biochemical discrimination, and depends on the biochemistry of net CO2 uptake (Griffiths et al., 2007).
When Δ and g m are known, Δ bio can be solved from equation 10, resulting in:
| (12) |
Because g m was obtained from combined measurement of Δ and gas exchange in the C3 species F. pringlei, Δ and g m are not independent and we could not estimate Δ bio from eq. 12. For the intermediate and C4 species, g m was calculated independently of the Δ measurements as described in the Materials and Methods section, so Δ bio could be estimated from eq. 12 for F. floridana, F. brownii and F. bidentis.
For modeling purposes, or when Δ is unknown, Δ bio can be derived from von Caemmerer’s (1992) equation A17:
where R i and R p are the molar abundance ratios of 13C/12C in the intercellular space and the photosynthetic product, respectively.
Thus:
| (13) |
The factor b 3 is the Rubisco fractionation, and b 4 is the combined fractionation of PEP carboxylation and the preceding isotope equilibrium during dissolution of CO2 and conversion to bicarbonate; s is the fractionation during leakage of CO2 out of the bundle sheath; e is the fractionation during mitochondrial respiration; f is the fractionation during photorespiration; R m and R s are the mitochondrial respiration rates in the mesophyll and the bundle sheath in the light, respectively. It was assumed that R d=R m+R s, and R m=R s=0.5R d. The factors F m and F s are the photorespiration rates derived from Rubisco oxygenation in the mesophyll and the bundle sheath, respectively. When pO2 is low, F m and F s are close to 0, so equation 13 simplifies to:
| (14) |
The parameter e needs to account for differences between the isotopic composition of CO2 during plant growth and during the measurements, because the substrates used during respiration are most likely carbohydrates assimilated before the experiment (Wingate et al., 2007). No fractionation during mitochondrial respiration was assumed in this work, so e was calculated as the difference between δ13C in the CO2 cylinder used during the experiments and δ13C in the atmosphere during growth conditions (e=δ13Ccylinder-δ13Catmosphere) (Tazoe et al., 2009; Pengelly et al., 2010). In this work, δ13Ccylinder was between −4.12‰ and −5.14‰, and δ13Catmosphere was assumed to be −8‰ (Table 1).
In vitro enzyme activity assays
Leaf discs (0.5cm2) were collected from the leaves used for gas exchange experiments and frozen in liquid nitrogen immediately after the experiment. Soluble protein was extracted by grinding one frozen leaf disc in a cold Tenbroeck homogenizer with 0.5ml extraction buffer [50mM HEPES, 1mM EDTA, 0.1% (v/v) Triton X-100, 10mM DTT, 1% (w/v) PVPP, 1% (v/v) protease inhibitor cocktail (Sigma), pH 7.8]. Extracts were centrifuged at 13000rpm for 30s. Spectrophotometric assays were performed to determine Rubisco and PEPC activities as described in Pengelly et al. (2010).
CA activity was measured in the same extract used for PEPC and Rubisco activity measurements, using a membrane inlet mass spectrometer to measure the rates of 18O exchange from labeled 13C18O2 to H2 16O at 25°C with a subsaturating total carbon concentration of 1mM (Badger and Price, 1989; von Caemmerer et al., 2004; Cousins et al., 2008). The hydration rates were calculated from the enhancement in the rate of 18O loss over the uncatalyzed rate, and the nonenzymatic first-order rate constant was applied at pH 7.4 (k c=6.22x10−11/[H+]+3.8x10−2=0.0396), appropriate for the mesophyll cytosol, at a CO2 concentration of 8μM, which is approximately the CO2 concentration in the mesophyll of F. bidentis (Jenkins et al., 1989; von Caemmerer et al., 2004). When CA is in the chloroplast, which is tipically the case in C3 plants like F. pringlei, our calculations underestimate its in planta activity by ~10% due to the effect of the higher chloroplastic pH on k c (k c=0.0442 at pH 8).
Results
O2 response of CO2 assimilation rate and compensation point
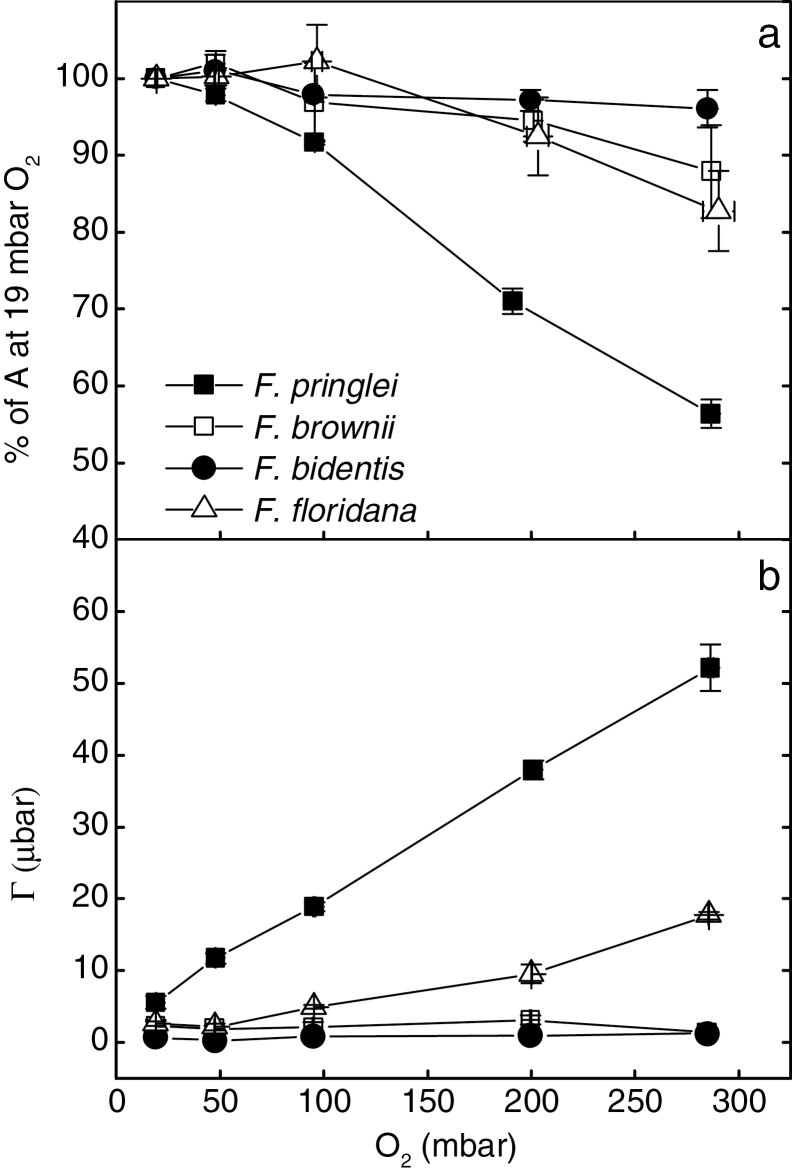
The effect of pO2 on CO2 assimilation rate and the compensation point (Γ) was measured at 380 μbar reference CO2, an irradiance of 1500 μmol quanta m−2 s−1 and 25 °C (Fig. 1).
Fig. 1.
The responses of (a) CO2 assimilation rate, A and (b) compensation point (Γ) in F. pringlei, F. floridana, F. brownii and F. bidentis to changes in atmospheric pO2. Assimilation rate is expressed as a percentage of the assimilation rate at 19mbar O2 (average of 28.7±1.13 μmol m−2 s−1 for F. pringlei, 24.2±1.52 for F. floridana, 20.6±1.2 for F. brownii and 21.7±0.49 for F. bidentis). Measurements were made at 25°C and 385 μbar CO2 (R), and an irradiance of 1500 μmol m−2 s−1. Values represent averages and standard error of four replicates.
In F. pringlei, increasing pO2 caused a decrease in CO2 assimilation rate, a response typical of a C3 plant. Consistent with this, the Γ increased with increasing pO2, ranging from 5.6 ubar at 19mbar O2 to 53 µbar at 285mbar O2.
In the C4 species F. bidentis, the effect of oxygen was very small, with only a 5% decrease in CO2 assimilation rate at the highest tested pO2. Γ in these plants barely changed with pO2, and ranged from 0.2 to 1.2 μbar.
The effect of O2 on Γ in F. brownii was also very small and similar to the C4 species F. bidentis, ranging from 1.3 to 3.1 μbar (Fig. 1b). However, the inhibitory effect of O2 on CO2 assimilation rate was more pronounced, and resulted in an intermediate response of CO2 assimilation rate to increasing pO2 (Fig. 1a).
The O2 response of Γ in F. floridana was intermediate between C3 and C4 species (2.3–18μbar; Fig. 1b), as has been previously shown (Ku et al., 1991). However, in our experiments the inhibitory effect of O2 on photosynthesis was smaller than that previously reported by these authors and strikingly similar to that in F. brownii when pO2 was 200mbar or lower, despite the important differences in the enzyme compartmentation between these two species (Fig. 1a). Only at 290mbar O2 the inhibition of photosynthesis was higher for F. floridana, with a reduction of a 22%, compared to that in F. brownii (15% inhibition).
Stomatal conductance and C i increased slightly with pO2, with the exception of F. bidentis, which remained stable, and were considerably higher in the C3 species F. pringlei at any pO2 (Supplementary Fig. S1 at JXB online).
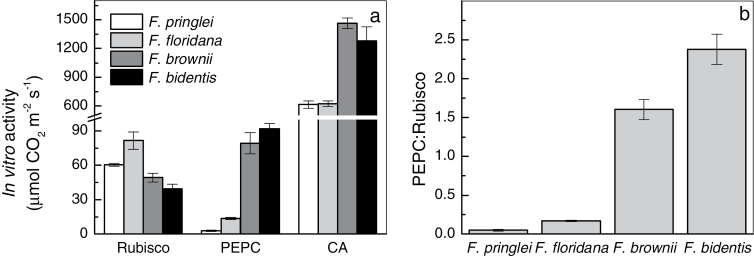
Rubisco, PEPC and CA activity
In vitro Rubisco, PEPC and CA activities were analyzed in extracts from the same leaves on which the concurrent gas exchange and Δ measurements were made (Fig. 2). Rubisco activity was higher in F. floridana (average of 74.9 μmol m−2 s−1), followed by F. pringlei (60.5 μmol m−2 s−1), F. brownii (49.2 μmol m−2 s−1) and F. bidentis (39.7 μmol m−2 s−1). PEPC activity was lowest in F. pringlei (2.9 μmol m−2 s−1) and, notably, four times higher in F. floridana (13.8 μmol m−2 s−1). F. brownii showed a PEPC activity closer to that of F. bidentis (79.3 and 91.8 μmol m−2 s−1 respectively). CA activity was similar and high in F. bidentis and F. brownii (1278.7 and 1464.5 μmol m−2 s−1 respectively), and lower in F. pringlei and F. floridana (614.9 and 623.6 μmol m−2 s−1 respectively).
Fig. 2.
(a) In vitro Rubisco, PEPC and CA activities in F. pringlei, F. floridana, F. brownii and F. bidentis, measured from samples of the same leaves used for gas exchange and expressed on a leaf area basis. (b) PEPC to Rubisco activity ratio in these experiments. Values represent mean and standard error of four experimental replicates.
The relative activity of PEPC to Rubisco was lowest in F. pringlei and highest in F. bidentis (Fig. 2b). F. floridana showed a PEPC:Rubisco ratio 3.4 times greater than the C3 species, and F. brownii was closer to the C4 species.
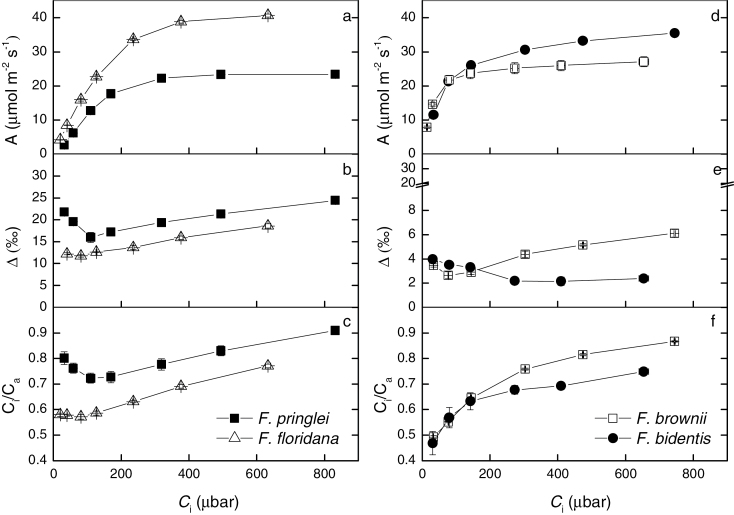
CO2 assimilation rate and carbon isotope discrimination
Measurements of carbon isotope discrimination concurrently with gas exchange were performed under a range of CO2 concentrations at 19mbar O2 on 3–4 plants from each species (Fig. 3). At this low pO2, photorespiration is greatly reduced and the effect of the C2 cycle is negligible. Thus, small differences in the level of C4 activity or mesophyll Rubisco activity are easier to detect.
Fig. 3.
Concurrent measurements of (a, d) CO2 assimilation rate, A, (b, e) carbon isotope discrimination, Δ, and (c, f) the ratio of intercellular to ambient CO2, C i/C a, as a function of intercellular CO2 (C i) in F. pringlei, F. floridana, F. brownii and F. bidentis. Values represent averages and standard error of 4 replicates. Measurements were made at 19 mbar O2, a leaf temperature of 25°C and an irradiance of 1500 μmol m−2s−1.
F. pringlei and F. bidentis showed the typical C3 and C4 response of CO2 assimilation rate to increasing C i, respectively (Fig. 3a). The initial slope of the A/C i curve in F. floridana was closer to that in the C3 species, F. pringlei, whereas that of F. brownii was more similar to that of the C4 species, F. bidentis, although in both intermediate species the sharp saturation typical of the C4 species was missing. The maximum apparent assimilation rates in both intermediates were higher than those of the C3 and C4 species.
Carbon isotope discrimination measured over the defined range of pCO2 provided clear differences between the four species (Fig. 3b). Δ was greatest in F. pringlei at any C i, ranging from 16‰ to 24.4‰. Discrimination in F. floridana followed a similar trend than that in the C3 species, with Δ generally increasing with C i, but Δ was lower than in F. pringlei across the whole experimental range, ranging from 12.2‰ to 18.6‰. The response of C i/C a to CO2 concentration was parallel to that of Δ in F. pringlei and F. floridana, reflecting the strong dependence of Δ on the ratio C i/C a in C3 species and also in F. floridana (Fig. 3c). The initial decrease of Δ in F. pringlei is also caused by a drop in C i/C a, which is in turn driven by a reduction of stomatal conductance with increasing C i when C i is lower than 200μbar.
In F. bidentis, as expected from a C4 plant, discrimination was low (2–4‰) and decreased slightly with increasing C i. Δ in F. brownii was similar to F. bidentis at C i under 95 μbar (3.5–2.6‰), but above that the value of Δ increased with increasing C i, to a maximum of 6.1‰.
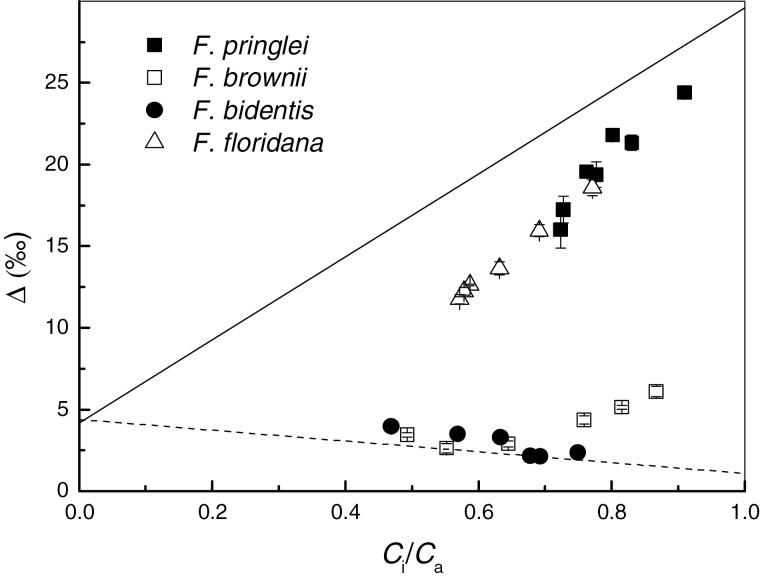
Measured Δ is shown with respect to C i/C a in Fig. 4. The theoretical lines assume infinite mesophyll conductance, which explains why both F. pringlei and F. floridana fell below the theoretical response for C3 plants, with Δ and C i/C a generally lower in F. floridana. In F. bidentis, the result was as predicted by a theoretical CO2 response of Δ for a C4 plant when whereas F. brownii only fitted the expected response at low C i/C a, with Δ higher than predicted at high C i/C a.
Fig. 4.
Observed carbon isotope discrimination, Δ expressed as a function of the ratio of intercellular to ambient CO2, C i/C a, in F. pringlei, F. floridana, F. brownii and F. bidentis. Values are the same as plotted in Fig. 3. Solid line represents the theoretical response of Δ to C i/C a in C3 plants ( ; (Roeske and O’Leary, 1984; Evans et al., 1994). Dashed line represents the theoretical response of Δ to C i/C a in C4 plants, (Henderson et al., 1992) when φ=0.25.
Modeling CO2 assimilation rate and carbon isotope discrimination in C3-C4 intermediate species
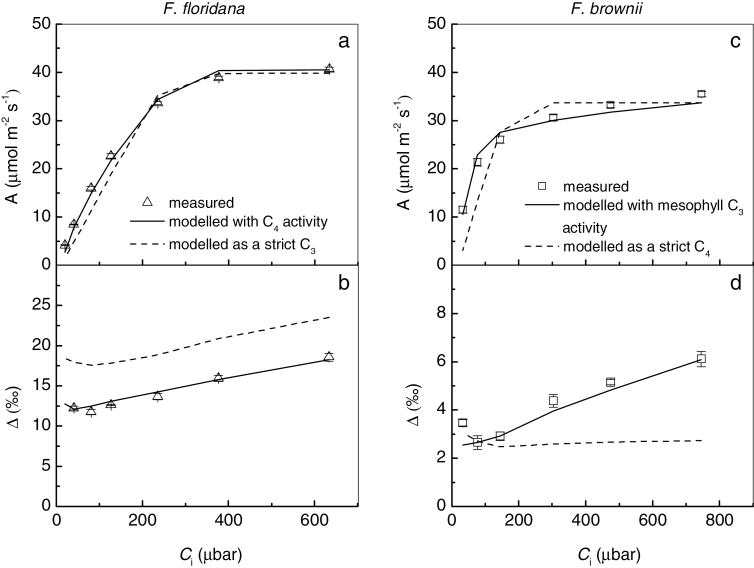
In order to evaluate the contribution of the C4 cycle to overall photosynthesis in the intermediate species F. floridana and F. brownii, the mathematical models proposed here for A and Δ responses to C i (eqs 6 and 10, respectively) were fitted concurrently to the observed results (Fig. 5). By simultaneously fitting both models using the same set of parameters, the accuracy of the predictions increases because some combinations of assigned constants that may result in a good fit for one of the models are unacceptable for the other. For comparison, the same strategy was also applied to the C3 and C4 species (see Supplementary Fig. S2).
Fig. 5.
Comparison between modeled and measured responses of CO2 assimilation rate, A, and carbon isotope discrimination, Δ, to variation in intercellular pCO2, C i, in the C3-C4 intermediate species F. floridana and F. brownii. Measured A (a) and Δ (b) as a function of C i in F. floridana (empty triangles), compared with the modeled responses predicted by C3-C4 photosynthetic model assuming an active C4 cycle (solid lines) or no C4 cycle activity (dashed lines). Measured A (c) and Δ (d) as a function of C i in F. brownii (white squares), compared with the modelled responses using the C3-C4 models assuming Rubisco activity in the mesophyll cells (solid lines) or a strict compartmentalization of Rubisco in the bundle sheath cells (dashed lines). Parameters used for model simulations are presented in Table 1.
Table 1 shows the values assigned for fitting purposes and their source. Rubisco K C and K O (Michaelis–Menten constants for CO2 and O2, respectively) in the four Flaveria species analyzed here have been previously reported (Kubien et al., 2008), and V c,max and V p,max are from our own in vitro experiments. We assigned reasonable values for maximum electron transport (J max). Leakiness was assigned so that the sum of the squares of the variances between the measured and modeled A, and between the measured and modeled Δ, was minimum. The distribution of Rubisco between the mesophyll and the bundle sheath in the intermediate species can be adjusted in the models by the assigned V m,max (maximum rate of Rubisco carboxylation in the mesophyll) value. When V m,max equals the V c,max observed in vitro, all Rubisco is in the mesophyll. A lower asigned V m,max indicates that part of the Rubisco activity is contained in the bundle sheath cells.
Mesophyll conductance (g m) for F. pringlei was calculated from concurrent gas exchange and carbon isotope discrimination measurements at 19mbar O2 and a range of reference pCO2 as previously described (Tazoe et al., 2011; Farquhar and Cernusak, 2012; Evans and von Caemmerer, 2013). Results show that g m decreases from 0.62±0.1 to 0.33±0.03mol m–2 s–1 bar–1 with increasing C i when atmospheric pCO2 is lower than ambient, and then remains stable at higher pCO2 (Fig. 6). The CO2 dependence of g m in F. pringlei is described by the polinomial function g m=10–6·C i 2−0.0013·C i+c, where c=0.666. In C4 and C3-C4 intermediate species, g m cannot be obtained from concurrent gas exchange and Δ 13C measurements, so the same CO2 dependence of g m was assumed for F. bidentis, F. brownii and F. floridana, and the constant c was calculated from model fitting so that the sum of variances between the measured and modeled A, and between the measured and modeled Δ, was minimum (Table 1). The resulting g m are shown in Fig. 6. Methods for obtaining g m in C4 and C3-C4 intermediate species, based on 18O discrimination measurements, are currently being developed (S. von Caemmerer, unpublished results).
Fig. 6.
Response of mesophyll conductance (g m) to changes in atmospheric pCO2. In F. pringlei, g m was calculated from concurrent gas exchange and Δ measurements made at 19mbar pO2. The values for F. floridana, F. brownii and F. bidentis were assigned assuming the same response of g m to C i as observed in F. pringlei, scaled from model fitting.
The A and Δ responses to increasing C i predicted with this strategy were reasonably close to the measured values for F. pringlei and F. bidentis (Supplementary Fig. S2).
In an exercise to prove the predictive value of these models for the presence of low levels of activity of the C4 component, we attempted to fit the models for F. floridana under two different premises. In one case, we assumed a certain level of effective C4 cycle contribution to overall carbon assimilation (Fig. 5a, b, solid lines). In the second case, we considered no C4 activity and values were assigned to obtain the best possible fitting ignoring the measured enzyme activities (Fig. 5a, b, dashed lines). The models could only be fitted to the measured values of Δ and A if some C4 activity, specified by a V p,max close to our in vitro measurements, was assumed.
A similar approach was used with F. brownii. In one case, the models were fitted assuming the presence of Rubisco in the mesophyll, and in the other case the model was fitted as if it were a strict C4 plant (Fig. 5c, d). The predicted responses approached the measured values only if ~30% of Rubisco activity was located in the mesophyll (V m,max =15 μmol m−2 s−1; observed in vitro V c,max =50 μmol m−2 s−1).
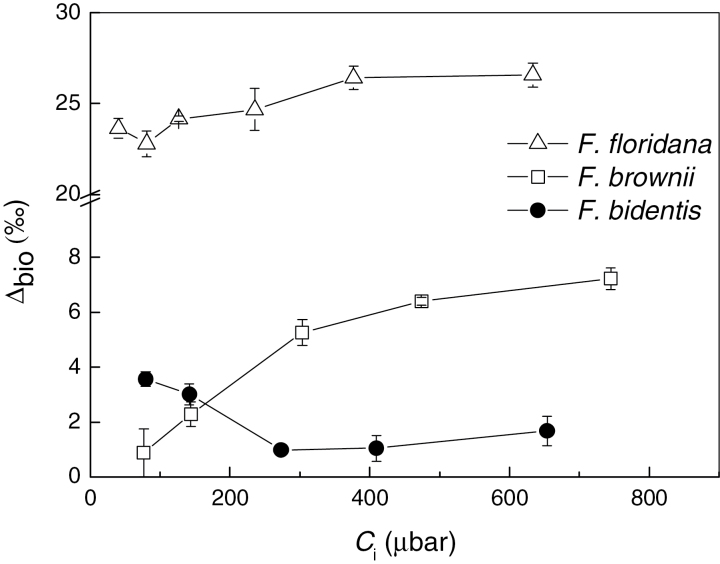
A comparison of Δ and Δ bio highlights the fact that CO2 diffusion processes have a large influence on Δ (Figs 3, 7). Δ bio was calculated from eq. 12 using gas exchange and Δ measured values. Calculation of Δ bio factors out the contribution from CO2 diffusion and shows that the biochemical fractionations are different in the species analyzed. In F. floridana, Δ bio was high and increasing with C i. In F. brownii, Δ bio also increased with increasing C i, whereas in the C4 species F. bidentis Δ bio generally decreases with C i.
Fig. 7.
Biochemical fractionation (Δ bio), as a function of intercellular CO2 (C i) in F. floridana, F. brownii and F. bidentis. Δ bio was calculated from eq. 12 using the combined gas exchange and Δ measurements shown in Fig. 3. Δ bio could not be calculated for F. pringlei because g m is obtained from Δ measurements in this species, so both factors are not independent. Values represent averages and standard error of four replicates.
The A and Δ responses to C i could be modeled assuming a constant g m without important differences (data not shown). However, the calculation of biochemical fractionation (Δ bio) from eq. 12 is dependent on g m, and thus the dependence of g m on C i must have an effect on Δ bio. To show the magnitude of this effect, the C i response of Δ bio was calculated from eq. 12 and the gas exchange and Δ measurements, assuming either variable g m, assigned as previously explained in this section, or constant g m, calculated as the average of the variable g m values obtained for each species (see Supplementary Fig. S3). As a reference, the C i response of Δ bio was calculated from eq. 14 (modelled Δ bio) after fitting the models for the C i responses of A and Δ using variable g m.
Estimation of the C4 (bundle sheath) photosynthesis contribution to total photosynthesis
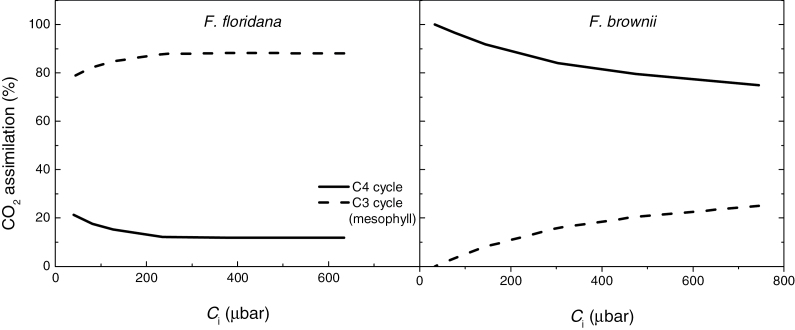
The relative contribution of the bundle sheath to total photosynthesis in the intermediate species was estimated from A s in eq. 2, after fitting the models to our observed results (Fig. 8). Because the experiments were performed under low O2, photorespiration is greatly reduced and it can be assumed that all the CO2 assimilated in the bundle sheath is transported by the C4 cycle. The contribution of the bundle sheath to total photosynthesis in both F. floridana and F. brownii decreased with increasing C i. In F. brownii, almost all carbon was fixed by Rubisco in the bundle sheath at very low C i, but up to 25% of fixation occurred via Rubisco in the mesophyll at high C i. In F. floridana, the maximum estimated contribution of the bundle sheath photosynthesis via the C4 cycle was 21% at very low C i and it dropped to 12% at the highest C i analyzed.
Fig. 8.
CO2 response of the estimated contribution of the C4 cycle and the mesophyll C3 cycle in the intermediate species F. floridana and F. brownii, expressed as a percent of total CO2 assimilation rate, under low pO2.
Discussion
Effect of O2 on carbon assimilation and compensation point
The oxygen responses of CO2 assimilation and the compensation point have been used in the past as a tool to identify and characterize C3-C4 intermediate species (Sayre and Kennedy, 1977; Monson et al., 1984; Dai et al., 1996; Vogan et al., 2007). As only mesophyll Rubisco is exposed to air oxygen, its effect on CO2 assimilation and Γ decreases with increasing proportions of the enzyme allocated to the bundle sheath. However, it is difficult to separate and quantify the effects of the C2 and C4 cycles from studies on the O2 response of CO2 assimilation, as both cycles contribute to reduce the negative effect of photorespiration in carbon assimilation and the compensation point. Moreover, the efficiency of the C2 cycle varies between different intermediate species, as does the contribution of the C4 cycle (Cheng et al., 1988; Keerberg et al., 2014).
In this work, the O2 response of carbon assimilation, and especially Γ, in F. brownii was very close to that of the C4 species F. bidentis. A highly efficient C2 cycle would have a greater impact on the O2 sensitivity of Γ than on carbon assimilation and that, combined with high in vitro PEPC and CA activities at the same level as the C4 species F. bidentis, eliminates the effect of pO2 on Γ almost completely (Cheng et al., 1988; Ku et al., 1991). Previous studies initially classified F. brownii as a C4 species, but it was later demonstrated that the enzyme compartmentation is incomplete in this plant (Monson et al., 1987; Ku et al., 1991). The small proportion of Rubisco present in the mesophyll is reflected in the sensitivity of assimilation rate to pO2.
CA activity in F. floridana is similar to F. pringlei but PEPC activity is four times higher (13.8 μmol m−2 s−1), consistent with Ku et al. (1991) and supporting the hypothesis of an active C4 cycle. However, PEPC activity is still low when compared with F. bidentis (91.8 μmol m−2 s−1), indicating that the activity of the C4 cycle in this plant is small. In our experiments, the O2 sensitivity of Γ in F. floridana is intermediate, and the O2 response of CO2 assimilation rate is remarkably close to that of F. brownii.
Previous studies have reported a C3-like O2 response in F. floridana (Dai et al., 1996; Monson et al., 1986), which differs from our observations. Although the reason for this discrepancy is not known, it must be noted that O2 sensitivity measurements are affected by variation of parameters like temperature or stomatal conductance between measurements at different pO2. These interactions increase the difficulty of estimating the activity of the C4 cycle from O2 response experiments.
Signature of C4 photosynthesis in the CO2 response of Δ in intermediate species
The different CO2 responses of Δ in the intermediate C3-C4 species, relative to the C3 or C4 species, can be attributed to the different ratios of PEPC/Rubisco activity in the mesophyll. The lower Δ observed in F. floridana, relative to F. pringlei, is partially attributable to a lower C i/C a, but their different Δ bio indicates an influence of the PEPC to Rubisco ratio, especially at low C i.
Interestingly, F. brownii and F. bidentis show similar Δ at low C i, but it increases in F. brownii with increasing pCO2 instead of decreasing as in the C4 plant. This particular response can be attributed to the activity of the small fraction of Rubisco in the mesophyll that would have a stronger influence at high pCO2. In F. floridana, Rubisco is abundant in the mesophyll but PEPC activity is low, and as a consequence the greatest effect of the C4 cycle activity is observed at very low pCO2, with a greater reduction of Δ compared to the C3 species. Both results indicate that the contribution of mesophyll Rubisco to overall assimilation is more important under high pCO2, and of the C4 cycle at low pCO2. The fact that environmental conditions affect the contribution of C4 photosynthesis may explain ambiguous results on previous analyses of dry matter δ13C in F. floridana and other intermediates, which showed C3-like ratios (Monson et al., 1988; Byrd et al., 1992). δ13C is a result of carbon discrimination during the leaf growth, thus it integrates the effect of variable environmental conditions. In the online experiments presented here, instant discrimination is measured under controlled conditions, highlighting their influence. By performing the analyses under low pO2, the effect of photorespiration and subsequent refixation through the C2 cycle is greatly reduced, emphasizing the differences in biochemical fractionation caused by the presence of C4 activity.
Although the CO2 response of A is also influenced by different relative activities of mesophyll Rubisco and PEPC, the effect of each enzyme in this case is difficult to separate. The greater initial slope of the A/C i curve in F. floridana, compared with F. pringlei, reflects the slightly greater PEPC activity detected in our in vitro assays, but could also be attributed to higher Rubisco activity. In the same sense, the initial slope of the A/C i curve in F. brownii and F. bidentis are similar and typically C4, whereas their Δ are different.
Concurrent model fitting reveals C4 activity in F. floridana
The strategy to evaluate the contribution of the C4 cycle to total carbon assimilation in intermediate species presented in this work is based on concurrently measuring and model-fitting the CO2 responses of carbon assimilation and discrimination.
Mathematical modeling has proved to be a powerful tool to get a deeper insight into the biochemical and physiological basis of the observed responses of carbon assimilation and discrimination, and it has been used to estimate parameters such as the maximum carboxylase activity of Rubisco in vivo (V C,max) and g m in C3 species, or V P,max and leakiness in C4 systems (Tazoe et al., 2011; Ubierna et al., 2011; Walker et al., 2013; Sharwood and Whitney, 2014). However, in most cases there is more than one unknown variable in the equations that represent those responses. This is especially problematic in intermediate species, where the number of factors affecting those responses is greater than in C3 or C4 plants. By concurrently fitting the CO2 responses of A and Δ in each experiment with the same set of constants, the range of values that can be assigned to these variables to obtain a satisfactory fitting is reduced. In this work, the activities of photosynthetic enzymes were analyzed in vitro to further reduce the number of unknowns, providing more accurate predictions. This method confirmed the presence of Rubisco activity in the mesophyll of F. brownii, which was already known (Cheng et al., 1988), but more interestingly indicated that F. floridana harbors an active C4 cycle. This C4 activity causes a change in the biochemical fractionation, compared to F. pringlei, which is evident at any C i analyzed. This is consistent with the increased activity of PEPC and previous observations based on 14CO2 pulse-chase experiments (Monson et al., 1986; von Caemmerer and Hubick, 1989). It is important to note that other studies based on δ13C analyses, metabolite dynamics and O2 response of carbon assimilation and Γ were unable to conclusively prove a contribution of the C4 cycle to overall photosynthesis in F. floridana, and the presence of a futile C4 cycle was proposed where most or all the CO2 released in the bundle sheath is not fixed and leaks back to the mesophyll (Monson et al., 1988; Leegood and von Caemmerer, 1994; Dai et al., 1996). However, other authors have already indicated that in F. floridana the C4 cycle may contribute up to 50% of the total CO2 fixation (Ku et al., 1991). In this work, the contribution of the mesophyll and the bundle sheath Rubisco to overall carbon assimilation was calculated for F. brownii and F. floridana. In both intermediate species, the contribution of the C4 cycle, or bundle sheath Rubisco, is highest at very low pCO2, and decreases with increasing pCO2. This reflects the lower apparent K c of PEPC compared to that of Rubisco (Bauwe, 1986; Kubien et al., 2008).
An improved equation describing CO2 response of Δ in intermediate species
An equation describing photosynthetic carbon isotope discrimination (Δ) that is applicable for C3, C4 and C3-C4 photosynthesis is provided and applied in this study. It allows the calculation of the biochemical fractionation occurring for the different photosynthetic pathways as a function of C i and takes into account g m and the ternary effects of transpiration rate. The biological relevance of g m, and its influence on Δ, has been reported extensively and incorporated in mathematical models for C3 species (Evans et al., 1986; von Caemmerer and Evans, 1991; Tazoe et al., 2011). When mesophyll conductance is considered in C3 species, C c (pCO2 at the site of Rubisco) can be estimated and is lower than C i, and this affects the estimates of Rubisco carboxylations. The same applies in intermediate species, where assimilation and discrimination by mesophyll Rubisco is dependent on the concentration of CO2 diffusing from the intercellular space. For model fitting purposes, the calculated C c was used as the available CO2 for both PEPC and mesophyll Rubisco in the case of the intermediate species. The models presented in this work assume that pCO2 is the same in the cytosol and the chloroplast.
The effect of pCO2 on g m has been studied by other authors, with results depending on the species analyzed. Whereas previous results showed that g m is not affected by pCO2 in wheat (Tazoe et al., 2009), other authors reported an inverse correlation in several C3 species (Flexas et al., 2007; Tazoe et al., 2011). We observed that g m is dependent on pCO2 in the C3 F. pringlei, and assumed that the same is true for the C4 and intermediate species analyzed. Although the effect of using either constant or variable g m on the models of the CO2 responses of carbon assimilation and discrimination has only a minor effect at low C i, it is important for the calculation of Δ bio and thus the contribution of the C4 and C3 cycles to overall carbon assimilation, especially at low C i. The fact that Δ bio is similar when calculated using either constant or variable g m in F. brownii and F. bidentis reflects the lower relevance of g m when the CO2 concentrating mechanism is expressed at high levels.
Conclusion
Concurrent Δ and gas exchange measurements and modeling provide a powerful diagnostic tool for C4 photosynthesis. Performing the measurements under controlled environmental conditions, especially low pO2, allows the detection and estimation of the C4 cycle activity in C3-C4 intermediate species even when it is low. This approach confirmed the presence of active Rubisco in the mesophyll of F. brownii, and revealed a contribution of the C4 cycle to total carbon assimilation in F. floridana. However, the carbon isotope signal is complex and not all its components are well understood, so some caution is required. We show for example that a CO2 dependence of gm affects the calculation of the biochemical fractionation, and thus the contribution of the C4 cycle to overall CO2 assimilation.
Supplementary data
Supplementary data are available from JXB online.
Figure S1. Responses of C i and stomatal conductance to changes in atmospheric pO2.
Figure S2. Models of CO2 response of assimilation rate and carbon isotope discrimination in the C3 and C4 species.
Figure S3. Effect of assuming constant or variable g m in the calculation of the biochemical fractionation.
Acknowledgments
We thank Soumi Bala for expert technical assistance with plant culture, biochemical assays, TDL and gas exchange measurements. We thank the High Resolution Plant Phenomics Centre (CSIRO, Australia) for the use of their TDL for some experiments. This research was supported by the Bill and Melinda Gates Foundation’s funding for the C4 Rice consortium and by the Australian Research Council Centre of Excellence for Translational Photosynthesis (CE140100015).
References
- Badger MR, Price GD. 1989. Carbonic anhydrase activity associated with the Cyanobacterium Synechococcus PCC7942. Plant Physiology 89, 51–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badger MR, Price GD. 1994. The role of carbonic anhydrase in photosynthesis. Annual Review of Plant Physiology and Plant Molecular Biology 45, 369–392. [Google Scholar]
- Bauwe H. 1986. An efficient method for the determination of Km values for HCO3- of phosphoenolpyruvate carboxylase. Planta 169, 356–360. [DOI] [PubMed] [Google Scholar]
- Bowling DR, Sargent SD, Tanner BD, Ehleringer JR. 2003. Tunable diode laser absorption spectroscopy for stable isotope studies of ecosystem–atmosphere CO2 exchange. Agricultural and Forest Meteorology 118, 1–19. [Google Scholar]
- Brown RH, Hattersley PW. 1989. Leaf anatomy of C3-C4 species as related to evolution of C4 photosynthesis. Plant Physiology 91, 1543–1550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown WV. 1975. Variations in anatomy, associations, and origins of Kranz tissue. American Journal of Botany 11, 395–402. [Google Scholar]
- Byrd GT, Brown RH. 1989. Environmental effects on photorespiration of C3-C4 species: I. Influence of CO2 and O2 during growth on photorespiratory characteristics and leaf anatomy. Plant Physiology 90, 1022–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrd GT, Brown RH, Bouton JH, Bassett CL, Black CC. 1992. Degree of C4 photosynthesis in C4 and C3-C4 Flaveria species and their hybrids: I. CO2 assimilation and metabolism and activities of phosphoenolpyruvate carboxylase and NADP-malic enzyme. Plant Physiology 100, 939–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng S-H, Moore BD, Edwards GE, Ku MSB. 1988. Photosynthesis in Flaveria brownii, a C4-like species: leaf anatomy, characteristics of CO2 exchange, compartmentation of photosynthetic enzymes, and metabolism of 14CO2 . Plant Physiology 87, 867–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousins AB, Badger MR, von Caemmerer S. 2008. C4 photosynthetic isotope exchange in NAD-ME- and NADP-ME-type grasses. Journal of Experimental Botany 59, 1695–1703. [DOI] [PubMed] [Google Scholar]
- Dai Z, Ku MB, Edwards G. 1996. Oxygen sensitivity of photosynthesis and photorespiration in different photosynthetic types in the genus Flaveria . Planta 198, 563–571. [DOI] [PubMed] [Google Scholar]
- Ehleringer JR, Sage RF, Flanagan LB, Pearcy RW. 1991. Climate change and the evolution of C4 photosynthesis. Trends in Ecology & Evolution 6, 95–99. [DOI] [PubMed] [Google Scholar]
- Evans JR, Sharkey TD, Berry JA, Farquhar GD. 1986. Carbon isotope discrimination measured concurrently with gas exchange to investigate CO2 diffusion in leaves of higher plants. Functional Plant Biology 13, 281–292. [Google Scholar]
- Evans JR, von Caemmerer S, Setchell BA, Hudson GS. 1994. the relationship between CO2 transfer conductance and leaf anatomy in transgenic tobacco with a reduced content of Rubisco. Functional Plant Biology 21, 475–495. [Google Scholar]
- Evans JR, von Caemmerer S. 2013. Temperature response of carbon isotope discrimination and mesophyll conductance in tobacco. Plant, Cell & Environment 36, 745–756. [DOI] [PubMed] [Google Scholar]
- Farquhar GD. 1983. On the Nature of carbon isotope discrimination in C4 species. Functional Plant Biology 10, 205–226. [Google Scholar]
- Farquhar GD, O’Leary MH, Berry J. 1982. On the relationship between carbon isotope discrimination and the intercellular carbon dioxide concentration in leaves. Functional Plant Biology 9, 121–137. [Google Scholar]
- Farquhar GD, Cernusak LA. 2012. Ternary effects on the gas exchange of isotopologues of carbon dioxide. Plant, Cell & Environment 35, 1221–1231. [DOI] [PubMed] [Google Scholar]
- Flexas J, Diaz-Espejo A, Galmés J, Kaldenhoff R, Medrano H, Ribas-Carbo M. 2007. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant, Cell & Environment 30, 1284–1298. [DOI] [PubMed] [Google Scholar]
- Griffis TJ, Baker JM, Sargent SD, Tanner BD, Zhang J. 2004. Measuring field-scale isotopic CO2 fluxes with tunable diode laser absorption spectroscopy and micrometeorological techniques. Agricultural and Forest Meteorology 124, 15–29. [Google Scholar]
- Griffiths H, Cousins AB, Badger MR, von Caemmerer S. 2007. Discrimination in the dark. Resolving the interplay between metabolic and physical constraints to phosphoenolpyruvate carboxylase activity during the crassulacean acid metabolism cycle. Plant Physiology 143, 1055–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatch MD. 1987. C4 photosynthesis – a unique blend of modified biochemistry, anatomy and ultraestructure. Biochimica et Biophysica Acta 895, 81–106. [Google Scholar]
- Hatch MD, Slack CR, Johnson HS. 1967. Further studies on a new pathway of photosynthetic carbon dioxide fixation in sugar-cane and its occurrence in other plant species. The Biochemical Journal 102, 417–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson SA, von Caemmerer S, Farquhar GD. 1992. Short-term measurements of carbon isotope discrimination in several C4 species. Functional Plant Biology 19, 263–285. [Google Scholar]
- Hibberd JM, Sheehy JE, Langdale JA. 2008. Using C4 photosynthesis to increase the yield of rice-rationale and feasibility. Current Opinion in Plant Biology 11, 228–231. [DOI] [PubMed] [Google Scholar]
- Holaday AS, Lee K, Chollet R. 1984. C3−C4 Intermediate species in the genus Flaveria: leaf anatomy, ultrastructure, and the effect of O2 on the CO2 compensation concentration. Planta 160, 25–32. [DOI] [PubMed] [Google Scholar]
- Jenkins CL, Furbank RT, Hatch MD. 1989. Mechanism of C4 photosynthesis: a model describing the inorganic carbon pool in bundle sheath cells. Plant Physiology 91, 1372–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karki S, Rizal G, Quick W. 2013. Improvement of photosynthesis in rice (Oryza sativa L.) by inserting the C4 pathway. Rice 6, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keerberg O, Pärnik T, Ivanova H, Bassüner B, Bauwe H. 2014. C2 photosynthesis generates about 3-fold elevated leaf CO2 levels in the C3–C4 intermediate species Flaveria pubescens . Journal of Experimental Botany 65, 3649–3656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ku MS, Monson RK, Littlejohn RO, Nakamoto H, Fisher DB, Edwards GE. 1983. Photosynthetic characteristics of C3-C4 intermediate flaveria species: i. leaf anatomy, photosynthetic responses to O2 and CO2, and activities of key enzymes in the C3 and C4 pathways. Plant Physiology 71, 944–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ku MSB, Wu J, Dai Z, Scott RA, Chu C, Edwards GE. 1991. Photosynthetic and photorespiratory characteristics of Flaveria species. Plant Physiology 96, 518–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubien DS, Whitney SM, Moore PV, Jesson LK. 2008. The biochemistry of Rubisco in Flaveria . Journal of Experimental Botany 59, 1767–1777. [DOI] [PubMed] [Google Scholar]
- Langdale JA. 2011. C4 cycles: past, present, and future research on C4 photosynthesis. The Plant Cell 23, 3879–3892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leegood RC. 2013. Strategies for engineering C4 photosynthesis. Journal of Plant Physiology 170, 378–388. [DOI] [PubMed] [Google Scholar]
- Leegood RC, von Caemmerer S. 1994. Regulation of photosynthetic carbon assimilation in leaves of C3–C4 intermediate species of Moricandia and Flaveria . Planta 192, 232–238. [Google Scholar]
- McKown AD, Moncalvo JM, Dengler NG. 2005. Phylogeny of Flaveria (Asteraceae) and inference of C4 photosynthesis evolution. American Journal of Botany 92, 1911–1928. [DOI] [PubMed] [Google Scholar]
- Monson RK, Edwards GE, Ku MSB. 1984. C3-C4 intermediate photosynthesis in plants. BioScience 34, 563–574. [Google Scholar]
- Monson RK, Moore Bd, Ku MSB, Edwards GE. 1986. Co-function of C3-and C4-photosynthetic pathways in C3, C4 and C3-C4 intermediate Flaveria species. Planta 168, 493–502. [DOI] [PubMed] [Google Scholar]
- Monson RK, Schuster WS, Ku MSB. 1987. Photosynthesis in Flaveria brownii AM Powell: a C4-Like C3-C4 intermediate. Plant physiology 85, 1063–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monson RK, Teeri JA, Ku MSB, Gurevitch J, Mets LJ, Dudley S. 1988. Carbon-isotope discrimination by leaves of Flaveria species exhibiting different amounts of C3-and C4-cycle co-function. Planta 174, 145–151. [DOI] [PubMed] [Google Scholar]
- Moore BD, Ku MSB, Edwards GE. 1989. Expression of C4-like photosynthesis in several species of Flaveria . Plant, Cell & Environment 12, 541–549. [Google Scholar]
- O’Leary MH. 1981. Carbon isotope fractionation in plants. Phytochemistry 20, 553–567. [Google Scholar]
- Pengelly JJ, Tan J, Furbank RT, von Caemmerer S. 2012. Antisense reduction of NADP-malic enzyme in Flaveria bidentis reduces flow of CO2 through the C4 cycle. Plant Physiology 160, 1070–1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pengelly JJL, Sirault XRR, Tazoe Y, Evans JR, Furbank RT, von Caemmerer S. 2010. Growth of the C4 dicot Flaveria bidentis: photosynthetic acclimation to low light through shifts in leaf anatomy and biochemistry. Journal of Experimental Botany 61, 4109–4122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rawsthorne S. 1992. C3–C4 intermediate photosynthesis: linking physiology to gene expression. The Plant Journal 2, 267–274. [Google Scholar]
- Roeske CA, O’Leary MH. 1984. Carbon isotope effects on enzyme-catalyzed carboxylation of ribulose bisphosphate. Biochemistry 23, 6275–6284. [DOI] [PubMed] [Google Scholar]
- Sage RF, Christin PA, Edwards EJ. 2011. The C4 plant lineages of planet Earth. Journal of Experimental Botany 62, 3155–3169. [DOI] [PubMed] [Google Scholar]
- Sage RF, Sage TL, Kocacinar F. 2012. Photorespiration and the evolution of C4 photosynthesis. Annual Review of Plant Biology 63, 19–47. [DOI] [PubMed] [Google Scholar]
- Sayre RT, Kennedy RA. 1977. Ecotypic differences in the C3 and C4 photosynthetic activity in Mollugo verticillata, a C3−C4 intermediate. Planta 134, 257–262. [DOI] [PubMed] [Google Scholar]
- Schulze S, Mallmann J, Burscheidt J, Koczor M, Streubel M, Bauwe H, Gowik U, Westhoff P. 2013. Evolution of C4 photosynthesis in the genus Flaveria: establishment of a photorespiratory CO2 pump. The Plant Cell 25, 2522–2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharwood RE, Whitney SM. 2014. Correlating Rubisco catalytic and sequence diversity within C3 plants with changes in atmospheric CO2 concentrations. Plant, Cell & Environment 37, 1981–1984. [DOI] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Badger MR, Evans JR. 2009. Light and CO2 do not affect the mesophyll conductance to CO2 diffusion in wheat leaves. Journal of Experimental Botany 60, 2291–2301. [DOI] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Estavillo GM, Evans JR. 2011. Using tunable diode laser spectroscopy to measure carbon isotope discrimination and mesophyll conductance to CO2 diffusion dynamically at different CO2 concentrations. Plant, Cell & Environment 34, 580–591. [DOI] [PubMed] [Google Scholar]
- Tholen D, Zhu XG. 2011. The mechanistic basis of internal conductance: a theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plant Physiology 156, 90–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubierna N, Sun W, Cousins AB. 2011. The efficiency of C4 photosynthesis under low light conditions: assumptions and calculations with CO2 isotope discrimination. Journal of Experimental Botany 62, 3119–3134. [DOI] [PubMed] [Google Scholar]
- Vogan PJ, Frohlich MW, Sage RF. 2007. The functional significance of C3–C4 intermediate traits in Heliotropium L. (Boraginaceae): gas exchange perspectives. Plant, Cell & Environment 30, 1337–1345. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S. 1992. Carbon isotope discrimination in C3-C4 intermediates. Plant, Cell & Environment 15, 1063–1072. [Google Scholar]
- von Caemmerer S. 2000. Biochemical Models of Leaf Photosynthesis . Vol. 2 CSIRO Publishing, Collingwood, Australia. [Google Scholar]
- von Caemmerer S. 2013. Steady-state models of photosynthesis. Plant, Cell & Environment 36, 1617–1630. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Evans JR. 1991. Determination of the average partial pressure of CO2 in chloroplast from leaves of several C3 plants. Australian Journal of Plant Physiology 18, 287–305. [Google Scholar]
- von Caemmerer S, Ghannoum O, Pengelly JJL, Cousins AB. 2014. Carbon isotope discrimination as a tool to explore C4 photosynthesis. Journal of Experimental Botany 65, 3459–3470. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Hubick KT. 1989. Short-term carbon-isotope discrimination in C3−C4 intermediate species. Planta 178, 475–481. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Quick WP. 2000. Rubisco: physiology in vivo. In: Leegood R, Sharkey T, von Caemmerer S, eds. Photosynthesis , Vol. 9: Springer; Netherlands, 85–113. [Google Scholar]
- von Caemmerer S, Quick WP, Furbank RT. 2012. The development of C4 rice: current progress and future challenges. Science 336, 1671–1672. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Quinn V, Hancock NC, Price GD, Furbank RT, Ludwig M. 2004. Carbonic anhydrase and C4 photosynthesis: a transgenic analysis. Plant, Cell & Environment 27, 697–703. [Google Scholar]
- Walker B, Ariza LS, Kaines S, Badger MR, Cousins AB. 2013. Temperature response of in vivo Rubisco kinetics and mesophyll conductance in Arabidopsis thaliana: comparisons to Nicotiana tabacum. Plant, Cell & Environment 36, 2108–2119. [DOI] [PubMed] [Google Scholar]
- Wang L, Czedik-Eysenberg A, Mertz RA, et al 2014. Comparative analyses of C4 and C3 photosynthesis in developing leaves of maize and rice. Nature Biotechnology 32, 1158–1165. [DOI] [PubMed] [Google Scholar]
- Whitney SM, Sharwood RE, Orr D, White SJ, Alonso H, Galmés J. 2011. Isoleucine 309 acts as a C4 catalytic switch that increases ribulose-1,5-bisphosphate carboxylase/oxygenase (rubisco) carboxylation rate in Flaveria . Proceedings of the National Academy of Sciences, USA 108, 14688–14693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wingate L, Seibt U, Moncrieff JB, Jarvis PG, Lloyd JON. 2007. Variations in 13C discrimination during CO2 exchange by Picea sitchensis branches in the field. Plant, Cell & Environment 30, 600–616. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.