Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1992 Mar 15;89(6):2471–2474. doi: 10.1073/pnas.89.6.2471

Rhythmogenic effects of weak electrotonic coupling in neuronal models.

A Sherman 1, J Rinzel 1
PMCID: PMC48680  PMID: 1549611

Abstract

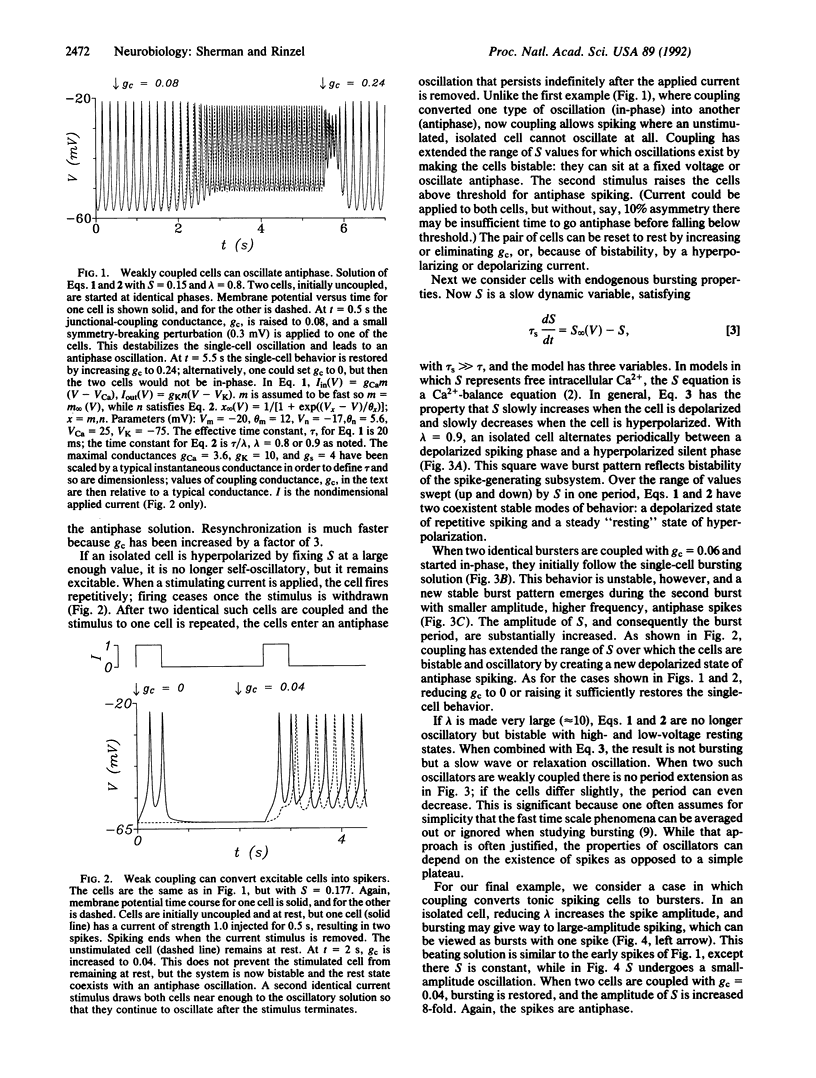
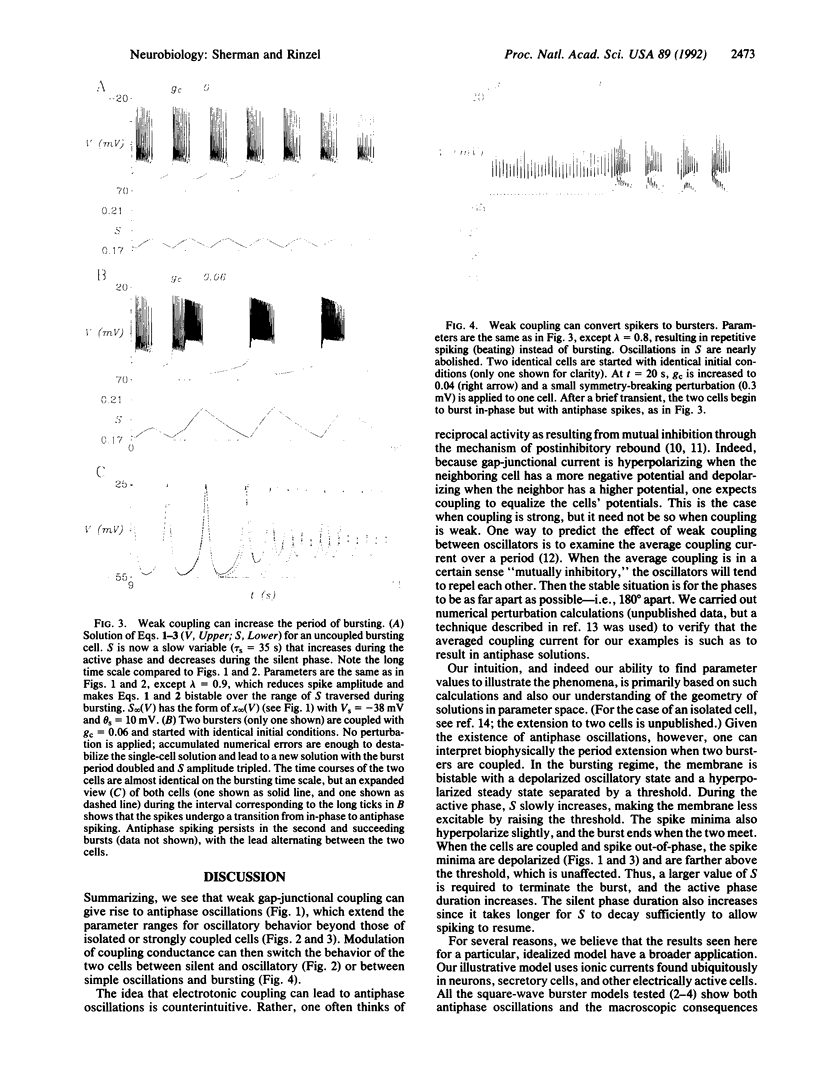
Strong gap-junctional coupling can synchronize the electrical oscillations of cells, but we show, in a theoretical model, that weak coupling can phase lock two cells 180 degrees out-of-phase. Antiphase oscillations can exist in parameter regimens where in-phase oscillations break down. Some consequences are (i) coupling two excitable cells leads to pacemaking, (ii) coupling two pacemaker cells leads to bursting, and (iii) coupling two bursters increases burst period. The latter shows that details of the fast spikes can affect macroscopic properties of the slow bursts. These effects hold in other models for bursting and may play a role in the collective behavior of cellular ensembles.

Full text

PDF
2471

Images in this article

2473Image
on p.2473
2473Image
on p.2473

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Hindmarsh J. L., Rose R. M. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond B Biol Sci. 1984 Mar 22;221(1222):87–102. doi: 10.1098/rspb.1984.0024. [DOI] [PubMed] [Google Scholar]
  2. Kawato M., Sokabe M., Suzuki R. Synergism and antagonism of neurons caused by an electrical synapse. Biol Cybern. 1979 Oct;34(2):81–89. doi: 10.1007/BF00365472. [DOI] [PubMed] [Google Scholar]
  3. Keizer J., Magnus G. ATP-sensitive potassium channel and bursting in the pancreatic beta cell. A theoretical study. Biophys J. 1989 Aug;56(2):229–242. doi: 10.1016/S0006-3495(89)82669-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kepler T. B., Marder E., Abbott L. F. The effect of electrical coupling on the frequency of model neuronal oscillators. Science. 1990 Apr 6;248(4951):83–85. doi: 10.1126/science.2321028. [DOI] [PubMed] [Google Scholar]
  5. Morris C., Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981 Jul;35(1):193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Perkel D. H., Mulloney B. Motor pattern production in reciprocally inhibitory neurons exhibiting postinhibitory rebound. Science. 1974 Jul 12;185(4146):181–183. doi: 10.1126/science.185.4146.181. [DOI] [PubMed] [Google Scholar]
  7. Satin L. S., Cook D. L. Calcium current inactivation in insulin-secreting cells is mediated by calcium influx and membrane depolarization. Pflugers Arch. 1989 May;414(1):1–10. doi: 10.1007/BF00585619. [DOI] [PubMed] [Google Scholar]
  8. Satterlie R. A. Reciprocal inhibition and postinhibitory rebound produce reverberation in a locomotor pattern generator. Science. 1985 Jul 26;229(4711):402–404. doi: 10.1126/science.229.4711.402. [DOI] [PubMed] [Google Scholar]
  9. Sherman A., Rinzel J., Keizer J. Emergence of organized bursting in clusters of pancreatic beta-cells by channel sharing. Biophys J. 1988 Sep;54(3):411–425. doi: 10.1016/S0006-3495(88)82975-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Sherman A., Rinzel J. Model for synchronization of pancreatic beta-cells by gap junction coupling. Biophys J. 1991 Mar;59(3):547–559. doi: 10.1016/S0006-3495(91)82271-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES