Abstract
It is widely established that proteins involved in reproduction diverge between species more quickly than other proteins. For male sperm proteins, rapid divergence is believed to be caused by post-copulatory sexual selection and/or sexual conflict. Here, we derive the expected levels of gene diversity within populations and divergence between them for male sperm protein genes evolving by post-copulatory, pre-zygotic fertility competition, i.e. the function imputed for some sperm and seminal fluid genes. We find that, at the mutation-selection equilibrium, both gene diversity within species and divergence between them are elevated relative to genes with similar selection coefficients expressed by both sexes. We show that their expected level of diversity is a function of the harmonic mean number of mates per female which affects the strength of fertility selection stemming from male-male sperm competition. Our predictions provide a null hypothesis for distinguishing between other selective hypotheses accounting for the rapid evolution of male reproductive genes.
Keywords: Sperm Proteins, Rapid Evolution, Relaxed Selection, Reproductive Genes, Sexual Selection
INTRODUCTION
A widely documented pattern in molecular evolution is that proteins involved in reproductive processes, including male reproductive proteins found in sperm and seminal fluid (Civetta and Singh 1995; Swanson et al. 2001; Andres et al. 2006; Van Dyken and Wade 2010; Walters and Harrison 2011), are more divergent among species than other proteins (Civetta and Singh 1995; Swanson and Vacquier 2002; Clark et al. 2006; Turner and Hoekstra 2008). This pattern is most often explained as an adaptive response to post-copulatory sexual selection (PCSS), where male sperm protein genes enhance male fertilization success in post-copulatory, pre-zygotic reproductive competition with other males (Parker 1970; Rice and Holland 1997; Birkhead and Pizzari 2002; Singh et al. 2002; Swanson and Vacquier 2002; Ramm et al. 2008; Turner and Hoekstra 2008). Support for this hypothesis comes from laboratory experiments showing that some male seminal fluid proteins affect sperm competition (Clark et al. 1995), sperm storage (Neubaum and Wolfner 1999; Tram and Wolfner 1999), female clutch size (Nilsson et al. 2002), and the length of a female's re-mating, refractory period (Chen et al. 1988). It has also been suggested that these proteins may play a role in reproductive isolation, thereby enhancing their diversification by limiting gene flow (Robinson et al. 1994; Wade et al. 1995; Civetta and Singh 1998; Jagadeeshan et al. 2011).
Increased divergence is consistent with rapid adaptive evolution and with relaxed purifying selection. In the extreme case, pseudogenes, which no longer experience selection, exhibit rapid, but ultimately non-adaptive, divergence relative to other genes (Lewis and Cowan 1986; Pritchard and Schaeffer 1997). Genes with sex-limited or conditional expression experience relatively weaker purifying selection, since unexpressed gene copies are not screened by selection (Whitlock and Wade 1995; Wade 1998; Barker et al. 2005; Cruickshank and Wade 2008; Wade et al. 2009; Van Dyken and Wade 2010; Van Dyken et al. 2011; Van Dyken and Wade 2012). For genes with sex-limited expression, like sperm protein genes, the efficacy of directional selection is reduced by half, slowing the initial spread of alleles with positive effects on fitness and diminishing the efficacy of purifying selection against rare deleterious alleles (Kimura 1962; Kimura 1964). For similar selection coefficients, the frequency at mutation-selection equilibrium of a deleterious allele is twice that of a gene expressed in both sexes (Whitlock and Wade 1995). Thus, relaxed selection may explain a significant portion of the elevated divergence observed in male reproductive genes, as has been shown for genes with female-limited expression (Barker et al. 2005; Demuth and Wade 2007; Cruickshank and Wade 2008; Wade et al. 2009).
Multiple mating by females is a prerequisite for sperm competition. Thus, the strength of sperm competition is reduced by the fraction of females with only one mate where there is no fertility competition (Simmons and Simmons 2001; Shuster and Wade 2003). We modeled the evolution of male sperm-competition protein genes under fertility selection to derive the expected levels of gene diversity and divergence. We find that both are a function of the harmonic mean number of mates per female. Our model provides a method for evaluating adaptive hypotheses regarding the rapid evolution of male reproductive genes.
METHODS
MODELS OF SPERM COMPETITION
We considered three different ways to model post-copulatory, pre-zygotic sperm competition: (1) haploid males with haploid sperm proteins; (2) diploid males and sperm proteins expressed via the haploid sperm genome; and (3) diploid males and sperm proteins expressed by the diploid male genome. Most sperm protein studies have been of species with diploid males (cases 2 and 3), rather than haploid males (case 1). With diploid males, haploid (case 2) or diploid selection (case 3) depends on when genes are expressed during spermatogenesis (Eddy 2002; Joseph and Kirkpatrick 2004). In the majority of species, most male reproductive genes experience diploid selection (case 3) because their mRNA is transcribed early in sperm development or they express shared protein products during the haploid stages of sperm development (Braun et al. 1989; Joseph and Kirkpatrick 2004). The haploid model applies to highly male-biased genes expressed late in spermatogenesis (Mank et al. 2010). Male accessory gland proteins are passed to the female with sperm during copulation, experience diploid selection.
The intensity of selection owing to sperm competition depends upon the genic variance (cases 1 and 2) or the genotypic variance (case 3) within females. For example, consider an autosomal, sperm protein gene, expressed only in haploid sperm, with two alleles, A and a, where the selective advantage of an A allele in competition for fertilizations with an a allele arises owing to an advantage in sperm-sperm competition or to a preference on the part of females for A sperm over a sperm via cryptic female choice. If the fitness of the A allele is 1 and that of an a allele is (1 – s), consider multiply inseminated female, i, with A sperm in frequency, pi, and a sperm in frequency, qi. The mean sperm fertility fitness within this female, W·i, is (1 – qiS). After competition, the frequency of the A allele in her fertilized eggs is and that of the alternative allele is . Thus, Δpi, the change in frequency of the A allele in her fertilized eggs owing to sperm competition equals where piqi is the genic variance in allele frequency within the i-th female.
The total change in allele frequency owing to sperm competition across all females depends on the average variance in allele frequency or in genotype frequency within females, which is a function of the mating system. If we assume that all females have the same number of eggs, then there is soft selection on the male sperm and the differences in W·i among females do not affect the selection dynamics. The solution is complicated because, although mating is random, fertilization is not. As a result, offspring genotypes at birth are not in Hardy-Weinberg equilibrium.
THE AVERAGE VARIANCE IN ALLELE FREQUENCY WITHIN FEMALES
1) Haploid Adults
With random mating, the number of haploid mates, k, determines the genetic variation among sperm within females as well as the genotypic variation among groups of k mates. When k is 1, the variance within females is zero, and, owing to the absence of sperm competition, both types of sperm are equally successful. When females have two mates (k = 2), there is sperm competition when one male is A and the other is a, which occurs with frequency 2pq, since males are haploid. The fertilization frequency of ‘A’ bearing sperm equals where W is . The change in allele frequency within females equals or . Averaging over both female genotypes, we find as the change in allele frequency within females owing to sperm competition and the differential fertilization that results from it (See Table 1). (Note that could also be written , where k = 2.) This is half of the total gene frequency change, because there is no selection on the alleles in females, so that .
With exactly three randomly chosen mates (k = 3), there is sperm competition when one male is A and the other two are a or when two males are A and the other is a. These possibilities occur with frequency 3pq2 and 3p2q, respectively, since males are haploid. With one A male, the fertilization frequency of ‘A’ bearing sperm equals where W is . The change in allele frequency in these cases equals or . With two A males, the fertilization frequency equals (2/3)(1/W) where W is (1 – [1/3]s). The change in allele frequency here equals or . Averaging over the A and a females, we find a change in allele frequency within females equal to . (Note that could also be written , where k = 3.) The total change in allele frequency in the population equals half of this or .
The form, , recurs because fertility selection caused by sperm competition depends upon the average genetic variance within females, which is . The total allele frequency change in the population is half this value:
| (1) |
Remember, the mean fitness of sperm within females, W, does not result in a change in female fecundity and, as a consequence, W does not appear in the denominator of the total frequency change.
In natural populations, females vary in mate numbers. Let Fk, be the frequency of females mated to exactly k males. The change in frequency of the A allele is the sum of the changes within females mated to k males weighted by Fk, the frequency of females mated to i males:
| (2a) |
| (2b) |
where H is the harmonic mean number of mates per female; i.e., . (Note that is the average genic variance among sperm proteins within mated females.) Since the harmonic mean is always less than the arithmetic mean, the strength of fertility selection depends most strongly on the fraction of females with one or a few mates. The total change, Δp, equals , half the change in frequency owing to male-male competition, since the alleles are not expressed in females. Our analysis assumed random mating but did not assume Hardy-Weinberg.
2) Diploid Adults, Haploid Expression of Sperm Proteins
In diploid species, late in spermatogenesis, sperm proteins expressed by the haploid sperm genome experience haploid, rather than diploid, selection. Heterozygous males produce both A and a bearing sperm, creating the potential for competition between the sperm of a single male. To simplify, we assume weak selection and Hardy-Weinberg (HW) proportions after fertility selection (see below and Supplementary Material). When each female has exactly k mates, the total change in the frequency of the A allele within the population is approximately equal to:
| (3) |
(See Supplemental Table 2). When k is so large that the genic variance within females is pq for all females, the exact solution (i.e., without assuming Hardy-Weinberg) is , which is the solution in the limit as k → infinity of eq. (3).
As in the first case, we can model variation among females in mate numbers, by letting Fi, be the frequency of females mated to exactly i males. Among all multiply-mated females (k > 1), the total change in frequency of the A allele is half the weighted average across females or approximately:
| (4) |
where H is the harmonic mean number of mates per female.
To determine degree of approximation owing to the HW assumption, we simulated the exact change in allele frequency assuming random mating between males and females, but not assuming a Hardy-Weinberg distribution of offspring genotypes. At the beginning of each simulated generation, male and females genotypes occur at the same frequency and are denoted by G1, G2 and G3, representing genotypes AA, Aa and aa, respectively. Selection occurs when both ‘A’ and ‘a’ bearing sperm are present within the same female reproductive tract (i.e. in the presence of sperm competition). As a result, female eggs are differentially fertilized and offspring genotypes are produced accordingly in frequencies, G1’, G2’, and G3’.
To determine the magnitude of the deviation between our approximate solution with the HW assumption and the exact solution, we determined the difference between Δp in our analytical approximation and our simulated results under the conditions at which the effect is expected to be the strongest, i.e., when p and q occur at equal frequency (p = 0.5) and when the number of mates per female is low. (Note, the analytic and approximate solutions converge to the same expression when k is very large.) When k = 1 or 2, the magnitude of the deviation between the exact and approximate solutions is s3, a third order effect (See Supplemental Figure 1). Models of autosomal genes with sex-differences in selection, like ours, employ the HW approximation and the deviation it causes is on the order of s2 (Charlesworth and Charlesworth 2010), larger than the deviation caused by our HW assumption. We believe that the trade-off between the precision of the exact solution and the tractability afforded to the approximate solution by the HW assumption (eq. [3]) is warranted for weak selection (s ≤ 0.05).
3) Diploid Adults, Diploid Somatic Expression of Sperm Proteins
Unlike the previous cases of competition between haploid sperm, competition here is between three sperm protein genotypes: AA, Aa, and aa. The fitness of AA sperm is equal to 1 and the fitnesses of Aa and aa sperm are 1-hs and 1-s, respectively, where h is the dominance coefficient. Absent competition, all genotypes have a fitness of 1. To simplify the model in a way that facilitates obtaining a solution (eq. [7] below), we again assume weak selection and Hardy-Weinberg (HW) proportions among adults after fertility selection. The expected change in frequency for a standard diploid gene expressed in both sexes with genotypic fitnesses, WAA = 1; WAa = 1 - hs; and, Waa = 1 – s, under weak selection (Charlesworth and Charlesworth 2010) is: Δp = spq(ph + q(1 – h)). This reduces to in the additive case (dominance coefficient h = 0.5). The total change in frequency of the A allele can be found by summing the change within females with i mates, weighted by their frequency, Fi:
| (5) |
where Gij is the frequency of genotype j in females of type i, pij is the frequency of A alleles in genotype j, and Wij is the fitness of genotype j in females of type i. The total change in the frequency of the A allele in the population, is equal to:
| (6) |
(See Table 3). Thus, when h = 0.5, , when h = 1, , and when h = 0, .
We evaluated the difference between Δp in our analytical approximation and our simulation of the exact genotypic transition equations when p and q occur at equal frequency (p = 0.5) and when the number of mates per female is low. When k = 2, the magnitude of the effect is s3, a third order effect as we found for Case 2 above (See Supplemental Figure 1). Thus, to the same order of approximation, the result assuming HW is reasonably close to the exact solution.
Thus, sperm competition genes that experience diploid selection evolve half as quickly as genes that experience haploid selection. Comparing, equations (4) and (6), we see that the difference in the effective strength of selection on a diploid-selected sperm protein is approximately half as strong as that on a haploid-selected sperm protein in the additive case (when h = 0.5).
THE EXPECTED LEVEL OF GENE DIVERSITY IN SPERM PROTEIN GENES
If the rate of mutation from A to a equals μ, then the frequency of the a allele at mutation-selection balance, assuming that both W and p are near 1, is for haploid proteins and for diploid proteins when h = 0.5. We can compare the expected level of gene diversity in sperm competition proteins, by modifying the strength of selection appropriately and observing the relative change in the expected level of gene diversity, q*. The expected mutation-selection equilibrium allele frequencies, q*, for sperm competition genes are:
| (7a) |
| (7b) |
| (7c) |
for Cases 1, 2, and 3, respectively. The expected relative level of gene diversity is equal to the quotient of mutation-selection balance for sperm competition proteins and the mutation-selection balance for standard constitutively expressed proteins .
Under the standard assumptions of large population size and independence among sites, we can use the equilibrium allele frequency under mutation-selection balance (q*) to determine the expected gene diversity (Van Dyken and Wade 2010). However, when drift dominates in small populations (Ne< 103), or when a large fraction of the non-synonymous sites evolve neutrally, our approximation will overestimate the expected relative level of gene diversity between sperm genes and standard constitutively expressed genes (Van Dyken and Wade 2010).
PROBABILITY OF FIXATION FOR NEW MUTATIONS IN SPERM PROTEIN GENES IN FINITE POPULATIONS
The deterministic population genetic model above assumed an infinite population, while natural populations are finite. As a result of random genetic drift, the equilibrium state of a population influenced by selection and mutation is a probability distribution of allele frequencies, rather than the single equilibrium allele frequency, q*, above. The distribution of allele frequencies under mutation, drift, and natural selection is given by the diffusion approximation (Kimura 1962). Diffusion theory shows that the probability of fixation of a new mutation (U) is a function of its selective effect, s, and effective population size, Ne (Kimura 1962; Kimura 1964). Assuming that a new mutation is introduced in a single copy at a frequency of 1/N in haploid organisms and 1/2N in diploid organism, the probability of fixation for a new mutation in a standard constitutively expressed protein is equal to:
| (8a) |
| (8b) |
where we use N to mean Ne following Kimura and assume additivity for diploid expression (Kimura 1962; Kimura 1964). Likewise, for sperm competition proteins, the selective effect of a new mutation is modified by the reduction in genic and genotypic variance, such that the probability of fixation for a new mutation becomes a function of the harmonic mean number of mates (H):
| (9a) |
| (9b) |
| (9c) |
The expected relative level of sequence divergence is equal to the ratio of the probability of fixation of a new mutation in a sperm competition protein (Eqns. 9a-c) and the probability of fixation of a new mutation in a constitutively expressed protein (Eqns. 8a,b).
The increased probability of fixation of deleterious mutations by drift, combined with the decreased probability of fixation of beneficial mutations by selection, results in an increase in sequence divergence between species for genes involved in fertility competition between males. Since the fitness effects of new mutations are believed to be predominantly deleterious, with beneficial mutations very rare, the increased probability of fixation of deleterious mutation due to relaxed selection outweighs the decreased probability of adaptive substitutions, increasing the rate of sequence divergence among species (Eyre-Walker and Keightley 2007). However, as with gene diversity, when drift dominates in small populations (Ne < 103), or when a large fraction of the non-synonymous sites evolve neutrally, our approximation will overestimate the expected relative probability of fixation of a new mutation between sperm genes and standard constitutively expressed genes.
THE EXPECTED RATIO OF SYNONYMOUS TO NON-SYNONYMOUS SUBSTITUTIONS
Comparing the frequency of non-synonymous to synonymous substitutions is a common test for the genetic signature of purifying versus positive selection (McDonald and Kreitman 1991). Purifying selection is indicated by more frequent synonymous than non-synonymous substitutions (dN/dS < 1) (Charlesworth and Charlesworth 2010). Conversely, if non-synonymous substitutions are significantly more frequent than synonymous substitutions (dN/dS > 1), it is indicative of positive or directional selection (McDonald and Kreitman 1991). A ratio of non-synonymous to synonymous substitutions that does not differ significantly from 1 is consistent with neutral evolution and is expected for pseudogenes. To determine the expected dN/dS ratio, we considered the ratio of the probability of fixation of a new mutation with selective effect s [see eqns. 9a-c] to the probability of fixation of a neutral mutation (1/N in haploid populations and 1/2N in diploid populations). Thus for a diploid, constitutively expressed gene, the expected dN/dS ratio is:
| (10a) |
when the selective effect of new mutations are generally weakly negative (Kimura 1957, 1962; Kimura 1964). Likewise, the expected dN/dS ratio for a diploid, sperm competition gene is:
| (10b) |
| (10c) |
RESULTS
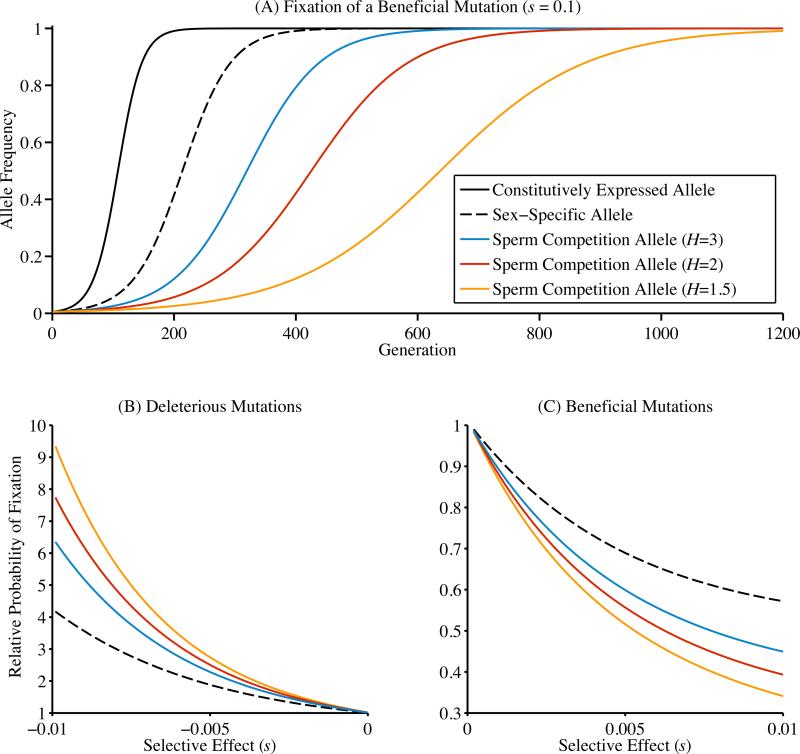
Our model shows that the strength of selection acting on sperm competition genes is a function of the harmonic mean number of mates per female (H). When H is low, sperm competition is infrequent and the effective strength of selection acting on sperm competition alleles is reduced. For example, consider an additive allele with sex-specific expression and selective benefit, s = 0.1, initially present at a low frequency (p = 0.01). This allele will take twice as long to near fixation as an equally beneficial allele that is constitutively expressed in both sexes (Figure 1A). If that same allele functions only in sperm competition, it can take several times longer to near fixation, as an inverse function of H (Figure 1A). Interestingly, if that same allele occurs in a sperm competition gene that exhibits haploid, gametic expression in a diploid species, within male sperm competition increases the strength of selection, again as a function of H, and that allele will near fixation more rapidly than a comparable sex-specific gene (Supplemental Figure 2).
Figure 1.
(A) Beneficial alleles (s = 0.1, h = 0.5) take longer to near fixation when they occur in sex-specific genes (dashed, black) in comparison to constitutively expressed genes (solid, black). If they occur in sex-specific genes that function primarily in sperm competition, the expected time near fixation increases as the harmonic mean number of mates per female (H) decreases (H=3, blue; H=2, red; H=1.5, yellow). (B) New deleterious mutations (s < 0, h = 0.5) have a higher probability of fixing in sex-specific gene relative to standard constitutively expressed genes (black, dashed). (C) Conversely, new beneficial mutations (s > 0, h = 0.5) have a lower probability of fixing in sex-specific gene relative to standard constitutively expressed genes. These effects are exaggerated in sex-specific genes that function primarily in sperm competition. Among sperm competition genes, the relative probability of fixation is a function of the harmonic mean number of mates per female (H). This figure illustrates the most common case (diploid adults with diploid expression of sperm and seminal fluid proteins). For the other cases, please see the supplementary material.
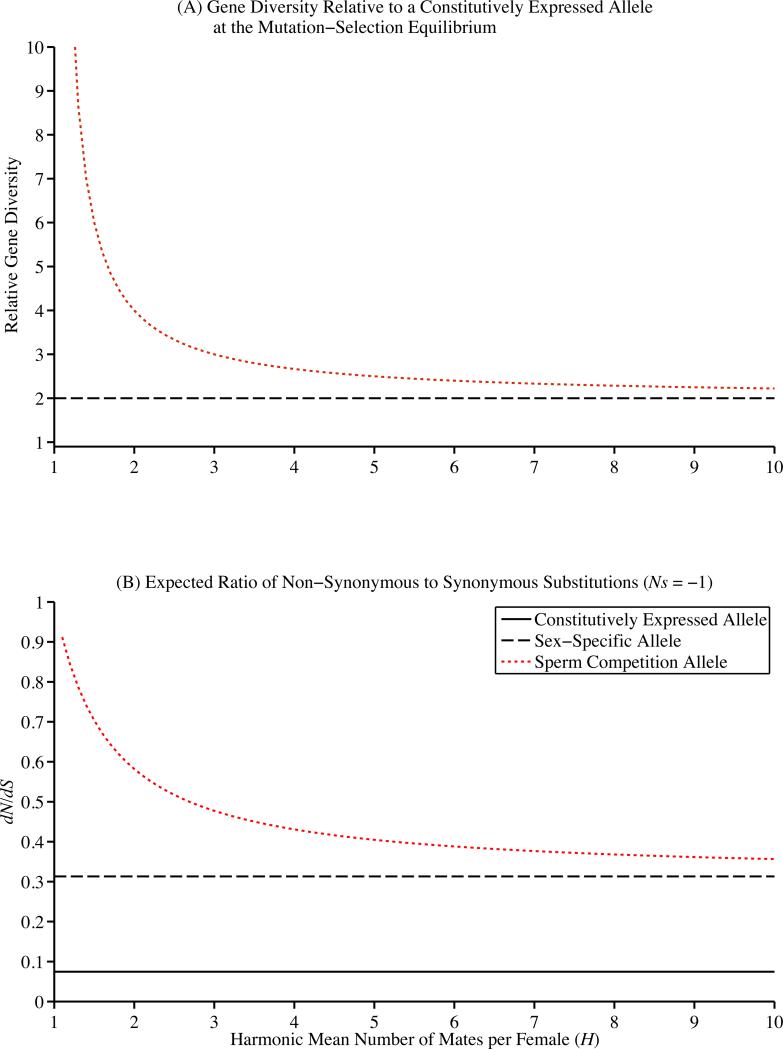
Similarly, as the strength of selection is reduced, the gene diversity expected at the mutation-selection balance increases. For example, the effective strength of selection is reduced by a half in genes that exhibit sex-specific expression (s/2). As a result, sex-specific genes are expected to be twice as diverse at the mutation-selection balance in comparison with a similarly selected allele with standard constitutive expression (Figure 2A; (Whitlock and Wade 1995; Wade 1998; Barker et al. 2005; Cruickshank and Wade 2008)). Our model shows that male-specific genes involved in sperm competition should exceed this two-fold increase in relative level of gene diversity, as an inverse function of H. For example, when H=1.5, sperm competition genes are expected to be 6-fold more variable within populations than standard constitutively expressed genes (Figure 2A). If the sperm competition gene exhibits gametic expression, and thus experience haploid selection, the expected levels of gene diversity are lower than those expected in a comparable sex-specific gene and approach the levels expected of a constitutively expressed gene as the harmonic mean number of mates per female (H) increases (Supplemental Figure 3).
Figure 2.
(A) Sex-specific genes are expected to exhibit twice as much gene diversity at the mutation-selection balance relative to standard constitutively expressed genes (black, dashed line). Sperm competition genes are expected to exhibit even higher levels of gene diversity relative to constitutively expressed genes (red, dotted line). The relative increase in gene diversity is a function of the harmonic mean number of mates per female (H) decreases. (B) Sperm competition (red, dotted line) and sex-specific genes (black, dashed line) are expected to exhibit elevated ratios of non-synonymous to synonymous substitutions (dN/dS) in comparison with standard, constitutively expressed genes (black, solid), given the same average selective effect of new mutations (Ns = −1). Among sperm competition genes, the expected dN/dS ratio increases with decreasing harmonic mean number of mates per female (H). This figure illustrates the most common case (diploid adults with diploid expression of sperm and seminal fluid proteins). For the other cases, please see the supplementary material.
The decrease in the strength of selection acting on sperm competition genes has dual effects on the probability of fixation of new mutations: (1) deleterious mutations become more likely to fix and (2) beneficial mutations become less likely to fix (Figure 1B). For example, a deleterious new mutation (s = 0.01) occurring in a sex-specific gene is approximately 1.8 times more likely to fix in a haploid population and approximately 4 times more likely to fix in a diploid population in comparison with a new mutation of the same deleterious effect arising in a standard constitutively expressed gene (Figure 1B). Likewise, if a new mutation with a deleterious effect of the same magnitude arises in a sperm competition allele, its relative probability of fixation further increases as a function of H (Figure 1B). If we instead consider a new mutation with a beneficial effect, its probability of fixation decreases when making the same comparison (Figure 1C). Both of these effects are reduced for new mutations that arise in sperm competition genes with gametic expression (Supplemental Figure 4).
The increased probability of fixation of new deleterious mutations on sex-specific and sperm competition genes significantly increases the expected divergence of these classes in genes in comparison with standard constitutively expressed genes (Figure 2B). For example, when Ns = −1, the expected dN/dS value for sex-specific genes is 0.3130, over 4-fold higher than the expected dN/dS value for standard, constitutively expressed genes (0.0746). Furthermore, the expected dN/dS value of sperm competition genes increases as a function the harmonic mean number of mates per female (H) (Figure 2B). As the harmonic mean number of mates per female approaches one (i.e. no sperm competition), the expected dN/dS value for sperm competition genes approaches one, i.e., neutrality. For the same example, when H = 1.5, the expected dN/dS value for sperm competition genes with somatic expression was 0.7034, almost 10-fold higher than the expected dN/dS value for standard, constitutively expressed genes. Even when females mate with multiple males (H = 4), the expected dN/dS value of sperm competition genes is notably elevated (0.4308) (Figure 2B). Consistent with our previous results, the expected dN/dS ratio for sperm competition genes with gametic expression is reduced and approaches the expected value for sex-specific genes as the harmonic mean number of mates per female decreases (Supplemental Figure 5).
DISCUSSION
Male reproductive genes have elevated levels of sequence divergence between species relative to genes expressed in both sexes (Civetta and Singh 1995; Swanson and Vacquier 2002; Clark et al. 2006; Turner and Hoekstra 2008). Many consider the elevated level of divergence to be evidence of post-copulatory sexual selection acting on males. However, reproductive genes, which tend to have sex-specific expression, experience significantly weaker selection than genes constitutively expressed in both sexes. All else being equal, the sex specificity of expression of reproductive genes alone, in theory, is sufficient to elevate the level of gene diversity two-fold. The effect can be even greater on the expected level of non-synonymous divergence, as a function of the product of effective population size and selective effect (Nes). Thus, among studies that rely upon comparisons of divergence between classes of genes, the inference of adaptive divergence for genes with sex-limited expression requires that the observed level of divergence exceed that expected owing to weaker, sex-limited selection. That is, theory tells us a priori that we should expect genes with sex-limited expression to exhibit greater divergence among species than genes expressed in both sexes, without invoking a special mechanism of adaptation. Few analyses of sequence divergence of reproductive genes have discussed how sex-limited selection alone enhances divergence.
In theory, sexual selection acting on males can be several times stronger than selection acting on females, whenever some males have more mates than others and consequently sire more offspring (Wade 1979; Shuster and Wade 2003). However, a feature of male-male reproductive competition, specific to sperm and seminal fluid proteins, weakens the argument for strong sexual selection: male-male sperm competition occurs only within multiply inseminated females, and not in singly inseminated females. Moreover, the effective strength of selection acting on sperm competition genes is a function of the harmonic mean number of mates per female (H), which affects the frequency and strength of male-male competition. This feature of sperm competition can elevate the level of expected gene diversity and divergence for sperm competition genes substantially above that for genes with sex-limited expression. The harmonic mean number of mates per female must be quite high (on the order of 8-10 mates per female) before the effective strength of selection rises to the level of a gene with sex-limited expression experiencing a similar selection coefficient. For example, while estimates of re-mating frequency for D. melanogaster vary, females likely mate with an average of 2-6 males (Harshman and Clark 1998; Imhof et al. 1998; Kuijper and Morrow 2009). Because the harmonic mean is less than or equal to the arithmetic mean, the females that mate with few males have a larger effect on H than a few females that mate with many males. Typically, papers analyzing evolutionary genetic patterns of male reproductive genes do not provide neither an estimates of the fraction of females multiply inseminated not the harmonic mean number of mates, a necessary component of the hypothesized frequency-dependent sperm competition.
Interestingly, the effects of sperm competition on the strength of selection are reversed in genes that exhibit gametic, rather than somatic, patterns of expression. These are male genes that are expressed late in spermatogenesis via the haploid sperm genome rather than the diploid male genome. As a result, there can be competition between the sperm of a heterozygous males, even if he is a female's only mate, increasing the overall strength of selection acting on these genes. However, only a minority of reproductive genes appears to exhibit haploid sperm expression (Braun et al. 1989; Joseph and Kirkpatrick 2004). Nonetheless, they provide the best targets for finding adaptive differentiation and evolution among reproductive genes. Our model specifically considers only alleles that influence sperm competitiveness. However, it is well documented that seminal fluid genes can also influence female fecundity (Chapman et al. 1995; Nilsson et al. 2002). In simple cases, such genes would simply behave as sex-specific genes, and thus still be expected to exhibit elevated polymorphism and divergence. However, more complicated interactions with female fecundity may produce non-intuitive effects on the effective strength of selection and would be an interesting future extension of this model.
Our theoretical approximations make direct predictions that can be applied to empirical data sets. Estimating the harmonic mean number of mates per female, H, is necessary to determine the degree to which variation in mating system can contribute to elevated diversity among reproductive genes specifically involved in post-copulatory sexual selection. Furthermore, the probability of fixation of a new mutation is a function of the product of effective population size and average selective effect, Ns. Given estimates of these two parameters, it is straightforward to apply our model to any system as long as the genes under study exhibit male-specific expression and function during sperm competition. If relaxed purifying selection is the predominant underlying cause of the elevated gene diversity and divergence observed among reproductive genes, we should expect to observe more than two-fold elevations of polymorphism and divergence in male sperm protein genes in comparison with standard constitutively expressed genes. Studies of sequence variation in D. melanogaster have documented both elevated levels of polymorphism (Begun et al. 2000; Wong et al. 2008) and divergence (Civetta and Singh 1995; Swanson et al. 2001; Findlay et al. 2008) that is many-fold greater than that observed among constitutively expressed control genes, consistent with our predictions. Unfortunately, neither estimates of H or Ns have been provided in the published literature on the rapid evolution of reproductive genes.
We are able to derive useful equations for predicting the expected diversity within and between species using standard assumptions of large population size and independence among sites. However, naturally occurring populations rarely experience the idealized conditions commonly assumed in population genetic theory. In particular, when drift dominates in small populations (Ne< 103), or when a large fraction of the non-synonymous sites evolve neutrally, our approximation will overestimate the expected relative level of gene diversity and diversity between sperm genes and standard constitutively expressed genes (Van Dyken and Wade 2010). However, this occurs because the strength of drift predominates across the genome, further reducing the opportunity for strong positive selection among reproductive genes. We also should note that relaxed purifying selection is not the only evolutionary scenario that predicts both elevated levels levels of diversity within species. Negative frequency dependent selection is a widely cited hypothesis that has empirical support within D. melanogaster (Clark et al. 2000; Clark 2002). However, because negative frequency dependent selection and/or balancing selection maintains variation within populations it has been viewed as an increase in Ne, and thus tends to reduce between-species diversification (Walsh and Lynch 2014). In some cases, it has lead to phylogenetically deep and persistent polymorphisms, i.e., ancient polymorphisms, which endure through speciation events, such as the polymorphism associated with the S-locus responsible for outcrossing in the plant family, Solanaceae (Igic et al. 2004). Our results highlight the importance of using population genetics tests that utilize within and between species variation, such as the allele frequency spectrum and the McDonald-Kreitman test, to distinguish between these alternate hypotheses (McDonald and Kreitman 1991). It is important to note our findings do not preclude reproductive genes from undergoing rapid adaptive evolution. They do indicate that adaptive differentiation of genes with sex-limited expression requires selection that is many-fold stronger than that generally observed among standard constitutively expressed genes.
In summary, the null hypothesis against which to test hypotheses of rapid diversification by sexual selection requires more than the observation of a significantly greater divergence relative to a set of genes constitutively expressed in both sexes. Rather, in evolutionary genetic analyses of reproductive genes with sex-limited expression, the correct null hypothesis is two-fold, or greater, elevated gene diversity and two-fold or greater divergence due to relaxed selection (Figure 2).
Supplementary Material
Acknowledgements
The authors thank J. Adrion and D. Drown for valuable discussion during the development of this manuscript. The research reported in this publication was supported by the National Institute of General Medical Science of the National Institute of Health (NIH) under award R01GM084238 to MJW. Additionally, ALD was supported by a National Science Foundation (NSF) Predoctoral Fellowship and an NSF Doctoral Dissertation Improvement Grant (1311167).
Works Cited
- Andres JA, Maroja LS, Bogdanowicz SM, Swanson WJ, Harrison RG. Molecular evolution of seminal proteins in field crickets. Mol. Biol. Evol. 2006;23:1574–1584. doi: 10.1093/molbev/msl020. [DOI] [PubMed] [Google Scholar]
- Barker MS, Demuth JP, Wade MJ. Maternal expression relaxes constraint on innovation of the anterior determinant, bicoid. PLoS Genet. 2005;1:527–530. doi: 10.1371/journal.pgen.0010057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begun DJ, Whitley P, Todd BL, Waldrip-Dail HM, Clark AG. Molecular population genetics of male accessory gland proteins in drosophila. Genetics. 2000;156:1879–1888. doi: 10.1093/genetics/156.4.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birkhead TR, Pizzari T. Postcopulatory sexual selection. Nat. Rev. Genet. 2002;3:262–273. doi: 10.1038/nrg774. [DOI] [PubMed] [Google Scholar]
- Braun RE, Behringer RR, Peschon JJ, Brinster RL, Palmiter RD. Genetically haploid spermatids are phenotypically diploid. Nature. 1989;337:373–376. doi: 10.1038/337373a0. [DOI] [PubMed] [Google Scholar]
- Chapman T, Liddle LF, Kalb JM, Wolfner MF, Partridge L. Cost of mating in Drosophila melanogaster females is mediated by male accessory-gland products. Nature. 1995;373:241–244. doi: 10.1038/373241a0. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Charlesworth D. Elements of evolutionary genetics. Roberts and Company Publishers; Greenwood Village: 2010. [Google Scholar]
- Chen PS, Stummzollinger E, Aigaki T, Balmer J, Bienz M, Bohlen P. A male accessory-gland peptide that regulates reproductive-behavior of female Drosophila melanogaster. Cell. 1988;54:291–298. doi: 10.1016/0092-8674(88)90192-4. [DOI] [PubMed] [Google Scholar]
- Civetta A, Singh RS. High divergence of reproductive tract proteins and their association with postzygotic reproductive isolation in Drosophila melanogaster and Drosophila virilis group species. J. Mol. Evol. 1995;41:1085–1095. doi: 10.1007/BF00173190. [DOI] [PubMed] [Google Scholar]
- Civetta A, Singh RS. Sex-related genes, directional sexual selection, and speciation. Mol. Biol. Evol. 1998;15:901–909. doi: 10.1093/oxfordjournals.molbev.a025994. [DOI] [PubMed] [Google Scholar]
- Clark AG. Sperm competition and the maintenance of polymorphism. Heredity. 2002;88:148–153. doi: 10.1038/sj.hdy.6800019. [DOI] [PubMed] [Google Scholar]
- Clark AG, Aguade M, Prout T, Harshman LG, Langley CH. Variation in sperm displacement and its association with accessory-gland protein loci in Drosophila melanogaster. Genetics. 1995;139:189–201. doi: 10.1093/genetics/139.1.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AG, Dermitzakis ET, Civetta A. Nontransitivity of sperm precedence in Drosophila. Evolution. 2000;54:1030–1035. doi: 10.1111/j.0014-3820.2000.tb00102.x. [DOI] [PubMed] [Google Scholar]
- Clark NL, Aagaard JE, Swanson WJ. Evolution of reproductive proteins from animals and plants. Reproduction. 2006;131:11–22. doi: 10.1530/rep.1.00357. [DOI] [PubMed] [Google Scholar]
- Cruickshank T, Wade MJ. Microevolutionary support for a developmental hourglass: gene expression patterns shape sequence variation and divergence in Drosophila. Evol. Dev. 2008;10:583–590. doi: 10.1111/j.1525-142X.2008.00273.x. [DOI] [PubMed] [Google Scholar]
- Demuth JP, Wade MJ. Maternal expression increases the rate of bicoid evolution by relaxing selective constraint. Genetica. 2007;129:37–43. doi: 10.1007/s10709-006-0031-4. [DOI] [PubMed] [Google Scholar]
- Eddy EM. Male germ cell gene expression. Recent Progress in Hormone Research. 2002;57:103–128. doi: 10.1210/rp.57.1.103. Vol 57. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 2007;8:610–618. doi: 10.1038/nrg2146. [DOI] [PubMed] [Google Scholar]
- Findlay GD, Yi XH, MacCoss MJ, Swanson WJ. Proteomics reveals novel Drosophila seminal fluid proteins transferred at mating. PLoS. Biol. 2008;6:1417–1426. doi: 10.1371/journal.pbio.0060178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harshman LG, Clark AG. Inference of sperm competition from broods of field-caught Drosophila. Evolution. 1998;52:1334–1341. doi: 10.1111/j.1558-5646.1998.tb02015.x. [DOI] [PubMed] [Google Scholar]
- Igic B, Bohs L, Kohn JR. Historical inferences from the self-incompatibility locus. New Phytol. 2004;161:97–105. [Google Scholar]
- Imhof M, Harr B, Brem G, Schlotterer C. Multiple mating in wild Drosophila melanogaster revisited by microsatellite analysis. Mol. Ecol. 1998;7:915–917. doi: 10.1046/j.1365-294x.1998.00382.x. [DOI] [PubMed] [Google Scholar]
- Jagadeeshan S, Haerty W, Singh RS. Is Speciation Accompanied by Rapid Evolution? Insights from Comparing Reproductive and Nonreproductive Transcriptomes in Drosophila. International Journal of Evolutionary Biology. 2011;2011:1–11. doi: 10.4061/2011/595121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph SB, Kirkpatrick M. Haploid selection in animals. Trends Ecol. Evol. 2004;19:592–597. [Google Scholar]
- Kimura M. Some problems of stochastic-processes in genetics. Annals of Mathematical Statistics. 1957;28:882–901. [Google Scholar]
- Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;47:713–&. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. Diffusion models in population genetics. J. appl. Prob. 1964;1:177–232. [Google Scholar]
- Kuijper B, Morrow EH. Direct observation of female mating frequency using time-lapse photography. Fly. 2009;3:118–120. doi: 10.4161/fly.8053. [DOI] [PubMed] [Google Scholar]
- Lewis SA, Cowan NJ. Tubulin pseudogenes as markers for hominoid divergence. J. Mol. Biol. 1986;187:623–626. doi: 10.1016/0022-2836(86)90340-2. [DOI] [PubMed] [Google Scholar]
- Mank JE, Nam K, Brunstrom B, Ellegren H. Ontogenetic Complexity of Sexual Dimorphism and Sex-Specific Selection. Mol. Biol. Evol. 2010;27:1570–1578. doi: 10.1093/molbev/msq042. [DOI] [PubMed] [Google Scholar]
- McDonald JH, Kreitman M. Adaptive protein evolution at the ADH locus in Drosophila. Nature. 1991;351:652–654. doi: 10.1038/351652a0. [DOI] [PubMed] [Google Scholar]
- Neubaum DM, Wolfner MF. Mated Drosophila melanogaster females require a seminal fluid protein, Acp36DE, to store sperm efficiently. Genetics. 1999;153:845–857. doi: 10.1093/genetics/153.2.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson T, Fricke C, Arnqvist G. Patterns of divergence in the effects of mating on female reproductive performance in flour beetles. Evolution. 2002;56:111–120. doi: 10.1111/j.0014-3820.2002.tb00853.x. [DOI] [PubMed] [Google Scholar]
- Parker GA. Sperm competition and its evolutionary consequences in insects. Biol. Rev. Cambridge Philosophic. Soc. 1970;45:525–&. [Google Scholar]
- Pritchard JK, Schaeffer SW. Polymorphism and divergence at a Drosophila pseudogene locus. Genetics. 1997;147:199–208. doi: 10.1093/genetics/147.1.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramm SA, Oliver PL, Ponting CP, Stockley P, Emes RD. Sexual selection and the adaptive evolution of mammalian ejaculate proteins. Mol. Biol. Evol. 2008;25:207–219. doi: 10.1093/molbev/msm242. [DOI] [PubMed] [Google Scholar]
- Rice WR, Holland B. The enemies within: intergenomic conflict, interlocus contest evolution (ICE), and the intraspecific Red Queen. Behav. Ecol. Sociobiol. 1997;41:1–10. [Google Scholar]
- Robinson T, Johnson NA, Wade MJ. Postcopulatory, prezygotic isolation - intraspecific and interspecific sperm precedence in Tribolium spp, flour beetles. Heredity. 1994;73:155–159. doi: 10.1038/hdy.1994.114. [DOI] [PubMed] [Google Scholar]
- Shuster SM, Wade MJ. Mating systems and strategies. Princeton University Press; 2003. [Google Scholar]
- Simmons LW, Simmons LW. Sperm competition and its evolutionary consequences in the insects. Princeton University Press; 2001. [Google Scholar]
- Singh SR, Singh BN, Hoenigsberg HF. Female remating, sperm competition and sexual selection in Drosophila. Genetics and Molecular Research. 2002;1:178–215. [PubMed] [Google Scholar]
- Swanson WJ, Clark AG, Waldrip-Dail HM, Wolfner MF, Aquadro CF. Evolutionary EST analysis identifies rapidly evolving male reproductive proteins in Drosophila. Proc. Natl. Acad. Sci. U. S. A. 2001;98:7375–7379. doi: 10.1073/pnas.131568198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson WJ, Vacquier VD. The rapid evolution of reproductive proteins. Nat. Rev. Genet. 2002;3:137–144. doi: 10.1038/nrg733. [DOI] [PubMed] [Google Scholar]
- Tram U, Wolfner MF. Male seminal fluid proteins are essential for sperm storage in Drosophila melanogaster. Genetics. 1999;153:837–844. doi: 10.1093/genetics/153.2.837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner LM, Hoekstra HE. Causes and consequences of the evolution of reproductive proteins. Int. J. Dev. Biol. 2008;52:769–780. doi: 10.1387/ijdb.082577lt. [DOI] [PubMed] [Google Scholar]
- Van Dyken JD, Linksvayer TA, Wade MJ. Kin Selection-Mutation Balance: A Model for the Origin, Maintenance, and Consequences of Social Cheating. Am. Nat. 2011;177:288–300. doi: 10.1086/658365. [DOI] [PubMed] [Google Scholar]
- Van Dyken JD, Wade MJ. The Genetic Signature of Conditional Expression. Genetics. 2010;184:557–570. doi: 10.1534/genetics.109.110163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dyken JD, Wade MJ. Detecting the Molecular Signature of Social Conflict: Theory and a Test with Bacterial Quorum Sensing Genes. Am. Nat. 2012;179:436–450. doi: 10.1086/664609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade MJ. Sexual selection and variance in reproductive success. Am. Nat. 1979;114:742–747. doi: 10.1086/424531. [DOI] [PubMed] [Google Scholar]
- Wade MJ. The evolutionary genetics of maternal effects. In: Mousseau TA, Fox CW, editors. Maternal effects as adaptations. Oxford University Press; New York, NY: 1998. pp. 5–21. [Google Scholar]
- Wade MJ, Chang NW, McNaughton M. Incipient speciation in the flour beetle, Tribolium confusum - Premating isolation between natural populations. Heredity. 1995;75:453–459. doi: 10.1038/hdy.1995.161. [DOI] [PubMed] [Google Scholar]
- Wade MJ, Priest NK, Cruickshank T. A theoretical overview of maternal genetic effects: evolutionary predictions and empirical tests using sequence data within and across mammalian taxa. In: Maestripieri D, Mateo JM, editors. Maternal effects in mammals. University of Chicago Press; 2009. pp. 38–63. [Google Scholar]
- Walsh B, Lynch M. Evolution and Selection of Quantitative Traits I : Foundations. 2014 http://nitro.biosci.arizona.edu/zbook/NewVolume_2/newvol2.html.
- Walters JR, Harrison RG. Decoupling of rapid and adaptive evolution among seminal fluid proteins in Heliconius butterflies with divergence mating systems. Evolution. 2011;65:2855–2871. doi: 10.1111/j.1558-5646.2011.01351.x. [DOI] [PubMed] [Google Scholar]
- Whitlock MC, Wade MJ. Speciation: founder events and their effects on X-linked and autosomal genes. Am. Nat. 1995;145:676–685. [Google Scholar]
- Wong A, Turchin MC, Wolfner MF, Aquadro CF. Evidence for positive selection on Drosophila melanogaster seminal fluid protease homologs. Mol. Biol. Evol. 2008;25:497–506. doi: 10.1093/molbev/msm270. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.