Abstract
This study investigated the hypothesis that a simple intensive code, based on mean firing rate, could explain the cortical representation of subjective roughness intensity and its invariance with scanning speed. We examined the sensitivity of neurons in the cutaneous, finger representation of primary somatosensory cortex (S1) to a wide range of textures [1 mm high, raised-dot surfaces; spatial periods (SPs), 1.5–8.5 mm], scanned under the digit tips at different speeds (40–115 mm/s). Since subjective roughness estimates show a monotonic increase over this range and are independent of speed, we predicted that the mean firing rate of a subgroup of S1 neurons would share these properties. Single-unit recordings were made in four alert macaques (areas 3b, 1 and 2). Cells whose discharge rate showed a monotonic increase with SP, independent of speed, were particularly concentrated in area 3b. Area 2 was characterized by a high proportion of cells sensitive to speed, with or without texture sensitivity. Area 1 had intermediate properties. We suggest that area 3b and most likely area 1 play a key role in signaling roughness intensity, and that a mean rate code, signaled by both slowly and rapidly adapting neurons, is present at the level of area 3b. Finally, the substantial proportion of neurons that showed a monotonic change in discharge limited to a small range of SPs (often independent of response saturation) could play a role in discriminating smaller changes in SP.
Keywords: tactile roughness, neuronal coding, passive touch, hierarchical processing
when we touch a surface, the tactile impression of smoothness/roughness is influenced by the physical structure of the surface. A number of factors contribute, including the number of projections (or tactile elements) that make up the surface, their spacing, density, size, form, degree of unevenness and the material from which they are constructed. Any tactile exploration of a surface necessarily activates all of the large-diameter cutaneous mechanoreceptive afferents that are involved in discriminative touch, including (in the monkey) slowly adapting type I (SA), rapidly adapting (RA) and Pacinian (PC) afferents. The discharge evoked by textured surfaces is complex, reflecting not only the surface structure, but also factors intrinsic to the exploration process, including scanning speed and contact force.
Although the nature of the relationship between subjective roughness and texture remains controversial, the bulk of the evidence suggests that, if the tactile elements are sufficiently high (≥1 mm), then there is a linear relation between subjective roughness and tactile element spacing [spatial period (SP), distance center-to-center between adjacent elements] for surfaces composed of gratings and raised dots (Dépeault et al. 2009; Lederman 1974; Meftah et al. 2000; Morley et al. 1983; Sathian et al. 1989; Sutu et al. 2013; Yoshioka et al. 2001; cf, Connor et al. 1990). A representative example of such a psychophysical curve is shown in Fig. 1 (Meftah et al. 2000): subjective roughness showed a monotonic increase across a wide range of dot spacings (1.5–8.5 mm SP), with identical results obtained when scanning speed was doubled on a trial-by-trial basis. Similar monotonic relations between roughness and SP are obtained using nonperiodically disposed raised dots (Dépeault et al. 2009) and tetragonal arrays of raised dots (Sutu et al. 2013). Taken together, the critical factor for subjective roughness intensity is the spacing between raised dots in the direction of the scan, and any neuronal code needs to reflect this.
Fig. 1.
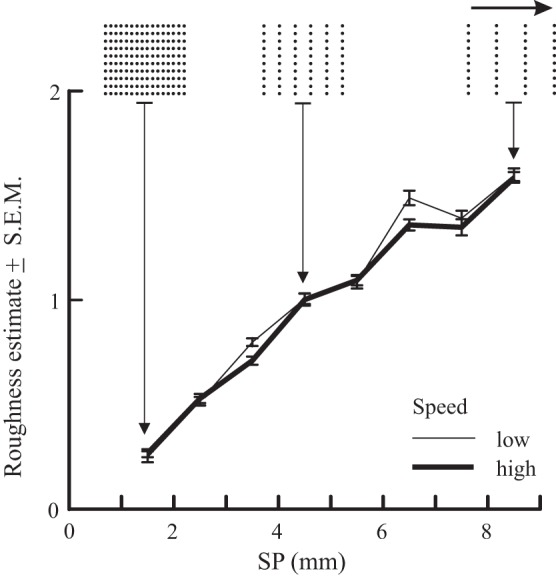
The subjective intensity of roughness (normalized) in humans (n = 4) shows a linear increase as the longitudinal spatial period (SP) of raised-dot surfaces is increased from 1.5 to 8.5 mm (n = 4 subjects). Scanning speed was doubled (from 50 to 94 mm/s), but roughness estimates were invariant. For each subject, data were normalized to the grand mean of all estimates in the session. Speed was varied on a trial-by-trial basis. Scanning direction is indicated by the arrow. [Data replotted, with permission, from Meftah et al. 2000.]
Given the complexity of the subject, it is not too surprising that it is difficult to define the neuronal bases underlying tactile roughness. A number of neuronal codes have been proposed to explain various aspects of roughness, including a spatial code restricted to SA afferents (Connor et al. 1990; Connor and Johnson 1992), a mean rate code based on the firing of SA and RA afferents (Goodwin and Morley 1987; Goodwin et al. 1989; Sathian et al. 1989) and a temporal code mainly involving RA and PC afferents (Cascio and Sathian 2001; Weber et al. 2013). Each code has its merit, and all may contribute in some fashion to the perception of roughness.
Our laboratory previously suggested that a simple intensive code, based on mean firing rate, could explain the cortical representation of subjective roughness intensity (Meftah et al. 2000). Previous studies, albeit with limited ranges of SPs, have shown that neurons in monkey primary somatosensory cortex (S1) show graded relations between mean rate and SP (Darian-Smith et al. 1982; Jiang et al. 1997; Sinclair and Burton 1991a). We suggested that an invariant representation of tactile roughness intensity could be generated centrally by a simple subtraction of speed-varying signals on-line from the multiplexed signal sensitive to both roughness and speed. Consistent with this suggestion, our laboratory recently identified a small proportion of S1 neurons whose mean rate covaried with tactile speed, independent of the SP of the textured surfaces scanned under the fingertips (Dépeault et al. 2013). Such neurons thus provide the template to generate an invariant representation of roughness independent of speed.
The present study was, therefore, designed to investigate the cortical neuronal mechanisms underlying the representation of the subjective intensity of tactile roughness. For this, we chose to base our analyses largely on a mean rate code. This choice is supported by our laboratory's recent demonstration (Dépeault et al. 2013) that a mean rate code signaled by cutaneous neurons in S1 is sufficient to explain the human ability to scale the subjective speed of tactile stimuli displaced over the skin (Dépeault et al. 2008). We reasoned that the same code should be able to explain the human ability to estimate the subjective roughness of textured surfaces.
Using the same data base as in Dépeault et al. (2013), we tested the hypothesis that S1 neurons use an intensive code, based on mean firing rate, to signal tactile roughness. Single-unit responses were compared with published psychophysical results (e.g., Fig. 1). We predicted that neurons would show monotonic increases in their discharge rate as raised-dot spacing was increased over the range of 1.5–8.5 mm (dot height, 1 mm), i.e., their discharge would be graded across a wide range of SPs. We further hypothesized that the discharge of a subset of these S1 neurons would be graded with dot spacing independent of scanning speed, consistent with observations of perceptual constancy for tactile roughness when scanning speed is increased (Lederman 1974, 1983; Meftah et al. 2000; Yoshioka et al. 2011). Preliminary results have been presented in abstract form (Dépeault et al. 2007; Meftah et al. 2014).
METHODS
Experiments were performed on four adult monkeys, Macaca mulatta (monkey B, 8.5 kg; monkey I, 11.2 kg; monkey J, 7.5 kg; monkey N, 7.3 kg), trained to rest the fingertips of digits 3 and 4 (D3/4) of one hand on the textured surfaces (Fig. 2A) that were rotated underneath the immobile digits (Fig. 2, B and C). Data were collected from the contralateral hemisphere (monkey B, both sides; monkeys I and J, right side; monkey N, left). The data from monkeys B and N were also used for another publication, focused on the cortical neuronal coding of tactile speed (Dépeault et al. 2013). Animal care and housing conformed with published guidelines of the Canadian Council on Animal Care. The experimental protocol was approved by the institutional ethics committee.
Fig. 2.
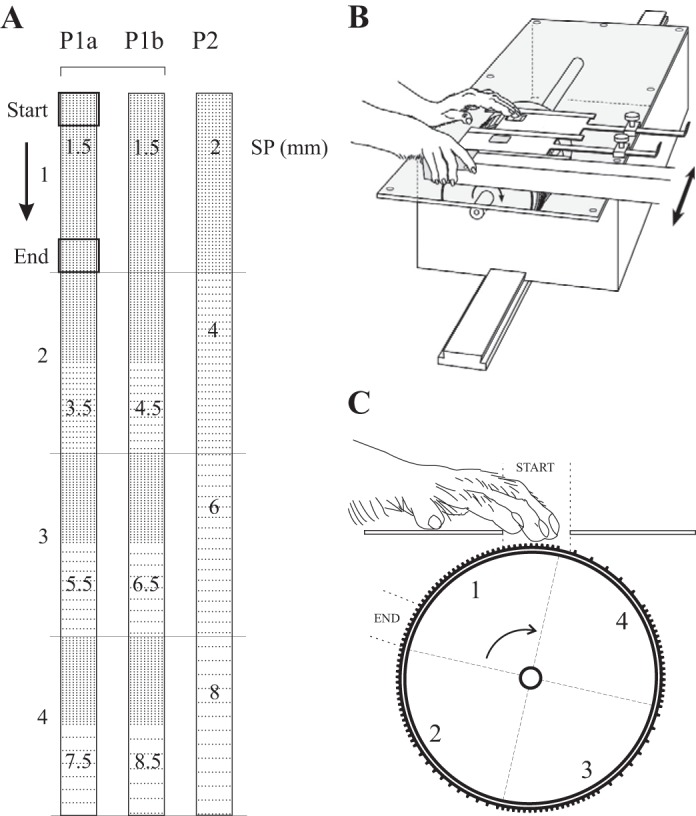
A: representation of the raised-dot surfaces used in the experiments (dot height 1 mm, dot diameter 0.6 or 0.8 mm). There were 3 series of periodic (P) surfaces, each divided into 4 segments (2 × 10 cm). Series P1a and b were used for recordings in monkeys I and J; P2 was used for monkeys B and N. For each segment, the SP (mm) is indicated. B: the tactile stimulator containing the drum to which the surfaces were attached, and the position of the monkey's hands during data acquisition, one on the surfaces and the other on the response lever. The surfaces were affixed to the drum (P1a/b or P2); the drum was shifted laterally between series P1a/b (see arrow) to ensure that the position relative to the stimulated hand was constant. C: lateral view of the drum showing the placement of one series, P1. The surface formed the floor of the aperture and was contacted with the tips of digits 3 and 4. The drum was rotated during a trial, going from the “start” position to the “end” position (see arrow).
Textured Surfaces
The textured surfaces were fabricated from flexible letterpress plate using a photographic process (CML Printing Plates, St. Léonard, QC, Canada). The results presented here come from three series of raised-dot surfaces, Fig. 2A. Each series consisted of four segments (2 × 10 cm, numbered 1–4) in a continuous strip. The surfaces consisted of truncated, cylindrical raised dots in a rectangular array (1 mm high, 0.6 or 0.8 mm diameter at the top). There were three series of periodic surfaces (P1a, P1b, P2). Series P1a and b were used for monkeys I and J; series P2 was used for recordings in monkeys B and N. Transverse SP (center-to-center distance between dots) was 1.5 mm for the P1 series and 2 mm for the P2 series. Longitudinal SP (direction of the scan, see arrow in Fig. 2A) varied from 1.5 to 7.5 (P1a) or 8.5 mm (P1b) for the P1 series, and from 2 to 8 mm for the P2 surfaces. Note that the longitudinal SP was constant across each segment for series P2. For the P1 series, the first half (5 cm) of the segment had a longitudinal SP of 1.5 mm; dot spacing was either the same (segment 1) or increased on the second half of the surface (segments 2–4: a, 3.5, 5.5, 7.5 mm; b, 4.5, 6.5, 8.5 mm). These surfaces covered a wide range of SPs across which humans show a linear increase in roughness (Dépeault et al. 2009; Meftah et al. 2000; Sutu et al. 2013) and extend the ranges studied previously, both in this laboratory (Chapman and Meftah 2005; Jiang et al. 1997; Meftah et al. 2002, 2009; Tremblay et al. 1996) and elsewhere (Darian-Smith et al. 1982; Sinclair and Burton 1988, 1991a).
Tactile Stimulator
The tactile stimulator has been described elsewhere (Tremblay et al. 1996). Briefly, it consisted of a drum (40 cm circumference) mounted on a drive shaft coupled to a DC motor through a 100:1 reduction gear. The position of the drum was monitored using a photoelectric system (precision 0.72°). Twinned rectangular apertures (1.9 × 2.2 cm) above the drum gave access to the textured surface that formed the floor of the aperture (Fig. 2B). The aperture was positioned in front of the stimulated arm. During training and recording sessions, the monkey was seated in a primate chair with the tactile stimulator mounted in front of the animal, at waist height, and firmly clamped to the chair. Vision of the apparatus was precluded by means of an opaque, horizontal barrier mounted just below the head. Each series was attached around the circumference of the drum with double-sided adhesive tape (Fig. 2C). During the recordings in monkeys I and J (series P1a/b), the tactile stimulator was displaced laterally so that, for all cells, the position of the textured surfaces relative to the monkey was the same (see arrow, Fig. 2B).
Tactile Stimulation
Prior to the recordings, monkeys I and J were trained to perform a texture discrimination task (respectively, 7.5 and 13 mo). In both cases, the monkeys were conditioned to rest the tips of D3/4 on the textured surface, and to remain immobile as the surface was scanned, proximal to distal, under the finger tips. The present recordings were, however, performed mainly outside of the context of the texture discrimination task: no-task condition (Chapman and Meftah 2005). Random drops of juice were presented in no particular relation to the presentation of the tactile stimuli, and the monkeys appeared alert throughout the recordings, with their eyes open and directed to the juice spigot immediately in front of the animal.
As described in detail elsewhere (Dépeault et al. 2013), monkeys B and N were also trained to rest their fingertips on the textured surface and to remain immobile during the texture presentation (duration of training, 1.5 and 2 mo). In this case they were trained in a diversionary task, discriminating an increase in light intensity (light affixed to the primate chair at eye-level, distance 35 cm), with the change in intensity occurring after the end of the texture presentation period. Their response was signaled by releasing a lever within a reaction time window (200–700 ms after the change); successful responses were rewarded with a drop of juice or water. In all cases, the tactile drum was repositioned during the intertrial interval (3–5 s), so that the start position of the chosen surface (Fig. 2C) formed the floor of the aperture. Monkeys I, J and N remained immobile during this period of drum rotation, while monkey B withdrew its fingers during repositioning. The position of the digits was visually verified by one of the experimenters and manually adjusted if necessary before the trial was initiated. Trials were rejected at acquisition if there was any movement during the surface presentation.
For monkeys I and J, each cell was tested with series P1a or P1b (Fig. 2A), systematically alternating from one cell to the next. For most cells, five scanning speeds were tested, covering a range of speeds that are often used during tactile exploration (Smith et al. 2002), 40–115 mm/s. The nominal speeds were 40, 60, 75, 95 and 115 mm/s. As reported previously, actual drum speed varied within about ±2 mm/s of the nominal values (Meftah et al. 2000). For monkeys B and N, all cells were tested with series P2; three nominal speeds were tested, usually 40, 75 and 100 mm/s.
Surgical Procedures
Access to the hand representation of S1 was achieved through a chronic recording chamber implanted, under aseptic conditions, over the hemisphere contralateral to the tactile stimulation (Meftah et al. 2002). Briefly, after sedation with ketamine + glycopyrolate (15 mg/kg im + 0.01 mg/kg), the animal was intubated for endotracheal administration of isoflurane (2–3%). Physiological parameters (temperature, heart rate, and respiration rate) were monitored during the surgery. Antibiotics (enrofloxacin: 5 mg/kg) were administered prior to surgery, and for 10 days postoperatively. Postoperative analgesia was provided for a minimum of 72 h (ketoprofen 0.1 mg/kg and buprenorphine 0.05 mg/kg).
Data Acquisition and Analysis
The data collection procedures have been described elsewhere (Chapman and Ageranioti-Belanger 1991; Meftah et al. 2002; Tremblay et al. 1996). Briefly, the monkey was seated in a primate chair, with the head immobilized. The activity of single neurons was recorded extracellularly with glass-coated tungsten microelectrodes. During each penetration, a record was kept of the depth at which the first sign of cell activity was encountered as well as the depth of each unit recorded. Cells were classified as responding to cutaneous stimuli (touch or hair) or deep stimuli (tapping over muscle bellies, joint manipulation). For each cutaneous cell, the location of the peripheral receptive field (RF) was carefully mapped using a variety of manually applied stimuli. For one monkey (N), the mapping was repeated and confirmed using a Von Frey filament (F = 0.02 N). Cutaneous cells were categorized according to their rate of adaptation to manually applied tactile stimuli: SA units showed discharge that persisted throughout 1–2 s of static stimulation; RA units showed only transient responses to the same stimulation.
Only neurons with a cutaneous RF that included the glabrous tips of D3/4 were tested for their responsiveness to texture stimulation. For series P1a/b, 160 trials were presented in a pseudorandom order (4 segments × 5 speeds × 8 replications). For series P2, there were 60 trials (4 segments × 3 speeds × 5 replications). During the recordings, sampling was periodically equalized across trial types (e.g., every 40 trials for series P1a/b). In addition, repetition of a single trial type was limited to a maximum of three consecutive trials.
The task and the data acquisition were under computer control. For each trial, the following data were collected: neural spike intervals (1 ms resolution), vertical contact force (digitization rate, 200 Hz), and specific timing data (drum onset and end, time of the change in texture for series P1a/b). Trial duration was 4.5–6.5 s. Discharge patterns were examined using rasters and post-event histograms (PEHs) aligned on different events in the trials.
For each trial, cell firing rate (imp/s) was measured in two intervals: 1) spontaneous discharge during the first 500 ms of data acquisition (digits resting on the stationary surface); and 2) during the surface scanning. For series P1a/b, firing rate was measured as the second half of the surface was moved under the digit tips. This corresponds to the portion of the surface over which SP was increased relative to the first half of the surface (texture change period) for three of four segments in each series. For series P2, SP was constant throughout the scan, so firing rate was measured during the entire stimulation period. The latter choice was justified by our observation that the r2 values from the regression analyses (below) were highest for this measure across the population of texture-sensitive cells. All cells showed a significant modulation of their discharge when the textures were displaced under the fingertips (interval 1 vs. 2, Wilcoxon test, P ≤ 0.05). All other analyses are focused on the discharge rate during the surface scanning.
The data of each cell were analyzed using a two-way analysis of variance (ANOVA) (dependent: firing rate during surface scanning; independent: SP and scanning speed). For all cells, firing rates during the scans were examined for normality (Shapiro-Wilks test) and homogeneity of variance (Bartlett test); a square root transformation was applied if necessary. The results were used to classify cells as texture and/or speed sensitive. The level of significance was set at P ≤ 0.05.
The nature of the relationship between firing rate and SP was evaluated using scatter plots and linear regression analyses. Cells were classified as graded if firing rate showed a monotonic change (increase or decrease) across the entire range of tested SPs. Cells that showed a monotonic increase or decrease in discharge over only a portion of the tested range (Jiang et al. 1997), with discharge plateauing for the remaining part of the range of SPs tested, were classified as partially graded. Secondary tests confirmed that discharge rate was stable across the plateau (ANOVA covering only the range of the observed plateau). Similar analyses were performed to evaluate the nature of the relation, if any, between firing rate and scanning speed, but in this case one additional test was added: cells also had to have a significant linear relation with speed. The latter results have been reported elsewhere (Dépeault et al. 2013). Finally, the χ2 test of independence was used for comparisons of frequencies. Additional analyses are detailed in results. Statistical analyses used Systat version 11.0 for Windows (SPSS, Chicago, IL).
The main analyses (above) were based on the assumption that the underlying neuronal code for roughness is based on mean firing rate. Using the same approach described in Dépeault et al. (2013), we tested the possibility that a spike count code might provide a better fit to SP as previously suggested for S1 coding of flutter vibration (Luna et al. 2005). As found for speed, the regressions were substantially weaker (lower r2 values), and so the analyses concentrated on a mean firing rate code.
Finally, we examined the timing of the spikes in each texture-related cell by computing autocorrelograms from the data during the period of texture scanning (second half of the surface only for cells tested with series P1), for each textured surface and each scanning speed (Poggio and Viernstein 1964). The resulting histograms were examined for evidence of periodic discharge.
Histology.
Near the end of the recording period, the monkeys were sedated (ketamine, 15 mg/kg), and electrolytic lesions made in selected tracks. After the final recordings, the animals were killed with an overdose of pentobarbital and perfused per cardium. Tracks were reconstructed from 50-μm parasagittal sections stained with cresyl violet. Neurons were assigned to areas 3b, 1 or 2 using the criteria described by Powell and Mountcastle (1959) and Jones et al. (1978). The histology from monkey I has been published (Meftah et al. 2009).
RESULTS
Classification of Cells
Neuronal data were collected from four monkeys as textured surfaces were scanned under the tips of D3 and D4. Sensitivity to texture and scanning speed was tested in 185 cells recorded from the S1 cutaneous digit representation of the hemisphere contralateral to the stimulated hand, 69 in area 3b, 75 in area 1 and 41 in area 2 (monkey B, 71; monkey I, 60; monkey J, 12; monkey N, 42). All cells had a cutaneous RF that included the glabrous tips of D3 and/or D4, and their discharge was significantly modulated during the presentation of the textured surfaces. The adaptation rate of the cells in response to manually applied, punctate stimuli was determined for 184/185 cells: 112 were categorized as SA and 72 as RA.
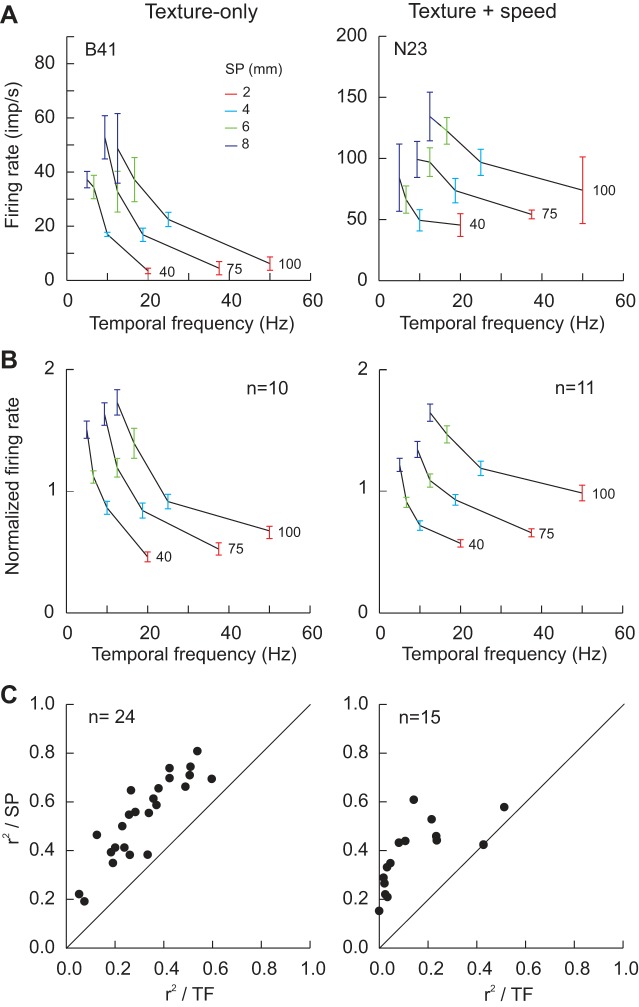
As described in methods, an ANOVA was applied to each cell to determine whether cell firing rate covaried with texture (SP) and/or scanning speed. The nature of the relation with each factor was examined with plots and linear regressions. As detailed in Table 1, 80% of the recorded cells were sensitive to surface texture (148/185), with almost all showing an increase in discharge with an increase in SP (144/148). A smaller proportion of cells (39%, 72/185) was sensitive to scanning speed, almost always in combination with texture sensitivity (57/72). Although all cells were modulated during the surface scanning, reflecting a bias in cell selection, a small number (12%, 22/185) were not sensitive to either surface texture or scanning speed. Single-cell examples of the main patterns of discharge with respect to surface texture are presented, followed by population analyses. Neuronal sensitivity to scanning speed has been addressed elsewhere (Dépeault et al. 2013).
Table 1.
Categorization of discharge patterns of 185 neurons as a function of sensitivity to spatial period, scanning speed, and cytoarchitectonic location
| Area 3b (n = 69) | Area 1 (n = 75) | Area 2 (n = 41) | |
|---|---|---|---|
| Texture only (n = 91) | 48 | 34 | 9 |
| Texture + speed (n = 57) | 16 | 20 | 21 |
| Speed only (n = 15) | 9 | 6 | |
| NS (n = 22) | 5 | 12 | 5 |
n, No. of neurons. NS, nonsignificant for texture or speed.
Discharge Properties of Cells
In these experiments, we sought a measure of neuronal discharge that would explain our psychophysical observations of increasing subjective roughness with increasing SP, independent of speed (Fig. 1). We reasoned that the invariance of roughness across different speeds necessarily ruled out a major role for a temporal code in signaling roughness intensity.
Periodicity.
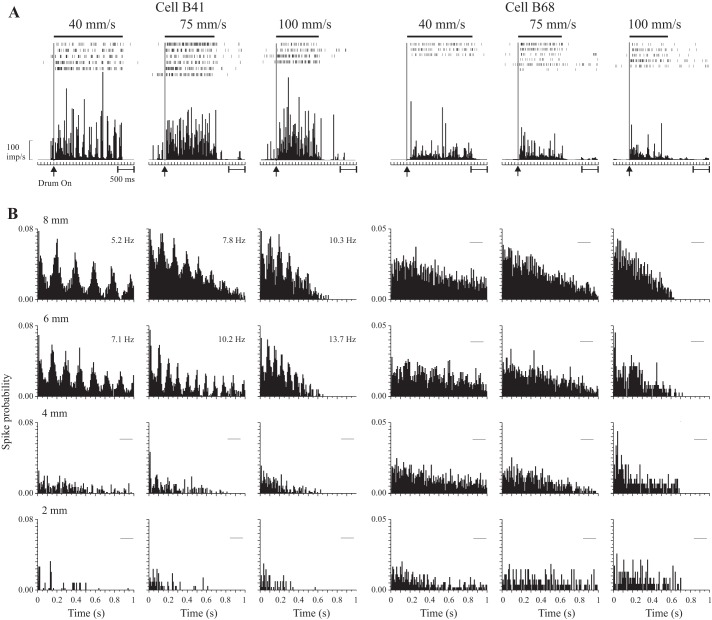
We did however, notice evidence of periodicity in some of the texture-related cells (e.g., Fig. 3A, cell B41) but not all (e.g., Fig. 3A, cell B68). We therefore performed an initial analysis using autocorrelograms to determine whether these signals contained sufficient evidence to provide a unique representation of the spatial characteristics of the surfaces, SP, independent of scanning speed. Figure 3B shows the results for the two example neurons. For this analysis, discharge is unfiltered, and the data show clear periodicity for one cell (left, B41) but not the other (right, B68). The periodicity was, moreover, limited to the two roughest surfaces (8 and 6 mm SP). No periodicity was observed for the smoother surfaces (4 and 2 mm SP). The measures of the temporal frequency of the discharge (displayed with each panel) varied with scanning speed. Thus they did not provide a unique measure of SP independent of speed. For each cell, in contrast, mean firing rate showed a progressive increase as SP was increased and was invariant with changes in scanning speed (see Fig. 4A, right, for cell B41).
Fig. 3.
A: post-event histograms (PEH; bin width, 25 ms) showed evidence for periodicity for some texture-related cells (left), but not others (right). Data are aligned on the onset of drum rotation; the bar (above) shows the approximate duration of the drum scan. B: autocorrelogram histograms for the same two cells (bin width, 8 ms) for each SP and speed tested. Cell B41 (left) displayed periodic discharge for rough surfaces (SPs of 6 and 8 mm), all 3 speeds tested, but not for smoother surfaces (2 and 4 mm SP). Cell B68 (right) showed no periodic discharge for any of the 12 conditions tested. For these examples, the autocorrelograms were based on all spikes recorded during the period of drum rotation. For cell B41, the measures of the temporal frequency of discharge (based on the peak timing of single peaks that exceeded baseline by 1 SD; Lebedev and Wise 2000) are given in each panel.
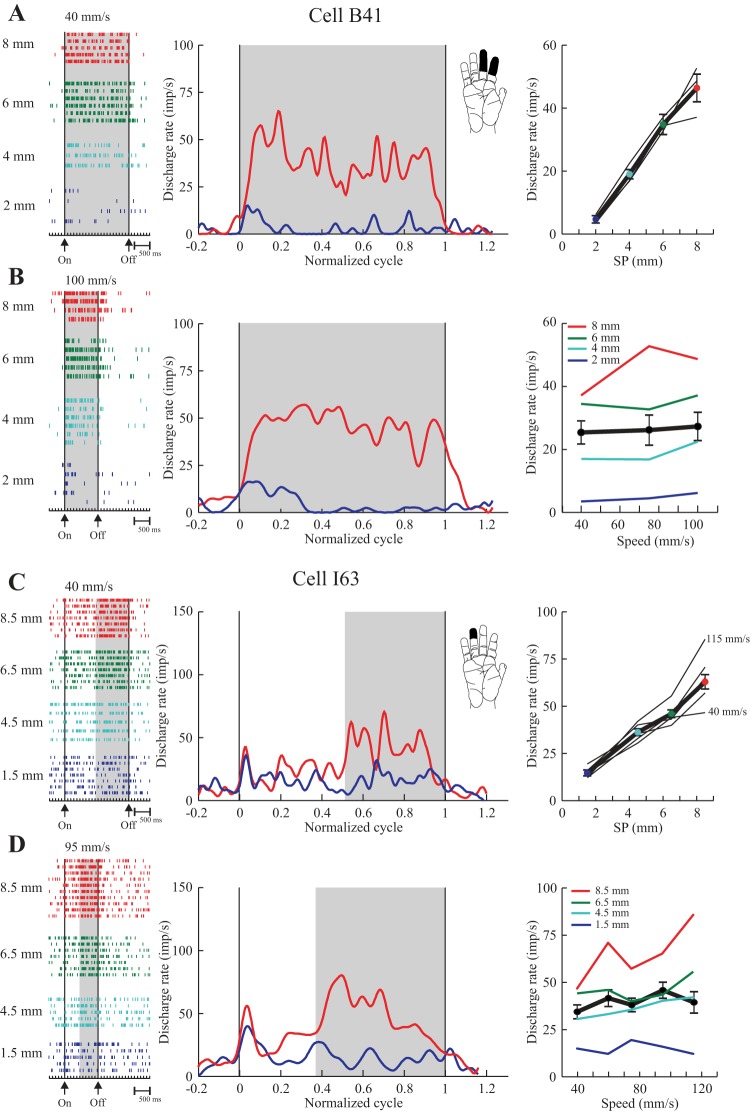
Fig. 4.
Examples of two texture-only cells (area 3b) that showed a monotonic increase in discharge as SP was increased (graded). A and B: cell tested with series P2 (2–8 mm SP; same cell as in Fig. 3, left). C and D: cell tested with series P1b (1.5–8.5 mm SP), with modified SP only over the second half of the surfaces (shaded region). For each cell, rasters (left) show data from individual trials aligned on drum onset (first vertical line, On). Drum stop is indicated by the second vertical line (Off). Trials are sorted according to SP and scanning speed (A and C, slow; B and D, fast). During acquisition, the surface and speed changed on a trial-by-trial basis. Discharge rate is shown in PEHs (middle), normalized to the duration of the surface scan (data during surface presentation divided into 256 equal bins, see Drew and Doucet 1991; Udo et al. 1982) so as to show data from low (A and C) and high (B and D) speeds on the same relative time scale. Baseline discharge is also shown (±20% of the duration of each scan, assigned to 12 bins pre- and 12 bins postscan). Discharge was convolved with a Gaussian (Gaussian standard deviation, 35.4 ms). PEHs are shown for the smoothest (blue) and roughest (red) surfaces. Summary plots (right) show mean discharge frequency as a function of SP (A and C) and scanning speed (B and D). The thick line is the mean across all trials (±SE). The thin lines show the individual plots for each SP (A and C) or speed (B and D). Scanning speed had little effect on the pattern of discharge so that the graded pattern was preserved across the range of speeds tested. These cells were both sensitive to light touch [see inset; A and B, rapidly adapting (RA); C and D, slowly adapting (SA)].
Approximately 70% of texture-related cells showed some evidence for periodicity when tested with the roughest surface at the slowest speed. For the smoothest surface, in contrast, almost none of the cells (<1%) showed periodicity when tested at higher speeds. Even for the slow speed, discharge was rarely periodic for the smoothest surface (11% of cells). Consequently, only a small proportion of cells tested showed periodic discharge with all four SPs tested (6%), and this only for the slowest speed. No cells showed periodic discharge for all test conditions (4 SPs × 3 speeds in monkeys B/N; 4 SPs × 5 speeds in monkeys I/J). Finally, periodic discharge was absent in a substantial proportion of cells categorized as texture-related on the basis of changes in firing rate (26%, Fig. 3, right).
These results show that periodic discharge patterns were limited to certain conditions and did not show the invariances expected to explain subjective roughness intensity. However, the fact that such periodic discharge was not seen in all conditions suggests that it is not a good candidate for a global descriptor of subjective roughness over a wide range. We therefore concentrate in the rest of this report on our hypothesis that a mean rate code can provide a unique descriptor of the spatial characteristics of rough surfaces, consistent with our psychophysical observations.
Mean firing rate.
For these analyses, firing rate on each trial was calculated over the entire period of surface scanning (only the second half of the scan for series P1, Fig. 2A) by counting the number of spikes and expressing this as the number of impulses per second.
GRADED.
Cells with a monotonic change in discharge rate across the entire range of SPs tested were classified as graded. Two representative examples are plotted in Fig. 4 [A and B: cell B41 (same cell as in Fig. 3A, left), range 2–8 mm; C and D: cell I63, range 1.5–8.5 mm]. For each cell, we show rasters (left) sorted according to SP for a low (A and C) and high speed (B and D), along with PEHs (middle) triggered by the onset of drum rotation. For the PEHs, discharge was normalized to the duration of the scan so that different speeds could be displayed on the same scale, and the traces are filtered to put the emphasis on the mean firing rate of the cell (see legend for details). The PEHs contrast the pattern of discharge obtained with the smoothest surface (blue) with that obtained with the roughest surface (red). The shaded regions give an indication of the windows used for data analysis.
For cell B41 (Fig. 4, A and B), the discharge patterns clearly distinguished the smooth and rough surfaces at low (A, 40 mm/s) and high speeds (B, 100 mm/s), with little change in firing rate when speed was more than doubled. This cell was tested with the P2 series (Fig. 2A), and so discharge rate on each trial was measured across the entire scanned segment (shaded region). The nature of the relation with SP was examined by plotting discharge rate as a function of SP (Fig. 4A, right). Here we show the individual curves from each speed tested and a summary curve (thick black line). Inspection shows that rate increased monotonically with SP. The individual curves are closely superimposed, consistent with the absence of any dependence on scanning speed. The pooled data were fit to a linear regression. Discharge rate varied significantly with SP (P < 0.0005) and explained a high proportion of the variability in cell discharge rate (r2, 0.70). The same data are also plotted as a function of speed (Fig. 4B, right). The dependence of rate on SP was clearly preserved across all speeds (individual color-coded curves). The pooled data (thick black line) had a slope close to zero, and there was no relation between rate and speed (P = 0.76). The ANOVA (dependent variable, firing rate in the shaded region; independent variables, SP and speed) confirmed these observations: rate varied with SP (P < 0.0005) but not speed (P = 0.24). This cell was thus categorized as having a graded relation to SP, independent of scanning speed.
Cell I63 (Fig. 4, C and D) was tested with series P1a. The first half of each segment had a uniform SP, 1.5 mm, while the second half was either identical, 1.5 mm, or incremented to 4.5, 6.5 or 8.5 mm, and so measures of discharge rate were restricted to the second half (shaded region). This cell showed a graded increase in rate across the entire range of SPs. In this case, there was a minor influence of scanning speed on firing rate, but this was restricted to the fastest speed tested, 115 mm/s (see summary plot, C), and the roughest surface (8.5 mm SP, illustrated in the PEH, D). The linear regression (rate vs. SP, pooled data) explained a high proportion of the variance in firing rate (r2, 0.61). The ANOVA, however, indicated that firing rate varied significantly with both SP (P < 0.0005) and speed (P = 0.004). As described in the methods, however, we further required that cells show a significant linear relation with speed to classify them as speed sensitive. In this case, the linear regression (rate vs. speed, pooled data: thick line, D) was not significant (P = 0.31), reflecting the fact that the pooled data had a slope close to zero. Thus this cell was also categorized as graded and speed insensitive.
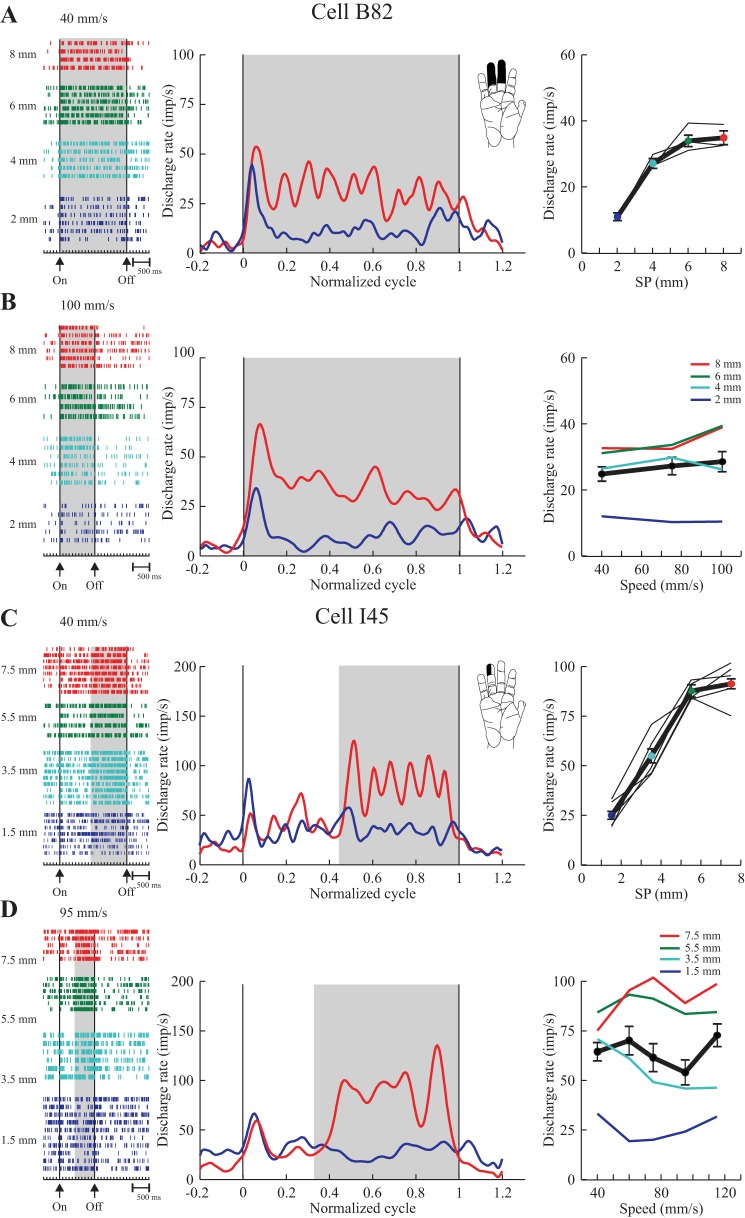
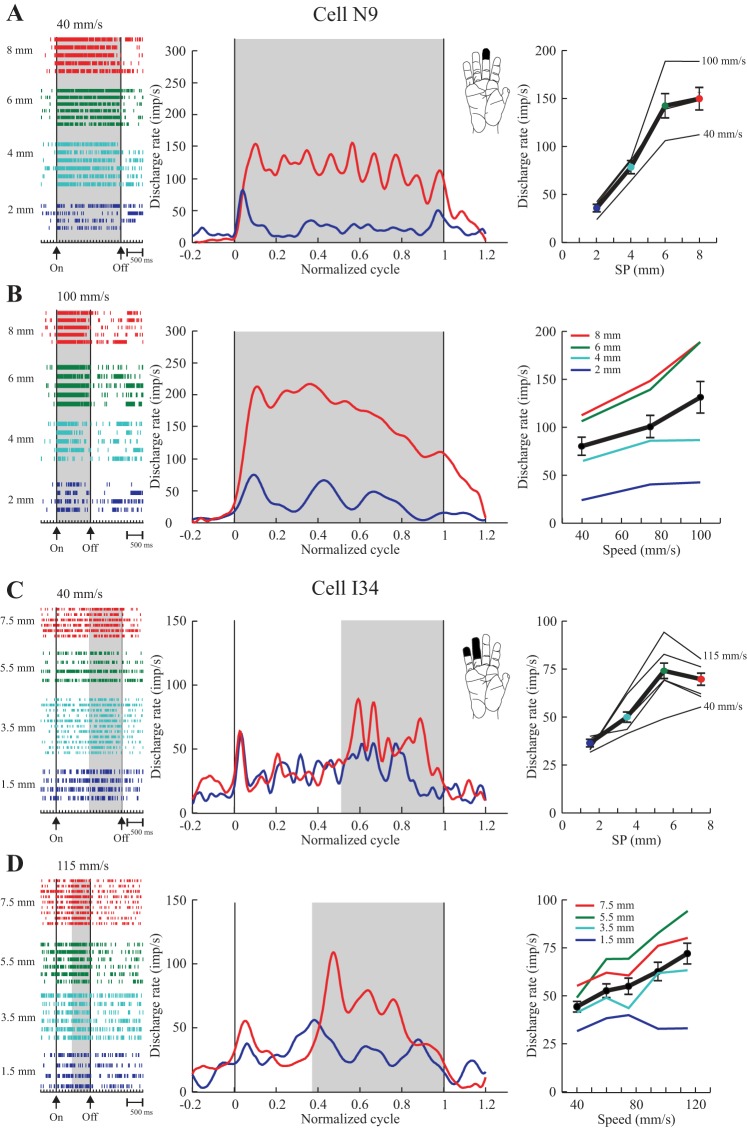
PARTIALLY GRADED.
Cells with a monotonic change in discharge rate restricted to only a portion of the tested range of SPs, and a plateau over the remaining part of the range were classified as partially graded (Figs. 5 and 6). As described in methods, the plateau in the discharge was always verified statistically, using either a paired t-test or an ANOVA. Two examples are shown in Fig. 5. In each case, the ANOVA indicated sensitivity to SP (P < 0.0005) but not speed (P > 0.2). Cell B82 (Fig. 5, A–B) showed an increase in rate across SPs ranging from 2 to 6 mm, with some decrease in the rate of rise over the larger SPs (4–6 mm). Further analyses (above) indicated that the plateau in discharge was restricted to the largest SPs tested, 6–8 mm (P = 0.7). Cell I45 (Fig. 5, C and D) showed a monotonic increase in rate across SPs, ranging from 1.5 to 5.5 mm; thereafter discharge plateaued (5.5–7.5 mm, P = 0.12). In both cases, the individual plots of discharge rate vs. SP (for each speed tested) are closely superimposed (A and C, right). The lack of speed-sensitivity is likewise evident in examining the plots of discharge rate vs. speed for the individual SPs (B and D, right). In these examples, it is possible that discharge may have saturated at higher SPs.
Fig. 5.
Examples of two texture-only cells (area 3b) with partially graded responses to SP. Data are plotted as in Fig. 4. A and B (tested with series P2, 2–8 mm SP): discharge increased steeply over SPs of 2–4 mm, reaching a plateau for SPs of 6–8 mm. C and D (tested with series P1a, 1.5–7.5 mm): discharge increased over SPs of 1.5–5.5 mm and then plateaued for SPs of 5.5–7.5 mm. In both cases, the discharge pattern was preserved across all scanning speeds (see summary plots, A and C). Both cells had a SA response to light touch.
Fig. 6.
Examples of two texture- and speed-sensitive cells (area 3b) with a partially graded texture response. Data are plotted as in Fig. 4. A and B (tested with series P2, 2–8 mm SP): discharge increased over SPs of 2–6 mm, plateauing thereafter (SPs of 6–8 mm). C and D (tested with series P1a, 1.5–7.5 mm): discharge increased over SPs of 1.5–5.5 mm, and then plateaued for SPs of 5.5–7.5 mm. Both cells showed a significant relation with scanning speed: higher rates with higher speeds. The pattern of discharge was preserved across all speeds, suggesting that the plateau was not explained by saturation in firing rates. Both units were sensitive to light touch (A and B, RA; C and D, SA).
Other cells, such as those shown in Fig. 6, were sensitive to both texture and speed (P < 0.0005). These two neurons are similar to those shown in Fig. 5 in that their discharge plateaued over the final 2 mm of dot spacings tested (P > 0.3). In contrast, discharge rates also covaried with speed, but in both cases their pattern of texture sensitivity was preserved across the range of speeds tested. This observation suggests that the plateau at higher SPs was not explained by saturation of discharge in either case (see Fig. 6, A and C, right).
OTHER RESPONSE PATTERNS.
In a few cells we observed an inverted U-shaped pattern in relation to SP, as described by Connor et al. (1990) for peripheral afferents. These cells showed an increase in firing rate up to SPs of 4 or 5.5–6.5 mm, followed by a decrease as SP was further increased. Such responses were uncommon (n = 8, Table 2). A further 11 cells (Table 2) showed a significant change in discharge across the range of SPs, but their discharge plateaued in the midrange.
Table 2.
Patterns of discharge seen in 148 texture-sensitive cells
| Area 3b | Area 1 | Area 2 | |
|---|---|---|---|
| Texture-only (n = 91) | |||
| Graded (26%) | 16 | 6 | 2 |
| Partially graded (62%) | 29 | 22 | 5 |
| Other* (12%) | 3 | 6 | 2 |
| Texture + speed (n = 57) | |||
| Graded (26%) | 7 | 3 | 5 |
| Partially graded (58%) | 9 | 12 | 12 |
| Other† (16%) | 5 | 4 |
n, No. of cells.
Includes 6 cells showing increased discharge across the range with a plateau for the intermediate spatial periods, 4 inverted-U cells, and 1 unclassified.
Includes 5 cells showing increased discharge across the range with a plateau for the intermediate spatial periods and 4 inverted-U cells.
Population Analyses
Temporal frequency.
We examined the extent to which mean firing rate covaried with the temporal frequency of the stimulation (speed/SP) in each texture-related cell. Since tactile roughness estimates in humans vary with SP and not temporal frequency (Meftah et al. 2000), we expected that neurons playing a role in texture scaling should share this property. Examples are shown in Fig. 7A for a graded texture-only cell (left, same cell as in Fig. 4, A and B) and a graded texture + speed cell (right). A family of three mostly non-overlapping curves resulted, one for each speed tested, with rate decreasing as temporal frequency increased. These results contrast with the plots with SP which are closely superimposed (e.g., Fig. 4A). Mean rate was relatively constant for each SP (see legend), despite large changes in temporal frequency. The data (all speeds) were fit to a linear regression (rate vs. temporal frequency). A significant result was obtained for the texture-only cell (P < 0.0005), but the coefficient of determination, r2, was considerably lower than for the regression with SP (0.44 vs. 0.7). The regression was not significant for the texture + speed cell. These two examples were representative of the sample of graded texture cells. Figure 5B plots normalized firing rate as a function of temporal frequency for all graded cells tested with these same speeds. These plots are very similar to those obtained when human roughness estimates are plotted as a function of temporal frequency (Fig. 5, Meftah et al. 2000). To quantify the observations, a linear regression was fit to the data of each texture-related cell. All but one texture-only graded cell showed a significant negative linear relation with temporal frequency (24/25), compared with 8 of 15 texture + speed-sensitive cells. We compared the r2 values for the analyses relative to SP and temporal frequency. The results, plotted in Fig. 7C, show that SP explained a higher proportion of firing rate variance than did temporal frequency for all of the graded texture-only, 54% vs. 32%, and the graded texture + speed cells, 38% vs. 14% (all points above the line of equality, P < 0.0005). Similar results were obtained when the analysis was extended to all texture-sensitive cells: 114 of 148 texture-sensitive cells showed a significant relation to temporal frequency (P < 0.0005), including 51/56 partially graded texture-only cells and 20/33 partially graded texture + speed cells.
Fig. 7.
Temporal frequency (speed/SP) analysis for single-cell examples (A) and for pooled data (B) as a function of cell classification (fully graded cells: texture-only, left; texture + speed, right). A: examples of graded texture-only (same cell as in Fig. 3A and Fig. 4, A and B) and texture + speed cells. Both cells showed a linear and graded increase in firing rate when this was plotted as a function of SP (e.g., Fig. 4A). When the data were plotted as a function of the temporal frequency of the stimuli, families of 3 non-overlapping curves were obtained, corresponding to the 3 speeds tested. B: pooled data from monkeys B and N (all graded cells tested with the same speeds). C: comparison of the coefficient of determination, r2, from regression analyses applied to all fully graded cells (firing rate vs. SP or temporal frequency). Inspection shows that the r2 values from the SP analysis were higher than those from the temporal frequency analysis: all points are distributed above the line of equality.
TEXTURE-ONLY CELLS.
A large proportion of cells were sensitive to SP independent of scanning speed (91/148, 61%; Table 1), and so were categorized as texture only. Examples are illustrated in Figs. 4 and 5. Such cells were encountered throughout the cutaneous hand representation but showed a rostral-caudal gradient, making up a larger portion of the sample in area 3b (70%) compared with areas 1 (45%) and 2 (22%). Overall, 53/72 cells tested with the P1 series were categorized as texture-only compared with 38/113 cells tested with the P2 series. The higher proportion of texture-only cells for the P1 series was explained by sampling bias: area 2 was not explored in the monkeys tested with the P1 series, and this region was dominated by speed-sensitive cells (Table 1).
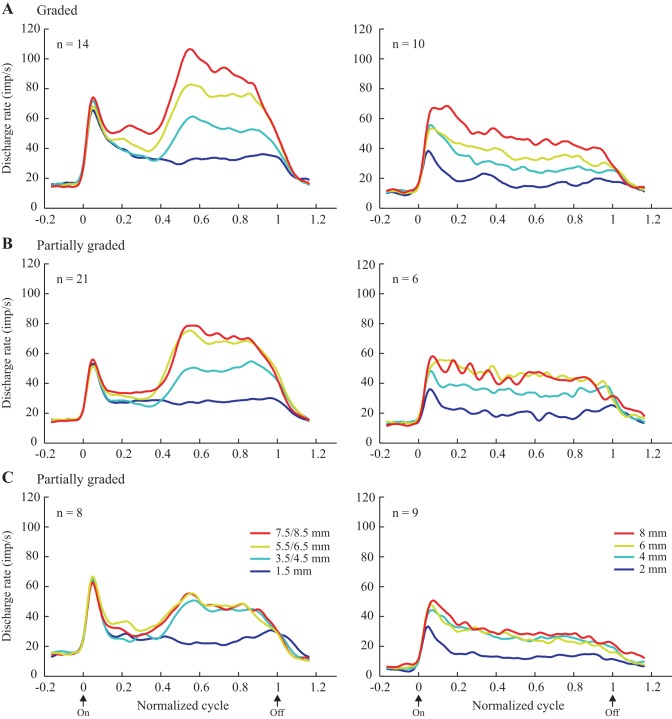
1) Graded texture-only cells. A substantial proportion of the texture-only neurons showed a graded increase in discharge rate across the entire range of SPs tested, spanning 6 or 7 mm. Examples are shown in Fig. 4. Overall, 24/91 (26%) texture-only cells showed this pattern of discharge, and the large majority of these, 16 (67%), was localized to area 3b (Table 2). Two-thirds were categorized as SA from the RF testing; the remainder were RA. Population ensemble averages, shown separately for the P1 (left, surfaces with modified SP over the second half of the scanned surfaces) and P2 series (right, surfaces with a single SP across the entire length of the scanned surfaces) are plotted in Fig. 8A. These averages were generated using all of the data collected and also multiple speeds. Examination shows that the discharge of the graded neurons clearly distinguished the different SPs presented, and that the difference was maintained throughout the period of the scan. This impression was confirmed with ANOVAs and linear regressions applied to the pooled data from each series: in both cases, firing rate varied with SP (P < 0.0005), and the pooled regression curves (rate vs. SP) showed a monotonic increase in rate with SP (P < 0.0005).
Fig. 8.
Ensemble averages for texture-only cells (plotted as in Fig. 4) grouped according to their discharge pattern and the series of surfaces employed (left, series P1a/b; right, series P2). Only cells showing an increase in discharge with SP are included here. A: graded cells showed an increase across all 4 SPs. B and C: partially graded cells showed an increase across 3 (B; surfaces 1, 2, and 3, Fig. 1A) or 2 (C; surfaces 1 and 2) of the surfaces. Data are aligned on the onset of drum rotation and normalized to the duration of the stimulation period (60–120 trials per cell).
When comparing across the two series of surfaces (left vs. right), discharge rates were generally higher for the P1 surfaces (left). Consequently, the slopes of the individual linear regressions, rate vs. SP, were steeper for the cells tested with the P1 surfaces (P = 0.004, Kruskal-Wallis test). This observation was unrelated to the spontaneous firing rate of the neurons (measured prior to the onset of the scans), since there was no difference either between the cells contributing to these averages or the entire sample (P > 0.15). It is more likely that the response evoked by the initial SP scanned under the fingertips (1.5 mm SP, P1) influenced the amplitude of the subsequent response to the modified SPs (rougher surfaces).
The initial response amplitude elicited by the standard SP of 1.5 mm (over first half of the scanned texture), however, shows some variability, most obviously for the roughest surface (red trace). The source of this variability is not known, but it may be related to some imperfection on the surface that allowed the monkeys to anticipate an upcoming change in surface roughness (note that both were trained to discriminate the change in roughness, although the recordings were made outside the context of the task). To address this, we applied a multiple regression to the data from each cell contributing to the average (Fig. 8A, left) to determine the relative contribution of SP (second half) and the discharge rate during the first half of the scan (1.5 mm SP) to the discharge rate measured over the second half of the scan. SP explained more than twice as much of the variance in firing rate over the second half of the scan than did the firing rate over the first half of the scan (56% vs. 24%, P = 0.002). Thus, while there was an interaction, the SP over the second, modified half of the surfaces was clearly the major factor influencing firing rates during the second half of the scan. It is, however, likely that the lack of response priming for the cells tested with the P2 series (Fig. 8, right) contributed to their lower discharge rates. This is further addressed in the discussion.
2) Partially graded texture-only cells. The majority of texture-only cells were categorized as partially graded (56/91, 62%), i.e., their firing rate showed a monotonic change over a part of the tested range of SPs and plateaued for further increases in SP. Examples are shown in Fig. 5. These examples were representative of the larger sample, since their discharge rate showed a graded increase across smaller SPs (e.g., 1.5–5.5 mm for Fig. 5C) and a plateau for the largest SPs tested (5.5–7.5 mm in this case). Overall, 50/56 cells showed such a pattern, with the plateau extending across 2–3 mm (n = 29) or 4–5 mm (n = 21), corresponding to, respectively, surfaces 3 and 4 and surfaces 2, 3 and 4 of the test series (Fig. 2A). In all but two cases, the sign of the response was positive, i.e., cell discharge was higher for larger SPs. Partially graded cells were found in all three areas, making up 56–65% of the texture-only cells. Both SA (n = 33) and RA (n = 23) responses to RF testing were observed.
Population ensemble averages are plotted in Fig. 8, B and C (only cells showing an increased discharge rate with an increase in SP). For this, cells were divided into two groups. The averages shown in Fig. 8B show the response profile for those units whose discharge rate plateaued for the two surfaces with the largest SP (verified statistically for each individual cell). ANOVAs applied to the pooled data confirmed the single-cell results: no variation in firing rate over the pair of surfaces with the largest SPs (P > 0.3), although SP was a significant factor across the entire range (P < 0.0005 for each series). Inspection shows that discharge was clearly graded over the other portion of the range of SPs tested, with the results being very similar for both series of surfaces and so the two groups of monkeys. The neurons illustrated in Fig. 8C plateaued over a wider range of SPs, only differentiating the smoothest surface from the other three rougher surfaces. ANOVAs applied to the pooled data confirmed the results of the single-cell analyses: there was no change in rate across the three rougher surfaces (P > 0.5), while SP was significant across the entire range of SPs tested (P < 0.0005). Again the pattern of modulation was very similar for the two series. Units with the response pattern shown in Fig. 8B were particularly localized to area 3b (19/29); those with the pattern depicted in Fig. 8C were found in all three areas, but especially area 1 (11/21). Finally, we compared the slopes of the regression curves (rate vs. SP) across the cells tested with P1 (left) and P2 (right). There was a trend for higher slopes for those tested with the P1 series, 8.1 ± 0.9 vs. 6.6 ± 0.9, but the difference was not significant (P = 0.109). As found for the graded cells (above), SP explained more than three times as much of the variance in firing rate over the second half of the scan than did the firing rate over the first half of the scan (44% vs. 12%, P < 0.0005).
The remaining partially graded cells (6/56) showed either a plateau for smoother surfaces along with a graded increase in discharge rate for large SPs (n = 3), or a more selective response only for the midrange SPs (plateaus for the low and high SPs, n = 3). These atypical cells were encountered in areas 3b and 1 (3 in each).
3) Adaptation rates. From the RF testing, the majority of texture-only cells were categorized as SA (62%, 56/91), while the remainder were RA (38%). In area 3b, SA neurons predominated (∼70%: 34 SA, 14 RA), while in caudal S1 there were approximately equal numbers of SA and RA neurons that were characterized as texture-only (area 1, 18 SA, 16 RA; area 2, 4 SA, 5 RA).
4) Relationship with RF geometry. RFs were characterized in a number of ways to describe their geometry. The database contained a high proportion of multidigit RFs, 128/185. Single- and multidigit RFs were differentially distributed across S1 (χ2 = 44.1, P < 0.0005): single-digit RFs made up 61% of the area 3b sample compared with 19% and 7% in areas 1 and 2. In the majority of cells, the RF covered the entire distal phalanx in contact with the surfaces (D3 and/or D4), 164/184 (extent not determined for 1 cell); no differences were, however, observed across S1 (χ2 = 2.56, P = 0.28). Finally, cells were categorized according to whether one or both of D3/4 had a RF in contact with the surfaces: 86 cells had a RF restricted to a single digit in contact, while 99 had a RF that spanned both digits. These categories were differentially distributed across S1 (χ2 = 28.5, P < 0.0005): area 3b neurons had mainly one digit with a RF in contact (48/69), while areas 1 and 2 were characterized by high numbers of RFs covering both D3 and D4 (respectively, 46/75 and 32/41).
We also measured the dimensions of the distal phalanges (D3/4) in all four monkeys from photos: means of 14 mm in the proximal-distal axis × 9 mm in the medial-lateral axis. The approximate area of contact on each digit was 11 × 9 mm (measures from a monkey from which we are currently recording; same size as those used here). With the largest SPs tested, 7.5, 8 or 8.5 mm, the RF would have been contacted by two rows or more at all times as long as it included the entire distal phalanx (see below). The exception would have been cells with a smaller RF restricted to the distal part of the phalanx. For comparison, measures were taken in two representative human subjects, in this case using a single digit, D3, as in our laboratory's psychophysical studies (Dépeault et al. 2009; Meftah et al. 2000; Sutu et al. 2013): the area of contact was 14 × 10 mm (dimensions of distal phalanx, respectively, 23 × 16 mm). The human digit was thus also contacted with two rows or more at all times.
We compared our measures of RF geometry across the fully and partially graded cells, including whether the RF included (or not) the entire distal phalanx, the number of digits with a RF in contact with the surfaces and the extent of the RF (single or multidigit). No differences were observed, including the comparison across larger and smaller RFs, suggesting that differences in the pattern of texture sensitivity could not be explained by the geometry of the peripheral RF. Thus some of our fully graded cells had a RF restricted to the most distal part of the distal phalanx (2/24), and most of the partially graded cells had RFs that included the entire glabrous surface of D3 and/or D4 (46/56).
TEXTURE- AND SPEED-SENSITIVE CELLS.
A smaller proportion of cells (57/148, 39%, Table 1) were sensitive to both texture and scanning speed (13, P1 surfaces; 44, P2 surfaces). These cells were particularly concentrated in posterior S1, making up 51% of the sample in area 2, compared with 23–27% in areas 3b and 1. The overall proportions of graded and partially graded responses were similar to those described for texture-only cells (Table 2), with partially graded responses being more frequent (58% vs. 26%). The adaptation rates of the cells were similarly distributed as well (graded: 9 SA, 6 RA; partially graded, 20 SA, 13 RA). Cell discharge rate increased as scanning speed increased for the vast majority of cells, 54/57 (Dépeault et al. 2013). The sign of the response with texture (SP) was likewise positive for all but two cells (partially graded). The pattern of the texture response was preserved across the range of speeds tested for the majority of cells (see Fig. 6), i.e., the response pattern was specific to the SPs tested and did not represent response saturation at higher speeds (51/57). As for the partially graded texture-only cells, the plateau for the partially graded texture + speed responses extended across 2–3 mm (n = 16) or 4–5 mm (n = 17). In contrast, however, there was a large proportion of atypical partially graded cells (9/33, 27%), including selective responses to the roughest SPs (n = 5) or midrange SPs (n = 4). The majority of the atypical cells were localized to area 2 (7/9); the others were in area 1.
As for the texture-only cells, we compared our RF measures across the graded and partially graded texture + speed cells, and no differences were observed. A comparison across the texture-only and texture + speed groups revealed one difference, a higher proportion of multidigit RFs for partially graded texture + speed cells (25/33) than for the corresponding texture-only cells (23/56, χ2 = 5.72, P = 0.017). Graded cells showed no difference.
QUANTIFICATION OF THE RELATIONSHIP BETWEEN CELL DISCHARGE AND SP.
Each cell was fit to a linear regression, mean firing rate vs. SP. Overall, graded cells had significantly higher slopes than partially graded cells, respectively, 8.1 ± 0.7 (means ± SE) and 4.8 ± 0.4 imp·s−1·mm−1 (P < 0.0005, Kruskal-Wallis test). This difference disappeared when the regression was repeated for the partially graded cells using a smaller range of SPs corresponding to the range over which cell discharge was graded (8.5 ± 0.6, P = 0.59). The r2 values were significantly higher for graded cells (respectively, 0.477 ± 0.028 and 0.319 ± 0.02, P < 0.0005), while there was no difference in the intercepts (P = 0.19). Although, the r2 values for partially graded cells remained significantly lower than for the graded cells when the regression was restricted in range (0.399 ± 0.022, P = 0.03), this may have reflected the lower number of trials, since the fully graded cells also showed lower r2 values when the regression was limited to the same ranges.
Figure 9 summarizes the distributions of the r2 values from the regressions (all SPs included) as a function of sensitivity to texture alone (top) or texture + speed (bottom). Cells are grouped according to their pattern of texture sensitivity (see legend). Texture-only cells had higher r2 values than did texture + speed-sensitive cells (Kruskal-Wallis test, P = 0.004). This was explained by higher r2 values for texture-only graded cells. The latter had higher r2 values than did the graded texture + speed cells (P = 0.007). No difference was observed for the partially graded cells (texture-only vs. texture + speed, P = 0.17). Within the partially graded cells, those that signaled texture changes over a wider range of SPs (green) had higher r2 values than those that signaled a texture change across a more limited range (orange), but only for the texture-only group (P < 0.0005). The mean r2 value for the texture-only graded cells was 0.537 ± 0.034. Overall, one-half of the texture-only neurons, 47/91, had a strong relation with SP (r2 ≥ 0.4), compared with only one-fourth of the texture + speed cells, 16/57. Concentrating on the graded cells, 75% of the texture-only cells had a strong relation with SP compared with only 53% of the texture + speed cells, and the former were almost entirely concentrated in rostral S1 (area 3b, n = 12; area 1, n = 5; area 2, n = 1).
Fig. 9.
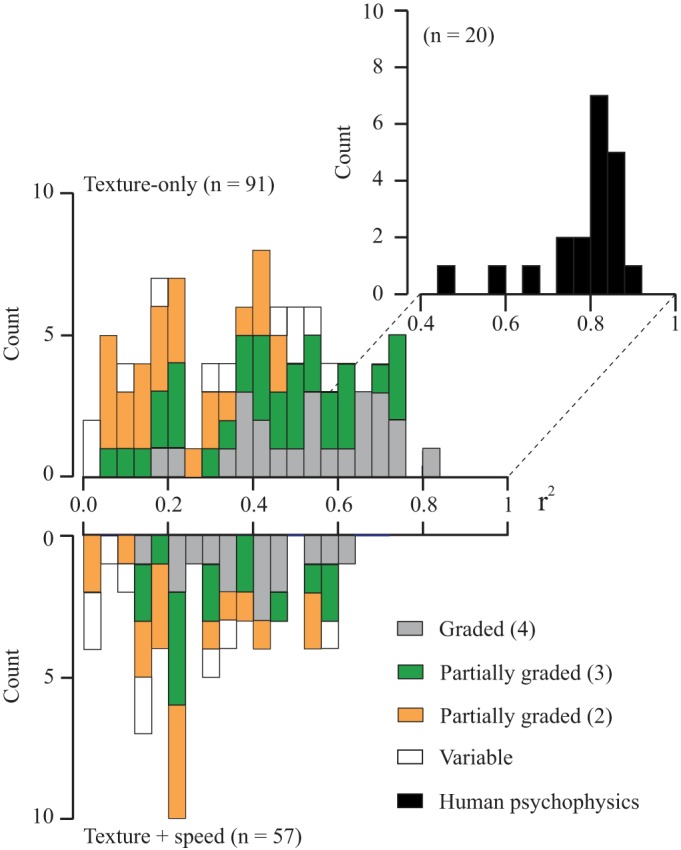
Distribution of r2 values from the linear regression analyses (discharge rate vs. SP) for 148 texture-sensitive neurons. The data are plotted separately as a function of whether their discharge varied only with texture (top) or with both texture + speed (bottom). Neurons were subdivided according to their pattern of texture responsiveness (see legend and Fig. 8). The corresponding r2 values from human psychophysical experiments (subjective roughness vs. SP) are also shown (inset: black histogram: pooled data from Dépeault et al. 2009 and Meftah et al. 2000). The graded, texture-only cells had the highest r2 values, partly overlapping the r2 values from the human data. The partially graded cells were divided into two groups, depending on the number of surfaces over which their discharge varied (2, orange; 3, green).
COMPARISON WITH ROUGHNESS SCALING.
The major aim of this study was to test our hypothesis that a simple intensive code (mean firing rate) could explain the cortical representation of subjective roughness intensity. As outlined in the Introduction, our psychophysical observations (Fig. 1) led us to predict that a subset of S1 cortical cells would show a graded increase in discharge across a wide range of SPs, independent of scanning speed, consistent with a role in encoding subjective tactile roughness. Overall, 24 neurons met these criteria: texture-only and graded response to SP. Such cells made up a relatively small proportion of the texture-sensitive cells in S1, 24/148 (16%). Their individual regression curves are plotted in Fig. 10A. For comparison, we also plot the individual curves, roughness estimates vs. SP, of 20 human subjects in Fig. 10B. The latter data come from earlier experiments using the same types of raised-dot surfaces (data from Dépeault et al. 2009; Meftah et al. 2000). For the human data, the estimates of each subject were normalized by dividing all values by the grand mean for the session to take into account the fact that different subjects used different rating scales. To facilitate comparison, the single-unit data were also normalized. A comparison of the two plots shows that the results were qualitatively very similar. The slopes of the curves varied from cell to cell and across subjects, but all showed a significant monotonic relation with SP.
Fig. 10.
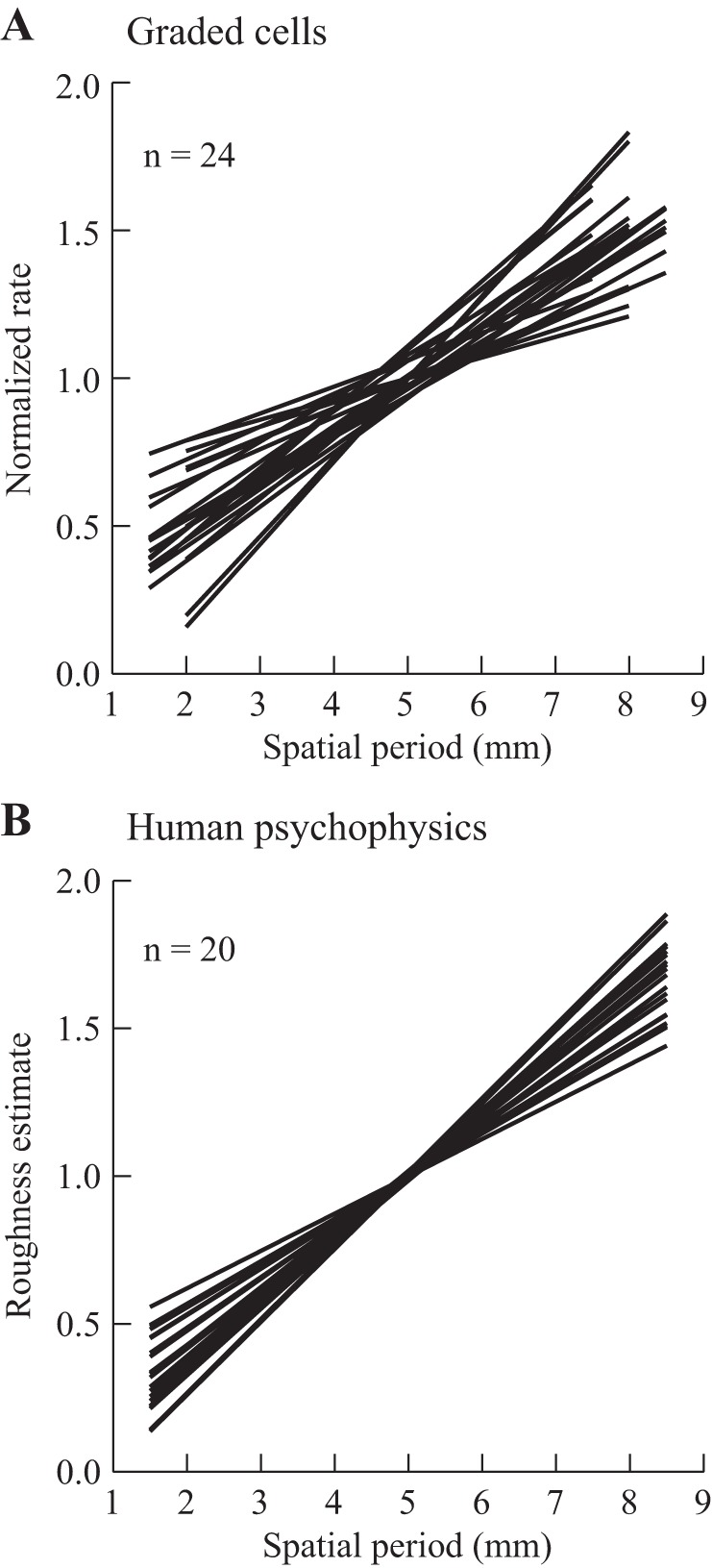
Neuronal sensitivity to SP (A) and human scaling of tactile roughness (B). A: linear regression curves for 24 texture-only cells with a fully graded response to SP. For each cell, data were normalized by dividing the discharge rate by the grand mean for all trials. B: linear regression curves from 20 subjects, plotting normalized roughness estimates as a function of SP (SPs of 1.5–8.5 mm; 1-mm increments in SP; dot heights of 1–1.8 mm). [Psychophysical data are replotted from Dépeault et al. (2009) and Meftah et al. (2000) with permission.]
We compared the parameters of the regression curves plotted in Fig. 10 (A vs. B). There was no difference in the slopes (P = 0.07, 0.16 ± 0.01 and 0.19 ± 0.01), but the intercepts were modestly lower in the humans (P = 0.034, 0.2 ± 0.06 and 0.04 ± 0.04). The distribution of the r2 values for the human psychophysical data is shown in Fig. 9 (black histogram). Their r2 values were higher (0.78 ± 0.03) compared with the neuronal data (0.54 ± 0.03, P < 0 .0005), but there was, nevertheless, considerable overlap.
DISCUSSION
In agreement with our primary hypothesis, we identified a population of S1 neurons showing a monotonic increase in their mean discharge rate across a wide range of dot spacings, i.e., their discharge was graded across the entire range of tested SPs. As predicted, a subset of these neurons was insensitive to scanning speed, consistent with them playing a role in subjective roughness scaling. We also identified a substantial proportion of neurons sensitive to smaller ranges of SPs, compatible with a role in discriminating smaller changes in tactile roughness.
S1 Cortical Representation of Surface Texture: Graded Responses to SP
This is the first demonstration that S1 cortical firing rate is monotonically graded across a wide range of surface textures, 1.5 to 8.5 mm SP, corresponding to a range over which roughness estimates also show a monotonic increase (see below). Overall, 26% of the texture-sensitive cells were categorized as graded. These observations confirm and extend our earlier report that S1 cutaneous neurons show a linear, monotonic relation to the SP of raised-dot surfaces over a smaller range of SPs, 2–5 mm (Jiang et al. 1997). We also found that the discharge of 61% of S1 texture-sensitive neurons was independent of scanning speed, including 75% of the texture-sensitive neurons in area 3b, corresponding to the major point of entry for cutaneous inputs to S1. This latter observation must reflect cortical processing, since the discharge of primary cutaneous mechanoreceptive afferents generally covaries with both SP and scanning speed (Goodwin and Morley 1987).
The graded texture-only neurons have properties consistent with playing a key role in encoding subjective roughness intensity. Estimates of tactile roughness show a monotonic increase across SPs of 1.5–8.5 mm and are invariant with scanning speed across the range tested here (Dépeault et al. 2009; Meftah et al. 2000). These properties are shared by the graded texture-only neurons identified here, which showed stronger correlations with SP than the other texture-sensitive neurons. In addition, their slopes (normalized) were similar to those obtained from our human psychophysical experiments (Fig. 10). We suggest that such neurons, which included both SA and RA neurons, play a key role in scaling subjective roughness. Although the r2 values for the psychophysical data were higher than for the neuronal data (see Fig. 9), this likely reflects the fact that subjective roughness is encoded by the discharge of a population of cells and not single neurons.
Results from a limited number of recordings in the present database (74 texture-related cells) suggest that some S1 cells are graded for SP independent of dot disposition (periodically or nonperiodically disposed raised dots), and this independent of scanning speed. Such observations are consistent with observations that subjective roughness is similar for periodic and nonperiodic surfaces (Dépeault et al. 2009).
S1 Cortical Representation of Surface Texture: Partially Graded Responses to SP
The majority of texture-sensitive cells, 60%, were sensitive to only a small range of SPs. Our results confirm and extend earlier results (Jiang et al. 1997; Sinclair and Burton 1991a; Sinclair et al. 1996). The higher proportion of partially graded responses here, in contrast to our laboratory's previous study, 14% (Jiang et al. 1997), reflects the larger range of SPs presented and differences in sampling across S1 (sampled mainly area 3b in Jiang et al.). For approximately one-third of the cells, we ruled out saturation of discharge as a contributing factor to this pattern since the plateau was present at both low and higher discharge rates associated with low and high speeds (examples in Fig. 6). For the remaining cells (not speed-sensitive), we cannot rule out saturation of discharge, but we do note that the population averages (Fig. 8, B and C) show that the discharge rates of these cells are relatively modest (peak rates <80 imp/s) and unlikely to represent the maximal firing rate for these cells.
We considered the possibility that these partially graded responses might be explained by RF geometry in relation to the range of SPs tested here. No evidence was found to suggest that these neurons had smaller RFs than did fully graded cells, and so it seems unlikely that this pattern could be explained by differences in RF geometry.
Sensitivity to a limited range of SPs is consistent with such cells playing a role in discriminating small changes in SP. Psychophysical results indicate that humans can discriminate changes in the spacing of tactile elements on manufactured surfaces (raised dots, gratings) in the order of 5% (Lamb 1983a; Morley et al. 1983; Sutu et al. 2013). This translates into a change in SP of 100 μm relative to a standard surface texture of 2 mm. Discrimination thresholds may be higher in monkeys (20–25% or 0.5 mm for a 2-mm standard), at least when exploration is limited to a single scan (Meftah et al. 2002; Sinclair and Burton 1991b). Consistent with a role in roughness discrimination, it is noteworthy that some cells signaled changes in SP at the lower end of the tested range, and others at the higher end. The existence of such tuning is critical to explaining the human ability to discriminate tactile roughness, since humans can discriminate differences in SP across the ranges presented here (Sutu et al. 2013). Interestingly, the present sample of neurons showed a definite preference to signal changes in SP across the lower part of the range tested, 1.5–4.5 mm (46/89), compared with the higher SPs (5/89 for the two highest SPs tested, e.g., 6 vs. 8 mm).
For the partially graded cells identified here, the average slope over the range of SPs to which they were sensitive was 8.5 Hz/mm. Monkeys can discriminate a SP change of 0.5 mm (above), and so discrimination would be based on a change in firing rate of ∼4 Hz. This value is almost identical to the discrimination threshold identified by Romo et al. (2000) for monkeys discriminating the frequency of trains of intracortical stimuli applied to area 3b, 4.6 Hz. Since our graded cells had slopes within the same range as identified for partially graded cells (mean, 8.1 Hz/mm), these cells may also contribute to discriminating differences in tactile roughness. This reasoning is, however, inherently unsatisfactory, since humans can clearly discriminate much smaller changes in the spacing of raised dot surfaces (above, 100 μm for a standard SP of 2 mm). If this ability were based on the relatively weak texture sensitivity seen here, then one would have to assume that subjects can detect changes in firing rate of <1 imp/s. This seems unlikely.
Our results may, however, represent an incomplete picture of the neuronal mechanisms underlying roughness discrimination. Of particular interest is the observation of Sinclair and Burton (1988) that, when monkeys scanned their fingers sequentially over pairs of surfaces, the SP of the first surface encountered sometimes influenced the response of S1 neurons to the SP on the second surface scanned. They called this a contrast response with reference to the brightness illusion seen in the visual system: the apparent brightness of a shade of gray is enhanced when presented on a dark (vs. light) background. This visual phenomenon is, however, considered to be peripheral in origin (Meister and Tessier-Lavigne 2013), and no such phenomenon has been reported for cutaneous mechanoreceptive afferents (Lamb 1983b). Inspection of our ensemble averages (Fig. 8) suggests, consistent with Sinclair and Burton, that the initial neuronal response to the standard SP influenced the subsequent response to the modified SPs. The cortical discharge rates evoked by closely similar SPs were considerably higher when this was preceded by a SP of 1.5 mm (Fig. 8, left) compared with uniform textures (Fig. 8, right). This increased level of discharge may have modified their sensitivity to SP, possibly changing their gain (Chance et al. 2002; Salinas and Abbott 1996; Shu et al. 2003). Consistent with this, the slopes of the regression curves (rate vs. SP) for the graded texture-only cells were twice as steep for the cells tested with the nonuniform P1 series compared with the uniform P2 series (P = 0.004, see Fig. 8A). There was a trend for steeper slopes for the partially graded cells tested with the P1 surfaces, but the differences were not significant (Fig. 8, B and C). The advantage of such a mechanism is that it could dynamically extend the working range of each neuron, enhancing its ability to signal changes in surface roughness, and this in a manner consistent with the highly developed abilities of humans to discriminate changes in tactile roughness (above). To test this suggestion, we are currently recording S1 neuronal responses to different ranges of SPs using surfaces similar to the P1 series here (Fig. 2). The SP over the first half of the surface is varied from one series of surfaces to the next. The SP over the second half of the surfaces is also systematically incremented, but using smaller increments closer to discrimination threshold. Our hypothesis is that a proportion of texture-sensitive neurons will show evidence for dynamic gain changes as a function of the SP encountered over the first half of the surface.
Comparison with Earlier Studies of Cortical Encoding of Tactile Roughness
The present results greatly extend previous studies that concentrated on smoother textured surfaces, limited to smaller SPs [0.75–3.65 mm for Darian-Smith et al. (1982) and Sinclair and Burton (1991a); 2–5 mm, Jiang et al. 1997]. Our results also confirm Sinclair and Burton's (1991a) observation of S1 sensitivity to SP, independent of speed. Their observations were made during a task involving active touch (voluntary movement made by the monkey), and so speed was not systematically varied. Here we extend this observation to a situation in which speed was systematically varied, and the surfaces were passively scanned under the immobile finger tips.
Coding of Tactile Roughness
Roughness intensity is a global measure that reflects the underlying spatial characteristics of textured stimuli (Fig. 1). In this study, we concentrated our analyses on a firing rate (intensive) code for tactile roughness, following on from a number of earlier studies that linked the firing rate of SA, RA and PC mechanoreceptive afferents to the increased roughness observed when the SP of periodic gratings is increased (Cascio and Sathian 2001; Goodwin et al. 1989; Sathian et al. 1989). Our results suggest a simple intensive code based on mean firing rate of S1 cortical neurons (SA and RA) is sufficient to explain the relation between subjective roughness intensity and SP (independent of scanning speed). This code is present in area 3b, the earliest level of processing within S1 (see below).
Roughness is, however, a complex quality with multiple different dimensions (Hollins et al. 1993), and so it is natural that multiple coding mechanisms may encode its different attributes. One influential hypothesis is that tactile roughness is signaled by a spatial variation code (Connor et al. 1990; Connor and Johnson 1992) carried by SA afferents. This code was not tested here, but it is worth noting that our results suggest that both SA and RA inputs contribute to roughness, and this in almost equal proportions among the fully graded cells. The high degree of spatial acuity carried by the spatial variation code, which is preserved up to area 3b (DiCarlo and Johnson 1999; 2000; DiCarlo et al. 1998; Phillips et al. 1988), may be particularly important for signaling local spatial form, e.g., Braille characters.
Temporal coding is another candidate code for the central representation of tactile roughness (Cascio and Sathian 2001; Lederman 1983), and this may, for finer textured surfaces, also include a contribution from RA and PC afferents (Weber et al. 2013; cf, Yoshioka et al. 2001). Indeed, there is good evidence to show that temporal coding of other qualities, including orientation of edges (Pruszynski and Johansson 2014) and vibration frequency (Harvey et al. 2013), contributes to encoding tactile inputs. For the types of surfaces studied here, we do not believe that a temporal code contributes to the central representation of the intensity of tactile roughness. Several observations support this suggestion. First, our psychophysical results show that tactile roughness scaling, for the types of surfaces used here, is dependent on the spatial characteristics of the surfaces and not the temporal characteristics of the scanned dot patterns (Fig. 1). Furthermore, roughness scaling is independent of periodicity, since roughness estimates are identical for surfaces with periodically and nonperiodically disposed raised dots matched for dot spacing in the direction of the scan (Dépeault et al. 2009). Second, the discharge rate of graded texture-only cells did not vary with the temporal frequency of the stimuli, as also found for human roughness estimates (Meftah et al. 2000). Third, the autocorrelograms applied to all texture-related cells showed that periodic discharge was mainly limited to the roughest surfaces presented (Fig. 3, left), often only for the slow speed, or was absent for all conditions (Fig. 3, right, 26% of texture-related cells). These latter observations are consistent with earlier reports using a more limited range of SPs (Sinclair et al. 1996; Tremblay et al. 1996) and with our suggestion that the spatial characteristics of the surfaces are the most important contributing factor to roughness intensity.
Our suggestion that rate coding underlies tactile roughness intensity is consistent with the results of single-unit recordings in the auditory cortex. Lu et al. (2001) identified a large proportion of neurons with limited stimulus-synchronized responses, and yet their discharge rates reliably encoded differences in acoustic trains. They suggested that the perceptual ability to discriminate fine temporal features, including (acoustic) roughness, is explained in part by a rate code. Temporal coding also contributed, but was restricted in its operating range to slower acoustic stimuli, in a manner similar to that seen here with the roughest SPs tested. Clearly further work is needed to assign a functional role to temporal coding in the central encoding of tactile roughness.
A mean rate code is widely thought to underlie neural coding in the visual and auditory systems (Kandel et al. 2013; Lemus et al. 2009). Even within the somatosensory system, most of the submodalities are signaled by a rate code. For example, tactile speed and contact force are both signaled with a mean rate code at the level of peripheral afferents and S1 cortex (Dépeault et al. 2013; Essick and Edin 1995; Wannier et al. 1991; Wheat et al. 2010). Muscle length and speed of stretch are likewise signaled by discharge rate (Matthews 1972). Amplitude of vibration is signaled by a mean rate code (Muniak et al. 2007) at least at the peripheral level. Finally, the work of Romo and collaborators suggests not only that S1 neurons use a rate code to discriminate differences in flutter vibration, but that the brain can discriminate differences in the rate of electrical, intracortical stimuli (area 3b) from mechanical (flutter) or electrical stimuli (Hernandez et al. 2000; Romo et al. 1998, 2000) based on a simple measure of the number of spikes or pulses. We cannot exclude the contribution of other coding mechanisms (spatial, temporal, long-range oscillations, etc.) to roughness, but our suggestion that tactile roughness intensity is signaled by a mean rate code is consistent with the general view that this is an important neural coding mechanism.
Areal Localization of Tactile Roughness
We found that neurons with properties that could account for a monotonic relation between subjective roughness and a wide range of SPs (graded, insensitive to speed) were almost entirely restricted to rostral S1 (22/24, areas 3b and 1), and two-thirds were in area 3b. In contrast, partially graded responses were widely distributed across all three cutaneous fields (range, 59–63%). Thus, texture sensitivity is distributed across the three fields that contain a cutaneous representation of the digits in S1: areas 3b, 1 and 2. This result confirms our laboratory's previous observations (Ageranioti-Bélanger and Chapman 1992; Chapman and Ageranioti-Bélanger 1991; Jiang et al. 1997; Meftah et al. 2002; Tremblay et al. 1996), as well as those of others for areas 3b and 1 (Darian-Smith et al. 1982; Sinclair and Burton 1991a).
There were differences across the three areas in the presence or absence of sensitivity to scanning speed. The overall portrait that emerged was that rostral S1 (area 3b) is predominantly composed of cells sensitive to texture independent of scanning speed; no speed-only cells were found here. In contrast, caudal S1 (area 2) is composed of cells sensitive to texture + speed, as well as cells sensitive only to scanning speed (Dépeault et al. 2013). Area 1 was intermediate: close to one-half of the cells were texture-only, but the proportion of speed-only cells was as high as in area 2 (12 vs. 15%). These classifications were, however, made within two particular contexts. First, the textures were passively displaced under the fingertips. This ensured that the stimulating conditions were similar for all recordings, but it is possible that the results may not extend to include other test conditions, e.g., active touch in which case the textures are explored by the animal, and so the latter determines the speed of exploration. Second, our data were recorded outside of the context of a texture discrimination task. We (Chapman and Meftah 2005) reported that ∼10% of S1 texture-sensitive cells lost their texture responsiveness when tested outside the context of a texture discrimination task involving directed attention. Thus the overall proportion of texture-sensitive cells here may have been modestly underestimated. Using the same logic, it is possible that the proportion of speed-sensitive cells was also underestimated.
Adaptation Rates of Texture-Sensitive S1 Neurons
Based on previous work (Darian-Smith et al. 1980; Lamb 1983b), the surfaces used here should have activated all three types of mechanoreceptive afferents involved in discriminative touch in the monkey: SA, RA and also PC afferents. No PC-like responses were identified in this sample of cortical recordings (large RF, very sensitive to touch, including a puff of air), reflecting the fact that such responses are rare in S1 (Hyvarinen and Poranen 1978; Iwamura et al. 1983a, 1985; Tremblay et al. 1996). Our sample thus included only SA and RA units. Consistent with our laboratory's earlier results, and those of others (Darian-Smith et al. 1982; Sinclair and Burton 1991a), both SA and RA S1 cortical neurons were texture sensitive (proportions of about 60:40% here for the texture-only cells). This suggests that both types of mechanoreceptive afferent contribute to encoding tactile roughness in S1.
Localization of Function in the S1 Digit Representation
We originally expected that neurons encoding lower level aspects of roughness would be sensitive to scanning speed as well as roughness, since the two signals are confounded in the discharge of primary afferents (Darian-Smith et al. 1980; Lamb 1983b). Such response properties were expected to be localized to area 3b, corresponding to the major gateway for lemniscal inputs to S1. Neurons involved in higher level aspects of roughness, signaling roughness independent of speed, were expected to be localized in higher level areas, including areas 1, 2 and secondary somatosensory cortex (S2). The results did not follow this expected pattern: only 25% of area 3b neurons were sensitive to both texture and speed, compared with 70% of area 2 neurons.
Taken together, our results suggest that the cutaneous representation of the hand in S1 is organized so that area 3b is specialized to process information about surface texture, extracting a representation of roughness independent of speed, which is critically important for our appreciation of subjective tactile roughness. In contrast, area 2 is specialized for processing moving cutaneous inputs, extracting a representation of tactile speed independent of roughness and so contributing to encoding subjective tactile speed (Dépeault et al. 2008, 2013). Area 1 contributes to both texture and speed, and it should be stressed that its role in texture appreciation is critical based both on lesion studies (Carlson 1981; Randolph and Semmes 1974) and single-unit recordings. In particular, the majority of attention-sensitive cutaneous cells in S1 (70%), studied in the context of a cross-modal manipulation of attention, are localized to area 1 (Meftah et al. 2009). Area 1 also had the highest proportion of texture-sensitive cells, as well as the highest proportion of neurons showing instructed delay discharge within the context of the same task (vs. areas 3b and 2). Thus area 1 signals texture differences, but its discharge also reflects the action of cognitive factors, including attention and instructions.
The areal localization of texture and speed processing seen here may reflect the results of parallel processing of somatic sensory inputs in S1, as originally proposed by Dykes (1983), combined with serial processing according to the widely accepted rostral-caudal hierarchy in S1 based on considerations of connectivity [denser thalamic inputs to rostral areas, 3a/b, vs. caudal, 1/2 (Jones 1983)], along with the appearance of larger and more complex RFs in caudal regions (Hyvarinen and Poranen 1978; Iwamura et al. 1983b, 1993). The net result is that each area plays a unique role in the processing of tactile inputs.
GRANTS
The research was supported by grants from the Canadian Institute of Health Research (CIHR) (individual grants to C. E. Chapman, MOP14454 and 111258; Group in Neurological Sciences), the National Sciences and Engineering Research Council, and the Groupe de Recherche sur le Système Nerveux Central (GRSNC; Fonds de la Recherche en Santé du Québec). S. Bourgeon was supported by a bursary from the GRSNC. A. Dépeault was supported by scholarships from the CIHR, including the Canada Graduate Scholarship.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: S.B., A.D., E.-M.M., and C.E.C. performed experiments; S.B., A.D., E.-M.M., and C.E.C. analyzed data; S.B., A.D., E.-M.M., and C.E.C. interpreted results of experiments; S.B., A.D., E.-M.M., and C.E.C. prepared figures; S.B., A.D., E.-M.M., and C.E.C. approved final version of manuscript; A.D., E.-M.M., and C.E.C. drafted manuscript; E.-M.M. and C.E.C. edited and revised manuscript; C.E.C. conception and design of research.
ACKNOWLEDGMENTS
We thank the following for excellent technical assistance: René Albert, Tommy Ariel, the late Richard Bouchoux, Marc Bourdeau, Philippe Drapeau, Marie-Thérèse Parent, Jean Soucy, and Christian Valiquette. We also thank Dr. Trevor Drew for helpful comments on the manuscript.
REFERENCES
- Ageranioti-Bélanger SA, Chapman CE. Discharge properties of neurones in the hand area of primary somatosensory cortex in monkeys in relation to the performance of an active tactile discrimination task II. Area 2 compared with areas 3b and 1. Exp Brain Res 91: 207–228, 1992. [DOI] [PubMed] [Google Scholar]
- Carlson M. Characteristics of sensory deficits following lesions of Brodmann's areas 1 and 2 in the postcentral gyrus of Macaca mulatta. Brain Res 204: 424–430, 1981. [DOI] [PubMed] [Google Scholar]
- Cascio CJ, Sathian K. Temporal cues contribute to tactile perception of roughness. J Neurosci 21: 5289–5296, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chance FS, Abbott LF, Reyes AD. Gain modulation from background synaptic input. Neuron 35: 773–782, 2002. [DOI] [PubMed] [Google Scholar]
- Chapman CE, Ageranioti-Bélanger SA. Discharge properties of neurones in the hand area of primary somatosensory cortex in monkeys in relation to the performance of an active tactile discrimination task I. Areas 3b and 1. Exp Brain Res 87: 319–339, 1991. [DOI] [PubMed] [Google Scholar]
- Chapman CE, Meftah EM. Independent controls of attentional influences in primary and secondary somatosensory cortex. J Neurophysiol 94: 4094–4107, 2005. [DOI] [PubMed] [Google Scholar]
- Connor CE, Hsiao SS, Phillips JR, Johnson KO. Tactile roughness: neural codes that account for psychophysical magnitude estimates. J Neurosci 10: 3823–3836, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor CE, Johnson KO. Neural coding of tactile texture: comparison of spatial and temporal mechanisms for roughness perception. J Neurosci 12: 3414–3426, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darian-Smith I, Davidson I, Johnson KO. Peripheral neural representation of spatial dimensions of a textured surface moving across the monkey's finger pad. J Physiol (Lond) 309: 135–148, 1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darian-Smith I, Sugitani M, Heywood J, Karita K, Goodwin A. Touching textured surfaces: cells in somatosensory cortex respond both to finger movement and to surface features. Science 218: 906–909, 1982. [DOI] [PubMed] [Google Scholar]
- Dépeault A, Meftah EM, Chapman CE. Tactile perception of roughness: neural correlates (Abstract). Neuroscience Meeting Planner 2007: 74 6, 2007. [Google Scholar]
- Dépeault A, Meftah EM, Chapman CE. Tactile speed scaling: contributions of time and space. J Neurophysiol 99: 1422–1434, 2008. [DOI] [PubMed] [Google Scholar]
- Dépeault A, Meftah EM, Chapman CE. Tactile perception of roughness: raised-dot spacing, density and disposition. Exp Brain Res 197: 235–244, 2009. [DOI] [PubMed] [Google Scholar]
- Dépeault A, Meftah EM, Chapman CE. Neuronal correlates of tactile speed in primary somatosensory cortex. J Neurophysiol 110: 1554–1566, 2013. [DOI] [PubMed] [Google Scholar]
- DiCarlo JJ, Johnson KO. Velocity invariance of receptive field structure in somatosensory cortical area 3b of the alert monkey. J Neurosci 19: 401–419, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiCarlo JJ, Johnson KO. Spatial and temporal structure of receptive fields in primate somatosensory area 3b: effects of stimulus scanning direction and orientation. J Neurosci 20: 495–510, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiCarlo JJ, Johnson KO, Hsiao SS. Structure of receptive fields in area 3b of primary somatosensory cortex in the alert monkey. J Neurosci 18: 2626–2645, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew T, Doucet S. Application of circular statistics to the study of neuronal discharge during locomotion. J Neurosci Methods 38: 171–181, 1991. [DOI] [PubMed] [Google Scholar]
- Dykes RW. Parallel processing of somatosensory information: a theory. Brain Res Rev 6: 47–115, 1983. [DOI] [PubMed] [Google Scholar]
- Essick GK, Edin BB. Receptor encoding of moving tactile stimuli in humans. II The mean response of individual low-threshold mechanoreceptors to motion across the receptive field. J Neurosci 15: 848–864, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin AW, Morley JW. Sinusoidal movement of a grating across the monkey's fingerpad: representation of grating and movement features in afferent fiber responses. J Neurosci 7: 2168–2180, 1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin AW, John KT, Sathian K, Darian-Smith I. Spatial and temporal factors determining afferent fiber responses to a grating moving sinusoidally over the monkey's fingerpad. J Neurosci 9: 1280–1293, 1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey MA, Saal HP, Dammann JF, Bensmaia SJ. Multiplexing stimulus information through rate and temporal codes in primate somatosensory cortex. PLoS Biol 11: e1001558, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez A, Zainos A, Romo R. Neuronal correlates of sensory discrimination in the somatosensory cortex. Proc Natl Acad Sci U S A 97: 6191–6196, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollins M, Faldowski R, Rao S, Young F. Perceptual dimensions of tactile surface texture: a multidimensional scaling analysis. Percept Psychophys 54: 697–705, 1993. [DOI] [PubMed] [Google Scholar]
- Hyvarinen J, Poranen A. Receptive field integration and submodality convergence in the hand area of the post-central gyrus of the alert monkey. J Physiol (Lond) 283: 539–556, 1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwamura Y, Tanaka M, Sakamoto M, Hikosaka O. Functional subdivisions representing different finger regions in area 3 of the first somatosensory cortex of the conscious monkey. Exp Brain Res 51: 315–326, 1983a. [Google Scholar]
- Iwamura Y, Tanaka M, Sakamoto M, Hikosaka O. Converging patterns of finger representation and complex response properties of neurons in area 1 of the first somatosensory cortex of the conscious monkey. Exp Brain Res 51: 327–337, 1983b. [Google Scholar]
- Iwamura Y, Tanaka M, Sakamoto M, Hikosaka O. Diversity in receptive field properties of vertical neuronal arrays in the crown of the postcentral gyrus of the conscious monkey. Exp Brain Res 58: 400–411, 1985. [DOI] [PubMed] [Google Scholar]
- Iwamura Y, Tanaka M, Sakamoto M, Hikosaka O. Rostrocaudal gradients in the neuronal receptive field complexity in the finger region of the alert monkey's postcentral gyrus. Exp Brain Res 92: 360–368, 1993. [DOI] [PubMed] [Google Scholar]
- Jiang W, Tremblay F, Chapman CE. Neuronal encoding of texture changes in the primary and the secondary somatosensory cortical areas of monkeys during passive texture discrimination. J Neurophysiol 77: 1656–1662, 1997. [DOI] [PubMed] [Google Scholar]
- Jones EG. Lack of collateral thalamocortical projections to fields in the first somatic sensory cortex in monkeys. Exp Brain Res 52: 375–384, 1983. [DOI] [PubMed] [Google Scholar]
- Jones EG, Coulter JD, Hendry SHC. Intracortical connectivity of architectonic fields in the somatic sensory, motor and parietal cortex of monkeys. J Comp Neurol 181: 291–347, 1978. [DOI] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessel TM, Siegelbaul SA, Hudspeth AJ. (Editors) Principles of Neural Science (5th Ed). New York: McGraw-Hill, 2013. [Google Scholar]
- Lamb GD. Tactile discrimination of textured surfaces: psychophysical performance measures in humans. J Physiol (Lond) 338: 551–565, 1983a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb GD. Tactile discrimination of textured surfaces: peripheral neural coding in the monkey. J Physiol (Lond) 338: 567–587, 1983b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebedev MA, Wise SP. Oscillations in the premotor cortex: single-unit activity from awake, behaving monkeys. Exp Brain Res 150: 195–215, 2000. [DOI] [PubMed] [Google Scholar]
- Lederman SJ. Tactile roughness of grooved surfaces: the touching process and effects of macro- and microsurface structure. Percept Psychophys 16: 385–395, 1974. [Google Scholar]
- Lederman SJ. Tactual roughness perception: spatial and temporal determinants. Can J Psychol 37: 498–511, 1983. [Google Scholar]
- Lemus L, Hernandez A, Romo R. Neural codes for perceptual discrimination of acoustic flutter in the primate auditory cortex. Proc Natl Acad Sci U S A 106: 9471–9476, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T, Liang L, Wang X. Temporal and rate representations of time-varying signals in the auditory cortex of awake primates. Nat Neurosci 4: 1131–1138, 2001. [DOI] [PubMed] [Google Scholar]
- Luna R, Hernandez A, Brody CD, Romo R. Neural codes for perceptual discrimination in primary somatosensory cortex. Nat Neurosci 8: 1210–1219, 2005. [DOI] [PubMed] [Google Scholar]
- Matthews PBC. Muscle Receptors. London: Arnold, 1972. [Google Scholar]
- Meftah EM, Belingard L, Chapman CE. Relative effects of the spatial and temporal characteristics of scanned surfaces on human perception of tactile roughness using passive touch. Exp Brain Res 132: 351–361, 2000. [DOI] [PubMed] [Google Scholar]
- Meftah EM, Bourgeon S, Chapman CE. Instructed delay discharge in primary and secondary somatosensory cortex within the context of a selective attention task. J Neurophysiol 101: 2649–2667, 2009. [DOI] [PubMed] [Google Scholar]
- Meftah EM, Bourgeon S, Dépeault A, Chapman CE. Neuronal correlates of tactile surface roughness in primary somatosensory cortex, S1, of the macaque monkey (Abstract). Neuroscience Meeting Planner 2014: 441 13, 2014. [Google Scholar]
- Meftah EM, Shenasa J, Chapman CE. Effects of a cross-modal manipulation of attention on somatosensory cortical neuronal responses to tactile stimuli in the monkey. J Neurophysiol 88: 3133–3149, 2002. [DOI] [PubMed] [Google Scholar]
- Meister M, Tessier-Lavigne M. Low-level visual processing: the retina. In: Principles of Neural Science (5th Ed), edited by Kandel ER, Schwartz JH, Jessel TM, Siegelbaum SA, Hudspeth AJ. New York: McGraw-Hill, 2013, p. 577–601. [Google Scholar]
- Morley JW, Goodwin AW, Darian-Smith I. Tactile discrimination of gratings. Exp Brain Res 49: 291–299, 1983. [DOI] [PubMed] [Google Scholar]
- Muniak MA, Ray S, Hsiao SS, Dammann JF, Bensmaia SJ. The neural coding of stimulus intensity: linking the population response of mechanoreceptive afferents with psychophysical behavior. J Neurosci 27: 11687–11699, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips JR, Johnson KO, Hsiao SS. Spatial pattern representation and transformation in monkey somatosensory cortex. Proc Nat Acad Sci U S A 85: 1317–1321, 1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poggio GF, Viernstein LF. Time series analysis of impulse sequences of thalamic somatic sensory neurons. J Neurophysiol 27: 517–545, 1964. [DOI] [PubMed] [Google Scholar]
- Powell TP, Mountcastle VB. The cytoarchitecture of the postcentral gyrus of the monkey Macaca mulatta. Bull Johns Hopkins Hosp 105: 108–131, 1959. [PubMed] [Google Scholar]
- Pruszynski JA, Johansson RS. Edge-orientation processing in first-order tactile neurons. Nat Neurosci 17: 1404–1409, 2014. [DOI] [PubMed] [Google Scholar]
- Randolph M, Semmes J. Behavioral consequences of selective subtotal ablations in the postcentral gyrus of Macaca mulatta. Brain Res 70: 55–70, 1974. [DOI] [PubMed] [Google Scholar]
- Romo R, Hernandez A, Zainos A, Brody CD, Lemus L. Sensing without touching: psychophysical performance based on cortical microstimulation. Neuron 26: 273–278, 2000. [DOI] [PubMed] [Google Scholar]
- Romo R, Hernandez A, Zainos A, Salinas E. Somatosensory discrimination based on cortical microstimulation. Nature 392: 387–390, 1998. [DOI] [PubMed] [Google Scholar]
- Salinas E, Abbott LF. A model of multiplicative neural responses in parietal cortex. Proc Natl Acad Sci U S A 93: 11956–11961, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sathian K, Goodwin AW, John KT, Darian-Smith I. Perceived roughness of a grating: correlation with responses of mechanoreceptive afferents innervating the monkey's fingerpad. J Neurosci 9: 1273–1279, 1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y, Hasenstaub A, Badoual M, Bal T, McCormick DA. Barrages of synaptic activity control the gain and sensitivity of cortical neurons. J Neurosci 23: 10388–10401, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinclair R, Burton H. Responses from area 3b of somatosensory cortex to textured surfaces during active touch in primate. Somatosens Res 5: 283–210, 1988. [DOI] [PubMed] [Google Scholar]
- Sinclair R, Burton H. Neuronal activity in the primary somatosensory cortex in monkeys (Macaca mulatta) during active touch of textured surface gratings: responses to groove width, applied force and velocity of motion. J Neurophysiol 66: 153–169, 1991a. [DOI] [PubMed] [Google Scholar]
- Sinclair RJ, Burton H. Tactile discrimination of gratings: psychophysical and neural correlates in human and monkey. Somatosens Mot Res 8: 241–248, 1991b. [DOI] [PubMed] [Google Scholar]
- Sinclair R, Pruett JR, Burton H. Responses in primary somatosensory cortex of rhesus monkey to controlled application of embossed grating and bar patterns. Somatosens Mot Res 13: 287–306, 1996. [DOI] [PubMed] [Google Scholar]
- Smith AM, Chapman CE, Deslandes M, Langlais JS, Thibodeau MP. The role of friction and tangential force in the subjective scaling of tactile roughness. Exp Brain Res 144: 211–223, 2002. [DOI] [PubMed] [Google Scholar]
- Sutu A, Meftah EM, Chapman CE. Physical determinants of the shape of the psychophysical curve relating estimated tactile roughness to raised-dot spacing: implications for neuronal coding of roughness. J Neurophysiol 109: 1403–1415, 2013. [DOI] [PubMed] [Google Scholar]
- Tremblay F, Ageranioti-Bélanger SA, Chapman CE. Cortical mechanisms underlying tactile discrimination in the monkey. I. Role of primary somatosensory cortex in passive texture discrimination. J Neurophysiol 76: 3382–3403, 1996. [DOI] [PubMed] [Google Scholar]
- Udo M, Kamei H, Matsukawa K, Tanaka K. Interlimb coordination in cat locomotion investigated with perturbation. II. Correlates in neuronal activity of Dieters cells of decerebrate walking cats. Exp Brain Res 46: 438–447, 1982. [DOI] [PubMed] [Google Scholar]
- Wannier TMJ, Maier MA, Hepp-Reymond MC. Contrasting properties of monkey somatosensory and motor cortex neurons activated during the control of force in precision grip. J Neurophysiol 65: 572–589, 1991. [DOI] [PubMed] [Google Scholar]
- Weber AI, Saal HP, Lieber JD, Cheng JW, Manfredi LR, Dammann JF, Bensmaia S. Spatial and temporal codes mediate the tactile perception of natural textures. Proc Natl Acad Sci U S A 110: 17107–17112, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheat HE, Salo M, Goodwin AW. Cutaneous afferents from the monkeys fingers: responses to tangential and normal forces. J Neurophysiol 103: 950–964, 2010. [DOI] [PubMed] [Google Scholar]
- Yoshioka T, Craig JC, Beck GC, Hsiao SS. Perceptual constancy of texture roughness in the tactile system. J Neurosci 31: 17603–17611, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshioka T, Gibb B, Dorsch AK, Hsiao SS, Johnson KO. Neural coding mechanisms underlying perceived roughness of finely textured surfaces. J Neurosci 21: 6905–6916, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]