Gradient-Based Algorithm for Determining Tumor Volumes in Small Animals Using Planar Fluorescence Imaging Platform

Abstract

Planar fluorescence imaging is widely used in biological research because of its simplicity, use of nonionizing radiation, and high-throughput data acquisition. In cancer research, where small animal models are used to study the in vivo effects of cancer therapeutics, the output of interest is often the tumor volume. Unfortunately, inaccuracies in determining tumor volume from surface-weighted projection fluorescence images undermine the data, and alternative physical or conventional tomographic approaches are prone to error or are tedious for most laboratories. Here, we report a method that uses a priori knowledge of a tumor xenograft model, a tumor-targeting near infrared probe, and a custom-developed image analysis planar view tumor volume algorithm (PV-TVA) to estimate tumor volume from planar fluorescence images. Our algorithm processes images obtained using near infrared light for improving imaging depth in tissue in comparison with light in the visible spectrum. We benchmarked our results against the actual tumor volume obtained from a standard water volume displacement method. Compared with a caliper-based method that has an average deviation from an actual volume of 18% (204.34 ± 115.35 mm³), our PV-TVA average deviation from the actual volume was 9% (97.24 ± 70.45 mm³; P < .001). Using a normalization-based analysis, we found that bioluminescence imaging and PV-TVA average deviations from actual volume were 36% and 10%, respectively. The improved accuracy of tumor volume assessment from planar fluorescence images, rapid data analysis, and the ease of archiving images for subsequent retrieval and analysis potentially lend our PV-TVA method to diverse cancer imaging applications.

Introduction

In recent years, optical imaging has been used with increasing regularity as an imaging modality. Historically, its primary use has been in the field of microscopy; however, technological advances have enabled many applications in small-animal in vivo imaging (1–3). Compared with conventional imaging modalities such as computed tomography (CT), positron emission tomography, and magnetic resonance imaging (MRI), optical imaging of small-animal models can serve as a high-throughput, accurate, low learning curve, and low-cost method for measuring pathophysiological parameters using nonionizing radiation. Therefore, thousands of laboratories worldwide have adopted planar optical imaging as the preferred imaging modality for assessing drug efficacy, developing new molecular imaging probes, and understanding the molecular basis of pathophysiological processes.

In cancer research, molecular probes targeting specific biomarkers have been developed to give insight into tissue-specific properties (4, 5). These probes allow for the rapid detection of tumors, assessment of tumor-associated protein expression levels, and evaluating the relative size of tumors. Targeted molecular fluorescence imaging has the potential to improve patient care by facilitating the understanding of tumor characteristics in small-animal models. In addition, preclinical testing of new cancer therapies is often conducted in small-animal models to determine therapeutic efficacy (2), with tumor volume assessment typically reported as a primary output in interventional studies.

Preclinical tumor volume is often estimated by measuring the length and width of a tumor using calipers, and then inputting the values in the equation $V=0.5\hspace{0.17em}\times \hspace{0.17em}L\hspace{0.17em}\times \hspace{0.17em}{W}^2$, where V is the tumor volume, L is the tumor length, and W is the tumor width. This approach is simple, fast, and fairly reliable (6). However, the potential for user-dependent variability introduces intractable errors in data analysis (7, 8). When the tumor grows in an infiltrative manner and invades the underlying tissue, identification of the tumor margin using calipers presents additional challenges. Moreover, if a measurement is not taken for a given day, the data cannot be obtained at a later time.

Using fluorescence imaging to determine tumor volume has been a challenge, largely because of the attenuation of light within the tissue. For in vivo imaging, light is reflected, scattered, and absorbed as it passes through a heterogeneous medium, thereby obscuring the true boundary of the target object within the tissue. There are 2 ways to solve the inverse problem of locating the boundaries of a fluorescent target: mathematically and empirically. Mathematical approaches based on stochastic modeling of light propagation through a medium have been developed. Further, 3-dimensional quantitative fluorescence imaging has been accomplished by using fluorescence molecular tomography (FMT) to measure tumor geometry (1, 3). The drawback of FMT is that it requires a complex setup that is not accessible to most biological laboratories. In addition, the process necessary to extract the signal can be computationally intensive and time consuming, limiting real-time feedback.

Because of the complexity of FMT, planar optical imaging platforms that use empirical methods have become the hallmark of most biological imaging studies. Empirical approaches have been successfully adopted for tumor cell viability testing with technologies such as bioluminescence imaging (BLI) (9). BLI projects light generated from the interaction of a bioluminescent enzyme with its substrate to the animal surface. Because light emanates spontaneously from cells expressing the bioluminescent protein without the need for external light excitation used in fluorescence, modern cameras can detect cancer cells with exceptionally high sensitivity. However, tumor volume measurements obtained from BLI are anecdotal because the method reports only viability of cells expressing the reporter protein, but not the actual tumor volume. As tumor cells proliferate, some of the daughter cells do not express the reporter protein, which confounds tumor volume assessment.

In this study, we sought to develop a simple optical method for determining tumor volume from planar fluorescence images. Currently, the inverse problem in tissue optics can be empirically solved if the target geometry dimensions are known and if parameters to compensate light attenuation are determined. Because small-animal imaging uses similar tumor models to screen for therapies, the empirical approach can be used with very few parameters necessary to obtain an adequate fit between the calculated volume and the actual volume. By using a cancer-targeting molecular probe, we were able to investigate the application of our model to diverse tumors. Compared with conventional methods, our new PV-TVA approach is simpler and more accurate. Automation of the algorithm will increase its potential adoption by current investigators with planar fluorescence imaging systems.

Methodology

Tumor Models

We used 2 tumor models in this study: HT1080 (human fibrosarcoma) to develop and test the algorithm, and 4T1-Luc (murine mammary cancer) to compare the algorithm to BLI, which requires transfected cells. HT1080 xenografts were generated by administering subcutaneous injection of 3 × 10⁶ cells into 8-week-old female athymic nude mice in either the right shoulder or the left flank region. The right shoulder region was used to determine the optimal time point for imaging (n = 2), and the left flank region was used for the development of the algorithm (n = 3). 4T1-Luc xenografts were generated by administering subcutaneous injection of 1 × 10⁶ cells into 6-week-old female Balb/c mice in the left flank region (n = 5). The longitudinal therapeutic study was conducted using the HT1080 flank model (n = 4). Tumors were allowed to develop until palpable, and length and width measurements were taken using calipers. Mice were anesthetized with isoflurane (3%–5%) during all experimental procedures, including inoculation of tumor cells, caliper tumor measurement, and image acquisition. All studies were conducted in compliance with the Washington University Animal Welfare Committee's requirements for the care and use of laboratory animals in research.

Fluorescence Imaging Studies

For imaging studies, the mice were injected with a 0.40 mg/kg or 0.80 mg/kg dose of cypate-cGRD, a near infrared (NIR) fluorescent probe (10). This molecular probe is known to target diverse tumors in vivo. Cypate-cGRD was suspended in 100 μL of Dulbecco's phosphate buffered saline and injected into the mouse xenografts through a lateral tail vein injection. Using excitation and emission wavelengths of 785 and 810 nm, respectively, fluorescence imaging was performed with the Pearl® Small Animal Imaging System (Li-Cor Biosciences, Inc., Lincoln, Nebraska). Animals were imaged from a dorsal view at either 0, 1, 4, 24, 48, and 96 hours post injection, or a single image at 24 hours post injection. After the final imaging time point, the mice were euthanized and the skin was reflected from the tumor surface. In situ length and width of the tumor were measured using calipers, and the tumor volume was calculated using the equation $V=0.5\hspace{0.17em}\times \hspace{0.17em}L\hspace{0.17em}\times \hspace{0.17em}{W}^2$. The tumors were then carefully excised using the tumor capsule as a guide, and the tumor volume was measured using a water displacement method. Grayscale fluorescence images from the 800 nm channel were output in .jpg format using PearlCam software (Li-Cor Biosciences, Inc.). Image processing and analysis were conducted via a custom code written in MATLAB (Mathworks, Inc., Natick, Massachusetts).

Bioluminescence Imaging Studies

Five 4T1-Luc xenograft mice expressing luciferase received an intraperitoneal injection of 150 mg/kg d-luciferin in phosphate buffered saline (Gold Biotechnology, St. Louis, Missouri) for BLI. Mice were then imaged at 10 minutes under isoflurane anesthesia with IVIS 50 (PerkinElmer, Waltham, Massachusetts; Living Image 4.3, 1- or 10-second exposures, bin8, field of view 12 cm, f/stop1 and open filter). The total photon flux (photons/second) was measured from software-defined contour regions of interest over the tumors using Living Image 2.6. Bioluminescence from viable tumor cells was used to estimate tumor burden.

Longitudinal Therapeutic Studies

One of the benefits of using the PV-TVA to measure the tumor volume is to determine the efficacy of therapy over time. To investigate the treatment response, we obtained longitudinal images using an HT1080 xenograft model. Four mice were injected with a 0.40 mg/kg dose of cypate-cGRD via the tail vein, once a week for 4 weeks. In 2 of the mice, doxorubicin was administered at a dose of 10 mg/kg after a baseline image was obtained. The doxorubicin was dissolved in dimethyl sulfoxide, and then mixed in Dulbecco's phosphate buffered saline to obtain the desired dose in 100 μL of solution.

Results

Algorithm Development

To calculate the tumor volume from planar images, we first determined a suitable fluorescent probe to use and the proper time point to image. We selected cypate-cGRD because of its versatility in targeting a number of different tumor types. We then determined the optimal time point to analyze the images. The fluorescent probe was injected into the tail vein of each mouse bearing HT1080 tumors. Imaging was performed at multiple time points post injection using Pearl Small Animal Imaging System (Supplemental Figure 1A). We compared the tumor region to an equivalently sized nontumor region. The maximum difference of the fluorescence signal from the tumor compared with that from the nontumor region was obtained at 24 hours post injection (Supplemental Figure 1B), exhibiting the maximum tumor-to-nontumor ratio (Supplemental Figure 1C), and optimal imaging time point.

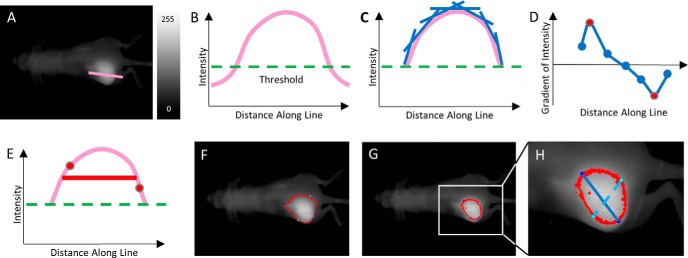
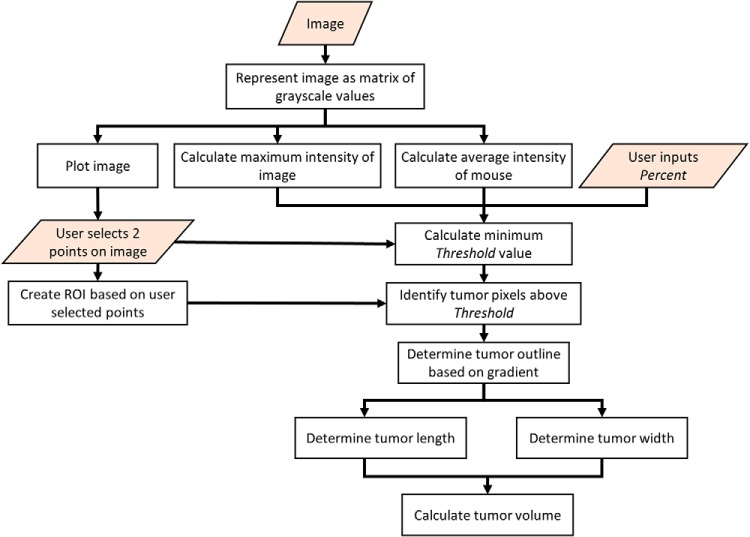
The next step was to determine the proper type of image to analyze. The Pearl Small Animal Imaging System has the ability to create images using a color map, grayscale, and numerous other visualization options. The color map image provides for a rapid method to visualize tumor contrast from the surrounding tissue; however, slight changes in the intensity scale may produce significant changes in the apparent tumor outline (Figure 1A). Color images rely on the user's visual interpretation to create the best guess for how to threshold the tumor boundary, therefore leading to variability. A more reliable approach is to reduce the need for perceptive input from the user. When analyzed, grayscale images produced a consistent tumor region as the contrast settings were varied (Figure 1B). To further standardize the approach, the grayscale images for output were selected by increasing the maximum intensity in the image until just below the point where the image became saturated. This technique allowed for maximum contrast between the signal and background without losing information in the image.

Figure 1.

Color images of a fluorescent tumor and surrounding tissue with the maximum intensity set to different values (from left to right): 1.0, 1.5, 2.0, 2.5, and 3.0 a.u. (A). Grayscale images of the same tumor set to the same maximum intensity values as the color images (B). Side and top images of light scattering in tissue, with the apparent width of the source at the top of the finger (red arrow) larger than the actual width of the light source (green arrow) (C) and (D). Illustration of a light-emitting fluorescent tumor (light source) within the scattering medium (E). The red arrow shows the observed width at the surface of the tissue, and the green arrow shows the actual width of the tumor within the surrounding tissue.

Despite the consistent tumor image produced by using grayscale, the light attenuation due to tissue scattering remained a confounding factor in determining the true tumor outline. This is similar to what is observed in Figure 1, C and D, where the light source is smaller than the observed light after it passes through the tissue. Image processing allows for an algorithm to account for the amount of scattering for a given tissue system. Because xenograft models of a particular tumor type are relatively consistent, the parameters to account for scattering can be set for all other samples once they are known for a given tumor model.

To initiate the PV-TVA, 2 points were selected by the user approximately along the horizontal axis of the tumor from the grayscale image. This line was long enough to go from uninvolved tissue, through the tumor, and back to the uninvolved tissue (Figure 2A). An intensity curve was created using the intensity values from the pixels along the length of the line (Figure 2B). The slope of the intensity curve was calculated for each point along the line using the subsequent number of pixels that the user specified (user-input parameter; Figure 2C). The use of a larger number of pixels to calculate the slope acted as a smoothing operation, making the algorithm less sensitive to local variability. Once the slopes were calculated along the length of the line, the maximum and minimum slope values were identified as the inflection points of the intensity plot along the line (Figure 2D). The average of these intensity values was used to determine the average value of the edge of intensity observed at the surface of the skin (Figure 2E). All values above this intensity were found within the user-selected region (Figure 2F). Once this procedure was completed, it became evident that the scattered light caused the apparent tumor outline to be larger than the actual tumor outline, as was later verified using postmortem in situ measurements.

Figure 2.

Input image with an illustrated user-selected line for region of interest identification (A). Intensity profile along the line (pink curve) with a Threshold value (green dashed line) (B). Moving slope (blue lines) of the intensity profile calculated along the line (C). Plot of the moving slopes (blue points) calculated along the line, with the inflection points of the intensity (red points) (D). Two inflection points identified (red points) and the average used for the tumor boundary determination (red line) (E). Algorithm-determined tumor outline overlaid on the image without using the Threshold value (F). Algorithm-determined tumor outline overlaid on image using the Threshold value to account for scattering (G). Tumor length (blue solid line) and tumor width (cyan dashed line) overlaid on image (H).

To account for this variability, a threshold value was created to decrease the outline of the tumor with the verified assumption that the scattered light contributes to increasing the imaged tumor outline dimensions. For example, a Threshold value of 0.25 would select the highest 25% of values that were along the user-selected line and calculate the inflection points based on only those values. Once the threshold was determined, the slopes of the intensity values were calculated using only the values that fell above that threshold value (Figure 2C). Adding a Threshold parameter to the PV-TVA resulted in a more accurate identification of the tumor from the images (Figure 2G).

The threshold was defined in Equation 1 as:

$$Threshold=I_{max}-Percent(I_{max}-I_{avg}),$$ (1)

where Threshold is the minimum intensity value accepted as potentially originating from the tumor tissue, I_max is the maximum intensity value originating from the mouse, I_avg is the average intensity value for the mouse, and Percent is a user-input value specific to the system being analyzed.

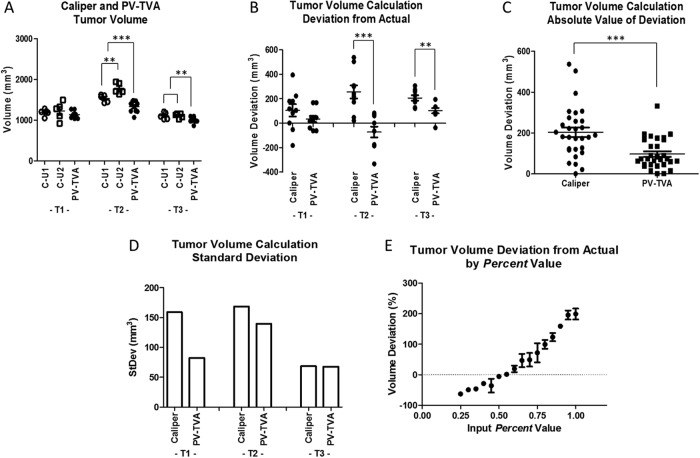
Percent was chosen as the user-input value rather than Threshold because inputting the Percent parameter allowed the incorporation of the intensity contrast between the tumor and the surrounding tissue for determining the threshold value. This approach balanced the need for tuning the threshold based on the system properties (the tumor morphological appearance, dye kinetics, and dye attenuation properties at the emission wavelength), with preserving the relationship of the tumor contrast within the image. By changing the Percent value, this tunable threshold allowed for versatility of the algorithm for different biological systems and dye concentrations. The Percent value was initially determined by using the postmortem tumor volume value from one mouse, and then that value was subsequently used to analyze the images for all the following mice. This Percent value was validated after the study by running the PV-TVA at various Percent values, and comparing each resultant tumor volume to the actual value (Figure 3E). The validation confirmed that the initially selected Percent was valid for all of the tumors of this type. Future study will explore the use of a receiver operating characteristic curve to estimate the optimal threshold per fluorescent imaging agent. This value will be input into the algorithm.

Figure 3.

Tumor volumes for 3 HT1080 tumors (T1, T2, and T3) as determined using the caliper measurement method for 2 users (C-U1 and C-U2), and the planar view tumor volume algorithm (PV-TVA) (Percent = 0.55) (A). Tumor volume calculation deviations from the actual volume as measured using postresection water displacement (B). Absolute value of the deviations of the tumor volume calculation methods to measure the accuracy (C). Average standard deviations of 10 measurements for each of the 3 tumors to measure the precision (D). Validation for the Percent value selected to calculate tumor volume (E). *P ≤ .05, **P ≤ .01, and ***P ≤ .001.

The final tumor volume was calculated by determining the length and width of the outlined tumor (Figure 2H). The length was defined as the longest distance between 2 points on the outline. The width was defined as the distance between the 2 points, on opposite sides of the line defining the length, with the maximum perpendicular distance from the line defining the length. The volume was calculated using the same equation as that in the caliper method.

There was a tradeoff between versatility and variability when conducting automated image analysis. Therefore, the PV-TVA had some inherent variability based on the initial 2 points that the user selected. Allowing the user to select the initial 2 points facilitated independent analysis of multiple tumors on the same mouse, and it was therefore an essential part of the algorithm. The potential variability from this was compared with the variability in the tumor volume caliper measurement method. The PV-TVA was run 10 times for a given set of images, with the user selecting different input points, to understand the precision and accuracy of the calculated values. The tumors were measured using calipers 10 times by 2 users who were blinded to the previous readings to capture the inherent variation in measurements using calipers.

Tumor Volume Calculations

Three HT1080 tumors were analyzed to test the capabilities of the PV-TVA. We used caliper measurements as our control, and then blinded the user to the previous caliper measurement. To capture inter-user variability, 2 users measured each tumor 5 times, for a total of 10 measurements. Figure 3A shows the caliper-measured tumor volumes separated by the user. T1 and T3 produced similar results; however, T2 showed a difference in caliper-calculated volume between users (P = .010). We binned the caliper measurements of both users for each tumor and repeated the PV-TVA 10 times for each tumor. The results were compared with the actual tumor volume obtained from the volume of water displaced by the tumor, and the deviations from the calculated versus actual tumor volume were compared for the caliper method and the PV-TVA method (Figure 3B). The accuracy of each method was assessed by calculating the average of the absolute value of the deviations for the caliper and PV-TVA methods. The caliper average deviation was 18% (204.34 ± 115.35 mm³) and the PV-TVA average deviation was 9% (97.24 ± 70.45 mm³; P < .001; Figure 3C). A comparison of the precision of each method using the standard deviations of the 10 calculations showed that the average standard deviations were 11% (131.95 mm³) and 8% (96.51 mm³) for the caliper and the PV-TVA methods, respectively (Figure 3D).

The in situ length and width were measured by reflecting the skin and measuring the tumor before complete resection. Our result showed that the absolute value of the length deviations from the in situ dimensions were, on average, 10% (1.21 ± 0.44 mm) for the calipers and 5% (0.68 ± 0.21 mm) for the PV-TVA (P < .001; Supplemental Figure 2, A and B) methods. The absolute value of the width deviations was, on average, 8% (0.81 ± 0.48 mm) for the calipers and 5% (0.55 ± 0.31 mm) for the PV-TVA (P = .001; Supplemental Figure 2C) methods.

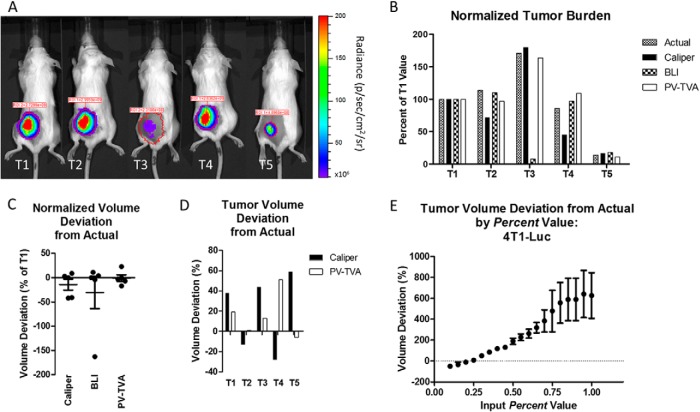
We next examined how this algorithm compared with other planar optical methods for determining tumor burden. BLI was conducted on a set of 4T1-Luc tumors, and the results were compared with those of the caliper and PV-TVA methods. Because BLI does not give the tumor volume, the measurements for 5 tumors were all normalized to the value of the first tumor (T1). This analysis allowed us to compare the trend in tumor burden between the different tumors. The same normalization to T1 was done using the actual tumor volumes as measured by the water displacement method and for the caliper and PV-TVA methods. The analysis revealed that the BLI measurements had a similar trend to the actual tumor volumes (Figure 4B), except for the case of T3 where the BLI would have predicted a much smaller tumor than what was observed (Figure 4A). In this case, the PV-TVA predicted a similar burden as the ground truth measurement obtained using the water displacement method. The deviations of each normalized value from the actual normalized value were calculated for the BLI, caliper, and PV-TVA methods (Figure 4C). When comparing the deviations, BLI, caliper, and the PV-TVA methods had absolute value average deviations of 36% of T1, 19% of T1, and 10% of T1, respectively. Normalization for comparative analysis allowed for the comparison of trends, but it did not give insight into the absolute deviations without extrapolation. Figure 4D shows the signed deviation from the actual deviation for the caliper and the PV-TVA methods. The average absolute value of the deviations was 37% (112.9 ± 93.62 mm³) for the calipers and 18% (60.52 ± 62.65 mm³) for the PV-TVA (P = .105) methods. The Percent value for this tumor model was 0.25. The PV-TVA was run at various Percent values and compared with the actual volume for validation (Figure 4E).

Figure 4.

BLI images for 5 4T1-Luc tumors (T1, T2, T3, T4, and T5) (A). Normalized tumor burden values for the actual volume, caliper, BLI, and the PV-TVA (B). All measurements were normalized to the T1 value for the specific type of measurement. The PV-TVA result was obtained using Percent = 0.25. Normalized tumor volume deviation from actual as a percentage of T1 for each method (C). Tumor volume percent deviation from the actual for the caliper and PV-TVA methods (D). Validation for the Percent value selected to calculate tumor volume using postmortem tumor volumes (E). The tumor volume deviations were calculated at various Percent values for the 4T1-Luc tumor model.

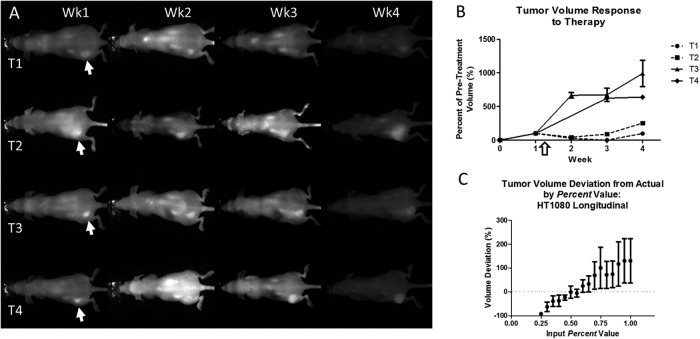
To assess the ability of the PV-TVA to monitor the tumor response to a given treatment, we used the HT1080 tumor model because it has previously shown a treatment response to doxorubicin. We took a baseline NIR image of each of the mice to establish the pretreatment tumor volume. Two of the mice were treated with doxorubicin, and all of the mice were followed for additional 3 weeks. The NIR images show the range of tumor-to-background signals obtained using planar fluorescence imaging (Figure 5A). Because the PV-TVA calculates a threshold based on a combination of a user-input Percent value and the inherent image contrast, the PV-TVA could calculate the tumor volume, despite the varied appearance of the images, in all but 1 of the images (T4-week 2). Regarding the image that did not produce a solution, there was insufficient contrast at the location of the tumor to calculate the tumor volume. To account for various initial tumor volumes at the time of treatment, the tumor response was calculated as a percentage of the pretreatment volume. At each time point, the PV-TVA was run 3 times. The doxorubicin-treated mice showed a tumor-growth suppression over time when compared with the control mice (Figure 5B). This result was obtained even when image properties such as tumor signal and average mouse signal varied (Supplemental Figure 3). We also confirmed that the Percent value used to calculate tumor volume did not change because of multiple fluorophore injections. The PV-TVA was run at the final time point (4th fluorophore injection), for various Percent values, to confirm that the original HT1080 Percent value remained valid (Figure 5C). A Percent value of 0.55 produced the smallest deviation from the actual value, consistent with the single time point study using an HT1080 tumor model (Figure 3E).

Figure 5.

NIR images of four HT1080 mice, with the left-flank tumors (T1, T2, T3, and T4) indicated by the arrows (A). Each mouse was imaged once a week for 4 weeks. Images had different tumor signals, average mouse signals, and tumor-to-mouse contrast. Tumor volumes, over time, normalized to the pretreatment volume. Doxorubicin-treated mice (dashed line) showed suppressed tumor growth compared with the control mice following the administered dose (white arrow) (B). Validation for the Percent value used in the HT1080 longitudinal treatment study after multiple fluorophore injections over time (Percent = 0.55) (C).

Discussion

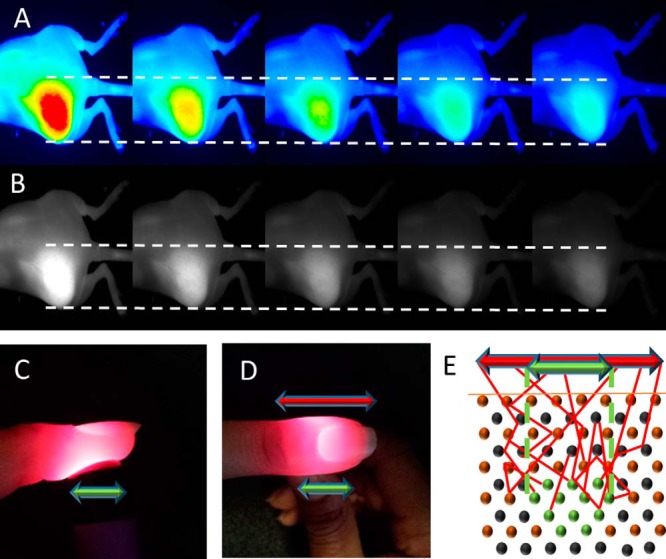
When determining the tumor volume, calipers are cost-effective and relatively straightforward. However, they introduce variability that is in excess of what we observed from our PV-TVA data. Using an algorithm-based approach minimizes the user-induced measurement variability. The PV-TVA works by allowing the user to input a fluorescence image, converting the image to a matrix of grayscale values, using user-selected points to determine the region of interest, and then using a gradient-based calculation to calculate the tumor volume (Figure 6). The gradient-based calculation accounts for light scattering of fluorescence in a given system, allowing the algorithm to select the apparent tumor outline in a number of different systems. By combining the inherent image properties, along with a user-input parameter, the tumor volume can be reproducibly calculated.

Figure 6.

Planar view tumor volume algorithm (PV-TVA) schematic. The user inputs the image and the Percent value, and then selects 2 points on the opposite sides of the tumor. The algorithm then calculates the tumor volume based on the gradient along the line connecting the 2 points that the user selected.

The user-input value, Percent, can be determined for different systems by acquiring empirical data. The Percent value used for the group of 4T1-Luc tumors in Figure 4 was different than the value used in the HT1080 group of tumors in Figure 3. It is important to note that the injected fluorescent probe concentration also differed among the groups. This emphasizes the versatility of the PV-TVA, along with the importance of calibration for a given system, for obtaining the ideal Percent value. Once this parameter is obtained, the value can be used on subsequent images that satisfy the same conditions. Moreover, we showed that this parameter remains consistent even after multiple fluorophore injections.

In addition to reducing variability, using an imaging approach has other advantages. Obtaining an image over a direct measurement allows for retrospective analysis and calculations to be made after the study has been completed. The PV-TVA can be used with any targeted fluorescent probe with enhanced signal within the tumor, making it highly versatile. Our current method is optimized for images using NIR fluorescence, which provides a larger gradient in the intensity of the surface-weighted projection fluorescence image, allowing for more extensive fine-tuning of the volume calculation. The ability to interrogate deeper tissues with NIR light, from diverse NIR fluorescent molecular probes and proteins, creates an opportunity to apply the PV-TVA method in data analysis for many studies. Because the PV-TVA relies on the gradient of the fluorescent signal, any image with an adequate contrast between the tumor and the surrounding tissue could use this approach to determine the tumor volume. Thus, the method can be extended to visible light images with adequate tumor-to-background contrast. A recalibration of the algorithm would be required to optimize the PV-TVA for use in the visible range, which can be accomplished in future studies.

A goal of this study is to provide a rapid and retrievable quantitative analysis using planar fluorescence images. We illustrated the application of the PV-TVA in subcutaneous tumor models because these models are extensively used in cancer research. For deep tumors, the algorithm could be calibrated for a type of tumor with a known depth. However, if the depth varied for a type of tumor model, additional a priori information from other sources such as CT or MRI would be required to develop a reliable metric for the PV-TVA. A similar challenge is applicable to metastatic tumors in deep tissues, but our method can longitudinally track the volume of subcutaneous tumor metastases, providing additional insights into tumor progression. Because of the large signal variability of deep tumors and metastasis, a more complex algorithm would be required, which is outside the scope of the current study.

The PV-TVA performed as well as, or better than, the BLI. The luciferin injection for BLI can be a variable factor in determining the resultant signal. This variability was evident in tumor T3 (Figure 4), where the tumor visibly appeared to be larger than the others, but only a small BLI signal was obtained. Several factors could mediate this observation, including an inadequate injection of the substrate, a reduced cellular division rate, cellular mutations, or other biologic variables. In contrast, a fluorescent probe can be used in nontransfected cells, thereby reducing much of this biological variability. For longitudinal studies, the fluorescent probe can be reinjected at subsequent time points to track the response of tumors to therapy. The longitudinal study was executed using a modified code that used a center-point slope calculation, rather than a forward-stepping slope calculation. Both methods produced similar results, which provide flexibility to the user in selecting the best logic for a given application.

Future studies will focus on improving some of the limitations of our approach. Occasionally, the algorithm selected an incorrect tumor width. The current algorithm provides the user with visual feedback of the width points identified. Although the width of an object is relatively apparent to the operator, designing an algorithmic logic to select the desired dimension on irregular shapes is desirable, but complex. A more robust approach for selecting tumor width will be examined in future revisions. After optimizing the logic for the final code, the algorithm will be benchmarked against additional imaging modalities such as CT, MRI, FMT, and multimodal imaging.

In summary, the fluorescent guided PV-TVA provides an alternative to physically measuring tumor volumes using calipers, other empirical optical methods such as BLI, or other optical methods such as FMT. An initial calibration study is needed for a given system before the PV-TVA can be run on subsequent images without any additional a priori information. The ability to measure tumor volume in a noninvasive, cost-effective manner is beneficial for rapid determination of this important parameter, particularly when retrospective analysis is desired. In combination with tumor-targeted molecular probes, our approach allows for accurate determination of tumor volumes without any additional action by the user.